PRELIMINARY SIMULATION
OF A M6.5
EARTHQUAKE ON THE SEATTLE FAULT
USING 3D FINITE-DIFFERENCE MODELING
by
William J. Stephenson1 and Arthur D. Frankel1
U.S. Geological Survey Open-File Report 00-339
1U.S. Geological Survey, Denver, CO
This report is preliminary and has not been reviewed for conformity with U.S. Geological Survey editorial standards or with the North American Stratigraphic Code. Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. U.S. Department of the Interior U.S. Geological Survey
U.S. Department of the Interior
U.S. Geological Survey
Abstract
A three-dimensional finite-difference simulation of a moderate-sized (M 6.5) thrust-faulting earthquake on the Seattle fault demonstrates the effects of the Seattle Basin on strong ground motion in the Puget lowland. The model area includes the cities of Seattle, Bremerton and Bellevue. We use a recently developed detailed 3D-velocity model of the Seattle Basin in these simulations. The model extended to 20-km depth and assumed rupture on a finite fault with random slip distribution. Preliminary results from simulations of frequencies 0.5 Hz and lower suggest amplification can occur at the surface of the Seattle Basin by the trapping of energy in the Quaternary sediments. Surface waves generated within the basin appear to contribute to amplification throughout the modeled region. Several factors apparently contribute to large ground motions in downtown Seattle: (1) radiation pattern and directivity from the rupture; (2) amplification and energy trapping within the Quaternary sediments; and (3) basin geometry and variation in depth of both Quaternary and Tertiary sediments
Introduction
The Puget Lowland in western Washington has
been recognized in recent years as an area of significant earthquake hazard (Figure 1). Although western Washington has experienced
six historic earthquakes of magnitude 6 or greater, only one, in 1872, is
believed to be from a shallow crustal event [Ludwin et al., 1991]. However,
recent evidence has clearly shown that active faults in the upper crust exist
and that they also pose a significant seismic hazard to the region [e.g.
Johnson et al., 1999]. The Seattle fault is foremost among these and of
particular concern because it underlies the heavily populated Seattle
metropolitan area (1996 U.S. Census Bureau estimate of 3.3 million). The
Seattle fault was first inferred from gravity data [Danes et al., 1965]; its
location and extent have since been defined from surface-geologic relationships
[Gower et al., 1985; Yount and Holmes, 1992] and most recently from seismic
reflection data [Johnson et al., 1994; 1999; Pratt et al., 1997]. Bucknam et
al. [1992] document as much as 7 m of co-seismic uplift on a Holocene marine
terrace 1000-1100 years ago that is believed to have formed during a large
(M7.0+) earthquake on the Seattle fault. Additional evidence of this large
earthquake is documented by a tsunami deposit in Puget Sound [Atwater and
Moore, 1992], rock slides in nearby mountains [Schuster et al., 1992] and
landslides in Lake Washington [Jacoby et al., 1992; Karlin and Abella, 1992].
|
Figure 1. Generalized geologic map of the Puget Lowland showing the approximate surface projection of the Seattle fault (from Johnson et al. [1999]) and area of model simulation. Seattle fault shown as heavy black line. Vertical black line is location of highlighted part of cross-section in Figure 2. Region of finite-difference simulation shown in red box and is also area of map views in Figures 4 and 5. |
We simulate long-period ground motion from a M6.5 earthquake on the Seattle fault near Seattle using a three-dimensional, staggered-grid, elastic finite-difference algorithm (methodology similar to that of Graves [1996]). The model region (Figure 1) includes a large part of the Seattle fault, the over-8-km-deep Seattle basin, and the Bremerton area to the west. We believe this preliminary study is an important step in more accurately assessing the earthquake hazard posed to the Puget Sound region by the Seattle fault.
Velocity and Density Models
Pratt et al. [1997] proposed the Puget
Lowland thrust system to explain stratigraphic and structural relationships
observed in marine seismic-reflection data in the Puget Sound region. This
thrust model consists of a north-moving thrust sheet underlying most of the
region, with the Seattle uplift near Seattle caused by fault-propagation folds
and the Kingston Arch caused by a ramp anticline (Figure
2). A decollement at 15 to 22 km depth, dipping at 1 to 2° is interpreted
as the base of the thrust system. The thrust sheet model generally explains the
trends of potential-field anomalies and the locations of many known geomorphic
(drainage patterns, uplifted marine terraces) and geologic (locations of Quaternary
basins) features in the area, and it also provides insights regarding the
current seismicity in the region. In this model, the Seattle fault is a major
thrust fault above the decollement dipping at 20° at depth and about 50°
up-dip, with dislocation occurring on the segment dipping at 20° only.
|
Figure 2. Partial cross-section of Puget lowland thrust sheet (from Pratt et al. [1997]). Highlighted gray box is the region where the velocity and density models were developed. Crescent Formation is assumed to be basement rock; Tertiary and Quaternary sedimentary deposits overlie the Crescent. Seattle fault is interpreted to dip at 20°S; overlying sub-thrusts interpreted at dips of 50-55°S.
|
Using the thrust-system as a geologic template, the three-dimensional velocity and density models used in this simulation were developed assuming two primary seismic impedance boundaries (Figure 2). These are the Quaternary/Tertiary sediment interface (data compiled by S. Johnson, U.S. Geological Survey) and the Tertiary sediment/Tertiary Crescent interface (depth-to-basement data from R. Blakely, U.S. Geological Survey). The Quaternary/Tertiary interface is based on borehole and seismic reflection data while the sediment/Crescent interface is derived from gravity inversion. As such, it is monotonic and smooth and probably does not accurately represent the inferred overthrust wedge of sediments seen in the footwall of the cross section (Figure 2). However, we assume that the surface is a reasonable approximation to the general Crescent Formation structure and is appropriate for the low frequencies used in our finite-difference simulation.
Velocity and density ranges were based on borehole data [Brocher and Ruebel, 1998], near surface (40 m and less) P- and S-wave refraction measurements [Williams et al., 1999], and industry-derived P-wave velocity functions from Puget Sound [e.g. Pratt et al., 1997]. The water column itself was not included in the model because it is relatively shallow through the model region. Model parameters were assigned at the top and bottom of each layer as well as at the surface and base of the model (Table 1). P-wave velocities ranged from 1200 m/s to 6700 m/s across the four layers (Fig. 6), with corresponding S-wave velocities ranging from 500 m/s to 3750 m/s. The velocity/density values within the model volume were then calculated by linear three-dimensional interpolation.
M6.5 Earthquake Simulation
A random thrust-slip distribution on a
200-km2 fault plane striking east-west and dipping at 20°S was used
for the simulation. Dislocation on the fault was pure dip-slip along its
length, from 8 to 17 km depth. The fractal slip variation had a Gaussian
distribution and a correlation distance of 2.0 km. Rupture velocity was set at
2500 m/s, or about 0.75 times the shear-wave velocity at the average depth of
the fault. Frequencies up to 0.5 Hz were modeled with a grid spacing of 200 m.
No attenuation was incorporated in the simulations; this was considered a
reasonable omission given the low frequencies and relatively small distances
(less than 40 km across the model) involved. M6.5 was chosen because it
is well within the magnitude range possible on the Seattle fault based on
paleo-seismic evidence [Bucknam et al., 1992].
|
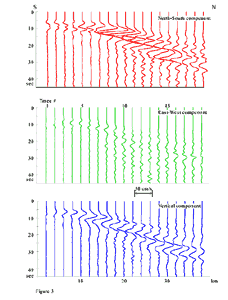
Figure 3. North-south, east-west, and vertical component synthetic seismograms from M6.5 Seattle fault earthquake simulation. Amplitudes are normalized by half of maximum velocity. Highest ground motion is in N-S direction. |
As observed in the synthetic seismograms in Figure 3, the north-south component has the highest
simulated ground motion. These unfiltered traces represent a series of
receivers at the ground surface aligned on a north-south transect through the
center of the model (red line on Figure 4). The effective frequency content of
these data is 0.2 to 0.5 Hz. Amplitudes of all traces have been normalized by
one-half of the maximum velocity in the synthetics. Highest ground motions in
the north-south direction and the change in polarity of the direct S-pulse in
the vicinity of trace 4 are caused by the radiation pattern of the thrust
mechanism and directivity effects. Peak amplitudes varied by over a factor of
four between the southern end of the model and the region over the deepest part
of the Seattle Basin, at about trace 9 in the north-south seismograms. Overall
ground shaking is significantly higher and of longer duration over the basin.
Peak amplification does not vary dramatically with distance in either the
east-west or vertical components. S-waves produce the highest ground motions up
to trace 11; more distant sites are dominated by a large phase about 8-10
seconds after the direct S-wave. Much of this energy at later time is believed
to be surface waves. We interpret the highest amplitude events at distances greater
than 10 km as a combination of surface waves and multi-path S-waves trapped
within the Quaternary sediments of the Seattle Basin. Apparent phase velocities
of the later high-amplitude events are on the order of 1500 to 2000 m/s. This
is consistent with surface waves travelling at velocities of the deepest part
of the Tertiary sediments.
|
Figure 4. Four vertical and surface time slices of M6.5 earthquake simulation on the Seattle fault. Vector magnitude of three velocity components (N-S, E-W, and vertical) are presented. Surface slices: red line is the location of vertical time slice, green 'S' is downtown Seattle, white lines are coastlines, and orange box is surface projection of fault plane. Vertical slices: magenta line is the Quaternary/Tertiary impedance boundary, black line is the top of Crescent, and green line is the fault plane. Much of the high-amplitude motion is focussed in the near-surface. |
Four horizontal and vertical time slice sets resulting from the moment-magnitude M6.5 earthquake simulation on the Seattle fault are shown in Figure 4. We analyze the vector magnitude of the north-south, east-west, and vertical components of velocity (i.e. Vm=(Vns2+Vew2+Vv2)1/2), which shows how overall particle motion varies with time. Most of the early seismic energy released by the earthquake is directed upward through basement rock (Figure 4A). At 9.3 seconds after rupture onset, the cumulative effect of both direct S and reflected S-waves as well as the initiation of surface waves cause significant ground motion over the southern edge of Seattle basin; the high-amplitude S phase is observed along the basin-edge bedrock interface at depth (Figure 4B).
The wave-field within the Quaternary sediments has a second linear band of high ground motion that sweeps south-to-north across Seattle (Figure 4C). This corresponds to the high-amplitude back swing of the strong motion phase observed at 9.3 seconds. Surface wave energy may also be contributing to the amplification. The linear bands are the approximate width of the rupture plane, and the narrowness of these pulses in both space and time are probably related to the rupture direction and apparent duration. Wave phases deeper in the Seattle basin, possibly surface waves, arc upward in apparent response to basin geometry and velocity gradients as they propagate northward. The general wave amplitude pattern seen at the ground surface in Figure 4D continues to the end of the simulation 45 seconds after onset, with much of the later motion being trapped within the Quaternary sediments. No high-amplitude southward-propagating wave fields are observed from the northern edge of the basin at later times.
As shown in Figure 5, the maximum ground motion computed from all time slices in the simulation using the three components of velocity is 53 cm/s (similar to the maximum value when calculated from just the north-south and east-west velocity components). The highest ground motions predicted by this simulation are under downtown Seattle. The largest peak is shifted east of the thickest section of Quaternary deposits and is almost directly over the thickest section of Tertiary sediments, suggesting a correlation with deeper basin geometry. A peak velocity at long periods as large as 53 cm/s is not unreasonable for such a shallow earthquake and most likely underestimates ground motion at short periods. The bulls-eye of high motion is also in an area of significant man-made fill that is currently not represented in the models. Williams et al. [1999] describe S-wave velocities of 200 m/s and less in an area of downtown Seattle on man-made fill and low-velocity deposits up to 45 m thick. Incorporating these thin low-velocity units could most likely increase ground motion in affected areas.
|
Figure 5. Peak ground motion from M6.5 earthquake simulation. Maximum velocity is 53 cm/s in the vicinity of downtown Seattle. |
Discussion and Conclusions
The inferred surface wave phases within the deeper part of the Seattle basin are probably caused by a combination of basin geometry, basin edge effects, and basin velocities and gradients. Graves et al. [1998] document the effects of different basin geometries across the Santa Monica fault and suggest shallow basin structure may contribute most to high amplification observed in the immediate vicinity of the fault after the 1994 Northridge earthquake. Conversely, Alex and Olsen [1998] describe possible focussing effects from deep basin structures across the Santa Monica fault. While the geometry of this fault may be similar in a gross sense to the Seattle fault, neither of these studies discusses what effects would be expected from an earthquake occurring on the Santa Monica fault. Pitarka et al. [1998] inferred that coupling of basin-edge effects and source directivity caused high ground-motion amplification during the 1995 Kobe earthquake. Likewise, we believe the geometry of the Seattle Basin as well as the location of, and rupture direction on, the Seattle fault play critical roles in predicted ground motions for an earthquake on this structure.
A second earthquake simulation, with the rupture plane at the same latitude but translated to the westernmost limit of the model region, yielded a similar maximum ground motion pattern to that obtained in Figure 5. Focussing of energy from the basin edge above the Seattle fault contributes to the region of the peak ground amplification. However, the recurrent location of the peak maximum ground motion, in an area generally east of the thickest section of Quaternary and Tertiary sediments, suggests deep basin geometry is an important factor in the Seattle area for low-frequency wave amplification from a thrust event.
Wave motions within the Tertiary basin sediments are amplified by transmission into the Quaternary sediments (Figure 4). Energy apparently becomes trapped in the Quaternary and leads to multiple arrivals. In cross-section, the thinning of the Quaternary deposits and the contact of the Tertiary sediments at the free surface seems to be a focus for amplification, at a distance of about 12 km from the southern edge of the model. Much of the high-amplitude linear bands of motion emanate from this region.
The current exclusion of an over-thrust sedimentary package from the model may be part of the reason for the peak ground motion pattern, even though best guess estimates would put only a few kilometers of sediment under bedrock [Pratt et al., 1997]. Such a feature should not dramatically affect the low-frequency wave-fields discussed here. However, higher frequency effects could be important to overall ground shaking across the Seattle Basin and will be addressed in future work with better three-dimensional constraints (e.g. from results of the recently completed SHIPS experiment [Fisher et al., 1999]). Similarly, including very low-velocity man-made fill deposits (S-wave velocities less than 200 m/s) that occur throughout the Seattle area could be important for frequencies greater than 0.5 Hz.
The M6.5 Seattle fault earthquake simulation of low frequency (0.5 Hz and less) ground motions has given an important first look at regions in the Seattle area that could be significantly impacted from such an event. Several factors contribute to large ground motions in downtown Seattle from this earthquake scenario. First, directivity and the radiation pattern from the rupture appear to have a significant effect on ground motion, especially in relation to basin geometry. Second, wave motions are amplified within the Quaternary sediments after travelling through the Tertiary basin sediments. Third, energy is trapped in the Quaternary deposits increasing the duration of ground shaking. Fourth, inferred surface waves propagating at high apparent phase velocities contribute to amplification patterns at the surface. Finally, the geometry of the basin, particularly its variation in depth seems to be an important factor in ground motion amplification and patterns within the Seattle area. Incorporation of a more detailed shallow velocity model and inclusion of attenuation and higher-frequency wave propagation effects are important factors to be considered for additional study.
Acknowledgements. We thank both Sam Johnson (Base-of-Quaternary Map, 1999) and Rick Blakely (preliminary depth to basement model of Puget lowland, 1998) for generously supplying their unpublished data sets used for the primary seismic impedance boundaries. The efforts of Susan Rhea with GIS support are also greatly appreciated. The National Earthquake Hazards Reduction Program financially supported this work.
References
Alex, C.M., and K.B. Olsen, Lens-effect in Santa Monica?, Geoph. Res. Lett., 25, 3441–3444, 1998.
Atwater, B.F., and A.L. Moore, A tsunami about 1000 years ago in Puget Sound, Washington, Science, 258, 1614–1617, 1992.
Brocher, T., and A.L. Ruebel, Compilation of 29 sonic and density logs from 23 oil test wells in western Washington state, U.S. Geological Survey, Open File Report, 1998.
Bucknam, R.C., E. Hemphill-Haley, and E.B. Leopold, Abrupt uplift within the past 1700 years in Puget Sound, Washington, Science, 258, 1611–1614, 1992.
Danes, Z.F., and nine others, Geophysical investigations of the southern Puget Sound area, Washington, J. Geophys. Res., 70, 5573–5579, 1965.
Fisher, M.A., and 19 others, Seismic survey probes urban earthquake hazards in the Pacific Northwest, EOS, 80, 13–17, 1999.
Gower, H.D., J.C. Yount, and R.S. Crosson, Seismotectonic map of the Puget Sound region, Washington: U.S. Geological Survey Map I-1613, Scale 1:250,000, 1985.
Graves, R.W., Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences, Bull. Seism. Soc. Am., 86, 1091–1106, 1996.
Graves, R.W., A. Pitarka, and P.G. Somerville, Ground-motion amplification in the Santa Monica area: effects of shallow basin-edge structure, Bull. Seism. Soc. Am., 88, 1224–1242, 1998.
Ludwin, R.S., C.S. Weaver, and R.S. Crosson, Seismicity of Washington and Oregon, in Slemmons, D.B., Engdahl, E.R., Blackwell, E., and Schwartz, D., eds., Neotectonics of North America, Decade of North American Geology, v. GSMV-1, Geol. Soc. Am., 77–98, 1991.
Jacoby, G.C., P.L. Williams, and B.M. Buckley, Tree ring correlation between prehistoric landslides and abrupt tectonic events in Seattle, Washington, Science, 258, 1621–1623, 1992.
Johnson, S.Y., C.J. Potter, and J.M. Armentrout, Origin and evolution of the Seattle basin and Seattle fault, Geology, 22, 71–74, 1994.
Johnson, S.Y., S.V. Dadisman, J.R. Childs, and W.D. Stanley, Active tectonics of the Seattle fault and central Puget Sound, Washington--implications for earthquake hazards, Geol. Soc. Am. Bull., 111, 1042–1053, 1999.
Karlin, R.E., and S.E.B. Abella, Paleoearthquakes in the Puget Sound region recorded in sediments from Lake Washington, U.S.A., Science, 258, 1617–1620, 1992.
Pitarka, A., K. Irijura, T. Iwata, and H. Sekiguchi, Three-dimensional simulation of the near-fault ground motion for the 1995 Hyogo-ken Nanbu (Kobe), Japan, earthquake, Bull. Seism. Soc. Am., 88, 428–440, 1998.
Pratt, T.L., S.Y. Johnson, C.J. Potter, W.J. Stephenson, and C. Finn, Seismic reflection images beneath Puget Sound: The Puget Lowland thrust sheet hypothesis, J. Geophys. Res., 102, 27469–27489, 1997.
Schuster, R.L., R.L. Logan, and P.T. Pringle, Prehistoric rock avalanches in the Olympic Mountains, Washington, Science, 258, 1620–1621, 1992.
Williams, R.A., W.J. Stephenson, A.D. Frankel, and J.K. Odum, Surface seismic measurements of near-surface P- and S-wave seismic velocities at earthquake recording stations, Seattle, Washington: Earthquake Spectra, 15, 565–584, 1999.
Yount, J.C., and M. Holmes, The Seattle fault - a possible Quaternary reverse fault beneath Seattle Washington: Geol. Soc. Am. Abstracts with Programs, 24, 93, 1992.
Table 1. Model
Parameters for Seattle area model
|
Interface |
Vp (m/s) |
Vs (m/s) |
Density (kg/m3) |
|
Free Surface |
1200 |
500 |
2000 |
|
Base Quaternary |
2000 |
1000 |
2100 |
|
Top Tertiary Seds. |
2400 |
1400 |
2400 |
|
Base Tertiary Seds. |
3400-4850* |
2000-2770* |
2500 |
|
Top Crescent |
4500-6300* |
2600-3600* |
2700 |
|
Base of Model |
6700 |
3750 |
2800 |
* Values varied linearly along interface as a function of depth