1Earthquake Research Institute, University of Tokyo, Tokyo 113, Japan.
The major June 15, 1991, eruption of Mount Pinatubo started with generation of pyroclastic flows in the afternoon, which were subsequently followed by a plinian eruption. This sequence of events is reflected in the stratigraphy of the fall deposits, which consists of a fine ash layer, a lapilli layer commonly including pumice grains of >1 centimeter in diameter, and a lapilli-bearing volcanic sand layer, in ascending order. A giant disc-shaped cloud covering an area of 60,000 square kilometers appeared in the satellite images at 1440 Philippine local time. The cloud expanded radially for 5 hours to an area more than 300,000 square kilometers. According to eyewitness accounts, there was heavy ash fall after 1400, intermittent lapilli fall starting at about 1420, and heavy and continuous lapilli fall starting widely at about 1500. The occurrence of the giant cloud roughly corresponded to the initiation of the intermittent lapilli fall. The satellite and grain-size data indicate that the volumetric flow rate of the umbrella cloud during the climactic plinian phase was 3 to 10x1010 cubic meters per second. According to the results of calculations on the dynamics of the eruption cloud, the volumetric flow rate of the eruption cloud is accounted for by a plinian eruption with a magma discharge rate of 4x108 to 2x109 kilograms per second. The total amount of the ejecta injected into the stratosphere during the climactic plinian eruption was 2 to 10 cubic kilometers dense-rock equivalent. The upper estimate is greater than the upper volume estimate of the tephra-fall deposits including fine ash observed in the South China Sea and Southeast Asia (2 cubic kilometers dense-rock equivalent). The discrepancy may be partly due to fine particles that were extensively dispersed in the atmosphere and could not be counted in the deposit.
Note to readers: Figures open in separate windows. To return to the text, close the figure's window or bring the text window to the front.
This study is an extension of recent work on the dynamics of eruption clouds of the 1991 Pinatubo eruption on the basis of the satellite images (Koyaguchi and Tokuno, 1993). According to the preliminary analyses of Koyaguchi and Tokuno on the basis of a fluid dynamic model of an eruption column (Woods, 1988), the expansion rate of the eruption cloud is accounted for by an injection of pyroclasts into the stratosphere at the rate of 109 kg/s. They concluded that the total amount of the pyroclasts is more than 1.8x1013 kg (7 km3 dense-rock equivalent, DRE), derived simply by multiplying the magma discharge rate by the time during which the eruption cloud continued to expand upwind (5 hours). This value is several factors greater than the published total volume of tephra-fall deposits (3 km3; Pinatubo Volcano Observatory Team, 1991). The discrepancy would be partly due to uncertainties of both the methods for estimating volumes of discharged magma and tephra-fall deposits, but there is another important possibility. The volume of deposits does not necessarily represent that of discharged magma if the ejecta consisted of fine particles and were widely dispersed in the atmosphere. If this possibility played a significant role, the discrepancy between the two quantities gives important information about the environmental effects of the eruption as a result of the dispersal of fine volcanic ash. I examine this problem of the volume estimations by different methods in more detail in this paper. I emphasize at the outset that the purpose of this study is not to judge which method gives the correct value of the volume of tephra deposits but to clarify the difference between implications of volume estimates based on fluid dynamics of eruption clouds and on geological methods. First, I describe tephra-fall deposits and the satellite data to clarify the chronological relation between the growth of the eruption cloud and the deposits. Second, the total volume of ejecta and that of the tephra-fall deposits is estimated on the basis of a dynamical model of the eruption cloud as well as geological methods. The sources of uncertainties of each step of these estimates are evaluated. Finally, the implications of the results of each volume estimate are discussed.
The major Pinatubo eruptions were recorded hourly in multispectral images by the Japanese Geostationary Meteorological Satellite Himawari 4 (Koyaguchi and Tokuno, 1993). Repetitive explosive eruptions at the volcano culminated in the afternoon of June 15. Eruption clouds repetitively pierced low-level white cloud in the morning of that day. A remarkable disc-shaped cloud was observed at 1440 (local Philippine time, fig. 1). This cloud expanded up to 280 km in diameter (60,000 km2), the center of which was located about 30 km west of Pinatubo. One hour later (1540) the cloud further expanded up to 400 km in diameter (120,000 km2). There was a several-kilometer-high dome-shaped swell at the center of the cloud at 1440 and 1540. The widths of shadows of the eruption cloud onto the surrounding white clouds indicate that the altitude of the cloud was approximately 25 km at its eastern edge and 34 km at its center at 1540 (Tanaka and others, 1991). The cloud expanded up to 250 km upwind until 1940, covering an area of 300,000 km2, and subsequently the east end of the cloud moved westward, at which time the cloud reached a stagnation point upwind but continued to grow downwind and crosswind. It is inferred from the position of the center of the cloud at 1440 and the wind velocity at the altitude of the cloud (typically 10 to 20 m/s southwestward) that the cloud began to expand at about 1420 or before. Average radial expansion velocity of the giant cloud was up to 102 m/s before 1440 and approximately 14 m/s between 1440 and 1540.
Figure 1. Visible satellite images at 1440 and 1540 Philippine local time, on June 15, 1991.
Infrared images indicate that the surface temperature of the eruption cloud before 1340 was approximately -80°C, which is slightly higher than the temperature at the tropopause (-83°C). The surface temperature of the giant cloud after 1440 was higher than the tropopause temperature by more than 10°C; the east half (upwind) of the cloud was mostly -80 to -70°C, that of the west half was slightly higher than -70°C, and there was a small hot spot (a few tens of kilometers in diameter) with temperatures up to -27°C at the center of the cloud at 1440. At 1540 the area of the surface temperature higher than -60°C with some hot spots of approximately -30°C spread in all directions. The area with surface temperatures higher than -60°C further expanded up to 100 km upwind at 1640 (Tokuno, 1991a,b; Tanaka and others, 1991; Koyaguchi and Tokuno, 1993).
The tephra-fall deposits can be divided into 5 units (fig. 2), designated as layers A, B, C1, C2, and D in ascending order. This lettering scheme is consistent with that used by Paladio-Melosantos and others (this volume); in it, layers C1, C2, and D correspond to layers C, D, and E, respectively, of Koyaguchi and Tokuno (1993). Layer A is a lapilli or volcanic sand layer enriched in grayish pumice grains and lithic fragments. It is the deposit of the eruption on June 12. Layer B is a silt-sized fine ash layer, the lower part of which was deposited between the eruptions of June 12 and the climactic eruption of June 15. Layer C1 is a lapilli layer commonly including pumice grains of >1 cm in diameter. Layer C2 is a lapilli-bearing volcanic sand layer. The uppermost part of layer B and all of layers C1 and C2 correlate with the sequence from heavy, fine ash fall to lapilli fall during the major eruption on June 15. Layer D is a fine ash layer, and it originated mainly from fallout of continuous, minor eruptions occurring during the period of June 16 to early July.
Figure 2. A columnar section for the tephra-fall deposits of the Pinatubo 1991 eruptions at location 1101, approximately 13 km southwest of the vent.
Figure 3 shows isopach maps of layers A, B, C1, and C2. In contrast to the narrow distribution of layer A, the isopach maps of layers B, C1, and C2 show wide distributions in all directions including upwind (northeast) of the vent, although they are slightly elongated in the wind direction. This observation is consistent with the observation in the satellite images that the eruption clouds of the major eruption on June 15 expanded in all directions.
The broad distribution of layer B (fig. 3) suggests that the fine ash in layer B is not distal deposits of a small eruption but originated from a large eruption cloud expanding against wind. Judging from this distribution and the depletion of coarse material, layer B is considered to be derived from an ash cloud that was produced from pyroclastic flows covering several tens of square kilometers (Koyaguchi and Tokuno, 1993). There were also pulses of fine ash fall, mainly downwind from Pinatubo, due to intermittent minor eruptions on June 13, 14, and in the morning of June 15 (Hoblitt, Wolfe, and others, this volume; Paladio-Melosantos and others, this volume), which could not be distinguished in this study from the fine ash deposits from the initial phase of the major eruption.
Figure 3. Isopach maps of layers A, B, C1, and C2 (after Koyaguchi and Tokuno, 1993). Star indicates the locality of Mount Pinatubo. Thicknesses are in millimeters. Data in parentheses are unpublished data by E.L. Listanco (Earthquake Research Institute and PHIVOLCS), from June 1991. The other data were collected in December, 1991. At some localities, thicknesses of layer C2 were less in December 1991 than in June 1991, as a result of erosion and compaction. In such cases, data of Listanco from June 1991 were used. +, trace.
Layers A and B
Layers C1 and C2
According to the eyewitness accounts of the major eruption collected at Subic Bay Naval Station, Clark Air Base, Magalang, and Angeles (summarized by Koyaguchi and Tokuno, 1993), fine ash fall with rain started in the morning of June 15 and became heavy after 1400, even in the region upwind of the vent. Intermittent lapilli fall started between 1400 and 1445 and became very heavy and continuous after 1500 even in the region upwind the volcano. Considering the time scale for pumice grains to reach the ground from the bottom of the cloud (approximately 20 minutes for grains of more than 1 cm in diameter; Walker and others, 1971; Wilson, 1972), I infer that the pumice grains started falling from the eruption cloud between 1400 and 1425. Thus, the deposition of layer C1 roughly corresponded to the occurrence of the giant cloud (1420 or before). The dynamics of the expanding umbrella cloud during the major eruption will be discussed on the basis of the granulometric data of layer C1 and the satellite images from 1440 in later sections.
The volume estimation of ejecta by means of a dynamic model of the eruption cloud is composed of three steps (fig. 4). The first step is the estimation of the volumetric flow rate of the cloud. There are at least three independent ways for estimating the volumetric flow rate of the cloud; one method is an estimation from grain-size data of deposits on the basis of a dispersal-sedimentation model of tephra, and the other two methods are estimations from satellite images on the basis of fluid dynamics models. The second step involves estimation of the magma discharge rate on the basis of the volumetric flow rate of the eruption clouds and fluid dynamics models. Finally, the total amount of the ejecta can be obtained by multiplying the discharge rate by the duration of the eruption in the third step. Temperature data in the satellite images also give important constraints on the dynamics of the eruption cloud. We will describe each step of these estimations below.
Figure 4. Flowchart of the volume estimation of ejecta and deposits.
Theoretical analyses (Sparks, 1986; Woods, 1988) have revealed that an eruption column convectively rises by buoyancy to a height where the column density equals that of the atmosphere and spreads laterally as a gravity current just above the neutral buoyancy level to form an umbrella cloud (fig. 5). The dispersal of tephra-fall deposits is generally controlled by many factors such as dynamics of the eruption cloud, its interaction with wind, and the overall grain-size distribution of the ejecta (Carey and Sparks, 1986; Bursik and others, 1992; Sparks and others, 1992; Koyaguchi, 1994).
Figure 5. Schematic illustration of an umbrella eruption cloud showing the definitions of cloud thickness.
Koyaguchi (1994) developed a method for estimating the volumetric flow rate of an umbrella cloud from grain-size data of tephra-fall deposits. The following five assumptions are made:
The model with these assumptions is simplified in order to elucidate basic relations between eruption cloud dynamics and grain-size variation of tephra-fall deposits. These assumptions will be evaluated later.
The principle of the present dispersal-sedimentation model is schematically illustrated in figure 6. As a specific volume of an umbrella cloud is conveyed laterally, particles are removed from the cloud, so that both the total mass of particles, M, and the probability distribution function (abbreviated as pdf hereafter) of settling velocity, f(v), in the specific volume will change with distance. The function f(v) is directly related to the grain size distribution if the density and the shape of the particles are uniform. Based on the third and fourth assumptions, the volumetric flow rate of the umbrella cloud, Q, can be approximated as
Figure 6. Schematic illustration of the dispersal-sedimentation model from an umbrella cloud. Variables are defined in the text.
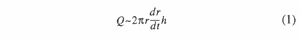
where r is the distance from the center of the umbrella cloud, h is the thickness of the umbrella cloud, and t is the time. When the wind velocity is negligible compared with the expansion velocity (the fifth assumption), r approximates the distance from the center line of the vent. According to Martin and Nokes' theory (1988) and the first and second assumptions, the decay of a mass of particles with a given settling velocity in the specific volume occurs at a rate given by

From equations 1 and 2, we obtain the simple solution
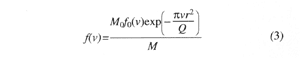
where M0 and f0(v) are the total mass of particles and the pdf in the specific volume of the cloud at r=0, respectively. Equation 3 means that the concentration of the coarser particles decreases more rapidly than the finer ones with distance in the specific volume of the cloud, and therefore the pdf changes with distance. Because the sedimentation rate is proportional to the terminal velocity of a particle (see fig. 6), the pdf in the deposit, fsed(v) should be expressed as

The pdf in the deposits is a function of the initial pdf of the ejecta. From equation 4, we obtain the ratio of the pdf in the deposits of two localities at distances from the vent r1 and r2, ln Rf, as:

The parameter A represents the ratio of the total mass of deposits between the two localities, and so it is a constant for a given pair of localities. An important implication of this result is that the first term of the right side of equation 5a is independent of the initial pdf and that the logarithm of the ratio of pdf has a linear relation with the settling velocity. Because the distance from the vent, r, is a known factor, we can estimate the value of Q from the slope of the line in the diagram of the logarithm of the ratio of pdf versus the settling velocity.
The ratio of pdf on the basis of the terminal velocity, Rf, is obtained from grain-size data as:

where g(![]() ) is the pdf of grain size based on the phi scale,
) is the pdf of grain size based on the phi scale, ![]() .The value of g(
.The value of g(![]() ) is given by dividing the mass fraction of the sample in the range with a certain interval of phi scale by the interval of the phi scale. On the other hand, the settling velocity of a particle with the size of
) is given by dividing the mass fraction of the sample in the range with a certain interval of phi scale by the interval of the phi scale. On the other hand, the settling velocity of a particle with the size of ![]() at high Reynolds number is calculated from the following formula:
at high Reynolds number is calculated from the following formula:

where d is the clast diameter, ![]() is the atmospheric density,
is the atmospheric density, ![]() is the clast density, g is the acceleration due to gravity, and Cd is the drag coefficient, which is approximately unity. B is the parameter which relates grain size in phi scale to terminal velocity for each grain. The values of B vary considerably depending on the atmospheric density (2.0x10-5 g/cm3 in the stratosphere and 1.3x10-3 g/cm3 near the surface). It should also be noted that equation 7 is valid only for particles larger than a few hundreds of microns and that for smaller particles it should be replaced by a different relationship. Because of these uncertainties in estimating the value of B, it would be practical to draw the diagram of ln Rf versus 2-
is the clast density, g is the acceleration due to gravity, and Cd is the drag coefficient, which is approximately unity. B is the parameter which relates grain size in phi scale to terminal velocity for each grain. The values of B vary considerably depending on the atmospheric density (2.0x10-5 g/cm3 in the stratosphere and 1.3x10-3 g/cm3 near the surface). It should also be noted that equation 7 is valid only for particles larger than a few hundreds of microns and that for smaller particles it should be replaced by a different relationship. Because of these uncertainties in estimating the value of B, it would be practical to draw the diagram of ln Rf versus 2-![]() /2 instead of that of ln Rf
versus v. The diagram of ln Rf versus 2-
/2 instead of that of ln Rf
versus v. The diagram of ln Rf versus 2-![]() /2 can be obtained from grain size data alone without any assumptions. In this case, the slope of the line represents
/2 can be obtained from grain size data alone without any assumptions. In this case, the slope of the line represents 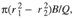 so that we can obtain the value of B/Q for two given localities. Consequently, the value of Q is estimated according to the assumed values of B.
so that we can obtain the value of B/Q for two given localities. Consequently, the value of Q is estimated according to the assumed values of B.
The pdf of the grain size of layer C1 is shown in figure 7. Fine particles (![]() >3) make up only a small fraction of the lapilli fall deposits except for those which fell with rain. The size distribution of layer C1 collected along the downwind axis systematically changes with distance; the fraction of coarser grains decreases with increasing distance (fig. 7). The value of B/Q is calculated from the diagram of ln Rf versus 2-
>3) make up only a small fraction of the lapilli fall deposits except for those which fell with rain. The size distribution of layer C1 collected along the downwind axis systematically changes with distance; the fraction of coarser grains decreases with increasing distance (fig. 7). The value of B/Q is calculated from the diagram of ln Rf versus 2-![]() /2 to be 5.7x10-14, 6.2x10-14, and 4.2x10-14 cm-2 for the pairs of localities of 15 km versus 13 km, 21 km versus 13 km, and 33 km versus 13 km, respectively (fig. 8). The volumetric flow rate of the umbrella cloud is, therefore, estimated to be about 4x1016 to 5x1016 cm3/s when the value of B for pumice grains in the stratosphere (2,200 cm/s) is adopted. By use of the obtained value of B/Q, the initial grain size distribution in the umbrella cloud can be calculated from the actual grain-size distribution data (Koyaguchi, 1994) as:
/2 to be 5.7x10-14, 6.2x10-14, and 4.2x10-14 cm-2 for the pairs of localities of 15 km versus 13 km, 21 km versus 13 km, and 33 km versus 13 km, respectively (fig. 8). The volumetric flow rate of the umbrella cloud is, therefore, estimated to be about 4x1016 to 5x1016 cm3/s when the value of B for pumice grains in the stratosphere (2,200 cm/s) is adopted. By use of the obtained value of B/Q, the initial grain size distribution in the umbrella cloud can be calculated from the actual grain-size distribution data (Koyaguchi, 1994) as:

Figure 7. Probability distribution functions of grain size for the tephra-fall deposits of the major eruption (layer C1) for the localities with variable distances from the vent. The numbers in parentheses are locality numbers from layer A in figure 3.
Figure 8. The ratio of the probability distribution functions of grain size from two localities against the settling velocities for determining the volumetric flow rate of an umbrella cloud of the 1991 Pinatubo eruption. Probability distribution functions of grain size from localities that are 15, 21, and 33 km from the vent are normalized to the pdf from a locality 13 km from the vent.
In order to confirm the above estimation of B/Q, the initial size distributions calculated from the actual grain-size data of different localities are compared. They converge onto a single distribution pattern for B/Q = 5x10-14 cm-2 (fig. 9).
Figure 9. Initial probability distribution functions of grain size for layer C1, calculated from the actual grain size data. The theoretical probability distribution function which explains exponential thinning behavior from r=0 to infinity for k=2.5x10-7 cm-1 and B/Q=5x10-14 cm-2 is shown by a solid curve; part of the theoretical probability distribution function for fine particles (![]() >3) is shown by a dashed curve. Variables are defined in the text.
>3) is shown by a dashed curve. Variables are defined in the text.
The present model is based on a number of simplifications that should be evaluated thoroughly. The most important effects would be those of wind. The major eruption occurred when a tropical typhoon, international code name Yunya, was passing 50 km north of Pinatubo. The lower tropospheric winds were strongly affected by the typhoon winds, while mid tropospheric and stratospheric winds (9,000 m and above) were essentially unaffected by the typhoon (Paladio-Melosantos and others, this volume). Because the eruption cloud expanded in the stratosphere, it blew generally southwestward, consistent with the wind direction in the stratosphere. There were some influences of wind at lower altitudes such as those of the typhoon. For example, the center of the isopach map of layer B and C1 is located about 10 km south of the vent. This may be due to a local influence of the wind within the typhoon.
The effect of the wind in the stratosphere will be evaluated first. The satellite images suggest that the center of the eruption cloud drifted southwestward at the velocity of approximately 10 m/s between 1440 and 1940 (Koyaguchi and Tokuno, 1993), while the cloud was radially expanding. Because of this effect, the distance from the vent does not give the distance from the center of the eruption cloud in the region more than a few tens of kilometers away from the vent, where the expansion velocity is comparable to wind velocity. If it is assumed that the thickness of the cloud is constant with time, the downwind distance from the vent, rvent, is approximated by

where Vw is the wind velocity. The downwind distances of 10 km and 30 km from the vent give approximately 3% and 10% overestimation of the distance from the center of the cloud, respectively, when Q is 5x1016 cm3/s, h is 5 km and Vw is 10 m/s. Although the evaluation of this effect on the estimation of Q is not straightforward, because the error of r depends on Q, the overestimation of r can lead to up to a few tens of percentage overestimation of Q when the pair of rvent=30 km and 10 km is used. Consequently, I propose the value of 3 to 4x1016cm3/s as the estimate of the volumetric flow rate from grain-size data.
Another important process in the stratosphere is that turbulent fluctuations in the ambient atmosphere can mix the cloud with the surrounding air so that the cloud may lose its coherence. This process would result in change in the effective thickness of the cloud. Furthermore, if the turbulence at the base of the cloud is sufficiently strong, fine particles may be kept in suspension and may not follow the second assumption. This effect would lead to the loss of fine particles in tephra-fall deposits.
The wind at the lower altitude is likely to affect the motion of tephra between the base of the cloud and its arrival on the ground. From equation 7, the settling velocities of particles of a few millimeters in diameter are estimated to be of order 1 to 10 m/s in the lower troposphere, which may be smaller than the wind velocity within the typhoon. This means that these particles can be dispersed laterally over considerable distances while they are falling through a distance of a few tens of kilometers from the umbrella cloud to the ground. These effects of turbulence at the higher and lower altitudes play an important role particularly in the dispersal of fine particles (see fig. 6). The grain-size distribution of coarser particles would give a more reliable estimation of the volumetric flow rate than would the grain-size distribution of fine particles.
Recent theoretical studies of a fluid dynamics model on eruption columns (Wilson and others, 1978; Settle, 1978; Sparks, 1986; Woods, 1988) allow us to relate eruption conditions (for example, discharge rate, temperature, and H2O content of magma) to dimension and dynamics of eruption clouds (for example, height, depth, temperature, and volumetric flow rate of the cloud). The volumetric flow rate at the neutral buoyancy level can be estimated from satellite data on the basis of the fluid dynamics models. The methods and the values of constants are the same as Woods' model (1988) for steady plinian eruption columns except that the tropical atmospheric conditions are taken into account in this study. Generally speaking, the conditions of plinian eruptions are governed by magma discharge rate, temperature, and H2O content of magma at the surface. The magma discharge rate is determined by two independent parameters, such as vent radius and initial velocity at the vent, when the temperature and H2O content of magma are fixed. We evaluate plausible ranges of temperature and water content of magma from viewpoints of petrological features of the Pinatubo pumice first, before the results of numerical calculations for variable magma discharge rates with different pairs of initial velocity and vent radius are shown.
Temperature of magma.--At least two important phenocrystic (or microphenocrystic) phases in the Pinatubo pumice constrain the preeruption temperature of magma: cummingtonite and hemoilmenite. According to the experimental results by Rutherford (1993), the presence of cummingtonite requires an H2O-rich fluid and pressure in the 150- to 350-MPa range at approximately 1060K (787°C) or less. On the other hand, considering the miscibility gap between ilmenite-hematite solid solution, high hematite content of hemoilmenite indicates that the temperature of magma was higher than 1070K (Imai and others, 1993; this volume). It is, therefore, concluded that the preeruption temperature of the magma was around 1060 to 1070K. The small discrepancy in the crystallization temperature between cummingtonite and hemoilmenite may be due to heterogeneity in the magma chamber or different stages of crystallization between the two minerals. It should be noted that the preeruption temperature does not necessarily represent the temperature of erupting magma at the surface; the temperature of vesiculating magma is significantly cooled by exsolution and expansion of gas phase. If there is good thermal equilibration between the magma and adiabatically expanding gas, the magma with several weight percent H2O is cooled by a few hundreds of degrees (Williams and McBirney, 1979). The presence of lithic fragments also decreases the effective magma temperature. However, I assumed that this effect is negligible in the present case, because lithic fragments are rarely observed in the tephra-fall deposits (<1%). Consequently, the initial temperature of the eruption cloud at the surface would be approximately 800 to 900K. In the following numerical calculations, a wider range, between 800 and 1200K, is assumed in order to elucidate the effects of magma temperature on the dynamics of the eruption column.
H2O content of magma.--The presence of hydrous phenocrysts (hornblende, biotite, and cummingtonite) indicates that the magma contained considerable water just prior to the eruption. Ion probe analyses of melt inclusions in plagioclase and quartz yield H2O contents of 5.5 to 6.5 wt%, which is slightly less than the solubility limit at 200 MPa (Rutherford, 1993). The estimation of H2O content by means of ion probe analyses of melt inclusions may overestimate H2O content in the magma because of the effect of overgrowth of the host crystals. In the following calculations, H2O contents between 1 and 6 wt% are assumed.
The results of the numerical calculations based on the fluid dynamic model (Woods, 1988) suggest that the volumetric flow rate at the neutral buoyancy level is closely related to the total height of the cloud (Bursik and others, 1992). One of the most interesting results is that the relation between the two quantities is not much affected by magmatic temperature, H2O content, or other conditions of eruption such as vent radius and initial velocity except for some conditions that are close to the critical conditions for column collapse (fig. 10). The total height of the cloud is estimated from the widths of shadows in the satellite images to be approximately 34 km (Tanaka and others, 1991). Although this method is the simplest way among the three methods, it has a disadvantage. The height estimates on the basis of the widths of shadows are largely dependent on the shape of the edge of clouds and contain considerable errors, which can be as large as the thickness of cloud (up to several kilometers). Taking this uncertainty into account, a volumetric flow rate at the buoyancy level is estimated from the height estimate to be approximately 5x1016 to 1x1017 cm3/s. It should be noted that the above value represent the volumetric flow rate at 1540, because the height estimate is based on the satellite image at 1540.
Figure 10. The results of numerical calculations on the fluid dynamics model of eruption clouds showing the relation between the total height of the cloud versus the volumetric flow rate at the neutral buoyancy level. The model by Woods (1988) is applied to the tropical atmospheric conditions. The temperature and H2O content of magma and the initial velocity are systematically varied in the ranges from 800 to 1200 K, 1 to 6 wt%, and 0 to 350 m/s, respectively.
The volumetric flow rate of the umbrella cloud can be estimated from the satellite data in another way. The satellite data indicate that the umbrella cloud expanded from 60,000 km2 to 120,000 km2 between 1440 and 1540 and continued to expand until by 1940 it covered an area of 300,000 km2. This fact suggests that the cloud expanded at the rate of 1.7x1011 cm2/s between 1440 and 1540 and almost steadily at the rate of 1.3x1011 cm2/s between 1540 and 1940. The volumetric flow rate of the umbrella cloud is obtained by multiplying the above rate by the cloud thickness. The largest source of the uncertainty of this method is the cloud thickness, which is obtained only by an indirect method. The maximum thickness of the umbrella cloud would be given by the difference between the altitudes of the cloud top and the neutral buoyancy level (see fig. 5). The difference between the altitudes of the cloud top and the neutral buoyancy level is also related to the volumetric flow rate at the neutral buoyancy level, and this relationship is not dependent on the magmatic or other conditions of eruption (fig. 11); it is constant (approximately 5 km) when the volumetric flow rate is less than 5x1015 cm3/s, and it increases from 5 km to 10 km as the volumetric flow rate increases from 1016 to 1017 cm3/s. According to the satellite images at 1540, there was a small dome-shaped swell (several kilometers high), which suggests that most of the cloud was thinner than the maximum thickness by several kilometers. I infer that the actual thickness of the cloud was 3 to 6 km. The volumetric flow rate between 1440 and 1540 is estimated to be 5x1016 to 1x1017 cm3/s by multiplying the spreading rate of the cloud (1.7x1011 cm2/s) by the thickness (3 to 6 km). Recent fluid dynamic considerations suggest that if an umbrella cloud expands as a gravity current, the thickness of the current decreases with time even for a constant volumetric flow rate (A.W. Woods, Institute of Theoretical Geophysics, Cambridge, written commun., 1993). Judging from the expansion rate (1.3x1011 cm2/s), I think it is reasonable to assume that the thickness of the cloud decreased after 1540, although no thickness estimate based on satellite images after 1540 is available. It is suggested that the volumetric flow rate decreased considerably after 1540.
Figure 11. The results of numerical calculations on the fluid dynamics model of eruption clouds showing the difference between the altitudes of the cloud top and the neutral buoyancy level against the volumetric flow rate at the neutral buoyancy level. The ranges of the temperature and H2O content of magma and the initial velocity are the same as in figure 10.
The two estimations from the satellite image give consistent values of 5x1016 to 1x1017 cm3/s, despite the fact that they are based on different kinds of data. On the other hand, the volume flow rate on the basis of the grain-size data gives slightly smaller values (3x1016 to 4x1016 cm3/s). It should be noted that the meanings of the volumetric flow rates obtained by the above three methods are slightly different. The estimate based on grain size gives the expansion rate of the region where particles are homogenized by turbulence, the estimate based on cloud height represents the volumetric flow rate at the neutral buoyancy level, and the estimate based on cloud thickness and area gives the actual volumetric flow rate of the cloud. Generally, the volumetric flow rate of the eruption cloud increases as its altitude increases because of decompression and entrainment of the ambient air. Because the umbrella cloud is diverted between the altitudes of the neutral buoyancy level and the cloud top, the actual volumetric flow rate would be between those at the neutral buoyancy level and the cloud top. Considering that the umbrella cloud flows as a gravity current, the main part of the current would be diverted just above the neutral buoyancy level (see fig. 5). Consequently, it is considered that the estimate based on grain size and that based on cloud area and thickness roughly represent the volumetric flow rate at the neutral buoyancy level at least near the vent, and they may increase to some extent with distance due to the entrainment of the ambient air during the expansion.
There are at least four possible explanations for the lower estimate of the volumetric flow rate from the grain-size data than estimates from the satellite data. First, the estimates based on satellite data represent the volumetric flow rate at 1540 or the averaged volumetric flow rate between 1440 and 1540, while the estimate based on the grain-size data represents the average volumetric flow rate during the deposition. The lower estimate based on grain size data may reflect the decrease of volumetric flow rate with time after 1540. Secondly, the effect of the entrainment during the expansion is more significant in the estimation from satellite images of the cloud that expanded more than 102 km in diameter than in the estimation from grain-size data near the vent. Third, the average clast density may be greater than that of pumice grains, which can cause the underestimation of the value of B and hence the underestimation of Q. Finally, pyroclastic flows may have been forming at the same time as the plinian fall layers (W.E. Scott and others, this volume), so some of the mass that contributed to rise of the eruption is not represented in the plinian fall deposits.
The volumetric flow rate at the neutral buoyancy level and that of the cloud top against variable magma discharge rate are shown in figure 12. The relation between the volumetric flow rate of the umbrella cloud and the magma discharge rate depends on the magmatic temperature at the vent but is insensitive to the changes in H2O content. If the magmatic temperature (at the vent) is 800K, the magma discharge rate is 4 to 8x108 kg/s for the volumetric flow rate of 3 to 4x1016 cm3/s. The discharge rate is up to 2x109 kg/s if the upper estimate of the volumetric flow rate on the basis of the satellite data (1x1017 cm3/s) is applied. Because the magma discharge rate rather sensitively depends on the volumetric flow rate as well as magmatic temperature at the vent, the second step of the volume estimation can be a source of serious errors. Furthermore, in contrast to the estimation of volumetric flow rate in the first step, the estimation of the magma discharge rate from the volumetric flow rate is not supported by different kinds of observations. The uncertainties of the results of numerical calculations largely depend on applied fluid dynamics models. Accordingly, the self consistency of the fluid dynamics model will be checked on the basis of the satellite data below.
Figure 12. The results of numerical calculations on the fluid dynamics model of eruption clouds showing the relation between the volumetric flow rate at the neutral buoyancy level and the magma discharge rate. The results of the volumetric flow rate at the cloud top are shown by a shaded zone for comparison. The ranges of the temperature and H2O content of magma and the initial velocity are the same as in figure 10.
Constraints from temperature data in the satellite images.--The temperature of an eruption cloud top is a function of many parameters related to the dynamics of the event, such as temperature and H2O content of magma and the vent radius. Woods and Self (1992) showed that the cloud top temperature deviates from the local temperature at the same altitude and thus could not be used to infer plume elevation. Cloud top temperature increases with decreasing initial velocity and with increasing vent radius if discharge rate and temperature and H2O content of magma are fixed. One of the most important features of the dynamics of plinian eruptions is that the column is unstable and collapses if the vent radius is greater than a critical value for a constant initial velocity or if initial velocity is less than a critical value for a constant vent radius (Woods, 1988). Because of this constraint, cloud top temperature has an upper limit for a given discharge rate, temperature, and H2O content of magma (Koyaguchi and Tokuno, 1993). Figure 13 shows the numerical results of cloud top temperature against magma discharge rate for magma temperature of 800, 1000 and 1200K, water content from 1 to 6 wt%, and variable pairs of vent radius and initial velocity on the basis of Woods' model (1988). The maximum cloud temperature for each magma temperature increases as the magma discharge rate increases. For the cloud top temperature to be as high as that in the satellite image (243K), the magma discharge rate should be greater than 7x108, 1x109 or 3x109 kg/s if the magma temperatures are 800, 1000 or 1200K, respectively. It is notable that the discharge rates estimated from the cloud temperature increase as assumed magmatic temperature increases (fig. 13), whereas those estimated from the volumetric flow rate decrease with the increasing magmatic temperature (fig. 12). The discharge rates estimated from the two different methods agree fairly well when the assumed temperature is 800K (4 to 8x108 kg/s vs >7x108 kg/s), while they give conflicting results when the assumed temperature is 1200K (2 to 3x108 kg/s vs >3x109 kg/s). We emphasize that the temperature data in the satellite images should be used only as a supporting constraint at present. Because the fluid dynamics model assumes an steady eruption column which has horizontally uniform temperature and other physical quantities, the numerically obtained temperature cannot be compared directly to the observed cloud top temperatures.
Figure 13. The results of numerical calculations on the fluid dynamics model of eruption clouds showing the relation between the temperature of the cloud top and the magma discharge rate. The temperature of the cloud at the neutral buoyancy level (NBL) is shown by small dots for comparison. The ranges of the temperature and H2O content of magma and the initial velocity are the same as figure 10.
Koyaguchi and Tokuno (1993) assumed that the duration of the eruption was approximately 5 hours on the basis of the duration in which the eruption cloud continued to expand upwind. However, the duration of the cloud expansion does not necessarily indicate the duration of the eruption, because the cloud can continue to expand even after the supply at its source ceases. Tahira and others (this volume) reported that infrasonic waves and acoustic-gravity waves generated by the major eruption of Mount Pinatubo on June were observed at Kariya, Japan. High amplitudes of these waves lasted about 3.5 hours. Because it is considered that the infrasonic waves reflect the intensity of magma discharge at the source, I adopt the duration of the high amplitudes of the infrasonic waves (3.5 hours) as the duration of the eruption.
The total volume of the ejecta can be estimated by multiplying the magma discharge rate by the duration of the eruption. It should be noted here that the magma discharge rates based on the satellite images represent those at 1540 or those between 1440 and 1540, while those based on grain-size data represent the average magma discharge rate during the deposition. It would be more reasonable to use the average discharge rate for the calculation of the total volume rather than the magma discharge rate at one moment. Accordingly, applying the values based on grain-size data, the total volume of the ejecta is 2 to 4 km3 DRE (5 to 10 km3 bulk volume assuming that the bulk density of the deposit is 1,000 kg/m3). If the values based on satellite images are used, the total volume is estimated to be up to 10 km3 DRE (25 km3 bulk volume).
It is quite difficult to estimate the whole amount of the ejecta by geological methods, because fine particles are likely to be dispersed in the atmosphere and cannot be counted in the deposits. Pyle (1989) and Fierstein and Nathenson (1992) showed that many deposits display an exponential decrease in thickness with square root of the area enclosed by an isopach contour. This means that the thickness, T, should be in the form as:

where S is the area enclosed by an isopach contour, T0 is the thickness at S=0, and k is the decay constant. They proposed that the volume of the tephra-fall deposits, V, can be estimated by integrating this empirical relationship from S=0 to S=![]() as:
as:

The validity of this empirical relation has been tested for the tephra-fall deposits during eruptions where the distal ash falls on land (for example, Mount St. Helens; Fierstein and Nathenson, 1992). However, this method should be applied with caution to eruptions where data from distal areas are sparse. In the case of the Pinatubo eruption, most of tephra-fall deposits fell in the South China Sea, where few thickness data are available. Figure 14 shows the relation between the logarithm of thickness and the square root of the area enclosed by an isopach contour of layers C1 and C2 (fig. 3) and their best fit lines. The decay constants of layers C1 and C2 are 2.7x10-7 and 2.4x10-7 (cm-1), respectively. The sum of the volumes of the two layers is calculated from equation 11 to be 1.2 km3 (the volumes of layers C1 and C2 are 0.5 and 0.7 km3, respectively). The areas enclosed by isopach contours less than 32 mm thick determined were by smoothly extrapolating the isopach contours obtained on land toward the South China Sea, and so the calculation would contain considerable errors. Similarly, the volume calculated from isopachs of the Pinatubo Volcano Observatory Team (1991) is 1.5 km3,which agrees well with the present results. An early extrapolation to include distal deposits (3 km3; Pinatubo Volcano Observatory Team, 1991), has more recently been updated by use of the dual-slope exponential thinning relationship (3.4 to 4.4 km3 bulk volume; Paladio-Melosantos and others, this volume; W.E. Scott and others, this volume).
Figure 14. The logarithm of thickness versus the square root of the area enclosed by an isopach contour for layers C1 and C2 (fig. 3). Uses terrestrial data only.
Discrepancies between various estimates of volumes are shown schematically in figure 15. By integrating equation 5b we can obtain a volume estimate from on-land grain-size data on the basis of the dispersal-sedimentation model, which yields an anomalously low estimate. Fine particles (![]() >3) make up only a small fraction of the Pinatubo tephra-fall deposits on land (fig. 7; see also fig. 9 for estimated initial grain-size distribution). The extreme depletion of the fine particles is not predicted by the present dispersal-sedimentation model alone, unless the ejecta were originally depleted in the fine particles. However, enough fine ash fell with rain or as accretionary lapilli that I do not suggest an initial paucity of fine particles. An alternative is that fine particles did not follow the present model but were instead widely dispersed in the atmosphere (see fig. 6). If the turbulence at the bottom of the cloud and between the cloud and the ground is sufficiently strong, fine particles may be kept in suspension and dispersed laterally over considerable distances.
>3) make up only a small fraction of the Pinatubo tephra-fall deposits on land (fig. 7; see also fig. 9 for estimated initial grain-size distribution). The extreme depletion of the fine particles is not predicted by the present dispersal-sedimentation model alone, unless the ejecta were originally depleted in the fine particles. However, enough fine ash fell with rain or as accretionary lapilli that I do not suggest an initial paucity of fine particles. An alternative is that fine particles did not follow the present model but were instead widely dispersed in the atmosphere (see fig. 6). If the turbulence at the bottom of the cloud and between the cloud and the ground is sufficiently strong, fine particles may be kept in suspension and dispersed laterally over considerable distances.
Figure 15. Volume estimation that is consistent with the dispersal-sedimentation model and volume estimates that are based on the assumption of the exponential thinning behavior.
Generally speaking, the total sedimentation rate and thickness at a given distance are determined by a specific range of grain size; they are determined by those of the larger particles in the proximal region but by those of the finer particles in the distal region. According to Koyaguchi (1994), the thickness-distance relation is basically determined by the sedimentation of coarse particles (![]() <0) in the region within 30 km from the vent when Q>1016 cm3/s. Therefore, the thickness-distance relation on land around Pinatubo was mainly determined by the observed coarse particles (
<0) in the region within 30 km from the vent when Q>1016 cm3/s. Therefore, the thickness-distance relation on land around Pinatubo was mainly determined by the observed coarse particles (![]() <0), but it is insensitive to the amount of fine particles. Koyaguchi (1994) analytically proved that the dispersal-sedimentation model successfully explained exponential thinning behavior from r=0 to r=
<0), but it is insensitive to the amount of fine particles. Koyaguchi (1994) analytically proved that the dispersal-sedimentation model successfully explained exponential thinning behavior from r=0 to r=![]() only for an initial grain-size distribution that is approximately log-normal with
only for an initial grain-size distribution that is approximately log-normal with ![]()
![]() = 2.5; otherwise, the model holds only in a limited range of distance. In figure 9 the theoretical initial grain-size distributions that predict exponential thinning behavior from the dispersal-sedimentation model are calculated for B/Q = 5x10-14 cm-2 and k=2.5x10-7 cm-1. The initial size distribution estimated from the actual grain-size data shows a substantially coarser distribution than the theoretical initial grain-size distribution. The difference between the theoretical and actual initial grain size is explained by the depletion of fine particles. If particles of size
= 2.5; otherwise, the model holds only in a limited range of distance. In figure 9 the theoretical initial grain-size distributions that predict exponential thinning behavior from the dispersal-sedimentation model are calculated for B/Q = 5x10-14 cm-2 and k=2.5x10-7 cm-1. The initial size distribution estimated from the actual grain-size data shows a substantially coarser distribution than the theoretical initial grain-size distribution. The difference between the theoretical and actual initial grain size is explained by the depletion of fine particles. If particles of size ![]() >3 are omitted from the theoretical initial grain-size distribution, the pdf of the rest shows a better agreement with the distribution deduced from the actual grain size data (fig. 9). Thus, the volume of the particles which follows the dispersal-sedimentation model is understandably smaller than the volume estimated from the data on land on the basis of the exponential thinning relationship.
>3 are omitted from the theoretical initial grain-size distribution, the pdf of the rest shows a better agreement with the distribution deduced from the actual grain size data (fig. 9). Thus, the volume of the particles which follows the dispersal-sedimentation model is understandably smaller than the volume estimated from the data on land on the basis of the exponential thinning relationship.
Volumes estimated from the fluid dynamic model and satellite data are higher than those estimated by Paladio-Melosantos and others (this volume) using the method of Fierstein and Nathenson (1992), even when fine ash observed far from the vent, in Southeast Asia and the South China Sea, is taken into account. Again, I judge that separation of fine ash explains the discrepancy.
The behavior of fine particles is an important problem not only in volcanology but also in relation to environmental effects of volcanic eruptions or to aviation safety. Walker (1980) developed another method for estimating the amount of lost fine vitric particles on the basis of the degree of the crystal concentration in the deposits. Crystal concentration studies are being carried out for the Pinatubo tephra-fall deposits in order to confirm the present conclusions. In the present study, the numerical calculations on the dynamics of the eruption columns were carried out using a wide ranges of magmatic temperatures, H2O contents, and other conditions of eruption, and the results were cross-checked by different kinds of observations. Nevertheless, the following uncertainties may still modify the present results to some extent:
Comments by S. Carey (Univ. of Rhode Island), A.W. Woods (Institute of Theoretical Geophysics, Cambridge), W.E. Scott (U.S. Geological Survey), Makoto Tahira (Aichi Univ. of Education), Toshitsugu Fujii (Univ. of Tokyo, Earthquake Research Institute), C.G. Newhall (U.S. Geological Survey), and an anonymous reviewer were helpful. E.L. Listanco (Earthquake Research Institute and PHIVOLCS) kindly allowed me to use his unpublished data. I wish to thank all of these people.
Bursik, M.I., Sparks, R.S.J., Gilbert, J.S., and Carey, S.N., 1992, Sedimentation of tephra by volcanic plumes. I. Theory and its comparison with a study of the Fogo A plinian deposit, Sao Miguel (Azores): Bulletin of Volcanology, v. 54, p. 324-344.
Carey, S.N., and Sparks, R.S.J., 1986, Quantitative models of the fallout and dispersal of tephra from volcanic eruption columns: Bulletin of Volcanology, v. 48, p. 109-125.
Fierstein, J., and Nathenson, M., 1992, Another look at the calculation of fallout tephra volumes: Bulletin of Volcanology, v. 54, p. 156-167.
Hoblitt, R.P., Wolfe, E.W., Scott, W.E., Couchman, M.R., Pallister, J.S., and Javier, D., this volume, The preclimactic eruptions of Mount Pinatubo, June 1991.
Imai, A., Listanco, E.L. and Fujii, T., 1993, Petrologic and sulfur isotopic significance of highly oxidized and sulfur-rich magma of Mount Pinatubo, Philippines: Geology, v. 21, p. 699-702.
------this volume, Highly oxidized and sulfur-rich dacitic magma of Mount Pinatubo: Implication for metallogenesis of porphyry copper mineralization in the Western Luzon arc.
Koyaguchi, T., 1994, Grain size variation of tephra derived from volcanic umbrella clouds: Bulletin of Volcanology, v. 56, p. 1-9.
Koyaguchi, T., and Tokuno, M., 1993, Origin of the giant eruption cloud of Pinatubo, June 15, 1991: Journal of Volcanology and Geothermal Research, v. 55, p. 85-96.
Martin, D., and Nokes, R., 1988, Crystal settling in a vigorously convecting magma chamber: Nature, v. 332, p. 534-536.
Paladio-Melosantos, M.L., Solidum, R.U., Scott, W.E., Quiambao, R.B., Umbal, J.V., Rodolfo, K.S., Tubianosa, B.S., Delos Reyes, P.J., and Ruelo, H.R., this volume, Tephra falls of the 1991 eruptions of Mount Pinatubo.
Pinatubo Volcano Observatory Team, 1991, Lessons from a major eruption: Mt. Pinatubo, Philippines: Eos, Transactions, American Geophysical Union, v. 72, p. 545-555.
Pyle, D.M., 1989, The thickness, volume and grainsize of tephra fall deposits: Bulletin of Volcanology, v. 51, p. 1-15.
Rutherford, M.J., 1993, Experimental petrology applied to volcanic processes: Eos, Transactions, American Geophysical Union, v. 74, p. 49-55.
Scott, W.E., Hoblitt, R.P., Torres, R.C., Self, S, Martinez, M.L., and Nillos, T., Jr., this volume, Pyroclastic flows of the June 15, 1991, climactic eruption of Mount Pinatubo.
Settle, M., 1978, Volcanic eruption clouds and thermal power output of explosive eruptions: Journal of Volcanology and Geothermal Research, v. 3, p. 309-324.
Sparks, R.S.J., 1986, The dimension and dynamics of volcanic eruption columns: Bulletin of Volcanology, v. 48, p. 3-15.
Sparks, R.S.J., Bursik, M.I., Ablay, G.J., Thomas, R.M.E., and Carey, S.N., 1992, Sedimentation of tephra by volcanic plumes. II. Controls on thickness and grain-size variation of tephra fall deposits: Bulletin of Volcanology, v. 54, p. 685-695.
Tahira, M., Nomura, M., Sawada, Y., and Kamo, K., this volume, Infrasonic and acoustic-gravity waves generated by the Mount Pinatubo eruption of June 15, 1991.
Tanaka, S., Sugimura, T., Harada, T., and Tanaka, M., 1991, Satellite observation of the diffusion of Pinatubo volcanic dust to the stratosphere: Journal of the Remote Sensing Society of Japan, v. 11, p. 91-99. (In Japanese with English abstract.)
Tokuno, M., 1991a, Observation of volcanic eruption clouds from Mt. Pinatubo, Philippines by GMS-4: Meteorological Satellite Center Technical Note, v. 23, p. 1-14.
------1991b, GMS-4 observations of volcanic eruption clouds from Mt. Pinatubo, Philippines: Journal of the Remote Sensing Society of Japan, v. 11, p. 81-89. (In Japanese with English abstract.)
Walker, G.P.L., 1980, The Taupo pumice: Products of the most powerful known (ultraplinian) eruption?: Journal of Volcanology and Geothermal Research, v. 8, p. 69-94.
Walker, G.P.L., Wilson, L., and Boswell, E.L.G., 1971, Explosive volcanic eruptions. I. The rate of fall of pyroclasts: Geophysical Journal of the Royal Astronomical Society, v. 22, p. 377-383.
Williams, H., and McBirney, A.R., 1979, Volcanology: San Francisco, Freeman, Cooper and Company, 397 p.
Wilson, L., 1972, Explosive volcanic eruptions. II. The atmospheric trajectory of pyroclasts: Geophysical Journal of the Royal Astronomical Society, v. 30, p. 381-392.
Wilson, L., Sparks, R.S.J., Huang, T.C., and Watkins, N.D., 1978, The control of volcanic column heights by eruption energetics and dynamics: Journal of Geophysical Research, v. 83, p. 1829-1836.
Woods, A.W., 1988, The fluid dynamics and thermodynamics of eruption columns: Bulletin of Volcanology, v. 50, p. 169-193.
Woods, A.W., and Self, S., 1992, Thermal disequilibrium at the top of volcanic clouds and its effect on estimates of the column height: Nature, v. 355, p. 628-630.
PHIVOLCS | University of Washington Press | U.S.Geological Survey
This page is <https://pubs.usgs.gov/pinatubo/koya/>
Contact: Chris Newhall
Last updated 06.11.99