Scientific Investigations Report 2005–5284
In cooperation with National Water Research Institute, Environment Canada National Assessment of Water Availability and Use Program
Shallow Ground-Water Recharge in the Great Lakes Basin
Box 1— Estimating Shallow Ground-Water Recharge in Michigan (by S.S. Aichele, USGS)
Figure 1. Study area and surficial geology of the Great Lakes Basin.
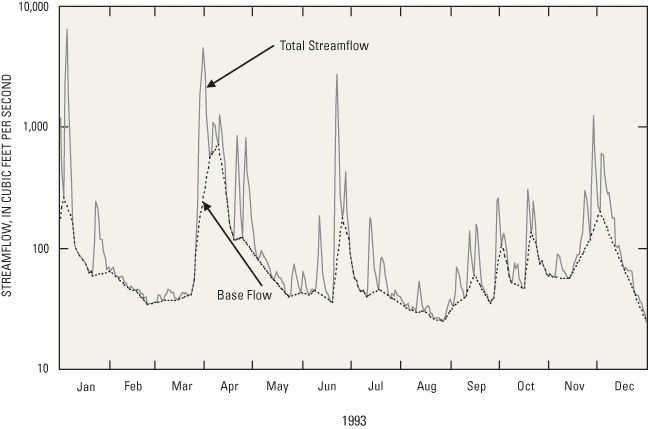
Figure 2. Hydrograph separation on Nith River at New Hamburg, Ontario, stre...
Figure 3. Regression between 30-year normal streamflow and length-of-record...
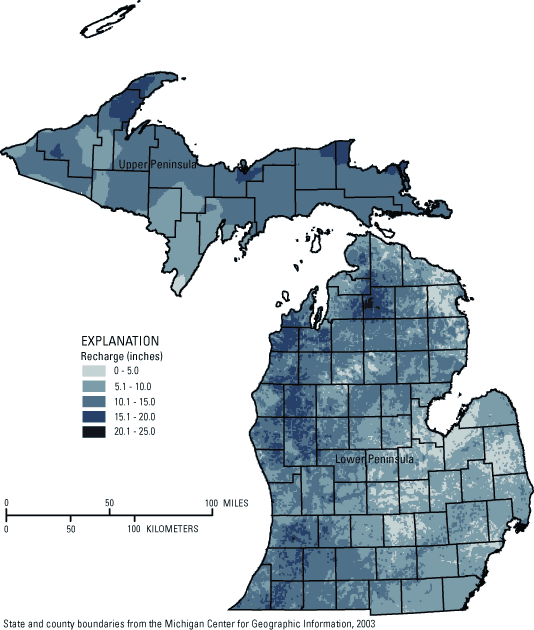
Figure 4. Shallow ground-water recharge rates in the Great Lakes Basin. [<,...
Figure 5. Comparison of UKIH-based recharge results with data reported in W...
Figure 6. The effect of interpolation and summation on base-flow index (BFI...
Table 1. Values of xg,j, the value of BFI assigned to geologic class j, use...
Table 2. Long-term average shallow ground-water recharge rates for watershe...
Table 3. Comparison of long-term trends in base flow and corresponding tren...
| Multiply | By | To obtain |
|---|---|---|
| Length | ||
| inch (in.) | 25.4 | millimeter (mm) |
| foot (ft) | 0.3048 | meter (m) |
| Area | ||
| square foot (ft2) | 0.0929 | square meter (m2) |
| square mile (mi2) | 2.590 | square kilometer (km2) |
| Volume | ||
| cubic foot (ft3) | 0.02832 | cubic meter (m3) |
Temperature in degrees Celsius (°C) may be converted to degrees Fahrenheit (°F) as follows:
°F=(1.8x°C)+32
Temperature in degrees Fahrenheit (°F) may be converted to degrees Celsius (°C) as follows:
°C=(°F-32)/1.8
Vertical coordinate information is referenced to the North American Vertical Datum of 1988 (NAVD 88).
Horizontal coordinate information is referenced to the North American Datum of 1983 (NAD 83) and the Albers projection.
Altitude, as used in this report, refers to distance above the vertical datum.
Knowledge of ground-water recharge is fundamental to understanding the availability and quality of ground water. As a prelude to the discussions in this report on natural recharge in the Great Lakes Basin, it is useful to review the value of recharge estimates in hydrologic studies and some caveats on their use.
Ground-water recharge includes recharge as a natural part of the hydrologic cycle and human-induced recharge either directly through spreading basins or injection wells or as a consequence of human activities such as irrigation and waste disposal. This report addresses the natural component of ground-water recharge to shallow aquifers (usually less than 100 feet deep), the dominant component of recharge at a regional scale in the Great Lakes Basin. Such discussion needs to be combined with estimates of deeper aquifer recharge and the effects of human activities where these estimates and activities affect ground-water recharge at the scale of interest.
Ground water flows from areas of recharge to areas of discharge. Discharge may occur to the atmosphere by transpiration from plants rooted below the water table; to streams, lakes, and other surface-water bodies; or to pumping wells. The balance between ground-water recharge and discharge controls ground-water levels and storage in a manner analogous to how deposits and withdrawals control savings in a bank account. Thus, recharge is an important component of the "ground-water savings account." If recharge exceeds discharge for some period, ground-water levels and storage will increase. Conversely, ground-water levels and storage will decrease during periods when discharge exceeds recharge.
Understanding ground-water recharge is commonly important to successfully calibrating computer models of ground-water systems. This understanding is particularly true in instances where model simulation is used to address concerns about the effects of ground-water pumping on surface-water resources. Also, recharge links climate with water resources, and contaminant transport to and through ground-water systems. In the process of calibrating and verifying these models, recharge rates are highly correlated with estimates of aquifer permeability. Thus, errors in recharge estimates can affect how well a model represents the actual hydrogeologic setting of interest.
Recharge rates are one of the major key controls on the rate of contaminant movement in ground water and the "flushing" rate of shallow aquifers. Thus, assessment of recharge is critical to assessment of ground-water contamination. Likewise, estimation of recharge at regional scales is integral to strategies that focus on aquifer protection by delineation of areas vulnerable to contamination. Areas of greatest vulnerability often correspond to areas of highest recharge. Many recharge estimates are limited to broad spatial average fluxes through the unsaturated zone to the water table and may not reflect preferential flow paths or areas of focused recharge as potential conduits for rapid contamination of the aquifer. For example, areas underlain by carbonate rocks commonly contain preferential flow paths that facilitate recharge and potential contamination of the aquifer.
Finally, it is important to clarify the relation of recharge to the concepts of safe yield or sustainability of an aquifer. A common misperception has been that the development of a ground-water system is "safe" if the average annual rate of ground-water withdrawal does not exceed the average annual rate of natural recharge. Thus, natural recharge sometimes is assumed, erroneously, to be equivalent to the basin sustainable yield. This concept has been referred to as the "Water Budget Myth" (Bredehoeft, 1997). Even further misinterpretations sometimes are made that if ground-water withdrawals are less than the recharge rate, then water levels and ground-water storage will not decline.
To understand the fallacy of the misperception described above, one needs to consider how ground-water systems respond to withdrawals. Under natural (non-pumping) conditions, a ground-water system is in long-term equilibrium. That is, averaged over some period (and without considering possible long-term climate change), the amount of water recharging the system is approximately equal to the amount of water leaving or discharging from the system. Ground-water withdrawals by pumping change the flow system. The water that is withdrawn must be supplied by some combination of (1) increased recharge, (2) decreased discharge, and (3) removal of water that was stored in the system.
Regardless of the amount of water withdrawn, the ground-water system will undergo some drawdown in water levels in pumping wells to induce the flow of water to these wells. Thus, some water is removed from storage. For most ground-water systems, the change in storage in response to pumping is a transient phenomenon that occurs as the system adjusts to the withdrawals. The relative contributions of changes in storage, changes in recharge, and changes in discharge evolve with time. If the system can come to a new equilibrium, the changes in storage will diminish to zero (at a new reduced level of ground-water storage), and inflows will again balance outflows. Thus, the long-term source of water to discharging wells becomes a change in the amount of water entering or leaving the system. The time that is required to bring a ground-water system into equilibrium is a function of the characteristics of the aquifer system, such as permeability, thickness, distance to hydrologic boundaries, and the placement of pumping wells.
In summary, natural recharge is a critical element for understanding the water balance, an important parameter in many computer-model simulations of aquifer systems, and is fundamental to understanding contaminant transport from the land surface. All of these aspects may factor into an analysis of the sustainability of a ground-water system. An estimate of natural recharge, by itself, however, should not be used to determine the amount of ground water that can be withdrawn on a sustained basis. The quantity of ground water available for use depends more upon how the changes in inflow and outflow that result from withdrawals affect the surrounding environment and the acceptable tradeoff between ground-water use and these changes. Achieving this tradeoff in the long term is a central theme in the evolving concept of sustainability (Alley and others, 1999; Alley and Leake, 2004).
This report presents the results of the first known integrated study of long-term average ground-water recharge to shallow aquifers (generally less than 100 feet deep) in the United States and Canada for the Great Lakes, upper St. Lawrence, and Ottawa River Basins. The approach used was consistent throughout the study area and allows direct comparison of recharge rates in disparate parts of the study area. Estimates of recharge are based on base-flow estimates for streams throughout the Great Lakes Basin and the assumption that base flow in a given stream is equal to the amount of shallow ground-water recharge to the surrounding watershed, minus losses to evapotranspiration. Base-flow estimates were developed throughout the study area using a single model based on an empirical relation between measured base-flow characteristics at streamflow-gaging stations and the surficial-geologic materials, which consist of bedrock, coarse-textured deposits, fine-textured deposits, till, and organic matter, in the surrounding surface-water watershed. Model calibration was performed using base-flow index (BFI) estimates for 959 stations in the U.S. and Canada using a combined 28,784 years of daily streamflow record determined using the hydrograph-separation software program PART.
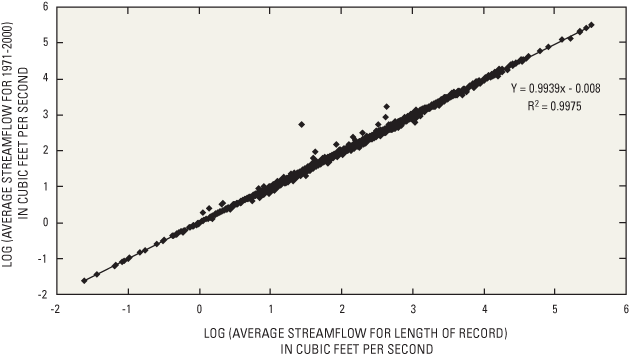
Results are presented for watersheds represented by 8-digit hydrologic unit code (HUC, U.S.) and tertiary (Canada) watersheds. Recharge values were lowest (1.6-4.0 inches/year) in the eastern Lower Peninsula of Michigan; southwest of Green Bay, Wisconsin; in northwestern Ohio; and immediately south of the St. Lawrence River northeast of Lake Ontario. Recharge values were highest (12-16.8 inches/year) in snow shadow areas east and southeast of each Great Lake. Further studies of deep aquifer recharge and the temporal variability of recharge would be needed to gain a more complete understanding of ground-water recharge in the Great Lakes Basin.
Information on the hydrologic budgets of watersheds is useful in many environmental and public-use settings. Examples where this information is useful include urban planning and water supply, fish and wildlife management, and environmental cleanup and remediation. This information is also useful to industrial and commercial interests such as thermoelectric and hydroelectric power generation, petroleum refining, irrigation of crops, mining, and the production of salt, fertilizer, and chemicals. Ground-water recharge (referred to as "recharge" in this report) is a primary component of a watershed water balance and is frequently unknown or difficult to quantify. In addition, recharge estimates can be applicable to many water-resource management issues, including the development of non-point source-water protection strategies. In this report, recharge is defined as precipitation that infiltrates the land surface, moves downward through the unsaturated zone, and enters the water table. For the purposes of this study, water that is evaporated or transpired by plant roots is not included as recharge.
Several estimates of ground-water recharge in portions of the Great Lakes Basin (fig. 1) have been reported (Holtschlag 1996; Cherkauer, 2001; Dumouchelle and Schiefer, 2002; Wolock, 2003; Gebert and others, in press; Geoff Delin, U.S. Geological Survey, written commun., 2005). At least one study (Wolock, 2003) estimated recharge over the U.S. portion of the Great Lakes Basin as part of a larger study to estimate recharge in the United States. Local or state-wide recharge studies within the Great Lakes Basin include Dumouchelle and Schiefer (2002), Cherkauer (2001), and Holtschlag (1996). To date (2005), no study has attempted to estimate recharge to shallow aquifers (generally less than 100 feet deep) in the entire Great Lakes Basin. Therefore, the U.S. Geological Survey, in cooperation with the National Water Research Institute, Environment Canada, began a study in 2005 to more accurately estimate recharge in all portions of the Great Lakes Basin as part of the Great Lakes Water Availability Pilot Project.
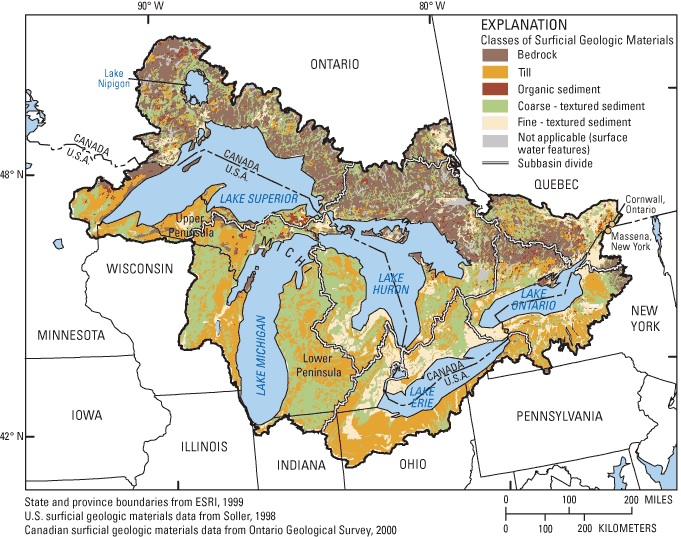
Figure 1. Study area and surficial geology of the Great Lakes Basin.
Options for estimating recharge over an area as large as the Great Lakes Basin are limited. Dumouchelle and Schiefer (2002) used a technique known as hydrograph separation to evaluate long-term (tens of years) streamflow records in Ohio to determine the component of streamflow that results from ground-water seepage into the stream, defined herein as base flow. The long-term average base flow was assumed to be equal to long-term average ground-water recharge in the surrounding watershed. This approach requires streamflow-gaging records, which are spatially and temporally limited in their availability. A hydrograph separation for a streamflow-gaging station in New Hamburg, Ontario, is shown in figure 2.
In the Great Lakes Basin, the approach most commonly used to estimate recharge in ungaged areas is to use regression equations to relate base-flow information in gaged areas to landscape attributes in the surrounding surface-water watershed. Then the regression equations are applied in ungaged areas based on the abundance of the respective landscape attributes in the ungaged areas (Gebert and others, in press; Neff and others, 2005; Holtschlag, 1996). This approach is used in this report and is appropriate for estimating long-term average recharge rates. This approach is limited in that variability of recharge over relatively short time scales (days and weeks) is not addressed and it is unclear at what spatial scale estimates can be reliably made. Spatially complete base-flow estimates reported in Neff and others (2005) are used in this report to estimate recharge throughout the Great Lakes Basin.
Other approaches to determine recharge are available. Direct measurement of recharge is possible using closed-bottom lysimeters buried beneath the rooting zone (Routson and Johnson, 1990). However, these measurements are difficult to make, and data collected with this approach cannot be applied to a broad area (Holtschlag, 1996). To avoid this problem, numerous approaches for estimating recharge indirectly have been developed. Some of these approaches seek to quantify ground-water seepage to surface-water bodies and relate that to recharge in the surrounding watershed, similar to what is done in this study. Such approaches utilize seepage runs (Lerner and others, 1990), seepage meters (Choi and Harvey, 2000), or conservative tracers such as heat (Stonestrom and Constantz, 2003) to estimate seepage. Numerical computer simulation has been used to quantify recharge in many studies and can be done multiple ways at a range of spatial and temporal scales (Singh, 1995; Arnold and others, 2000). Analysis of chloride tracers has been used to estimate recharge rates (Prych, 1995), as has using tracers, such as chlorofluorocarbons (CFCs) or tritium, to date ground water and infer recharge rates (Cook and Walker, 1995). One approach utilizes information on water-table fluctuations and specific yield of shallow aquifers to estimate recharge (Healy and Cook, 2002). A thorough description and comparison of recharge estimation techniques is provided in Scanlon and others (2002).
The base flow of a stream or river is the amount of ground water discharged from an aquifer to the stream. This discharge occurs year-round and fluctuates seasonally depending on the ground-water levels in the aquifer. Over the course of a year, assuming there is no long-term trend in the quantity of water stored in the aquifer or losses due to underflow, the total base flow is assumed to equal the total ground-water recharge for a watershed. This base flow is supplemented by direct runoff during and immediately after precipitation or snowmelt events, resulting in peaks on a hydrograph showing streamflow through time. The process of dividing these peaks into base flow and direct runoff is called hydrograph separation.
The separation of total streamflow into base flow and direct runoff by hydrograph separation has been described as "one of the most desperate analysis techniques in use in hydrology" (Hewlett and Hibbert, 1967) and "that fascinating area of fancy and speculation" (Appleby, 1970). It is, nonetheless, widely used to estimate base flow and recharge over broad areas. In more localized applications, the use of numerical models or seepage meters is more appropriate and more likely to accurately represent the many processes governing discharge of ground water to streams.
Base-flow separation was performed in Michigan Department of Environmental Quality (MDEQ, 2005) using the HYSEP – local minimum method developed by Pettyjohn and Henning (1979) as implemented in Sloto and Crouse (1996). This method was selected from the many competing methods for two reasons. First, watershed size is incorporated into the estimation. Second, this method is easily reproducible in a variety of software packages and virtually no assumptions are made about the response of ground water to increased inputs of runoff.
As part of MDEQ (2005), base-flow separations were completed on streamflow records for all USGS stations in Michigan with more than 10 years of daily record. Records were excluded that were clearly affected by impoundments (lakes, dams) upstream. No attempt was made to detect or correct for trends in the data. The resulting dataset contained records for 208 stations. Watersheds were delineated for each of the 208 stations, and the state was divided into three regions based on the distribution of base-flow yields (base flow per unit area)—the eastern Lower Peninsula, the western Lower Peninsula, and the Upper Peninsula.
Various landscape attributes of the watersheds were related to base flow using a series of multivariate linear regression models developed for each of the three regions. Within the eastern Lower Peninsula, the significant predictive attributes were agricultural land use, urban land use, annual growing degree days, annual precipitation, and percentage of the watershed underlain by lacustrine deposits. Within the western Lower Peninsula, the significant predictive variables were winter (December through March) precipitation, the percentage of the watershed underlain by till, and the percentage of the watershed covered by forests. In the Upper Peninsula, the significant predictive variables were growing degree days and winter precipitation. These variables, combined with the watershed area, were used to estimate base flow in each stream segment of the 1:100,000 scale National Hydrography Dataset (NHD, available online at http://nhd.usgs.gov/).
To estimate shallow ground-water recharge, a "base" recharge was estimated within each of the three regions, defined as the mean base-flow yield for all streamflow-gaging stations in the region. This mean was multiplied by the watershed area for each station as an initial estimate. A residual was then calculated by subtracting the observed base flow at each station from the area-based prediction. A second set of linear-regression models was created to predict these residuals based on the same watershed attributes described previously. The resulting regression models were then applied to estimate the residual in each section of the state (section in this context denotes surveyed 1 mi2 sections, or 1/36th of a township). The residual was then added to the initial estimated yield to arrive at an estimate of total recharge for each section.
Spatial resolution of estimates of recharge in the Upper Peninsula are limited by the density of the streamflow-gaging station network in that area. These stations did not provide a sufficient number of observations to support incorporation of land cover or surficial geology into the models. The recharge map for the Upper Peninsula is therefore less detailed than in the Lower Peninsula. In addition, the effects of surficial geology, such as the reduction in recharge and base flow associated with the low-permeability lacustrine deposits in the eastern Upper Peninsula, and land cover, are ignored in the estimates.
Selecting a method to estimate recharge is largely an exercise of weighing trade-offs and making concessions between scale and resolution. Recharge is widely variable over space and time. For example, recharge rates can range widely from the top of a small hill to the bottom of the same hill only yards away. Also, recharge in these areas is likely to be different in the middle of the winter than it is in late spring, or before and after a given precipitation event. Approaches to quantify this variability are available, but they are often resource-intensive and applicable for short-term (up to a month) or small-scale (at a specific location or within a watershed) studies. No approach to recharge estimation can capture the true spatial and temporal variability in recharge across a broad area such as the Great Lakes Basin. In general, the finer the scale that a given approach can describe spatial or temporal variability in recharge, the more limited the areal extent of the study area.
Recent advancements in technologies, such as geographic information systems (GIS), remote sensing, and personal computing, are allowing researchers to more fully utilize established approaches. To a limited extent, the allocation of new technologies and additional resources can overcome the fundamental issues of scale and resolution. It is possible that a creative combination of approaches and technologies can be used to estimate recharge in the Great Lakes Basin at a resolution previously not thought possible.
In this report, the term "basin" is used to describe the Great Lakes Basin, and the term "watershed" is used to describe the watersheds of streams tributary to the Great Lakes. The term "station" is hereafter used to describe a streamflow-gaging station unless otherwise stated. The term "gaged area" is used to describe the area tributary to a given gage or gages. The term "ungaged area" is used to describe areas that are not tributary to any stations used in this study. In general, ungaged areas in this study are watersheds represented by 8-digit hydrologic unit codes (HUCs) for the U.S. and tertiary watersheds for Canada. These watersheds are relatively large (generally larger than 700 mi2) and frequently contain one or more gaged areas within their boundaries. For example, HUC 04060102, Muskegon River, Michigan, encompasses the entire area tributary to the Muskegon River in Michigan, but not all areas in this watershed are gaged. There are six current or past stations on this river. The 8-digit HUC and tertiary watersheds were used to take advantage of the availability of digitized datasets for these watersheds. Recharge estimates could have been made at a finer scale, such as 10- or 12-digit HUC and Quaternary watersheds, but digitized datasets describing these watersheds were not available for all areas within the study area.
This report presents estimates of long-term (tens of years) average recharge to shallow aquifers (usually less than 100 ft deep) for the portions of Ontario and the eight Great Lakes States that lie within the Great Lakes Basin, the upper St. Lawrence River Basin extending downstream to the cities of Massena, New York, and Cornwall, Ontario, and the Ottawa River Basin, an area of approximately 300,000 mi2. The study area is collectively referred to as the Great Lakes Basin in this report. Fifty-nine percent of the study area is in the U.S. and 41 percent is in Canada. The model used to generate base-flow/recharge estimates described in this report was calibrated using long-term daily streamflow records from 959 gaged watersheds within the Great Lakes Basin.
Alternate approaches are also presented that have been used to estimate recharge in parts of the Great Lakes Basin. Results are presented as single recharge values for 8-digit HUC watersheds (U.S.) and tertiary (Canada) watersheds in the Great Lakes, the upper St. Lawrence River, and the Ottawa River Basins, including parts of Ontario, Canada, and the States of Illinois, Indiana, Michigan, Minnesota, New York, Ohio, Pennsylvania, and Wisconsin (fig. 1). These recharge estimates refer to long-term averages, rather than temporally varying estimates of recharge. Recharge estimates are based on base-flow estimates for streams tributary to the Great Lakes (Neff and others, 2005). The approach used to estimate shallow ground-water recharge does not include evapotranspiration from the unsaturated zone as recharge or identify water that is lost to deeper ground-water flow systems that do not discharge to local streams.
Recharge estimates over limited portions of the Great Lakes Basin, but at a smaller spatial resolution than is presented for the whole study area, are featured in three "text boxes" in the report. These estimates were derived from other studies and are presented to demonstrate the potential for estimating shallow ground-water recharge at finer resolutions than are presented in the main text.
The climate of the Great Lakes Basin varies widely seasonally and from a generally northwest to southeast direction. Mean daily air temperature in January ranges from approximately 28°F in Indiana and Ohio to -4°F in the northern reaches of the basin near Lake Nipigon. Mean daily air temperature for July ranges from over 77°F in southern Michigan, Ohio, Indiana and Illinois to under 63°F in the areas north and east of Lake Superior (Government of Canada and U.S. Environmental Protection Agency, 1995, p. 8). Air temperature over the lakes and in nearshore areas is strongly affected by lake-water temperature. Precipitation also varies considerably within the study area. Mean annual precipitation ranges from less than 27 in. west of Lake Superior to more than 47 in. east of Lake Ontario (Government of Canada and U.S. Environmental Protection Agency, 1995, p. 8). Mean annual snowfall is more variable than rainfall because of the average temperature differences from north to south across the basin and because of lake-effect snow. Areas receiving substantial snowfall generally are located immediately to the south and east of each lake (Eichenlaub, 1979).
Surficial geologic material in the study area includes unconsolidated glacial deposits and bedrock outcrops (fig 1). Bedrock, predominantly of Precambrian and Paleozoic ages, crops out in much of the northern Canadian and northwestern U.S. portions of the Great Lakes Basin. The bedrock outcrops cover 5.1 and 30.8 percent of the study area in the U.S and Canada, respectively, and are likely to have varying capacities to recharge ground water. Unconsolidated materials can be generally classified as coarse sediment, fine sediment, till, and organic sediment. Coarse and fine sediments cover 27.4 and 7.6 percent of the study area, respectively. Till covers 55.6 percent and 35.6 percent of the U.S. and Canadian portions of the study area, respectively. Organic sediments are minimal in extent and primarily are present in northern Canadian watersheds. Only 0.9 and 1.8 percent of the study area in the U.S. and Canada contain organic sediment, respectively. Lakes and wetlands cover 12.4 and 7.6 percent of the U.S. and Canadian portions of the basin, respectively, and are not assigned a particular classification in this report. The types of surficial geologic materials present are thought to be a dominant factor in controlling recharge. Additional information on the geology of the Great Lakes region is given in Dorr and Eschman (1970).
Sources of additional information (including hydrologic and water-quality data) on the Great Lakes Basin include Coordinating Committee on Great Lakes Basic Hydraulic and Hydrologic Data (1977), Eichenlaub (1979), Government of Canada and U.S. Environmental Protection Agency (1995), Great Lakes Commission (2003), Great Lakes Regional Assessment Group (2000), Manninen and Gauthier (1999), the HYDAT CD-ROM (Environment Canada, 2002), and annual data reports published by USGS for each State.
The approach described in Neff and others (2005) to estimate base flow to the Great Lakes is summarized in the following subsections. Selected base-flow estimates reported in Neff and others (2005) are used to estimate shallow ground-water recharge throughout the basin. The underlying assumptions of the base flow to recharge conversion are described below.
Base-flow estimates used in this study were obtained from reports describing base flow throughout the Great Lakes Basin (Neff and others, 2005). Hydrograph separation was performed using the PART computer program (Rutledge, 1998) on length-of-record streamflow data from 959 stations in the study area to estimate base-flow index (BFI), defined here as the ratio of base flow to total streamflow. Of these 959 stations, 441 were sited in Ontario and 518 were in the Great Lakes States. A 5-tier surficial-geology classification was designed to classify the relative coarseness of surficial material (bedrock, coarse-textured sediment, fine-textured sediment, till, organic sediment). This classification was applied to available surficial-geology datasets (fig. 1) and the relative abundance of each surficial geologic material was calculated for each gaged watershed, HUC watershed, and tertiary watershed. The empirical relation between each surficial geologic material and BFI in each gaged watershed was determined by stepwise regression and used to assign a value of BFI to each surficial geologic material. To prevent surface-water features from inflating base-flow estimates, the effect of surface water on gaged-area BFI results was accounted for using an attenuation function in this calculation. Specifically, this accounting was done by comparing estimated and calculated BFI values and minimizing the error function (E) with respect to xg,j and xw using a nonlinear optimization algorithm, as follows:
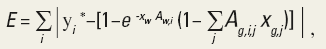 (1)
(1)
where:
yi* are the values of BFI calculated using the hydrograph-separation information,
e-Xw Aw,i is the surface-water attenuation function, where xw is greater than or equal to 0 and is a parameter that regulates the attenuation and Aw,i is the proportion of surface-water features within the watershed, expressed as a decimal between 0 and 1,
Ag,i,j is the proportion of geologic class j within watershed i, expressed as a decimal between 0 and 1, and
xg,j is the value of BFI for geologic class j. Values of xg,j are summarized in table 1.
| Surficial-Geologic Material | xg,j |
|---|---|
| Bedrock | 0.78 |
| Coarse-textured sediments | .89 |
| Fine-textured sediments | .25 |
| Till | .52 |
| Organic sediments | .09 |
The BFI for each HUC and tertiary watershed was then based on the coefficient assigned to each surficial geologic material and the relative distribution of each type within the watershed. The mathematical statement of the model is
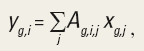 (2)
(2) where:
yg,j is the value of BFI for watershed i that results because of geological factors,
Ag,i,j is proportion of geology class j within watershed i, expressed as a decimal between 0 and 1, and
xg,j represents ground-water discharge to the stream and is the value of BFI assigned to geology class j.
The mathematical form of the model is given in equation 3 and an example of the BFI computation is shown in equation 4 for the HUC watershed 04060102, Muskegon River, Michigan. The coefficients in equation 4 are the proportions of each respective surficial geologic material occurring within this watershed.
(Bedrock*0.78) + (Coarse *0.89) + (Fine*0.25) + (Till*0.52) + (Organic*0.09). (3)
(0.00*0.78) + (0.54 *0.89) + (0.00*0.25) + (0.45*0.52) + (0.00*0.09) = 0.71. (4)
In this example, BFI is estimated to be 0.71. This estimate is meant to approximate the proportion of streamflow originating from ground-water discharge and to eliminate the effect of surface-water features that appear to be base flow on hydrographs (fig. 2). For comparison, using PART and the streamflow record on the most downstream station on the Muskegon River retained for model development (04122000), the BFI was estimated to be 0.75.
To calculate base flow (volume of flow per unit time) from BFI (the ratio of base flow to total streamflow), it was necessary to estimate long-term average streamflow in each HUC and tertiary watershed. To do this estimation, a value of streamflow was assigned to each gaged watershed in terms of depth of watershed per year of recharge, termed a "flow ratio." Flow ratios are derived using a unit conversion of observed average streamflow from the commonly used cubic feet per second (ft3/s) to [feet (ft) times watershed area in square feet (ft2)]/year. The gaged watersheds were then intersected with 8-digit HUC and tertiary watersheds. A weight (w) was determined for each gaged watershed that fell within a given HUC or tertiary watershed and given as
w = Intersected area / (Ungaged area + Gaged area – Intersected area). (5)
The weights were then applied to the flow ratios for each of the gaged watersheds (i) within a given HUC or tertiary watershed to determine the flow ratio for each respective HUC or tertiary watershed and given as
FHUC = ∑ (w(i) * F(i)) / ∑ w(i), (6)
where FHUC is the flow ratio of each HUC and tertiary watershed, w(i) is the weight of station i, and F(i) is the flow ratio of station i. Total streamflow was determined by multiplying the calculated flow ratio by the area of the HUC or tertiary watershed. Base flow was then determined by multiplying model-simulated BFI by the estimated total streamflow for each HUC or tertiary watershed. As an example, long-term average runoff for HUC 04060102 is 2,182 ft3/s. When this value is multiplied by the long-term average BFI for this HUC watershed (calculated above as 0.71), the result is 1,549 ft3/s of estimated long-term average base flow.
Recharge was estimated from base-flow estimates by summing the quantity of base flow in one year and dividing by the area of each respective watershed. The resulting recharge dataset is given in inches of recharge per year. For example, the long-term average base flow of HUC watershed 04060102 (calculated above as 1,549 ft3/s), was converted from ft3/s to ft3/year (48,856,202,000 ft3/year) and divided by the surface area of the HUC watershed (76,334,100,466 ft2) to calculate recharge as a depth of watershed in feet (0.64 ft/year). Multiplying feet of recharge by 12 yields inches of recharge for HUC watershed 04060102 (7.7 in/year). The above calculations used values that were rounded and the result differs slightly from the result listed in table 2 (back of report).
In summary, the steps taken to generate recharge estimates in each HUC and tertiary watershed were:
1. Estimated BFI in gaged watersheds from length-of-record streamflow data at each station using the hydrograph-separation program PART.
2. Related BFI to surficial geologic materials and surface-water features in gaged areas using a regression model.
3. Used the regression model to estimate BFI due to ground-water discharge in each HUC and tertiary watershed.
4. Estimated total streamflow in each HUC and tertiary watershed by interpolating the ratio of long-term average streamflow per unit area observed at each station within each HUC or tertiary watershed.
5. Multiplied long-term average runoff by long-term average BFI to estimate long-term average base flow.
6. Converted long-term average base flow to recharge by summing the quantity of base flow in one year within a given watershed and dividing by the area of the respective watershed. The result is a depth of recharge per year within the watershed.
Trends in streamflow and base flow in some Great Lakes Basin streamflow records (Gebert and Krug, 1996) affect uncertainty in recharge estimates. Base-flow and BFI values calculated using the entire period of streamflow record and a 30-year subset of the streamflow record (1970-99) for five stations in Wisconsin are compared in table 3. Base-flow/recharge values for these five stations all indicate an increase in the 1970-99 dataset from the length-of-record dataset. The magnitude of the change in base flow is variable, but was as high as 39 percent at one station. Changes to agricultural practices are thought to be the primary cause for these changes (Gebert and Krug, 1996), although the exact relation among climate, land use, and recharge is presently (2005) unknown.
[ft3/s, cubic feet per second; data provided by W. Gebert, U.S. Geological Survey]
| Streamflow-gaging station name and identifier number | Base flow (ft3/s) | Base-flow index (BFI) | ||||||
|---|---|---|---|---|---|---|---|---|
| All years of record | 1970-99 | Trend in mean base flow (percent) | All years of record | 1970- 99 | Trend in mean BFI (percent) | |||
| Bois Brule River at Brule, Wisconsin (04025500) | 149 | 152 | 2 | 0.869 | 0.873 | 0.5 | ||
| Peshtigo River at Peshtigo, Wisconsin (04069500) | 566 | 604 | 7 | 0.608 | 0.635 | 4.4 | ||
| Fox River at Berlin, Wisconsin (04073500) | 941 | 1,127 | 20 | 0.822 | 0.872 | 6.1 | ||
| Sheboygan River at Sheboygan, Wisconsin (04086000) | 115 | 146 | 27 | 0.474 | 0.511 | 7.8 | ||
| Milwaukee River at Milwaukee, Wisconsin (04087000) | 209 | 291 | 39 | 0.481 | 0.55 | 14.4 | ||
The effect of trends in the streamflow record on the regression model used to estimate base flow and recharge can be mitigated multiple ways. The most direct approach is to truncate all streamflow data used to estimate recharge to a specific period of time such as a 30-year normalized period. This approach, however, eliminates many potentially useful streamflow records from inclusion in the dataset. Without these records, it would be difficult to estimate recharge in many parts of the Great Lakes Basin, particularly northern Ontario.
A second approach to mitigate the effect of trends in the streamflow record on the regression model used to estimate base flow and recharge is to use BFI rather than base flow to develop the regression model. One important property of BFI is that BFI values are relatively stable over time as compared to base flow (Neff and others, 2005). In other words, the partitioning of water between surface runoff and recharge is primarily dependent on watershed characteristics and this partitioning is relatively stable. In contrast, total base flow is sensitive to changes in total runoff that are affected largely by climate variability. The trend in BFI is attenuated compared to the trend in total base flow. This result is illustrated by comparing 1970-99 and length-of-record averages of BFI for the same five stations described above (table 3). In all cases, the shift in BFI was roughly one-half to one-third the magnitude of the shift in base flow.
A third approach to diminish the effect of trends in the streamflow record on the regression model used to determine base flow and recharge is to calibrate the regression model to streamflow records from nearly 1,000 stations located throughout the Great Lakes Basin. This third approach diminishes the relative importance of isolated cases of trending streamflow records.
To evaluate the effect of trends in the streamflow record on length-of-record streamflow data, 1971-2000 average streamflow was calculated for 555 stations in Ontario and 1,936 stations in the eight Great Lakes States and compared to length-of-record (extending for various lengths of time beyond 1971-2000) total streamflow reported in Neff and others (2005). Results show no systematic difference in average streamflow calculated for the two periods (fig. 3). Although trends in Great Lakes Basin streamflow may be present, the results of this study show that no widespread trend is evident when comparing year 2000 30-year normalized streamflow to length-of-record total streamflow for these particular streamflow records. This observation may indicate that trends occur in isolated areas of the basin or that they may be present on time scales too short to be captured in 30-year normalized average streamflow records or that they tend to average out when considering nearly a thousand 30-year and length-of-record streamflow records. No further attempt was made to index base-flow or recharge estimates to a specific time period.
The importance of spatial variability in recharge. As discussed previously, many methods for estimating recharge are not tenable when operating at a scale as large as the Great Lakes Basin. However, it is conceivable that average areal values calculated using large areas such as the 8-digit HUC of Neff and others (2005) miss smaller scale variability within a given watershed. An investigation of spatial variability at smaller watershed scales was performed in the Lake Michigan Basin in the State of Wisconsin (Gebert and others, in press).
Base-flow derived recharge values from sites within larger watersheds were calculated with the methods of Gebert and others (in press)—an approach not practical at the scale of the Great Lakes Basin. Whereas both the recharge estimation methods of Neff and others (2005) and Gebert and others (in press) utilize base-flow separation and watershed area, the approach of Gebert and others (in press) obtains estimates of base-flow information from miscellaneous discharge measurements in addition to streamflow-gaging stations, which allows direct estimation of recharge from small basins without stations. A comparison of results from the two methods show a large range of recharge rates within the average value of large-scale 8-digit HUC watershed value (see figure below). Considerable variability of recharge is present within the 8-digit HUC watershed scale, reflected in the result attained using the approach of Gebert and others (in press). These results underscore the spatial variability in recharge even when using similar approaches. Moreover, the range in recharge can be expected to increase as the spatial scale becomes smaller, or different techniques are used.
The importance of temporal variability in recharge. As discussed in the section titled Effect of Trends in Streamflow on Recharge Estimates, trends in streamflow and base flow can affect uncertainty in recharge estimates determined directly from base-flow estimates. Both changes in climate and land use can affect how precipitation falling on the land surface is distributed between surface-water stormflow and recharge-derived base flow. Thus, the period investigated can affect the recharge rate calculated. For example, at five stations in Wisconsin, values calculated using the entire period of record were compared to a recent 30-year subset of the entire period of record (1970-99; table B2). Although base flow was calculated using the same technique, base flow and the resulting recharge values differed by as much as 39 percent. As discussed by Gebert and Krug (1996), changes to agricultural practices are thought to be the primary driver for these changes, although the exact relation among climate, land use, and recharge are still active areas of research. Regardless of the exact driver, the results in table B2 underscore the need to match the time period studied to the time period that estimates are being made.
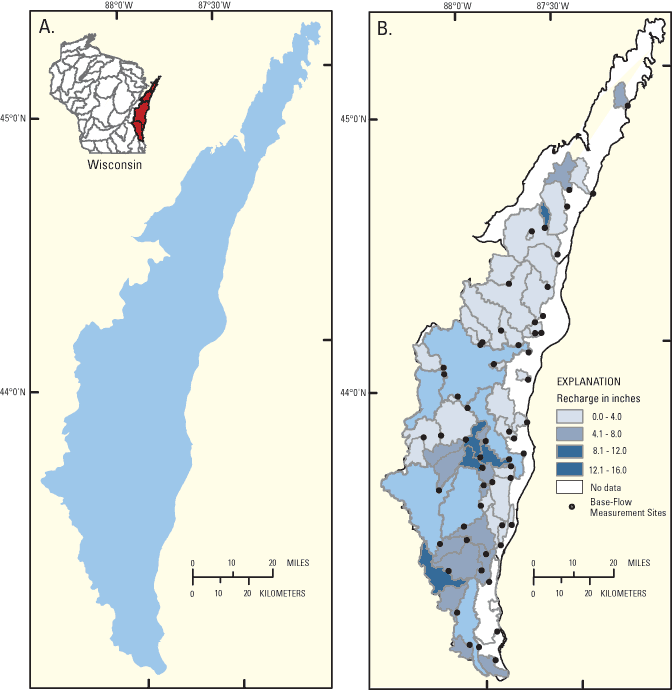
An approach described as the regional regression recharge (RRR) model was developed to estimate ground-water recharge in Minnesota (Geoff Delin, written commun., 2005; figure B3). In this model, watershed scale estimates of recharge, precipitation, evapotranspiration, and average specific yield are used to predict recharge. Recharge estimates represent long-term average values and are mapped on the scale of STATSGO (1994) soil associations. The RRR model was calibrated using estimates of recharge for 38 gaged watersheds using the program RORA (Rutledge, 1998, 2000). RORA uses streamflow records as an input and estimates recharge. Results are applied to the surrounding surface-water watershed for each streamflow-gaging station and the assumption is made that the shallow ground-water watershed is coincident with the surface-water watershed. It is also assumed that recharge is reflected in the streamflow record and is not affected by evapotranspiration from the water table, water withdrawals, standing surface water (wetlands) within the watershed, or dam regulation.
Estimates of recharge are mapped at the STATSGO mapping unit scale (about 50 mi2), which provides relatively fine spatial resolution to long-term average recharge estimates made using the RRR model. Recharge estimates based on the RRR model are greater than the estimates shown for Minnesota in figure 4 for at least two reasons. First, the theory behind the RORA (Rutledge, 2000) and PART (Rutledge, 1998) methods of hydrograph separation differs (T.C. Winter, U.S. Geological Survey, oral commun., 2004), which could explain part of this difference in estimates. Also, estimates presented in figure 4 discount the effect of surface water on hydrographs that would otherwise lead to an overestimation of base flow by hydrograph separation. Temporal resolution of the RRR model is limited to averages of a decade or longer.
Recharge rates estimated with the RRR model compare well with rates estimated from seven previous studies in Minnesota where recharge was estimated with the water-table-fluctuation approach (Ruhl and others, 2002; Lindgren, 1996; Stark and others, 1991). Mean recharge estimated with the RRR model was 0.25 in/yr less than mean recharge calculated with the water-table-fluctuation approach used in the previous studies, an absolute difference of 31 percent. Ground-water flow models were constructed in all but one of those studies and the mean absolute difference between the model-calibrated recharge and recharge determined with the water-table-fluctuation approach was 39 percent. These differences indicate some of the inherent difficulties in estimating shallow ground-water recharge.
Estimates of ground-water recharge are presented for 8-digit HUC (U.S.) and tertiary (Canada) watersheds. Recharge estimates are presented in table 2 (back of the report) and figure 4.
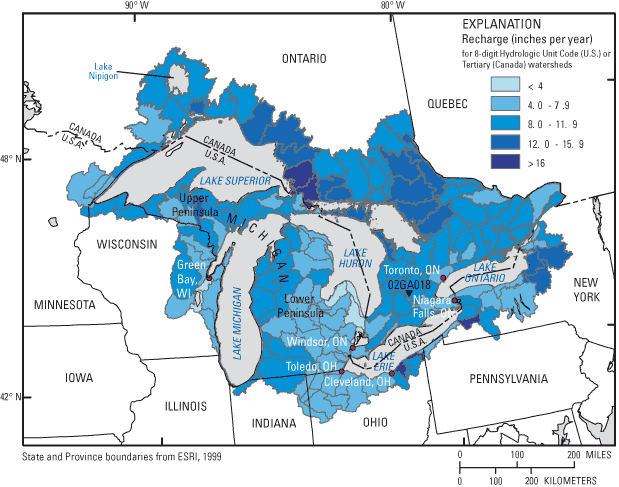
The lowest recharge rates identified in this study (1.6-4.0 in) occurred in the eastern lower peninsula of Michigan; southwest of Green Bay, Wisconsin; near the southwestern shore of Lake Erie near Toledo, Ohio; and in portions of southeastern Ontario near Windsor, Niagara, and west of Toronto. In contrast, the highest recharge rates occurred in the snow-shadow areas east and southeast of the Great Lakes.
Recharge rates provided in previous studies largely fall within the range of values reported in the current study. Prior estimates of average annual recharge or base flow in Ontario are few, but values listed by Singer and others (1997) for selected stations in southern Ontario are comparable to values determined using the approach described here. Recharge rates published for Ohio (Dumouchelle and Schiefer, 2002) are spatially limited to gaged areas, but agree relatively well in areas of overlap. For example, low recharge rates (approximately 2.5 – 5 in/year) were reported for areas south of the southwestern shoreline of Lake Erie near Toledo, Ohio. Likewise, high recharge rates (greater than 8 in/year) were reported near the south-central coast of Lake Erie, east of Cleveland, Ohio. Recharge rates determined during this study are higher for this area than previously published results (Dumouchelle and Schiefer, 2002), perhaps because recharge estimates determined for the current study were spatially situated in areas more likely to receive high amounts of lake-effect snow. Recharge estimates for northeastern Ohio agree almost exactly between the two studies (approximately 4 in/year).
Comparison of results in the Lower Peninsula of Michigan with the previous study of Holtschlag (1996) is difficult because recharge results in the current study are reported for 8-digit HUC watersheds, whereas results in Holtschlag (1996) are presented in a gridded dataset. This difference causes recharge estimates in the previous study to range considerably on a small spatial scale. Because digital datasets were not available, a robust quantitative comparison was not possible. However, the results of Holtschlag (1996) were visually estimated for each HUC and compared to the results of the current study. For example, low recharge rates were reported in both studies for the eastern and southeastern Lower Peninsula of Michigan. Recharge rates for the north-central portion of the peninsula averaged between 7 and 10 in/year in both studies, and in the snow-shadow area on the western side of the central Lower Peninsula, recharge rates ranged between 10 and 13 in/year for both studies.
Wolock (2003) used BFI to estimate BFI and ground-water recharge rates for the U.S. Wolock (2003) used a method similar to the UKIH method (developed at the United Kingdom's Institute of Hydrology; Piggott and others, 2005) to produce a gridded recharge map. To compare recharge published in Wolock (2003) to the current study, recharge was recalculated using UKIH calibrated base-flow model results from Neff and others (2005). Wolock's (2003) gridded dataset was then averaged within each 8-digit HUC polygon and a single value of recharge was compared to each value of UKIH (fig. 5).
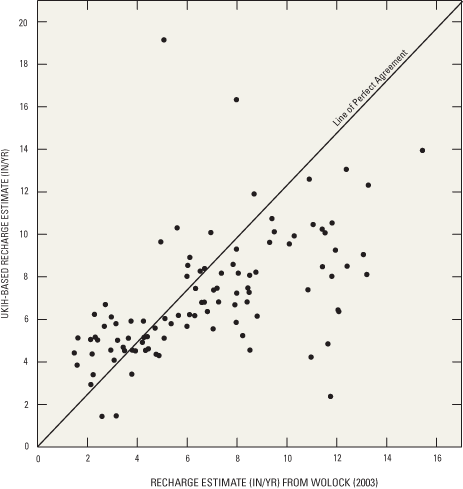
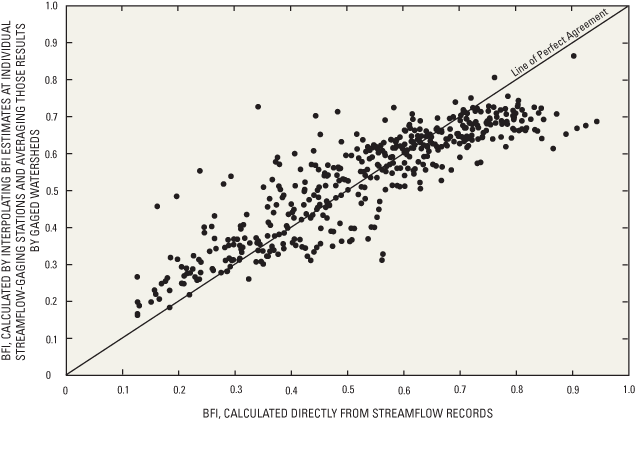
The recharge estimates shown in figure 5 indicate considerable variability in the relation of estimates. This variability likely results from three sources. First, results presented in Wolock (2003) were regionalized by interpolating estimates of BFI at individual streamflow-gaging stations. In contrast, the methods in this study regionalized BFI based on surficial geologic material. Surficial geology has been shown to be a measure of factors that control BFI (Piggott and others, 2002) and is known to be highly variable over short distances (less than 1 mi), a characteristic that interpolation may not easily capture. Second, variability between the Wolock dataset and the results of the current study may result from how the two methods accounted for the effect of lakes and wetlands on base flow. Base-flow data used in Wolock (2003) were taken directly from hydrograph-separation results, which are often affected by lakes and wetlands. Analyses in Neff and others (2005) that were used in the current study specifically addressed this issue and generated estimates of BFI and base flow designed to eliminate the effects of lakes and wetlands on the streamflow record. Third, the mathematical operations of regionalizing BFI by interpolating station-based data and then averaging those results by gaged watersheds (as was done with the Wolock (2003) dataset in the above comparison) will introduce considerable noise to the dataset. To demonstrate this result, station based BFI data presented in Neff and others (2005) were treated similarly and evaluated (fig. 6). The initial station-based values of BFI (for example, x-y points with values of BFI determined from UKIH hydrograph separation) were interpolated using a standard inverse-distance weighted approach. The gridded values were then averaged over the gaged watersheds and compared with the original BFI values for each gaged watershed. Ideally, the two sets of results would match, but the interpolation process seems to generate considerable scatter (fig. 6). Considering these sources of variability and uncertainty, recharge results determined during this study are difficult to compare to those presented by Wolock (2003).
The use of base-flow results to develop recharge estimates is based on several assumptions that introduce uncertainty to estimates and limit their applicability. Scanlon and others (2002) and Halford and Mayer (1999) describe some of the limiting assumptions related to the use of hydrograph-separation techniques to estimate recharge, including the effects of pumping, evapotranspiration, and underflow.
The approach of defining base flow as equivalent to recharge assumes that all base flow in a given stream is from recharge and is not affected by a change in aquifer storage. To account for this assumption, estimates are limited to long-term averages based on another assumption that on a long enough time scale, the significance of change in aquifer storage diminishes. Use of this approach cannot properly describe the seasonal and annual variability of recharge. Another assumption inherent in the base-flow/recharge equivalence is that base flow in a stream is equal to the sum of recharge in the contributing surface-water watershed minus evapotranspiration. Uncertainties result from instances where the ground-water watershed is not coincident with the surface-water watershed or where the local ground-water-flow system interacts with deep aquifers that do not interact exclusively with the nearest stream. Limiting recharge estimates to large spatial (8-digit HUC and tertiary watersheds) and long temporal scales (length of record averages) mitigates these concerns, but prevents an accurate description of the small-scale variability of recharge.
Uncertainty in base-flow estimates arises from the effect of upstream surface-water features (for example, wetlands), dam operation, effluent from wastewater-treatment plants, and water withdrawals on streamflow records. To mitigate these factors, equation 1 was designed and used to attenuate base-flow estimates proportionally to the abundance of surface-water features within the watershed. In other words, surface-water features such as wetlands tend to retain water during peak streamflows and slowly drain accumulated water during times of reduced streamflow. The effect of this retention and draining on streamflow hydrographs is to cause an apparent increase in base flow. However, this increased base flow does not result from ground-water seepage into the stream. Equation 1 was used to adjust base-flow estimates in this study according to the proportion of surface water features within the watershed in question. This additional step removes or reduces the effect of surface-water features on the results. However, some uncertainty arises from the process of extrapolating base-flow estimates from gaged areas to ungaged areas.
The largest source of uncertainty associated with base-flow results arises from the selection of one hydrograph-separation method over another. Estimates of base flow using hydrograph separation are sensitive to the method of hydrograph separation used. Neff and others (2005) presented estimates of long-term average base flow at 3,936 stations in the 8 Great Lakes States and Ontario using 6 different methods of hydrograph separation. The hydrograph-separation methods used include the fixed-interval, sliding-interval, and local minimum HYSEP methods developed by Pettyjohn and Henning (1979) as implemented by Sloto and Crouse (1996), PART (Rutledge, 1998), BFLOW (Arnold and Allen, 1999), and UKIH (Piggott and others, 2005). Whereas the patterns of base flow observed with each hydrograph-separation method were similar, the average range in the magnitude of BFI estimates for each station was 0.24 BFI, an average of 41 percent, depending on the method used. In other words, all of these methods identified the same stations as having relatively high or low BFI, but the methods showed substantial disagreement with respect to how high and how low the BFI was at specific stations. For simplicity, only the estimates of base flow and recharge derived using the PART method of hydrograph separation was used here. The PART method was chosen because the results from PART compared reasonably well with manual base-flow-recession estimation in the eastern United States (Rutledge, 1998). The variability in base-flow estimates calculated using different hydrograph-separation methods causes significant uncertainty in the magnitude of recharge estimates, but relatively little uncertainty in the relative distribution of recharge.
Recharge estimates presented in this report are generalized spatially and temporally. Spatially, recharge estimates are made for relatively large 8-digit HUC and tertiary watersheds (typically about 750 mi2). Temporally, recharge results reflect long-term (years to tens of years) averages, and do not describe seasonal or interannual variation in recharge. Nevertheless, these results provide a point of reference for future studies.
The common approach of relating landscape attributes to base flow by way of regression and extrapolating to broad areas does not address important issues of temporal variability in recharge over short time scales (days and weeks). Additionally, estimates made using this approach are only as good as the hydrograph-separation results used, and recharge estimates can vary widely depending on which hydrograph-separation method was used to estimate base flow (Neff and others, 2005). In addition, some factors, such as the presence of wetlands within a watershed, can lead to overestimation of base flow by hydrograph separation. It is unclear at what spatial and temporal scales this approach is valid.
Other approaches are available to estimate recharge. No one approach is ideal for making detailed estimates on a large spatial scale; each approach is better suited to examine recharge at particular spatial and temporal scales and particular hydrologic settings, and some approaches may not be applicable in the Great Lakes Basin. In general, the approaches that provide estimates at fine spatial and temporal scales are limited in the areal extent to which they can be applied. Consequently, using a combination of approaches may prove to be the best method for estimating shallow ground-water recharge in the Great Lakes Basin.
The estimation of recharge is important for proper management of the water resources of the Great Lakes Basin. Previous estimates of shallow ground-water recharge in parts of the Great Lakes Basin are useful, but usually do not extend basinwide and may be inaccurate for some areas. Therefore, the U.S. Geological Survey, in cooperation with the National Water Research Institute, Environment Canada, began a study in 2005 to more accurately estimate recharge in the Great Lakes Basin. This study was conducted as part of the Great Lakes Water Availability Pilot Project. The study area is approximately 300,000 mi2 and includes the portions of Ontario and the eight Great Lakes States that lie within the Great Lakes Basin, the upper St. Lawrence River Basin extending downstream to the cities of Massena, New York, and Cornwall, Ontario, and the Ottawa River Basin.
Ground-water recharge in the study area is defined in this report as precipitation in the form of rain and snow that infiltrates the land surface, moves downward through the unsaturated zone, and enters the water table. Water that is evaporated or transpired by plant roots as it percolates to the water-table surface is not counted as recharge in this study.
Shallow ground-water recharge estimates are based on base-flow estimates throughout the study area and the assumption that water that has been discharged to a stream as base flow must have originated as shallow ground-water recharge in the adjacent watershed. One problem inherent to this approach is that the base-flow estimates determined using hydrograph separation may overestimate the quantity of streamflow that results from ground-water discharge to the stream. Wetlands and other surface-water features within a watershed tend to retain water during peak streamflows and slowly drain accumulated water during times of reduced streamflow. The effect of this retention and draining on streamflow hydrographs is to cause an apparent increase in base flow. However, this increased base flow does not result from ground-water seepage into the stream. Care must be taken to consider this effect when estimating shallow-aquifer recharge using base-flow estimates.
Another difficulty inherent to this study is that many different methods are available to estimate base flow from streamflow records and the accuracy of different methods is not well understood. For example, this study estimated base flow at streamflow gages using the PART hydrograph-separation method to surficial geology. Other hydrograph-separation methods are available and yield results that vary in a similar pattern, but are different in magnitude. Further, this study related surficial geologic material to hydrograph separation results to regionalize base flow. Other variables could have been used such as slope, land use, vegetation type, latitude, and others.
Results presented in this report represent the first unified estimate of recharge over the entire Great Lakes, upper St. Lawrence, and Ottawa River Basins. The approach used in this study was consistent throughout the study area and allows a reasonable comparison of recharge rates in disparate areas of the Great Lakes, upper St. Lawrence, and Ottawa River Basins. Results are limited to long-term averages, broad spatial scales of 8-digit hydrologic unit code (HUC, U.S.) and tertiary (Canada) watersheds, and do not capture deep aquifer recharge (>100 ft). Uncertainty in the recharge estimates made herein results from various assumptions inherent to the approach used.
Key findings presented in this report include:
Recharge estimates presented here are only one component of the hydrologic budget needed to better describe water availability within the Great Lakes Basin; these recharge estimates are not meant to define safe yield of shallow aquifers underlying the basin. Additional research to characterize deep aquifer recharge and the effect of human activity on the hydrologic system would be needed before sustainability issues could be addressed. Users of these results are cautioned not to assume that natural recharge is equivalent to the basin sustainable yield. This concept has sometimes led to the incorrect assumption that pumping less than the recharge rate means that water levels and ground-water storage will not decline.
The authors appreciate the important contributions of the Ontario Ministry of Natural Resources, the Ontario Ministry of the Environment, and Environment Canada's Meteorological Service of Canada in providing data and information during the course of this study. Additionally, this report benefited from many important individual contributions made by the following U.S. Geological Survey employees: W.M. Alley, who authored the foreword, S.S. Aichele and D.L. Lorenz, who authored the text boxes on ground-water recharge research in Michigan and Minnesota, respectively, and W.A. Gebert, J.L. Kennedy, and R.J. Hunt, who authored the text box describing recharge rates in HUC watershed 04030102, Door-Kewaunee, Wisconsin. This report was enhanced by diligent and thorough technical reviews by D.W. Risser and G.E. Groschen, and editorial review by Angel Martin.
Alley, W.M., and Leake, S.A., 2004, The journey from safe yield to sustainability: Ground Water, v. 42, no. 1, p.12–16.
Alley, W.M., Reilly, T.E., and Franke, O.L., 1999, Sustainability of ground-water resources: U.S. Geological Survey Circular 1186, 79 p. Available on the World Wide Web at URLhttps://pubs.water.usgs.gov/circ1186.
Appleby, V.C., 1970, Recession and the base flow problem: Water Resources Research, v. 6, no. 5, p. 1398–1403.
Arnold, J.G., and Allen, P.M., 1999, Automated methods for estimating baseflow and groundwater recharge from stream flow records: Journal of American Water Resources Association, v. 35 p. 411–424.
Arnold, J.G., Muttiah, R.S., Srinivasan, R., and Allen, P.M., 2000, Regional estimation of baseflow and groundwater recharge in the Upper Mississippi river basin: Journal of Hydrology, v. 227, no. 1–4, p. 21–40.
Bredehoeft, J.D., 1997, Safe yield and the water budget myth: Ground Water, v. 35, no. 6, p. 929.
Cherkauer, D.S., 2001, Distribution of ground-water recharge in southeastern Wisconsin: Open-File Report to Source Water Protection Program, Wisconsin Department of Natural Resources, 31 p.
Choi, J., and Harvey, J.W., 2000, Quantifying time-varying groundwater discharge and recharge in wetlands—A comparison of methods in the Florida Everglades: Wetlands, v. 20, no. 3, p. 500–511.
Cook P.G., and Walker G.R., 1995, An evaluation of the use of 3H and 36Cl to estimate groundwater recharge in arid and semi-arid environments, in Proceedings of IAEA International Symposium on Isotopes in Water Resources Management, Vienna, Austria: p. 20–24.
Coordinating Committee on Great Lakes Basic Hydraulic and Hydrologic Data, 1977, Coordinated Great Lakes physical data: Detroit, Mich., and Burlington, Ont., 12 p.
Dorr, J.A., and Eschman, D.F., 1970, Geology of Michigan: Ann Arbor, Mich., University of Michigan Press, 488 p.
Dumouchelle, D.H., and Schiefer, M.C., 2002, Use of streamflow records and basin characteristics to estimate ground-water recharge rates in Ohio: Ohio Department of Natural Resources, Division of Water, Bulletin 46, 45 p.
Eichenlaub, V.L., 1979, Weather and climate of the Great Lakes region: Notre Dame, Ind., University of Notre Dame Press, 335 p.
ESRI, 1999, ArcView GIS 3.2, Environmental Systems Research Institute, Inc., Redlands, California. http://www.esri.com/data/.
Gebert, W.A., Lange, M.J., Considine, E.J.,and Kennedy, J.L., in press, Use of streamflow data to estimate baseflow/ground-water recharge for Wisconsin: Journal of the American Water Resources Association.
Gebert, W.A., and Krug,W.R., 1996, Streamflow trends in Wisconsin's driftless area: Water Resources Bulletin, v. 32, no. 4, p. 733–744.
Government of Canada and U.S. Environmental Protection Agency, 1995, The Great Lakes—An environmental atlas and resource book (3rd ed.): Toronto, Ont., and Chicago, Ill., 46 p.
Great Lakes Commission, 2003, Toward a water resources management decision support system for the Great Lakes–St. Lawrence River Basin: Great Lakes Commission for the Great Lakes States and Provinces, 142 p.
Great Lakes Regional Assessment Group, 2000, Preparing for a changing climate; The potential consequences of climate variability and change—Great Lakes overview (edited by P.J. Sousounis and J.M. Bisanz): Ann Arbor, Mich., University of Michigan, 106 p.
Halford, K.J., and Mayer, G.C., 1999, Problems associated with estimating ground water discharge and recharge from stream-discharge records: Ground Water, v. 38, p. 331–342.
Healy, R.W., and Cook, P.G., 2002, Using groundwater levels to estimate recharge: Hydrogeology Journal, v. 10, no. 1, p. 91–109.
Hewlett, J.D., and Hibbert, A.R., 1967, Factors affecting the response of small watersheds to precipitation in humid areas, in W.E. Sopper and H.W. Lull, eds., Forest hydrology: New York, Pergamon Press, p. 275–290.
Holtschlag, D.J., 1996, A generalized estimate of ground-water recharge rates in the lower peninsula of Michigan: U.S. Geological Survey Water-Supply Paper 2437, 37 p.
Environment Canada, 2002, HYDAT CD Version 2.01: Ottawa, Ontario.
Lerner, D.N., Issar, A., and Simmers, I., 1990, Groundwater recharge—A guide to understanding and estimating natural recharge: International Contributions to Hydrogeology, v. 8. 147 p.
Lindgren, R.J., 1996, Availability and quality of water from drift aquifers in Marshall, Pennington, Polk, and Red Lake Counties, northwestern Minnesota: U.S. Geological Survey Water-Resources Investigations Report 95–4201, 144 p.
Manninen, C., and Gauthier, R., 1999, Living with the lakes—Understanding and adapting to Great Lakes water level changes: Ann Arbor, Mich., and Detroit, Mich., Great Lakes Commission and U.S. Army Corps of Engineers, 39 p.
Michigan Department of Environmental Quality, 2005, Public Act 148—Groundwater Inventory and Map Project, Executive Summary: State of Michigan, August 18, 2005, 31 p., http://gwmap.rsgis.msu.edu/.
Michigan Geographic Framework, 2003, Statewide County Layer, http://www.mcgi.state.mi.us/mgdl/framework/statewide/metadata/Counties%20MI%20DDv3b.pdf
Ministry of Natural Resources, 2002, Land Information Ontario, Watersheds, Tertiary: Queen's Printer for Ontario.
Neff, B.P., Day, S.M., Piggott, A.R., and Fuller, L.M., Base flow in the Great Lakes Basin: U.S. Geological Survey Scientific Investigations Report 2005–5217, 23 p.
Ontario Geological Survey, 2000, Quaternary geology—Seamless coverage of the Province of Ontario: ERLIS Data Set 14.
Pettyjohn, W.A., and Henning, Roger, 1979, Preliminary estimate of ground-water recharge rates, related streamflow and water quality in Ohio: Columbus, Ohio, Ohio State University Water Resources Center, Project Completion Report 552, 323 p.
Piggott, A., Brown, D., and Moin, S., 2002, Calculating a groundwater legend for existing geological mapping data, in Stolle, D., Piggott, A.R., and Crowder, J.J., eds., Ground and Water—Theory to Practice: Proceedings of the 55th Canadian Geotechnical and 3rd Joint IAH-CNC and CGS Groundwater Specialty Conferences, October 20–23, 2002, Southern Ontario Section of the Canadian Geotechnical Society, Niagara Falls, Ontario, p. 863–871.
Piggott, A.R., Moin, S., and Southam, C., 2005, A revised approach to the UKIH method for the calculation of baseflow: Hydrological Sciences Journal, v. 50, no. 5, p. 911–920.
Prych, E.A., 1995, Using chloride and chlorine-36 as soil-water tracers to estimate deep percolation at selected locations on the U.S. Department of Energy Hanford site, Washington: U.S. Geological Survey Open-File Report 94–514, 125 p.
Routson, R.C., and Johnson, V.G., 1990, Recharge estimates of the Hanford Site 200 Areas Plateau: Northwest Science, v. 64, no. 3, p. 150–158.
Ruhl, J.F., Kanivetsky, R., and Shmagin, B., 2002, Estimates of recharge to unconfined aquifers and leakage to confined aquifers in the seven-county metropolitan area of Minneapolis-St. Paul, Minnesota: U.S. Geological Survey Water-Resources Investigations Report 02–4092, 32 p.
Rutledge, A.T., 1998, Computer programs for describing the recession of ground-water discharge and for estimating mean ground-water recharge and discharge form streamflow data—Update: U.S. Geological Survey Water-Resources Investigations Report 98–4148, 43 p.
Rutledge, A.T., 2000, Considerations for use of the RORA program to estimate groundwater recharge from streamflow records: U.S. Geological Survey Open-File Report 00–156, 44 p.
Scanlon, B.R., Healy, R., and Cook, P.G., 2002, Choosing appropriate techniques for quantifying groundwater recharge: Hydrogeology Journal, v. 10, p. 18–39.
Singer, S.N., Cheng, C.K., and Scafe, M.G., 1997, The hydrogeology of southern Ontario: Toronto, Ont., Ministry of Environment and Energy, Hydrogeology of Ontario Series (Report 1), 80 p.
Singh, V. P., ed., 1995, Computer models of watershed hydrology: Highlands Ranch, Colo., Water Resource Publications, 1130 p.
Sloto, R.A., and Crouse, M.Y., 1996, HYSEP: A computer program for streamflow hydrograph separation and analysis: U.S. Geological Survey Water-Resources Investigations Report 96–4040, 46 p.
Soller, D.R., 1998, Map showing the thickness and character of Quaternary sediments in the glaciated United States east of the Rocky Mountains—Character of selected significant, buried Quaternary sediments: U.S. Geological Survey Digital Data Series DDS–38.
Stark, J.R., Busch, J.P., and Deters, M.H., 1991, Hydrogeology and water quality of glacial-drift aquifers in the Bemidji-Bagley area, Beltrami, Clearwater, Cass, and Hubbard Counties, Minnesota: U.S. Geological Survey Water-Resources Investigations Report 89–4136, 135 p.
STATSGO, 1994, State Soil Geographic (STATSGO) Database: U.S. Department of Agriculture, Natural Resources Conservation Service, Fort Worth, Tex. Available on the World Wide Web at URL http://www.ncgc.nrcs.usda.gov/products/datasets/statsgo/
Stonestrom, D.A., and Constantz, J., eds., 2003, Heat as a tool for studying the movement of ground water near streams: U.S. Geological Survey Circular 1260, 96 p. Available on the World Wide Web at URL https://pubs.water.usgs.gov/circ1260
Wolock, D.M., 2003, Estimated mean annual natural ground-water recharge in the conterminous United States: U.S. Geological Survey Open-File Report 03–311, digital data set. Available on World Wide Web at URL http://water.usgs.gov/lookup/getspatial?rech48grd
[Information including graphical descriptions of each HUC watershed is available at http://water.usgs.gov/GIS/huc.html. Information including graphical descriptions and metadata of each tertiary watershed is in Ministry of Natural Resources (2002).]
| Watershed Number | Watershed Name | Recharge (inches) | Watershed Number | Watershed Name | Recharge (inches) | |
|---|---|---|---|---|---|---|
| 04010101 | Baptism-Brule | 9.9 | 04060105 | Boardman-Charlevoix | 8.8 | |
| 04010102 | Beaver-Lester | 6.0 | 04060106 | Manistique | 11.2 | |
| 04010201 | St. Louis | 7.0 | 04060107 | Brevoort-Millecoquins | 7.9 | |
| 04010202 | Cloquet | 5.6 | 04070001 | St. Marys | 5.0 | |
| 04010301 | Beartrap-Nemadji | 7.7 | 04070002 | Carp-Pine | 9.4 | |
| 04010302 | Bad-Montreal | 9.0 | 04070003 | Lone Lake-Ocqueoc | 9.2 | |
| 04020101 | Black-Presque Isle | 8.9 | 04070004 | Cheboygan | 11.0 | |
| 04020102 | Ontonagon | 7.7 | 04070005 | Black | 7.4 | |
| 04020103 | Keweenaw Peninsula | 11.6 | 04070006 | Thunder Bay | 6.4 | |
| 04020104 | Sturgeon | 10.7 | 04070007 | Au Sable | 8.5 | |
| 04020105 | Dead-Kelsey | 13.2 | 04080101 | Au Gres-Rifle | 8.9 | |
| 04020201 | Betsy-Chocolay | 10.7 | 04080102 | Kawkawlin-Pine | 4.9 | |
| 04020202 | Tahquamenon | 7.0 | 04080103 | Pigeon-Wiscoggin | 3.8 | |
| 04020203 | Waiska | 8.2 | 04080104 | Birch-Willow | 3.0 | |
| 04030101 | Manitowoc-Sheboygan | 4.5 | 04080201 | Tittabawassee | 7.1 | |
| 04030102 | Door-Kewaunee | 5.5 | 04080202 | Pine | 6.2 | |
| 04030103 | Duck-Pensaukee | 4.9 | 04080203 | Shiawassee | 5.3 | |
| 04030104 | Oconto | 6.4 | 04080204 | Flint | 5.0 | |
| 04030105 | Peshtigo | 7.1 | 04080205 | Cass | 5.6 | |
| 04030106 | Brule | 6.6 | 04080206 | Saginaw | 5.0 | |
| 04030107 | Michigamme | 12.5 | 04090001 | St. Clair | 3.7 | |
| 04030108 | Menominee | 8.0 | 04090002 | Lake St. Clair | 2.0 | |
| 04030109 | Cedar-Ford | 7.0 | 04090003 | Clinton | 6.2 | |
| 04030110 | Escanaba | 8.6 | 04090004 | Detroit | 5.2 | |
| 04030111 | Tacoosh-Whitefish | 8.6 | 04090005 | Huron | 6.3 | |
| 04030112 | Fishdam-Sturgeon | 11.1 | 04100001 | Ottawa-Stony | 5.1 | |
| 04030201 | Upper Fox | 7.3 | 04100002 | Raisin | 5.5 | |
| 04030202 | Wolf | 8.6 | 04100003 | St. Joseph | 2.5 | |
| 04030203 | Lake Winnebago | 3.0 | 04100004 | St. Marys | 5.9 | |
| 04030204 | Lower Fox | 3.7 | 04100005 | Upper Maumee | 3.5 | |
| 04040001 | Little Calumet-Galien | 9.0 | 04100006 | Tiffin | 3.1 | |
| 04040002 | Pike-Root | 6.7 | 04100007 | Auglaize | 5.0 | |
| 04040003 | Milwaukee | 5.6 | 04100008 | Blanchard | 4.4 | |
| 04050001 | St. Joseph | 8.9 | 04100009 | Lower Maumee | 5.4 | |
| 04050002 | Black-Macatawa | 11.2 | 04100010 | Cedar-Portage | 4.7 | |
| 04050003 | Kalamazoo | 8.4 | 04100011 | Sandusky | 5.4 | |
| 04050004 | Upper Grand | 5.8 | 04100012 | Huron-Vermilion | 6.1 | |
| 04050005 | Maple | 5.5 | 04110001 | Black-Rocky | 6.3 | |
| 04050006 | Lower Grand | 7.7 | 04110002 | Cuyahoga | 10.2 | |
| 04050007 | Thornapple | 6.8 | 04110003 | Ashtabula-Chagrin | 9.0 | |
| 04060101 | Pere Marquette-White | 10.6 | 04110004 | Grand | 8.4 | |
| 04060102 | Muskegon | 7.8 | 04120101 | Chautauqua-Conneaut | 10.1 | |
| 04060103 | Manistee | 12.1 | 04120102 | Cattaraugus | 11.8 | |
| 04060104 | Betsie-Platte | 9.6 | 04120103 | Buffalo-Eighteenmile | 12.0 | |
| 04120104 | Niagara | 8.3 | 2FA | North Grey Sauble Bruce Peninsula Watersheds | 13.1 | |
| 04130001 | Oak Orchard-Twelvemile | 4.3 | 2FB | Owen Sound Watersheds | 10.8 | |
| 04130002 | Upper Genesee | 9.2 | 2FC | Saugeen | 11.7 | |
| 04130003 | Lower Genesee | 7.5 | 2FD | Penetangore | 10.6 | |
| 04140101 | Irondequoit-Ninemile | 5.4 | 2FE | Maitland | 11.3 | |
| 04140102 | Salmon-Sandy | 5.4 | 2FF | Ausable | 8.3 | |
| 04140201 | Seneca | 7.7 | 2GA | Upper Grand | 8.0 | |
| 04140202 | Oneida | 16.3 | 2GB | Lower Grand | 6.3 | |
| 04140203 | Oswego | 10.0 | 2GC | Big Creek | 9.3 | |
| 04150101 | Black | 3.6 | 2GD | Upper Thames | 8.2 | |
| 04150102 | Chaumont-Perch | 6.0 | 2GE | Lower Thames | 7.9 | |
| 04150301 | Upper St. Lawrence | 1.9 | 2GF | Rondeau Watersheds | 6.5 | |
| 04150302 | Oswegatchie | 8.1 | 2GG | Sydenham | 6.4 | |
| 04150303 | Indian | 4.0 | 2GH | Cedar Creek | 4.1 | |
| 2AA | Arrow | 10.1 | 2HA | Niagara | 4.4 | |
| 2AB | Dog | 7.2 | 2HB | Credit River - 16 Mile Creek | 8.1 | |
| 2AC | Black Sturgeon | 8.3 | 2HC | Humber - Don Rivers | 6.1 | |
| 2AD | Nipigon | 11.7 | 2HD | Ganaraska | 10.9 | |
| 2AE | Jackpine | 12.6 | 2HE | Prince Edward Bay | 11.6 | |
| 2BA | Little Pic | 11.5 | 2HF | Gull | 11.8 | |
| 2BB | Pic | 11.0 | 2HG | Scugog | 7.5 | |
| 2BC | White | 12.3 | 2HH | Kawartha Lakes | 9.7 | |
| 2BD | Michipicoten - Magpie | 13.0 | 2HJ | Otonabee | 7.7 | |
| 2BE | Agawa | 13.2 | 2HK | Crowe | 10.4 | |
| 2BF | Goulais | 16.8 | 2HL | Moira | 10.7 | |
| 2CA | Garden | 16.8 | 2HM | Napanee | 9.9 | |
| 2CB | Wenebegon | 11.8 | 2JC | Englehart | 9.0 | |
| 2CC | Mississagi | 12.4 | 2JD | Montreal | 11.0 | |
| 2CD | Serpent | 14.6 | 2JE | Upper Ottawa - Kipawa | 12.6 | |
| 2CE | Spanish | 11.3 | 2KA | Petawawa | 9.2 | |
| 2CF | Onaping | 10.2 | 2KB | Deep | 10.7 | |
| 2CG | Manatoulin Islands | 13.9 | 2KC | Bonnechere | 6.9 | |
| 2CH | Killarney Channel | 11.0 | 2KD | Upper Madawaska | 10.8 | |
| 2DA | North Wanapitei | 11.8 | 2KE | Lower Madawaska | 10.0 | |
| 2DB | South Wanapitei | 11.3 | 2KF | Mississippi | 9.7 | |
| 2DC | Sturgeon | 12.5 | 2LA | Rideau | 8.8 | |
| 2DD | French | 12.2 | 2LB | Lower Ottawa - South Nation | 7.7 | |
| 2EA | Magnetawan | 14.2 | 2MA | Cataraqui | 11.0 | |
| 2EB | Muskoka | 15.5 | 2MB | Upper St. Lawrence - Thousand Islands | 10.5 | |
| 2EC | Black River - Lake Simcoe | 9.3 | 2MC | Upper St. Lawrence - Raisin | 8.6 | |
| 2ED | Nottawasaga | 8.3 |
Document Accessibility: Adobe Systems Incorporated has information about PDFs and the visually impaired. This information provides tools to help make PDF files accessible. These tools convert Adobe PDF documents into HTML or ASCII text, which then can be read by a number of common screen-reading programs that synthesize text as audible speech. In addition, an accessible version of Adobe Reader, which contains support for screen readers, is available. These tools and the accessible reader may be obtained free from Adobe at Adobe Access.
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|