

In cooperation with: La Crosse County, Wisconsin Department of Natural Resources, Wisconsin Geological and Natural History Survey
1U.S. Geological Survey, 2Wisconsin Geological and Natural History Survey
Conceptualization of the Ground-Water-Flow System
Hydraulic Properties of the Ground-Water-Flow System
Three-Dimensional Simulation of the Ground-Water-Flow System
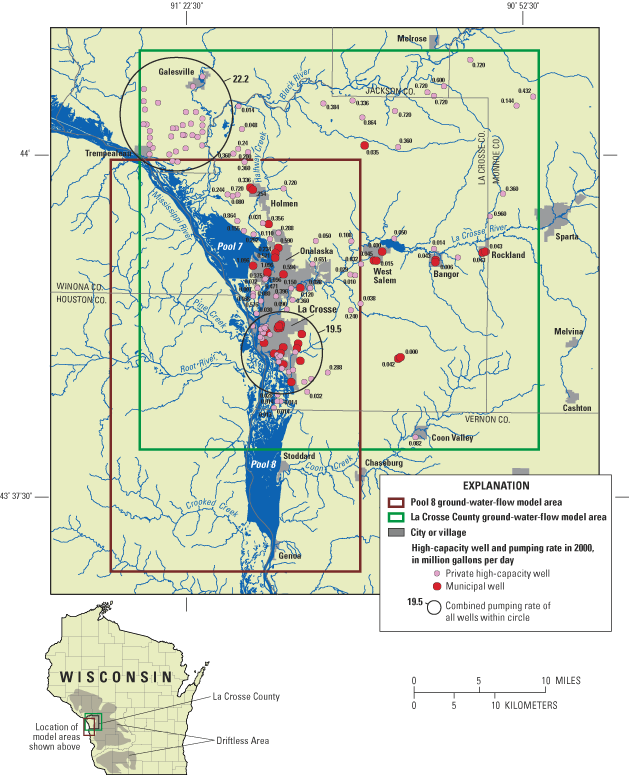
Figure 1. Location and extent of the La Crosse County and Pool 8 ground-wat...
Figure 2a. Conceptual model of ground-water-flow system.
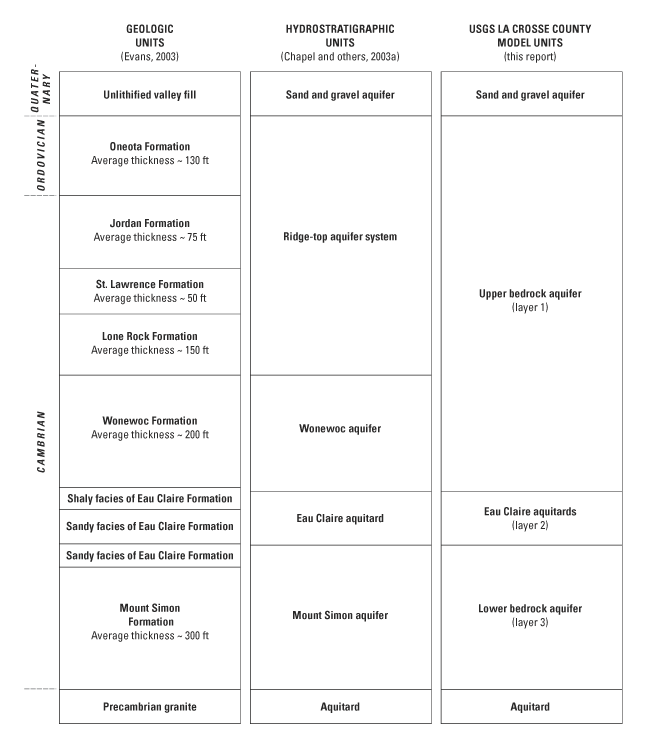
Figure 2b. Geologic and hydrostratigraphic units of La Crosse County. The L...
Figure 3. Extent of the analytic element model (GFLOW) and MODFLOW model gr...
Figure 4a. Model layers and hydraulic properties used for final calibrated ...
Figure 4b. Block diagrams showing La Crosse County MODFLOW model layers, K ...
Figure 5. Finite-difference grids, model boundary conditions, and water-lev...
Figure 6. Measured ground-water levels plotted against simulated ground-wat...
Figure 7. Simulated water-table elevation and target residuals for La Cross...
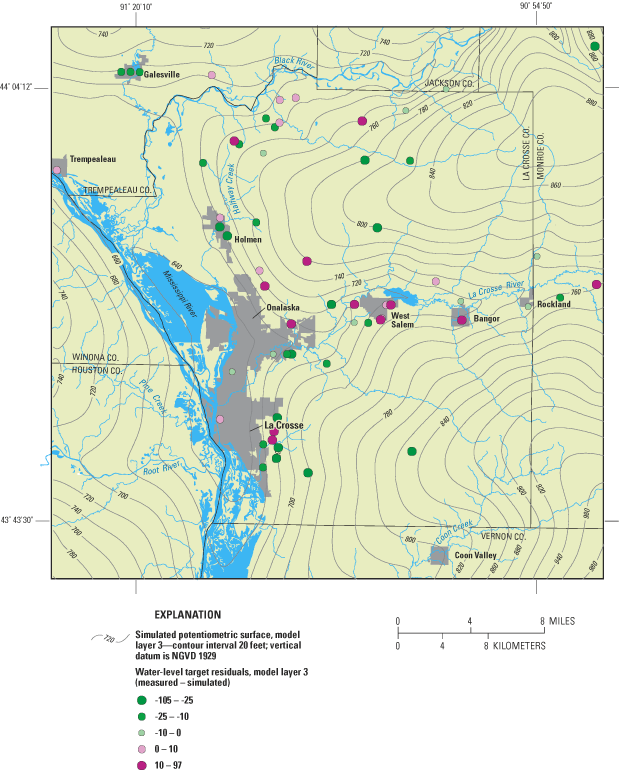
Figure 8. Simulated potentiometric-surface elevation and target residuals f...
Figure 9. Plot of model parameter sensitivity; sum of square weighted resid...
Figure 10a. Simulated water-table decline from predevelopement to 2000 for ...
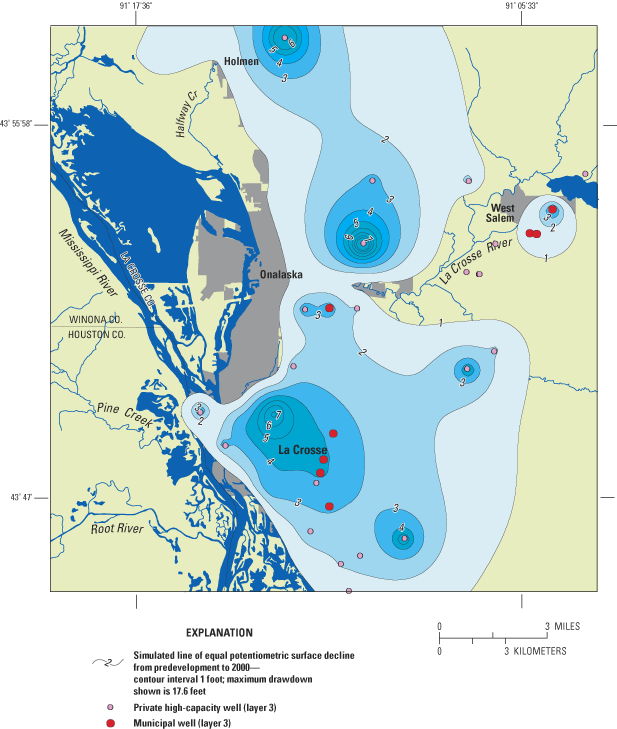
Figure 10b. Simulated potentiometric-surface decline from predevelopement t...
Figure 11a. Predevelopment ground-water/surface-water interaction.
Figure 11b. Postdevelopment ground-water/surface-water interaction. Note ar...
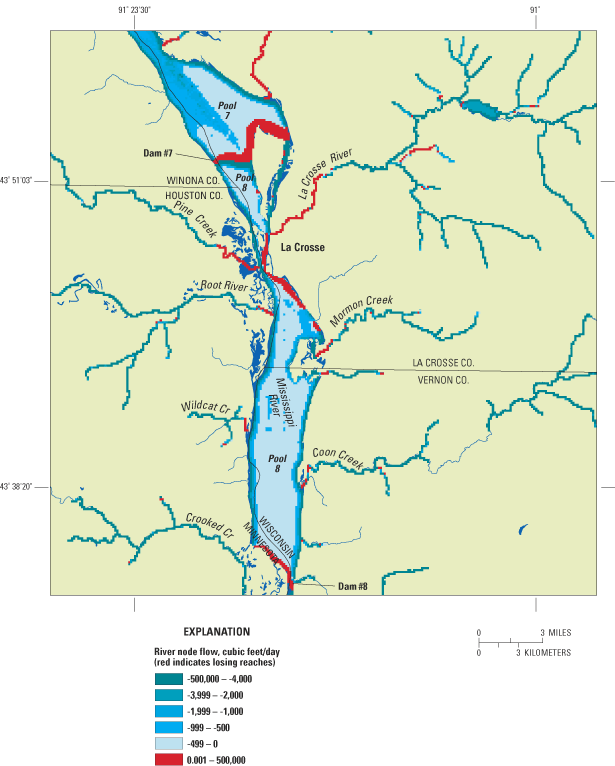
Figure 12. Simulated river flow for the lower portion of Pool 7 and Pool 8 ...
Table 1. Measured and simulated horizontal hydraulic conductivity values (f...
Table 2. UCODE weights and final model calibration statistics
Appendix. La Crosse County area ground-water withdrawals by model layer, ro...
This report describes a two-dimensional regional screening model and two associated three-dimensional ground-water flow models that were developed to simulate the ground-water flow systems in La Crosse County, Wisconsin, and Pool 8 of the Mississippi River. Although the geographic extents of the three-dimensional models were slightly different, both were derived from the same geologic interpretation and regional screening model, and their calibrations were performed concurrently. The objectives of the La Crosse County (LCC) model were to assess the effects of recent (1990s) and potential future ground-water withdrawals and to provide a tool suitable to evaluate the effects of proposed water-management programs. The Pool 8 model objectives were to quantify the magnitude and distribution of ground-water flow into the Pool. The Wisconsin Geological and Natural History Survey and the U.S. Geological Survey developed the models cooperatively. The report describes: 1) the conceptual hydrogeologic model; 2) the methods used in simulating flow; 3) model calibration and sensitivity analysis; and 4) model results, such as simulation of predevelopment conditions and location and magnitude of ground-water discharge into Pool 8 of the Mississippi.
Three aquifer units underlie the model area: 1) a shallow unconsolidated sand and gravel aquifer; 2) an upper bedrock aquifer, composed of Cambrian and Ordovician sandstone and dolomite; and 3) a lower bedrock aquifer composed of Cambrian sandstone of the Eau Claire Formation and the Mount Simon Formation. A shale layer that is part of the Eau Claire Formation forms a confining unit separating the upper and lower bedrock aquifers. This confining unit is absent in the Black River and parts of the La Crosse and Mississippi River valleys. Precambrian crystalline basement rock forms the lower base of the ground-water flow system.
The U.S. Geological Survey ground-water flow model code, MODFLOW, was used to develop the La Crosse County (LCC) and Pool 8 ground-water flow models. Boundary conditions for the MODFLOW model were extracted from an analytic element screening model of the regional flow system surrounding La Crosse County. Model input was obtained from previously published and unpublished geologic and hydrologic data. Pumpages from municipal and high-capacity wells were also simulated.
Model calibration included a comparison of modeled and field-measured water levels and field-measured base flows to simulated stream flows. At calibration, most measured water levels compared favorably to model-calculated water levels. Simulated streamflows at two targets were within 3 percent of estimated measured base flows. Mass balance results from the LCC and Pool 8 models indicated that 63 to 74 percent of ground water was from recharge and 19 to 26 percent was from surface-water sources. Ground-water flow out of the model was to rivers and streams (85 to 87 percent) and pumping wells (11 and 13 percent).
The model demonstrates the effects of development on ground water in the study area. The maximum simulated water-level decline in the city of La Crosse metropolitan area is 9.3 feet. Simulated stream losses are similar to the amount of ground water pumped by wells. This indicates that ground water withdrawn by La Crosse County wells is water that under predevelopment conditions discharged to streams and lakes.
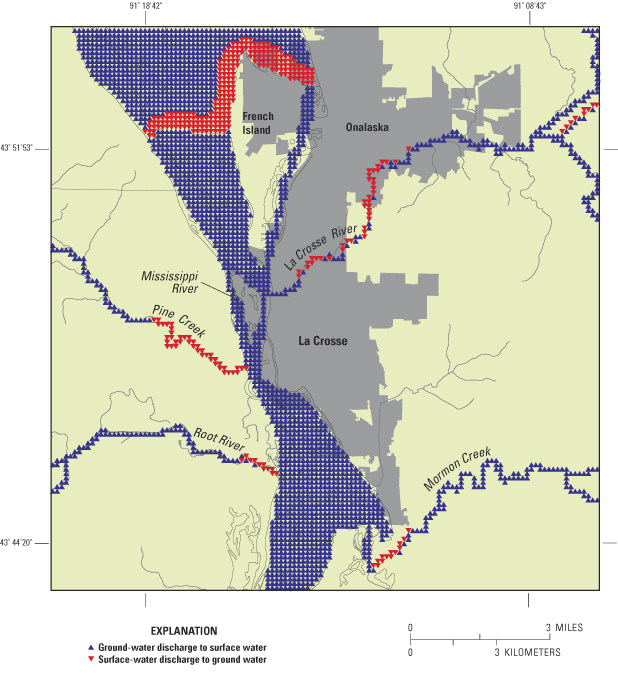
The models provide estimates of the locations and amount of ground-water flow into Pool 8 and the southern portion of Pool 7 of the Mississippi River. Ground-water discharges into all areas of the pools, except along the eastern shore in the vicinity of the city of La Crosse and immediately downgradient from lock and dam 7 and 8. Ground-water flow into the pools is generally greatest around the perimeter with decreasing amounts away from the perimeter. An area of relatively high ground-water discharge extends out towards the center of Pool 7 from the upper reaches of the pool and may be associated with the absence of the Eau Claire confining unit in this vicinity.
Ground water is the sole source of residential water supply in La Crosse County and the Pool 8 area ("Pool 8" refers to the impoundment of the Mississippi River near La Crosse, Wisconsin, resulting from the lock and dam system). There are currently 9 municipal supply systems with 36 active wells (fig. 1) operating in La Crosse County (Chapel and others, 2003a,b). Approximately 80,000 people or 75 percent of the residents are served by municipal water-supply systems located along the Mississippi and La Crosse River valleys. Water-supply systems along the Mississippi River valley withdraw ground water from a sand and gravel aquifer. This aquifer may be susceptible to contamination because of its shallow depth to ground water and lack of an areally extensive protective confining unit. The importance of protecting this aquifer is underscored by the fact that there are over 160 ground-water contamination sites in La Crosse County, mostly in the vicinity of the cities of La Crosse and Onalaska (Charles Cameron, WDNR, written commun., November 4, 1999). East of the Mississippi River valley, bedrock aquifers are used for municipal water supply.
Although ground water is widely recognized as an important drinking water source, it also sustains surface-water features such as streams and wetlands. Urban and county planners are commonly faced with decisions that balance the need for increased ground-water withdrawals while maintaining the quantity and quality of ground-water-supported surface-water resources such as trout streams. Managing and protecting the ground- and surface-water (or "hydrologic") resources requires a basic understanding of hydrologic systems. Information about the ground-water system such as the extent of aquifer units, their water-bearing properties, and their recharge and discharge areas, allows assessments of the susceptibility of water supplies to over-use and contamination. In this regional ground-water study, data from topographic and geologic maps, well construction reports, water-level measurements, and surface-water features are synthesized to produce a conceptual model of aquifer units and the regional ground-water-flow system (Chapel and others, 2003a). Although the data and maps produced in a regional study provide basic hydrogeologic information for water-resource management, this information also provides the basis for constructing ground-water-flow models. These models are a mathematical simulation of the natural system that can be used to simulate how water flows through the system, and how it will react to stress (such as increased pumping from wells).
Large ground-water withdrawals concentrated near the city of La Crosse are expected to have an effect on regional and local ground-water flow. For example, large amounts of municipal pumping have lowered water levels in the shallow sand and gravel aquifer, creating downward leakage of surface water into the aquifers, which could result in migration of associated contaminants to some municipal wells. Analyses of water from city of La Crosse wells have indicated that sodium concentrations have increased in all municipal wells over the last 17 years (Tom Berendes, City of La Crosse Water Utility, written commun., February 2003,); in 6 municipal wells, sodium concentrations more than doubled over that period. In addition, volatile organic chemicals and nitrate have been detected in some private and public wells (Charles Cameron, WDNR, written commun., November 4, 1999).
Previous work in the area included a number of local ground-water-flow models (EarthTech, 1999; Davy Engineering, 2002). The modeling described in this report differs from the previous work in the following ways. It is much larger in extent, and includes all of La Crosse County, parts of surrounding counties, and the Pool 8 area. It includes recently collected geologic and hydrologic data that improved the conceptualization and parameterization of the regional ground-water-flow system. Moreover, recent improvements in computational power facilitate high-resolution models that provide a more detailed simulation of the regional ground-water-flow systems and associated hydrologic features. These models can be constructed using complementary techniques (for example, analytic element and finite difference) that are then coupled so that insight gained from one can be translated into the other. These large models, and the software needed to pre- and post-process the datasets, run rapidly on today's computers. The resulting model can be used to identify major areas of ground-water recharge and discharge, estimate the amount of ground water discharging to surface-water bodies, and quantify ground-water flow rates. The model can also be used in a "what if" capacity to simulate effects of ground-water withdrawals, both existing and potential, and the effects of proposed water-management programs.
This report presents the results of a hydrologic investigation in the La Crosse area that consisted of two complementary modeling efforts. The first was a regional ground-water flow model of La Crosse County. The second was a ground-water-flow model of the Pool 8 vicinity. The purpose of the two models was to: 1) improve understanding of the ground-water-flow system and its relation to surface water, and 2) to develop a ground-water flow model for use on an ongoing basis by water-resource managers.
This study was a cooperative effort that included La Crosse County, Wisconsin Department of Natural Resources, Wisconsin Geological and Natural History Survey (WGNHS), and the U.S. Geological Survey (USGS). The work was divided into three phases. The first phase was to refine the conceptual understanding of the ground-water system and establish a hydrogeologic database (see Chapel and others, 2003a). The second phase was to develop and calibrate the three-dimensional ground-water flow models. The third phase was to simulate zones of contributions for the municipal water-supply wells. This report represents phase 2 of the study and describes: 1) the conceptual hydrogeologic model, 2) the methods used in simulating ground-water flow, 3) the calibrated model parameters and sensitivity, and 4) the limitations of the model.
Appreciation is expressed to Jeff Bluske from La Crosse County and Jeff Helmuth of the Wisconsin Department of Natural Resources for their support for the project. Funding for this project was received from the County of La Crosse and Wisconsin Department of Natural Resources. Special thanks are given to Tom Berendes and Mark Johnson of the City of La Crosse Water Utility for their help in understanding the hydrologic system and the pumping stresses operating therein.
The two model areas are adjacent and, in some locations, overlap. The La Crosse County (LCC) model includes the entire County, parts of four adjacent counties in southwestern Wisconsin, and two counties in Minnesota (fig. 1). The Pool 8 model has significant overlap with the LCC model but extends farther south (fig. 1). The models were constructed using the same methods and were calibrated simultaneously. Aquifer and confining-unit thickness and hydraulic properties for the entire model domain were determined from published and unpublished maps; methods used are described by Chapel and others (2003a).
Prior to the construction of the three-dimensional ground-water-flow models, a conceptual model of the system was developed on the basis of previously collected data and the interpretation of data collected during Phase 1 of the study. Using the methodology described by Hunt and others (1998a, 1998b), a two-dimensional analytic-element ground-water-flow model (GFLOW, Haitjema, 1995) was used as a simplified screening model to quickly test the conceptual model and derive hydrologic boundaries for the three-dimensional LCC and Pool 8 models. A complete description of analytic element modeling is beyond the scope of this report; a brief overview is given below. Strack (1989) and Haitjema (1995) provide detailed discussions of the analytic element method.
Analytic element modeling assumes an aquifer of infinite extent. The problem domain does not require a grid or involve interpolation between cells. To construct an analytic element model, features important to ground-water flow (for example, wells) and surface-water bodies are entered as mathematical elements or strings of elements. The amount of detail specified for each feature depends on distance from the area of interest. Each element corresponds to an analytic solution, and these solutions are superposed or added together in the model to arrive at a solution for the ground-water-flow system. Because the solution is not confined to a grid, as it is in the finite-difference method, ground-water levels and flows can be computed anywhere in the model domain without nodal averaging. In the GFLOW model used here, the analytic elements are two-dimensional and are used only to simulate steady-state conditions (that is, ground-water levels do not vary with time). A comparison of analytic element to finite-difference numerical modeling techniques is discussed in Hunt and Krohelski (1996) and Hunt and others (1998a; 1998b).
MODFLOW96 (Harbaugh and others, 1996), a USGS block-centered finite-difference code, was used to simulate the three-dimensional flow system in the LLC and Pool 8 models. MODFLOW requires input arrays (gridded data) that describe hydraulic parameters such as hydraulic conductivity and recharge, top and bottom elevation of aquifers, and boundary conditions. Detailed discussions of finite-difference methods, MODFLOW input requirements, and theory are provided by McDonald and Harbaugh (1988) and Anderson and Woessner (1992). Three steps were used to create the input arrays required by MODFLOW. First, geographic information system (GIS) coverages of aquifer top and bottom elevations and hydraulic conductivity of bedrock and unconsolidated materials were developed during phase 1 of this study (Chappel and others, 2003a) using well logs and previous reports (Mandle and Kontis, 1992; Young, 1992; Earth Tech, 1999; Davey Engineering, 2001). Second, these GIS coverages were intersected with the model grid using Groundwater Vistas (Rumbaugh and Rumbaugh, 2001), a ground-water modeling preprocessor. Third, boundary conditions at the model perimeter were extracted directly from the analytic-element model. The details of the technique are described in more detail by Hunt and others (1998b).
The analytic element and MODFLOW models were calibrated using parameter-estimation techniques. The primary benefit of parameter estimation is the ability to automatically calculate parameter values (for example, hydraulic conductivity and recharge) that are a quantified best fit between simulated model output and observed data (for example, ground-water levels and streamflows). Other benefits also include quantification of the quality of the calibration, parameter correlation (for example, hydraulic conductivity and recharge), and parameter sensitivity. This study used the parameter estimation code UCODE (Poeter and Hill, 1998).
Prior to simulating the ground-water system, a conceptualization of the system is essential because it forms the basis for model development. The conceptualization is a necessary simplification of the natural system because inclusion of all of the complexities of the natural system into a computer model is not feasible given the existing knowledge of the subsurface and current computer capabilities. Steps in the development of the conceptual model include: 1) definition of aquifers and confining units, 2) identification of sources and sinks of water, and 3) identification and delineation of hydrologic boundaries encompassing the area of interest. The first two of these steps were accomplished by review and interpretation of existing and new geologic and hydrogeologic data. The third step was accomplished by using a screening model.
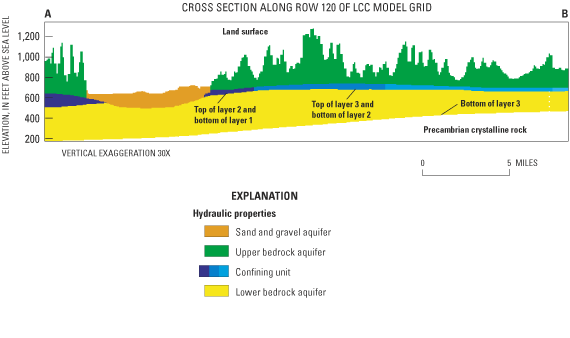
Three regional aquifers and one regional confining unit occur in the La Crosse County area, based on existing and new geologic and hydrologic data (Chapel and others, 2003a). The conceptual model of the ground-water flow system is shown in figure 2. The stratigraphic names used in this report use the nomenclature of Ostrom (1967) and Evans (2003). A shallow sand and gravel aquifer is made up of unconsolidated glacial and alluvial materials overlying the bedrock. Except in narrow alluvial valleys and the broader Mississippi River valley, the sand and gravel aquifer is thin or absent in the model area (fig. 2). The upper bedrock aquifer underlies the unconsolidated deposits. It is made up of sandstone and dolomite, and (if present) includes the Prairie du Chien and Tunnel City Groups, but is dominated by the Wonewoc Formation. A shaly facies within the Eau Claire Formation underlies the upper bedrock aquifer and forms a confining unit. This confining unit is largely absent in eroded valleys of the Black River valley and is partially absent in the La Crosse River and Mississippi River valleys. The Mount Simon Formation and sandstone within the Eau Claire Formation form the lower bedrock aquifer that overlies Precambrian crystalline basement rock. The Precambrian crystalline basement rock is assumed to be impermeable and forms the lower boundary of the ground-water flow system. Most municipal water-supply systems use the sand and gravel aquifer or the lower bedrock aquifer. Most ridge-top communities are on private water supply and use the Wonewoc sandstone or a combination of the Wonewoc sandstone and the Tunnel City Group.
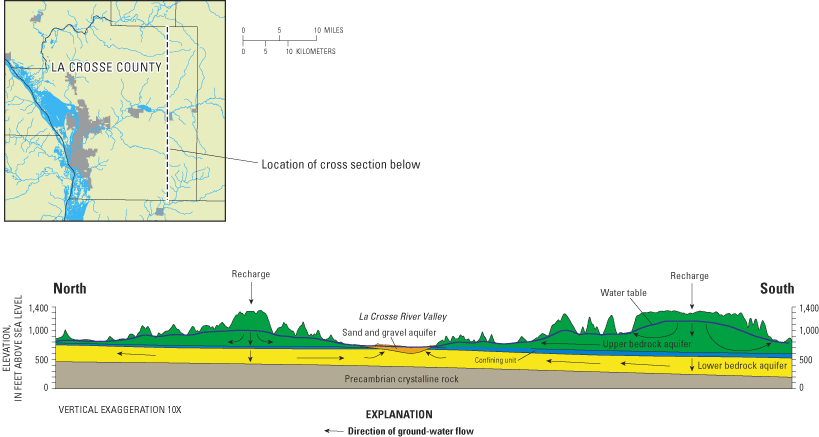
Water enters the ground-water-flow system as recharge to the water table. Recharge takes place primarily in upland areas throughout La Crosse County. Rates of recharge are variable because of differing soil percolation rates, slope, and relative topographic position. Ground-water-flow paths may be local or regional. As shown in figure 2, local systems with short flow paths are common in the sand and gravel and upper bedrock aquifers; regional flow with longer flow paths takes place in the lower bedrock aquifer. A portion of recharging water moves downward to the sand and gravel or upper bedrock aquifers, travels a short horizontal distance and then moves upward, discharging to a stream or wetland. Recharge may move downward through the confining unit into the lower bedrock aquifer. In areas where the confining unit is absent, recharge may move through the sand and gravel aquifer directly to the lower bedrock aquifer. Because of the conductive nature of the lower bedrock aquifer and the nearly impermeable Precambrian rock forming the lower boundary of the system, flow paths in the lower bedrock aquifer are primarily horizontal. Pumping wells, an important sink of ground water, can be open to the sand and gravel aquifer (for example, in municipalities along the Mississippi River valley such as the city of La Crosse) or to the bedrock aquifer (for example, municipalities along the La Crosse River valley such as the village of West Salem). The pumping associated with the wells captures a portion of the ground water that under predevelopment conditions would have discharged to streams and wetlands. In places where large withdrawals of ground water occur, streams may recharge the ground-water system.
An analytic element screening model based on the code GFLOW (Haitjema, 1995) was used to construct boundary conditions representing the regional ground-water flow system at the edge of the three-dimensional model domains (fig. 3). The screening model is a simplified representation of the natural system because: 1) the flow system is assumed to be two-dimensional, and vertical components of flow and the three-dimensional nature of the geologic deposits are ignored; 2) recharge is grouped into broad zones within the entire model; 3) the aquifer system is also zoned into watersheds with constant values of hydraulic conductivity; 4) surface-water/ground-water interactions are simulated using coarse representations; and 5) the system is at steady-state (that is, water levels are not changing over time). Although the advantage of such simplification is that the model can be constructed with minimal time and data, the screening model may not generally be suitable for extensive use in land-use planning or other applications because of the limitations associated with these simplifications. The screening model is able to serve, however, as a foundation upon which to build the more complex, realistic, three-dimensional MODFLOW models.
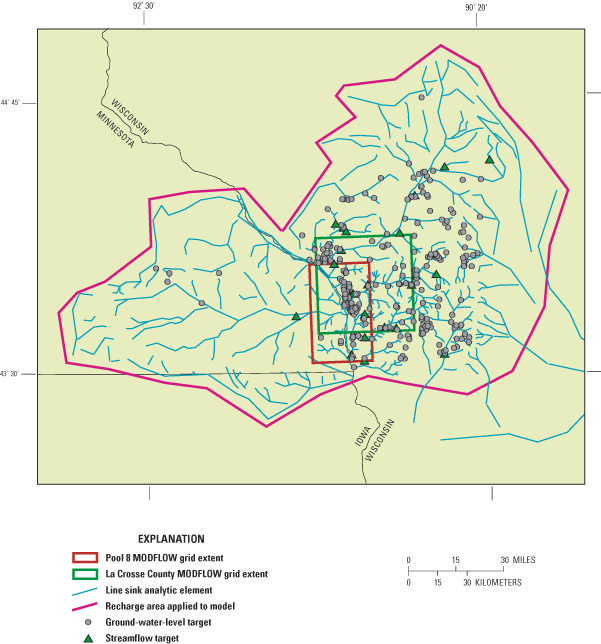
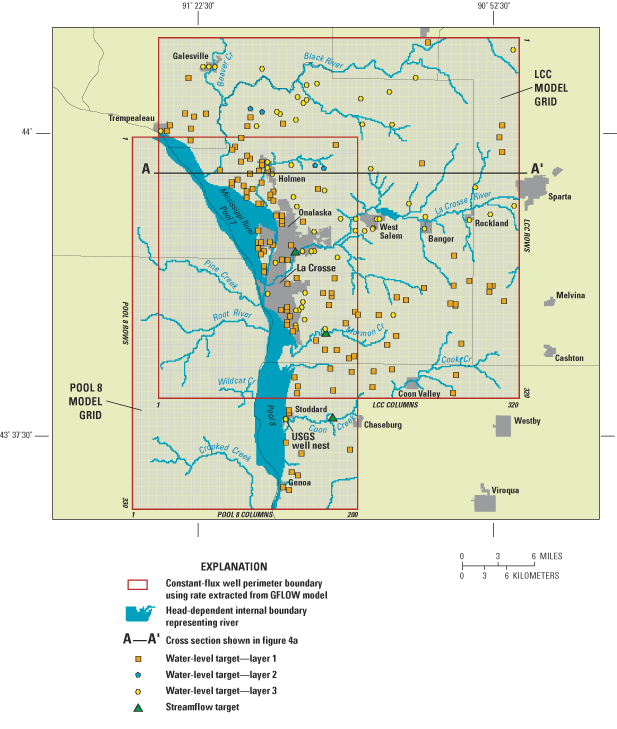
The analytic element screening model was developed by digitizing surface-water features and assigning representative hydrologic properties to the aquifer. Surface-water features were simulated with line sinks with and without hydraulic resistance. Resistance represents the restriction to flow caused by low conductivity sediments that line the stream channels; all streams with resistance were assigned a value of 0.3 days, which corresponds to a sediment thickness of 0.3 feet and a vertical hydraulic conductivity of 1 ft/d. A stream resistance of 0.3 days is within the range reported by Krohelski and others (2000). Moreover, this parameter has been reported to be insensitive for values less than 200 days in a nearby watershed (Gaffield and others, 1998). A single layer representing the bulk average properties of the sand and gravel and bedrock aquifers was simulated, and conductivity was zoned by watershed. A global uniform recharge rate was varied to obtain a reasonable fit for ground-water levels and base flow measured in the area. The area simulated included a much larger area than La Crosse County (fig. 3), and included 22 current and historical USGS streamflow-gaging stations for flow calibration. The values of hydraulic conductivity and recharge were varied automatically until the best match to the measured ground-water level and flow data was obtained. The final hydrologic parameters used in the screening model were horizontal hydraulic conductivity of 1 to 5 ft/d, and a calibrated recharge rate representative of the La Crosse area of 8.5 in/yr. Once the analytic element model was calibrated, flux-specified boundary conditions for the three-dimensional model were extracted (Haitjema 1995; Hunt and others, 1998b) as input files for the well (WEL) package in MODFLOW. The extracted extents were designed such that the model boundaries were distant from areas of hydrologic stress (for example, pumping centers) and included areas outside of the immediate La Crosse County and Pool 8 areas (fig. 1).
Initial estimates of hydraulic conductivity, recharge, and streambed leakance for the three-dimensional ground-water-flow models were based on existing and on new geologic and hydrologic data. A complete discussion of the collection and interpretation of these data is presented in Chapel and others (2003a). The following is a brief description of these estimates.
The hydrogeologic system is characterized by a mature drainage network developed in the Paleozoic bedrock units typical of the Driftless Area (fig. 1, inset map). The river and streams cut into the upper bedrock (here defined as the bedrock above the shaly facies of the Eau Claire Formation) and are filled with sand and gravel sediments of relatively high hydraulic conductivity. The lower bedrock represents the units below the shaly portion of the Eau Claire Formation and is dominated by the Mt. Simon Sandstone.
The saturated horizontal hydraulic conductivities of the geologic units in the La Crosse County area (table 1) were estimated using data from specific capacity and aquifer tests (Chapel and others, 2003a). Horizontal hydraulic conductivity of the sand and gravel aquifer generally ranges from 3 to 1,500 ft/d (table 1), with a geometric mean value equal to 51.7 ft/d, on the basis of 904 specific capacity tests. Specific capacity tests for wells in the bedrock above and below the shaly facies of the Eau Claire Formation provided a smaller range of values (generally between 0.05 to 25 ft/d), with a geometric mean value of 0.3 and 3.1 ft/d for the upper and lower bedrock, respectively. The geometric mean of estimated horizontal hydraulic conductivity of 5 tests of the Eau Claire Formation is 1.2 ft/d. No measurements of the vertical hydraulic conductivity of these rock units have been made in the La Crosse County area to date. Although these ranges are useful for characterizing the system, the model requires specific values for the hydraulic conductivity variation in the system. Thus, the zones were treated as calibration parameters and final values used in the modeling described here were determined using the parameter estimation code and evaluated using the range of field measurements.
| Saturated geologic unit(s) well is open to | Measured minimum | Measured maximum | Geometric mean of measured values | Number of estimates | Modellayer | Simulated value |
|---|---|---|---|---|---|---|
| Eau Claire Formation (sandstone and shale) | 0.9 | 1.6 | 1.2 | 5 | 2 | 2.2 |
| Mount Simon Formation (sandstone) | .4 | 18.1 | 4.9 | 21 | 3 | 12 |
| Mount Simon & Eau Claire Formations (sandstone and shale) | .09 | 8.5 | 2.3 | 30 | NA | |
| Mount Simon & Wonewoc Formations (sandstone) | .6 | 8.6 | 3.4 | 6 | NA | |
| Wonewoc Formation (sandstone) | .08 | 12.3 | 2.3 | 9 | 1 | 8 |
| Wonewoc Formation & Tunnel City Group (sandstone and shale) | .03 | 6.8 | .1 | 23 | 1 | 8 |
| Tunnel City Group or Tunnel City Group & St. Lawrence Formation (sandstone and shale) | .03 | 25.9 | .2 | 20 | 1 | 8 |
| Tunnel City Group & Jordan Formation (sandstone and shale) | .09 | .5 | .2 | 9 | 1 | 8 |
| Jordan Formation (sandstone) | .07 | 3.3 | .5 | 5 | 1 | 8 |
| Unconsolidated (all valleys) (sand and gravel) | 2.6 | 1486 | 51.7 | 904 | 1 | |
| Unconsolidated (Mississippi River Valley) (sand and gravel) | 2.6 | 1486 | 52.0 | 831 | 1 and 2 | 420 |
| Unconsolidated (La Crosse River Valley) (sand and gravel) | 12.2 | 130 | 33.3 | 33 | 1 | 40 |
| Unconsolidated (Black River Valley) (sand and gravel) | 6.5 | 455 | 69.8 | 40 | 1 | 200 |
| Lower Bedrock (below Eau Claire Shale)1 (sandstone) | .09 | 18.1 | 3.1 | 51 | 3 | 12 |
| Upper Bedrock (above Eau Claire Shale) (sandstone and shale) | .03 | 25.9 | .6 | 65 | 1 | 8 |
1Lower Bedrock includes wells open to Mount Simon and Eau Claire Formations.
The zonation of recharge areas and associated rates were determined (Chapel and others, 2003a) by developing a mass-balance model for the La Crosse County area using a modified Thornthwaite and Mather (1957) water-balance method (Dripps, 2003). This method incorporates many parameters such as soil percolation rate, soil moisture storage, land-use type, temperature, and precipitation and evapotranspiration rates. Results of this method indicate that the highest rates of recharge within La Crosse County occur near hilltops and on the undeveloped sand and gravel terraces along the Mississippi River valley. Ground-water discharge occurs predominantly in the river bottoms. The recharge rate ranged between 0.0 to 29.9 in/yr and had an average value of 9.3 in/yr with a standard deviation of 3.6 in/yr. Because the approach used is an unconstrained estimate of recharge (not compared to field measurements of water flow), the ground-water-flow model used the relative recharge distribution calculated by the water-balance model. The parameter estimation then increased or decreased the relative recharge rates by the same percent. Therefore, although the simulated recharge rate for a given area was changed, the relative difference between areas was maintained.
Estimates of streambed leakance were needed to simulate the interaction between surface water and ground water. Streambed leakance is equal to the reciprocal of hydraulic streambed resistance (discussed previously); thus, streambed leakance is the vertical hydraulic conductivity of the streambed divided by its thickness. In this study, streambed leakance was estimated as 1 ft/day/ft, which is an intermediate value between the measured values reported for Dane County, Wisconsin, (1.6 to 37 ft/d/ft) by Krohelski and others (2000) and the simulated value used in the adjacent Kickapoo watershed (0.05 ft/d/ft) by Gaffield and others (1998). The streambed leakance is not expected to severely limit flows to and from the stream due to the high conductivity of the underlying sand and gravel aquifer and frequent local erosion events that occur in the streams (Gaffield and others, 1998). Moreover, the model was not sensitive to values of streambed leakance when varied by ±75 percent around this value (see sensitivity section).
Current municipal supply accounts for about 31 percent of the total high-capacity ground-water use in the La Crosse County model domain. The city of La Crosse, the largest single consumer, accounts for about 25 percent of this. Generally, municipal withdrawals in the city of La Crosse have remained between 11.5 and 15.5 mgd since early 1977. The largest pumping volumes occurred during the 1980s, and the smallest annual pumping volume was recorded in 2002 (Thomas Berendes, city of La Crosse, written commun., March 25, 2003).
The sand and gravel aquifer is the primary water supply in the Mississippi River valley. The upper bedrock aquifer is used for rural domestic supplies; the lower bedrock aquifer is the primary water supply for municipal systems east of the Mississippi River valley. Large-diameter wells open to the large thicknesses of the sand and gravel aquifer generally yield 1,000 to 2,000 gpm, and large-diameter wells completed in the bedrock may yield as much as 600 gpm. Pumping rates are variable over time; thus, rates representative of the 1990s were used (Appendix). These rates were based on a 10-year average rate, or in the case where a10-year average rate was unavailable, an average rate over the period the well was operated at a typical pumping schedule.
Normal water use reported to the Wisconsin Department of Natural Resources for 147 nonmunicipal high-capacity wells within the La Crosse County model domain is 45.4 mgd (Appendix 1). Pumpage from these wells was sufficiently large to include in the ground-water flow model. Pumpage from individual private wells in the county is not included in the model because the discharge of these wells is relatively small, widely distributed, and does not have a significant effect on the overall regional water balance.
The LCC and Pool 8 three-dimensional models are mathematical representations of ground-water flow and use the USGS MODFLOW96 code (Harbaugh and McDonald, 1996). Although they cover different areas, the two models have similar construction and are discussed together below. The steps involved in developing the three-dimensional models were: 1) input boundary conditions identified by the screening model and select appropriate aquifers and confining units as identified in the conceptual model; 2) construct a finite-difference grid for each model domain; 3) assemble hydrologic data (for example, aquifer and confining unit geometry and hydraulic conductivities, recharge rate, and leakance of streambeds); 4) input pumping rates and locations of simulated wells; 5) calibrate the models by adjusting parameters over realistic ranges until there is a reasonable match between measured and simulated ground-water levels and measured and simulated surface-water flows; and 6) ensure that the models are in mass balance; that is, the volume of water entering the model approximates the volume of water being withdrawn or leaving the model.
As currently implemented, the models simulate a steady-state ground-water system; that is, ground-water levels are not changing with time. The steady-state assumption is appropriate because of the good hydraulic connection between aquifers and between aquifers and surface water, which mitigates the effect of pumping. The results of simulations made with the screening model, which is also a steady-state model, compare favorably to observed conditions in the ground-water system.
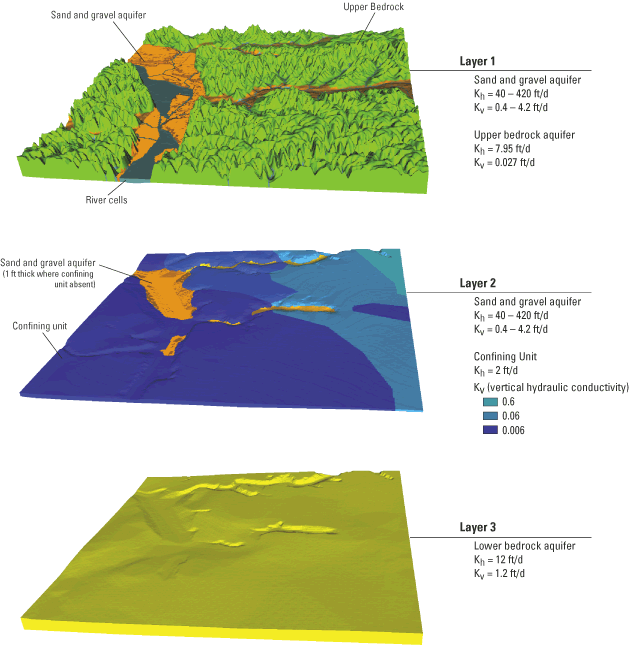
As specified in the conceptual model, the sand and gravel aquifer is in the uppermost model layer (layer 1 – figs. 4a and 4b). The sand and gravel deposits are associated predominantly with alluvial valley settings. Measured hydraulic conductivities were widely variable (table 1). For modeling purposes, the sand and gravel aquifer in the alluvial valleys was divided into three zones, two representing sediments in the tributary valleys of the Black and La Crosse Rivers, and one zone representing the Mississippi River valley sediments.
The bedrock units were combined into three model layers. Layer 1 consists of the sand and gravel aquifer and upper bedrock units above the confining unit (figs. 4a and 4b). Layer 2 in the model represents the confining unit (shaly facies of the Eau Claire Formation). This unit has relatively low horizontal hydraulic conductivity values (table 1); the vertical hydraulic conductivity for layer 2 was also relatively low and was zoned based upon estimated locations of facies changes where the unit is sandier (Chapel and others, 2003a). In areas where the confining unit was eroded away, the nodes were given properties of the sand and gravel aquifer. The lower bedrock aquifer (layer 3) represents the rock units below the shaly facies of the Eau Claire formation and is dominated by the Mount Simon Sandstone. This layer is bounded by the relatively impermeable Precambrian basement that forms the model base. The three model layers are hydraulically connected by a leakance term (McDonald and Harbaugh, 1988, p. 5-13, eq. 51) that takes into account the vertical hydraulic conductivities and thickness of the adjacent aquifers and confining unit.
The two MODFLOW model domains have perimeter boundary conditions extracted from the analytic-element screening model. The perimeter of the grids is assigned as specified flux nodes (using the MODFLOW well package). Flux values were determined from a single-layer MODFLOW extraction from the corresponding area of the GFLOW model. The flux values were added to multiple layers of the MODFLOW model using analytic element wells in the MODFLOW pre-processor Groundwater Vistas (Rumbaugh and Rumbaugh, 2001). This allows the constant flux to be automatically partitioned between model layers based on transmissivity on a cell-by-cell basis. Internal boundaries include streams and lakes within the model domains. These boundaries are head-dependent; ground-water flow to or from these surface-water bodies depends on the difference in surface-water and ground-water levels, the vertical conductivity and thickness of the streambed (leakance), and the length and width of the stream or lake. The assumed streambed leakance (1 ft/d/ft) indicates a good hydraulic connection; that is, the hydraulic conductivity of the streambeds are such that stream stages have a substantial effect on the water table. Pool 8 and the Mississippi River are also assumed to be head-dependent boundaries.
In addition to boundary conditions, initial input to the models includes the top and bottom elevations of each model layer, hydraulic conductivities, recharge rates, and pumping rates and locations of wells. Initial model input represents a node average of the aquifer properties and the recharge rate estimated by Chapel and others (2003a).
The LCC three-dimensional finite-difference ground-water-flow model covers a 30- by 30-mile area (fig. 5) that is subdivided into 307,200 nodes (320 rows, 320 columns, and 3 layers). The Pool 8 model covers a 31- by 19-mile area and uses 330 rows, 200 columns, and 3 layers for a total of 198,000 active nodes (fig. 5). The row and column dimension of each node is uniform throughout the model area, with each node measuring 500 feet on a side and having an area of about 5.7 acres. This uniformly spaced grid was used to simulate all parts of the flow system.
The model was calibrated using UCODE (Poeter and Hill, 1998). The UCODE optimization automatically adjusted input parameters in a series of model runs. After each model run, simulated ground-water levels and stream gains were compared to measured water levels and base flow by UCODE. Runs continued until simulated water levels and base flow agreed with measured water levels and base flow. Parameters values used in the sand and gravel aquifer zones were later modified to be consistent with independent estimates of surface-water capture (see Chapel and others, 2003b). These new values for the sand and gravel aquifer are included in the model described here, and had little effect on overall model calibration.
Although a steady-state model was used (in which ground-water levels do not change with time), measured water levels used during calibration spanned many years and the location of the measurements is somewhat uncertain. Because of these uncertainties, perfect agreement between the simulated and measured values was not expected. A formal evaluation of data quality is included in the calibration via the UCODE weight assigned each target (table 2). These weights provide an indication of the quality of measured data; the weighted residuals between measured and simulated values were used by UCODE to determine the best fit. The locations of a subset of the wells used as ground-water-level targets were checked by comparing location information on well logs with topographic maps and by comparing the well owner names to historic plat book records; these are given more importance in the calibration (smaller uncertainty). Finally, the USGS monitoring wells in Stoddard, Wis. (fig. 1), have accurate locations and a long record of measurements; thus, these two ground-water-level targets were given a relatively low uncertainty based on the magnitude of fluctuation observed (table 2). Streamflow measurements made during 1999 were used to estimate base flow. These base-flow estimates were compared to simulated stream gains as part of the model calibration. Only a subset of all possible parameters was optimized by UCODE. Parameters were excluded if they were unsuitable for optimization (for example, vertical leakance between layers) or insufficiently sensitive. In these cases, the parameter value was set equal to a value within the measured range and those given by (Young, 1992).
| UCODE weights | |||
|---|---|---|---|
| Number of targets | Weight | Weight type | |
Ground-water levels |
|||
| Stoddard Monitoring Wells | |||
| Water-table well | 1 | 0.7 feet | standard deviation |
| Mt. Simon wells1 | 1 | 0.6 feet | standard deviation |
| Water levels from wells checked using topographic maps and plat books | 215 | 10 feet | standard deviation |
| Water levels from other wells | 72 | 25 feet | standard deviation |
Streamflows |
|||
| La Crosse River | 1 | 0.05 | coefficient of variation |
| Mormon Creek | 1 | 0.05 | coefficient of variation |
| Coon Creek | 1 | 0.1 | coefficient of variation |
| Model results | |||
Unweighted ground-water-level calibration statistics
(feet) |
Water table(layer 1) | Potentiometric surface (layer 3) | |
| Mean Error | 5.0 | -4.7 | |
| Mean Absolute Error | 20.1 | 21.8 | |
| Root Mean Square Error | 31.3 | 29.9 | |
Streamflow Calibration |
Measured base flow (ft3/s) |
Simulated base flow(ft3/s) |
|
| La Crosse River | 131.4 | 135.8 | |
| Mormon Creek | 11.0 | 11.0 | |
| Coon Creek | 4.2 | 6.9 | |
1Average of 2 monitoring wells in Mt. Simon aquifer
Values for hydraulic conductivities used in the final calibrated model are shown in table 1 and on figure 4b. The horizontal hydraulic conductivity of the upper bedrock aquifer was 8 ft/d and that of the lower bedrock aquifer was 12 ft/d. The confining unit has a horizontal hydraulic conductivity value equal to 2 ft/d for the entire model domain that represents the ability of the confining unit to transmit water laterally through the sandstone portion of the unit. The ratio of horizontal to vertical hydraulic conductivity (Kh:Kv) is 100:1 for the sand and gravel aquifer (layer 1). The Kh:Kv ratio is 300:1 for the upper bedrock reflecting the laterally extensive layering of aquifers and confining units and 10:1 for the relatively homogenous lower bedrock aquifer. The confining unit is zoned with a relatively high Kv in the northeast (Kh:Kv ratio of 3:1), an intermediate Kv in the middle of the model domain (Kh:Kv ratio of 33:1), and a lower Kv in the southwest (Kh:Kv ratio of 333:1).
Field-measured ground-water levels were compared to model-calculated ground-water levels at specific model nodes. Water-level measurements from 178 drillers' construction reports spanning approximately the last 50 years, which provide data on the water table in the sand and gravel aquifer or the upper bedrock aquifer, were compared to model-calculated water levels. Water levels from 59 wells open to the lower bedrock aquifer represent the potentiometric surface of the lower bedrock aquifer or, in places, a combination of the water levels in the upper and lower bedrock aquifers when open to bedrock above and below the confining unit. Water levels measured in these wells were also compared to model-calculated water levels in the lower bedrock aquifer. Of special importance were data from the USGS monitoring well nest in Stoddard, Wis. (fig. 5). At this nest, the deepest well was drilled to the Precambrian bedrock and piezometers were installed above and below the confining unit to measure the vertical gradient. This area is within the Pool 8 model domain and water levels above and below the confining unit were closely simulated (within 0.1 ft).
Most model-calibrated water-table levels compare favorably to measured water-table levels. However, figure 6 shows that the maximum simulated water table is about 933 ft above sea level and that a few wells had measured water levels exceeding 960 ft (and one well over 1,050 ft) above sea level. This phenomenon was noted in another model that included simulation of the Driftless Area (Krohelski and others, 2000), and is likely caused by the inability of the regional model to simulate localized high ground-water levels. This is a result of the large number of head-dependent boundaries (interior streams) and the excellent hydraulic connection between the surface-water features and the underlying aquifer. The highest stream-surface elevation assigned to the head-dependent boundaries is about 1,000 feet above sea level. The simulated ground-water-flow system does not support a water table at an elevation much higher than 1,000 feet above sea level because the relatively low water levels near the streams are efficiently transmitted to portions of the aquifer distant from the streams.
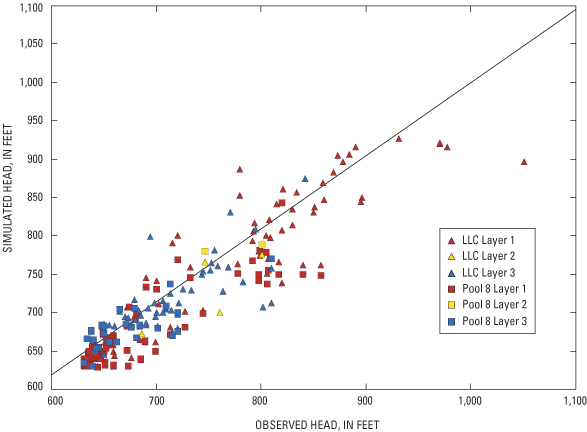
The summary statistics for the ground-water level calibration from the LCC and Pool 8 models are similar to what has been observed in other regional models in Wisconsin (table 2). The average error of all the ground-water level targets (a measure of the model bias) is 2.27 feet; the average error of the water table and potentiometric surface is 5.0 and –4.7 feet, respectively. A root mean square (RMS) difference between measured and simulated water levels for the water table and the potentiometric surface is 31.3 and 29.9 feet, respectively. The mean absolute difference (MAD) is 20.1 feet for the water table and 21.8 ft for the potentiometric surface. These RMS and MAD values represent less than 8 percent of the total range of observed water-levels across the model area.
In addition to comparing measured and modeled water levels using summary statistics, a spatial comparison between the measured and simulated water table and potentiometric surfaces was made (figs. 7 and 8). The "matches" between measured and model-calculated water levels of both the water table and the potentiometric surface are better along the valley bottoms than the ridge-tops, but no obvious banding of residuals occurs. The poorer match in ridgetop areas is due to multiple ground-water-flow systems in the upper bedrock aquifers having large vertical gradients between systems (for examples, see Juckem, 2003). Perched water tables and local confining conditions are probably common in the upper bedrock aquifers along the ridgetops (Chapel and others, 2003a). Multiple ground-water-flow systems are not well simulated by a single layer (layer 1) where all properties, ground-water levels, and flows are average values. As a result, there can be large differences between measured and simulated water levels. Moreover, this simplification of the upper bedrock aquifer may be partly responsible for the outliers observed in figure 6 and discussed previously. However, in many cases, areas with large over-simulation of ground-water levels are near areas with large under-simulations. Thus, a systematic bias in the model results was not observed.
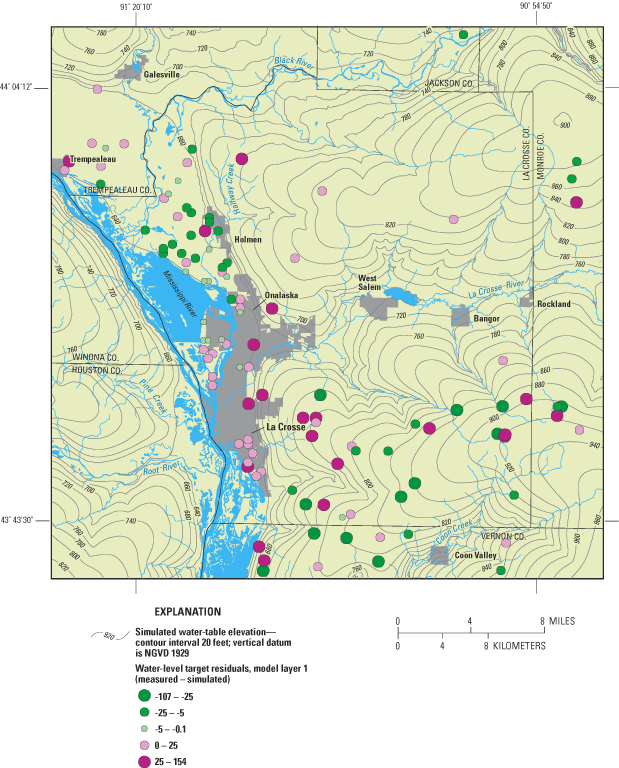
Measured base flows were compared to simulated base flows at three locations (fig. 5); however only the La Crosse River and Mormon Creek targets were considered most important because the Coon Valley target was near a model boundary (table 2). Measured streamflow was used to estimate base flow for each site. The two primary water-level targets simulated within the MODFLOW model domain were sufficient to constrain the recharge rate in the MODFLOW model. The magnitude of recharge rates varied by node and ranged from 0.0 to 27.6 in/year; when averaged over the model domains, the average areal recharge rates were 8.5 and 8.6 in/year for the LCC and Pool 8 model, respectively. The range and average areal recharge rate are similar to rates simulated by the water-balance model in Chapel and others (2003a).
Calibrated model results indicate two major sources of inflow to the ground-water flow system. Recharge accounts for 74 percent (571 cubic feet per second, or ft3/s) in the LLC model and 63 percent (373 ft3/s) in the Pool 8 model. Seepage from internal rivers, streams, and lakes accounts for about 19 percent (150 ft3/s) in the LLC model and 26 percent (152 ft3/s) in the Pool 8 model. The majority of the river contributions occur in the Mississippi River valley where the tributary rivers flow across the permeable sand and gravel aquifer. The river source is larger in the Pool 8 model than in the LLC model because the Mississippi River flats include a larger portion of the Pool 8 model domain. Ground-water drawdowns from high-capacity wells near the rivers can also result in induced ground-water recharge. A minor amount of flow is from outside the model domains through the boundaries (less than 7 percent and 11 percent for the LLC and Pool 8 models, respectively). In the LLC model these sources of water are balanced by flow from the aquifers to internal rivers (85 percent or 654 ft3/s), to pumping wells (13 percent or 100 ft3/s), and to the boundaries of the model domain (2 percent or 19 ft3/s). Similarly, in the Pool 8 model, sources of water are balanced by flow from the aquifers to internal rivers (87 percent or 511 ft3/s), to pumping wells (11 percent or 63 ft3/s), and to the boundaries of the model domain (2 percent or 13 ft3/s). The mass balance indicates that the source of ground water withdrawn by pumping wells is water recharged within the modeled area (either from terrestrial recharge or induced recharge from surface water) and is water that otherwise would have discharged to or remained in local surface water features.
There is always some uncertainty about the accuracy of models because the model parameters are never exactly known. The importance of each input parameter and its effect on simulation results can be evaluated through sensitivity tests, in which the value of a hydraulic parameter, such as hydraulic conductivity, is adjusted above or below the calibrated value and the magnitude of change in simulated ground-water levels and flows is quantified. In this report, UCODE was used to calculate the measure of model goodness of fit; specifically, the "sum of square weighted residual", or SOSWR, was used (Poeter and Hill, 1998). This statistic allows a measure of sensitivity that includes dissimilar types of observed data (in these models, ground-water levels and base flow). This combined sensitivity represents the sensitivity of the model to all the observed data used to calibrate the model rather than a commonly used approach that uses only ground-water-level data (for example, Anderson and Woessner, 1992). Because the SOSWR is a measure of difference between the measured and simulated data, lower numbers reflect a better model fit. Sensitivity analysis of the LLC and Pool 8 models is limited to primary hydrologic parameter inputs into the model (horizontal and vertical hydraulic conductivity, recharge, and leakance of the Pools and selected streams).
The most sensitive parameter (that is, the parameter where the smallest change caused the largest degradation in calibration) was recharge (fig. 9), as evidenced by a ±25 percent change causing the largest deviation from the calibrated residual. The following example may help to put this change in SOSWR into more familiar terms. A recharge rate that is 25 percent higher than the calibrated case results in a degradation in SOSWR of about 139 (fig. 9). This increase in recharge causes the measured ground-water levels in the model domain to be more poorly simulated by 0.24 ft when compared using the unweighted mean absolute difference (MAD). Although this change in mean absolute difference is somewhat modest, the simulated flows were much more poorly simulated; simulated flows that were within 3 percent of measured flows (La Crosse River and Mormon Creek) in the calibrated model were more than 30 percent over-simulated when recharge was increased by 25 percent. Moreover, the relation of SOSWR and MAD (or any ground-water-level summary statistic) will change depending on the parameter, as some parameters affect the ground-water-level unweighted calibration more than others, and the SOSWR includes weighted residuals of both ground-water levels and streamflow.
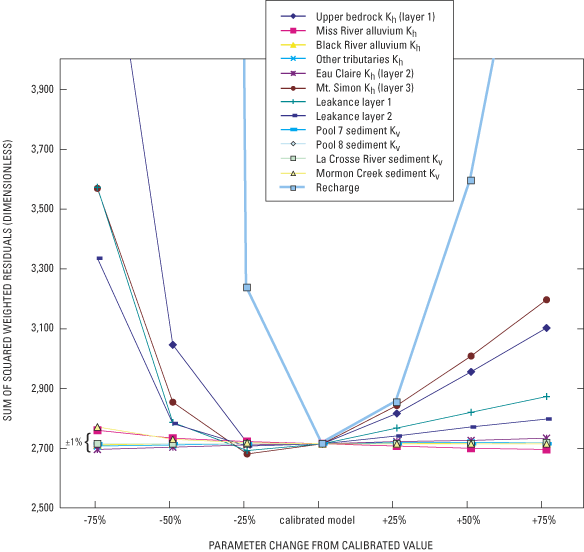
Horizontal hydraulic conductivities (Kh) of the upper bedrock aquifer (layer 1), the lower bedrock aquifer (layer 3), and the degree of vertical connection between layers (leakance layer 1 and leakance layer 2) were also sensitive, especially when varied at least +25 percent and –50 percent (fig. 9). However, the change between the calibrated value and –25% was not large for these aquifer parameters, and in some cases resulted in a small improvement in SOSWR (for example, a reduction of 25 percent in the Kh of layer 3). In practice, changes in SOSWR of less than ±1 percent (shown on fig. 9 for reference) can be considered an indication that one parameter value is not superior to another (for example, Poeter and Hill, 1998, page 26). Given how little change is observed in the SOSWR between the calibrated model and –25 percent, it is conceivable that model parameters other than recharge may be as much as 25 percent lower than the final calibrated values reported here. However, some information can be lost when looking at summary statistics such as the SOSWR. For example, the most accurate ground-water-level measurement from layer 3 (the USGS monitoring wells in the lower bedrock aquifer at Stoddard, Wis.) was better simulated (residual less than 0.1 ft) in the calibrated case than in the case where the Kh of layer 3 was reduced by 25 percent (residual = 3.64 ft).
Horizontal hydraulic conductivity of the sand and gravel aquifer in the valleys of the Mississippi and Black Rivers, and in tributary river valleys, and the vertical hydraulic conductivity of sediments that line these surface-water features were relatively insensitive. That is, large changes in these parameters did not result in a substantial change in the model calibration. The insensitivity of the sand and gravel Kh likely results from ground-water-level targets in these deposits being overly affected by nearby surface-water features. The insensitivity of the low conductivity sediments that line the surface-water features has been observed in other models in Wisconsin (for example, Hunt, 2002) and reflects the inability of commonly collected ground-water level and streamflow field data (such as was used here to calibrate the models) to assess this parameter when the sediments do not have extremely low vertical conductivities.
Simulations designed to address specific hydrologic questions can be run after the models are calibrated. These simulations can include past and present conditions, or future scenarios. Past and current (1990s) conditions are discussed in this section.
The calibrated La Crosse County model can be used to address the affects of pumping (past, current, and future) on the ground-water resource. In this study, predevelopment conditions were compared to current pumping conditions. The pre-development conditions were simulated using the calibrated model input and excluding pumping wells.
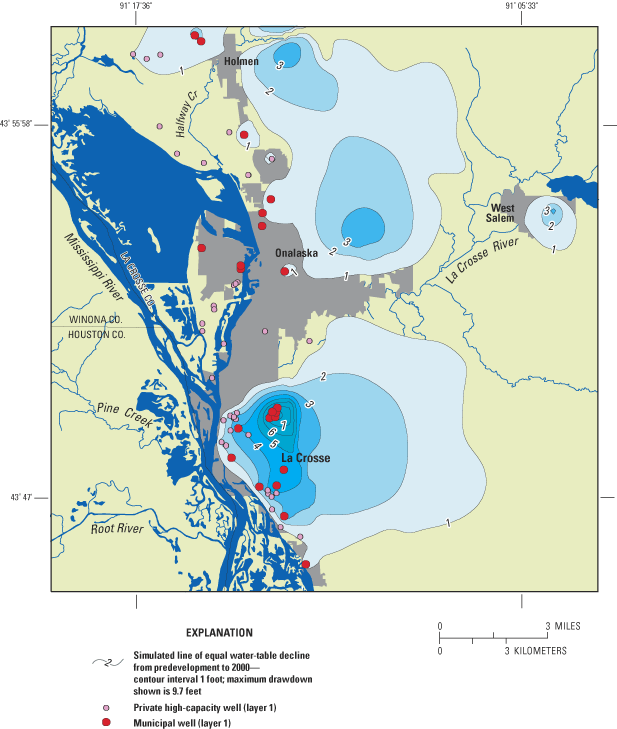
The model simulations show appreciable declines in ground-water levels beneath the city of La Crosse metropolitan area where high capacity wells are located in discrete clusters, but little to no effects were observed in other areas of the county where pumping wells are much more dispersed and discharge at lower rates. The estimated total current pumping from high-capacity wells in the metropolitan area is 19 mgd from 42 wells, most of which are drawing water from the sand and gravel aquifer. The simulated predevelopment (no pumping withdrawals) water table and potentiometric surface beneath the city of La Crosse slope gradually east-to-west toward the Mississippi River. With current pumping conditions, the water table and potentiometric surfaces beneath the city of La Crosse have each declined more than 3 feet from the predevelopment level, with the largest decline at the center of a cone of depression beneath a cluster of municipal wells (city wells #13, 14, 15, 20, and 21) near the University of La Crosse campus. The cone of depression beneath this area is more than 9 feet in the water table (fig. 10a) and about 7 feet in the potentiometric surface (fig. 10b).
Prior to development, all ground water in both the sand and gravel and the underlying lower bedrock aquifers beneath the city of La Crosse discharged into the Mississippi River. Model simulations show that with current pumping conditions, less ground water is discharging into the river and in many areas surface water from the Mississippi and La Crosse Rivers is recharging the sand and gravel aquifer (Figure 11a and 11b). The amount of ground water diverted from discharging into the river in addition to the amount of surface water pulled into the aquifer is approximately equal to the total pumpage from the high-capacity wells in the metropolitan area. Recently collected water isotope data and capture-zone modeling for La Crosse municipal wells indicate surface-water contributions to some city of La Crosse municipal wells (see Chapel and others, 2003b).
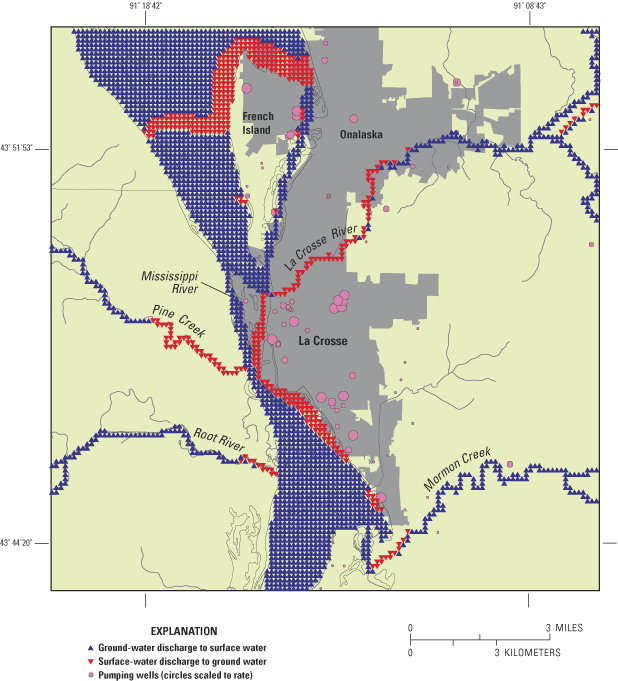
Current pumping conditions have also changed the vertical flow in the lower bedrock aquifer beneath some areas of the city. Prior to development, all vertical flow in the sandstone was upward into the sand and gravel aquifer and/or into the river. With pumping from certain wells beneath the city of La Crosse the potentiometric surface has been lowered below the water table and the vertical flow is now downward.
Ground-water flow into Pools 7 and 8 of the Mississippi River was evaluated using output from the calibrated ground-water-flow models. Modeled flows for each river node were color-coded using a GIS to show gaining and losing reaches (fig. 11). Ground-water discharges into all areas of the pools, except along the eastern shore in the vicinity of the City of La Crosse and immediately downgradient from lock and dam numbers 7 and 8 (fig. 12). Ground-water flow into the pools is generally greatest around the perimeter with decreasing amounts away from the perimeter. Ground-water flow generally decreases to a relatively uniform rate within about 3 to 4 river nodes (1,500-2,000 ft) from the edge of the widest parts of the pools. An area of relatively high ground-water discharge extends out toward the center of Pool 7 from the upper reaches of the pool. This may be associated with the absence of the confining unit in this vicinity.
As is the case with all ground-water-flow models, the LLC and Pool 8 models are a simplification of the "real world" ground-water system, and have corresponding limitations in model precision and how the model can be used. For example, the MODFLOW model discretization (node) is 500 feet by 500 feet. As a result of this discretization, the conditions within the node (ground-water level, ground-water flow) are reduced to one average value for the entire node. Therefore, even though the resolution of the model grid is relatively high, the model is not suitable for analysis of site-specific problems or issues. Hydrologic parameters and aquifer and confining unit geometry in portions of the model area are not well known at this scale. For instance, aquifer thickness and hydraulic conductivity can change vertically at intervals smaller than the current model resolution, especially near the valley bluffs.
Hydrologic and geologic data are more abundant and of better quality in the city of La Crosse portion of the model than in the other model areas. This area of the model can therefore be considered better constrained than other areas. The match between measured and simulated ground-water levels is not as good elsewhere, due largely to the fact that the bedrock geology and the hydrogeology of the Driftless Area are complex. Perched water tables and local confining conditions are common in the Driftless Area, and reported water levels may not always be representative of the water levels of the regional aquifers simulated by the model. Moreover, although the model simulated the bedrock above the Eau Claire unit as one layer, the section actually consists of several layered aquifers and confining units. Thus, if simulation of the distribution of ground-water flow in this upper bedrock is an important modeling objective, layer 1 will need to be divided into additional hydrostratigraphic layers (for example, Juckem 2003). Because of these inherent simplifying assumptions, the ground-water-flow model cannot simulate small-scale complexities of the ground-water-flow system. Finally, a modeling artifact (dry nodes) affected simulated ground-water levels and flows in the Black River valley area. Although simulation of the regional flow is representative, modeling flow near the dry nodes (Black River Bluffs area) will require additional refinement to the model.
The LLC and Pool 8 ground-water-flow models could be improved with additional hydrologic and geologic research, data collection and interpretation, and the use of additional MODFLOW options and packages. As new data become available, the model could be updated and recalibrated. The following is a list of research, data collection needs, and MODFLOW options that could enable refinements, and in turn increase the utility of the ground-water-flow models.
Ground water is the sole source of residential water supply in La Crosse County, Wis., and the Pool 8 area. Commonly, urban and county planners are faced with decisions that balance the need for increased ground-water withdrawals while maintaining the quantity and quality of ground-water-fed surface-water resources such as trout streams. Managing and protecting the ground- and surface-water resources requires an understanding of hydrologic systems. The La Crosse County (LCC) and Pool 8 models described in this report were developed to address this need. Specific objectives of the modeling were to provide a tool to locate source areas for large ground-water withdrawals by high-capacity municipal wells, and quantify ground-water discharge occurring to the Mississippi River in the La Crosse area. These models were constructed for La Crosse County and the Wisconsin Department of Natural Resources in collaboration with the Wisconsin Geologic and Natural History Survey.
The ground-water-flow models described in this report simulate the major hydrogeologic features of the modeled area, including bedrock and surficial aquifers, ground-water/surface-water interactions, and ground-water withdrawals from high-capacity wells. Simulations made with the model reproduce ground-water levels and stream base flows representative of current (1990s) conditions, and reproduce ground-water-flow patterns and directions delineated on water-table and potentiometric-surface maps. As currently calibrated, the models are suitable for use as regional water-management tools. Because of their regional focus, however, these models cannot be used for site-specific simulations. Regardless, they provide a valuable framework (regional flow patterns, boundary conditions, aquifer parameters) within which site-specific studies can be carried out.
For most efficient use, the model would require periodic updates and improvements as field data and better assessments of future hydrologic stressors become available. The model could be updated and improved with additional data collection to improve characterization of the aquifers, springs, and wetlands, and recharge distribution and magnitude. Transient calibration and the use of the Stream Routing "packages" of the MODFLOW code could improve the calibration and explicitly couple the ground-water system to the surface-water system.
Anderson, M.P., and Woessner, W.W., 1992, Applied groundwater modeling: Academic Press, Inc., San Diego, Calif., 381 p.
Chapel, D.M., Bradbury, K.R., Hunt, R.J., and Hennings, R.G., 2003a, Hydrogeology of La Crosse County, Wisconsin: Wisconsin Geological and Natural History Survey Open-File Report 2003–03, 75 p.
Chapel, D.M., Bradbury, K.R. and Hunt, R.J., 2003b, Delineation of 5-year zones of contribution for municipal wells in La Crosse County, Wisconsin: Wisconsin Geological and Natural History Survey Open-File Report 2003–02, 42 p.
Davey Engineering, 2002, Wellhead protection plan phase I—Delineation Onalaska, Wisconsin: Unpublished report to the City of Onalaska, 11 p.
Dripps, Weston, 2003, The spatial and temporal variability of ground water recharge within the Trout Lake Basin of northern Wisconsin: Madison, University of Wisconsin, Department of Geology and Geophysics, Ph.D. dissertation, 250 p.
Earth Tech, 1999, Delineation of wellhead protection areas: Unpublished report to the city of La Crosse, unpaginated.
Evans, Thomas J., 2003, Geology of La Crosse County, Wisconsin: Wisconsin Geological and Natural History Survey Bulletin 101, 33 p. and 1 plate.
Gaffield, S.J., Bradbury, K.R., and Potter, K.W., 1998, Hydrologic assessment of the Kickapoo Watershed, southwestern Wisconsin: Wisconsin Geological and Natural History Survey Open-File Report 1998–08, 81 p.
Haitjema, H.M., 1995, Analytic element modeling of groundwater flow: San Diego, Calif., Academic Press, 394 p.
Harbaugh, A.W., and McDonald, M.G., 1996, User's documentation for MODFLOW-96, an update to the U.S. Geological Survey modular finite-difference ground-water flow model: U.S. Geological Survey Open-File Report 96–485, 56 p.
Hunt, R.J., and Krohelski, J.T., 1996, The application of an analytic element model to investigate groundwater-lake interactions at Pretty Lake, Wisconsin: Journal of Lakes and Reservoir Management, v. 12, no 4., p. 487–495.
Hunt, R.J., Anderson, M.P., and Kelson, V.A., 1998a, Improving a complex finite difference groundwater-flow model through the use of an analytic element screening model. Ground Water, v. 36, no. 6, p. 1011–1017.
Hunt, R.J., Kelson, V.A., and Anderson, M.P., 1998b, Linking an analytic element flow code to MODFLOW—Implementation and benefits., MODFLOW '98, in 3rd International Conference of the International Ground Water Modeling Center, Proceedings: Golden, Colo., Colorado School of Mines. p. 497–504.
Hunt, R.J., 2002, Evaluating the importance of future data collection sites using parameter estimation and analytic element groundwater flow models, in XIV International Conference on Computational Methods in Water Resources Conference, Proceedings. Deflt, The Netherlands, p. 755-762.
Juckem, P.F., 2003, Spatial patterns and temporal trends in groundwater recharge, Upper Coon Creek Watershed, southwest Wisconsin: Madison, University of Wisconsin, Department of Geology and Geophysics, MS Thesis, 161 p.
Krohelski, J.T., Bradbury, K.R., Hunt, R.J., and Swanson, S.K., 2000, Numerical simulation of ground-water flow in Dane County, Wisconsin: Wisconsin Geological and Natural History Survey Bulletin 98, 31 p.
Mandle, R.J., and Kontis, A.L., 1992, Simulation of regional ground-water flow in the Cambrian-Ordovician aquifer system in the Northern Midwest, United States: U.S. Geological Survey Professional Paper 1405–C, p. 97.
McDonald, M.G., and Harbaugh, A.W., 1988, A modular three-dimensional finite-difference ground-water flow model: U.S. Geological Survey Techniques of Water-Resources Investigations, book 6, chap. A1, 586 p.
Ostrom, M.E., 1967, Paleozoic stratigraphic nomenclature for Wisconsin: Wisconsin Geologic and Natural History Survey Information Circular 8, 1 sheet.
Poeter, E.P., and Hill, M.C., 1998, Documentation of UCODE, a computer code for universal inverse modeling: U.S. Geological Survey Water-Resources Investigations Report 98–4080, 116 p.
Rumbaugh, J.O., and Rumbaugh, D.B., 2001, Groundwater Vistas version 3: Environmental Simulations Inc., Herndon, Va., 242 p.
Strack, O.D.L. 1989, Groundwater Mechanics: Englewood Cliffs, New Jersey, Prentice-Hall, 732 pp.
Thornthwaite, C.W., and Mather, J.R., 1957, Instructions and tables for computing potential evaporation and the water balance: Publications in Climatology, v. 10, no 3.
Young, H.L., 1992, Hydrogeology of the Cambrian-Ordovician aquifer system in the Northern Midwest, United States: U.S. Geological Survey Professional Paper 1405–B, p. 99.
[mgd, million gallons per day; DNR, Wisconsin Department of Natural Resources]
| MUNICIPAL HIGH-CAPACITY WELLS | |||||
|---|---|---|---|---|---|
| Layer | Row | Column | Rate mgd (1990 average) | DNR permit no. | County |
| 1 | 173 | 91 | 1.0954 | 626 | La Crosse |
| 3 | 162 | 195 | .4000 | 1770 | La Crosse |
| 3 | 162 | 278 | .0435 | 2906 | La Crosse |
| 1 | 140 | 104 | .3563 | 2869 | La Crosse |
| 1 | 220 | 114 | .9831 | 80909 | La Crosse |
| 1 | 110 | 89 | .3356 | 80939 | La Crosse |
| 3 | 168 | 238 | .1296 | 80899 | La Crosse |
| 3 | 170 | 238 | .0060 | 80900 | La Crosse |
| 1 | 112 | 91 | .2539 | 80903 | La Crosse |
| 1 | 235 | 100 | .3998 | 80905 | La Crosse |
| 1 | 238 | 116 | .4384 | 80906 | La Crosse |
| 1 | 223 | 111 | .9995 | 80907 | La Crosse |
| 1 | 223 | 113 | 1.0925 | 80908 | La Crosse |
| 1 | 243 | 113 | 1.3700 | 80910 | La Crosse |
| 1 | 243 | 108 | 1.0926 | 80911 | La Crosse |
| 1 | 226 | 102 | 1.2569 | 80913 | La Crosse |
| 1 | 222 | 113 | 1.6376 | 80914 | La Crosse |
| 1 | 221 | 112 | 1.3829 | 80915 | La Crosse |
| 1 | 252 | 116 | 1.6075 | 80916 | La Crosse |
| 1 | 179 | 103 | 1.0960 | 80917 | La Crosse |
| 1 | 178 | 103 | 1.0960 | 80918 | La Crosse |
| 1 | 246 | 210 | .0001 | 80921 | La Crosse |
| 1 | 248 | 208 | .0423 | 80922 | La Crosse |
| 3 | 228 | 130 | .0268 | 80923 | La Crosse |
| 3 | 249 | 129 | .0167 | 80924 | La Crosse |
| 3 | 239 | 127 | .0418 | 80925 | La Crosse |
| 3 | 235 | 127 | .0331 | 80926 | La Crosse |
| 3 | 77 | 181 | .0350 | 80927 | La Crosse |
| 1 | 163 | 109 | .2338 | 80930 | La Crosse |
| 1 | 167 | 109 | .5206 | 80931 | La Crosse |
| 1 | 159 | 112 | .5897 | 80932 | La Crosse |
| 3 | 163 | 275 | .0435 | 80934 | La Crosse |
| 3 | 169 | 190 | .0153 | 80935 | La Crosse |
| 3 | 169 | 188 | .0153 | 80936 | La Crosse |
| 1 | 266 | 122 | 1.0296 | 80937 | La Crosse |
| 1 | 180 | 116 | .5941 | 80938 | La Crosse |
| 3 | 242 | 125 | .0120 | 90182 | La Crosse |
| 1 | 195 | 91 | .0070 | 90237 | La Crosse |
| 20.3299 | TOTAL RATE | ||||
| MUNICIPAL HIGH-CAPACITY WELLS | |||||
|---|---|---|---|---|---|
| Layer | Row | Column | Rate mgd (1990 average) | DNR permit no. | County |
| 3 | 151 | 205 | 0.0500 | 386 | La Crosse |
| 1 | 55 | 51 | .8401 | 454 | Trempealeau |
| 3 | 257 | 124 | .0360 | 535 | La Crosse |
| 3 | 257 | 124 | .0380 | 536 | La Crosse |
| 3 | 181 | 173 | .0050 | 560 | La Crosse |
| 3 | 180 | 170 | .0290 | 561 | La Crosse |
| 3 | 153 | 170 | .1080 | 819 | La Crosse |
| 3 | 181 | 173 | .0050 | 828 | La Crosse |
| 1 | 198 | 110 | .1260 | 929 | La Crosse |
| 1 | 198 | 110 | .1260 | 930 | La Crosse |
| 1 | 198 | 110 | .0720 | 931 | La Crosse |
| 1 | 198 | 110 | .0720 | 932 | La Crosse |
| 3 | 45 | 303 | .1440 | 1041 | Monroe |
| 3 | 172 | 139 | .5760 | 1110 | La Crosse |
| 1 | 82 | 87 | .2000 | 1186 | La Crosse |
| 1 | 223 | 101 | .0950 | 1189 | La Crosse |
| 1 | 223 | 101 | .1700 | 1246 | La Crosse |
| 3 | 172 | 139 | .0750 | 1255 | La Crosse |
| 1 | 222 | 102 | .1250 | 1345 | La Crosse |
| 1 | 276 | 111 | .0280 | 1430 | La Crosse |
| 1 | 282 | 111 | .0140 | 1431 | La Crosse |
| 1 | 282 | 111 | .0650 | 1432 | La Crosse |
| 1 | 287 | 108 | .0140 | 1433 | La Crosse |
| 1 | 287 | 108 | .0130 | 1434 | La Crosse |
| 1 | 282 | 111 | .0070 | 1435 | La Crosse |
| 3 | 282 | 114 | .0140 | 1437 | La Crosse |
| 3 | 209 | 170 | .2400 | 1476 | La Crosse |
| 1 | 228 | 105 | .1200 | 1900 | La Crosse |
| 1 | 116 | 79 | .7200 | 1926 | La Crosse |
| 1 | 21 | 51 | .3240 | 2042 | Trempealeau |
| 1 | 222 | 100 | .3420 | 2076 | La Crosse |
| 1 | 117 | 75 | .0800 | 2135 | La Crosse |
| 3 | 208 | 119 | .0900 | 2203 | La Crosse |
| 1 | 79 | 37 | .7200 | 2250 | Trempealeau |
| 3 | 8 | 266 | .0720 | 2274 | Monroe |
| 1 | 60 | 6 | .0060 | 2558 | Trempealeau |
| 1 | 60 | 6 | .0060 | 2559 | Trempealeau |
| 1 | 60 | 3 | .0040 | 2562 | Trempealeau |
| 3 | 111 | 116 | .7200 | 2725 | La Crosse |
| 1 | 224 | 98 | .2500 | 2733 | La Crosse |
| 1 | 223 | 101 | .2000 | 2774 | La Crosse |
| 1 | 245 | 113 | .2450 | 2968 | La Crosse |
| 1 | 244 | 111 | .5760 | 3000 | La Crosse |
| 1 | 246 | 112 | .2160 | 3001 | La Crosse |
| 1 | 89 | 27 | .8641 | 3003 | Trempealeau |
| 3 | 282 | 111 | .0180 | 3118 | La Crosse |
| 1 | 223 | 101 | .0720 | 3427 | La Crosse |
| 1 | 223 | 101 | .2000 | 3496 | La Crosse |
| 3 | 34 | 231 | .7200 | 12101 | Jackson |
| 3 | 37 | 237 | 0.7200 | 12102 | Jackson |
| 3 | 29 | 244 | .6000 | 12103 | Jackson |
| 1 | 255 | 115 | .3600 | 14201 | La Crosse |
| 3 | 191 | 137 | .0280 | 14203 | La Crosse |
| 1 | 83 | 76 | .3600 | 14204 | La Crosse |
| 1 | 63 | 82 | .0480 | 14205 | La Crosse |
| 3 | 54 | 179 | .8641 | 14208 | La Crosse |
| 3 | 49 | 205 | .7200 | 14209 | La Crosse |
| 1 | 137 | 79 | .8641 | 14210 | La Crosse |
| 3 | 41 | 171 | .3360 | 14211 | La Crosse |
| 3 | 43 | 148 | .3840 | 14212 | La Crosse |
| 1 | 79 | 80 | .2400 | 14213 | La Crosse |
| 3 | 172 | 178 | .0320 | 14214 | La Crosse |
| 3 | 78 | 208 | .3600 | 14215 | La Crosse |
| 1 | 90 | 85 | .3600 | 14216 | La Crosse |
| 1 | 147 | 112 | .2880 | 14217 | La Crosse |
| 3 | 133 | 281 | .9601 | 20212 | Monroe |
| 3 | 37 | 316 | .4320 | 20216 | Monroe |
| 3 | 115 | 292 | .3600 | 20221 | Monroe |
| 1 | 60 | 35 | .7200 | 31903 | Trempealeau |
| 1 | 63 | 30 | .7200 | 31905 | Trempealeau |
| 1 | 63 | 27 | .7200 | 31906 | Trempealeau |
| 1 | 66 | 51 | .7200 | 31908 | Trempealeau |
| 1 | 78 | 11 | .8641 | 31910 | Trempealeau |
| 1 | 70 | 9 | .7200 | 31911 | Trempealeau |
| 1 | 41 | 4 | 1.2961 | 31913 | Trempealeau |
| 1 | 50 | 46 | .5760 | 31917 | Trempealeau |
| 1 | 69 | 26 | .8641 | 31918 | Trempealeau |
| 1 | 81 | 29 | .7561 | 31919 | Trempealeau |
| 1 | 70 | 47 | .7200 | 31920 | Trempealeau |
| 1 | 68 | 36 | 1.2001 | 31922 | Trempealeau |
| 1 | 50 | 38 | .7200 | 31925 | Trempealeau |
| 1 | 68 | 43 | .7200 | 31926 | Trempealeau |
| 1 | 31 | 4 | .7200 | 31929 | Trempealeau |
| 1 | 76 | 51 | .8641 | 31930 | Trempealeau |
| 1 | 68 | 35 | .7200 | 31931 | Trempealeau |
| 1 | 60 | 51 | .7200 | 31932 | Trempealeau |
| 1 | 59 | 42 | .7200 | 31933 | Trempealeau |
| 1 | 65 | 9 | .7200 | 31934 | Trempealeau |
| 1 | 42 | 15 | .7200 | 31935 | Trempealeau |
| 1 | 48 | 5 | .7200 | 31937 | Trempealeau |
| 1 | 84 | 24 | .7200 | 31938 | Trempealeau |
| 1 | 90 | 31 | .7200 | 31939 | Trempealeau |
| 1 | 245 | 111 | .1280 | 51202 | La Crosse |
| 1 | 231 | 98 | .3027 | 51206 | La Crosse |
| 1 | 148 | 92 | .0660 | 51215 | La Crosse |
| 1 | 148 | 92 | .0660 | 51216 | La Crosse |
| 1 | 148 | 92 | 0.1600 | 51217 | La Crosse |
| 1 | 145 | 84 | .0250 | 51219 | La Crosse |
| 3 | 191 | 122 | .1500 | 51220 | La Crosse |
| 1 | 200 | 123 | .3600 | 51221 | La Crosse |
| 1 | 145 | 84 | .1300 | 51223 | La Crosse |
| 3 | 231 | 98 | .2000 | 51224 | La Crosse |
| 1 | 230 | 97 | 1.1520 | 51225 | La Crosse |
| 1 | 211 | 94 | .0300 | 51226 | La Crosse |
| 1 | 250 | 112 | .2000 | 51227 | La Crosse |
| 1 | 250 | 112 | .2000 | 51228 | La Crosse |
| 3 | 221 | 91 | .0489 | 71861 | La Crosse |
| 3 | 221 | 91 | .0050 | 71862 | La Crosse |
| 3 | 221 | 91 | .1320 | 71863 | La Crosse |
| 3 | 221 | 91 | .1320 | 71864 | La Crosse |
| 1 | 258 | 120 | .0280 | 80802 | La Crosse |
| 1 | 258 | 120 | .0280 | 80803 | La Crosse |
| 1 | 139 | 99 | .0060 | 80810 | La Crosse |
| 1 | 139 | 99 | .0250 | 80811 | La Crosse |
| 1 | 223 | 101 | .0620 | 80812 | La Crosse |
| 3 | 274 | 135 | .0300 | 80813 | La Crosse |
| 1 | 274 | 135 | .0020 | 80814 | La Crosse |
| 3 | 203 | 178 | .0380 | 80816 | La Crosse |
| 1 | 191 | 95 | .0800 | 80818 | La Crosse |
| 3 | 45 | 80 | .0080 | 80819 | La Crosse |
| 3 | 45 | 80 | .0060 | 80820 | La Crosse |
| 1 | 183 | 102 | .3753 | 80821 | La Crosse |
| 1 | 184 | 101 | .4709 | 80822 | La Crosse |
| 1 | 184 | 101 | .8017 | 80823 | La Crosse |
| 1 | 198 | 91 | .1680 | 80824 | La Crosse |
| 1 | 190 | 95 | .0720 | 80825 | La Crosse |
| 3 | 166 | 256 | .1680 | 80826 | La Crosse |
| 3 | 264 | 133 | .0110 | 80827 | La Crosse |
| 3 | 266 | 133 | .0150 | 80828 | La Crosse |
| 1 | 116 | 71 | .1480 | 80829 | La Crosse |
| 3 | 153 | 142 | .0500 | 80832 | La Crosse |
| 1 | 201 | 98 | .5760 | 80833 | La Crosse |
| 1 | 152 | 105 | .0100 | 80834 | La Crosse |
| 1 | 152 | 105 | .1000 | 80835 | La Crosse |
| 1 | 116 | 71 | .0960 | 80836 | La Crosse |
| 3 | 259 | 151 | .2880 | 80837 | La Crosse |
| 3 | 159 | 237 | .0140 | 80838 | La Crosse |
| 1 | 223 | 101 | .1750 | 80841 | La Crosse |
| 1 | 223 | 101 | .0200 | 80843 | La Crosse |
| 1 | 227 | 100 | .2160 | 80844 | La Crosse |
| 3 | 191 | 129 | .1200 | 80933 | La Crosse |
| 1 | 29 | 43 | .2200 | 86851 | Trempealeau |
| 1 | 84 | 8 | .2520 | 86859 | Trempealeau |
| 1 | 76 | 8 | .2520 | 86860 | Trempealeau |
| 1 | 311 | 222 | .0820 | 87063 | Vernon |
| 45.3324 | TOTAL RATE | ||||
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|