USGS Bulletin 1450: Coal Resource Classification System

COAL RESOURCE CLASSIFICATION SYSTEM OF THE U.S. BUREAU OF MINES AND U.S. GEOLOGICAL SURVEY

Mineral Resource Classification Systems of the U.S. Bureau of Mines and the U.S. Geological Survey

A report published jointly by the U.S. Bureau of Mines and U.S. Geological Survey. Definitions of coal resource classification terms used by the U.S. Bureau of Mines and U.S. Geological Survey.

In order to use mineral resource terms with precision and common understanding and to compare resource data effectively, a joint U.S. Bureau of Mines and U.S. Geological Survey work group developed a standardized, definitive, broadly applicable classification system to derive uniform, coordinated resource estimates. The principles of the system are given in Chapter A of this series (Bulletin 1450-A). This chapter presents the classification system for coal resources. Future chapters will present classification terms for other specific commodities.

This method of classification is in conformity with the provisions of the Joint Geological Survey-Bureau of Mines Resource Classification Agreement of November 21, 1973, covering all mineral resources and will be used in future resource/reserve studies on coal conducted by agencies of the Department of the Interior. All resource and reserve estimates will be dated.

Within this system, the term "coal resource" designates the estimated quantity of coal in the ground in such form that economic extraction is currently or potentially feasible. The "coal reserve" is that part of the resource for which rank, quality, and quantity have been reasonably determined and which is deemed to be minable at a profit under existing market conditions.

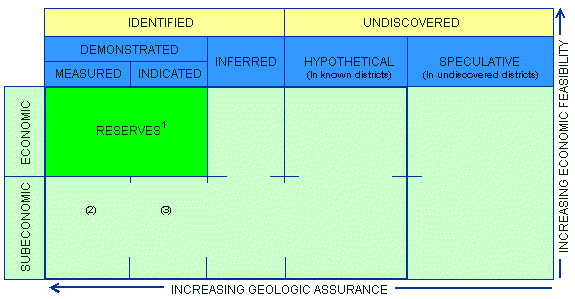
This system employs a concept by which coal beds are classified in terms of their degree of geologic identification and economic and technologic feasibility of recovery. In the following conceptual diagram (figure 1) showing the relationship of the various factors involved, coal resources are located on the horizontal scale, increasingly to the left, according to their degree of geological assurance of existence, and on the vertical scale, increasingly upward, according to their degree of economic and technologic feasibility of recovery.

Figure 1. Classification of coal resources.

¹Recovery factor = _________.
² Includes ______ billion tons of Reserve Base coal that are not currently minable. (see recovery factor)
³Includes ______ billion tons of Reserve Base that are not currently minable. (see recovery factor)

Total Remaining Resources _______.
Cumulative Production __________.
Total Original Resources _________.

Average Production, (5 yr. period) ________ million short tons.
Production, (most recent year) ___________ million short tons.

The following general definitions of coal resource categories are amplified by the criteria for resource identification, which follow the Glossary. The criteria may be revised to reflect changing conditions without affecting the definitions.

Resources: Concentrations of coal in such forms that economic extraction is currently or may become feasible.

Identified Resources: Specific bodies of coal whose location, rank, quality, and quantity are known from geologic evidence supported by engineering measurements.

Undiscovered Resources: Unspecified bodies of coal surmised to exist on the basis of broad geologic knowledge and theory.

Reserve Base: That portion of the Identified Coal Resource from which Reserves are calculated.

Reserve: That portion of the Identified Coal Resource that can be economically mined at the time of determination. The reserve is derived by applying a Recovery Factor to that component of the Identified Coal Resource designated as the Reserve Base.

Recovery Factor: The percentage of total tons of coal estimated to be recoverable from a given area in relation to the total tonnage estimated to be in the Reserve Base in the ground.

Identified Subeconomic Resources: The part of coal resources that occurs in Demonstrated and Inferred Resources that is not now minable economically.

Hypothetical Resources: Undiscovered Coal Resources in beds that may reasonably be expected to exist in known mining districts under known geologic conditions. In general, Hypothetical Resources are in broad areas of coal fields where points of observation are absent and evidence is from distant outcrops, drill holes, or wells. Exploration that confirms their existence and reveals quantity and quality will permit their reclassification as a Reserve or Identified Subeconomic Resource.

Speculative Resources: Undiscovered coal in beds that may occur either in known types of deposits in a favorable geologic setting where no discoveries have been made, or in deposits that remain to be recognized. Exploration that confirms their existence and reveals quantity and quality will permit their reclassification as Reserves or Identified Subeconomic Resources.

The following definitions are applicable to both the Reserve and Identified Subeconomic Resource components:

Measured: Coal for which estimates of the rank, quality, and quantity have been computed, within a margin of error of less than 20 percent, from sample analyses and measurements from closely spaced and geologically well-known sample sites.

Indicated: Coal for which estimates of the rank, quality, and quantity have been computed partly from sample analyses and measurements and partly from reasonable geologic projections.

Demonstrated: A collective term for the sum of coal in both Measured and Indicated Resources and Reserves.

Inferred: Coal in unexplored extensions of Demonstrated Resources for which estimates of the quality and size are based on geologic evidence and projection.

Rank: The classification of coals relative to other coals, according to their degree of metamorphism, or progressive alteration, in the natural series from lignite to anthracite (Classification of Coal by Rank, 1938, American Society for Testing Materials, ASTM Designation D-388-38, p. 77-84).

Quality or Grade: Refers to individual measurements such as heat value, fixed carbon, moisture, ash, sulfur, phosphorus, major, minor, and trace elements, coking properties, petrologic properties, and particular organic constituents. The individual quality elements may be aggregated in various ways to classify coal for such special purposes as metallurgical, gas, petrochemical, and blending usages.

Estimates of the different classes of coal resources and reserves are arbitrarily based upon three criteria: (1) thickness, rank, and quality of the coal bed, (2) depth of the coal bed, and (3) the proximity of the coal resource data upon which the estimate was based. Depth and thickness are criteria because they control economic and technologic feasibility of recovery. The criteria for each class are described below and summarized in table 1 and will be used in preparing all Department of the Interior coal resource/ reserve estimates from January 1, 1975, until further revised.

These criteria apply only to those coal bodies that are or will be economically extractable by underground, surface, and/or in situ methods. Coal thinner than 14 inches (35 cm) (anthracite and bituminous) and 30 inches (75 cm) (subbituminous and lignite) and all coal deeper than 6,000 feet (1,800 m) is excluded. These thinner and deeper coals will be considered at a later date. Coal containing more than 33 percent ash is excluded from resource and reserve estimates.

Identified Resources: Include beds of bituminous coal and anthracite 14 inches (35 cm) or more thick and beds of subbituminous coal and lignite 30 inches (75 cm) or more thick that occur at depths to 6,000 feet (1,800 m), and whose existence and quantity have been delineated within specified degrees of geologic assurance as measured, indicated, or inferred. Include also thinner and/or deeper beds that presently are being mined or for which there is evidence that they could be mined commercially.

Undiscovered Resources: Include beds of bituminous coal and anthracite 14 inches (35 cm) or more thick and beds of subbituminous coal and lignite 30 inches (75 cm) or more thick that are presumed to occur in unmapped and unexplored areas to depths of 6,000 feet (1,800 m).

Remaining Resources: Includes the sum of the Identified and Undiscovered Resources as of the date of the estimate.

Cumulative Production: Includes the sum of all production prior to the date of the estimate.

Total Original Resources: Includes the sum of the Remaining Resources and Cumulative Production as of the date of the estimate.

Reserve Base: Includes beds of bituminous coal and anthracite 28 inches (70 cm) or more thick and beds of subbituminous coal 60 inches (150 cm) or more thick that occur at depths to 1,000 feet (300 m). Includes also thinner and/or deeper beds that presently are being mined or for which there is evidence that they could be mined commercially at this time. Includes beds of lignite 60 inches (150 cm) or more thick which can be surface minedCgenerally those that occur at depths no greater than 120 feet (40 m).

Reserve: Includes that portion of the Reserve Base that can be mined at the time of classification (See Recovery Factor).

Recovery Factor: On a national basis, the estimated Recovery Factor for the total Reserve Base is 50 percent. More precise recovery factors can be computed by determining the total coal in place and the total coal recoverable in any specific locale.

Subeconomic Resources: Include all Identified Resources that do not fall into the Reserve category. Include in this category beds of bituminous coal and anthracite 14 inches (35 cm) to 28 inches (70 cm) thick and beds of subbituminous coal 30 inches (75 cm) to 60 inches (150 cm) thick that occur at depths to 1,000 feet (300 m). Include also beds of bituminous coal and anthracite 14 inches (35 cm) or more thick and beds of subbituminous coal 30 inches (75 cm) or more thick that occur at depths between 1,000 (300 m) and 6,000 feet (1,800 m). Include lignite beds 30 inches (75 cm) or more thick that cannot be surface minedCgenerally those that occur at depths greater than 120 feet (40 m), and lignite beds 30 inches (75 cm) to 60 inches (150 cm) thick that can be surface mined. Include the currently nonrecoverable portion of the Reserve Base.

The following criteria are applicable to both the Reserve and Subeconomic Resources components:

Measured: Resources are computed from dimensions revealed in outcrops, trenches, mine workings, and drill holes. The points of observation and measurement are so closely spaced and the thickness and extent of coals are so well defined that the tonnage is judged to be accurate within 20 percent of true tonnage. Although the spacing of the points of observation necessary to demonstrate continuity of the coal differs from region to region according to the character of the coal beds, the points of observation are no greater than 1/2 mile (0.8 km) apart. Measured coal is projected to extend as a 1/4-mile (0.4 km) wide belt from the outcrop or points of observation or measurement.

Indicated: Resources are computed partly from specified measurements and partly from projection of visible data for a reasonable distance on the basis of geologic evidence. The points of observation are 1/2 (0.8 km) to 1 1/2 miles (2.4 km) apart. Indicated coal is projected to extend as a l/2-mile (0.8 km) wide belt that lies more than l/4 mile (0.4 km) from the outcrop or points of observation or measurement.

Inferred: Quantitative estimates are based largely on broad knowledge of the geologic character of the bed or region and where few measurements of bed thickness are available. The estimates are based primarily on an assumed continuation from Demonstrated coal for which there is geologic evidence. The points of observation are 1 1/2 (2.4 km) to 6 miles (9.6 km) apart. Inferred coal is projected to extend as a 2 1/4-mile (3.6 km) wide belt that lies more than 3/4 mile (1.2 km) from the outcrop or points of observation or measurement.

Hypothetical Resources: Quantitative estimates are based on a broad knowledge of the geologic character of a coal bed or region. Measurements of coal thickness are more than 6 miles (9.6 km) apart. The assumption of continuity of a coal bed is supported only by geologic evidence.

Speculative Resources: Quantitative estimates are based on geologic assumptions that undiscovered coal may occur in known types of deposits or in favorable geologic settings.