[an error occurred while processing this directive]
C
Statistical Design of Water-Level Monitoring Networks
U.S. Geological Survey Circular 1217
Previous Section: Uses and
Importance of Long-Term Water-Level Data
Next Section: Status of Water-Level
Data-Collection Programs
Return to Table of Contents
Return to Home Page
Statistical techniques have found limited application to the design of water-level
monitoring networks for several reasons. First, sufficient data are needed to
reliably estimate the parameters required by the techniques. Second, water-level
monitoring networks typically have multiple objectives, some of which are difficult
to express quantitatively. Despite these limitations, statistical analysis of
data from existing networks can provide useful guidance in evaluating these
networks and a firmer basis for network modifications. Examples of the use of
two well-known statistical techniques, geostatistical analysis and principal-components
analysis, are described here.
Geostatistical Analysis
Geostatistics encompasses a set of probabilistic techniques aimed at determining
estimates of spatial data (in this case, water levels) at unmeasured locations
as combinations of nearby measured values. The method provides estimates of
uncertainty that can be used to aid network design.
A typical application of geostatistics is to evaluate the relation between
the number or density of monitoring wells and the uncertainty of a potentiometric
map. Olea (1984) presented an example of
this type of application for the Equus Beds aquifer, an intensively used aquifer
in central Kansas. A map of the water-table elevation in the Equus Beds aquifer,
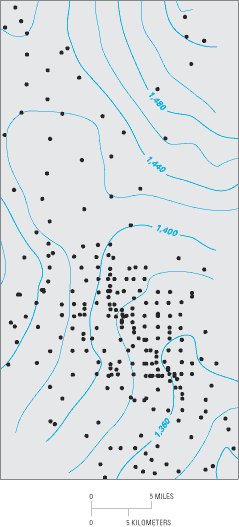
based on data from the existing network of 244 observation wells, is shown in
Figure C–1. Note that the density of monitoring wells
in Figure C–1 is not homogeneous—about 80 percent
of the wells are located in the southern half of the area. From this network,
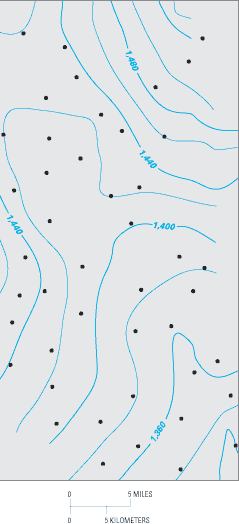
Olea (1984) identified a reduced network
of 47 wells by laying a regular hexagonal pattern (Figure C–2)
over the area and randomly selecting from among the existing monitoring wells
in each hexagon. A map of water-table elevation based on the revised network
of 47 wells is shown in Figure C–3 and is similar
to the map shown in Figure C–1. About 95 percent of
the values in the two contour map grids differ by less than 5 percent. From
the geostatistical analysis, the estimated average standard error of the water-table
elevations increased about 20 percent from 10 feet for the map of Figure
C–1 to 12 feet for the map shown in Figure C–3.
|
|
| Figure C–1. Water-table elevation in the
Equus Beds aquifer, based on data from network of 244 observation
wells. Circles show locations of observation wells. (Modified
from Olea, 1984.) |
|
|
|
|
| Figure C–2. Example of hexagonal sampling.
Olea (1984) found the hexagonal
pattern to be more efficient than a square pattern for selecting
wells. |
|
|
|
| Figure C–3. Water-table elevation in the Equus
Beds aquifer, based on data from network of 47 wells selected using 16-square-mile
hexagons. Circles show locations of observation wells. (Modified
from Olea, 1984.) |
Information provided by the previously described type of analysis may lead to
reductions in the number of monitoring wells in some areas. The savings can
be used to establish additional monitoring wells in areas with less adequate
coverage, to increase the frequency of measurement, or to otherwise upgrade
the network. The limitations of this type of analysis should be kept fully in
mind, however, in that the analysis focuses on the overall ability to accurately
represent a regional potentiometric surface. Other objectives of the network
might need to be factored into any decisions about network design, such as objectives
to quantify drawdowns in particular areas, to identify possible flow paths for
water-quality analysis, or to evaluate the interactions of ground water and
surface water. Likewise, geostatistical analysis assumes that further ground-water
development will not greatly alter the estimated spatial correlations.
Principal-Components Analysis
Principal-components analysis (PCA) is a data transformation technique used
to search for structure in multivariate data sets. The goal of PCA is to determine
a few linear combinations (principal components) of the original variables that
can be used to summarize the data without losing much information. An example
of PCA applied to water-level measurements near Williams Lake in Minnesota is
discussed here (Winter and others, 2000).
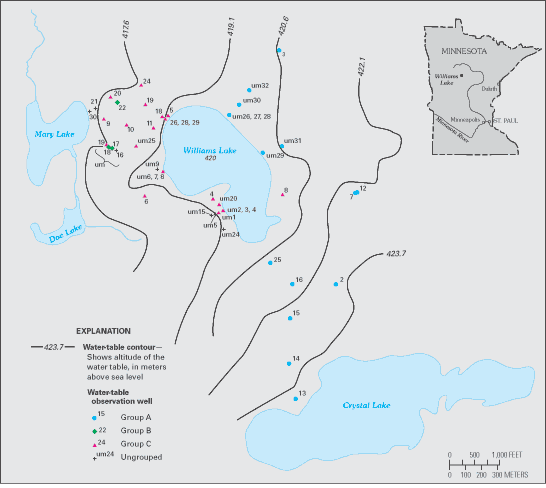
Williams Lake is located in the glacial terrain of northern Minnesota. More
than 300 measurements of water levels were made at each of 50 wells surrounding
the lake (Figure C–4). In applying PCA to these data,
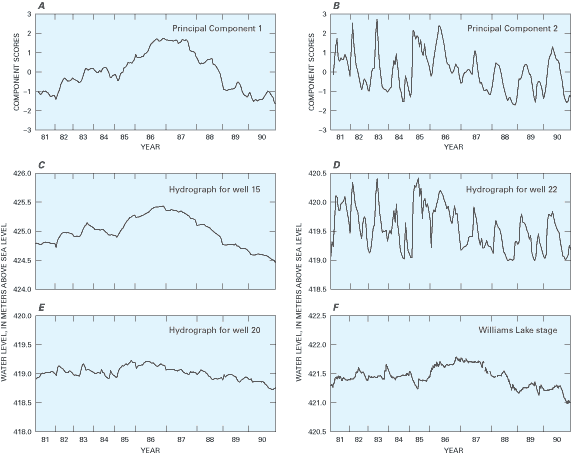
the first two principal components (PC–1 and PC–2) were found to mimic
basic patterns of water-level fluctuations in the wells and together accounted
for 93 percent of the variance (variability) in the water-level data. For example,
in Figure C–5, compare the hydrograph of water levels
for well 15 with the graph of component scores for PC–1. Likewise, compare
the hydrograph of water levels for well 22 with the graph of component scores
for PC–2. A third hydrograph, for well 20, appears to be a mixture of PC–1
and PC–2.
|
|
| Figure C–4. Location of observation wells near
Williams Lake in Minnesota. Well groups are based on the delineations shown
in Figure C–6 and discussed in the text. (Modified
from Winter and others, 2000.) |
|
|
| Figure C–5. Selected graphs for the Williams Lake
area of Minnesota, including (A) component scores for principal component
1, (B) component scores for principal component 2, (C) water level in well
15, (D) water level in well 22, (E) water level in well 20, and (F) stage
of Williams Lake. The variable spacing for each year on the x-axis reflects
the number of measurements made for the year at each site. Principal-components
analysis requires that measurements be made for all wells for each date
used in the analysis, but the number of measurements per year can vary.
(Modified from Winter and others, 2000.) |
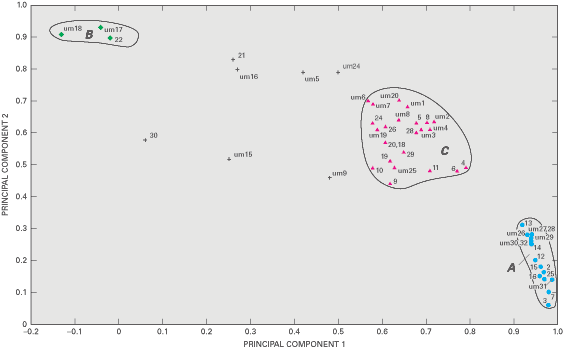
The relative weighting of the water-level patterns represented by PC–1
and PC–2 for a well are reflected in the principal-component loadings.
The component loadings are the correlation coefficients between the water-level
measurements for the well and each principal component. A plot of the component
loadings for each well with respect to PC–1 and PC–2 (Figure
C–6) indicates that most wells fall into three groups. A large number
of wells have high loadings on PC–1 and low loadings on PC–2 (Group
A). At the other extreme, a few wells have high loadings on PC–2 and low
loadings on PC–1 (Group B). Many wells have relatively high loadings on
both PC–1 and PC–2 (Group C). Wells 15, 22, and 20, whose hydrographs
are plotted in Figure C–5, are examples of wells from
Groups A, B, and C, respectively.
The three patterns of water-table fluctuations reflect variations in recharge
as related to the depth to the water table and whether the wells are upgradient
or downgradient from the lake. For example, all Group A wells are upgradient
from Williams Lake, and the water table is relatively deep at these wells. In
contrast, the water table is very shallow at the three Group B wells. All but
one of the Group C wells are downgradient from Williams Lake, and the pattern
of water-table fluctuations shows some similarity to the stage of Williams Lake
(Figure C–5).
The results of the PCA thus provide some basic insights into the similarities
and dissimilarities in patterns of water-level fluctuations among the wells
and might be useful in selecting wells for long-term monitoring. For example,
a first consideration might be to select wells from each of the three groups.
In addition, wells that fall outside the three groups might be individually
reviewed to consider whether they represent critical hydrologic settings for
long-term monitoring not represented by wells in the three groups.
Return to top
[an error occurred while processing this directive]