Fact Sheet 2006-3004
U.S. GEOLOGICAL SURVEY
Fact Sheet 2006-3004
Prepared in cooperation with the Bureau of Land Management
By Blakemore E. Thomas
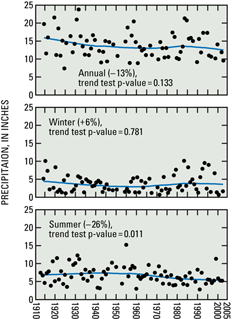
Figure 3. Trends in annual and seasonal pre-cipitation at Tombstone, Arizona. Lines are LOWESS fit to data.
Total annual streamflow of the San Pedro River at Charleston in southeastern Arizona (fig. 1) decreased by about 66 percent from 1913 to 2002 (fig. 2). The San Pedro River is one of the few remaining free-flowing perennial streams in the arid Southwestern United States, and the riparian forest along the river supports several endangered species and is an important habitat for migratory birds. The decreasing trend in streamflow has led to concerns that riparian habitat may be damaged and that overall long-term water supply for a growing population may be threatened. Resource managers and the public have an interest in learning more about the trend and the possible causes of the trend.
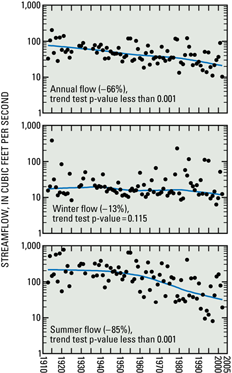
Figure 2. Trends in annual and seasonal streamflow of San Pedro River at Charleston, Arizona. Lines are LOWESS fit to data.
Thomas and Pool (2006) investigated the decreasing trends in streamflow of the San Pedro River. Their study evaluated trends in seasonal streamflows and trends in the relation between precipitation and streamflow. The purpose of this fact sheet is to summarize results of the detailed study by Thomas and Pool (2006).
Changes in total annual streamflow of the San Pedro River at Charleston, Arizona, were greater than changes in annual precipitation at Tombstone, Arizona, for the same period (1913–2002; figs. 2 and 3). Annual precipitation decreased by 13 percent, and annual streamflow decreased by 66 percent. Winter precipitation and streamflow changed by a small amount, but summer precipitation decreased by 26 percent, and summer streamflow decreased by 85 percent.
Possible factors that could have caused the decreasing trends in streamflow were trends in precipitation, changes in watershed characteristics, and human activities. The variation in streamflow caused by variation in precipitation was statistically removed. Thus, the remaining variation or trend in streamflow can be attributed to factors other than precipitation.
Two methods were used to partition the variation in streamflow and to determine trends in the partitioned variation: (1) regression analysis between precipitation and streamflow and statistical tests of time trends in regression residuals, and (2) development of regression equations between precipitation and streamflow for three time periods (early, middle, and late parts of the record) and testing to determine if the three regression equations (rainfall-runoff relations) are significantly different. Method 1 was applied to monthly values of total flow (average flow) and low flow (3-day low flow), and method 2 was applied to total flows. The low flows are roughly analogous to base flow, which is ground-water discharge to the river.
| Month of total streamflow1 | Months of precipitation used in LOWESS regression equation2 | R2 for regression equation |
|---|---|---|
| Jan. | Oct., Nov., Dec., Jan. | 0.81 |
| Feb. | Dec., Jan., Feb. | .80 |
| Mar. | Jan., Feb., Mar. | .66 |
| Apr. | Jan., Feb., Mar. | .50 |
| May | Jan., Feb., Mar. | .52 |
| June | Dec., Jan., Mar., June | .73 |
| July | Jan., May., June, July | .70 |
| Aug. | Feb., July, Aug. | .64 |
| Sept. | May, Aug., Sept. | .62 |
| Oct. | May, Sept., Oct. | .77 |
| Nov. | June, Oct., Nov. | .74 |
| Dec. | Oct., Nov., Dec. | .78 |
|
1Time period for analysis was 1913–2002. 2LOWESS regression model: log Qn = log P1 + log P2 + log Pn, where Qn is average streamflow for month n, in cubic feet per second, and Pn is precipitation for month n, in inches. |
||
| Month of total streamflow1 | Months of precipitation used in LOWESS regression equation2 | R2 for regression equation |
|---|---|---|
| Jan. | Oct., Nov., Dec., Jan. | 0.80 |
| Feb. | Nov., Dec., Jan. | .82 |
| Mar. | Jan., Feb., Mar. | .58 |
| April | Jan., Feb., Mar. | .60 |
| May | Nov., Dec., Jan., Mar. | .75 |
| June | Dec., Jan., June | .57 |
| July | Apr., May, June, July | .81 |
| Aug. | Dec., July, Aug. | .67 |
| Sept. | Jan., Aug., Sept. | .60 |
| Oct. | May, Aug., Sept. | .66 |
| Nov. | Aug. and Oct. | .65 |
| Dec. | Aug., Oct., Nov. | .59 |
|
1Time period for analysis was 1913–2002. 2LOWESS regression model: log Qn = log P1 + log P2 + log Pn, where Qn is average streamflow for month n, in cubic feet per second, and Pn is precipitation for month n, in inches. |
||
An important feature of the statistical analysis in the study is that it provides objective criteria for making decisions and interpretations about the data The statistical tests for trends result in a p-value. The p-value is a measure of the strength of evidence (data) for determining if the change in flow over time is a random occurrence or if it is a significant trend that did not occur by chance. As the p-value decreases, the evidence to support a conclusion for a trend becomes stronger. A threshold significance level of 0.05 was used in the study; a p-value of less than 0.05 means that the trend is considered significant. A p-value of 0.05 means that there is a 5-percent probability that the conclusion for a trend is incorrect.
The regression analysis between precipitation and streamflow (method 1) was done by using a regression-smoothing technique called locally weighted scatterplot smoothing (LOWESS) (Cleveland, 1979; Insightful, 2001). This nonlinear technique was used because the relation between precipitation and streamflow is not linear. Examples of the nonlinear relations are shown for February and July in figure 4.
The LOWESS analyses were successful in explaining much of the variation in streamflow (tables 1 and 2). Generally, precipitation for the same month as streamflow and precipitation for several preceding months were used in the LOWESS equations. The R2 values shown in tables 1 and 2 represent the amount of variation in streamflow that is explained by precipitation. Thus, precipitation in December, January, and February explained 80 percent of the variation in total streamflow for February. The advantage of using several months of precipitation instead of just one month of precipitation is evident in the comparison of the R2 values of single-variable LOWESS equations to the R2 values of multivariable equations. For February, the R2 value was 0.36 for a single-variable equation and 0.80 for a multivariable equation; for July, the R2 value was 0.33 for one variable and 0.70 for multiple variables (table 1 and fig. 4).
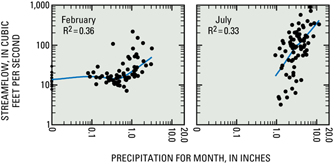
Figure 4. Examples of LOWESS fits to precipitation at Tombstone and streamflow of the San Pedro River at Charleston, Arizona, February and July.
To determine if factors other than precipitation caused trends in total flows and low flows, the residuals from the LOWESS multivariable analyses were tested for trends using a Kendall tau statistical test (Helsel and Hirsch, 1992). The LOWESS residual (measured minus predicted value) represents streamflow with the variability caused by precipitation removed. Trends in the residuals are trends caused by factors other than variation in precipitation. Residual trends are also trends in the relation between precipitation and streamflow.
Factors other than precipitation caused significant trends in total flows for June-December and did not cause significant trends for January-May (table 3). For low flows, factors other than precipitation caused significant trends for May, June, and August-December and did not cause significant trends for January-April and July (table 4). Thus, a seasonal pattern was determined with significant trends in summer, fall, and early winter flows, and no significant trends in late winter and spring flows. Examples of trends in streamflow and trends in streamflow adjusted for variation in precipitation (LOWESS residuals) are shown for February and July in figure 5.
| Month | Total streamflow, 1913–2002 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kendall tau trend test | |||||||||||||
| Streamflow and time | Adjusted streamflow and time1 | ||||||||||||
| Slope2 | p-value | Slope2 | p-value | ||||||||||
| Jan. | n | 0.017 | n | 0.208 | |||||||||
| Feb. | n | .930 | p | .428 | |||||||||
| Mar. | n | .996 | p | .487 | |||||||||
| Apr. | p | .542 | p | .638 | |||||||||
| May | n | .081 | n | .449 | |||||||||
| June | n | .001 | n | <.001 | |||||||||
| July | n | <.001 | n | .007 | |||||||||
| Aug. | n | <.001 | n | .001 | |||||||||
| Sept. | n | <.001 | n | <.001 | |||||||||
| Oct. | n | .029 | n | <.001 | |||||||||
| Nov. | n | <.001 | n | <.001 | |||||||||
| Dec. | n | .018 | n | <.001 | |||||||||
|
1Variation in streamflow that was caused by variation in precipitation was removed by LOWESS regression analysis. 2Slope of trend: n is negative and p is positive. |
|||||||||||||
| |||||||||||||
| Month | Low flow, 1931–2002 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kendall tau trend test | |||||||||||||
| Streamflow and time | Adjusted streamflow and time1 | ||||||||||||
| Slope2 | p-value | Slope2 | p-value | ||||||||||
| Jan. | n | 0.014 | n | 0.089 | |||||||||
| Feb. | n | .292 | n | .965 | |||||||||
| Mar. | p | .527 | p | .342 | |||||||||
| Apr. | n | .139 | n | .293 | |||||||||
| May | n | <.001 | n | .007 | |||||||||
| June | n | <.001 | n | .002 | |||||||||
| July | n | <.001 | n | .073 | |||||||||
| Aug. | n | <.001 | n | .002 | |||||||||
| Sept. | n | <.001 | n | <.001 | |||||||||
| Oct. | n | <.001 | n | .003 | |||||||||
| Nov. | n | .007 | n | <.001 | |||||||||
| Dec. | n | .003 | n | <.001 | |||||||||
|
1Variation in streamflow that was caused by variation in precipitation was removed by LOWESS regression analysis. 2Slope of trend: n is negative and p is positive. |
|||||||||||||
| |||||||||||||
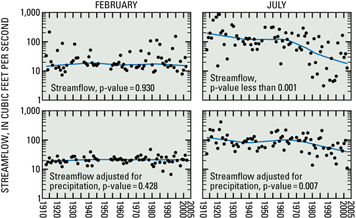
Figure 5. Trends in streamflow and adjusted streamflow for February and July, San Pedro River at Charleston, Arizona. Lines are LOWESS fit to data.
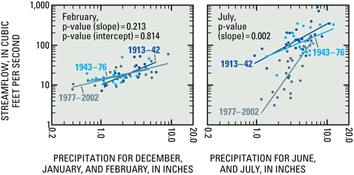
Figure 6. Trends in rainfall-runoff relations for February and July, San Pedro River at Charleston, Arizona, 1913 to 2002.
Trends in rainfall-runoff relations for three time periods were evaluated by comparing regression relations between precipitation and streamflow for 1913–42, 1943–76, and 1977–02. The difference among regression relations was determined with a nested F-test (Helsel and Hirsch, 1992). The results of the nested F-tests were similar to results of the LOWESS residual tests—trends in summer, fall, and late winter flows were significant, and trends in other parts of the year were not significant (table 5). Examples of trends in rainfall-runoff relations for February and July are shown in figure 6.
The primary factors that could have caused decreasing streamflow trends and changes in rainfall-runoff relations are decreases in precipitation, natural or human-induced changes in watershed characteristics, and increases in ground-water pumping. Examples of watershed characteristics that can change over time are riparian vegetation, upland vegetation, and stream-channel morphology. Annual precipitation decreased by 13 percent from 1913 to 2002, and the decrease likely resulted in some of the decrease in streamflow; however, statistical analyses provide strong evidence that other factors also contributed to the decrease in streamflow.
Changes in upland and riparian vegetation were likely major factors in the decreasing trends in total streamflows and low flows. Factors other than precipitation caused significant trends in total flows and low flows in the summer and fall, but those factors did not cause significant trends in late winter flows. The significant trends coincide with high rates of transpiration from vegetation in the summer, and the nonsignificant trends coincide with low rates of transpiration in the late winter. Another piece of evidence that implicates vegetation as a cause of decreased flows is that the upland and riparian vegetation of the San Pedro River Basin changed during the 20th century. The relative proportions of different species changed in upland vegetation (woody plants increased and grasses decreased), and the areal extent and density of riparian vegetation increased substantially (Rojo and others, 1999; Kepner and Edmonds, 2002; as referenced in Thomas and Pool, 2006).
Ground-water pumping in the upper San Pedro watershed in Mexico and the United States had a mixed influence on streamflow trends at Charleston. Pumping increased from less than 2,500 acre-ft/yr before 1940 to about 53,000 acre-ft/yr in 2002 (Thomas and Pool, 2006). Statistical analyses indicate that seasonal pumping from wells near the river for irrigation in the spring and summer was a major factor in the decrease in low flows. The analyses also indicate that year-round pumping from wells in the regional aquifer away from the river was not a major factor in the decrease in low flows. If regional pumping had caused a trend, the pumping should have affected low flows for all months of the year, but factors other than precipitation did not cause significant trends in low flows for January, February, March, and April (table 4). These conclusions are for trends from 1913–2002, and regional pumping in the United States and Mexico could affect streamflow at Charleston in the future, because regional ground-water pumping can have a delayed effect on streamflows (Alley and others, 1999).
| Month | Months of cumulative precipita-tion used for explantory variable1 | p-values for significance tests of difference among regression relations for three time periods2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slope3 | Intercept4 | |||||||||||
| Jan.5 | --- | --- | --- | |||||||||
| Feb. | 3 | 0.213 | 0.814 | |||||||||
| Mar. | 3 | 0.663 | 0.961 | |||||||||
| Apr. | 63 | 0.302 | 0.810 | |||||||||
| May | 63 | 0.188 | 0.198 | |||||||||
| June | 1 | 0.451 | 0.008 | |||||||||
| July | 2 | 0.002 | (7) | |||||||||
| Aug. | 1 | 0.239 | <0.001 | |||||||||
| Sept. | 2 | 0.889 | <0.001 | |||||||||
| Oct. | 2 | 0.014 | (7) | |||||||||
| Nov. | 3 | 0.731 | 0.002 | |||||||||
| Dec. | 3 | <0.001 | (7) | |||||||||
|
1Precipitation for same month as streamflow and indicated number of previous months (2 months is the same month and the previous month) 2Data were grouped into three time periods (1913–42, 1943–76, and 1977–2002). For each time period, a linear regression analysis was made between precipitation and monthly average streamflow. The difference among regression relations was tested with a nested F-test. 3Slope of regression relations. 4Intercept of regression relations. 5Linear regression relations could not be fit. 6Months of cumulative precipitation are January, February, and March. 7Significance test for difference among regression intercepts is not valid when the slopes are significantly different. |
||||||||||||
| ||||||||||||
Alley, W.M., Reilly, T.E., and Franke, O.L., 1999, Sustainability of ground-water resources: U.S. Geological Survey Circular 1186, 79 p.
Cleveland, W.S., 1979, Robust locally weighted regression and smoothing scatterplots: Journal of the American Statistical Association, v. 74, p. 829– 836.
Helsel, D.R., and Hirsch, R.M., 1992, Statistical methods in water resources: New York, Elesevier Science Publishing Company, Inc., 522 p.
Insightful, 2001, S-Plus 6 for windows guide to statistics, V. 1, Seattle, Washington, Insightful Corporation, 730 p.
Thomas, B.E., and Pool, D.R., 2006, Trends in streamflow of the San Pedro River, southeastern Arizona, and trends in precipitation and streamflow in northwestern New Mexico and southeastern Arizona: U.S. Geological Survey Professional Paper 1712, 79 p.
Blakemore E. Thomas
U.S. Geological Survey
Arizona Water Science Center
520 North Park Avenue, Suite 221
Tucson, Arizona, 85719-5035
Email: bthomas@usgs.gov
or visit home page at http://az.water.usgs.gov
This report is available online in Portable Document Format (PDF). If you do not have the Adobe Acrobat PDF Reader, it is available for free download from Adobe Systems Incorporated.
Document Accessibility: Adobe Systems Incorporated has information about PDFs and the visually impaired. This information provides tools to help make PDF files accessible. These tools convert Adobe PDF documents into HTML or ASCII text, which then can be read by a number of common screen-reading programs that synthesize text as audible speech. In addition, an accessible version of Acrobat Reader 7.0 for Windows (English only), which contains support for screen readers, is available. These tools and the accessible reader may be obtained free from Adobe at Adobe Access.
For more information about USGS activities in Arizona, visit the USGS Arizona Water Science Center home page.