This report is available in pdf 533KB.
Estimates of the magnitude and frequency of flood-peak discharges and flood hydrographs are used for a variety of purposes, such as for the design of bridges, culverts, and flood-control structures; and for the management and regulation of flood plains. To provide simple methods of estimating flood-peak discharges, the U.S. Geological Survey (USGS) has developed and published equations for every State, the Commonwealth of Puerto Rico, American Samoa, and a number of metropolitan areas in the United States. In 1993, the USGS, in cooperation with the Federal Emergency Management Agency and the Federal Highway Administration, compiled all current USGS statewide and metropolitan area equations into a computer program, titled “The National Flood-Frequency (NFF) Program” (Jennings and others, 1994).
Since 1993, new or updated equations have been developed by the USGS for various areas of the Nation. These new equations have been incorporated into an updated version of the NFF Program.
This Fact Sheet describes the application of the updated NFF Program to streams that drain rural and urban areas in North Carolina. Information on obtaining the NFF software and fact sheets for other areas of the Nation is provided at the end of this Fact Sheet.
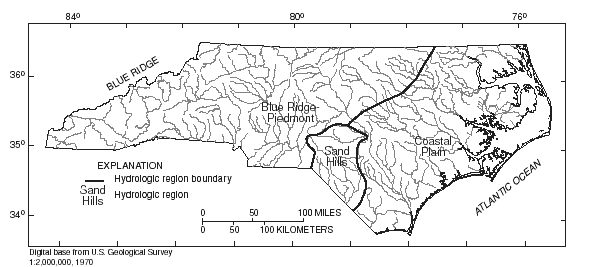
North Carolina is divided into three hydrologic regions (fig. 1) on the basis of physiography, soil characteristics, and analysis of geographic patterns in the differences between observed and estimated peak discharges for the stations used in the regression analyses. Pope and Tasker (2001) developed regression equations for estimating peak discharges (QT), in cubic feet per second, that have recurrence intervals (T) that range from 2 to 500 years for unregulated, nontidal, rural streams in each of these regions. Regression equations were developed based on the generalized-least-squares regression technique for each of the hydrologic regions of North Carolina. Peak-discharge records available through 1996 at 317 streamflow-gaging stations were used to develop the equations. Regression equations were also developed based on the region-of-influence regression technique for the Blue Ridge Piedmont and the Coastal Plain region. Pope and Tasker (2001) did not develop region-of-influence regression equations for the Sand Hills region because not enough stations were available in the region for the analysis.
 |
| Figure 1. Hydrologic regions of North Carolina |
Robbins and Pope (1996) developed regression equations for estimating peak discharges (QT), in cubic feet per second, that have recurrence intervals (T) that range from 2 to 100 years for small, urban watersheds in North Carolina. The regression equations were based on generalized-least-squares regression techniques. Synthetic peak-discharge data that resulted from calibrated rainfall-runoff model simulations using long-term rainfall and evaporation data were used for 34 sites, and observed peak-discharge data were used for 5 sites to develop the equations for urban areas of North Carolina.
Recurrence interval is the reciprocal of the annual exceedance probability and represents the average number of years between exceedances. For example, a flood-peak discharge with an exceedance probability of 0.01 has a recurrence interval of 100 years. This does not imply that the 100-year flood will be equaled or exceeded each 100 years, but that it will be equaled or exceeded on the average once every 100 years.
The regression equations for both rural and urban areas are based on the inch-pound system of units, but the NFF Program will accept and report either the inch-pound or metric system of units. Only the regression equations based on the generalized-least-squares regression technique (Pope and Tasker, 2001) are implemented in the NFF Program. The region-of-influence regression equations are considered secondary to the generalized-least-squares equations. Pope and Tasker (2001) developed a computer program for estimating both sets of rural equations, which can be downloaded from the World Wide Web at URL <http://nc.water.usgs.gov/reports/wri014207/apps.html>, and used as an alternate to the NFF program for North Carolina.
Drainage area (A), in square miles, is the only explanatory basin variable that
is used in the rural equations. The drainage area is the total area that contributes
runoff upstream of the stream site of interest, and is determined from the best
available topographic map.
The regression equations, the average standard errors of prediction, the equivalent years of record, and the range of drainage area for which the equations are applicable are shown in table 1. The average standard error of prediction is a measure of the accuracy of an equation when used to estimate peak discharges for ungaged watersheds similar to those that were used to derive the regression equations. Errors in the estimates for about two thirds of the ungaged sites will be within the given standard errors. The standard error of prediction increases appreciably when any explanatory watershed variable is near or beyond the range limits shown in table 1. The equivalent years of record is the number of years of streamflow record needed to achieve the same accuracy as the equation.
| Table 1.
Flood-peak discharge regression equations and associated statistics for
streams that drain rural areas in North Carolina (modified
from Pope and Tasker, 2001) [QT, rural peak discharge for recurrence interval T, 2 to 100 years; A, drainage area, in square miles; Do., ditto] |
|||
|
|
|||
| Regression equation | Average standard error of prediction, in percent |
Equivalent years of record |
Applicable range of drainage area, in square miles |
|---|---|---|---|
|
|
|||
| Blue Ridge-Piedmont | |||
| Q2 = 135A0.702 | 41.2 | 2.0 | 0.1–8,386 |
| Q5 = 242A0.677 | 41.2 | 3.0 | Do. |
| Q10 = 334A0.662 | 42.0 | 4.1 | Do. |
| Q25 = 476A0.645 | 43.6 | 5.4 | Do. |
| Q50 = 602A0.635 | 45.9 | 6.4 | Do. |
| Q100 = 745A0.625 | 47.0 | 7.2 | Do. |
| Q200 = 908A0.616 | 48.9 | 7.9 | Do. |
| Q500 = 1,160A0.605 | 51.6 | 8.7 | Do. |
| Sand Hills | |||
| Q2 = 33.5A0.712 | 38.4 | 2.1 | 0.1–1,228 |
| Q5 = 55.5A0.701 | 42.6 | 2.7 | Do. |
| Q10 = 72.9A0.697 | 45.6 | 3.4 | Do. |
| Q25 = 98.1A0.693 | 49.8 | 4.2 | Do. |
| Q50 = 120A0.691 | 53.1 | 4.6 | Do. |
| Q100 = 143A0.688 | 56.6 | 5.0 | Do. |
| Q200 = 170A0.686 | 60.2 | 5.4 | Do. |
| Q500 = 210A0.684 | 65.1 | 5.7 | Do. |
| Coastal Plain | |||
| Q2 = 64.7A0.673 | 37.9 | 2.9 | 0.3–8,671 |
| Q5 = 129A0.635 | 35.9 | 4.9 | Do. |
| Q10 = 188A0.615 | 36.3 | 6.7 | Do. |
| Q25 = 281A0.593 | 38.0 | 8.8 | Do. |
| Q50 = 367A0.579 | 39.8 | 10.1 | Do. |
| Q100 = 468A0.566 | 42.0 | 11.1 | Do. |
| Q200 = 586A0.554 | 44.2 | 11.9 | Do. |
| Q500 = 773A0.539 | 47.3 | 12.7 | Do. |
|
|
|||
The explanatory variables used in the equations for the urban areas are as follows:
Drainage area (A), in square miles, similarly defined as in rural areas. However, in urban areas, runoff from sub-watersheds may be diverted out of or into the drainage area of interest by stormwater sewers. The areas of such subwatersheds should be subtracted or added, as appropriate, to the drainage area of interest to compute the effective drainage area.
Impervious Area (IA) is the percentage of the drainage area, A, that is
covered by impervious surfaces and can be estimated by examination of maps or
aerial photos and the use of the grid-sampling method or planimeters and from
field reconnaissance of the basin.
Rural peak discharge (QT), in cubic feet per second, is generated by using the equations of Gunter and others (1987) for the equivalent recurrence interval (T).
The equations of Gunter and others (1987) are not included
in the NFF Program
because they have been superceded by the rural equations of Pope and Tasker
(2001);therefore, the urban equations of Robbins and Pope
(1996) have been restated in this Fact Sheet to incorporate
the rural equations of Gunter and others (1987). The restated
equations use only drainage area and impervious area as independent variables.
The equations, the average standard errors of prediction, and the ranges over
which the explanatory watershed variables are applicable in urban areas are
shown in Table 2.
| Table 2. Flood-peak
discharge regression equations and associated statistics for streams that
drain urban basins in North Carolina (modified from Robbins and Pope, 1996) [UT, urban peak discharge for recurrence interval T, 2 to 100 years, in cubic feet per second; A, drainage area; IA, impervious area; RQT, rural equivalent peak discharge for recurrence interval T, 2 to 100 years; Do., ditto] |
|||
|
|
|||
|---|---|---|---|
| Urban flood-frequency equations | Average standard error of prediction, in percent | Applicable range of drainage area, in square miles |
Applicable range of total impervious
area, in percent |
|
|
|||
| Blue Ridge-Piedmont | |||
| U2 = 33.3DA0.739IA0.686 | 40.4 | 0.04–41.0 | 2–54.6 |
| U5 = 78.9DA0.681IA0.572 | 38.5 | Do. | Do. |
| U10 = 122DA0.655IA0.515 | 38.3 | Do. | Do. |
| U25 = 228DA0.611IA0.436 | 38.7 | Do. | Do. |
| U50 = 296DA0.602IA0.396 | 37.8 | Do. | Do. |
| U100 = 374DA0.593IA0.358 | 37.8 | Do. | Do. |
| Sand Hills | |||
| U2 = 21.0DA0.752IA0.686 | 40.4 | 0.04–41.0 | 2–54.6 |
| U5 = 49.6DA0.700IA0.572 | 38.5 | Do. | Do. |
| U10 = 75.6DA0.677IA0.515 | 38.3 | Do. | Do. |
| U25 = 128DA0.644IA0.436 | 38.7 | Do. | Do. |
| U50 = 170DA0.637IA0.396 | 37.8 | Do. | Do. |
| U100 = 217DA0.630IA0.358 | 37.8 | Do. | Do. |
| Coastal Plain | |||
| U2 = 26.9DA0.722IA0.686 | 40.4 | 0.04–41.0 | 2–54.6 |
| U5 = 68.2DA0.655IA0.572 | 38.5 | Do. | Do. |
| U10 = 109DA0.625IA0.515 | 38.3 | Do. | Do. |
| U25 = 209DA0.570IA0.436 | 38.7 | Do. | Do. |
| U50 = 280DA0.558IA0.396 | 37.8 | Do. | Do. |
| U100 = 363DA0.547IA0.358 | 37.8 | Do. | Do. |
|
|
|||
The equations are not applicable to basins with significant in-channel detention or basin storage. The computed urban peak discharge may be less than the computed rural peak discharge in basins with impervious areas less than 10 percent, and hydrologic judgement is required to determine which peak-discharge estimate should be used or if a weighted estimate should be developed.
The U.S. Water Resources Council (1981, appendix 8) described weighting techniques to improve estimates of peak discharge at gaged locations by combining the estimates derived from analysis of gage records with estimates derived from other means, including regression equations. The weights of the two independent estimates are based on the length of the gage record (in years) and the equivalent years of record of the applicable regression equation. The weighted estimate of peak discharge is computed as:
where
| QT(G)w | is the weighted estimate of peak discharge, QT, for recurrence interval T at the gage location, |
| QT(G)s | is the estimate of QT derived from analysis of the systematic gage records, |
| QT(G)r | is the estimate of QT derived from application of the appropriate regression equation in table 1, |
| N | is the number of years in the gage record used to compute QT(G)s, and |
| EQ | is the equivalent years of record (table 1). |
The accuracy of the weighted discharge estimate, in equivalent years of record,
is equal to N + EQ. The NFF Program contains an algorithm to perform
these computations, which differs slightly from the computations described by
Pope and Tasker (2001).
Pope and Tasker (2001) showed how the weighted estimate for peak discharge at a gaged site can be used to improve estimates of peak discharge at an ungaged site on the same stream that has a drainage area that is between 0.5 and 1.5 times the drainage area of the gaged site. The regression estimate for the ungaged site is multiplied by an adjustment factor, which is computed as:
where
| AF | is the adjustment factor, |
| ΔA | is the absolute value of difference in drainage area between the gaged site (AG) and the ungaged site (AU), |AG -AU|, and |
| R | is the ratio of the weighted peak-discharge estimate to the regression estimate for the gaged site, QT(G)w/QT(G)r. |
The adjustment to the weighted estimate at the gage site can be used when the
drainage area at the ungaged site is within 50 to 150 percent of the drainage
area at the gaged site. Otherwise, the estimate at the ungaged site should be
based only on the appropriate regression equation from table
1.
At times, flood-frequency estimates may be desired for an ungaged site that
is between two gaged sites on the same stream. In this case, select the gaged
site for which ΔA/AG is less than 0.5, compute
AF, and apply as described above. If A/AG is
less than 0.5 for both gages, compute AF for each. If both correction
factors are less than 1.0, use the smaller AF. If one correction factor
is greater than 1.0 and the other is smaller than 1.0, an average of the two
correction factors should be used. Sites in Transition Zones When the drainage
area of the site of interest is in more than one region, a weighted estimate
of the peak discharge should be computed. The equations for the appropriate
regions should be applied to the total drainage area for the site, as if the
entire basin was in each region. The weighted estimate is then computed by multiplying
each regional estimate against the fraction of the drainage area in that region
and summing the products. The NFF Program provides an algorithm for this computation.
Gunter, H.C., Mason, R.R., and Stamey, T.C., 1987, Magnitude and frequency of floods in rural and urban basins of North Carolina: U.S. Geological Survey Water-Resources Investigations Report 87–4096, 52 p.
Jennings, M.E., Thomas, W.O., Jr., and Riggs, H.C., comps., 1994, Nationwide summary of U.S. Geological Survey regional regression equations for estimating magnitude and frequency of floods for ungaged sites, 1993: U.S. Geological Survey Water-Resources Investigations Report 94–4002, 196 p.
Pope, B.F., and Tasker, G.D., 2001, Estimating the magnitude and frequency of floods in rural basins of North Carolina -- revised: U.S. Geological Survey Water-Resources Investigations Report 01–4207, 44 p.
Robbins, J.C., and Pope, B.F., 1996, Estimation
of flood-frequency characteristics of small urban streams in North Carolina:
U.S. Geological Survey Water-Resources Investigations Report 96–4084, 21
p.
For more information contact:
U.S. Geological Survey
Office of Surface Water
415 National Center
Reston, Virginia 20192
(703) 648-5301
USGS hydrologic analysis software is available for electronic retrieval through
the World Wide Web (WWW) at:
http://water.usgs.gov/software/
and through anonymous File Transfer Protocol (FTP) from water.usgs.gov (directory:
/pub/software). The WWW page
and FTP directory from which the National Flood-Frequency software and user
documentation can be retrieved are http://water.usgs.gov/software/nff.html
and /pub/software/surface_water/nff,
respectively.
Additional earth science information is available from the USGS through the
WWW at http://www.usgs.gov/ or by calling
1-888-ASK-USGS.
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|