This report is available in pdf 470KB.
Estimates of the magnitude and frequency of flood-peak discharges and flood hydrographs are used for a variety of purposes, such as for the design of bridges, culverts, and flood-control structures; and for the management and regulation of flood plains. To provide simple methods of estimating flood-peak discharges, the U.S. Geological Survey (USGS) has developed and published regression equations for every State, the Commonwealth of Puerto Rico, American Samoa, and a number of metropolitan areas in the United States. In 1993, the USGS, in cooperation with the Federal Emergency Management Agency and the Federal Highway Administration, compiled all current USGS statewide and metropolitan area regression equations into a computer program, titled “The National Flood-Frequency (NFF) Program” (Jennings and others, 1994).
Since 1993, new or updated regression equations have been developed by the USGS for various areas of the Nation. These new equations have been incorporated into an updated version of the NFF Program.
This Fact Sheet describes the application of the updated NFF Program to streams that drain rural and urban areas in Missouri. Information on obtaining the NFF software and fact sheets for other areas of the Nation is provided at the end of this Fact Sheet.
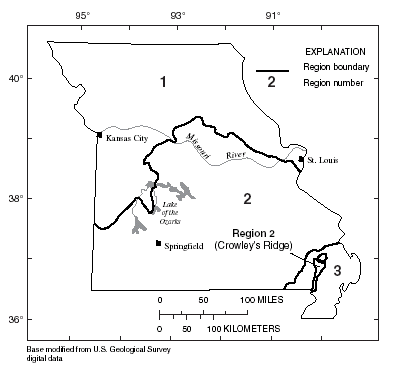
Missouri is divided into three hydrologic regions (fig. 1) on the basis of physiography and major drainage boundaries. Alexander and Wilson (1995) developed regression equations for estimating peak discharges (QT), in cubic feet per second, that have recurrence intervals (T) that range from 2 to 500 years. The regression equations are not applicable to sites subject to diversion, regulation, or urbanization. Alexander and Wilson (1995) defined an urban site as one in which greater than 5 percent of the drainage area is subject to commercial, industrial, or residential development.
 |
| Figure 1. Hydrologic regions of Missouri. |
Becker (1986) developed two sets of alternative regression equations for estimating peak discharges (QT), in cubic feet per second, that have recurrence intervals (T) that range from 2 to 100 years for small, urban watersheds in Missouri. Either set of regression equations may be used, depending on the availability of explanatory variable data. The equations are not applicable to basins with substantial in-channel detention or basin storage.
Recurrence interval is the reciprocal of the annual exceedance probability, and represents the average number of years between peak discharges of the same or greater magnitude. For example, the 100- year flood occurs, on average, once in 100 years, and has a 0.01 exceedance probability. This does not imply that the 100-year flood will be exceeded each 100 years, but that it has a 1 percent probability of occurring in any given year.
The equations for both the rural and urban basins are based on the inch-pound system of units, but the NFF Program will accept and report either the inch-pound or metric system of units. The explanatory watershed variables used by Alexander and Wilson for rural basins (1995) are as follows:
Drainage area (A), in square miles, is the total area that contributes runoff upstream of the stream site of interest determined from either 1:24,000- or 1:62,000-scale USGS topographic maps.
Main channel slope (S), in feet per mile, is the difference in elevation at points 10 and 85 percent of the distance along the main channel (measured from the location of the desired peak discharge to the drainage divide) divided by the distance between the points.
The regression equations, the average standard errors of prediction, and the equivalent years of record are shown in table 1. The standard error of prediction is a measure of the accuracy of the regression equations when estimating peak discharges for ungaged watersheds similar to watersheds that were used to derive the regression equations. About two thirds of estimates for ungaged watersheds will have errors less than or equal to the standard errors of prediction. The standard error of prediction increases appreciably when any explanatory watershed variable is near or beyond the range limits shown in table 2. The equivalent years of record is the number of years of streamflow records needed to achieve the same accuracy as the regression equations.
| Table 1. Flood-peak discharge regression
equations and associated statistics for streams that drain rural areas in
Missouri (modified from Alexander and Wilson, 1995) [QT, peak discharge for recurrence interval T, 2 to 500 years, in cubic feet per second; A, drainage area, in square miles; S, main channel slope, in feet per mile] |
||
|
|
||
|---|---|---|
| Regression equation | Average standard error of prediction, in percent |
Equivalent years of record |
|
|
||
| Region 1 | ||
| Q2= 69.4A0.703S0.373 | 34 | 4 |
| Q5 = 123A0.690S0.383 | 32 | 5 |
| Q10 = 170A0.680S0.378 | 34 | 6 |
| Q25 = 243A0.668S0.366 | 36 | 7 |
| Q50 = 305A0.660S0.356 | 38 | 8 |
| Q100 = 376A0.652S0.346 | 40 | 9 |
| Q500 = 569A0.636S0.321 | 45 | 10 |
| Region 2 | ||
| Q2 = 77.9A0.733S0.265 | 43 | 3 |
| Q5 = 99.6A0.763S0.355 | 36 | 5 |
| Q10 = 117A0.774S0.395 | 34 | 7 |
| Q25 = 140A0.784S0.432 | 32 | 11 |
| Q50 = 155A0.789S0.453 | 31 | 13 |
| Q100 = 170A0.794S0.471 | 32 | 15 |
| Q500 = 203A0.804S0.503 | 34 | 18 |
| Region 3 | ||
| Q2= 88.0A0.658 | 34 | 2 |
| Q5 = 145A0.627 | 36 | 2 |
| Q10 = 187A0.612 | 38 | 2 |
| Q25 = 244A0.595 | 41 | 3 |
| Q50 = 288A0.585 | 44 | 3 |
| Q100 = 334A0.576 | 46 | 3 |
| Q500 = 448A0.557 | 54 | 3 |
|
|
||
The regression equations were developed using peak-discharge data for stream- flow-gaging stations with at least 10 years of record at 278 locations in Missouri, Iowa, Kansas, and Arkansas. Alexander and Wilson (1995) summarized the watershed variables and peak-discharge estimates for the 278 streamflow-gaging stations used to develop the regression equations.
| Table 2. Range of explanatory variables
for which the rural regression equations are applicable in Missouri [--, not applicable] |
||
|
|
||
|---|---|---|
| Hydrologic region |
Drainage area, in square miles |
Main channel slope, in feet per mile |
|
|
||
|
1
|
0.13–11,500 | 1.35–150 |
|
2
|
.13–14,000 | 1.20–279 |
|
3
|
.48–1,040 | -- |
|
|
||
Becker (1986) developed two sets of regression equations to estimate flood magnitudes at selected recurrence intervals, ranging from 2 to 100 years. One set of equations used contributing drainage area and a basin development factor as explanatory variables; the other set of equations used contributing drainage area and percent impervious area in the basin as explanatory variables. Either set of equations may be used, depending on the type of available data. The explanatory watershed variables used by Becker (1986) for urban basins are as follows:
Drainage area (A), in square miles, is the total area that contributes runoff upstream of the location of the stream site of interest. In urban areas, runoff from subwatersheds may be diverted out of or into the drainage area of interest by stormwater sewers. The areas of subwatersheds should be subtracted or added, as appropriate, to the drainage area of interest to compute the effective drainage area.
Impervious area (I) is the percentage of the drainage area, A, that is covered by impervious surfaces and can be estimated by examination of maps or aerial photo- graphs, and the use of the grid-sampling method or planimeters and field reconnaissance of the basin.
Basin development factor (BDF), ranging from 0 to 12, is an index of development based on improvements to the basin drainage system (Sauer and others, 1983). The BDF is determined by first dividing the basin into upper, middle, and lower thirds such that each subarea contains approximately one-third of the total basin area and the travel distances of streams within a given subarea are approximately equal (note this does not mean the travel distances of streams in different thirds are equal). A value of 0 or 1 is assigned to each subarea for each of the following four development categories:
Channel improvements.—If more than 50 percent of the combined lengths of the main drainage channel and the principal tributaries have been straightened, enlarged, deepened, cleared, and (or) have other improvements, then a code 1 is assigned to this category in the subarea; otherwise, code 0 is assigned.
Channel linings.—If more than 50 percent of the combined lengths of the main drainage channel and the principal tributaries have been lined with an impervious material, then a code 1 is assigned to this category in the subarea; otherwise, code 0 is assigned. The presence of channel linings obviously would indicate the presence of channel improvements as well.
Storm drains (storm sewers).—If more than 50 percent of the secondary tributaries in a subarea are enclosed by drainage structures, such as storm drains and storm sewers, then a code 1 is assigned to this category; otherwise, a code 0 is assigned. If more than 50 percent of the main drainage channels and principal tributaries are enclosed, then channel improvements and linings also would be assigned a code 1.
Curb-and-gutter streets.—If more than 50 percent of a basin-third subarea has residential, commercial, or industrial development, individually or in combination, and if more than 50 percent of the roadways in the subarea have curb-and-gutter construction, then a code 1 is assigned for that category in the subarea; otherwise, a code 0 is assigned.
The sum of the values assigned to the four development categories for each subarea is the BDF (the maximum value for a fully developed drainage system would be 12). Values assigned to development categories can be determined from field inspection, or from available or planned zoning maps or planning documents. The BDF is subtracted from a constant of 13 by the NFF Program; the user enters the actual value of BDF.
The urban regression equations and the standard errors of estimate are shown in table 3. The average standard error of estimate is a measure of the goodness of fit between the equation and the data used to derive the equation. Errors in the urban flood-peak discharge estimates for about two-thirds of the stations used in the regression analyses were within the given standard errors. Errors in the estimates for ungaged sites are somewhat larger than the standard errors of estimate shown in table 3. Errors increase appreciably when any of the basin characteristics used in the equations are near or beyond the range limits shown in table 4.
| Table 3. Flood-peak discharge regression
equations and associated statistics for streams that drain urban areas in
Missouri (modified from Becker, 1986) [[QT, peak discharge for recurrence interval T, 2 to 100 years, in cubic feet per second; A, drainage area, in square miles; BDF, basin development factor; I, impervious area, in percent] |
|
|
|
|
|---|---|
| Regression equation | Standard error of estimate, in percent |
|
|
|
| Q2 = 801A0.747(13 - BDF)-0.400 | 32.9 |
| Q5 = 1,150A0.746(13 - BDF)-0.318 | 29.4 |
| Q10 = 1,440A0.755(13 - BDF)-0.300 | 28.4 |
| Q25 = 1,920A0.764(13 - BDF)-0.307 | 27.3 |
| Q50 = 2,350A0.773(13 - BDF)-0.319 | 26.5 |
| Q100 = 2,820A0.783(13 - BDF)-0.330 | 26.4 |
| Q2 = 224A0.793I0.175 | 32.3 |
| Q5 = 424A0.784I0.131 | 29.5 |
| Q10 = 560A0.791I0.124 | 28.6 |
| Q25 = 729A0.800I0.131 | 27.2 |
| Q50 = 855A0.810I0.137 | 26.1 |
| Q100 = 986A0.821I0.144 | 25.9 |
|
|
|
| Table 4. Range of explanatory variables for which regression equations are applicable in Missouri (modified from Becker, 1986) | ||
|
|
||
|---|---|---|
| Drainage area, in square miles |
Basin development factor |
Impervious area, in percent |
|
|
||
|
0.28-38.9
|
0-11 | 1-34 |
|
|
||
The regression equations were based on regression of synthetic peak-discharge data that were derived from calibrated rainfall-runoff model simulations using long-term rainfall and evaporation data for 9 sites and observed peak-discharge data at 18 sites in urban areas and 10 sites in rural areas of Missouri.
--Prepared by Scott M. Knowles and Robert R. Mason, Jr.
Alexander, T.W., and Wilson, G.L., 1995, Technique for estimating the 2- to 500-year flood discharges on unregulated streams in rural Missouri: U.S. Geological Survey Water-Resources Investigations Report 95–4231, 33 p.
Becker, L.D., 1986, Techniques for estimating flood-peak discharges from urban basins in Missouri: U.S. Geological Survey Water-Resources Investigations Report 86–4322, 38 p.
Jennings, M.E., Thomas, W.O., Jr., and Riggs, H.C., comps., 1994, Nationwide summary of U.S. Geological Survey regional regression equations for estimating magnitude and frequency of floods for ungaged sites, 1993: U.S. Geological Survey Water- Resources Investigations Report 94– 4002, 196 p.
Sauer, V.B., Thomas, W.O., Jr., Stricker, V.A., and Wilson, K.V., 1983, Flood characteristics of urban watersheds in the United States: U.S. Geological Survey Water-Supply Paper 2207, 63 p.
For more information contact:
U.S. Geological Survey
Office of Surface Water
415 National Center
Reston, Virginia 20192
(703) 648-5301
USGS hydrologic analysis software is available for electronic retrieval through the World Wide Web (WWW) at: http://water.usgs.gov/software/ and through anonymous File Transfer Protocol (FTP) from water.usgs.gov (directory:/pub/software). The WWW page and FTP directory from which the National Flood-Frequency software and user documentation can be retrieved are http://water.usgs.gov/software/nff.html and /pub/software/surface_water/nff, respectively.
Additional earth science information is available from the USGS through the
WWW at http://www.usgs.gov/ or by calling
1-888-ASK-USGS.
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|