[an error occurred while processing this directive]

The National Flood-Frequency Program—Methods for Estimating Flood Magnitude and Frequency for Natural Basins in Texas, 2001

U.S. Geological Survey Fact Sheet 022-01
February, 2001

Introduction

Estimates of the magnitude and frequency of flood-peak discharges and flood hydrographs are used for a variety of purposes, such as for the design of bridges, culverts, and flood-control structures; and for the management and regulation of flood plains. To provide simple methods of estimating flood-peak discharges, the U.S. Geological Survey (USGS) has developed and published regression equations for every State, the Commonwealth of Puerto Rico, American Samoa, and a number of metropolitan areas in the United States. In 1993, the USGS, in cooperation with the Federal Emergency Management Agency and the Federal Highway Administration, compiled all current USGS statewide and metropolitan area regression equations into a computer program, titled “The National Flood-Frequency (NFF) Program” (Jennings and others, 1994).

Since 1993, new or updated regression equations have been developed by the USGS for various areas of the Nation. These new equations have been incorporated into an updated version of the NFF Program.

This Fact Sheet describes the application of the updated NFF Program to streams that drain natural (rural and unregulated) basins in Texas. Information on obtaining the NFF software and Fact Sheets for other areas of the Nation is provided at the end of this Fact Sheet.

Overview

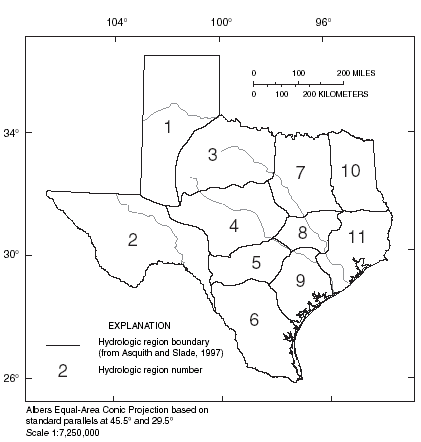
Asquith and Slade (1997) developed regional regression equations to estimate peak discharges (Q_T) in natural basins in Texas, with recurrence intervals (T) ranging from 2 to 100 years. These equations are included in the NFF Program. Asquith and Slade (1997) defined a natural basin as a basin with less than 10 percent impervious cover, less than 10 percent of its drainage area controlled by reservoirs, and no other human-related factors affecting streamflow. Separate sets of equations were developed for each of 11 hydrologic regions in Texas (fig. 1), which were determined on the basis of physiography and climatic conditions. For 5 of the 11 regions, the relation between peak discharge frequency and contributing drainage area was non-linear, requiring that one set of equations be developed for drainage areas less than 32 square miles and another set be developed for drainage areas greater than 32 square miles, giving rise to 16 sets of equations for the state (table 1).

Map showing hydrologic regions of Texas.

Figure 1. Hydrologic regions of Texas.


Table 1. Regression equations for estimating peak-streamflow frequency for hydrologic regions of Texas (from Asquith and Slade, 1997) [Q_T, peak discharge, in cubic feet per second for recurrence interval, T, in years; A, contributing drainage area, in square miles; SH, basin shape factor, dimensionless; and SL, stream slope, in feet per mile]
Regression equation	Weighted standard error of estimate, in percent

Region 1
Q₂ =16.lA^1.04 SH^-0.537	160
Q₅ =53.2A^0.958SH^-0.444	111
Q₁₀ =96.0A^0.921SH^-0.400	103
Q₂₅ =178 A^0.885SH^-0.356	103
Q₅₀ =263 A^0.864SH^-0.330	111
Q₁₀₀ =371 A^0.847SH^-0.307	120
Region 2
Q ₂ =826A^0.376SL^-0.689SH^0.869	120
Q₅=6,500A^0.372SL^-0.933SH^0.738	92
Q₁₀ =18,100A^0.369SL^-1.05SH^0.673	88
Q₂₅ =55,300A^0.366SL^-1.19SH^0.604	92
Q₅₀=108,000A^0.363SL^-1.27SH^0.566	99
Q₁₀₀=199,000A^0.361SL^-.134SH^0.531	107
Region 3
(Sites with contributing drainage areas less than 32 square miles)
Q₂ =119A^0.592	75
Q₅ =252A^0.629	78
Q₁₀ =373A^0.652	88
Q₂₅ =566A^0.679	103
Q₅₀ =743A^0.698	120
Q₁₀₀ =948A^0.715	134
Region 3
(Sites with contributing drainage areas greater than 32 square miles)
Q₂ =8.05A^0.668 SL^0.659 SH^0.189	60
Q₅ =42.0A^0.626 SL^0.574	57
Q₁₀ =91.9A^0.579 SL^0.537	60
Q₂₅ =233 A^0.523 SL^0.476	66
Q₅₀ =448 A^0.484 SL^0.425	72
Q₁₀₀ = 835 A^0.447 SL^0.372	92
Region 4
(Sites with contributing drainage areas less than 32 square miles)
Q₂ = 97.1A^0.626	134
Q₅ =196 A^0.650 SH^0.257	96
Q₁₀ =293 A^0.697 SH^0.281	92
Q₂₅ =455 A^0.741 SH^0.311	99
Q₅₀ =53A^0.927 SL^0.558 SH^0.333	107
Q₁₀₀ =51A^0.968 SL^0.627 SH^0.353	120
Region 4
(Sites with contributing drainage areas greater than 32 square miles)
Q₂ =0.0066A^1.29SL^2.09	72
Q₅ =0.0212A^1.24 SL^2.18	51
Q₁₀ =0.0467A^1.20 SL^2.18	49
Q₂₅ =0.102A^1.16 SL^2.18	54
Q₅₀ =0.166A^1.13 SL^2.19	60
Q₁₀₀ =0.252A^1.11 SL^2.19	69
Region 5
(Sites with contributing drainage areas less than 32 square miles)
Q₂ = 159 A^0.680	75
Q₅ = 396 A^0.773	63
Q₁₀ = 624 A^0.820	66
Q₂₅ = 997 A^0.866	69
Q₅₀ = 278 A^0.973SL^0.360	72
Q₁₀₀ = 295 A^1.01 SL^0.405	78
Region 5
(Sites with contributing drainage areas greater than 32 square miles)
Q₂ = 377 A^0.498	43
Q₅ = 1,270 A^0.534 SH^-0.145	28
Q₁₀ = 2,310 A^0.552SH^-0.221	28
Q₂₅ = 4,330 A^0.571SH^-0.307	31
Q₅₀ = 6,450 A^0.583SH^-0.366	36
Q₁₀₀ = 9,180 A^0.594SH^-0.420	41
Region 6
Q₂ = 66.2A^0.630 SH^-0.423	96
Q₅ = 931A^0.424 SL^-0.410	60
Q₁₀ = 1,720A^0.410 SL^-0.419	49
Q₂₅ = 3,290A^0.398 SL^-0.428	51
Q₅₀ = 4,970A^0.391 SL^-0.434	63
Q₁₀₀ = 1,780A^0.440	75
Region 7
(Sites with contributing drainage areas greater than 32 square miles)
Q₂ = 129A^0.578SL^0.364	66
Q₅ = 133A^0.605SL^0.578	54
Q₁₀ = 178A^0.644SL^0.699SH-^0.239	51
Q₂₅ = 219A^0.651SL^0.776SH-^0.267	51
Q₅₀ = 261A^0.653SL^0.817SH-^0.291	54
Q₁₀₀ = 313A^0.654SL^0.849SH-^0.316	60
Region 8
Q₂ = 30.7A^0.672SL^0.652	51
Q₅ = 87.6A^0.668SL^0.520	43
Q₁₀ = 134A^0.675SL^0.475	43
Q₂₅ = 191A^0.690SL^0.444	46
Q₅₀ = 229A^0.703SL^0.443	49
Q₁₀₀ = 261A^0.718SL^0.429	51
Region 9
Q₂ = 278A^0.526	54
Q₅ = 329A^0.645SL^0.220SH-^0.246	49
Q₁₀ = 350A^0.691SL^0.343SH-^0.321	46
Q₂₅ = 382A^0.743SL^0.466SH-^0.413	49
Q₅₀ = 409A^0.778SL^0.541SH-^0.477	49
Q₁₀₀ = 438A^0.811SL^0.607SH-^0.539	54
Region 10
(Sites with contributing drainage areas less than 32 square miles)
Q₂ = 54.9A^0.788SL^0.279	54
Q₅ = 80.7A^0.835SL^0.330	40
Q₁₀ = 98.2A^0.860SL^0.359	38
Q₂₅ = 122A^0.887SL^0.390	38
Q₅₀ = 141A^0.904SL^0.408	41
Q₁₀₀ = 159A^0.920SL^0.426	43
Region 10
(Sites with contributing drainage areas greater than 32 square miles)
Q₂ = 16.9A^0.798SL^0.777	63
Q₅ = 33.0A^0.790SL^0.795	51
Q₁₀ = 51.3A^0.775SL^0.785	43
Q₂₅ = 87.9A^0.752SL^0.760	38
Q₅₀ = 129A^0.733SL^0.735	36
Q₁₀₀ = 187A^0.713SL^0.708	36
Region 11
Q₂ = 159A^0.669SH-^0.262	43
Q₅ = 191A^0.696SL^0.130SH-^0.186	43
Q₁₀ = 199A^0.718SL^0.221SH-^0.151	49
Q₂₅ = 201A^0.713SL^0.313	54
Q₅₀ = 207A^0.735SL^0.380	60
Q₁₀₀ = 213A^0.755SL^0.442	66

The regression equations were developed from peak-discharge records through 1993 at 527 streamgaging stations with natural streamflow conditions in Texas. Asquith and Slade (1997) summarized streamgaging-station information, peak-discharge records, and peak-discharge estimates for 559 gaging stations in Texas, and 105 streamgaging stations in Arkansas, Louisiana, New Mexico, and Oklahoma.

Additional regression equations have been developed for some distinct areas in Texas, including streams in the vicinity of Highland Lakes, central Texas (Asquith, Slade, and Lanning-Rush, 1996), and tributaries to the Brazos River (Raines, 1998) and the Colorado River (Asquith, 1998). These additional regression equations are not included in the NFF Program. Users interested in documentation for these equations should contact the Texas District Office of the USGS, Austin, TX.

Asquith and Slade (1999) also developed a computer program that uses a site-specific approach to construct a unique set of regression equations to estimate Q_T for recurrence intervals ranging from 2–100 years for specific ungaged sites in natural basins in Texas. The computer program uses only streamgaging stations with basin characteristics similar to those for the ungaged site to develop the site-specific equations. A cluster analysis selects the stations from a data base that contains a total of 664 streamgaging stations, 559 in Texas and 105 in Arkansas, Louisiana, New Mexico, and Oklahoma. The program then uses multivariate generalized least-squares linear regression to develop the equations. Because a new set of equations is developed each time the program is run, no equations for this method are included in this fact sheet and the program is not included in the NFF Program. The report and the software required to run the program is available on the World Wide Web at URL https://pubs.water.usgs.gov/wri994172/. Users interested in the site-specific approach may also contact the Texas District Office of the USGS, Austin, TX.

Procedure

The explanatory variables used in the regional regression equations of Asquith and Slade (1997) are expressed in the inch-pound system of units; however, the NFF Program will accept and report either the inch-pound or the metric system of units. The explanatory variables used in the equations are:

Contributing drainage area (A), in square miles, is the area of the basin contributing to flow in the stream, determined from USGS topographic maps.

Basin shape factor (SH), dimensionless, is the ratio of the square of the stream length to the contributing drainage area and represents the ratio of the longest stream length to the mean width of the basin. Stream length, in miles, is the length of the longest mapped channel, from the gaging station to the headwaters and is determined from USGS, 1:100,000-scale topographic maps.

Stream slope (SL), in feet per mile, is the ratio of the change in elevation of the longest mapped channel from the gaging station to the headwaters to the length of the longest mapped channel determined from USGS, 1:100,000-scale topographic maps.

The regional regression equations of Asquith and Slade (1997) and the weighted standard errors of estimate in percent are shown in table 1. The weighted standard error of estimate is a measure of the goodness of fit between a regression equation and the data used to derive the equation. Errors in the Q_T estimates for about two thirds of the stations used in the regression analyses were within the given standard errors. Errors in the Q_T estimates for ungaged sites are somewhat larger than the standard errors of estimate shown in table 1, and errors increase appreciably when any of the basin characteristics used in the equations are near or beyond the range limits shown in table 2. Asquith and Slade (1997) provide procedures to compute the confidence intervals associated with flood estimates computed from the regression equations, as well as procedures that can assess the applicability of an equation to a given set of basin characteristics.

Hydrologic region	A	SH	SL
Table 2. Range of explanatory variables for which regression equations are applicable (from Asquith and Slade, 1997) [mi², square miles; A, contributing drainage area (mi²); SH, basin shape factor - ratio of length of longest mapped channel (stream length) squared to contributing drainage area (dimensionless); SL, stream slope - ratio of change in elevation of (1) longest mapped channel from site to headwaters to (2) length of longest mapped channel (feet per mile)]


Region 1	1.15-2,956	0.11-80.9	2.49-132
Region 2	0.32-4,305	0.51-14.8	9.67-130
Region 3	(Sites with A less than 32 mi2)
	0.10-97.0	0.16-9.32	10.7-105
	(Sites with A greater than 32 mi²)
	11.8-14,635	1.71-75.0	4.81-36.3
Region 4	(Sites with A less than 32 mi2)
	0.19-81.1	0.05-6.52	13.5-226
	(Sites with A greater than 32 mi²)
	12.0-19,819	0.49-19.7	3.52-36.1
Region 5	(Sites with A less than 32 mi²)
	0.18-22.3	0.50-84.9	20.9-224
	(Sites with A greater than 32 mi2)
	45.0-1,861	3.14-20.8	9.86-48.8
Region 6	(Sites with A less than 32 mi2)
	0.36-15,428	0.011-10.9	6.88-98.9
Region 7	(Sites with A less than 32 mi2)
	0.20-78.7	0.037-36.6	7.25-116
	(Sites with A greater than 32 mi2)
	13.0-2,615	1.66-36.6	3.85-31.9
Region 8	0.75-7,065	1.94-24.8	3.83-39.5
Region 9	0.24-5,198	0.091-30.1	2.77-70.0
Region 10	(Sites with A less than 32 mi2)
	0.21-100	0.008-1.05	2.00-138
	(Sites with A greater than 32 mi²)
	23.4-6,507	1.77-16.9	1.48-24.5

In regions for which the relation between peak discharge and contributing drainage area is non-linear and two sets of equations are presented in table 1 (Regions 3, 4, 5, 7, and 10), a weighting procedure is suggested to combine the estimates from the two sets of equations if the contributing drainage area is between 10 and 100 square miles. The weighted estimate, Q_TW, is computed as:

where

Q_TW	is the weighted peak discharge associated with T-year recurrence interval,
Q_T1	is the peak discharge associated with the equations for sites with contributing drainage areas less than 32 square miles,
Q_T2	is the peak discharge associated with the equations for sites with contributing drainage areas greater than 32 square miles, and
log(A)	is the common (base 10) logarithm of the contributing drainage area for the ungaged site.

This weighting procedure is not included in the NFF software. Users of the software should obtain the estimates from the two sets of equations provided in NFF and then manually solve the weighted estimate equation.

Prepared by Stephen S. Sumioka and Kernell G. Ries III

References

Asquith, W.H., 1998, Peak-flow frequency for tributaries of the Colorado River downstream of Austin, Texas: U.S. Geological Survey Water-Resources Investigations Report 98-4015, 19 p.

Asquith, W.H., and Slade, Raymond, Jr., 1997, Regional equations for estimation of peak-stream flow frequency for natural basins in Texas: U.S. Geological Survey Water-Resources Investigations Report 96-4307, 68p.

———1999, Site-specific estimation of peak-stream flow frequency using generalized least squares regression for natural basins in Texas: U.S. Geological Survey Water-Resources Investigations Report 99-4172, 19 p.

Asquith, W.H., Slade, R.M., Jr., and Lanning-Rush, Jennifer, 1996, Peak-flow frequency and extreme flood potential for streams in the vicinity of the Highland Lakes, central Texas: U.S. Geological Survey Water-Resources Investigations Report 96-4072, 1 sheet.

Jennings, M.E., Thomas, W.O., Jr., and Riggs, H.C., comp., 1994, Nationwide summary of U.S. Geological Survey regional regression equations for estimating magnitude and frequency of floods for ungaged sites, 1993, U.S. Geological Survey Water-Resources Investigations Report 94-4002, 196 p.

Raines, T.H., 1998, Peak-discharge frequency and potential extreme peak discharge for natural streams in the Brazos River Basin, Texas: U.S. Geological Survey Water-Resources Investigations Report 98-4178, 42 p.

For more information contact:

U.S. Geological Survey
Office of Surface Water
415 National Center
Reston, Virginia 20192
(703) 648-5301

USGS hydrologic analysis software is available for electronic retrieval through the World Wide Web (WWW) at: http://water.usgs.gov/software/ and through anonymous File Transfer Protocol (FTP) from water.usgs.gov (directory: /pub/software). The WWW page and FTP directory from which the National Flood-Frequency software and user documentation can be retrieved are http://water.usgs.gov/software/nff.html and /pub/software/surface_water/nff, respectively.

Additional earth science information is available from the USGS through the WWW at http://www.usgs.gov/ anonymous or by calling 1-888-ASK-USGS.

Accessibility FOIA Privacy Policies and Notices
U.S. Department of the Interior, U.S. Geological Survey Persistent URL: http://pubsdata.usgs.gov/pubs/fs/fs-022-01/ Page Contact Information: USGS Publishing Network Last modified: Tuesday, November 29 2016, 05:53:28 PM