This report is available in pdf 618KB.
Estimates of the magnitude and frequency of flood-peak discharges and flood hydrographs are used for a variety of purposes, such as for the design of bridges, culverts, and flood-control structures; and for the management and regulation of flood plains. To provide simple methods of estimating flood-peak discharges, the U.S. Geological Survey (USGS) has developed and published equations for every State, the Commonwealth of Puerto Rico, American Samoa, and a number of metropolitan areas in the United States. In 1993, the USGS, in cooperation with the Federal Emergency Management Agency and the Federal Highway Administration, compiled all current USGS statewide and metropolitan area equations into a computer program, titled “The National Flood-Frequency (NFF) Program” (Jennings and others, 1994).
Since 1993, new or updated equations have been developed by the USGS for various areas of the Nation. These new equations have been incorporated into an updated version of the NFF Program.
Fact sheets that describe application of the updated NFF Program to various areas of the Nation are available. This fact sheet describes the application of the updated NFF Program to streams that drain rural areas in Nevada.
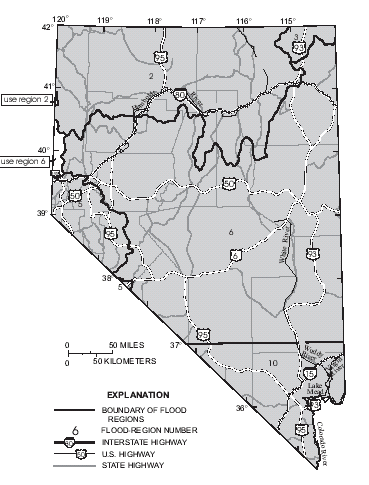
The State of Nevada is mostly located within a regional flood study area that encompasses the arid lands of the southwestern United States (Thomas and others, 1997). The study area is divided into 16 hydrologic flood regions, of which 6 include portions of Nevada (fig. 1). These regions were delineated on the basis of regional flood sources (snowmelt, summer thunderstorms, or cyclonic rainfall), elevation, and analysis of flood yields and residuals of preliminary regional flood-frequency relations. Within Nevada, sites greater in elevation than a threshold that varies with latitude (fig. 2) are considered to be in region 1. Sites located at or below the threshold may belong to regions 2,3,5,6, or 10 on the basis of geographic location (fig. 1). Two small areas along the western border of Nevada were not included in the regionalization study. The equations for region 2, however, can be extended to cover the small area just south of latitude 41 degrees (fig. 1) and the equations for region 6 can be extended to cover the second area north and south of latitude 40 degrees on the basis of similar hydrologic settings.
 |
| Figure 1. Hydrologic flood regions for Nevada. |
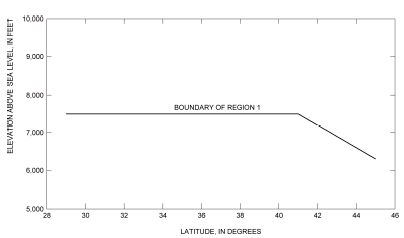 |
| Figure 2. Estimated elevation threshold for region 1 (from Thomas and others, 1997) |
Thomas and others (1997) developed regression equations for estimating peak discharges (QT), in cubic feet per second, that have recurrence intervals that range from 2 to 100 years for ungaged, unregulated rural streams. The NFF Program provides estimates of the 500-year discharge on the basis of extrapolation. Although some sites with drainages greater than 200 square miles were used to develop the equations, applications are best limited to 200 square miles or less.
The equations are based on the inch-pound system of units, but the NFF Program will accept and report either the inch-pound or metric system of units. The explanatory watershed variables used in the regression equations are as follows:
Drainage area (AREA), in square miles, is the total area that contributes runoff upstream of the location of the stream site of interest.
Mean annual precipitation (PREC), in inches, is the average mean annual precipitation for the basin as determined from isohyetal maps developed by the U.S. Weather Bureau (1959-61). The average is best determined by use of grid sampling techniques. Lines of equal precipitation from the Weather Bureau map are intersected with (drawn on to) a map of the drainage basin, a grid with equal-size cells is overlaid on the map, the mean annual precipitation is determined at each grid intersection, and the values are averaged.
Mean basin elevation (ELEV), in feet above sea level (National Vertical Datum of 1929), is also determined by grid sampling techniques. The elevations of a minimum of 20 equally spaced points are determined, and the average of the points is taken. As many as 100 points may be needed for large basins.
Latitude (LAT), in decimal degrees, is the latitude for the stream site of interest.
The regression equations, the average standard errors of prediction, and the equivalent years of record for regions 1, 2, 3, and 5 are given in table 1. The average standard errors of prediction are an average measure of the accuracy of the regression equations when estimating peak-discharge values for ungaged watersheds similar to those that were used to derive the regression equations. The equivalent years of record is the number of years of streamflow record needed to achieve the same accuracy as the regression equation.
| Table 1. Flood-peak discharge
regression equations and associated statistics for regions 1, 2, 3, and
5 in Nevada (modified from Thomas and others, 1997) [QT, peak discharge for recurrence interval T, 2 to 100 years, in cubic feet per second; AREA, drainage area, in square miles; PREC, mean annual precipitation, in inches; ELEV, mean basin elevation, in feet above sea level (NGVD of 1929); LAT, latitude in decimal degrees] |
||
|
|
||
|---|---|---|
| Regression equation | Average standard error of prediction, in percent |
Equivalent years of record |
|
|
||
| Region 1 - 165 stations (For sites located at elevations greater than elevation threshold from figure 2) |
||
| Q2 = 0.124AREA0.845PREC1.44 | 59 | 0.16 |
| Q5 = 0.629AREA0.807PREC1.12 | 52 | .62 |
| Q10 = 1.43AREA0.786PREC0.958 | 48 | 1.34 |
| Q25 = 3.08AREA0.768PREC0.811 | 46 | 2.50 |
| Q50 = 4.75AREA0.758PREC0.732 | 46 | 3.37 |
| Q100 = 6.78AREA0.750PREC0.668 | 46 | 4.19 |
| Region 2 - 108 stations | ||
| Q2 = 13.1AREA0.713 | 72 | 0.96 |
| Q5 = 22.4AREA0.723 | 66 | 1.80 |
| Q10 = 55.7AREA0.727(ELEV/1,000)-0.353 | 61 | 3.07 |
| Q25 = 84.7AREA0.737(ELEV/1,000)-0.438 | 61 | 4.64 |
| Q50 = 113AREA0.746(ELEV/1,000)-0.511 | 64 | 5.47 |
| Q100 = 148AREA0.752(ELEV/1,000)-0.584 | 68 | 6.05 |
| Region 3 - 35 stations | ||
| Q2 = 0.444AREA0.649PREC1.15 | 86 | 0.29 |
| Q5 = 1.21AREA0.639PREC0.995 | 83 | .49 |
| Q10 = 1.99AREA0.633PREC0.924 | 80 | .77 |
| Q25 = 3.37AREA0.627PREC0.849 | 78 | 1.23 |
| Q50 = 4.70AREA0.625PREC0.802 | 77 | 1.57 |
| Q100 = 6.42AREA0.621PREC0.757 | 78 | 1.92 |
| Region 5 - 37 stations | ||
| Q2 = 0.0333AREA0.853(ELEV/1,000)2.68[(LAT – 28)/10]4.1 | 135 | 0.21 |
| Q5 = 2.42AREA0.823(ELEV/1,000)1.01[(LAT – 28)/10]4.1 | 101 | .73 |
| Q10 = 28.0AREA0.826[(LAT – 28)/10]4.3 | 84 | 1.69 |
| Q25 = 426AREA0.812(ELEV/1,000)-1.10[(LAT – 28)/10]4.3 | 87 | 2.62 |
| Q50 = 2,030AREA0.798(ELEV/1,000)-1.71[(LAT – 28)/10]4.4 | 91 | 3.26 |
| Q100 = 7,000AREA0.782(ELEV/1,000)-2.18[(LAT – 28)/10]4.6 | 95 | 3.80 |
|
|
||
The regression equations for regions 6 and 10 were developed using an iterative regression method (Hjalmarson and Thomas, 1992) and a modified form of the station year statistical analysis method (Fuller, 1914). The regression equations, the estimated average standard errors of regression, and the equivalent years of record for regions 6 and 10 are given in table 2. The average standard error of regression is an estimate of the predictive accuracy of these regression equations and is determined by a direct sampling method.
| Table 2. Flood-peak
discharge equations and associated statistics for regions 6 and 10 in Nevada
(modified from Thomas and others, 1994) [Q, peak discharge for recurrence interval T, 2 to 100 years, in cubic feet per second; AREA, drainage area, in square miles; ELEV, mean basin elevation, in feet above sea level (NGVD of 1929)] Estimated average standard error of regression for these equations includes much of the within-station residual variance and therefore is not comparable to standard error of estimate from an ordinary-least-squares regression. |
||
|
|
||
| Regression equation | Estimated average standard error of regression, in log units |
Equivalent years of record |
|---|---|---|
|
|
||
| Region 6 - 80 stations | ||
| Q2 = 0 | -- | -- |
| Q5 = 32AREA0.80(ELEV/1,000)-0.66 | 1.47 | 0.233 |
| Q10 = 590AREA0.62(ELEV/1,000)-1.6 | 1.12 | .748 |
| Q25 = 3,200AREA0.62(ELEV/1,000)-2.1 | .796 | 2.52 |
| Q50 = 5,300AREA0.64(ELEV/1,000)-2.1 | 1.10 | 1.75 |
| Q100 = 20,000AREA0.51(ELEV/1,000)-2.3 | 1.84 | .794 |
| Region 10 - 104 stations | ||
| Q2 = 12 AREA0.58 | 1.14 | 0.618 |
| Q5 = 85 AREA0.59 | .602 | 3.13 |
| Q10 = 200 AREA0.62 | .675 | 3.45 |
| Q25 = 400 AREA0.65 | .949 | 2.49 |
| Q50 = 590 AREA0.67 | .928 | 3.22 |
| Q100 = 850 AREA0.69 | 1.23 | 2.22 |
|
|
||
The approximate ranges of the explanatory watershed variables over which the equations are applicable are shown in table 3. Thomas and others (1997) presented the actual ranges of applicability as two-dimensional clusters of explanatory variables plotted against one another. The ranges shown in table 3 define a rectangular space that brackets the clusters and, therefore, include pairs of values of the explanatory variables near the corners of the rectangle that are outside of the clusters. Application of the equations for values of the variables near the extremes of a range should be done cautiously. The standard errors increase appreciably when any explanatory watershed variable is near or outside the quoted range.
| Table 3. Range of
explanatory variables for which regression equations are applicable [--, not applicable.] |
||||
|
|
||||
| Hydrologic study region |
Drainage area, in square miles1 |
Mean basin elevation, in feet above sea level2 |
Mean annual precipitation, in inches |
Latitude in decimal degrees |
|---|---|---|---|---|
|
|
||||
| Region 1 | 0.6-1,060 | -- | 11-43 | -- |
| Region 2 | 0.8–1,680 | 3,540-7,950 | -- | -- |
| Region 3 | 2.2-1,450 | -- | 10-41 | -- |
| Region 5 | 4.1-360 | 5,770-10,500 | -- | 36.44-39.50 |
| Region 6 | 0.2-210 | 4,770–9,960 | -- | -- |
| Region 10 | 0.1-1,000 | -- | -- | -- |
| 1For best results, applications should be limited to basins of less than 200 square miles. | ||||
| 2NGVD of 1929. | ||||
|
|
||||
The U.S. Water Resources Council (1981, appendix 8) described weighting techniques to improve estimates of peak discharge at gaged locations by combining the estimates derived from analysis of gage records with estimates derived by other means, including regression equations.
The weights for these two estimates are based on the length of the stream gage record (in years) and the equivalent years of record of the applicable regression equation. The weighted estimate of peak discharge is computed as:
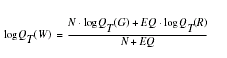
where
| QT(W) | is the weighted estimate for recurrence interval T at the gaged site, |
| QT(G) | is the estimate of QT derived from analysis of the gage records, |
| QT(R) | is the estimate of QT derived from application of the regression equation, |
| N | is the number of years of stream gage record, and |
| EQ | is the equivalent years of record (tables 1 and 2). |
The accuracy of the weighted discharge estimate, in equivalent years of record, is equal to N + EQ. The NFF Program contains the appropriate algorithms for this computation, which differs slightly from that described by Thomas and others (1997).
Thomas and others (1997) showed how the weighted estimate of peak discharge at a gaged site can be used to estimate the peak discharge of an ungaged site on the same stream that has a drainage area that is between 50 and 150 percent of the drainage area of the gaged site. The weighted estimate is computed as:
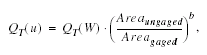
where
| QT(u) | is the weighted peak-discharge estimate for the recurrence interval T at the ungaged site, |
| QT(W) | is the weighted estimate of peak discharge at the gaged site, |
| AREA | ungaged and AREAgaged are the drainage areas of the ungaged and gaged sites, respectively, and |
| b | is an exponent for each region as follows: |
| Region | Exponent |
| 1 | 0.8 |
| 2 | .7 |
| 3 | .7 |
| 5 | .8 |
| 6 | .6 |
| 10 | .6 |
The adjustment to the weighted estimate of peak discharge at the gaged site can be used when the drainage area at the ungaged site is within 50 to 150 percent of the drainage area of the gaged site. Otherwise, the estimate at the ungaged site should be based on the appropriate regression equation only.
When the drainage area of the site of interest is in more than one of the regions 2, 3, 5, 6, or 10 a weighted estimate of the peak discharge should be computed. The equations for the appropriate regions should be applied independently by using basinwide estimates of the required explanatory variables. The weighted estimate is then computed by multiplying each regional estimate against the fraction of the drainage area in that region and summing the products. The NFF Program provides an algorithm for this computation.
When the elevation of the stream site of interest is between 6,800 and 7,500 feet, a weighted estimate of the peak discharge should be computed by using the equations for region 1 and the other regions in which the basin is located. The applicable equations are each applied by using basinwide estimates of the required explanatory variables, and the region estimates are weighted as a function of elevation as follows:
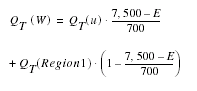
| QT(W) | is the weighted of peak-discharge estimate for the recurrence interval T at the site of interest, |
| QT(u) | is the estimate of peak discharge using the equations for regions 2, 3, 5, 6, or 10 as appropriate, |
| QT | (Region 1) is the estimate of the peak discharge using the equations for region 1, and |
| E | is the elevation of the stream site of interest. |
The NFF Program does not provide an algorithm for this weighting computation. Thomas and others (1997) summarized the basin characteristics, the estimates of peak discharge, and the weighted estimates of peak discharge for most of the 1,323 sites used in the study, including 148 sites in Nevada.
Fuller, W.E., 1914, Flood flows: American Society of Civil Engineers Transactions, v. 77, no. 1293, p. 564-617.
Hjalmarson, H.W., and Thomas, B.E., 1992, A new look at regional flood-frequency relations for arid lands: American Society of Civil Engineers, Journal of Hydraulic Engineering, v. 118, no. 6, p. 868-886.
Jennings, M.E., Thomas, W.O., Jr., and Riggs, H.C., comps., 1994, Nationwide summary of U.S. Geological Survey regional regression equations for estimating magnitude and frequency of floods for ungaged sites, 1993: U.S. Geological Survey Water-Resources Investigations Report 94–4002, 196 p.
Thomas, B.E., Hjalmarson, H.W., and Waltemeyer, S.D., 1997, Methods for estimating magnitude and frequency of floods in the southwestern United States: U.S. Geological Survey Water-Supply Paper 2433, 195p.
U.S. Water Resources Council, 1981, Guidelines for determining flood flow frequency: U.S. Water Resources Council Bulletin 17B, 28p. 14 appendixes.
U.S. Weather Bureau, 1959--61, Climates of the States: U.S. Department of Commerce Weather Bureau, Climatography of the United States, No. 60 [Section for each state}.
For more information contact:
U.S. Geological Survey
Office of Surface Water
415 National Center
Reston, Virginia 20192
(703) 648-5301
USGS hydrologic analysis software is available for electronic retrieval through the World Wide Web (WWW) at: http://water.usgs.gov/software/ and through anonymous File Transfer Protocol (FTP) from water.usgs.gov (directory: /pub/software). The WWW page and FTP directory from which the National Flood-Frequency software and user documentation can be retrieved are http://water.usgs.gov/software/nff.html and /pub/software/surface_water/nff, respectively.
Additional earth science information is available from the USGS through the WWW at http://www.usgs.gov/ or by calling 1-888-ASK-USGS.
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|