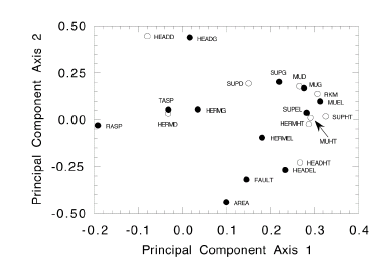
A principal-component analysis of the drainage-basin data for eastern Grand Canyon identified 9 redundant variables (fig. 14). Variables measuring height above and channel distance to the river were eliminated in favor of elevation and gradient variables, respectively. The river kilometer variable was also removed, as it strongly reflects the variation in Muav Limestone. The elevation and gradient of Muav Limestone were also strongly related, but both were retained as their removal had no effect on model outcome.
 |
| Figure 14. Graph showing the principal-component scores for variables used in the logistic regression model of eastern Grand Canyon. Variable names are given in table 4. Solid circles indicate variables that were retained for the logistic regression; open circles indicate variables that were removed from consideration in logistic regression. |
A significance threshold of 0.10 was used in modeling the binomial frequency of debris flows from the remaining 12 drainage-basin variables. Backwards, stepwise elimination removed eight variables as statistically insignificant (table 5). Overall model significance, ρm, is 0.86, indicating no significant difference between the final, five- variable and the original, twelve-variable model. This implies that there is a clear distinction between significant and non-significant variables. Model accuracy in predicting observed binomial frequencies is 76 percent, and ρC > 0.41, suggesting an adequate fit to the observed data. The verification set generated a model with the same group of significant variables (table 6), indicating that the calibration model is robust.
| Table 5. Calibration model for debris-flow frequency in tributaries of eastern Grand Canyon, Arizona | |||||||
|
|
|||||||
| Drainage-basin variable | Variable Coefficient (βv) |
Wald Statistic (W) |
Variable Signifi- cance1 (ρv) |
Log Odds (Ψ) |
Model Signifi- cance (ρm) |
Model Accuracy (α) |
Goodness- of-fit Signifi- cance2 (ρC) |
|---|---|---|---|---|---|---|---|
|
|
|||||||
| Intercept | 2.981 | 2.155 | 0.142 | -- | 0.86 | 0.76 | 0.41 |
| River aspect | 3.246 | 9.889 | 0.002 | 25.7 | |||
| Log of drainage-basin area | 2.192 | 4.124 | 0.042 | 9.0 | |||
| Log of channel gradient | 0.955 | 3.565 | 0.059 | 2.6 | |||
| to Hermit Shale | |||||||
| Log of channel gradient | 3.558 | 3.048 | 0.801 | 35.1 | |||
| Elevation of Hermit Shale | -0.002 | 2.991 | 0.084 | 1.0 | |||
|
|
|||||||
| Notes: Threshold of significance
= 0.10; n = 78 observations. 1 Based on a χ2 distribution of the Wald statistic. 2 Based on a χ2 distribution of the Hosmer-Lemeshow goodness-of-fit statistic (C) with 8 degrees of freedom (Hosmer and Lemeshow, 1989). |
|||||||
| Table 6. Verification model for debris-flow frequency in tributaries of eastern Grand Canyon, Arizona | |||||||
|
|
|||||||
| Drainage-basin variable | Variable Coefficient (βv) |
Wald Statistic (W) |
Variable Signifi- cance1 (ρv) |
Log Odds (Ψ) |
Model Signifi- cance (ρm) |
Model Accuracy (α) |
Goodness- of-fit Signifi- cance2 (ρC) |
|---|---|---|---|---|---|---|---|
|
|
|||||||
| Intercept | 2.199 | 1.726 | 0.189 | -- | 0.70 | 0.72 | 0.70 |
| River aspect | 2.850 | 12.01 | 0.001 | 17.3 | |||
| Elevation of Hermit Shale | -0.001 | 3.42 | 0.064 | 1.0 | |||
| Log of channel gradient | 2.891 | 2.917 | 0.088 | 18.0 | |||
| Log of drainage-basin area | 1.345 | 2.593 | 0.107 | 3.8 | |||
| Log of channel gradient to Hermit Shale | 0.614 | 2.416 | 0.120 | 18.0 | |||
|
|
|||||||
| Notes: Threshold of significance
= 0.10; n = 103 observations. 1 Based on a χ2 distribution of the Wald statistic. 2 Based on a χ2 distribution of the Hosmer-Lemeshow goodness-of-fit statistic (C) with 8 degrees of freedom (Hosmer and Lemeshow, 1989). |
|||||||
The high statistical significance of a climatic variable, river aspect (ρv = 0.002), reflects both the essential role of precipitation in debris-flow initiation and regional structure. A positive correlation with debris-flow frequency indicates that more debris flows occur where the river corridor trends northeast to southwest, directly along the path of most severe storms that track across the canyon. This correlation most likely relates to the general morphology of Grand Canyon, which is a narrow, deep canyon cut into a large plateau. Where the canyon trends southeast to northwest, perpendicular to the vector of severe weather and regional structure, storms may quickly cross the canyon and dissipate without dropping into it. This quick passage and dissipation results in less precipitation and limits intense precipitation to drainage headwaters. In contrast, where the canyon parallels the storm vector, storms can move quickly down into tributaries, impinging on canyon walls and directly affecting debris-flow source areas.
Standard morphometric measures of drainage-basin area and channel gradient are also significant and positively correlated with debris-flow frequency. Larger drainages provide more source material and are more likely than smaller drainages to be hit by localized thunderstorms. Larger drainages also have more waterfalls and produce more runoff during widespread precipitation, especially those basins with large drainage areas above the canyon rim, such as Prospect Creek (river mile 179.4-L). Steep gradients maximize the transport energy of a given debris flow by minimizing travel distance and energy loss for a given potential energy of failure.
The positive correlation of debris-flow frequency with two variables that are inversely proportional to each other — drainage area and channel gradient — reflects the complexity of the debris-flow initiation process. Using the linear relation between drainage area and gradient (fig. 15), we calculated the relative ratio of the log odds of the two variables: -1:12. This ratio indicates that for a given increase in drainage-basin area, the odds of debris-flow reaching the river will increase but the channel gradient decreases, which results in a twelve-fold decrease in the same odds. Thus, although both area and channel gradient are statistically significant in the process of debris-flow initiation and transport, an increase in gradient has more impact than an increase in drainage area. This results, in part, from a non-linear relation between debris-flow frequency and drainage area; there is likely an optimal size of drainage area above which no additional debris flows are produced. Large tributaries produce as many debris flows as smaller tributaries, but fewer may reach the river as channel gradient and transport energy decrease.
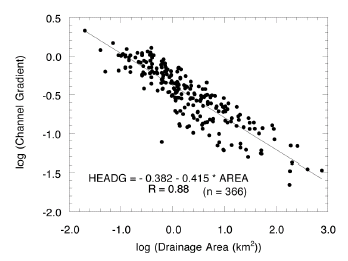 |
| Figure 15. The relation between the log of the drainage-basin area and the log of the channel gradient for tributaries in eastern Grand Canyon. Variable names are given in table 4. |
The model for eastern Grand Canyon also contained a source-area component in the form of two measures of the Hermit Shale: its elevation and the channel gradient to its base. These variables reflect the dominant role of the Hermit Shale as the primary source of debris flows in eastern Grand Canyon. The presence of the gradient variable reinforces the importance of channel gradient in general to debris-flow transport. The selection of the elevation variable most likely has less to do with climatic effects than debris-flow energetics. The elevation variable is inversely related to debris- flow frequency, linking lower elevations of Hermit Shale to increased debris-flow occurrence. This relation likely is non-linear, with debris-flow frequency increasing with the elevation of shales to an optimum and then decreasing. As bedrock units rise higher above the river they also are farther away, increasing travel distance and energy dissipation. Eventually, energy loss over travel distance outweighs the gain in potential energy from increased height.
All elevation data for the Hermit Shale used in the eastern model have values greater than 100 m above river level. If even a small majority of these values lie above the hypothesized optimum, the linear relation between height and frequency fit by logistic regression would have the very slight negative slope calculated for the model. In contrast, the relation between elevation and debris-flow occurrence on the basis of precipitation should be strictly linear and positive within the range of elevations present in Grand Canyon.
A principal-component analysis of the drainage-basin data for western Grand Canyon indicated 9 redundant variables (fig. 16). As in eastern Grand Canyon, variables measuring height above and channel distance to river were eliminated in favor of elevation and gradient variables respectively. The remaining variables — the elevation and channel gradient to the Hermit Shale — were also highly correlated. When both variables were left in the data set, channel gradient to the Hermit Shale was selected as statistically significant. Removal of the elevation of the Hermit Shale had no effect on the model and so it was retained in the initial data set.
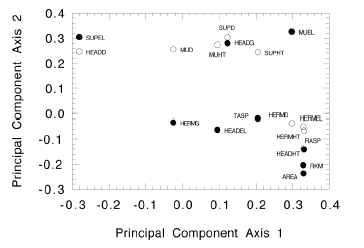 |
| Figure 16. Graph showing the principal-component scores for variables used in the logistic regression model of western Grand Canyon. Variable names are given in table 4. Solid circles indicate variables that were retained for the logistic regression; open circles indicate variables that were removed from consideration in logistic regression. |
Backwards stepwise elimination with a significance threshold of 0.10 removed eight more variables as statistically insignificant (table 7). The overall model significance (ρm) is 0.18, indicating no significant difference between the final, five- variable and the original, thirteen variable model. The low value, however, suggests that the distinction between significant and insignificant variable is not as definite as in the eastern canyon. This decreased robustness is expected with the increased variability of a larger data set drawn from a diverse geographic area. Model accuracy in predicting observed debris-flow frequencies is 74 percent, with ρC > 0.99, indicating an excellent fit to the observed data. The verification data generated exactly the same group of significant variables, suggesting a robust model (table 8).
| Table 7. Calibration model for debris-flow frequency in tributaries of western Grand Canyon, Arizona | |||||||
|
|
|||||||
| Drainage-basin variable | Variable Coefficient (βv) |
Wald Statistic (W) |
Variable Signifi- cance1 (ρv) |
Log Odds (Ψ) |
Model Signifi- cance (ρm) |
Model Accuracy (α) |
Goodness- of-fit Signifi- cance2 (ρC) |
|---|---|---|---|---|---|---|---|
|
|
|||||||
| Intercept | 3.367 | 4.450 | 0.035 | n.a. | 0.18 | 0.74 | 0.99 |
| Log of drainage-basin area | -2.226 | 9.324 | 0.002 | 0.1 | |||
| Log of channel gradient to Hermit Shale | 0.715 | 7.823 | 0.005 | 2.0 | |||
| Log of channel gradient | -5.221 | 7.144 | 0.007 | 0.01 | |||
| Elevation of Muav Limestone | -0.003 | 7.373 | 0.007 | 1.0 | |||
| Log of channel gradient to Muav Limestone | 0.768 | 3.319 | 0.068 | 2.2 | |||
|
|
|||||||
| Notes: Threshold of significance
= 0.10; n = 86 observations. 1 Based on a χ2 distribution of the Wald statistic. 2 Based on a χ2 distribution of the Hosmer-Lemeshow goodness-of-fit statistic (C) with 8 degrees of freedom (Hosmer and Lemeshow, 1989). |
|||||||
| Table 8. Calibration model for debris-flow frequency in tributaries of western Grand Canyon, Arizona | |||||||
|
|
|||||||
| Drainage-basin variable | Variable Coefficient (βv) |
Wald Statistic (W) |
Variable Signifi- cance1 (ρv) |
Log Odds (Ψ) |
Model Signifi- cance (ρm) |
Model Accuracy (α) |
Goodness- of-fit Signifi- cance2 (ρC) |
|---|---|---|---|---|---|---|---|
|
|
|||||||
| Intercept | 1.774 | 1.924 | 0.165 | n.a. | 0.70 | 0.68 | 0.80 |
| Log of drainage-basin area | -2.011 | 10.258 | 0.001 | 0.1 | |||
| Log of channel gradient | -4.632 | 8.289 | 0.004 | 0.01 | |||
| Log of channel gradient to Muav Limestone | 0.737 | 5.404 | 0.020 | 2.1 | |||
| Elevation of Muav Limestone | -0.002 | 5.139 | 0.023 | 1.0 | |||
| Log of channel gradient to Hermit Shale | 0.338 | 2.515 | 0.113 | 1.4 | |||
|
|
|||||||
| Notes: Threshold of significance
= 0.10; n = 86 observations. 1 Based on a χ2 distribution of the Wald statistic. 2 Based on a χ2 distribution of the Hosmer-Lemeshow goodness-of-fit statistic (C) with 8 degrees of freedom (Hosmer and Lemeshow, 1989). |
|||||||
The significant variables selected for western Grand Canyon are drainage area, channel gradient, and variables representing the shales, which is similar to the model for eastern Grand Canyon. In western Grand Canyon, drainage area and channel gradient are inversely correlated with debris-flow frequency; smaller drainages and shallow gradients produce more debris flows. Using the linear relation between drainage area and channel gradient (fig. 17) the ratio of the log odds for area and gradient is -150:1. Thus, a given decrease in drainage area results in an increase in the odds of debris-flow occurrence that is 150 times greater than the decrease in odds resulting from the concurrent decrease in slope gradient. At face value, this relation is an inversion of the relation between area, gradient, and debris-flow frequency established in eastern Grand Canyon. However, considering the close correlation between drainage area and channel gradient (fig. 17), gradient and area may act as proxies for each other. In this case, an increase in drainage area in the west, represented in the model as a decrease in gradient, produces more debris flows. An increase in gradient, represented as a decrease in area, also produces more debris flows. This interpretation also maintains the dominant role of channel gradient on debris-flow frequency evident in the eastern canyon.
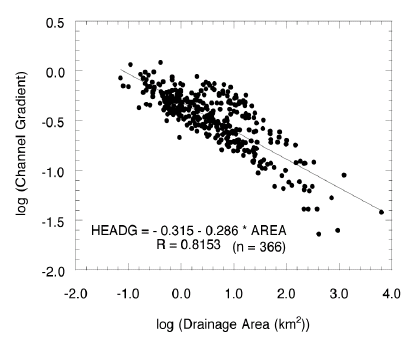 |
| Figure 17. The relation between the log of the drainage-basin area and the log of the channel gradient for tributaries in western Grand Canyon. Variable names are given in table 4. |
In western Grand Canyon, the primary debris- flow source area shifts from the Hermit Shale, which is at its highest elevation in the western canyon, to the Muav Limestone and its associated colluvial wedges. As in the model for eastern Grand Canyon, steeper gradients and low elevations are both selected for their role in debris-flow energy loss. The Hermit Shale, however, continues to be significant. Although it has risen to a fairly constant elevation since its appearance at river level in the eastern canyon, variations in drainage shape create variations in channel gradient to the Hermit Shale. Steep gradients to this important source area again correlate with increased debris-flow occurrence.
River aspect, Θ, is notably absent from the list of statistically significant variables in western Grand Canyon. Because precipitation decreases across Grand Canyon from east to west, the impact of climatic effects on debris-flow frequency is likely to be weaker in the west than in the east. Also, regional structure is controlled by large fault systems in western Grand Canyon (for example, Huntoon and others, 1981). In general, most climatic variables were not selected as significant at either end of the canyon. Tributary aspect is clearly not as important as the overall aspect of the river in producing debris flows. Although many side tributaries have narrow, slick-rock bottoms, in general they open wide to the river, spreading out along the margins of the canyon. This is especially true at the height of debris-flow source areas. Only in the most constricted basins would tributary aspect control precipitation effects. Elevation variables were selected in both models, but they apparently serve as proxies for the energy of source failures instead of runoff-generating variables. Improved measures of climatic effects, such as direct measure of precipitation in the tributaries, may be more significantly related to debris-flow initiation.
The secondary role of the Supai Group as a debris-flow source lithology is indicated by the absence in both models of variables representing the Supai Group. This emphasizes the role of the Supai Group as a secondary producer of colluvium that accumulates downslope, rather than as a direct source of debris flows. The variable measuring total fault length in each basin was also not significant. Clearly, fault-derived source material is locally important in several drainages within Grand
Canyon, but it is not a primary contributor in the overall pattern of debris-flow probability. Although faults control the locations of tributaries (Dolan and others, 1978; Potochnik and Reynolds, 1990), the area and volume of fractured material produced by faulting does not appear to be important in initiating debris flows, except locally.
Back: Initiation of debis flows
Next: Discussion and Conclusions
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|