USGS Home
Contact USGS
Search USGS

Processing and Interpretation of Aeromagnetic Data for the Santa Cruz Basin—Patagonia Mountains Area, South-Central Arizona

By

Jeffrey D. Phillips

Introduction

In 1997, the U.S. Geological Survey (USGS) contracted with Sial Geosciences Inc. for a detailed aeromagnetic survey of the Santa Cruz basin and Patagonia Mountains area of south-central Arizona. The contractor's Operational Report is included as an Appendix in this report. This section describes the data processing performed by the USGS on the digital aeromagnetic data received from the contractor. This processing was required in order to remove flight line noise, estimate the depths to the magnetic sources, and estimate the locations of the magnetic contacts. Three methods were used for estimating source depths and contact locations: the horizontal gradient method, the analytic signal method, and the local wavenumber method. The depth estimates resulting from each method are compared, and the contact locations are combined into an interpretative map showing the dip direction for some contacts.

Removal of flight line noise

The aeromagnetic data were collected along east-west flight lines spaced 250 meters apart. Data were also collected along several widely-spaced north-south tie lines. The tie line data were collected for the purpose of leveling the flight line data, and were not used in this analysis. The aeromagnetic map gridded from the contractor's flight line data (plate 1) shows significant streaking or "corrugation" along the flight line direction resulting from level shifts between adjacent flight lines. Because the depth analysis techniques require the computation of derivatives from the magnetic field, and because differentiation amplifies noise, it is important that this flight line noise be removed from the data prior to depth analysis. The process of removing this noise is called "decorrugation".

Several factors can lead to level shifts in the magnetic field between adjacent flight lines. These include elevation differences between flight lines, inadequate compensation for the magnetic field of the aircraft, and inadequate removal of time-varying (diurnal) magnetic field variations.

Although the contractor performed standard compensation and diurnal corrections and leveling, the rugged terrain and widely spaced tie lines prevented complete removal of flight line noise.

To remove the residual flight line noise from the gridded aeromagnetic map, a matched bandpass and azimuthal filtering approach was used (Syberg, 1972). Under this approach the power spectrum of the aeromagnetic map was "matched" to the power spectrum of a model consisting of several equivalent magnetic layers at different depths (using programs MFINIT and MFDESIGN from Phillips, 1997). For each equivalent layer a corresponding bandpass filter was applied to the aeromagnetic data to extract the magnetic field of the equivalent layer (using program MFFILTER from Phillips, 1997). One of the bandpassed fields was found to contain nearly all of the flight line noise. This bandpass was azimuthally filtered to remove most power in the direction of the flight lines (again using program MFFILTER). The azimuthally filtered bandpass was summed with the other bandpasses to produce the decorrugated aeromagnetic map (plate 2). Figure 1 shows how the decorrugation process affected one small part of the aeromagnetic map.

A similar matched filtering procedure was applied to the radar altimeter data, which also showed significant flight line noise. The filtered radar altimeter data was used to correct the various magnetic depth estimates for the height of the aircraft.

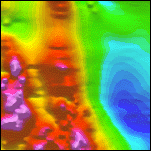
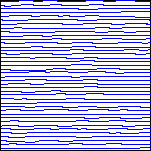
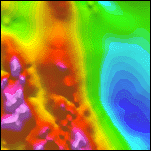
Figure 1. Results of decorrugation filtering. Illumination is from the north.

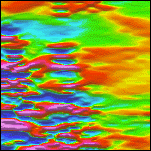1a. Detail of the aeromagnetic map gridded from contractor-supplied data. Intensities range from -336 (deep blue) to 956 nT (magenta).	1b. Flight line locations within the 10 km by 10 km detail area.	1c. Detail of the decorregated aeromagnetic map. Intensities range from -333 to 923 nT.	1d. Flight line noise removed by decorregation filtering. Intensities range from -65 to 65 nT.

Depth estimates and contact locations

In order to estimate source depths from gridded aeromagnetic data, it is first necessary to estimate the locations of the magnetic contacts. This is done by constructing a function from the aeromagnetic data that is peaked over the contacts. Several such functions have been suggested in the literature including the magnitude of the horizontal gradient (Cordell and Grauch, 1982, 1985; Blakely and Simpson, 1986), the amplitude of the analytic signal (Nabighian, 1972; Roest and others, 1992; Roest and Pilkington, 1993), and the local wavenumber (Thurston and Smith, 1997; Smith and others, 1998). In each case, the same function that is used to locate the contacts can be used to estimate the source depths at the contact locations.

Horizontal Gradient Method

The horizontal gradient method is in many ways the simplest approach to estimating contact locations and depths. It requires the greatest number of assumptions about the sources, but is the least susceptible to noise in the data, because it only requires calculation of the two first-order horizontal derivatives of the magnetic field. If M(x,y) is the magnetic field then the horizontal gradient magnitude HGM(x,y) is given by

(1)

This function is peaked over magnetic contacts under the following assumptions: (1) the regional magnetic field is vertical, (2) the source magnetizations are vertical, (3) the contacts are vertical, (4) the contacts are isolated, and (5) the sources are thick. Violations of the first four assumptions can lead to shifts of the peaks away from the contacts. Violations of the fifth assumption can lead to secondary peaks parallel to the contacts.

In order to partially satisfy the first two assumptions, it is usually necessary to perform a standard phase shift operation known as "reduction to the pole" on the observed magnetic field. Once the field has been reduced to the pole, the regional magnetic field will be vertical and most of the source magnetizations will be vertical, except for sources with strong remanent magnetization such as basic volcanic rocks.

Crests in the horizontal gradient magnitude can be located by passing a small 3 by 3 window over the HGM grid and searching for maxima (Blakely and Simpson, 1986). Program HDEP from Phillips (1997) uses a similar approach within a 5 by 5 window to both locate the crests and determine their strike direction. Once a crest is located and the strike direction is known, data within the window and within a belt perpendicular to the strike can be used to determine the depth of the contact by performing a least squares fit to the theoretical shape of the HGM over a contact. If h is the horizontal distance to the contact, d is the depth to the top of the contact and K is a constant, then the theoretical curve is given by

(2)

(Roest and Pilkington, 1993). The least squares fit gives an estimate of both the depth and its standard error, which can be expressed as a percentage of the depth. Typically only depth estimates with standard errors of 15% or better are retained in the final interpretation.

Due to the assumption of thick sources, the depth estimates obtained using the above procedure represent minimum depths. It is also possible to assume very thin sources and use a standard "pseudogravity" transformation instead of reduction to the pole (Roest and Pilkington, 1993). In this case the same analysis is done on the HGM of the pseudogravity field, and the depth estimates represent maximum depths.

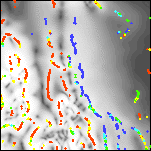
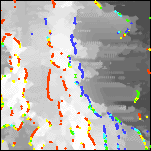
The horizontal gradient method has been applied to the decorrugated Patagonia aeromagnetic data in order to estimate contact locations and the minimum depths to magnetic sources. Figure 2 shows the processing sequence on a small part of the aeromagnetic map. Plate 3 shows the reduced-to-pole magnetic field. Plate 4 shows the terraced reduced-to-pole field along with identified crests of the HGM. Terracing is a filtering method that forces all horizontal gradients to become vertical and flattens the field between gradients (Cordell and McCafferty, 1989; Phillips, 1992, 1997). When displayed as a color or graytone image, the terraced reduced-to-pole aeromagnetic map resembles a geologic map, in which the colors or shades approximate the relative magnetizations of the geologic units. Note that the east-west streaking in the terraced map in low gradient areas results from a lack of control points rather than from flight line noise. Plate 5 shows the terraced reduced-to-pole magnetic field as a graytone image with color-coded horizontal gradient depth estimates representing minimum source depths with standard errors of 15% or less. In Plate 6 the depth estimates of Plate 5 have been gridded to form a surface passing through the minimum source depths

Figure 2. Sequence of images illustrating the horizontal gradient method for estimating contact locations and the minimum depths to magnetic sources. Illumination is from the northeast.

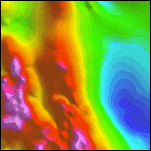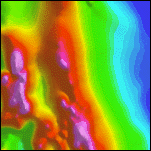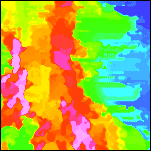2a. A 10 by 10 km detail of the decorrugated aeromagnetic map. Intensities range from -333 (deep blue) to 923 nT (magenta). For a similar map of the full area see Plate 2.	2b. Detail of the reduced-to-pole aeromagnetic map. Intensities range from -191 to 1330 nT. For a similar map of the full area see Plate 3.	2c. Detail of the terraced reduced-to-pole aeromagnetic map. Intensities range from -192 to 1329 nT. The east-west streaking in the terraced map in low gradient areas results from a lack of control points rather than from flight line noise.
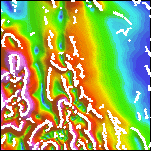2d. Detail of the horizontal gradient magnitude of the reduced-to-pole aeromagnetic map. Intensities range from 0.1 to 3476 nT/km.	2e. Detail of the horizontal gradient magnitude with identified contact locations superimposed along the crests.	2f. Detail of the terraced reduced-to-pole aeromagnetic map with horizontal gradient contact locations superimposed. For a similar map of the full area see Plate 4.
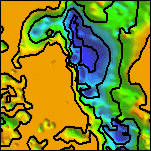2g. Grayscale detail of the horizontal gradient magnitude of the reduced-to-pole aeromagnetic map with color-coded depth estimates. Red sources are at or above ground level; yellows are within 0 to 100 meters; greens are within 100 to 200 meters; cyans are within 200 to 300 meters; and blues are deeper.	2h. Grayscale detail of the terraced reduced-to-pole aeromagnetic map with color-coded depth estimates. Only depth estimates with standard errors of 15% or less are shown. For a similar map of the full are see Plate 5.	2i. Detail of a surface gridded from the depth estimates, and representing the minimum depth to magnetic sources. Locations of depth estimates are shown in white. Depths range from 0 (orange) to 898 meters below ground level (deep blue). For a similar map of the full area see Plate 6.

Analytic Signal Method

The function used in the analytic signal method is the analytic signal amplitude of the observed magnetic field, defined by (Roest and others, 1992)

(3)

The analytic signal amplitude peaks over isolated magnetic contacts. As with the horizontal gradient method, the assumption of thick sources leads to minimum depth estimates. Because the analytic signal method requires the computation of the vertical derivative (using Fourier transforms), it is more susceptible to noise than the horizontal gradient method; however, there is no reduction-to-the-pole transformation required.

In a manner identical to that used in the horizontal gradient method, crests in the analytic signal amplitude are located by passing a 5 by 5 window over the grid and searching for maxima. When a crest is found, the local strike direction within the window is determined, and the minimum source depth and its standard error are estimated by a least squares fit to the equation for a two-dimensional analytic signal (Nabighian, 1972)

(4)

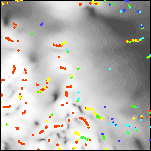
The analytic signal method has been applied to the decorrugated Patagonia aeromagnetic data in order to estimate contact locations and the minimum depths to magnetic sources. Figure 3 shows the processing sequence on a small part of the aeromagnetic map. Notice that some of the flight line noise removed from the aeromagnetic map by decorrugation has reappeared in the analytic signal amplitude as a result of the derivative calculations. Plate 7 shows the terraced reduced-to-pole magnetic field, along with identified crests of the analytic signal amplitude. Plate 8 shows the terraced reduced-to-pole magnetic field as a graytone image with color-coded analytic signal depth estimates representing minimum source depths with standard errors of 15% or less. In Plate 9 the depth estimates of Plate 8 have been gridded to form a surface passing through the minimum source depths.

Figure 3. Sequence of images illustrating the analytic signal method for estimating contact locations and the minimum depths to magnetic sources. Illumination is from the northeast.

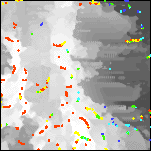
3a. A 10 by 10 km detail of the decorrugated aeromagnetic map. Intensities range from -333 (deep blue) to 923 nT (magenta). For a similar map of the full area see Plate 2.	3b. Detail of the analytic signal amplitude of the decorrugated aeromagnetic map. Intensities range from 14 to 4291 nT/km.	3c. Detail of the analytic signal amplitude with contact locations superimposed along the crests.	3d. Detail of the reduced-to-pole aeromagnetic map with analytic signal contact locations superimposed. For a similar map of the full area see Plate 7.
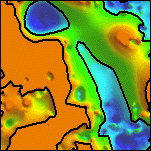
3e. Grayscale detail of the analytic signal amplitude of the decorrugated aeromagnetic map with color-coded depth estimates. Red sources are at or above ground level; yellows are within 0 to 100 meters; greens are within 100 to 200 meters; cyans are within 200 to 300 meters; and blues are deeper.	3f. Grayscale detail of the reduced-to-pole aeromagnetic map with color-coded depth estimates. Only depth estimates with standard errors of 15% or less are shown. For a similar map of the full area see Plate 8.	3g. Detail of a surface gridded from the depth estimates, and representing the minimum depth to magnetic sources. Locations of depth estimates are shown in white. Depths range from 0 (orange) to 754 meters below ground level (deep blue). For a similar map of the full area see Plate 9.

Local Wavenumber Method

In this method, the function used is the local wavenumber (Thurston and Smith, 1997) given by

(5)

The local wavenumber is peaked over isolated contacts. Depths can be estimated without assumptions about the thickness of the source bodies (Smith and others, 1998); therefore the depth estimates may be more accurate than the minimum (or maximum) depths calculated by the other two methods. In addition to the depth, the method yields a parameter called the structural index, which defines the geometry of the source. The edge of a thick body has a structural index of zero. As the thickness of the body decreases, the structural index of the edge moves toward unity. The structural index of a pipe is two; and that of a dipole is three.

Because the local wavenumber requires the calculation of second derivatives, it is very susceptible to noise in the data. It is usually necessary to improve the signal-to-noise ratio of the data by upward continuation of the aeromagnetic data grid prior to calculation of the local wavenumber. In the case of the Patagonia data, an upward continuation of 200 meters was applied to the decorrugated aeromagnetic grid.

A computer algorithm similar to the ones used by the other two methods was developed to locate maxima of the local wavenumber within a 5 by 5 window, estimate the local strike direction, and perform a least squares fit to estimate depth and the standard error in the depth. The structural index was then calculated from the depth estimate and the peak value of the local wavenumber.

Figure 4 shows the processing sequence on a small part of the aeromagnetic map. Again notice that some of the flight line noise removed from the aeromagnetic map by decorrugation has reappeared in the horizontal gradient as a result of the derivative calculations. Plate 10 shows the terraced reduced-to-pole magnetic field, along with identified crests of the local wavenumber. Plate 11 shows the terraced reduced-to-pole magnetic field as a graytone image with color-coded local wavenumber depth estimates having standard errors of 15% or less. In Plate 12 the depth estimates of Plate 11 have been gridded to form a minimum source depth surface. The structural indices corresponding to the depth estimates are color coded in Plate 13.

Figure 4. Sequence of images illustrating the local wavenumber method for estimating contact locations and depths to magnetic sources. Illumination is from the northeast.

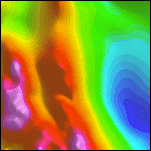
4a. A 10 by 10 km detail of the decorrugated aeromagnetic map. Intensities range from -333 (deep blue) to 923 nT (magenta). For a similar map of the full area see Plate 2.	4b. Detail of the aeromagnetic map after upward continuation 200 m. Intensities range from -303 to 491 nT.	4c. Detail of the local wavenumber computed from the upward continued aeromagnetic map. Intensities range from -19 to 22 1/km.
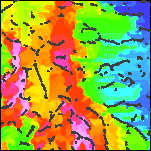
4d. Detail of the local wavenumber with estimated contact locations superimposed along the crests.	4e. Detail of the reduced-to-pole aeromagnetic map with local wavenumber contact locations superimposed. For a similar map of the full area see Plate 10.
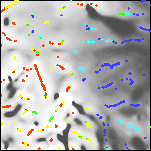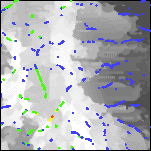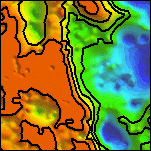4f. Grayscale detail of the local wavenumber of the upward continued aeromagnetic map with color-coded depth estimates. Red sources are at or above ground level; yellows are within 0 to 200 meters; greens are within 200 to 400 meters; cyans are within 400 to 600 meters; and blues are deeper.	4g. Grayscale detail of the reduced-to-pole aeromagnetic map with color-coded depth estimates. Only depth estimates with standard errors of 15% or less are shown. For a similar map of the full area see Plate 11.	4h. Detail of a surface gridded from the depth estimates, and representing the depth to magnetic sources. Locations of depth estimates are shown in white. Depths range from 0 (orange) to 2487 meters below ground level (deep blue). Selected contours at 0, 200, 400, and 600 meters. For a similar map of the full area see Plate 12.	4i. Grayscale detail of the reduced-to-pole aeromagnetic map with color-coded structural indices. Blue sources are contacts; yellows are sheets; greens are pipes; and reds are dipoles. For a similar map of the full area see Plate 13.

Interpretation

Contact Locations

The three sets of contact locations resulting from the three analysis methods can be combined as a color composite image to aid in the final interpretation of preferred contact locations. In figure 5 and plate 14, the horizontal gradient contacts are colored cyan, the analytic signal contacts are colored magenta, and the local wavenumber contacts are colored yellow. In the composite image (figure 5d and plate 14) overlapping contacts are colored red (analytic signal and local wavenumber), green (horizontal gradient and local wavenumber), blue(horizontal gradient and analytic signal), or black (all three methods). Whereas overlapping contacts may be judged more reliable than isolated contacts, overlap is not the only criterion for choosing preferred contact locations. The relative reliability of the three methods is also a factor.

The horizontal gradient method provides contacts that are highly continuous and generally parallel to the contours of the reduced-to-pole aeromagnetic field. For this reason, the horizontal gradient method is used to determine the locations of physical property (magnetization) boundaries during terracing. Recall, however, that the horizontal gradient method requires many assumptions, and that violations of these assumptions can result in displacement of the contacts away from their true locations. The displacement is typically down dip from the true contact location (Grauch and Cordell, 1987 ). The analytic signal method does not make the same assumptions, and does not result in displaced contacts. However, the analytic signal contacts are less continuous and their directions can be influenced by flight line and other noise in the data. The local wavenumber contacts are even less continuous and even more susceptible to noise.

Based on these factors, the following criteria were used to interpret the final contact locations shown in figure 5e and plate 15: (1) Where horizontal gradient contacts (cyan) are isolated, they represent the best available contact location. (2) Where horizontal gradient contacts (cyan) are parallel to and slightly offset from analytic signal contacts (magenta), the analytic signal contact represents the true contact location and the horizontal gradient contact indicates the down dip direction (indicated by tic marks). (3) Where analytic signal contacts (magenta) are isolated and not aligned with flight lines or other known noise directions, they provide reliable contact locations. (4) Where the analytic signal contacts (magenta) are discontinuous due to noise effects, they may be supplemented by local wavenumber contacts (yellow).

Figure 5. Sequence of images illustrating how contact locations are synthesized. The background image is the terraced reduced-to-pole aeromagnetic map.

5a. A 10 by 10 km detail of the estimated locations of contacts according to the horizontal gradient method (cyan).	5b. A 10 by 10 km detail of the estimated locations of contacts according to the analytic signal method (magenta).	5c. A 10 by 10 km detail of the estimated locations of contacts according to the local wavenumber method (yellow).
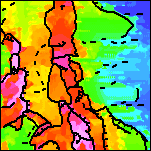5d. Detail of the color composite of the three sets of contact locations. For a similar map of the full area see Plate 14.	5e. Detail of the interpreted contact locations. tic marks show contact dip direction. Possible non-contacts (pipelines, flightline noise, minor faults) are indicated by dashes. For a similar map of the full area see Plate 15.

Depth Estimates

All three analysis methods were generally successful in locating deeper magnetic sources within basins along established drainages, and shallower magnetic sources in areas of outcropping bedrock. For the horizontal gradient and analytic signal methods we assumed thick sources, which resulted in minimum depths to magnetic sources. The local wavenumber depths are generally deeper than these minimum depths, reflecting the model-independent character of the local wavenumber method.

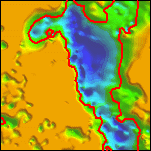
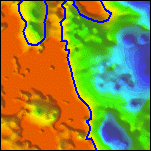
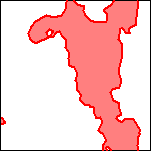
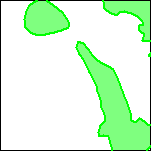
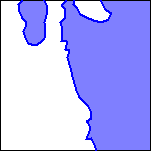
In order to compare and contrast the results from the three methods, 200 meter contours were extracted from each of the gridded surfaces (figure 6a,b,c). The areas deeper than 200 meters were filled in with color: light red for the horizontal gradient method, light green for the analytic signal method, and light purple for the local wavenumber method (figure 6d,e,f). Finally a color composite image was constructed (figure 6g and plate 16). In this image, white areas indicate that all methods predicted sources at depths shallower than 200 meters, gray areas indicate that all methods predicted magnetic sources at depths exceeding 200 meters, and other colors indicate some disagreement among the methods. Areas colored light cyan, light yellow, or light magenta indicate only two methods predicted magnetic sources at depths exceeding 200 meters. Areas colored light red, light green or light purple indicate only one method predicted magnetic sources at depths exceeding 200 meters.

Figure 6. Sequence of images illustrating construction of the basin depth composite map.

6a. A 10 by 10 km detail of the surface gridded from the reliable (15% standard errors or less) horizontal gradient depth estimates, with the 200 meter contour highlighted in red.	6b. Detail of the surface gridded from the reliable (15% standard errors or less) analytic signal depth estimates, with the 200 meter contour highlighted in green.	6c. Detail of the surface gridded from the reliable (15% standard errors or less) local wavenumber depth estimates, with the 200 meter contour highlighted in blue.
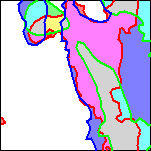6d. Detail of the area of the horizontal gradient surface deeper than 200 meters (red)	6e. Detail of the area of the analytic signal surface deeper than 200 meters (green)	6f. Detail of the area of the local wavenumber surface deeper than 200 meters (blue)	6g. Detail of the color composite of the three basin area estimates. In the gray areas, all three methods indicate a basin exceeding 200 meters depth. In the cyan, magenta, and yellow areas, two methods predict a basin exceeding 200 meters in depth. For a similar map of the full area see Plate 16.

References

• Blakely, R.J., and Simpson, R.W., 1986, Approximating edges of source bodies from magnetic or gravity anomalies: Geophysics, v.51, no.7, p.1494-1498.
• Cordell, Lindrith, and Grauch, V.J.S., 1982, Mapping basement magnetization zones from aeromagnetic data in the San Juan Basin, New Mexico: Society of Exploration Geophysicists, 52^nd Annual Meeting, Abstracts and Bibliographies, p.246-247.
• Cordell, Lindrith, and Grauch, V.J.S., 1985, Mapping basement magnetization zones from aeromagnetic data in the San Juan basin, New Mexico in Hinze, W.J., ed., The utility of regional gravity and magnetic anomaly maps: Society of Exploration Geophysicists, p.181-197.
• Cordell, Lindrith, and McCafferty, A.E., 1989, A terracing operator for physical property mapping with potential field data: Geophysics, v.54, no.5, p.621-634.
• Grauch, V.J.S., and Cordell, Lindrith, 1987, Limitations on determining density or magnetic boundaries from the horizontal gradient of gravity or pseudogravity data: Geophysics, v.52, no.1, p.118-121.
• Nabighian, M.N., 1972, The analytic signal of two-dimensional magnetic bodies with polygonal cross-section: its properties and use for automated anomaly interpretation: Geophysics, v.37, no.3, p.507-517.
• Phillips, J.D., 1992, TERRACE: A terracing procedure for gridded data, with Fortran programs, and VAX command procedure, Unix C-shell and DOS batch file implementations: U.S. Geological Survey Open-File Report 92-5, 27p., 1 diskette.
• Phillips, J.D., 1997, Potential-field geophysical software for the PC, version 2.2: U.S. Geological Survey Open-File Report 97-725, 34p.
• Roest, W.R., and Pilkington, Mark, 1993, Identifying remanant magnetization effects in magnetic data: Geophysics, v.58, no.5, p.653-659.
• Roest,W.R., Verhoef, Jacob, and Pilkington, Mark, 1992, Magnetic interpretation using the 3-D analytic signal: Geophysics, v.57, no.1, p.116-125.
• Smith, R.S., Thurston, J.B., Dai, Ting-Fan, and MacLeod, I.N., 1998, iSPI^tm - the improved source parameter imaging method: Geophysical Prospecting, v.46, p.141-151.
• Syberg, F.J.R., 1972, A Fourier method for the regional-residual problem of potential fields: Geophysical Prospecting, v.20, p.47-75.
• Thurston, J.B., and Smith, R.S., 1997, Automatic conversion of magnetic data to depth, dip, and susceptibility contrast using the SPI^tm method: Geophysics, v.62, no.3, p.807-813