

In cooperation with the Michigan Department of Environmental Quality
Figure 1. Secchi-disk transparency and chlorophyll a sample locations, Mich...
Figure 2. Radiometric-correction (top of atmosphere) reflectance values com...
Figure 3. Predicted and actual secchi-disk transparency for (A) path 21, ro...
Figure 4. Computed trophic state index from predicted secchi-disk transpare...
Figure 5. Predicted and actual chlorophyll a for path 21, row 29.
Figure 6. Computed trophic state index from predicted chlorophyll a for Lan...
Table 1. Lake trophic states and classification ranges for trophic state...
Table 2. MODTRAN4 atmospheric-correction parameters and input.
Table 3. R2 values and Fisher's Transformation significance tests used to...
Table 4. Stepwise regression trials and R2 values to predict trophic state...
| Multiply | By | To obtain |
|---|---|---|
| Length | ||
| foot (ft) | 0.3048 | meter (m) |
| mile (mi) | 1.609 | kilometer (km) |
| kilometer (km) | 0.6214 | mile (mi) |
| Area | ||
| acre | 0.001562 | square mile (mi2) |
| acre | 0.4047 | hectare (ha) |
| micrometer (µm) | 0.001 | millimeter (mm) |
| Concentration | ||
| micrograms per liter (µg/L) | 0.001 | milligrams per liter (mg/L) |
Abbreviated water-quality units used in this report: Chemical concentrations for Chlorophyll a and phosphorus are given in micrograms per liter (µg/L). Micrograms per liter is a unit expressing the concentration of chemical constituents in solution as a weight (micrograms) of solute per unit volume (liter) of water.
Inland lakes are an important economic and environmental resource for Michigan. The U.S. Geological Survey and the Michigan Department of Environmental Quality have been cooperatively monitoring the quality of selected lakes in Michigan through the Lake Water Quality Assessment program. Through this program, approximately 730 of Michigan's 11,000 inland lakes will be monitored once during this 15-year study. Targeted lakes will be sampled during spring turnover and again in late summer to characterize water quality. Because more extensive and more frequent sampling is not economically feasible in the Lake Water Quality Assessment program, the U.S. Geological Survey and Michigan Department of Environmental Quality investigate the use of satellite imagery as a means of estimating water quality in unsampled lakes. Satellite imagery has been successfully used in Minnesota, Wisconsin, and elsewhere to compute the trophic state of inland lakes from predicted secchi-disk measurements. Previous attempts of this kind in Michigan resulted in a poorer fit between observed and predicted data than was found for Minnesota or Wisconsin. This study tested whether estimates could be improved by using atmospherically corrected satellite imagery, whether a more appropriate regression model could be obtained for Michigan, and whether chlorophyll a concentrations could be reliably predicted from satellite imagery in order to compute trophic state of inland lakes. Although the atmospheric-correction did not significantly improve estimates of lake-water quality, a new regression equation was identified that consistently yielded better results than an equation obtained from the literature. A stepwise regression was used to determine an equation that accurately predicts chlorophyll a concentrations in northern Lower Michigan.
The State of Michigan has more than 11,000 inland lakes; approximately 3,500 of these lakes are greater than 25 acres in size. Nearly all of these lakes greater than 25 acres have developed communities with permanent residences or vacation homes. The general public has access to launches or beaches at about 1,300 lakes in Michigan. Recreational value, property values, and ecological value are all closely related to the quality of water in these inland lakes (Krysel and others, 2003). Tourism in Michigan, much of which involves recreation at inland lakes, accounts for nearly $15 billion of economic activity each year (Stynes, 2002). Thus, inland lakes are important economic and ecological resources to Michigan.
The U.S. Geological Survey (USGS) and the Michigan Department of Environmental Quality (MDEQ) have been cooperatively monitoring the quality of inland lakes in Michigan through the Lake Water Quality Assessment (LWQA) monitoring program funded by the Clean Michigan Initiative. Through this program, the USGS will sample approximately 730 lakes over 25 acres in size with public access during a 15-year period. The 730 lakes are grouped into 45 major watershed management units. In a given year, a set of 7 to 10 of the 45 major watershed management units is chosen for sampling and lakes to be sampled are randomly selected from this set. After 5 years, at least some lakes in each of the 45 major watershed management units will have been sampled. This 5-year rotation will continue until year 2015, when all targeted 730 lakes have been sampled once. In addition, each year the MDEQ will provide data from their Cooperative Lakes Monitoring Program (CLMP), which is a volunteer network monitoring more than 200 lakes. Data from those two sampling networks are used to characterize baseline water quality and compute trophic state of monitored inland lakes.
Measured water-quality characteristics of inland lakes are critical factors in determining their recreational use, habitat and species diversity, and the economic return from the tourism industry. The USGS and the MDEQ monitor many inland lakes, but it is not economically feasible to monitor the quality of all 11,000 inland lakes in Michigan by use of conventional sampling techniques. Knowledge of the biological productivity of unsampled inland lakes is needed to assist resource managers in their efforts to help protect and manage the quality in all of Michigan's inland lakes.
Satellite imagery has been successfully used in Minnesota (Olmanson and others, 2001), Wisconsin (Batzli, 2003), and elsewhere (Baban, 1993; Dekker and Peters, 1993; Mayo and others 1995; Giardino and others, 2001) to estimate water quality for unsampled inland lakes. In previous studies in Michigan (Nelson and others, 2002; Wianwang, 2002) researchers attempted to use existing models for relating satellite imagery to specific water-quality variables; however, they were unable to obtain as high a coefficient of determination (R2), which indicates the strength of a statistical relation, as previous studies in Minnesota and Wisconsin. A better method to predict trophic characteristics from satellite imagery would increase the knowledge every year about more of Michigan's inland lakes.
The purpose of this report is to describe the methods and techniques used to develop estimates of Michigan lake-water quality on the basis of satellite images. Specifically, this report presents a brief overview of the conceptual basis for predicting trophic state on the basis of satellite images, describes methods used to develop a new alternative regression model for predicting secchi-disk transparency, and offers a new regression equation for predicting chlorophyll a concentrations in northern Lower Michigan. These two measures can further be used to estimate the trophic state of Michigan inland lakes.
Naumann (1919) proposed a classification of lake-water quality ranging from oligotrophic (low phytoplankton populations and low primary productivity) to eutrophic (high phytoplankton populations and high primary productivity). Carlson (1977) proposed to quantify the trophic state by using a Trophic State Index (TSI), which can be used to group lakes into basic classes of oligotrophic, mesotrophic, eutrophic, and hypereutrophic. The natural progression of a lake from oligotrophic to eutrophic can be computed from measures of total phosphorus (TP), secchi-disk transparency (SDT), and chlorophyll a (Chl-a).
TP is measured directly by sampling and chemical analysis. SDT is a commonly used, low-cost technique that measures water clarity (Specifically, a black and white disk is lowered into the lake until it can no longer be seen). Water clarity is related to the quantity of phytoplankton in the water, although non-algal turbidity and tannic acids also can reduce water clarity. Chl-a measurements correlate with the concentration of phytoplankton within a given volume of lake water and are not affected by sediment or acids in the water. The formulas for computing TSI values are (Carlson, 1977):

The range of TSI values and how each measure is classified into oligotrophic, mesotrophic, eutrophic, and hypereutrophic is listed in table 1.
[Based on Michigan Department of Environmental Quality report (1982) and modified by the State of Michigan to account for regional characteristics. TSI, Trophic State Index; SDT, secchi-disk transparency; Chl-a, chlorophyll a; TP, Total Phosphorus; ft, feet; µg/L, micrograms per liter]
| Lake trophic condition | Carlson TSI | SDT (ft) | Chl-a (µg/L) | TP (µg/L) |
|---|---|---|---|---|
| Oligotrophic | <38 | >15 | <2.2 | <10 |
| Mesotrophic | 38–48 | 7.5–15 | 2.2–6 | 10–20 |
| Eutrophic | 49–61 | 3–7.4 | 6.1–22 | 20.1–50 |
| Hypereutrophic | >61 | <3 | >22 | >50 |
Typically, computing TSI values for a single lake using all three formulas should yield similar results. Increasing the phosphorus concentration generally results in increased phytoplankton concentration, which results in reduced water clarity. Yet at specific times of the year, results from the three formulas may not be congruous because of phosphorus nutrient uptake by macrophytes. Therefore, substantial amounts of macrophytes in a lake may alter the relation of the three TSI values. Of the three measures, SDT and Chl-a concentration have been quantified by use of satellite imagery techniques (Mayo and others, 1995; Zilioli and Brivio, 1997; Cox and others, 1998; Kloiber and others, 2000; Giardino and others, 2001; Kloiber and others, 2002).
Satellites have been used to predict water characteristics since the 1970s. For example, the National Aeronautics Space Administration (NASA) Earth Resources Technology Satellite (ERTS-1) was used to determine an algal bloom in Lake Erie in 1972 (Strong, 1974). NASA's Landsat satellite series improved the spatial, spectral, and radiometrical resolutions allowing more water-quality parameters to be studied. The idea to relate SDT to satellite imagery started in the late 1970s and studies involving Chl-a, turbidity, and other water-quality characteristics soon followed (Scarpace and others, 1979; Lillesand and others, 1983; Verdin, 1985; Lathrop and Lillesand, 1986; Dekker and Peters, 1993; Mayo and others, 1995; Zilioli and Brivio, 1997). Landsat bands 1 through 4 signifying the visible and near infrared portions of the electromagnetic spectrum, were found to correlate well with water-quality characteristics (Lathrop and Lillesand, 1986). However, Lathrop (1992) found it difficult to use the same regression equation to characterize the water quality of different lakes. Recent studies found that, with improved methods, it was possible to predict water quality for unsampled lakes by use of regression equations relating existing measurements to remotely sensed data (Pulliainen and others, 2001; Kloiber and others, 2002; Thiemann and Kaufmann, 2002). These most recent studies form the basis for this project.
Imagery used in this study was collected by the Landsat 7 Enhanced Thematic Mapper Plus (ETM+) satellite launched in 1999 by NASA. The satellite orbits at an altitude of approximately 705 km with a sun-synchronous 98-degree inclination and a descending equatorial crossing time of 10:00 a.m. (Williams, 2003). Every 16 days, the satellite will repeat coverage for each scene coinciding with the Landsat Worldwide Reference System (WRS), which records satellite scenes into a grid reference system made up of 233 paths and 248 rows. The Landsat 7 ETM+ sensor collects information in nine bands, distinct portions of the electromagnetic spectrum. Bands 1, 2, 3, 4, and 8 are sensed within a spectral range between 0.4 and 1 µm. Bands 1, 2, and 3 correspond to the visible spectrum of blue, green, and red, and band 4 is infrared; together, these bands span the spectral range of 0.45 to 0.90 µm. Bands 5 and 7 are short-wavelength infrared bands sensed within a spectral range between 1 and 3 µm. Bands 6a and 6b are thermal long wavelengths sensed within a spectral range between 8 and 12 µm. Band 8 is the panchromatic band that combines bands 2, 3, and 4 with a spectral range of 0.52 to 0.90 µm (Williams, 2003). Data are reported in digital numbers as 8-bit integers, ranging from 1 to 256.
Several distortion factors affect satellite imagery. These factors include geometric distortions that are the result of small imprecisions in maneuvering the sensor; radiometric distortions that arise from small differences in the calibration of the sensor and geometry of the earth, sun, and satellite; and atmospheric distortions that arise from scattering of light by moisture and particulates in the atmosphere. However, procedures have been developed to help correct for these factors. Geometric and radiometric corrections can be made with little or no field data. However, most studies of this scope suggest that the imagery should be geometrically, radiometrically, and atmospherically corrected (Brivio and others, 2001; Zilioli and Brivio, 1997; Kloiber and others, 2002).
A variety of equations relating satellite imagery to STD have been tested in different settings and with different sensors. Researchers that use imagery from the Landsat 7 ETM+ satellite (Kloiber and others, 2002) have generally used the following equation:
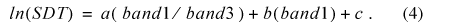
The variables a, b, and c are empirically derived coefficients from the regression equation.
Nelson and others (2002) used raw digital numbers from the images and the regression equation identified in Kloiber and others (2002) to estimate SDT for lakes in Lower Michigan. Kloiber and others (2002) reported predictions with R2 values between 0.72 and 0.93. Nelson and others (2002) achieved an R2 of only 0.43 for Landsat ETM+ scenes in path 21, rows 29, 30, and 31. Wiangwang (2002) used the same imagery and field data as Nelson and others (2002) but radiometrically corrected the images before determining regression equations. This type of correction is termed "Top of Atmosphere" (TOA) reflectance because, although it accounts for differences in illumination angle and sensor performance, it does not adjust for haze or diffusion within the atmosphere. The R2 value using SDT and Landsat 7 ETM+ TOA corrected imagery for path 21, rows 29, 30, and 31 was 0.558 (Wiangwong, 2002). This result suggests that a full atmospheric-correction of the imagery could in theory further improve the R2 values. The combination of all of these techniques in the same case study should improve the regression equations, and thus lead to better methodology to estimate water quality from satellite imagery.
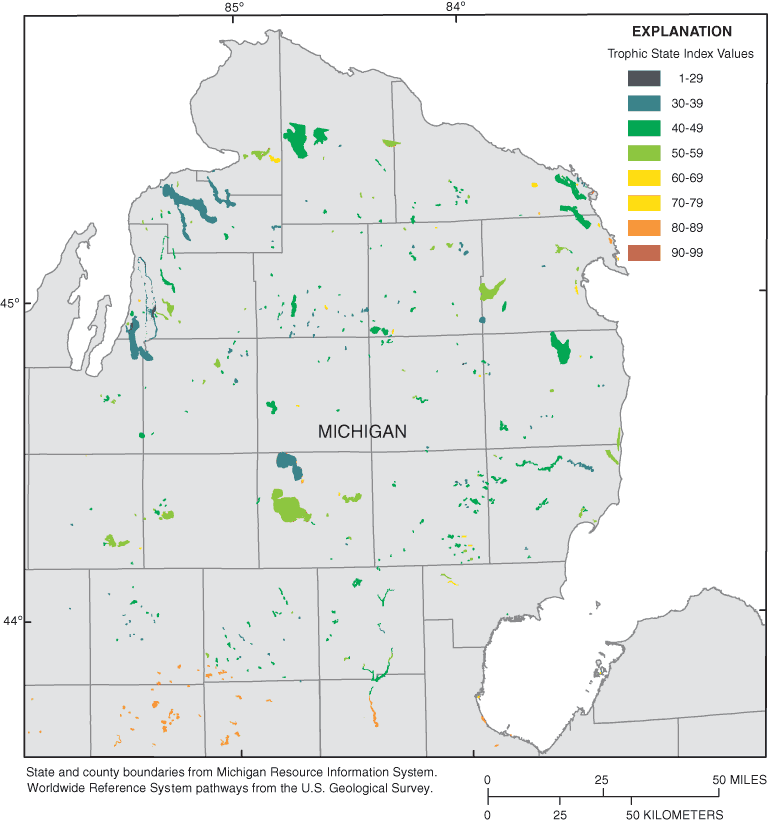
The study area was determined by the location of LWQA sampling planned for the 2002 water year (the 2002 water year was a portion of the inland lakes chosen to be sampled from 10 out of the 45 basins in Michigan). Most measurements fell within five Landsat 7 ETM+ satellite scenes covering the majority of Lower Michigan. The locations of the satellite scenes and the lakes with collected SDT measurements within a window of plus or minus 7 days of the imagery acquisition, are shown in figure 1.
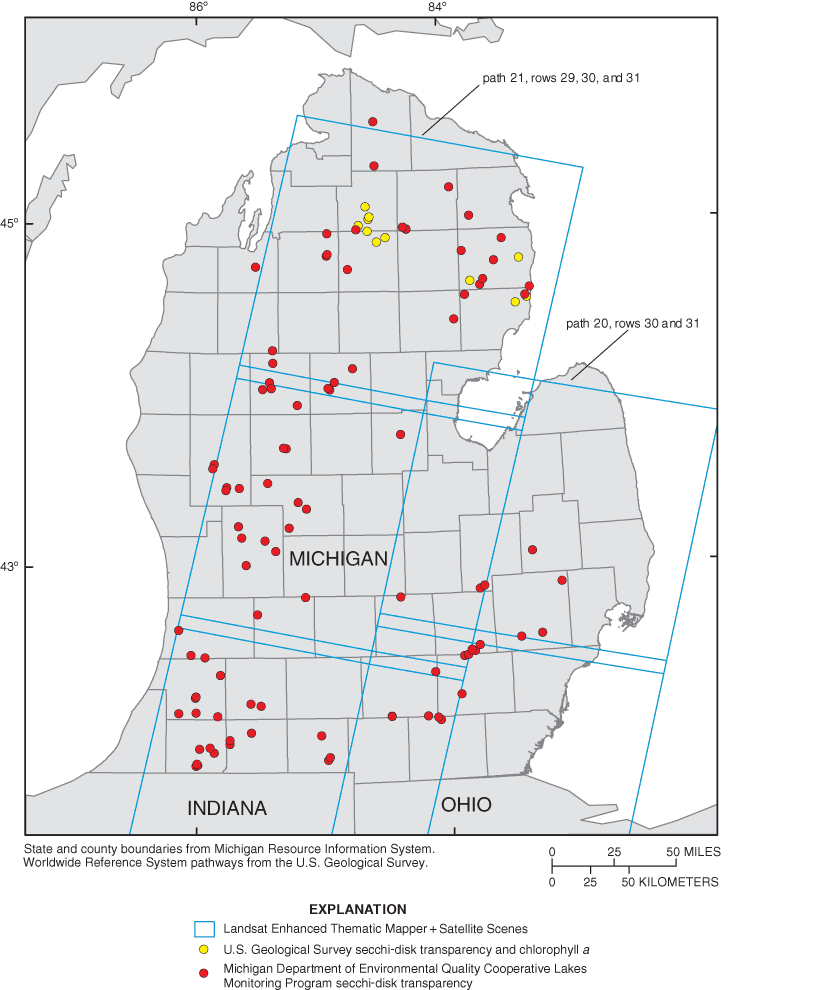
Figure 1. Secchi-disk transparency and chlorophyll a sample locations, Michigan, August 2002.
The general process to predict SDT and Chl-a measurements from satellite imagery involves several steps. First, field data must be obtained and digitized. Second, cloud-free satellite imagery from approximately the same date as the field data collection must be obtained. Third, the imagery must be corrected to compensate for geometric, radiometric, and atmospheric distortions in the imagery. Fourth, the field data must be compared to the imagery through the creation of Areas of Interest (AOI) within the satellite image. Fifth, a regression model must be developed for each scene to relate the field data to the spectral data collected in each AOI. Finally, the regression equation must be applied to all lakes over 25 acres in the satellite scene, to predict the water-quality characteristics at unmeasured locations.
USGS scientists and community volunteers from the CLMP routinely measure SDT in various lakes in Michigan. A secchi disk is a common tool for measuring the overall clarity of water. The Secchi disk is an 8-in. diameter circular disk painted black and white in alternating quadrants. The disk is lowered into the water, and the depth at which the disk is no longer visible is called the secchi depth. Chl-a, TP, several forms of nitrogen, and major ions are also measured at USGS sample sites. Samples from both the CLMP and USGS were used from the months of August and September 2002. This late-summer index period, when a lake is at the maximum biological productivity, was found to be the best period for relating SDT and Chl-a samples to satellite imagery (Kloiber and others, 2000).
USGS measurements were referenced by coordinates obtained from the Global Positioning System (GPS) and were used to create a shapefile. A shapefile is the file format ArcGIS software uses to store the location, shape, and attribute information. The SDT measurements from CLMP were recorded on paper and did not include precise coordinates for the measurements; however, a bathymetric map for each lake marked in the approximate location for each measurement. With this information, another shapefile was made by manually digitizing the correct location for all data within the lakes.
Volunteer SDT measurements have been studied and proven to be comparable with those made by professionals (Canfield and others, 2002; Obrecht and others, 1998). However, careful consideration was involved in choosing which CLMP SDT measurements were used in this study. Only measurements that were clearly marked on attached bathymetric maps were digitized. Some volunteer data were excluded where multiple measurements were made in a single lake (only one measurement per lake was chosen within the deepest basin) and when the location of measurements could not be determined from the published bathymetric maps.
Only measurements collected within 7 days of an image acquisition date were used. This restriction was shown to produce the best results in predictive SDT models (Kloiber and others, 2002). The final exclusions for all measurements were dependent upon the satellite imagery. Measurements when clouds or cloud shadows covered the lake or measurement location were excluded. Clouds and shadows are limiting factors and are the reason imagery should be chosen on clear satellite overpass days. (For a summary of sample numbers per scene refer to table 4.)
Five Landsat 7 ETM+ scenes were purchased from the Tropical Rain Forest Information Center, a member of NASA Federation of Earth Science Information Partners at the Center for Global Change and Earth Observations, Michigan State University. The scenes from path 20, rows 30 and 31, and path 21, rows 29, 30, and 31 were chosen because they had minimal cloud cover and were acquired closest to the dates when the measurements were collected. For reference, see figure 1, which depicts satellite scene locations with the placement of SDT and Chl-a measurements.
The data arrived with a geometric systematic correction, which helped ensure that the image cells would correspond to the data-collection points as closely as possible. The systematic correction refers to the type of geometric correction. "The end result is a geometrically rectified product free from distortions related to the sensor (e.g. jitter, view angle effects), satellite (e.g. attitude deviations from nominal), and earth (e.g. rotation, curvature)" (National Aeronautics Space Administration, 2003). However, the geometric correction did not use ground-control points to ensure complete geodetic accuracy, and NASA only claimed residual error to 250 m in flat terrain at sea level. When each image was compared with the Michigan transportation framework developed by the Michigan Center for Geographic Information, however, it was found to be accurate to within 2 cells, or about 60 m.
The satellite imagery was also radiometrically corrected by use of a radiative transfer model. Radiometric corrections are needed because the brightness of each pixel in a satellite image is "affected by sun angle, atmospheric interference, changes in detector response, and numerous other factors" (Kloiber and others, 2002). The atmospheric-correction method used was MODTRAN4, released by the Air Force Research Lab, Space Vehicles Directorate, in March 1999. This model is an atmospheric radiative transfer code and algorithm (Hoke, 1999).
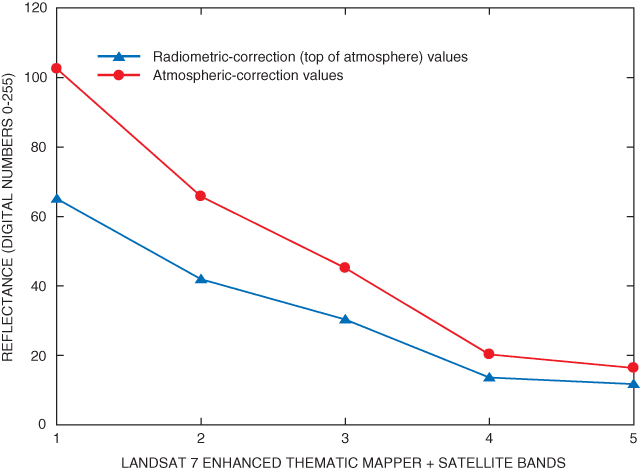
To test whether atmospherically correcting the imagery would achieve better fit regression equations, path 21, rows 29, 30, and 31 were atmospherically corrected. The atmospheric correction model MODTRAN4 (Hoke, 1999) was used. Each satellite scene was run seven times through the model, keeping all parameters constant for each scene except the surface percent reflectance, which started at 0.1 and increased to 0.7. The different surface percent reflectances were used to construct regression equations that accounted for atmospheric scattering of both incoming solar radiation and outgoing reflected radiation. The results were equations describing the relation between reflected radiation and radiation measured at the sensor. These equations were then applied to their corresponding bands to atmospherically correct the imagery. The inputs are listed in table 2. The output slope and intercept coefficients for each band were used in an Erdas IMAGINE model (Erdas Inc, 2001) to build the equations to compute atmospherically corrected images. The equations take into account that shorter wavelengths, such as band 1, scatter more than longer wavelengths, such as band 5. The values for all bands generally increase with this correction, but band 1 shows the most increase and band 5, the least. Typical change between the TOA reflectance values and the resulting atmospheric-correction values for Lake Lansing in Ingham County are shown in figure 2.
Table 2. MODTRAN4 atmospheric-correction parameters and input.
[km, kilometers]
| Parameter | Input |
|---|---|
| Surface percent reflectance | 0.1 to 0.7 |
| Atmospheric model | Midlatitude summer |
| Aerosol model | Rural extinction (default visibility = 23 km) |
| Season | Spring-summer |
| Visibility | 23 km |
| Day of year | Dependent upon satellite scene |
| Latitude and longitude | Varied depending on center of satellite scene |
| Greenwich mean time of image acquisition | 1430 |
The six shapefiles that were created corresponding to the SDT and Chl-a measurements for each scene were opened on top of the appropriate satellite scene in Erdas IMAGINE. Areas of Interest (AOIs) were digitized around the SDT measurements for five scenes, and Chl-a measurements for one scene. An area was drawn around each measurement to include pixels surrounding the measurements to help smooth radiometric noise. The AOI sizes depended on the size of the lake but were between the minimum of 8 pixels and the maximum of 1,000 pixels set by Olmanson and others (2001). The smallest AOI was 8 pixels, the mean was 12 pixels, and the maximum was 33 pixels.
Once all the AOIs were drawn around measurements within a satellite scene, each one was added to the signature file and the minimum, maximum, standard deviation, and mean value for each band within the AOI was computed. These results were then exported into a datafile format for further calculation. Results for the measurement values within the corresponding AOIs can be found in Appendix A.
A few steps were performed in Erdas IMAGINE to extract pixels in each image that would correspond to an inland lake greater than 25 acres. First, an unsupervised classification identified the water pixels (30-m cells). Next, the pixels were grouped into contiguous bodies of water to identify the inland lakes that were greater than 25 acres or 125 pixels. Finally, the pixels that corresponded to an inland lake greater than 25 acres were coded to a value of 1, with all other pixels coded to a no-data value to complete the water-only images.
In preparation for regression analysis, the band1/band3 ratio, the natural log of SDT (in meters) were computed. The data were then transferred into S-Plus 2000 (Data Analysis Products Division, 1999) for multiple regression calculations based on scene and type of measurement. (The combinations used in the regression equations are listed in table 3).
[ln, natural log; ETM+, Enhanced Thematic Mapper Plus; TOA, Radiometric-correction values of Top of Atmosphere Reflectance; ATM, Atmospheric-Correction; R2, R Squared; Eq, equation; ☐, Not tested]
| Equation 1 | Independent variable: ln (secchi depth in meters) | |||
|---|---|---|---|---|
| Secchi-disk transparency | Dependent variables: band 1/band 3, and band 1 | |||
| Landsat 7 ETM+ scenes | Samples | TOA R2 | ATM R2 | |
| path 20, row 30 | 15 | 0.5075 | ☐ | |
| path 20, row 31 | 13 | .3003 | ☐ | |
| path 21, row 29 | 28 | .6640 | 0.6737 | |
| path 21, row 30 | 29 | .7995 | .7995 | |
| path 21, row 31 | 25 | .6014 | .6072 | |
| Equation 2 | Independent variable: ln (secchi depth in meters) | |||
|---|---|---|---|---|
| Secchi-disk transparency | Dependent variables: band 1, band 2, band 3 | |||
| Landsat 7 ETM+ scenes | Samples | TOA R2 | ATM R2 | |
| path 20, row 30 | 15 | 0.7190 | ☐ | |
| path 20, row 31 | 13 | .6659 | ☐ | |
| path 21, row 29 | 28 | .7824 | 0.7875 | |
| path 21, row 30 | 29 | .7964 | .7964 | |
| path 21, row 31 | 25 | .6058 | .6101 | |
| Fisher's Transformation: R2 Equation 1 and Equation 2, R2 TOA and ATM ( >1.96 = significant) | ||||||
| Secchi-disk transparency | Samples | Eq1 & Eq2 TOA | Eq1 & Eq2 ATM | Eq 1 TOA & ATM | Eq 2 TOA & ATM | |
|---|---|---|---|---|---|---|
| Landsat 7 ETM+ scenes | ||||||
| path 20, row 30 | 15 | 1.199 | ☐ | ☐ | ☐ | |
| path 20, row 31 | 13 | 1.637 | ☐ | ☐ | ☐ | |
| path 21, row 29 | 28 | 1.233 | 1.212 | 0.065 | 0.086 | |
| path 21, row 30 | 29 | .043 | .043 | .000 | .000 | |
| path 21, row 31 | 25 | .032 | .022 | .032 | .043 | |
The equation developed by Kloiber and others (2000):
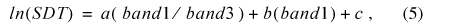
was applied to each TOA and atmospherically corrected scene. The variables a, b, and c were derived coefficients from the regression equation. In an effort to improve the goodness of fit for the model, various combinations of bands were tested. For the Kloiber (2000) equation, TOA and atmospherically corrected R2 values were compared. A new, alternative equation also was developed during the project. For the new alternative equation,
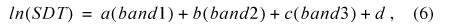
TOA and atmospherically corrected R2 values were compared.
To test whether there was a statistically significant difference between the R2 values, Fisher's Transformation was used:
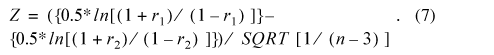
In the equation, r1 and r2 represent the two R2 values that were being tested, ln refers to base e and n refers to the number of samples. The results of Fisher's Transformation had to surpass 1.96 for a 95-percent confidence interval. This test was also used to determine whether there was any difference between the two equations to compute TSI from the predicted natural log of SDT and to test whether there was any difference between using the TOA or atmospherically corrected scenes from path 21.
To identify the best-fit regression equation for predicting Chl-a, a stepwise regression was used. In this process the natural log of measured Chl-a and various combinations of bands were used in four separate trials to determine the bands or combinations of bands with the best coefficients. For a list of the variables tested, refer to table 4.
Table 4. Stepwise regression trials and R2 values to predict trophic state index from chlorophyll a.
[TM, Landsat ETM + band; R2, R-squared; *, Landsat ETM+ satellite bands used for regression in each trial; --, Landsat ETM+ satellite bands not used]
| Stepwise regression trials | |||
|---|---|---|---|
| Trial 1 | Best coefficients | Trial 2 | Best coefficients |
| TM 1 | -- | TM 4 / TM 3 | -- |
| TM 2 | * | TM 2 / TM 3 | -- |
| TM 3 | * | TM 2 - TM 3 | -- |
| TM 4 | -- | TM 1 / TM 2 | -- |
| TM 5 | -- | TM 3 / TM 1 | * |
| TM 7 | * | R2 value | 0.6341 |
| R2 value | 0.8101 | ||
| Trial 3 | Best coefficients | Trial 4 | Best coefficients |
| (TM 2 + TM 3) / TM 2 | -- | TM 2 | -- |
| TM 22 | -- | TM 3 | * |
| TM 32 | * | TM 7 | * |
| (TM 1 + TM 2) / 2 | -- | TM 3 / TM 1 | -- |
| (TM 1 + TM 3) / 2 | * | TM 32 | -- |
| TM 3 / TM 4 | -- | (TM 1 + TM 3) / 2 | * |
| R2 value | 0.6592 | R2 value | 0.8045 |
An initial expectation for this project was that use of atmospherically corrected images would produce higher R2 values than use of the radiometrically corrected images. However, the R2 results were not significantly different. In some cases, the atmospheric-correction produced slightly higher R2 values than the radiometric-correction and in others produced slightly lower R2 values (these differences in the R2 values were only in the hundredths).
When Fisher's Transformation was used to test for the difference between R2 values for the atmospherically corrected imagery and R2 values for the radiometrically corrected imagery (tested on the R2 values resulting from both regression equations), the values for each scene ranged between 0.000 and 0.086. Therefore, imagery atmospherically corrected by use of MODTRAN4 did not produce a better-fit equation or statistically higher R2 values than did the radiometrically corrected imagery. The result from this test was that atmospherically corrected imagery was not necessary, and that radiometrically corrected imagery would be used to compute TSI values in this report. The R2 values from atmospherically corrected imagery or radiometrically corrected imagery for either regression equation are listed in table 3.
In comparison of results for the equation of Kloiber and others (2002),
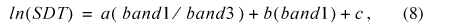
and the alternative regression equation that was derived and tested during the project,
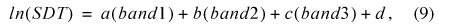
the alternative regression equation produced a better-fit equation and returned higher R2 values for four of the five scenes with very little difference in values for the fifth scene. Figure 3 shows the predicted and actual SDT for path 21, row 30, (which returned the highest R2 value), and for path 21, row 31, (which produced the lowest R2 value).
When Fisher's Transformation was used to test for differences between R2 values for the alternative regression equation and R2 values from the first equation (tested on the R2 values resulting from the atmospherically corrected imagery, and the radiometrically corrected imagery), the values for each scene were between 0.022 and 1.637. For each scene, the alternative regression equation had a higher R2 value, but the difference was not statistically significant (table 4). Because the alternative regression equation improved the R2 values for most scenes, it was substantially used to predict SDT for computing TSI values for lakes within the imagery. The computed TSI values for all lakes within the satellite imagery are shown on figure 4.
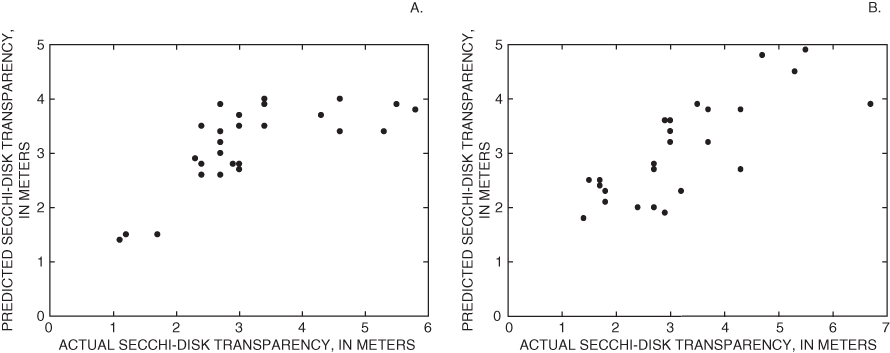
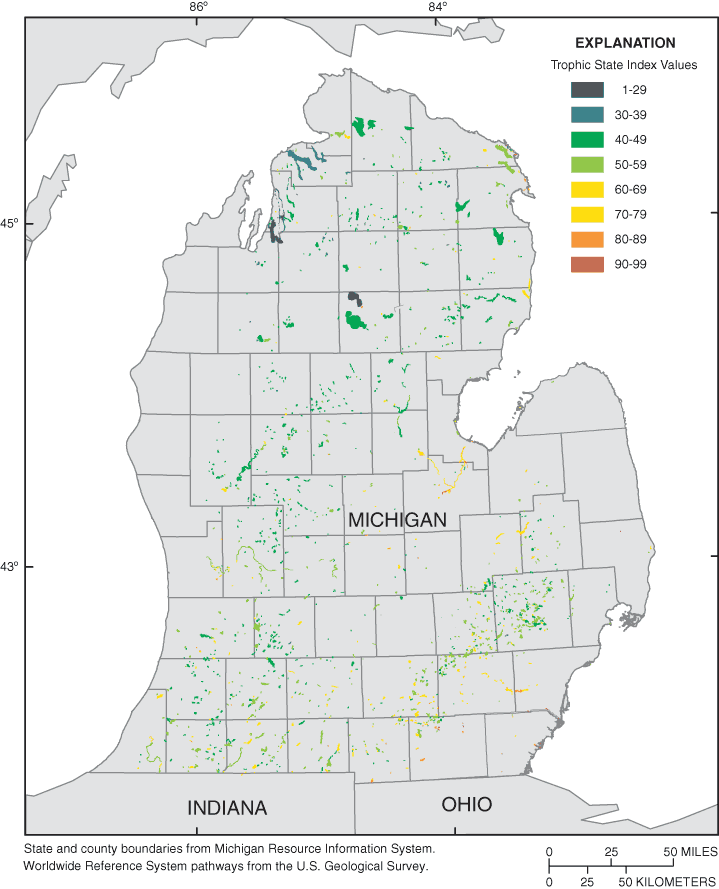
Figure 4. Computed trophic state index from predicted secchi-disk transparency, August 2002.
In the stepwise regression used to identify an equation for relating the natural log of Chl-a to satellite imagery, the combination of band 2 (Green), band 3 (Red), and band 7 (short wave infrared) produced the highest R2 values:
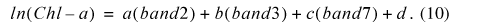
The resulting R2 value for predicting Chl-a measurements for path 21, row 29 was 0.81. Figure 5 shows predicted values and actual Chl-a values, figure 6 shows the computed TSI results from predicted Chl-a, and table 3 lists details of the stepwise regression variables and results.
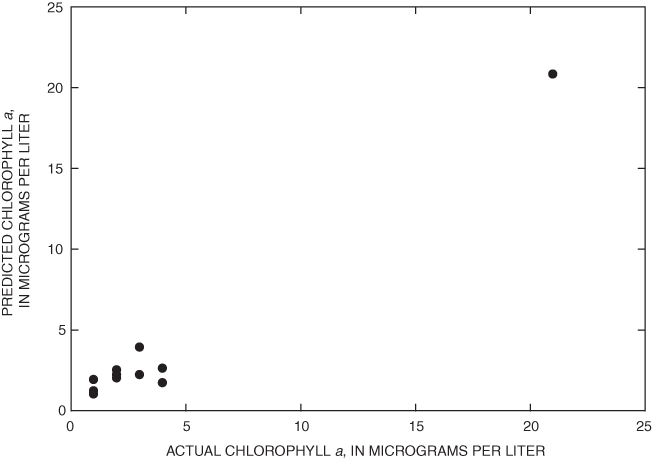
Figure 5. Predicted and actual chlorophyll a for path 21, row 29.
The USGS and MDEQ have been cooperatively monitoring the quality of inland lakes in Michigan through the Lake Water Quality Assessment (LWQA) monitoring program funded by the Clean Michigan Initiative. The LWQA and MDEQ Cooperative Lakes Monitoring Program monitor water quality for selected inland lakes each year. Since Michigan has many inland lakes, it is impossible to physically collect the necessary data to compute TSI values for all inland lakes. Remote sensing is an effective and economical tool to enhance the value of conventional sampling data by producing regression equations to predict SDT and Chl-a measurements from satellite imagery. From these predictions of SDT and Chl-a, TSI values can be computed for most of Michigan's inland lakes.
This study focused on 5 Landsat 7 ETM+ satellite scenes within Michigan, 87 SDT measurements, and 12 Chl-a measurements to find the best methods of predicting TSI values for inland lakes. As part of the study, atmospherically corrected images were tested against radiometrically corrected images to determine whether the atmospheric corrections would significantly improve the prediction of SDT. Differences between the R2 values, for the two sets of images were small and not statistically significant.
A second part of the study was to test was whether an alternative regression equation would fit the SDT data better and produce higher R2 values than a previously published equation from Kloiber and others (2000).
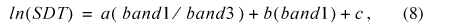
This equation produced R2 values ranging from 0.30 to 0.80. An alternative equation was found to produce a better correlation and higher R2 values ranging from 0.61 to 0.80.
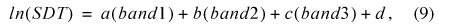
The improvement in R2 values was not statistically significant but it was adopted for subsequent prediction of SDT on account of the higher R2 values.
Finally, a stepwise regression was used to determine the best-fit equation between existing Chl-a measurements and various bands within the satellite imagery. This equation was developed for path 21, row 29 because that was the only scene with Chl-a measurements within plus or minus 7 days of the acquiring the imagery. The result of the stepwise regression was a regression equation that produced an R2 value of 0.81.
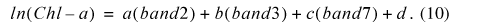
In addition to providing TSI estimates in unsampled lakes, remote-sensing techniques provide a cost-effective means of measuring both change through time and variability of water quality within a lake. Although TSI derived from satellite imagery is only an estimate of what the actual field sampled value might be, the cost per lake is dramatically lower compared to sampling. By using the high-quality measurements from the LWQA and CLMP programs, estimates can be made for entire Landsat scenes for approximately 10 percent the cost of field sampling. Operating both the field program and the remote sensing program will provide spatially continuous estimates of TSI for all lakes 25 acres or larger in size across Michigan, not just those selected for monitoring, and will increase temporal coverage because satellite-based estimates can be made for the same lakes on an annual or semiannual basis.
Mr. Ralph Bednarz of the Michigan Department of Environmental Quality and the volunteers of the Cooperative Lake Monitoring Program were invaluable in providing much of the field data used in the project. Dr. Jiagou Qi of the Michigan State University Department of Geography provided technical assistance with the atmospheric-correction process. Finally, Dr. Stacy Nelson, now at North Carolina State University, and Mrs. Naruman Wianwang of Michigan State University graciously provided assistance with this project.
Baban, S.M.J., 1993, Detecting water quality parameters in the Norfolk Broads, UK, using Landsat imagery: International Journal of Remote Sensing, v. 14, no. 7, p. 1247–1267.
Batzli, S., 2003, Mapping lake clarity: About the map, accessed February 2003 at URL http://www.lakesat.org/maptext1.php
Booth, B., 2000, Getting started with ArcInfo 8: ESRI Incorporated, 230 p.
Brivio P.A., Giardino, C., and Zilioli, E., 2001, Validation of satellite data for quality assurance in lake monitoring applications: Science of the Total Environment, v. 268, p. 3–18.
Canfield, D.E., Brown, C.D., Bachmann, R.W., and Hoyer, M.V., 2002, Volunteer lake monitoring-testing the reliability of data collected by the Florida LAKEWATCH Program: Lake and Reservoir Management, v. 18, no. 1, p. 1–9.
Carlson, R.E., 1977, A trophic state index for lakes: Limnology and Oceanography, v. 22, p. 361–369.
Carpenter, D.J., and Carpenter, S.M., 1983, Modeling inland water quality using landsat data: Remote Sensing of Environment, v. 13, p. 345–352.
Cox, R.M., Forsythe, R.D., Vaughan, G.E., and Olmsted, L.L., 1998, Assessing water quality in Catawba River reservoirs using Landsat thematic mapper satellite data: Lake and Reservoir Management, v. 14, no. 4, p. 405–416.
Data Analysis Products Division, 1999, S-Plus 2000-modern statistics and advanced graphics: Seattle, Wash., Mathsoft, Inc., 868 p.
Dekker, A.G., and Peters, S.W.M., 1993, The use of the Thematic Mapper for the analysis of utrophic lakes–a case study in the Netherlands: International Journal of Remote Sensing, v. 4, no. 5, p. 799–821.
Erdas, Inc., 2001, Erdas IMAGINE-Tour guides: Atlanta, Ga., Erdas, Inc., 662 p.
Giardino, C., Pepe, M., Brivio, P.A., Ghezzi, P., and Zilioli, E., 2001, Detecting chlorophyll, secchi-disk depth and surface temperature in a sub-alpine lake using Landsat imagery: Science of the Total Environment, v. 268, p. 19–29.
Hoke, Mike, 1999, MODTRAN v4.0 r00 Software, accessed February 2003 at URL http://www.vs.afrl.af.mil/Division/VSBYB/modtran4.html
Kendall, M.G., 1951, The advanced theory of statistics, v. 2 (3d ed.): New York, Hafner Publishing Company, p. 116–117.
Kloiber, S.M., Anderle, T.H., Brezonik, P.L., Olmanson, L., Bauer, M.E., and Brown, D.A., 2000, Trophic state assessment of lakes in the Twin Cities (Minnesota, USA) region by satellite imagery: Archive Hydrobiologie Special Issues, Advances in Limnology, v. 55, p. 137–151.
Kloiber, S.M., Brezonik, P.L., Olmanson, L.G., and Bauer, M.E., 2002, A procedure for regional lake water clarity assessment using Landsat multispectral data: Remote Sensing of Environment, v. 82, p. 38–47.
Krysel, C., Boyer, E.M., Parson, C., and Welle, P., 2003, Evidence from property sales in the Mississippi Headwaters Region, accessed September 2003 at URL http://info.bemidjistate.edu/News/currentnews/lakestudy/lakestudy.pdf
Lathrop, R.G., 1992, Landsat Thematic Mapper monitoring of turbid inland water quality: Photogrammetric Engineering and Remote Sensing, v. 58, no. 4, p. 465–470.
Lathrop, R.G., and Lillesand, T.M., 1986, Use of Thematic Mapper data to assess water quality in Green Bay and Central Lake Michigan: Photogrammetric Engineering and Remote Sensing, v. 52, no. 5, p. 671–680.
Lillesand, T.M., Johnson, W.L., Deuell, R.L., Lindstrom, O.M., and Meisner, D.E., 1983, Use of Landsat data to predict the trophic state of Minnesota lakes: Photogrammetric Engineering and Remote Sensing, v. 49, no. 2, p. 219–229.
Mayo, M., Gitelson, A., Yacobi, Y.Z., and Ben-Avraham, Z., 1995, Chlorophyll distribution in Lake Kinneret determined from Landsat Thematic Mapper data: International Journal of Remote Sensing, v. 16, no. 1, p. 175–182.
Michigan Department of Natural Resources, 1982, Michigan Inland Lake Project-Identification, Survey and Classification: Lansing, Mich., Clean Lake Agreement No. S 005511-01.
National Aeronautics Space Administration, 2003, Chapter 11–Data products, Landsat 7 science data users handbook, accessed March 2003 at URL http://ltpwww.gsfc.nasa.gov/IAS/handbook/handbook_htmls/chapter11/chapter11.html#section13
Naumann, E., 1919, Some aspects of the ecology of the limnoplankton, with special reference to the phytoplankton: Svensk Botanisk Tidskrift, v. 13, no. 2, p. 129–163.
Nelson, S.A.C., Soranno, P.A., Cheruvelil, K.S., Batzli, S.A., and Skole, D.L., 2002, Assessing regional lake water clarity using Landsat and the role of inter-lake variability, accessed February 2003 at URL http://foliage.geo.msu.edu/mdeq/docs/Nelson_RS-Secchi_text_2002__09.pdf
Obrecht, D.V., Milanick, M., and Perkins, B.D., 1998, Evaluation of data generated from lake samples collected by volunteers: Lake and Reservoir Management, v. 14, no. 1, p. 21–27.
Olmanson, L.G., Kloiber, S.M., Bauer, M.E., and Brezonik, P.L., 2001, Image processing protocol for regional assessments of lake water quality: St. Paul, Minn., Water Resources Center and Remote Sensing Laboratory, University of Minnesota, p. 1–13.
Pulliainen, J., Kallio, K., Eloheimo, K., Koponen, S., Servomaa, H., Hannonen, T., Auriainen, S., and Allikainen, M., 2001, A semi-operative approach to lake water quality retrieval from remote sensing data: Science of the Total Environment, v. 268, p. 79–93.
Scarpace, F.L., Holmquist, K.W., and Fisher, L.T., 1979, Landsat analysis of lake quality: Photogrammetric Engineering and Remote Sensing, v. 45, no. 5, p. 623–633.
Strong, A.E., 1974, Remote sensing of algal blooms by aircraft and satellite in Lake Erie and Utah Lake: Remote Sensing of Environment, v. 3, p. 99–107.
Stynes, D.J., 2002, Michigan statewide tourism spending and economic impact estimates 1998-2000, accessed November 2003 at URL http://www.prr.msu.edu/miteim/MichiganSatExec.pdf
Thiemann, S., and Kaufmann, H., 2002, Lake water quality monitoring using hyperspectral airborne data–A semiempirical multisensor and multitemporal approach for the Mecklenburg Lake District, Germany: Remote Sensing of Environment, v. 81, p. 228–237.
Verdin, J.P., 1985, Monitoring water quality conditions in a large western reservoir with Landsat imagery: Photogrammetric Engineering and Remote Sensing, v. 51, no. 3, p. 343–353.
Wiangwang, N., 2002, Water clarity/trophic condition monitoring by using satellite remote sensing data: Michigan State University, Department of Geography Graduate Program, East Lansing, Mich., Masters paper.
Williams, D., 2003, The Landsat 7 Satellite, instrument and data, accessed February 2003 at URL http://landsat.gsfc.nasa.gov/project/satellite.html
Zilioli, E., and Brivio, P.A., 1997, The satellite derived optical information for the comparative assessment of lacustrine water quality: Science of the Total Environment, v. 196, p. 229–245.
Results and computations from the Areas of Interest created from the Landsat 7 Enhanced Thematic Mapper Plus satellite scenes in Lower Michigan by use of radiometrically corrected imagery and atmospherically corrected imagery
[Abbreviations: AOI, Area of Interest; ft, feet; m, meters; ln, natural log; SDT, secchi-disk transparency; TOA, radiometrically corrected top of atmosphere reflectance values; MDEQ, Michigan Department of Environmental Quality; CLMP, Cooperative Lakes Monitoring Program; ATM, atmospherically corrected values; Chl-a, chlorophyll-a; USGS, U.S. Geological Survey; µg/L, micrograms per liter; band values recorded in digital numbers (0–255)]
| Satellite scene/ Lake name | AOI pixels | band 1 | band 2 | band 3 | band 4 | band 5 | band 1/ band 3 | SDT (ft) | SDT (m) | ln (SDT m) |
|---|---|---|---|---|---|---|---|---|---|---|
| path 20, row 30 TOA MDEQ CLMP | ||||||||||
| Lake Nepessing | 77 | 73.9870 | 48.8961 | 36.5325 | 17.4935 | 12.3507 | 2.0252 | 10.00 | 3.05 | 1.114 |
| Baseline | 57 | 65.5263 | 42.3509 | 31.0702 | 14.0526 | 11.3158 | 2.1090 | 11.50 | 3.51 | 1.254 |
| Bass | 37 | 69.3243 | 48.1351 | 33.0540 | 14.2432 | 11.6216 | 2.0973 | 9.83 | 3.00 | 1.097 |
| East Crooked | 50 | 67.0200 | 43.3600 | 31.7600 | 14.3400 | 11.9400 | 2.1102 | 10.00 | 3.05 | 1.114 |
| West Crooked | 26 | 66.0385 | 42.6154 | 31.7692 | 14.4231 | 11.8846 | 2.0787 | 6.50 | 1.98 | .684 |
| Ore | 48 | 76.2500 | 58.8542 | 38.1250 | 14.5625 | 11.9167 | 2.0000 | 6.00 | 1.83 | .604 |
| Strawberry | 33 | 68.7273 | 48.3636 | 34.9091 | 14.8182 | 11.7576 | 1.9688 | 6.17 | 1.88 | .632 |
| Zukey | 24 | 75.0417 | 55.3750 | 37.2083 | 14.4583 | 11.8750 | 2.0168 | 8.34 | 2.54 | .933 |
| Green | 26 | 71.8846 | 47.0000 | 32.9615 | 15.8462 | 12.3077 | 2.1809 | 14.00 | 4.27 | 1.451 |
| Lakeville | 37 | 73.1892 | 50.1892 | 36.8108 | 17.3243 | 12.2973 | 1.9883 | 12.00 | 3.66 | 1.297 |
| Walled | 48 | 70.5208 | 45.3750 | 32.9167 | 14.6250 | 11.9375 | 2.1424 | 17.75 | 5.41 | 1.688 |
| White Lake | 22 | 68.6818 | 43.2727 | 31.0454 | 15.0455 | 11.8182 | 2.2123 | 20.00 | 6.10 | 1.808 |
| Byram | 18 | 70.2778 | 48.8333 | 34.5556 | 16.0000 | 12.4444 | 2.0338 | 7.00 | 2.13 | .758 |
| Ponemah | 29 | 69.1724 | 45.7241 | 34.2759 | 15.4483 | 11.9310 | 2.0181 | 8.17 | 2.49 | .912 |
| Lansing | 88 | 78.8182 | 52.6818 | 40.4545 | 20.0909 | 13.6477 | 1.9483 | 10.00 | 3.05 | 1.114 |
| path 20, row 30 ATM MDEQ CLMP | ||||||||||
| Lake Nepessing | 77 | 120.5974 | 79.5065 | 56.0779 | 26.9740 | 17.4026 | 2.1505 | 10.00 | 3.05 | 1.114 |
| Baseline | 57 | 106.5439 | 68.7895 | 47.8421 | 21.1404 | 16.1754 | 2.2270 | 11.50 | 3.51 | 1.254 |
| Bass | 37 | 112.7838 | 78.2162 | 50.8649 | 21.5405 | 16.5405 | 2.2173 | 9.83 | 3.00 | 1.097 |
| East Crooked | 50 | 109.0600 | 70.3000 | 48.9200 | 21.6800 | 16.9600 | 2.2294 | 10.00 | 3.05 | 1.114 |
| West Crooked | 26 | 107.4231 | 69.1539 | 48.8462 | 21.8846 | 16.8462 | 2.1992 | 6.50 | 1.98 | .684 |
| Ore | 48 | 124.1875 | 95.5833 | 58.4583 | 22.1250 | 16.9375 | 2.1244 | 6.00 | 1.83 | .604 |
| Strawberry | 33 | 111.9697 | 78.6364 | 53.5758 | 22.6364 | 16.7273 | 2.0899 | 6.17 | 1.88 | .632 |
| Zukey | 24 | 122.3333 | 89.8750 | 57.0000 | 21.9167 | 16.7917 | 2.1462 | 8.34 | 2.54 | .933 |
| Green | 26 | 117.1154 | 76.2692 | 50.6923 | 24.6923 | 17.3846 | 2.3103 | 14.00 | 4.27 | 1.451 |
| Lakeville | 37 | 119.3243 | 81.4865 | 56.4865 | 26.6757 | 17.3243 | 2.1124 | 12.00 | 3.66 | 1.297 |
| Walled | 48 | 114.8125 | 73.6250 | 50.5833 | 22.2500 | 16.9167 | 2.2698 | 17.75 | 5.41 | 1.688 |
| White Lake | 22 | 111.7727 | 70.0909 | 47.9545 | 23.0909 | 16.7727 | 2.3308 | 20.00 | 6.10 | 1.808 |
| Byram | 18 | 114.5000 | 79.5000 | 53.1111 | 25.0000 | 17.5000 | 2.1559 | 7.00 | 2.13 | .758 |
| Ponemah | 29 | 112.5517 | 74.2414 | 52.5517 | 23.8966 | 16.9310 | 2.1417 | 8.17 | 2.49 | .912 |
| Lansing | 88 | 128.4204 | 85.4773 | 62.0909 | 31.0114 | 19.2046 | 2.0683 | 10.00 | 3.05 | 1.114 |
| path 20, row 31 TOA MDEQ CLMP | ||||||||||
| Baseline | 57 | 65.9649 | 42.7193 | 31.3684 | 14.1228 | 11.4561 | 2.1029 | 11.50 | 3.51 | 1.254 |
| Bass | 37 | 69.3784 | 48.2162 | 33.1351 | 14.2162 | 11.7297 | 2.0938 | 9.83 | 3.00 | 1.097 |
| Coon | 15 | 65.3333 | 41.5333 | 31.4667 | 15.2000 | 12.5333 | 2.0763 | 5.50 | 1.68 | .517 |
| East Crooked | 50 | 67.0000 | 43.5200 | 31.8000 | 14.4400 | 11.9800 | 2.1069 | 10.00 | 3.05 | 1.114 |
| West Crooked | 26 | 66.3461 | 42.7692 | 31.7692 | 14.3077 | 11.8846 | 2.0884 | 6.50 | 1.98 | .684 |
| Ore | 48 | 76.3125 | 58.7917 | 38.0417 | 14.5625 | 11.8542 | 2.0060 | 6.00 | 1.83 | .604 |
| Strawberry | 33 | 69.0000 | 48.4545 | 35.2121 | 14.8788 | 11.7273 | 1.9595 | 6.17 | 1.88 | .632 |
| Zukey | 24 | 75.0417 | 55.2917 | 36.9167 | 14.4583 | 11.8333 | 2.0327 | 8.34 | 2.54 | .933 |
| Walled | 48 | 70.4375 | 45.6042 | 33.3542 | 14.7917 | 11.9167 | 2.1118 | 17.75 | 5.41 | 1.688 |
| Portage | 82 | 65.7927 | 42.8902 | 30.5732 | 13.5488 | 11.2317 | 2.1520 | 13.40 | 4.08 | 1.407 |
| Clear | 59 | 67.7966 | 44.7458 | 31.2034 | 15.6441 | 12.1525 | 2.1727 | 9.00 | 2.74 | 1.009 |
| Pleasant | 24 | 66.6250 | 43.8750 | 32.3333 | 15.0000 | 12.0417 | 2.0606 | 7.08 | 2.16 | .769 |
| Vineyard | 20 | 77.8000 | 52.6000 | 38.4000 | 18.7500 | 13.1000 | 2.0260 | 10.50 | 3.20 | 1.163 |
| path 20, row 31 ATM MDEQ CLMP | ||||||||||
| Baseline | 57 | 109.6316 | 70.2807 | 48.3509 | 21.2807 | 16.3333 | 2.2674 | 11.50 | 3.51 | 1.254 |
| Bass | 37 | 114.8378 | 79.1081 | 50.9730 | 21.4595 | 16.6487 | 2.2529 | 9.83 | 3.00 | 1.097 |
| Coon | 15 | 108.6000 | 68.2667 | 48.4000 | 23.4000 | 17.6000 | 2.2438 | 5.50 | 1.68 | .517 |
| East Crooked | 50 | 111.2400 | 71.5200 | 49.0400 | 21.8800 | 17.0200 | 2.2683 | 10.00 | 3.05 | 1.114 |
| West Crooked | 26 | 110.1539 | 70.3077 | 48.8846 | 21.6538 | 16.8462 | 2.2533 | 6.50 | 1.98 | .684 |
| Ore | 48 | 126.4375 | 96.5000 | 58.3333 | 22.1250 | 16.8542 | 2.1675 | 6.00 | 1.83 | .604 |
| Strawberry | 33 | 114.4242 | 79.4242 | 54.0303 | 22.7576 | 16.6667 | 2.1178 | 6.17 | 1.88 | .632 |
| Zukey | 24 | 124.4583 | 90.7500 | 56.5833 | 21.9167 | 16.7500 | 2.1996 | 8.34 | 2.54 | .933 |
| Walled | 48 | 116.7083 | 74.6458 | 51.2708 | 22.6250 | 16.8958 | 2.2763 | 17.75 | 5.41 | 1.688 |
| Portage | 82 | 109.2073 | 70.5122 | 47.0854 | 20.5122 | 16.0976 | 2.3194 | 13.40 | 4.08 | 1.407 |
| Clear | 59 | 112.4407 | 73.3729 | 48.0508 | 24.2034 | 17.1525 | 2.3400 | 9.00 | 2.74 | 1.009 |
| Pleasant | 24 | 110.7083 | 72.1667 | 49.8333 | 23.0000 | 17.0417 | 2.2216 | 7.08 | 2.16 | .769 |
| Vineyard | 20 | 128.9500 | 86.2500 | 58.9500 | 28.7500 | 18.4000 | 2.1875 | 10.50 | 3.20 | 1.163 |
| path 24, row 28 TOA USGS LWQA | ||||||||||
| Arfelin | 18 | 56.1667 | 33.5556 | 23.6111 | 12.1667 | 11.2778 | 2.3788 | 22.00 | 6.71 | 1.903 |
| Witch | 19 | 55.2105 | 33.1053 | 24.4737 | 12.1579 | 11.6316 | 2.2559 | 15.00 | 4.57 | 1.520 |
| Horseshoe | 16 | 54.3125 | 34.2500 | 24.3750 | 12.0000 | 11.0625 | 2.2282 | 8.00 | 2.44 | .891 |
| Keewaydin | 17 | 54.1765 | 32.4706 | 23.6471 | 13.4706 | 11.4706 | 2.2910 | 9.00 | 2.74 | 1.009 |
| Silver | 10 | 54.4000 | 32.6000 | 24.7000 | 13.0000 | 11.7000 | 2.2024 | 10.00 | 3.05 | 1.114 |
| Buck | 18 | 54.9444 | 34.3889 | 24.2222 | 12.0000 | 11.1111 | 2.2683 | 8.00 | 2.44 | .891 |
| Indian | 14 | 56.7857 | 35.7143 | 24.2143 | 11.8571 | 10.8571 | 2.3451 | 15.00 | 4.57 | 1.520 |
| Emily | 16 | 55.6250 | 34.5625 | 25.9375 | 12.0625 | 10.8750 | 2.1446 | 8.00 | 2.44 | .891 |
| Ottawa | 21 | 56.9524 | 34.8571 | 23.8571 | 11.4762 | 10.4286 | 2.3872 | 19.00 | 5.79 | 1.756 |
| path 24, row 28 ATM USGS LWQA | ||||||||||
| Arfelin | 18 | 91.3333 | 54.6111 | 36.2222 | 18.3333 | 16.1111 | 2.5215 | 22.00 | 6.71 | 1.903 |
| Witch | 19 | 89.6316 | 54.0000 | 37.4211 | 18.5263 | 16.5263 | 2.3952 | 15.00 | 4.57 | 1.520 |
| Horseshoe | 16 | 88.1875 | 55.6250 | 37.3125 | 18.3125 | 15.7500 | 2.3635 | 8.00 | 2.44 | .891 |
| Keewaydin | 17 | 88.0000 | 52.8824 | 36.2941 | 20.5294 | 16.3529 | 2.4246 | 9.00 | 2.74 | 1.009 |
| Silver | 10 | 88.4000 | 52.9000 | 37.8000 | 19.8000 | 16.7000 | 2.3386 | 10.00 | 3.05 | 1.114 |
| Buck | 18 | 89.2778 | 55.8889 | 37.1667 | 18.1111 | 16.0000 | 2.4021 | 8.00 | 2.44 | .891 |
| Indian | 14 | 92.1429 | 57.7857 | 37.0714 | 17.9286 | 15.6429 | 2.4855 | 15.00 | 4.57 | 1.520 |
| Emily | 16 | 90.3125 | 56.0000 | 39.5625 | 18.3125 | 15.6875 | 2.2828 | 8.00 | 2.44 | .891 |
| Ottawa | 21 | 92.5714 | 56.5238 | 36.4286 | 17.4286 | 14.8571 | 2.5412 | 19.00 | 5.79 | 1.756 |
| path 21, row 29 TOA USGS LWQA | ||||||||||
| Brownlee | 15 | 63.4667 | 41.6000 | 29.6000 | 13.4000 | 12.6000 | 2.1441 | 6.00 | 1.83 | .604 |
| Alcona Dam Pond | 15 | 59.6000 | 37.4667 | 27.5333 | 13.5333 | 12.2667 | 2.1646 | 15.00 | 4.57 | 1.520 |
| Jewell | 11 | 64.7273 | 43.4545 | 31.2727 | 16.0909 | 13.5455 | 2.0698 | 11.00 | 3.35 | 1.210 |
| Van Etten | 14 | 64.2857 | 46.7143 | 34.9286 | 13.9286 | 11.9286 | 1.8405 | 4.00 | 1.22 | 0.198 |
| Foote Dam Pond | 14 | 60.8571 | 36.5000 | 27.3571 | 12.7143 | 12.0714 | 2.2245 | 21.00 | 6.40 | 1.856 |
| Shupac | 19 | 63.1053 | 39.3158 | 27.0526 | 14.3158 | 11.9474 | 2.3327 | 26.00 | 7.92 | 2.070 |
| West Twin | 18 | 62.4444 | 40.3333 | 27.3333 | 12.8889 | 10.7778 | 2.2846 | 10.00 | 3.05 | 1.114 |
| Dixon | 12 | 64.6667 | 42.2500 | 28.1667 | 15.8333 | 12.7500 | 2.2959 | 16.00 | 4.88 | 1.584 |
| Opal | 9 | 63.8889 | 40.3333 | 27.0000 | 14.6667 | 12.0000 | 2.3663 | 12.00 | 3.66 | 1.297 |
| K.P. | 13 | 62.0000 | 38.8462 | 27.4615 | 14.3077 | 12.0000 | 2.2577 | 9.00 | 2.74 | 1.009 |
| Emerald | 12 | 59.5000 | 37.4167 | 26.3333 | 15.0000 | 12.3333 | 2.2595 | 11.00 | 3.35 | 1.210 |
| Heart | 12 | 63.3333 | 39.9167 | 27.4167 | 16.1667 | 12.7500 | 2.3100 | 22.00 | 6.71 | 1.903 |
| path 21, row 29 ATM USGS LWQA | ||||||||||
| Brownlee | 15 | 101.2667 | 66.2000 | 44.7333 | 20.4000 | 17.5333 | 2.2638 | 6.00 | 1.83 | .604 |
| Alcona Dam Pond | 15 | 95.0667 | 59.4000 | 41.6667 | 20.5333 | 17.2667 | 2.2816 | 15.00 | 4.57 | 1.520 |
| Jewell | 11 | 103.1818 | 69.0000 | 47.2727 | 24.3636 | 19.0909 | 2.1827 | 11.00 | 3.35 | 1.210 |
| Van Etten | 14 | 102.6429 | 74.2857 | 52.5714 | 21.0714 | 16.7143 | 1.9524 | 4.00 | 1.22 | .198 |
| Foote Dam Pond | 14 | 97.1429 | 57.9286 | 41.3571 | 19.2143 | 16.7143 | 2.3489 | 21.00 | 6.40 | 1.856 |
| Shupac | 19 | 100.7368 | 62.5789 | 40.7895 | 21.6842 | 16.6842 | 2.4697 | 26.00 | 7.92 | 2.070 |
| West Twin | 18 | 99.7778 | 64.1667 | 41.3333 | 19.5556 | 14.9444 | 2.4140 | 10.00 | 3.05 | 1.114 |
| Dixon | 12 | 103.3333 | 67.0833 | 42.4167 | 23.9167 | 17.9167 | 2.4361 | 16.00 | 4.88 | 1.584 |
| Opal | 9 | 102.0000 | 64.3333 | 40.7778 | 22.2222 | 16.8889 | 2.5014 | 12.00 | 3.66 | 1.297 |
| K.P. | 13 | 99.0769 | 61.7692 | 41.5385 | 21.6154 | 16.7692 | 2.3852 | 9.00 | 2.74 | 1.009 |
| Emerald | 12 | 95.0000 | 59.3333 | 39.7500 | 22.8333 | 17.2500 | 2.3899 | 11.00 | 3.35 | 1.210 |
| Heart | 12 | 101.1667 | 63.5833 | 41.3333 | 24.5000 | 18.0000 | 2.4476 | 22.00 | 6.71 | 1.903 |
| path 21, row 29 TOA MDEQ CLMP | ||||||||||
| Vaughn | 27 | 58.1852 | 35.2593 | 25.3704 | 14.9259 | 12.2593 | 2.2934 | 11.00 | 3.35 | 1.210 |
| Jewell | 22 | 64.6818 | 42.6818 | 30.7727 | 15.3636 | 13.5000 | 2.1019 | 9.00 | 2.74 | 1.009 |
| Arnold | 42 | 62.0476 | 38.5714 | 27.2619 | 14.7143 | 12.2143 | 2.2760 | 15.00 | 4.57 | 1.520 |
| Lake Margrethe | 91 | 64.5824 | 40.4725 | 27.6923 | 12.6154 | 11.0000 | 2.3321 | 12.00 | 3.66 | 1.297 |
| Sage | 42 | 58.7857 | 36.3333 | 25.9762 | 12.6190 | 11.1667 | 2.2631 | 12.50 | 3.81 | 1.338 |
| North | 21 | 59.7619 | 37.4286 | 26.7619 | 14.4286 | 12.4762 | 2.2331 | 14.00 | 4.27 | 1.451 |
| Lake George | 17 | 62.1765 | 39.2941 | 28.1765 | 16.0588 | 12.4706 | 2.2067 | 10.00 | 3.05 | 1.114 |
| Shingle | 15 | 62.4667 | 39.2000 | 28.8000 | 16.2667 | 13.2000 | 2.1690 | 11.00 | 3.35 | 1.210 |
| Chain | 12 | 58.3333 | 36.7500 | 25.9167 | 13.8333 | 12.3333 | 2.2508 | 12.00 | 3.66 | 1.297 |
| Cub | 21 | 65.2857 | 41.2381 | 27.8095 | 15.1905 | 12.2381 | 2.3476 | 19.00 | 5.79 | 1.756 |
| Starvation | 25 | 65.6800 | 40.4400 | 28.4000 | 15.7200 | 11.9600 | 2.3127 | 26.17 | 7.98 | 2.077 |
| Avalon | 109 | 67.6606 | 41.4495 | 26.7064 | 13.0917 | 10.9908 | 2.5335 | 25.00 | 7.62 | 2.031 |
| East Twin | 83 | 64.2892 | 42.5904 | 29.3012 | 13.1205 | 10.8554 | 2.1941 | 10.00 | 3.05 | 1.114 |
| West Twin | 38 | 62.4474 | 40.7105 | 27.3421 | 12.5789 | 10.8421 | 2.2839 | 11.00 | 3.35 | 1.210 |
| Austin | 16 | 63.6250 | 39.4375 | 28.5625 | 15.5000 | 12.5000 | 2.2276 | 10.00 | 3.05 | 1.114 |
| Center | 22 | 66.2273 | 41.0909 | 30.2727 | 18.2727 | 13.5909 | 2.1877 | 18.50 | 5.64 | 1.730 |
| Wells | 14 | 63.7857 | 39.7857 | 28.2857 | 15.6429 | 12.7143 | 2.2551 | 17.50 | 5.33 | 1.674 |
| Stone Ledge | 22 | 65.5455 | 42.2273 | 30.9545 | 16.0455 | 12.8182 | 2.1175 | 8.00 | 2.44 | .891 |
| Beaver | 57 | 65.2807 | 43.0000 | 29.1228 | 13.4912 | 11.3158 | 2.2416 | 10.00 | 3.05 | 1.114 |
| Crooked | 16 | 59.0000 | 37.0625 | 25.6875 | 13.7500 | 11.9375 | 2.2968 | 16.50 | 5.03 | 1.615 |
| Hubbard | 769 | 61.1534 | 38.5176 | 26.1222 | 11.0988 | 10.2263 | 2.3410 | 17.00 | 5.18 | 1.645 |
| Cedar - Schmidt's Point | 44 | 67.8182 | 51.6364 | 35.3864 | 11.8182 | 10.7045 | 1.9165 | 3.42 | 1.04 | .042 |
| Mullett - Red Pine Point | 243 | 66.6872 | 43.0000 | 28.9959 | 12.0000 | 10.6049 | 2.2999 | 15.42 | 4.70 | 1.548 |
| Wildwood | 16 | 62.5625 | 39.1875 | 28.9375 | 14.1875 | 11.8750 | 2.1620 | 9.80 | 2.99 | 1.094 |
| Lily | 20 | 62.4500 | 38.3000 | 28.2000 | 14.7000 | 11.8000 | 2.2145 | 11.25 | 3.43 | 1.232 |
| Bear | 42 | 67.4762 | 40.8571 | 27.4048 | 14.0952 | 11.4286 | 2.4622 | 32.50 | 9.91 | 2.293 |
| Indian | 17 | 64.0000 | 39.8235 | 27.5294 | 16.1765 | 12.5882 | 2.3248 | 19.00 | 5.79 | 1.756 |
| Big Bradford | 28 | 62.8929 | 39.5714 | 26.7500 | 14.1786 | 11.9286 | 2.3511 | 16.00 | 4.88 | 1.584 |
| path 21, row 29 ATM MDEQ CLMP | ||||||||||
| Vaughn | 27 | 93.0741 | 56.1111 | 38.3704 | 22.5926 | 17.0741 | 2.4257 | 11.00 | 3.35 | 1.210 |
| Jewell | 22 | 103.2273 | 67.8182 | 46.4091 | 23.3636 | 19.0455 | 2.2243 | 9.00 | 2.74 | 1.009 |
| Arnold | 42 | 99.1190 | 61.2857 | 41.1905 | 22.4048 | 17.0714 | 2.4064 | 15.00 | 4.57 | 1.520 |
| Lake Margrethe | 91 | 103.1319 | 64.4725 | 41.8462 | 19.1978 | 15.2857 | 2.4645 | 12.00 | 3.66 | 1.297 |
| Sage | 42 | 93.9762 | 57.8571 | 39.3095 | 19.1905 | 15.5000 | 2.3907 | 12.50 | 3.81 | 1.338 |
| North | 21 | 95.3333 | 59.4286 | 40.3333 | 22.0000 | 17.5714 | 2.3636 | 14.00 | 4.27 | 1.451 |
| Lake George | 17 | 99.2353 | 62.4706 | 42.5294 | 24.1176 | 17.4706 | 2.3333 | 10.00 | 3.05 | 1.114 |
| Shingle | 15 | 99.8000 | 62.2667 | 43.4000 | 24.5333 | 18.6000 | 2.2995 | 11.00 | 3.35 | 1.210 |
| Chain | 12 | 93.0833 | 58.4167 | 39.2500 | 21.0000 | 17.2500 | 2.3715 | 12.00 | 3.66 | 1.297 |
| Cub | 21 | 104.2381 | 65.6667 | 41.9048 | 23.0476 | 17.1905 | 2.4875 | 19.00 | 5.79 | 1.756 |
| Starvation | 25 | 104.7200 | 64.4800 | 42.8800 | 23.7600 | 16.7600 | 2.4422 | 26.17 | 7.98 | 2.077 |
| Avalon | 109 | 107.8624 | 65.9633 | 40.2385 | 20.0092 | 15.2294 | 2.6806 | 25.00 | 7.62 | 2.031 |
| East Twin | 83 | 102.6265 | 67.6024 | 44.1928 | 20.0723 | 15.0723 | 2.3222 | 10.00 | 3.05 | 1.114 |
| West Twin | 38 | 99.7105 | 64.8158 | 41.2368 | 19.1053 | 15.0000 | 2.4180 | 11.00 | 3.35 | 1.210 |
| Austin | 16 | 101.6250 | 62.8125 | 43.1875 | 23.5000 | 17.4375 | 2.3531 | 10.00 | 3.05 | 1.114 |
| Center | 22 | 105.5000 | 65.4545 | 45.7273 | 27.5909 | 19.1818 | 2.3072 | 18.50 | 5.64 | 1.730 |
| Wells | 14 | 101.9286 | 63.3571 | 42.7143 | 23.5714 | 17.6429 | 2.3863 | 17.50 | 5.33 | 1.674 |
| Stone Ledge | 22 | 104.6364 | 67.0455 | 46.7273 | 24.2273 | 17.9091 | 2.2393 | 8.00 | 2.44 | .891 |
| Beaver | 57 | 104.1930 | 68.2632 | 43.9474 | 20.4211 | 15.6842 | 2.3709 | 10.00 | 3.05 | 1.114 |
| Crooked | 16 | 94.3125 | 58.8750 | 38.8125 | 20.8125 | 16.6875 | 2.4300 | 16.50 | 5.03 | 1.615 |
| Hubbard | 769 | 97.6112 | 61.1664 | 39.4421 | 16.9025 | 14.2471 | 2.4748 | 17.00 | 5.18 | 1.645 |
| Cedar - Schmidt's Point | 44 | 108.1136 | 82.2045 | 53.2955 | 17.9091 | 14.8182 | 2.0286 | 3.42 | 1.04 | .042 |
| Mullett - Red Pine Point | 243 | 106.2798 | 68.2798 | 43.7407 | 18.2099 | 14.6914 | 2.4298 | 15.42 | 4.70 | 1.548 |
| Wildwood | 16 | 99.9375 | 62.2500 | 43.7500 | 21.4375 | 16.5625 | 2.2843 | 9.80 | 2.99 | 1.094 |
| Lily | 20 | 99.7000 | 60.7500 | 42.5500 | 22.4000 | 16.4000 | 2.3431 | 11.25 | 3.43 | 1.232 |
| Bear | 42 | 107.5952 | 65.0238 | 41.3810 | 21.2381 | 15.8571 | 2.6001 | 32.50 | 9.91 | 2.293 |
| Indian | 17 | 102.2941 | 63.4706 | 41.5882 | 24.4118 | 17.7059 | 2.4597 | 19.00 | 5.79 | 1.756 |
| Big Bradford | 28 | 100.4643 | 63.0000 | 40.3929 | 21.5000 | 16.7143 | 2.4872 | 16.00 | 4.88 | 1.584 |
| path 21, row 30 TOA MDEQ CLMP | ||||||||||
| Lansing | 50 | 65.1600 | 41.9600 | 30.3200 | 13.6200 | 11.7400 | 2.1491 | 10.00 | 3.05 | 1.114 |
| Clear | 29 | 64.5862 | 42.3448 | 30.3103 | 14.5172 | 12.9655 | 2.1308 | 9.00 | 2.74 | 1.009 |
| Sanford | 39 | 64.8974 | 40.5897 | 30.2821 | 14.8974 | 11.7692 | 2.1431 | 9.50 | 2.90 | 1.063 |
| Lake George | 16 | 62.1250 | 39.6250 | 27.7500 | 16.1875 | 12.3125 | 2.2387 | 10.00 | 3.05 | 1.114 |
| Shingle | 12 | 62.5833 | 39.0833 | 28.7500 | 16.0000 | 13.2500 | 2.1768 | 11.00 | 3.35 | 1.210 |
| Bostwick | 54 | 65.6852 | 43.8333 | 29.5741 | 13.2407 | 11.2593 | 2.2210 | 8.00 | 2.44 | .891 |
| Freska | 12 | 61.9167 | 39.0000 | 27.5000 | 15.6667 | 12.5000 | 2.2515 | 9.00 | 2.74 | 1.009 |
| Murray | 30 | 65.1000 | 42.2667 | 29.4000 | 15.2000 | 12.1667 | 2.2143 | 7.50 | 2.29 | .827 |
| Reeds | 43 | 68.0465 | 48.8605 | 33.4651 | 13.5814 | 11.2791 | 2.0334 | 4.10 | 1.25 | .223 |
| Derby | 43 | 64.0698 | 39.9302 | 27.1860 | 14.0465 | 11.6977 | 2.3567 | 18.00 | 5.49 | 1.702 |
| Brooks | 31 | 66.8710 | 48.3871 | 34.0968 | 14.5161 | 11.5484 | 1.9612 | 3.50 | 1.07 | .065 |
| Hess | 150 | 68.7667 | 54.0600 | 39.0333 | 13.4133 | 10.7133 | 1.7617 | 3.00 | .91 | -.089 |
| Robinson | 22 | 62.6818 | 38.3182 | 27.5000 | 14.0000 | 11.6818 | 2.2793 | 11.00 | 3.35 | 1.210 |
| Austin | 13 | 63.3077 | 39.5385 | 28.5385 | 15.5385 | 12.5385 | 2.2183 | 10.00 | 3.05 | 1.114 |
| Big | 43 | 65.5349 | 41.7907 | 30.0465 | 15.0698 | 11.7907 | 2.1811 | 9.83 | 3.00 | 1.097 |
| Wells | 13 | 63.7692 | 40.1538 | 28.3846 | 15.8462 | 12.5385 | 2.2466 | 17.50 | 5.33 | 1.674 |
| Hutchins | 38 | 64.8421 | 41.8947 | 28.8947 | 13.3947 | 11.6053 | 2.2441 | 9.00 | 2.74 | 1.009 |
| Barlow | 16 | 66.1250 | 43.0625 | 27.6875 | 13.9375 | 11.6250 | 2.3883 | 9.00 | 2.74 | 1.009 |
| Jordan | 38 | 65.6842 | 48.7895 | 33.1053 | 13.6579 | 11.2895 | 1.9841 | 5.50 | 1.68 | .517 |
| Lily | 31 | 62.3226 | 38.4194 | 27.9032 | 14.6452 | 12.0000 | 2.2335 | 11.25 | 3.43 | 1.232 |
| Camp | 31 | 63.7419 | 39.4516 | 27.9032 | 13.9677 | 11.6452 | 2.2844 | 14.00 | 4.27 | 1.451 |
| Blue | 23 | 64.0435 | 42.0000 | 29.5217 | 13.6957 | 11.3913 | 2.1694 | 10.00 | 3.05 | 1.114 |
| Round | 23 | 63.9130 | 40.3043 | 29.0435 | 14.4348 | 12.1304 | 2.2006 | 9.00 | 2.74 | 1.009 |
| Baldwin | 9 | 63.4444 | 40.5556 | 27.8889 | 14.1111 | 11.7778 | 2.2749 | 8.00 | 2.44 | .891 |
| Clifford | 18 | 62.6667 | 39.6111 | 28.6111 | 14.0000 | 11.7778 | 2.1903 | 15.00 | 4.57 | 1.520 |
| Indian Lake | 40 | 63.0250 | 39.6250 | 28.7250 | 14.0250 | 11.3750 | 2.1941 | 9.00 | 2.74 | 1.009 |
| Bills | 29 | 67.3793 | 44.4483 | 28.7241 | 13.5517 | 11.4138 | 2.3457 | 8.00 | 2.44 | .891 |
| Crystal | 63 | 64.1429 | 39.1905 | 27.3016 | 13.9206 | 11.7302 | 2.3494 | 15.00 | 4.57 | 1.520 |
| Indian | 21 | 64.0000 | 39.9524 | 27.5238 | 16.4286 | 12.6190 | 2.3253 | 19.00 | 5.79 | 1.756 |
| path 21, row 30 ATM MDEQ CLMP | ||||||||||
| Lansing | 50 | 102.5400 | 65.7800 | 45.1800 | 20.2800 | 16.3600 | 2.2696 | 10.00 | 3.05 | 1.114 |
| Clear | 29 | 101.6897 | 66.3103 | 45.2414 | 21.5172 | 17.9655 | 2.2477 | 9.00 | 2.74 | 1.009 |
| Sanford | 39 | 102.1795 | 63.6667 | 45.2051 | 22.0513 | 16.4359 | 2.2604 | 9.50 | 2.90 | 1.063 |
| Lake George | 16 | 97.8750 | 62.0000 | 41.3750 | 24.1875 | 17.2500 | 2.3656 | 10.00 | 3.05 | 1.114 |
| Shingle | 12 | 98.5833 | 61.3333 | 42.9167 | 23.9167 | 18.2500 | 2.2971 | 11.00 | 3.35 | 1.210 |
| Bostwick | 54 | 103.3148 | 68.7593 | 44.1667 | 19.5741 | 15.5741 | 2.3392 | 8.00 | 2.44 | .891 |
| Freska | 12 | 97.5833 | 61.2500 | 40.9167 | 23.2500 | 17.3333 | 2.3849 | 9.00 | 2.74 | 1.009 |
| Murray | 30 | 102.4000 | 66.1000 | 43.9000 | 22.4333 | 17.0000 | 2.3326 | 7.50 | 2.29 | .827 |
| Reeds | 43 | 107.1860 | 76.6047 | 50.0000 | 20.1628 | 15.6279 | 2.1437 | 4.10 | 1.25 | .223 |
| Derby | 43 | 100.8837 | 62.6512 | 40.5581 | 20.9767 | 16.3256 | 2.4874 | 18.00 | 5.49 | 1.702 |
| Brooks | 31 | 105.0968 | 75.8387 | 50.8710 | 21.5161 | 16.0323 | 2.0659 | 3.50 | 1.07 | 0.065 |
| Hess | 150 | 108.2933 | 84.8267 | 58.3133 | 19.8600 | 14.8000 | 1.8571 | 3.00 | .91 | -.089 |
| Robinson | 22 | 98.7273 | 60.0909 | 40.9545 | 20.8182 | 16.2273 | 2.4107 | 11.00 | 3.35 | 1.210 |
| Austin | 13 | 99.6923 | 62.0000 | 42.5385 | 23.0769 | 17.4615 | 2.3436 | 10.00 | 3.05 | 1.114 |
| Big | 43 | 103.0233 | 65.4419 | 44.8140 | 22.2791 | 16.4651 | 2.2989 | 9.83 | 3.00 | 1.097 |
| Wells | 13 | 100.3846 | 63.0000 | 42.1538 | 23.6154 | 17.3846 | 2.3814 | 17.50 | 5.33 | 1.674 |
| Hutchins | 38 | 102.0526 | 65.5526 | 43.1053 | 19.9211 | 16.2368 | 2.3675 | 9.00 | 2.74 | 1.009 |
| Barlow | 16 | 103.8750 | 67.3750 | 41.1875 | 20.8750 | 16.2500 | 2.5220 | 9.00 | 2.74 | 1.009 |
| Jordan | 38 | 103.3421 | 76.4474 | 49.3947 | 20.2368 | 15.6842 | 2.0922 | 5.50 | 1.68 | .517 |
| Lily | 31 | 98.1613 | 60.3871 | 41.5806 | 21.6452 | 16.7097 | 2.3607 | 11.25 | 3.43 | 1.232 |
| Camp | 31 | 100.3871 | 61.9677 | 41.6452 | 20.7097 | 16.1613 | 2.4105 | 14.00 | 4.27 | 1.451 |
| Blue | 23 | 100.7391 | 65.7391 | 44.0435 | 20.4348 | 15.7826 | 2.2873 | 10.00 | 3.05 | 1.114 |
| Round | 23 | 100.5652 | 63.1739 | 43.2174 | 21.4348 | 16.9565 | 2.3270 | 9.00 | 2.74 | 1.009 |
| Baldwin | 9 | 99.8889 | 63.5556 | 41.6667 | 20.7778 | 16.4444 | 2.3973 | 8.00 | 2.44 | .891 |
| Clifford | 18 | 98.6111 | 62.2222 | 42.6667 | 20.7778 | 16.3333 | 2.3112 | 15.00 | 4.57 | 1.520 |
| Indian Lake | 40 | 99.2750 | 62.1500 | 42.9000 | 20.7500 | 15.8500 | 2.3141 | 9.00 | 2.74 | 1.009 |
| Bills | 29 | 105.9655 | 69.7586 | 42.8276 | 20.0690 | 15.8276 | 2.4742 | 8.00 | 2.44 | .891 |
| Crystal | 63 | 100.9683 | 61.5556 | 40.6508 | 20.6984 | 16.3651 | 2.4838 | 15.00 | 4.57 | 1.520 |
| Indian | 21 | 100.7143 | 62.7143 | 41.0000 | 24.4286 | 17.5714 | 2.4564 | 19.00 | 5.79 | 1.756 |
| path 21, row 31 TOA MDEQ CLMP | ||||||||||
| Randall | 55 | 62.5636 | 42.0545 | 30.3091 | 13.8909 | 11.6000 | 2.0642 | 4.50 | 1.37 | .316 |
| Coldwater | 124 | 63.9597 | 44.6210 | 30.1048 | 13.1774 | 12.2500 | 2.1246 | 6.00 | 1.83 | .604 |
| Birch | 68 | 70.0441 | 45.0147 | 28.3824 | 14.3529 | 11.7353 | 2.4679 | 14.00 | 4.27 | 1.451 |
| Diamond | 95 | 66.9263 | 43.2737 | 28.2211 | 13.4842 | 11.2000 | 2.3715 | 10.00 | 3.05 | 1.114 |
| Clear | 56 | 64.5357 | 42.4464 | 30.1250 | 14.5000 | 12.9286 | 2.1423 | 9.00 | 2.74 | 1.009 |
| Corey | 93 | 67.2258 | 44.2258 | 28.3118 | 13.2043 | 11.1075 | 2.3745 | 9.50 | 2.90 | 1.063 |
| Long | 16 | 59.5625 | 38.5000 | 28.6250 | 14.6250 | 12.6250 | 2.0808 | 5.00 | 1.52 | .421 |
| Farwell | 22 | 77.0909 | 54.6818 | 30.8636 | 14.8182 | 12.8636 | 2.4978 | 9.00 | 2.74 | 1.009 |
| Vineyard | 35 | 63.6286 | 43.8571 | 29.6286 | 13.4286 | 11.9143 | 2.1475 | 10.50 | 3.20 | 1.163 |
| Indian | 53 | 69.4151 | 50.4340 | 31.0943 | 13.2830 | 11.1509 | 2.2324 | 8.00 | 2.44 | .891 |
| Evans | 32 | 59.2813 | 37.2188 | 26.0938 | 13.1250 | 11.9375 | 2.2719 | 18.00 | 5.49 | 1.702 |
| Clear.0 | 46 | 63.0870 | 38.8913 | 27.3478 | 13.5000 | 11.7609 | 2.3068 | 11.50 | 3.51 | 1.254 |
| Cedar | 51 | 63.6667 | 38.8824 | 26.8039 | 13.0980 | 11.6667 | 2.3753 | 17.50 | 5.33 | 1.674 |
| Fish | 10 | 62.6000 | 39.8000 | 28.1000 | 14.9000 | 12.1000 | 2.2278 | 10.00 | 3.05 | 1.114 |
| Lake of the Woods | 39 | 63.0769 | 38.4872 | 27.3846 | 13.8974 | 11.6923 | 2.3034 | 12.00 | 3.66 | 1.297 |
| Eagle | 43 | 63.2326 | 38.7674 | 26.5349 | 13.4186 | 11.6047 | 2.3830 | 15.50 | 4.72 | 1.553 |
| Hutchins | 53 | 65.2830 | 41.6792 | 28.8868 | 13.4151 | 11.5094 | 2.2600 | 9.00 | 2.74 | 1.009 |
| Osterhout | 30 | 63.8333 | 39.8000 | 27.9333 | 14.4333 | 11.9000 | 2.2852 | 10.00 | 3.05 | 1.114 |
| Christiana | 53 | 64.5094 | 41.1698 | 29.3019 | 14.0189 | 11.4906 | 2.2015 | 5.50 | 1.68 | .517 |
| Juno | 90 | 64.1778 | 40.2778 | 29.1111 | 14.2444 | 11.4000 | 2.2046 | 5.50 | 1.68 | .517 |
| Painter | 32 | 64.2813 | 39.8438 | 29.4063 | 14.8750 | 12.0313 | 2.1860 | 6.00 | 1.83 | 0.604 |
| Gourdneck | 40 | 63.1500 | 38.9750 | 28.0750 | 13.4000 | 11.2500 | 2.2493 | 12.00 | 3.66 | 1.297 |
| Keeler | 45 | 66.5778 | 43.2000 | 30.4444 | 14.6889 | 12.7111 | 2.1869 | 9.50 | 2.90 | 1.063 |
| Reynolds (lower) | 16 | 63.5625 | 40.3750 | 28.8125 | 15.5000 | 13.1250 | 2.2061 | 14.00 | 4.27 | 1.451 |
| Reynolds (upper) | 27 | 63.7407 | 39.5926 | 27.4444 | 13.5556 | 11.4815 | 2.3225 | 22.00 | 6.71 | 1.903 |
| path 21, row 31 ATM MDEQ CLMP | ||||||||||
| Randall | 55 | 95.5455 | 64.3273 | 44.0909 | 19.9818 | 15.6727 | 2.1670 | 4.50 | 1.37 | .316 |
| Coldwater | 124 | 97.6774 | 68.1532 | 43.7419 | 18.9677 | 16.6210 | 2.2330 | 6.00 | 1.83 | .604 |
| Birch | 68 | 107.2941 | 68.7353 | 41.3382 | 20.7353 | 15.8382 | 2.5955 | 14.00 | 4.27 | 1.451 |
| Diamond | 95 | 102.2421 | 66.1368 | 41.0421 | 19.4526 | 15.0211 | 2.4912 | 10.00 | 3.05 | 1.114 |
| Clear | 56 | 98.6250 | 64.9464 | 43.8750 | 20.9821 | 17.5893 | 2.2479 | 9.00 | 2.74 | 1.009 |
| Corey | 93 | 102.7204 | 67.5806 | 41.2258 | 19.2043 | 14.9032 | 2.4917 | 9.50 | 2.90 | 1.063 |
| Long | 16 | 91.0625 | 58.8750 | 41.6250 | 21.1250 | 17.1875 | 2.1877 | 5.00 | 1.52 | .421 |
| Farwell | 22 | 117.8182 | 83.8182 | 44.7273 | 21.5000 | 17.5000 | 2.6341 | 9.00 | 2.74 | 1.009 |
| Vineyard | 35 | 97.2286 | 67.0286 | 43.1429 | 19.4286 | 16.0857 | 2.2536 | 10.50 | 3.20 | 1.163 |
| Indian | 53 | 106.3019 | 77.0377 | 45.1321 | 19.2264 | 15.0189 | 2.3554 | 8.00 | 2.44 | .891 |
| Evans | 32 | 90.6875 | 57.0938 | 37.9063 | 18.9688 | 16.0938 | 2.3924 | 18.00 | 5.49 | 1.702 |
| Clear.0 | 46 | 96.4130 | 59.5652 | 39.7609 | 19.5217 | 15.8913 | 2.4248 | 11.50 | 3.51 | 1.254 |
| Cedar | 51 | 97.2157 | 59.5294 | 38.9020 | 18.8824 | 15.8039 | 2.4990 | 17.50 | 5.33 | 1.674 |
| Fish | 10 | 95.5000 | 60.9000 | 40.9000 | 21.7000 | 16.5000 | 2.3350 | 10.00 | 3.05 | 1.114 |
| Lake of the Woods | 39 | 96.4359 | 59.0513 | 39.8205 | 19.9231 | 15.6667 | 2.4218 | 12.00 | 3.66 | 1.297 |
| Eagle | 43 | 96.6047 | 59.4186 | 38.5581 | 19.4186 | 15.5814 | 2.5054 | 15.50 | 4.72 | 1.553 |
| Hutchins | 53 | 99.7358 | 63.8679 | 42.0566 | 19.4151 | 15.5094 | 2.3715 | 9.00 | 2.74 | 1.009 |
| Osterhout | 30 | 97.5333 | 60.9667 | 40.6333 | 20.8667 | 16.0333 | 2.4003 | 10.00 | 3.05 | 1.114 |
| Christiana | 53 | 98.4906 | 63.0189 | 42.6604 | 20.1509 | 15.4528 | 2.3087 | 5.50 | 1.68 | .517 |
| Juno | 90 | 98.0667 | 61.6556 | 42.3889 | 20.5444 | 15.3778 | 2.3135 | 5.50 | 1.68 | .517 |
| Painter | 32 | 98.1875 | 60.9375 | 42.7500 | 21.6563 | 16.2813 | 2.2968 | 6.00 | 1.83 | .604 |
| Gourdneck | 40 | 96.4250 | 59.7250 | 40.8500 | 19.4000 | 15.0750 | 2.3605 | 12.00 | 3.66 | 1.297 |
| Keeler | 45 | 101.6889 | 66.0444 | 44.3333 | 21.3333 | 17.2889 | 2.2937 | 9.50 | 2.90 | 1.063 |
| Reynolds (lower) | 16 | 97.0000 | 61.7500 | 42.0000 | 22.5625 | 17.9375 | 2.3095 | 14.00 | 4.27 | 1.451 |
| Reynolds (upper) | 27 | 97.3333 | 60.6296 | 39.9259 | 19.5926 | 15.4444 | 2.4378 | 22.00 | 6.71 | 1.903 |
[Abbreviations: AOI, Area of Interest; ft, feet; m, meters; ln, natural log; SDT, secchi-disk transparency; TOA, radiometrically corrected top of atmosphere reflectance values; MDEQ, Michigan Department of Environmental Quality; CLMP, Cooperative Lakes Monitoring Program; ATM, atmospherically corrected values; Chl-a, chlorophyll-a; USGS, U.S. Geological Survey; µg/L, micrograms per liter; band values recorded in digital numbers (0–255)]
| Satellite scene/ Lake name | AOI Pixels | band 1 | band 2 | band 3 | band 4 | band 5 | band 7 | Chl-a (µg/L) | ln (Chl-a) | |
|---|---|---|---|---|---|---|---|---|---|---|
| path 21, row 29 USGS Chl-a | ||||||||||
| Brownlee | 13 | 62.92308 | 41.69231 | 29.69231 | 13.30769 | 12.69231 | 11.30769 | 3 | 1.10 | |
| Alcona Dam Pond | 9 | 59.88889 | 37.66667 | 27.11111 | 13.77778 | 12.22222 | 11.11111 | 1 | .00 | |
| Jewell | 12 | 64.83333 | 43.41667 | 31.16667 | 16.08333 | 13.41667 | 11.66667 | 2 | .69 | |
| Van Etten | 10 | 64.30000 | 47.30000 | 35.20000 | 15.60000 | 12.30000 | 10.30000 | 21 | 3.04 | |
| Foote Dam Pond | 13 | 61.30769 | 37.38462 | 26.92308 | 12.76923 | 12.38462 | 10.76923 | 2 | .69 | |
| East Twin | 18 | 65.16667 | 42.72222 | 28.77778 | 12.88889 | 11.00000 | 10.22222 | 4 | 1.39 | |
| Shupac | 12 | 63.75000 | 39.50000 | 26.58333 | 14.50000 | 12.08333 | 11.00000 | 1 | .00 | |
| West Twin | 13 | 62.84615 | 41.69231 | 28.30769 | 12.84615 | 11.07692 | 9.76923 | 3 | 1.10 | |
| Dixion | 14 | 65.71429 | 43.92857 | 29.21429 | 15.57143 | 12.85714 | 11.07143 | 1 | .00 | |
| Opal | 11 | 64.90909 | 42.00000 | 27.18182 | 14.63636 | 12.18182 | 10.36364 | 1 | .00 | |
| Emerald | 8 | 59.50000 | 37.37500 | 26.37500 | 14.87500 | 12.50000 | 10.87500 | 4 | 1.39 | |
| Heart | 9 | 63.44444 | 40.22222 | 27.55556 | 16.11111 | 12.88889 | 10.55556 | 2 | .69 | |
For more information concerning the research in this report, contact:
Jim Nicholas, District Chief
U.S. Geological Survey
6520 Mercantile Way, Suite 5
Lansing, MI 48911-5991
Document Accessibility: Adobe Systems Incorporated has information about PDFs and the visually impaired. This information provides tools to help make PDF files accessible. These tools convert Adobe PDF documents into HTML or ASCII text, which then can be read by a number of common screen-reading programs that synthesize text as audible speech. In addition, an accessible version of Acrobat Reader 6.0, which contains support for screen readers, is available. These tools and the accessible reader may be obtained free from Adobe at Adobe Access.
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|