
|
|
|
||||
| Scientific Investigations Report 2005–5153 |
in cooperation with the Ohio Department of Transportation and the U.S. Department of Transportation, Federal Highway Administration
Collection of Geomorphic Data at Study Sites
Determination of Bankfull Discharge and Recurrence Interval
Development of Methods to Estimate Bankfull Characteristics of Ohio Stream...
Relations Between Bankfull Characteristics and Peak Streamflows
Geographic Information System Data Set
Figure 1. Schematic diagram showing geomorphic features of a str...
Figure 2. Locations of the 50 selected study sites in Ohio.
Figure 3. Example plan-view plot for Skull Fork near Londonderry...
Figure 4. Example bankfull-profile plot for the right bank for S...
Figure 5. Example cross-section plot for Skull Fork near Londond...
Figure 6. Examples of computed bed-material plots for Walnut Cre...
Figure 7. Bankfull regions A and B and locations of the 50 selec...
Figure 8. Regional curves for bankfull width for Ohio.
Figure 9. Regional curves for bankfull mean depth for Ohio.
Figure 10. Regional curves for bankfull cross-sectional area for...
Figure 11. Regional curves for bankfull discharge for Ohio.
Table 1. Station identification information, geographical coordi...
Table 2. Selected geomorphic data for the 50 study sites in Ohio...
Table 3. Selected bed-material size-distribution data for the 50...
Table 4. Selected bank-material size-distribution data for t...
Table 5. Data used for Rosgen Level II (Rosgen, 1996) classifica...
Table 6. Bankfull discharges, associated recurrence interval...
Table 7. Simple-regression (drainage-area-only) equations fo...
Table 8. Multiple-regression equations for estimating bankfu...
Table 9 . Multiple-regression equations for estimating bankfu...
Table 10. Values of all explanatory variables in tables 7, 8...
Table 11. Five areas of Ohio and associated counties where o...
Table 12. Summary statistics of explanatory variables by region.
Table 13. Simple-regression equations for estimating flood-peak ...
Table 14. Values of the log-Pearson Type III flood-frequency...
Table 15. Comparison of simple-regression equations for estimati...
| Multiply | By | To obtain |
| millimeter (mm) | 0 .03937 | inch (in.) |
| inch (in.) | 25.4 | millimeter (mm) |
| foot (ft) | 0.3048 | meter (m) |
| mile (mi) | 1.609 | kilometer (km) |
| foot per mile (ft/mi) | 0.1894 | meter per kilometer (m/km) |
| square inch (in2) | 6.452 | square centimeter (cm2) |
| square mile (mi2) | 2.590 | square kilometer (km2) |
| cubic foot (ft3) | 0.02832 | cubic meter (m3) |
| acre-foot (acre-ft) | 1,233 | cubic meter (m3) |
| cubic foot per second (ft3/s) | 0.02832 | cubic meter per second (m3/s) |
Vertical coordinate information is referenced to the National Geodetic Vertical Datum of 1929 (NGVD of 1929).
The following are definitions of selected abbreviations as they are used in this report; they are not necessarily the only valid definitions for these abbreviations.
| AAC | Active-channel cross-sectional area (in square feet) -- Cross-sectional area of the stream channel at active-channel stage (SAC) measured perpendicular to the streamflow at active-channel stage. |
|---|---|
| ABF | Bankfull cross-sectional area (in square feet) -- Cross-sectional area of the stream channel at bankfull stage (SBF) measured perpendicular to the streamflow at bankfull stage. |
| BED50 | Bed-material particle size of which 50 percent is finer (in millimeters) -- For this study, bed-material particle size was determined at each cross section by means of Wolman pebble counts (Wolman, 1954). About 100 samples were collected across the streambed at the head of each riffle between the bottoms of the streambanks and extending downstream from riffle head about one-fourth of the bankfull width of channel. Bed material was sampled in a random grid pattern so that samples were equally distributed within the sample area. |
| BEDXX | Bed-material particle size of which XX percent is finer (in millimeters) -- For this study, bed-material particle size was determined at each cross section by means of Wolman pebble counts (Wolman, 1954). |
| BNKXX | Bank-material particle size of which XX percent is finer (in millimeters) -- For this study, bank-material samples were analyzed by means of standard dry-sieve analyses with sieve sizes of 3.0, 2.0, 1.0, 0.75, 0.50, 0.375, 0.25, 0.10, 0.025, and 0.005 inches. Particle-size analysis was done in accordance with American Society of Testing Materials method D422 (American Society of Testing Materials, 1998). |
| DA | Drainage area (in square miles) -- The surface area that contributes surface runoff to a specified location on a stream, measured in a horizontal plane. Computed (by planimeter, digitizer, or grid method) from U.S. Geological Survey 7.5-minute topographic quadrangle maps. A geographic information system (GIS) also may be used to determine drainage area provided that the GIS data are of sufficiently high resolution. |
| DAC | Active-channel mean depth (in feet) -- Mean depth of the channel at active-channel stage (SAC), computed as the active-channel cross-sectional area (AAC) divided by the active channel width (WAC). |
| DBF | Bankfull mean depth (in feet) -- Mean depth of the channel at bankfull stage (SBF), computed as the bankfull cross-sectional area (ABF) divided by the bankfull width (WBF). |
| DECLAT | Latitude expressed in decimal degrees (in degrees) |
| DECLONG | Longitude expressed in decimal degrees (in degrees) |
| ELEV | Average main-channel elevation index (in feet above National Geodetic Vertical Datum of 1929) -- Determined by averaging main-channel elevations (in feet) at points 10 and 85 percent of the distance from a specified location on the main channel to the topographic divide (following the longest path), as determined from U.S. Geological Survey 7.5-minute topographic quadrangle maps (Thomas and Benson, 1970). |
| FOR | Forested area (in percent) -- The percentage of the total drainage area occupied by forest cover, as determined by measuring the green-tinted areas on U.S. Geological Survey 7.5-minute topographic quadrangle maps. |
| I24,2 | 2-year, 24-hour rainfall intensity (in inches) -- Annual maximum 24-hour rainfall having a 2-year recurrence interval. Determined at study site from U.S. Weather Bureau Technical Paper 40 (Hershfield, 1961). |
| MCSL | Main-channel slope (in feet per mile) -- Computed as the difference in elevations (in feet) at points 10 and 85 percent of the distance along the main channel from a specified location on the channel to the topographic divide (following the longest path), divided by the channel distance (in miles) between the two points, as determined from U.S Geological Survey 7.5-minute topographic quadrangle maps (Benson, 1962; Thomas and Benson, 1970). |
| LCSL | Local-channel slope (in feet per mile) -- For this study, local-channel slope was computed by dividing the difference in channel-centerline elevation at the most upstream bankfull cross section and channel-centerline elevation at the most downstream bankfull cross section (in feet) by the distance between the two points (in miles). All bankfull cross sections were surveyed at the crests of riffles. |
| LG | Main-channel length (in miles) -- Distance measured along the main channel from a specified location to the topographic divide (following the longest path), as determined from U.S. Geological Survey 7.5-minute topographic quadrangle maps. |
| PREC | Average annual precipitation (in inches) -- Determined at study site from Ohio Department of Natural Resources Water Inventory Report No. 28 (Harstine, 1991). |
| QBF | Bankfull discharge (in cubic feet per second) -- Stream discharge at bankfull stage (SBF) that would fill the main channel to an elevation equal to that of the active flood plain. |
| Qt | Peak discharge (in cubic feet per second) -- Annual peak discharge with recurrence interval of t years. |
| SAC | Active-channel stage (in feet) -- Elevation at the top of the active channel, which is the area of stream bottom and banks that normally coincides with the lower limit of permanent vegetation. The active channel frequently is submerged, and its boundaries typically are composed of sediment particles moved by the stream (Natural Resources Conservation Service, 2005). |
| SBF | Bankfull stage (in feet) -- The elevation of the water surface during bankfull discharge (QBF). It is the stage at which a stream first begins to overflow its natural banks onto the active flood plain (Wolman and Leopold, 1957). |
| STOR | Storage area (in percent) -- That part of the contributing drainage area occupied by lakes, ponds, and swamps, as shown on U.S. Geological Survey 7.5-minute topographic quadrangle maps. Temporary storage as a result of detention basins or ponding upstream of roadway embankments is not included. |
| WAC | Active-channel width (in feet) -- Width of the channel at active-channel stage (SAC) measured perpendicular to the streamflow at active-channel stage. |
| WBF | Bankfull width (in feet) -- Width of the channel at bankfull stage (SBF) measured perpendicular to the streamflow at bankfull stage. |
Regional curves, simple-regression equations, and multiple-regression equations were developed to estimate bankfull width, bankfull mean depth, bankfull cross-sectional area, and bankfull discharge of rural, unregulated streams in Ohio. The methods are based on geomorphic, basin, and flood-frequency data collected at 50 study sites on unregulated natural alluvial streams in Ohio, of which 40 sites are near streamflow-gaging stations. The regional curves and simple-regression equations relate the bankfull characteristics to drainage area. The multiple-regression equations relate the bankfull characteristics to drainage area, main-channel slope, main-channel elevation index, median bed-material particle size, bankfull cross-sectional area, and local-channel slope. Average standard errors of prediction for bankfull width equations range from 20.6 to 24.8 percent; for bankfull mean depth, 18.8 to 20.6 percent; for bankfull cross-sectional area, 25.4 to 30.6 percent; and for bankfull discharge, 27.0 to 78.7 percent. The simple-regression (drainage-area only) equations have the highest average standard errors of prediction. The multiple-regression equations in which the explanatory variables included drainage area, main-channel slope, main-channel elevation index, median bed-material particle size, bankfull cross-sectional area, and local-channel slope have the lowest average standard errors of prediction.
Field surveys were done at each of the 50 study sites to collect the geomorphic data. Bankfull indicators were identified and evaluated, cross-section and longitudinal profiles were surveyed, and bed- and bank-material were sampled. Field data were analyzed to determine various geomorphic characteristics such as bankfull width, bankfull mean depth, bankfull cross-sectional area, bankfull discharge, streambed slope, and bed- and bank-material particle-size distribution. The various geomorphic characteristics were analyzed by means of a combination of graphical and statistical techniques.
The logarithms of the annual peak discharges for the 40 gaged study sites were fit by a Pearson Type III frequency distribution to develop flood-peak discharges associated with recurrence intervals of 2, 5, 10, 25, 50, and 100 years. The peak-frequency data were related to geomorphic, basin, and climatic variables by multiple-regression analysis. Simple-regression equations were developed to estimate 2-, 5-, 10-, 25-, 50-, and 100-year flood-peak discharges of rural, unregulated streams in Ohio from bankfull channel cross-sectional area. The average standard errors of prediction are 31.6, 32.6, 35.9, 41.5, 46.2, and 51.2 percent, respectively.
The study and methods developed are intended to improve understanding of the relations between geomorphic, basin, and flood characteristics of streams in Ohio and to aid in the design of hydraulic structures, such as culverts and bridges, where stability of the stream and structure is an important element of the design criteria. The study was done in cooperation with the Ohio Department of Transportation and the U.S. Department of Transportation, Federal Highway Administration.
Under natural conditions, streams will display geomorphic characteristics that are ultimately governed by a balance of energy associated with the flow of water combined with erosion, transport, and deposition of sediments. Spatially varying landscape factors such as topography, climate, geologic setting, vegetative cover, and position within the drainage network affect the energy balance and consequently lead to spatial variation in geomorphic form. Many of these same factors also affect peak streamflow characteristics, so a strong relation between peak streamflows and stream channel dimensions is common (Thomas and Benson, 1970).
One geomorphic characteristic of particular interest is the bankfull stage, the stage at which a stream first begins to overflow its natural banks onto the active flood plain (Wolman and Leopold, 1957). In addition to its obvious importance for flood awareness, the bankfull stage is also important geomorphically because flows at or near bankfull stage tend to move large amounts of sediment over the long term. Consequently, flows at (or near) bankfull stage can be important in forming the channel (Leopold and Maddock, 1953; Wolman and Miller, 1960).
In the past, the design of hydraulic structures such as culverts and bridges was based predominantly on their hydraulic characteristics. Attention to the consequences of these structures on stream geomorphology was mostly focused on ensuring the stability of the structures. Increased environmental awareness has led to an expanded focus that extends the concern for geomorphic consequences appreciably upstream and downstream from the structures. Reconstruction of stream channels to natural geomorphic dimensions can result in more stable channels, which can in turn improve the stability of the structures. Addressing that expanded focus will require an improved understanding of the relation between stream geomorphic characteristics — such as bankfull stage — and the physical, geological, and meteorological conditions that influence them.
In August 2000, the U.S. Geological Survey (USGS), in cooperation with the Ohio Department of Transportation (ODOT) and the U.S. Department of Transportation, Federal Highway Administration (FHWA), began a study to (1) collect geomorphic data at 50 unregulated natural alluvial streams in Ohio, (2) develop methods to estimate bankfull characteristics of Ohio streams, and (3) relate geomorphic characteristics of Ohio streams to their peak streamflows. Methods to estimate bankfull characteristics can also be helpful in the design of stream channels for stream-restoration projects.
This report presents methods to estimate bankfull characteristics of rural, unregulated streams in Ohio. The methods
consist of scatterplots, simple-regression equations, and multiple-regression equations in which bankfull width, bankfull depth, bankfull cross-sectional area, and bankfull discharge can be estimated from drainage area and other explanatory variables. The report also presents simple-regression equations to estimate peak streamflows for various recurrence intervals from bankfull cross-sectional area. The methods developed are based on geomorphic, drainage-basin, and flood-peak data collected for the study sites whose drainage areas range from 0.29 to 685 mi 2 . Methods of data collection and analysis for the study are summarized along with all data used in the analyses. The equations and methods developed are applicable to natural alluvial channels in Ohio with basin characteristics similar to those of the study sites. An example is given showing how to use the methods along with comparisons of explanatory variables required and estimates of accuracy of the methods.
The concept of "bankfull" is important for an understanding of morphology of stream channels. Bankfull stage (SBF, fig. 1) is the elevation at which a stream first begins to overflow its natural banks onto the active flood plain (Wolman and Leopold, 1957). The active flood plain is a relatively flat depositional surface adjacent to a stream. The active flood plain is continually formed by sediment suspended and delivered by the stream, and it floods frequently. An abandoned flood plain (or terrace) is a flat depositional surface adjacent to and higher than the active flood plain and it floods infrequently, if at all.
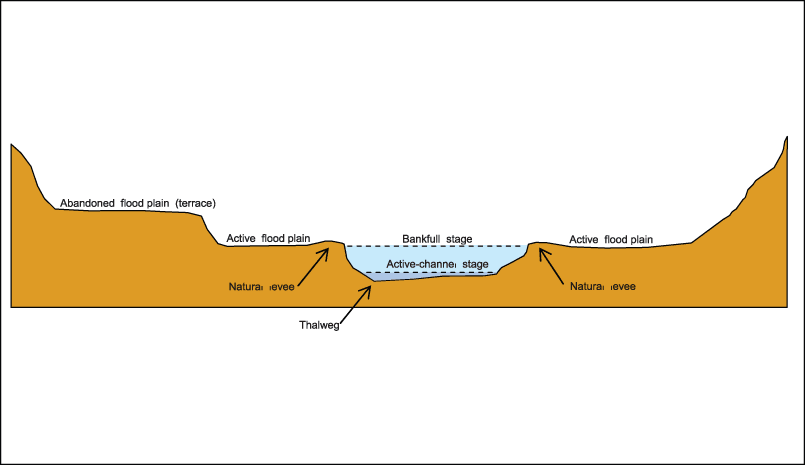
Figure 1. Schematic diagram showing geomorphic features of a stream channel.
Bankfull discharge (QBF) is the discharge that would fill the main channel to an elevation equal to bankfull stage. Bankfull discharge has often been referred to as the "effective discharge" or "channel-forming discharge." This concept is misleading because there is no single channel-forming discharge but rather a wide range of flows that might be considered effective in the formation of the main channel. More appropriately, the bankfull discharge can be considered a surrogate for this range of flows (Emmett, 2004). Over the years, moderate flood flows near bankfull stage do much work in terms of moving sediment and forming the main channel (Leopold and others, 1964). Large floods move great amounts of sediment, but they are rare; small floods occur frequently but move lesser amounts of sediment (Wolman and Miller, 1960). Under average conditions, bankfull discharge might occur about every 1 to 2 years; for some streams, however, bankfull discharge could be associated with recurrence intervals of less than 1 year or greater than 2 years. As flood flows overtop the streambanks, the abrupt decrease in velocity over the active flood plain often results in deposition of sediments just past the tops of the banks, resulting in the formation of natural levees (fig. 1).
Accurate identification of bankfull stage in the field is crucial for a study of bankfull characteristics. Generally, several types of field indicators are used to determine bankfull stage. Good results may be achieved if a combination of bankfull indicators is used. Some of the indicators of bankfull stage used for this study were: the elevation of depositional features such as point bars (deposits of alluvium found on the inside bank of a meander bend); changes in slope, vegetation, or bank material; recent deposits of fine material or debris on the active flood plain; and bank undercuts. More detailed information on field indicators of bankfull stage is given by Fitzpatrick and others (1998) and Harrelson and others (1994), and is shown in a video by the U.S. Department of Agriculture (2003).
Active-channel stage (SAC, fig. 1), within the context of this study, is the elevation at the top of the active channel, which is the area of stream bottom and banks that generally coincides with the lower limit of permanent vegetation. The active channel frequently is submerged, and its boundaries typically are composed of sediment particles moved by the stream (Natural Resources Conservation Service, 2005). The thalweg (fig. 1) is the minimum elevation of a stream cross section.
Terms that are commonly used throughout this report are bankfull width (WBF), bankfull mean depth (DBF), bankfull cross-sectional area (ABF), and bankfull discharge (QBF). All of the abbreviations for terms used in this report are defined at the beginning of the report.
The age of quantitative geomorphology essentially began with R.E. Horton's studies of drainage basin characteristics (Horton, 1945). Eight years later, Luna Leopold and Thomas Maddock, Jr., published a USGS Professional Paper in which they presented quantitative empirical relations between streamflow and stream morphology (Leopold and Maddock, 1953). In 1964, the classic text "Fluvial Processes in Geomorphology" (Leopold and others, 1964) was published, wherein the concepts of bankfull stage and its relation to flood frequency were presented. Leopold and others used the phrase "dynamic equilibrium" to explain that even though the locations of pools, riffles, bends, and straight portions changed and adjusted after large flood events, the general shape and form of a stream appeared to remain fairly constant over the years.
The need for geomorphic data has long been appreciated. In 1968, Emmett and Hadley, of the USGS, published a report on the Vigil Network (Emmett and Hadley, 1968), a database designed to preserve geomorphic data and make those data more accessible. Bankfull hydraulic geometry relations, also called "regional curves," were first developed by Dunne and Leopold (1978) to relate bankfull-channel dimensions (width, mean depth, and cross-sectional area) to drainage area. The primary reason for developing regional curves is to aid in estimating bankfull dimensions of natural alluvial channels. In Ohio, the regional curves developed by Dunne and Leopold (1978) for the eastern United States have been used by ODOT and other government agencies to estimate bankfull dimensions and discharge.
Two prior USGS studies in cooperation with ODOT and FHWA (Webber and Roberts, 1981; Roth, 1985) have been conducted in Ohio to estimate flood characteristics from geomorphic characteristics. In the 1981 study, regression equations were developed to estimate peak discharges of selected recurrence intervals (2, 5, 10, 25, 50, and 100 years) for alluvial streams in Ohio from active-channel width (WAC). The equations developed for alluvial streams are based on data collected at 160 streamflow-gaging stations in Ohio. The 1985 study confirmed the equations developed in the 1981 study and presented new equations for estimating peak discharges of selected recurrence intervals for bedrock or firm channels in Ohio from active-channel width (WAC) and bankfull depth (DBF). The equations developed for bedrock or firm channels are based on data collected at 20 streamflow-gaging stations in Ohio.
Other studies and sources of information regarding stream-restoration and regional curves for Ohio include those completed by Mecklenburg (2003), Chang and others (2004), and Ward and others (2004).
Site-selection criteria were developed to ensure that collection and analysis of the field data would meet the objectives of the study. An inventory of all streamflow-gaging stations (active and discontinued) in Ohio was done to identify sites that might potentially meet these criteria. A map- and field-based reconnaissance was begun to identify potential sites for data collection and analysis. Special emphasis was placed on locating appropriate sites near rural, unregulated streamflow-gaging stations for which flood frequency estimates had been developed. Site selection was coordinated with the ODOT and the Ohio Department of Natural Resources (ODNR), Division of Soil and Water Conservation. During site selection process, a geographic information system (GIS) database was developed to facilitate the selection and the planned regionalization analyses.
Field surveys were done at 50 selected sites to collect geomorphic data. Bankfull indicators were identified and evaluated, cross-section and longitudinal profiles were surveyed, and bed and bank material were sampled according to methods described by Harrelson and others (1994). Those methods were modified slightly or augmented to obtain information consistent with the project data requirements.
Field data were analyzed to determine various geomorphic characteristics such as bankfull width, bankfull mean depth, bankfull cross-sectional area, bankfull discharge, streambed slope, and bed and bank particle-size distribution for the 50 study sites.
The various geomorphic characteristics were regionalized by means of a combination of graphical and statistical techniques. These techniques resulted in a set of regional curves, simple-regression equations, and multiple-regression equations to estimate geomorphic characteristics from basin characteristics. Multiple-regression equations also were developed to estimate flood-peak discharges from geomorphic characteristics.
One of the most important phases of this study was the reconnaissance and selection of the 50 sites. Two broad categories of characteristics controlled and guided the selection process: (1) geomorphic characteristics of the potential study site, which were evaluated in the field and would influence the quality of data that could be collected at the site, and (2) basin characteristics, which were evaluated in the office by means of physiographic databases. A wide range of basin characteristics was desired to ensure general applicability of the regional curves and statewide regression models this study proposed to develop.
Special emphasis was placed on locating sites near unregulated streamflow-gaging stations with at least 10 years of record and available flood-frequency estimates. Active gaging stations were preferred over discontinued gaging stations. Reliability of the indicators used to identify bankfull stage at each gaging station also was a major consideration. The definitions of bankfull stage are numerous as are the multitude of methods for identifying bankfull stage. As stated by Borghese (ca. 1957, p. 2) "At some of the gaging stations, the designation of a so-called bankful stage is fraught with much uncertainty if not an impossibility insofar as a meaningful value for practical purposes." Williams (1978) found that the elevation of bankfull stage can be identified by at least 11 different methods, which could yield 11 different bankfull-stage elevations at the same stream cross section. Therefore, gaging stations having well-defined and consistent indicators of bankfull stage were highly ranked during the site-selection process. Forty of the sites selected are near streamflow-gaging stations; the remaining 10 sites are on ungaged streams. The 50 sites range in drainage area from 0.29 to 685 mi 2 and are uniformly distributed throughout Ohio.
Criteria were developed to guide the site-selection process. The following characteristics were considered desirable:
In Ohio, as of 2003, there were 133 active streamflow-gaging stations where hydrologic information was being collected; there were 228 discontinued gaging stations. Drainage areas ranged from 0.01 to 7,947 mi 2 , with a mean drainage area of 425 mi 2 . Streamflow record lengths ranged from 1 to 106 years, and the mean record length was 33 years. Of the total of 361 gaging stations, 241 were considered to be unregulated and to have at least 10 years of streamflow record. Because it was anticipated that methods developed to estimate geomorphic characteristics would most often be applied to projects on small streams (less than 50 mi 2 ), it was decided that most (about 40) of the 50 study sites should be in the 0 to 50 mi 2 range and the remainder (about 10) should range from 50 to 1,000 mi 2 . Because of the general paucity of gaging stations with drainage areas between 0 and 50 mi 2 , the number of potential study sites for consideration at gaging stations was greatly reduced.
After the initial screening of all 361 streamflow-gaging stations based on the site-selection criteria, 105 potential study sites at streamflow-gaging stations having drainage areas between 0 and 200 mi 2 were map- and field-checked for suitability for data collection and analysis. Site suitability was determined by use of a rating system based on the geomorphic characteristics of the stream and the reliability of the indicators of bankfull stage. Potential locations for cross-section surveys also were identified during reconnaissance. Sites were eliminated from further consideration if they were found to have bedrock channels, human-influenced channels (mostly channelization), and (or) the lack of well-defined indicators of bankfull stage. Some sites at discontinued gaging stations also were eliminated from further consideration because locating previously established gaging-station reference marks was not possible. Of the 105 potential sites, 36 were found to be suitable on the basis of field reconnaissance; however, not all 36 could be used because of an imbalance in their geographical distribution. Because of difficulty finding gaging stations with small drainage areas that also met the site-selection criteria, it was decided to select 40 sites near streamflow-gaging stations and 10 sites on small ungaged streams (0.1 to 30 mi 2 in drainage area) that appeared to have stable, natural channels with no apparent human influence. The 10 ungaged sites supplemented the gaged sites in the 0.1- to 30-mi 2 range and served as a check on the geomorphic characteristics of the gaged sites (of which many had some minor human influence). During the site-selection process, the consistent and pronounced differences in bankfull characteristics for low- and high-gradient streams was readily apparent. To facilitate analyses and quantification of the differences, efforts were made to broaden the range of channel slopes of sites selected by choosing more sites having extreme slope characteristics.
As a result of the initial map and field reconnaissance, strong relations were developed between what was documented in the field and what was indicated on the U.S. Geological Survey 7.5-minute topographic quadrangle maps. Potential study sites that were ranked "good" in the field were often indicated on the maps as having sinuous blue lines (meanders) in green-tinted (forested) areas, whereas potential study sites that were ranked "poor" in the field were often indicated on the maps as having straight blue lines (ditches) in white-tinted (non-forested) areas. On the basis of these relations, a statewide map reconnaissance effort resulted in the identification for field reconnaissance of 41 additional potential study sites at streamflow-gaging stations. In addition to the 41 gaged sites, map and field reconnaissance was also done at 88 ungaged streams in the State having drainage areas between 0.48 and 31.6 mi 2 that appeared to have stable, natural channels with no apparent human influence. Of the 41 gaged sites, 20 were found to be suitable for data collection and analysis, bringing the total number of suitable gaged sites to 56; additionally 17 of the 88 ungaged sites were found to be suitable, bringing the total number of suitable gaged and ungaged sites to 73.
An analysis to evaluate the geographical distribution and drainage area distribution of the 73 suitable sites resulted in the selection of 40 of the 56 suitable sites at streamflow-gaging stations for data collection and analysis, as well as 10 of the 17 suitable ungaged sites, bringing the total number of selected sites to 50. In total, 234 sites were field checked, and many hundreds more were map checked. The locations of the 50 selected study sites are shown in figure 2. Station-identification information, geographical coordinates, drainage areas, and annual peak discharge information for the 50 study sites are listed in table 1.
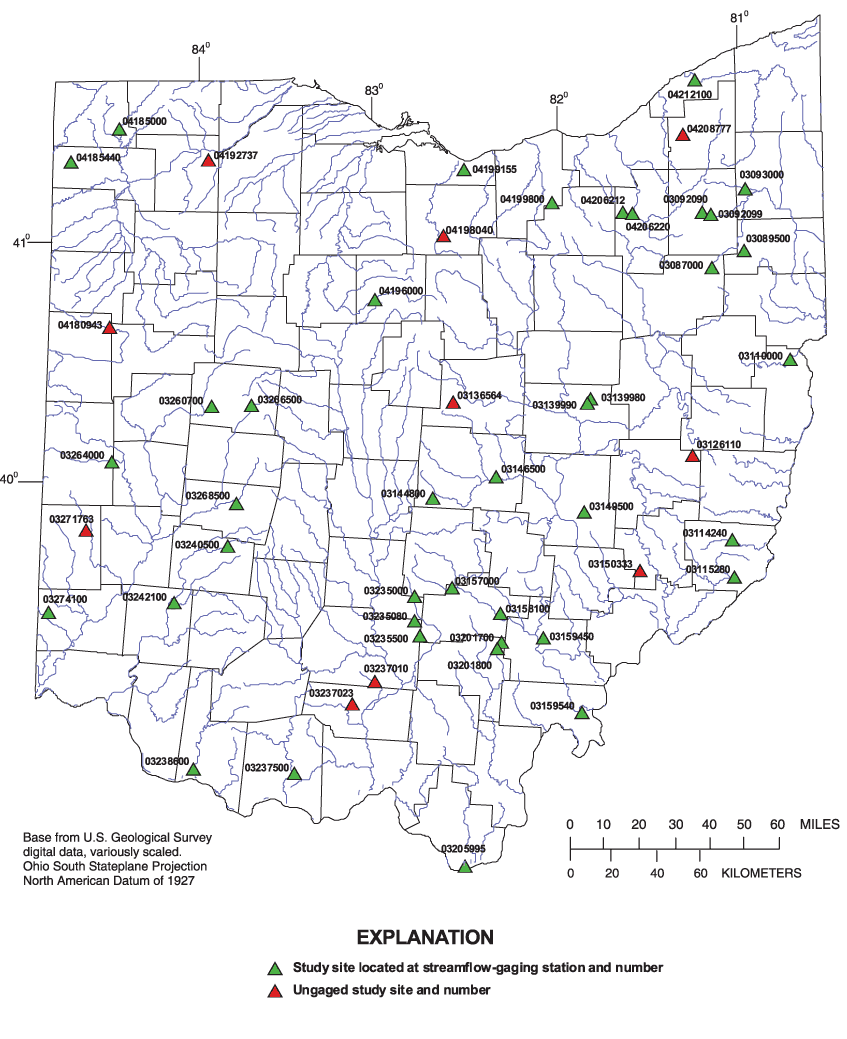
Figure 2. Locations of the 50 selected study sites in Ohio.
[ ---, ungaged study site, no annual peak discharge information ]
| Station number | Station name | Latitude | Longitude | Drainage area (mi2) | Record | Largest recorded discharge | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Years | Period used | Calendar year | Magnitude (ft3/s) | ||||||||||
| 03087000 | Beech Creek near Bolton | 40o | 55' | 50" | 81o | 08' | 50" | 17.4 | 12 | 1944-1954, 1959 | 1950 | 2,210 | |
| 03089500 | Mill Creek near Berlin Center | 41o | 00' | 01" | 80o | 58' | 07" | 19.1 | 36 | 1942-1977 | 1946 | 1,900 | |
| 03092090 | West Branch Mahoning River near Ravenna | 41o | 09' | 41" | 81o | 11' | 50" | 21.8 | 36 | 1966-2001 | 1979 | 2,810 | |
| 03092099 | Hinkley Creek at Charlestown | 41o | 09' | 16" | 81o | 08' | 51" | 7.85 | 13 | 1970-1982 | 1979 | 2,120 | |
| 03093000 | Eagle Creek at Phalanx Station | 41o | 15' | 40" | 80o | 57' | 16" | 97.6 | 72 | 1927-1934, 1938-2001 | 1979 | 8,150 | |
| 03110000 | Yellow Creek near Hammondsville | 40o | 32' | 16" | 80o | 43' | 31" | 147 | 61 | 1941-2001 | 1952 | 9,580 | |
| 03114240 | Wood Run near Woodsfield | 39o | 46' | 56" | 81o | 03' | 21" | 0.53 | 10 | 1978-1987 | 1981 | 240 | |
| 03115280 | Trail Run near Antioch | 39o | 37' | 29" | 81o | 02' | 54" | 5.45 | 10 | 1978-1987 | 1981 | 2,020 | |
| 03126110 | Skull Fork near Londonderry | 40o | 08' | 22" | 81o | 16' | 00" | 26.9 | --- | --- | --- | --- | |
| 03136564 | Dry Run near Bangs | 40o | 22' | 17" | 82o | 34' | 24" | 0.50 | --- | --- | --- | --- | |
| 03139980 | Little Mill Creek near Coshocton | 40o | 23' | 03" | 81o | 49' | 04" | 4.02 | 35 | 1937-1971 | 1957 | 1,590 | |
| 03139990 | Little Mill Creek near Coshocton | 40o | 21' | 51" | 81o | 50' | 20" | 7.16 | 36 | 1935, 1937-1971 | 1935 | 9,020 | |
| 03144800 | Etna Creek at Etna | 39o | 58' | 08" | 82o | 40' | 55" | 1.10 | 18 | 1966-1982, 1990 | 1979 | 365 | |
| 03146500 | Licking River near Newark | 40o | 03' | 33" | 82o | 20' | 23" | 537 | 62 | 1940-2001 | 1959 | 45,000 | |
| 03149500 | Salt Creek near Chandlersville | 39o | 54' | 31" | 81o | 51' | 38" | 75.7 | 14 | 1935-1947, 2001 | 1940 | 5,240 | |
| 03150333 | Keith Fork at Keith | 39o | 39' | 25" | 81o | 33' | 22" | 8.56 | --- | --- | --- | --- | |
| 03157000 | Clear Creek near Rockbridge | 39o | 35' | 18" | 82o | 34' | 43" | 89.0 | 62 | 1940-2001 | 1948 | 16,000 | |
| 03158100 | Hayden Run near Haydenville | 39o | 28' | 57" | 82o | 19' | 06" | 1.04 | 12 | 1966-1977 | 1968 | 370 | |
| 03159450 | Mill Creek near Chauncey | 39o | 22' | 46" | 82o | 05' | 04" | 1.48 | 10 | 1978-1987 | 1981 | 265 | |
| 03159540 | Shade River near Chester | 39o | 03' | 49" | 81o | 52' | 55" | 156 | 36 | 1966-2001 | 1997 | 15,600 | |
| 03201700 | Big Four Hollow Creek near Lake Hope | 39o | 21' | 48" | 82o | 18' | 51" | 1.01 | 13 | 1971-1983 | 1974 | 1,200 | |
| 03201800 | Sandy Run near Lake Hope | 39o | 20' | 01" | 82o | 19' | 56" | 4.99 | 21 | 1958-1978 | 1958 | 3,770 | |
| 03205995 | Sandusky Creek near Burlington | 38o | 25' | 03" | 82o | 30' | 36" | 0.73 | 10 | 1978-1987 | 1979 | 242 | |
| 03235000 | Salt Creek at Tarlton | 39o | 33' | 20" | 82o | 46' | 51" | 11.5 | 31 | 1947-1977 | 1968 | 5,360 | |
| 03235080 | Bull Creek near Adelphi | 39o | 27' | 11" | 82o | 46' | 46" | 3.13 | 11 | 1977-1987 | 1983 | 1,560 | |
| 03235500 | Tar Hollow Creek at Tar Hollow State Park | 39o | 23' | 22" | 82o | 45' | 03" | 1.35 | 32 | 1947-1978 | 1968 | 957 | |
| 03237010 | Crooked Creek at Alma | 39o | 11' | 31" | 82o | 59' | 25" | 8.01 | --- | --- | --- | --- | |
| 03237023 | No Name Creek at No Name | 39o | 05' | 52" | 83o | 06' | 55" | 3.82 | --- | --- | --- | --- | |
| 03237500 | Ohio Brush Creek near West Union | 38o | 48' | 13" | 83o | 25' | 16" | 387 | 70 | 1927-1935, 1941-2001 | 1997 | 77,700 | |
| 03238600 | Higgins Run near Higginsport | 38o | 49' | 10" | 83o | 57' | 28" | 0.55 | 12 | 1966-1977 | 1966 | 930 | |
| 03240500 | North Fork Massie Creek at Cedarville | 39o | 45' | 25" | 83o | 47' | 25" | 28.9 | 14 | 1955-1968 | 1963 | 3,030 | |
| 03242100 | Wayne Creek at Waynesville | 39o | 31' | 08" | 84o | 04' | 47" | 1.01 | 16 | 1966-1981 | 1974 | 880 | |
| 03260700 | Bokengehalas Creek near De Graff | 40o | 20' | 50" | 83o | 53' | 28" | 36.3 | 44 | 1958-2001 | 1959 | 1,780 | |
| 03264000 | Greenville Creek near Bradford | 40o | 06' | 08" | 84o | 25' | 48" | 193 | 71 | 1913, 1932-2001 | 1913 | 18,200 | |
| 03266500 | Mad River at Zanesfield | 40o | 21' | 01" | 83o | 40' | 28" | 7.31 | 33 | 1947-1979 | 1972 | 2,100 | |
| 03268500 | Beaver Creek near Springfield | 39o | 56' | 26" | 83o | 44' | 56" | 39.2 | 21 | 1943-1959, 1973-1976 | 1948 | 4,980 | |
| 03271763 | Price Creek near Brennersville | 39o | 48' | 50" | 84o | 34' | 01" | 20.7 | --- | --- | --- | --- | |
| 03274100 | Blake Run near Reily | 39o | 27' | 59" | 84o | 45' | 22" | 0.29 | 36 | 1939-1940, 1942-1943, 1947-1978 | 1960 | 307 | |
| 04180943 | Gallman Creek near Monticello | 40o | 39' | 55" | 84o | 27' | 30" | 1.90 | --- | --- | --- | --- | |
| 04185000 | Tiffin River at Stryker | 41o | 30' | 16" | 84o | 25' | 47" | 410 | 70 | 1913, 1922-1928, 1937, 1941-2001 | 1982 | 7,800 | |
| 04185440 | Unnamed tributary to Lost Creek near Farmer | 41o | 21' | 42" | 84o | 41' | 28" | 4.23 | 16 | 1986-2001 | 1998 | 1,770 | |
| 04192737 | Big Creek at McClure | 41o | 22' | 52" | 83o | 55' | 57" | 18.1 | --- | --- | --- | --- | |
| 04196000 | Sandusky River near Bucyrus | 40o | 48' | 13" | 83o | 00' | 21" | 88.8 | 49 | 1926-1935, 1939-1951, 1959, 1964-1981, 1987, 1996-2001 | 1959 | 13,500 | |
| 04198040 | Walnut Creek near Boughtonville | 41o | 04' | 02" | 82o | 37' | 32" | 4.96 | --- | --- | --- | --- | |
| 04199155 | Old Woman Creek at Berlin Road near Huron | 41o | 20' | 54" | 82o | 30' | 50" | 22.1 | 13 | 1988-1994, 1996-2001 | 1997 | 1,940 | |
| 04199800 | Neff Run near Litchfield | 41o | 12' | 33" | 82o | 01' | 26" | 0.76 | 17 | 1966-1982 | 1969 | 152 | |
| 04206212 | North Fork at Bath Center | 41o | 10' | 08" | 81o | 38' | 04" | 5.58 | 13 | 1992-2004 | 2003 | 1,820 | |
| 04206220 | Yellow Creek at Botzum | 41o | 09' | 47" | 81o | 35' | 02" | 30.7 | 13 | 1992-2004 | 2003 | 2,960 | |
| 04208777 | Chagrin River at Fullertown | 41o | 29' | 26" | 81o | 17' | 40" | 31.4 | --- | --- | --- | --- | |
| 04212100 | Grand River near Painesville | 41o | 43' | 08" | 81o | 13' | 41" | 685 | 27 | 1975-2001 | 1986 | 18,700 | |
Field surveys were done at each of the 50 selected sites to collect geomorphic data. The datum used for surveys at streamflow-gaging stations was the gage datum, which is generally an arbitrary datum that is established below the elevation of the lowest expected range of stage or near the stream bottom. The datum used for surveys at ungaged sites was an arbitrary datum established below the lowest expected elevation of the survey. All recoverable benchmarks and reference marks were surveyed at streamflow-gaging stations. To aid in the resurvey of cross sections in the future at bridge sites, four points on the bridge were described in field notes and surveyed (but not marked), the four points being the intersections of the inside of the abutments and the outside of the bridge deck at the top of the abutments. To aid in the resurvey of cross sections in the future at culvert sites, points were described in field notes and surveyed (but not marked), the points being the ends of the upstream and downstream headwalls, wingwalls, and top centers of culverts.
Bankfull indicators and cross-section locations were further identified, evaluated, and flagged. All cross-section and profile surveys were done by means of conventional total-station surveying methods. Because of the long distance between cross sections, real-time kinematic global positioning system (GPS) surveying methods were used at one study site (04185000) to establish reference marks at each cross section. After the reference marks at 04185000 were established, the cross-section and profile surveys were done by conventional total-station surveying methods.
Longitudinal profiles were surveyed for left and right bankfull, left and right active channel, and thalweg. Each bankfull ground point was rated good, fair, or poor, depending on the reliability of the bankfull indicators near the ground point. Active-channel profiles were surveyed at the elevation near the bottom of the bank; this generally coincided with the lower limit of permanent vegetation. Thalweg profiles were surveyed as the minimum-elevation points along the channel. In an attempt to obtain a maximum amount of channel-slope data, thalweg profiles often were surveyed for greater distances than were the bankfull or active-channel profiles.
Five cross sections that were representative of the general physical characteristics of the stream were surveyed at most of the 50 study sites. Fewer than five cross sections were surveyed at some study sites where conditions for the surveying of five cross sections were unsuitable. All bankfull cross sections were surveyed at the crests of riffles and perpendicular to the bankfull flow direction. A tagline was used to ensure a consistently straight cross-section survey. For most cross sections, the minimum elevations of the endpoints of the cross-section survey were at least 3 times the maximum bankfull depth, and the minimum length of the cross-section survey was at least 3 times the bankfull width. The minimum cross-section endpoint elevation and minimum length requirements were necessary to ensure adequate data for computation of entrenchment ratio (described later). For studies of bankfull characteristics of streams, it is important that the survey procedures allow for resurvey all cross sections at some time in the future. Thus, all cross-sections were monumented with 5/8-in.-diameter by 4-ft-long steel reinforcing bar set flush with the ground at either the left end or right end of the cross section. The coordinates of each monument were surveyed to permit accurate future resurveys of cross-section locations at each study site. Manning's n roughness coefficient was estimated for each cross section by use of a method developed by Cowan (1956). A photograph was taken looking downstream at each cross section.
At sites where a bridge crossed the stream, a bridge cross section and approach cross section also were surveyed in addition to the bankfull cross sections. At sites where a culvert conveyed the stream, culvert dimensions were measured and an approach cross section was surveyed. At the 40 gaged sites, a cross section was surveyed at the location of the stage sensor. Cross sections at the stage sensor were usually in a pool, in which case they were not used in the geomorphic analyses.
The composition of the streambed and streambank is an important geomorphic characteristic of the study site that would be included on the subsequent graphical and statistical analyses. Bed-material particle size was sampled at each cross section by means of Wolman pebble counts (Wolman, 1954). About 100 samples were taken across the streambed at the head of each riffle between the bottoms of the streambanks and extending downstream from riffle head about one-fourth of the bankfull width of channel. Bed material was sampled in a random grid pattern so that samples were equally distributed within the sample area. A composite sample of the top 4 inches of the left and right bank material for all cross sections was collected by use of a core sampling method (U.S. Department of Agriculture, Soil Conservation Service, 1982).
Graphical, mathematical, and statistical analyses of the geomorphic field data were used to plot and analyze plan views, longitudinal profiles, cross sections, particle-size distributions, and discharge. The plan-view plots of all surveyed data points facilitated visual checking of data-point locations and cross-section orientation (whether cross sections were straight and perpendicular to the streambanks). The plan views served to document locations of bridges, culverts, monuments, and other permanent features. In addition, the plan views were used to create a centerline-adjusted thalweg profile by creating a copy of the thalweg profile, adjusting the locations of each thalweg ground point perpendicular to the bankfull flow direction, and relocating the ground point halfway between the left and right bankfull profiles. Because the thalweg tends to meander back and forth across the main channel, the creation of the centerline-adjusted thalweg profile was necessary for proper computation of mid-channel thalweg length and local-channel slope (thalweg fall/thalweg length). An example plan-view plot is shown in figure 3 for Skull Fork near Londonderry, Ohio (03126110).
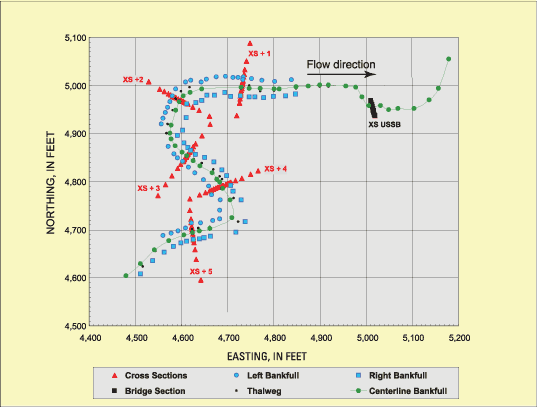
Figure 3. Example plan-view plot for Skull Fork near Londonderry, Ohio (03126110).
Following are step-by-step procedures used in the geomorphic data analyses.
A longitudinal profile of the centerline-adjusted thalweg was plotted and used as follows:
Longitudinal profiles of the left and right bankfull elevations were plotted and used as follows:
An example plot showing the right bankfull longitudinal profile at Skull Fork near Londonderry, Ohio (03126110), is shown in figure 4.
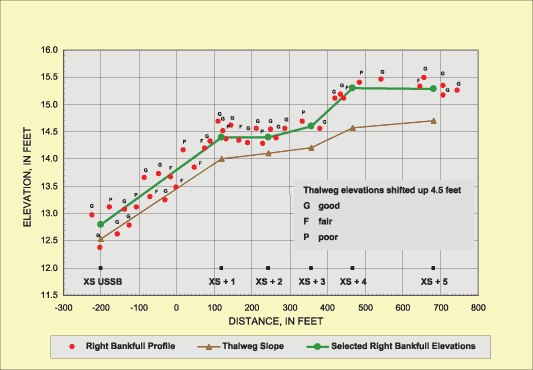
A process similar to that used to estimate bankfull elevations was used to estimate left and right active-channel elevations. All longitudinal profiles (centerline-adjusted thalweg, left and right bankfull, and left and right active-channel) were then plotted on a single plot as a final visual check of the elevation estimates.
Each cross section at each study site was plotted and analyzed as follows:
An example cross-section plot with measured and computed characteristics is shown in figure 5 for Skull Fork near Londonderry, Ohio (03126110). For the cross section shown in figure 5, the elevation of the active flood plain just beyond the natural levees was used as the representative bankfull elevation. Values for bankfull width, mean depth, and cross-sectional area and active-channel width, mean depth, and cross-sectional area were based on the final (overall) bankfull and active-channel elevations. For bankfull and active-channel calculations, mean depth was computed as the cross-sectional area divided by the width. Values for bankfull width/depth ratio, bankfull maximum depth, and entrenchment ratio (described later) also were computed for stream classification.
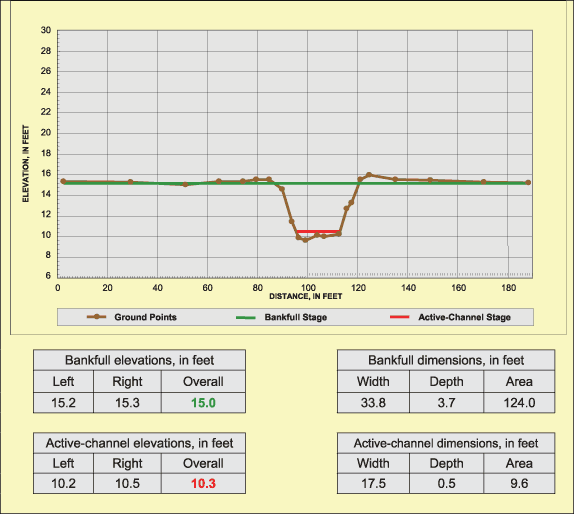
Figure 5. Example cross-section plot for Skull Fork near Londonderry, Ohio (03126110).
Summary statistics were calculated for all geomorphic values, and distribution plots were prepared to assess variability and check for outliers. In general, variability of characteristics among cross sections in a given reach was small, and no significant outliers were found. Mean values of all characteristics at a given site were used for subsequent statistical and graphical analyses relating geomorphic characteristics to basin characteristics. Selected geomorphic data and other site information for the 50 study sites are listed in table 2.
Table 2. Selected geomorphic data for the 50 study sites in Ohio
[ WBF, bankfull width, in feet; DBF, bankfull depth, in feet; ABF, bankfull cross-sectional area, in square feet; WAC, active-channel width, in feet; DAC, active-channel depth, in feet; AAC, active-channel cross-sectional area, in square feet]
| USGS Station number | Station name | WBF | DBF | ABF | WAC | DAC | AAC | ||
|---|---|---|---|---|---|---|---|---|---|
| 03087000 | Beech Creek near Bolton | 42.0 | 3.52 | 148.3 | 24.9 | 0.40 | 10.2 | ||
| 03089500 | Mill Creek near Berlin Center | 37.3 | 3.21 | 118.2 | 22.8 | 0.52 | 11.8 | ||
| 03092090 | West Branch Mahoning River near Ravenna | 56.3 | 3.48 | 194.0 | 28.1 | 0.57 | 15.7 | ||
| 03092099 | Hinkley Creek at Charlestown | 39.7 | 2.67 | 106.0 | 14.7 | 0.47 | 6.7 | ||
| 03093000 | Eagle Creek at Phalanx Station | 109.3 | 4.56 | 475.4 | 52.5 | 0.91 | 48.3 | ||
| 03110000 | Yellow Creek near Hammondsville | 126.2 | 4.85 | 605.3 | 85.3 | 0.82 | 71.0 | ||
| 03114240 | Wood Run near Woodsfield | 24.9 | 1.64 | 40.4 | 13.6 | 0.56 | 7.5 | ||
| 03115280 | Trail Run near Antioch | 34.5 | 3.22 | 111.1 | 19.7 | 0.53 | 10.3 | ||
| 03126110 | Skull Fork near Londonderry | 35.5 | 3.43 | 119.5 | 16.2 | 0.41 | 6.4 | ||
| 03136564 | Dry Run near Bangs | 15.3 | 1.09 | 16.8 | 9.1 | 0.34 | 3.1 | ||
| 03139980 | Little Mill Creek near Coshocton | 33.1 | 2.40 | 77.5 | 9.6 | 0.50 | 4.9 | ||
| 03139990 | Little Mill Creek near Coshocton | 35.4 | 3.21 | 113.1 | 20.6 | 0.56 | 11.5 | ||
| 03144800 | Etna Creek at Etna | 14.8 | 1.27 | 18.9 | 7.0 | 0.36 | 2.5 | ||
| 03146500 | Licking River near Newark | 248.0 | 7.61 | 1855.0 | 166.9 | 1.11 | 187.7 | ||
| 03149500 | Salt Creek near Chandlersville | 98.5 | 6.60 | 629.5 | 36.1 | 0.47 | 17.3 | ||
| 03150333 | Keith Fork at Keith | 41.9 | 2.85 | 119.0 | 31.0 | 0.89 | 26.0 | ||
| 03157000 | Clear Creek near Rockbridge | 71.9 | 6.94 | 499.1 | 53.6 | 1.04 | 55.0 | ||
| 03158100 | Hayden Run near Haydenville | 15.5 | 1.68 | 26.0 | 10.2 | 0.28 | 2.8 | ||
| 03159450 | Mill Creek near Chauncey | 19.0 | 1.50 | 28.5 | 10.1 | 0.28 | 2.8 | ||
| 03159540 | Shade River near Chester | 89.3 | 7.58 | 650.2 | 46.9 | 0.87 | 36.0 | ||
| 03201700 | Big Four Hollow Creek near Lake Hope | 21.5 | 1.13 | 24.2 | 10.5 | 0.33 | 3.1 | ||
| 03201800 | Sandy Run near Lake Hope | 31.4 | 2.74 | 86.1 | 20.0 | 0.63 | 12.5 | ||
| 03205995 | Sandusky Creek near Burlington | 14.4 | 1.42 | 20.4 | 7.5 | 0.37 | 2.8 | ||
| 03235000 | Salt Creek at Tarlton | 54.9 | 2.95 | 160.9 | 40.3 | 0.61 | 24.2 | ||
| 03235080 | Bull Creek near Adelphi | 21.8 | 2.81 | 60.7 | 14.7 | 0.54 | 7.4 | ||
| 03235500 | Tar Hollow Creek at Tar Hollow State Park | 25.4 | 1.90 | 48.1 | 13.5 | 0.47 | 6.0 | ||
| 03237010 | Crooked Creek at Alma | 85.0 | 3.29 | 278.5 | 23.8 | 0.51 | 11.8 | ||
| 03237023 | No Name Creek at No Name | 47.2 | 2.44 | 115.1 | 24.4 | 0.45 | 11.0 | ||
| 03237500 | Ohio Brush Creek near West Union | 209.3 | 12.08 | 2527.4 | 156.4 | 1.72 | 266.5 | ||
| 03238600 | Higgins Run near Higginsport | 39.8 | 2.02 | 80.4 | 25.3 | 0.69 | 17.8 | ||
| 03240500 | North Fork Massie Creek at Cedarville | 45.9 | 2.99 | 136.7 | 23.9 | 0.60 | 13.6 | ||
| 03242100 | Wayne Creek at Waynesville | 20.8 | 1.81 | 37.5 | 12.1 | 0.50 | 5.9 | ||
| 03260700 | Bokengehalas Creek near De Graff | 62.9 | 2.67 | 164.7 | 33.8 | 0.91 | 30.2 | ||
| 03264000 | Greenville Creek near Bradford | 142.5 | 4.50 | 641.4 | 101.9 | 0.97 | 96.2 | ||
| 03266500 | Mad River at Zanesfield | 36.7 | 2.36 | 84.6 | 21.5 | 0.44 | 9.2 | ||
| 03268500 | Beaver Creek near Springfield | 52.2 | 4.02 | 209.8 | 38.0 | 1.30 | 49.1 | ||
| 03271763 | Price Creek near Brennersville | 58.7 | 3.30 | 194.0 | 34.6 | 0.58 | 19.4 | ||
| 03274100 | Blake Run near Reily | 13.7 | 0.89 | 12.1 | 7.7 | 0.19 | 1.5 | ||
| 04180943 | Gallman Creek near Monticello | 17.1 | 1.54 | 26.2 | 9.8 | 0.30 | 3.0 | ||
| 04185000 | Tiffin River at Stryker | 121.4 | 8.08 | 981.9 | 85.3 | 1.69 | 144.2 | ||
| 04185440 | Unnamed tributary to Lost Creek near Farmer | 29.2 | 2.91 | 84.9 | 17.6 | 0.46 | 7.7 | ||
| 04192737 | Big Creek at McClure | 42.9 | 4.26 | 181.5 | 19.0 | 0.65 | 12.5 | ||
| 04196000 | Sandusky River near Bucyrus | 97.4 | 4.36 | 424.6 | 51.6 | 0.77 | 39.0 | ||
| 04198040 | Walnut Creek near Boughtonville | 33.6 | 2.27 | 76.1 | 15.0 | 0.27 | 4.0 | ||
| 04199155 | Old Woman Creek at Berlin Road near Huron | 45.7 | 4.49 | 205.3 | 15.2 | 0.31 | 4.7 | ||
| 04199800 | Neff Run near Litchfield | 15.0 | 1.08 | 15.6 | 5.0 | 0.32 | 1.6 | ||
| 04206212 | North Fork at Bath Center | 31.0 | 2.26 | 70.0 | 14.6 | 0.59 | 8.3 | ||
| 04206220 | Yellow Creek at Botzum | 63.3 | 3.54 | 223.8 | 52.6 | 0.62 | 32.4 | ||
| 04208777 | Chagrin River at Fullertown | 68.8 | 3.20 | 221.2 | 60.3 | 0.77 | 45.3 | ||
| 04212100 | Grand River near Painesville | 314.9 | 6.11 | 1916.4 | 149.6 | 1.41 | 208.2 | ||
| Maximum | 314.9 | 12.08 | 2527.4 | 166.9 | 1.72 | 266.5 | |||
| Minimum | 13.7 | 0.89 | 12.1 | 5.0 | 0.19 | 1.5 | |||
| Mean | 61.1 | 3.45 | 305.2 | 35.7 | 0.64 | 32.7 | |||
| Median | 40.9 | 2.97 | 118.6 | 22.2 | 0.55 | 11.6 |
Bed-material field data collected by means of Wolman pebble counts (Wolman, 1954) were used to create particle-size distribution plots and to calculate percentages of bed-material particle-size ranges, percentages of substrate type, and particle-size quantile values corresponding to 16, 35, 50, 84, and 95 percent finer for each cross section at each study site. Grain-size ranges given for bed-material particle-size ranges and percentages of substrate type are based on the modified Wentworth scale (American Geological Institute, 1982). An example of particle-size distribution plot, particle-size quantile values, and percentages of substrate type for Walnut Creek near Boughtonville (04198040) are shown in figure 6.
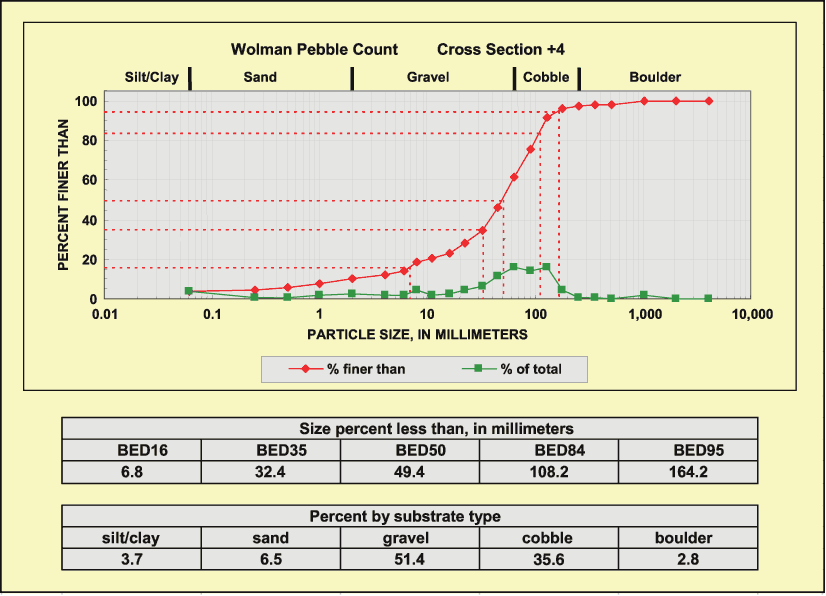
Summary statistics were calculated and distribution plots were prepared for all computed bed-material and riffle-slope values for all cross sections to assess variability and to assess relations between bed-material particle size and riffle slope. At most study sites, relations between bed-material particle size and riffle slope were evident. The computed means of the five bed-material particle size quantiles (16, 35, 50, 84, and 95 percent) for all cross sections were used for subsequent statistical and graphical analyses relating geomorphic characteristics to basin characteristics. Selected bed-material size-distribution data for the 50 study sites are listed in table 3.
Table 3. Selected bed-material size-distribution data for the 50 study sites in ohio.
[BEDXX, particle size of which XX percent of bed material is finer, in millimeters]
| Station number | Particle-size quantile | Percent by substrate type | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BED16 | BED35 | BED50 | BED84 | BED95 | Silt/clay | Sand | Gravel | Cobble | Boulder | ||
| < 0.062 mm | 0.062 to 2.0 mm | 2.0 to 64 mm | 64 to 256 mm | 256 to 4096 mm | |||||||
| 03087000 | 2.46 | 8.35 | 11.13 | 23.27 | 40.43 | 3.8 | 14.6 | 78.8 | 2.8 | 0.0 | |
| 03089500 | 6.04 | 26.97 | 45.05 | 103.24 | 144.54 | 0.0 | 10.9 | 54.8 | 34.0 | 0.3 | |
| 03092090 | 4.32 | 19.48 | 39.20 | 106.47 | 158.86 | 3.2 | 7.9 | 53.6 | 34.5 | 0.8 | |
| 03092099 | 2.62 | 7.96 | 12.94 | 32.87 | 50.49 | 1.2 | 14.8 | 78.7 | 5.3 | 0.0 | |
| 03093000 | 0.13 | 1.38 | 4.16 | 17.33 | 33.82 | 1.5 | 40.0 | 58.5 | 0.0 | 0.0 | |
| 03110000 | 6.23 | 25.73 | 54.12 | 225.82 | 358.20 | 1.0 | 5.7 | 49.0 | 32.7 | 11.6 | |
| 03114240 | 10.14 | 28.90 | 51.83 | 196.68 | 318.84 | 0.8 | 4.5 | 51.3 | 34.2 | 9.2 | |
| 03115280 | 2.87 | 10.59 | 18.66 | 67.46 | 133.27 | 1.7 | 12.5 | 69.6 | 15.2 | 1.0 | |
| 03126110 | 0.04 | 0.38 | 3.47 | 12.60 | 20.84 | 54.2 | 30.1 | 13.2 | 2.3 | 0.2 | |
| 03136564 | 6.39 | 16.20 | 27.85 | 79.44 | 131.71 | 0.6 | 5.0 | 71.5 | 22.7 | 0.2 | |
| 03139980 | 4.25 | 16.30 | 28.72 | 86.24 | 169.19 | 3.6 | 9.7 | 61.7 | 22.9 | 2.1 | |
| 03139990 | 3.70 | 16.34 | 29.17 | 109.27 | 183.10 | 3.2 | 12.4 | 57.8 | 24.0 | 2.6 | |
| 03144800 | 0.70 | 5.12 | 15.17 | 68.35 | 106.06 | 9.8 | 17.2 | 54.6 | 17.8 | 0.6 | |
| 03146500 | 2.00 | 9.71 | 14.71 | 35.38 | 54.50 | 1.0 | 15.0 | 80.5 | 3.5 | 0.0 | |
| 03149500 | 0.37 | 6.05 | 13.83 | 30.63 | 43.55 | 2.2 | 28.2 | 68.1 | 1.5 | 0.0 | |
| 03150333 | 1.73 | 6.73 | 11.43 | 30.39 | 53.52 | 4.2 | 17.0 | 75.2 | 3.6 | 0.0 | |
| 03157000 | 1.10 | 11.52 | 31.23 | 137.57 | 254.80 | 2.3 | 17.7 | 53.3 | 20.7 | 6.0 | |
| 03158100 | 3.48 | 7.04 | 10.60 | 26.71 | 47.39 | 1.0 | 11.2 | 85.5 | 2.3 | 0.0 | |
| 03159450 | 2.68 | 9.56 | 14.20 | 35.57 | 55.07 | 0.4 | 14.4 | 81.6 | 3.6 | 0.0 | |
| 03159540 | 1.54 | 9.78 | 17.90 | 51.07 | 116.12 | 7.5 | 13.0 | 68.0 | 10.5 | 1.0 | |
| 03201700 | 4.22 | 9.06 | 13.43 | 32.41 | 49.29 | 0.0 | 9.2 | 88.0 | 2.8 | 0.0 | |
| 03201800 | 1.45 | 3.54 | 5.54 | 12.67 | 21.79 | 1.0 | 34.2 | 64.4 | 0.4 | 0.0 | |
| 03205995 | 2.49 | 10.52 | 16.99 | 42.38 | 63.98 | 1.4 | 13.3 | 81.0 | 4.3 | 0.0 | |
| 03235000 | 6.96 | 23.36 | 41.44 | 114.74 | 173.45 | 1.6 | 7.0 | 56.1 | 34.1 | 1.2 | |
| 03235080 | 2.09 | 7.73 | 12.41 | 37.11 | 63.67 | 0.5 | 15.0 | 79.8 | 4.7 | 0.0 | |
| 03235500 | 3.40 | 7.52 | 11.03 | 32.22 | 50.38 | 4.6 | 10.0 | 82.2 | 3.2 | 0.0 | |
| 03237010 | 8.58 | 28.41 | 55.27 | 154.62 | 249.46 | 1.0 | 2.6 | 50.4 | 41.2 | 4.8 | |
| 03237023 | 17.53 | 43.66 | 71.90 | 217.39 | 432.00 | 0.0 | 0.6 | 45.8 | 41.0 | 12.6 | |
| 03237500 | 6.43 | 22.13 | 37.93 | 97.22 | 149.94 | 3.2 | 7.6 | 59.9 | 29.0 | 0.3 | |
| 03238600 | 11.43 | 49.75 | 94.86 | 269.68 | 387.54 | 3.3 | 3.3 | 33.6 | 42.7 | 17.1 | |
| 03240500 | 1.45 | 6.13 | 8.40 | 16.19 | 24.53 | 8.7 | 8.3 | 83.0 | 0.0 | 0.0 | |
| 03242100 | 8.23 | 28.24 | 48.98 | 145.69 | 257.87 | 1.4 | 11.6 | 46.5 | 35.7 | 4.8 | |
| 03260700 | 3.24 | 12.49 | 17.73 | 37.78 | 55.61 | 2.5 | 11.8 | 83.0 | 2.7 | 0.0 | |
| 03264000 | 8.71 | 16.52 | 27.86 | 75.67 | 122.74 | 1.6 | 5.0 | 73.9 | 18.2 | 1.3 | |
| 03266500 | 2.14 | 8.36 | 11.69 | 23.63 | 42.13 | 5.2 | 11.7 | 81.5 | 1.6 | 0.0 | |
| 03268500 | 1.83 | 9.46 | 15.62 | 59.96 | 93.24 | 7.1 | 13.0 | 67.1 | 12.2 | 0.6 | |
| 03271763 | 8.00 | 22.29 | 36.57 | 82.57 | 160.26 | 0.0 | 8.8 | 65.2 | 24.0 | 2.0 | |
| 03274100 | 8.77 | 23.17 | 38.63 | 113.06 | 184.90 | 8.2 | 1.0 | 60.5 | 28.1 | 2.2 | |
| 04180943 | 0.10 | 2.01 | 5.23 | 15.33 | 25.33 | 15.6 | 19.1 | 65.1 | 0.2 | 0.0 | |
| 04185000 | 0.03 | 0.10 | 0.21 | 3.49 | 8.62 | 27.1 | 53.7 | 19.2 | 0.0 | 0.0 | |
| 04185440 | 0.30 | 2.88 | 7.03 | 27.26 | 59.50 | 6.3 | 26.3 | 62.7 | 4.4 | 0.3 | |
| 04192737 | 0.37 | 2.44 | 4.80 | 18.61 | 39.57 | 9.8 | 30.9 | 57.1 | 2.2 | 0.0 | |
| 04196000 | 10.33 | 26.56 | 44.30 | 111.02 | 181.48 | 1.4 | 5.2 | 55.0 | 37.2 | 1.2 | |
| 04198040 | 2.92 | 21.62 | 41.34 | 99.25 | 156.28 | 5.1 | 11.3 | 52.3 | 29.7 | 1.6 | |
| 04199155 | 0.93 | 7.44 | 15.17 | 58.92 | 89.24 | 12.2 | 24.2 | 52.1 | 10.5 | 1.0 | |
| 04199800 | 0.08 | 5.93 | 9.78 | 22.66 | 38.47 | 18.5 | 2.5 | 77.8 | 1.2 | 0.0 | |
| 04206212 | 3.97 | 16.42 | 28.23 | 84.09 | 140.14 | 3.7 | 11.0 | 63.0 | 22.0 | 0.3 | |
| 04206220 | 2.18 | 21.90 | 59.83 | 167.20 | 232.52 | 4.7 | 10.7 | 35.7 | 46.3 | 2.6 | |
| 04208777 | 9.85 | 43.56 | 60.68 | 134.11 | 217.40 | 0.3 | 8.3 | 44.0 | 43.3 | 4.1 | |
| 04212100 | 12.85 | 48.48 | 74.93 | 187.35 | 343.11 | 1.0 | 2.7 | 42.0 | 44.0 | 10.3 | |
| Maximum | 17.53 | 49.75 | 94.86 | 269.68 | 432.00 | 54.2 | 53.7 | 88.0 | 46.3 | 17.1 | |
| Minimum | 0.03 | 0.10 | 0.21 | 3.49 | 8.62 | 0.0 | 0.6 | 13.2 | 0.0 | 0.0 | |
| Mean | 4.27 | 15.51 | 27.46 | 79.41 | 131.77 | 5.2 | 13.6 | 61.9 | 17.2 | 2.1 | |
| Median | 2.90 | 10.55 | 17.81 | 63.71 | 111.09 | 2.4 | 11.5 | 62.2 | 13.7 | 0.3 | |
Table 4. Selected bank-material size-distribution data for the 50 study sites in Ohio.
| [BNKXX, particle size of which XX percent of bank material is finer, in millimeters; ---, not determined] |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station number | Particle-size quantile | Percent by substrate type | ||||||||||
| BNK16 | BNK35 | BNK50 | BNK84 | BNK95 | Silt/clay | Sand | Gravel | Cobble | Boulder | |||
| < 0.062 mm | 0.062 to 2.0 mm | 2.0 to 64 mm | 64 to 256 mm | 256 to 4096 mm | ||||||||
| 03087000 | 0.010 | 0.060 | 0.098 | 0.302 | 13.500 | 35.0 | 55.0 | 10.0 | 0.0 | 0.0 | ||
| 03089500 | 0.005 | 0.049 | 0.089 | 0.264 | 0.710 | 39.0 | 60.0 | 1.0 | 0.0 | 0.0 | ||
| 03092090 | 0.013 | 0.097 | 0.134 | 0.209 | 0.325 | 27.0 | 73.0 | 0.0 | 0.0 | 0.0 | ||
| 03092099 | 0.026 | 0.081 | 0.117 | 0.343 | 4.750 | 26.0 | 67.0 | 7.0 | 0.0 | 0.0 | ||
| 03093000 | 0.019 | 0.087 | 0.128 | 0.296 | 0.490 | 26.0 | 74.0 | 0.0 | 0.0 | 0.0 | ||
| 03110000 | 0.007 | 0.064 | 0.104 | 0.370 | 1.680 | 34.0 | 61.0 | 5.0 | 0.0 | 0.0 | ||
| 03114240 | --- | 0.006 | 0.032 | 0.830 | 6.400 | 60.0 | 30.0 | 10.0 | 0.0 | 0.0 | ||
| 03115280 | --- | 0.028 | 0.076 | 0.240 | 0.420 | 45.0 | 55.0 | 0.0 | 0.0 | 0.0 | ||
| 03126110 | --- | --- | 0.007 | 0.042 | 0.090 | 91.0 | 9.0 | 0.0 | 0.0 | 0.0 | ||
| 03136564 | --- | 0.024 | 0.080 | 0.400 | 2.010 | 46.0 | 48.0 | 6.0 | 0.0 | 0.0 | ||
| 03139980 | 0.005 | 0.037 | 0.081 | 0.196 | 0.328 | 42.0 | 57.0 | 1.0 | 0.0 | 0.0 | ||
| 03139990 | 0.006 | 0.038 | 0.077 | 0.185 | 0.310 | 43.0 | 57.0 | 0.0 | 0.0 | 0.0 | ||
| 03144800 | --- | 0.012 | 0.044 | 0.214 | 0.760 | 57.0 | 41.0 | 2.0 | 0.0 | 0.0 | ||
| 03146500 | 0.008 | 0.040 | 0.067 | 0.161 | 0.258 | 47.0 | 53.0 | 0.0 | 0.0 | 0.0 | ||
| 03149500 | 0.005 | 0.031 | 0.069 | 0.167 | 0.262 | 47.0 | 53.0 | 0.0 | 0.0 | 0.0 | ||
| 03150333 | --- | 0.011 | 0.038 | 0.206 | 0.560 | 59.0 | 39.0 | 2.0 | 0.0 | 0.0 | ||
| 03157000 | 0.018 | 0.084 | 0.137 | 0.220 | 0.325 | 28.0 | 72.0 | 0.0 | 0.0 | 0.0 | ||
| 03158100 | 0.005 | 0.024 | 0.068 | 0.166 | 0.260 | 47.0 | 53.0 | 0.0 | 0.0 | 0.0 | ||
| 03159450 | 0.006 | 0.049 | 0.094 | 0.247 | 0.396 | 39.0 | 61.0 | 0.0 | 0.0 | 0.0 | ||
| 03159540 | --- | 0.018 | 0.061 | 0.170 | 0.280 | 50.0 | 50.0 | 0.0 | 0.0 | 0.0 | ||
| 03201700 | 0.009 | 0.075 | 0.120 | 0.280 | 0.670 | 32.0 | 67.0 | 1.0 | 0.0 | 0.0 | ||
| 03201800 | 0.011 | 0.098 | 0.143 | 0.246 | 0.420 | 30.0 | 70.0 | 0.0 | 0.0 | 0.0 | ||
| 03205995 | 0.005 | 0.039 | 0.139 | 1.410 | 13.700 | 39.0 | 47.0 | 14.0 | 0.0 | 0.0 | ||
| 03235000 | --- | 0.020 | 0.069 | 0.540 | 0.760 | 49.0 | 41.0 | 10.0 | 0.0 | 0.0 | ||
| 03235080 | 0.007 | 0.045 | 0.084 | 0.239 | 0.560 | 41.0 | 58.0 | 1.0 | 0.0 | 0.0 | ||
| 03235500 | --- | 0.019 | 0.357 | 0.221 | 1.120 | 67.0 | 30.0 | 3.0 | 0.0 | 0.0 | ||
| 03237010 | --- | 0.023 | 0.048 | 1.530 | 9.500 | 54.0 | 32.0 | 14.0 | 0.0 | 0.0 | ||
| 03237023 | --- | 0.012 | 0.034 | 1.550 | 9.500 | 59.0 | 27.0 | 14.0 | 0.0 | 0.0 | ||
| 03237500 | --- | 0.008 | 0.028 | 0.089 | 0.133 | 70.0 | 30.0 | 0.0 | 0.0 | 0.0 | ||
| 03238600 | --- | 0.061 | 0.480 | 30.800 | 37.700 | 35.0 | 24.0 | 41.0 | 0.0 | 0.0 | ||
| 03240500 | --- | 0.006 | 0.027 | 0.117 | 0.238 | 68.0 | 32.0 | 0.0 | 0.0 | 0.0 | ||
| 03242100 | 0.008 | 0.080 | 0.176 | 1.480 | 7.500 | 31.0 | 56.0 | 13.0 | 0.0 | 0.0 | ||
| 03260700 | --- | 0.016 | 0.050 | 0.218 | 0.820 | 55.0 | 42.0 | 3.0 | 0.0 | 0.0 | ||
| 03264000 | --- | 0.014 | 0.052 | 0.231 | 0.660 | 54.0 | 44.0 | 2.0 | 0.0 | 0.0 | ||
| 03266500 | --- | 0.011 | 0.039 | 0.170 | 0.420 | 60.0 | 37.0 | 3.0 | 0.0 | 0.0 | ||
| 03268500 | 0.010 | 0.078 | 0.112 | 0.237 | 0.359 | 29.0 | 71.0 | 0.0 | 0.0 | 0.0 | ||
| 03271763 | --- | 0.012 | 0.058 | 0.204 | 0.353 | 52.0 | 48.0 | 0.0 | 0.0 | 0.0 | ||
| 03274100 | --- | 0.007 | 0.021 | 0.083 | 0.420 | 78.0 | 21.0 | 1.0 | 0.0 | 0.0 | ||
| 04180943 | --- | --- | 0.022 | 0.151 | 0.346 | 65.0 | 35.0 | 0.0 | 0.0 | 0.0 | ||
| 04185000 | --- | --- | 0.008 | 0.062 | 0.149 | 84.0 | 16.0 | 0.0 | 0.0 | 0.0 | ||
| 04185440 | 0.007 | 0.068 | 0.105 | 0.240 | 0.382 | 33.0 | 67.0 | 0.0 | 0.0 | 0.0 | ||
| 04192737 | --- | 0.012 | 0.052 | 0.224 | 0.740 | 54.0 | 44.0 | 2.0 | 0.0 | 0.0 | ||
| 04196000 | --- | 0.037 | 0.075 | 0.237 | 0.460 | 45.0 | 55.0 | 0.0 | 0.0 | 0.0 | ||
| 04198040 | --- | 0.028 | 0.073 | 0.220 | 0.377 | 46.0 | 54.0 | 0.0 | 0.0 | 0.0 | ||
| 04199155 | --- | 0.012 | 0.040 | 0.176 | 0.420 | 59.0 | 40.0 | 1.0 | 0.0 | 0.0 | ||
| 04199800 | --- | 0.010 | 0.029 | 0.300 | 0.740 | 61.0 | 37.0 | 2.0 | 0.0 | 0.0 | ||
| 04206212 | 0.015 | 0.082 | 0.143 | 0.660 | 5.350 | 29.0 | 61.0 | 10.0 | 0.0 | 0.0 | ||
| 04206220 | 0.012 | 0.064 | 0.107 | 4.750 | 17.700 | 34.0 | 48.0 | 18.0 | 0.0 | 0.0 | ||
| 04208777 | 0.006 | 0.049 | 0.087 | 0.268 | 0.910 | 40.0 | 57.0 | 3.0 | 0.0 | 0.0 | ||
| 04212100 | 0.005 | 0.024 | 0.052 | 0.232 | 0.625 | 54.0 | 44.0 | 2.0 | 0.0 | 0.0 | ||
| Maximum | 0.026 | 0.098 | 0.480 | 30.800 | 37.700 | 91.0 | 74.0 | 41.0 | 0.0 | 0.0 | ||
| Minimum | 0.005 | 0.006 | 0.007 | 0.042 | 0.090 | 26.0 | 9.0 | 0.0 | 0.0 | 0.0 | ||
| Mean | 0.010 | 0.039 | 0.089 | 1.048 | 2.943 | 47.9 | 48.1 | 4.0 | 0.0 | 0.0 | ||
| Median | 0.008 | 0.031 | 0.074 | 0.235 | 0.525 | 46.5 | 49.0 | 1.0 | 0.0 | 0.0 | ||
Samples of bank material collected from the left and right bank material that were composited from all cross sections at each site were analyzed by means of standard dry-sieve analyses with sieve sizes of 3.0, 2.0, 1.0, 0.75, 0.50, 0.375, 0.25, 0.10, 0.025, and 0.005 in. Particle-size analysis was done in accordance with American Society of Testing Materials method D422 (American Society of Testing Materials, 1998). These analyses were used to calculate percentages of bank-material particle-size ranges, percentages of substrate type, and bank-material particle-size quantile values corresponding to 16, 35, 50, 84, and 95 percent finer for each study site. Selected bank-material size-distribution data for the 50 study sites are listed in table 4.
A variety of stream-classification methods (Center for Watershed Protection and others, 1999; Johnson and others, 1999; Montgomery and Buffington, 1997; Rosgen, 1996; Simon, 1989) have been used to assess the characteristics of a stream for a variety of purposes (geomorphic, water-quality, biologic, and land-use purposes, among others). Stream-classification methods are a means of grouping streams by their common characteristics and (or) processes. Recently, stream-classification concepts have been adopted and used by various state and Federal government agencies for purposes such as describing stream habitat, monitoring time-based trends in fluvial and geomorphic conditions, and making stream-management decisions regarding stream restoration and (or) rehabilitation. The need to make such stream-management decisions has prompted several studies in which regional relations of geomorphic characteristics were compiled (Andrews, 1980; Williams, 1978; Annabel, 1995; Moody and Odem, 1999; Smith and Turrini-Smith, 1999).
For this study, an appropriate method to classify the 50 study sites would be one that is well known and commonly used for stream-restoration purposes. The Rosgen Level II classification method (Rosgen, 1996) was selected to classify the 50 study sites. The data used to determine the Rosgen Level II classification and the stream type are presented in table 5.
| Station number | Station name | Entrenchment ratio (ft/ft) | Width/depth ratio (ft/ft) | Slope (ft/ft) | Dominant channel material | Rosgen II classification |
|---|---|---|---|---|---|---|
| 03087000 | Beech Creek near Bolton | 7.02 | 12.0 | 0.0029 | Gravel | E4 |
| 03089500 | Mill Creek near Berlin Center | 8.70 | 12.0 | 0.0031 | Gravel | E4 |
| 03092090 | West Branch Mahoning River near Ravenna | 6.48 | 16.5 | 0.0039 | Gravel | C4 |
| 03092099 | Hinkley Creek at Charlestown | 6.97 | 15.1 | 0.0016 | Gravel | C4 |
| 03093000 | Eagle Creek at Phalanx Station | 6.50 | 25.9 | 0.0005 | Gravel | C4c- |
| 03110000 | Yellow Creek near Hammondsville | 3.16 | 26.6 | 0.0033 | Gravel | C4 |
| 03114240 | Wood Run near Woodsfield | 1.88 | 15.6 | 0.0397 | Gravel | B4 |
| 03115280 | Trail Run near Antioch | 7.99 | 10.7 | 0.0051 | Gravel | E4 |
| 03126110 | Skull Fork near Londonderry | 7.42 | 10.9 | 0.0001 | Silt/Clay | E6 |
| 03136564 | Dry Run near Bangs | 6.12 | 14.2 | 0.0127 | Gravel | C4 |
| 03139980 | Little Mill Creek near Coshocton | 9.35 | 14.4 | 0.0049 | Gravel | C4 |
| 03139990 | Little Mill Creek near Coshocton | 6.94 | 11.2 | 0.0060 | Gravel | E4 |
| 03144800 | Etna Creek at Etna | 6.35 | 11.7 | 0.0078 | Gravel | E4 |
| 03146500 | Licking River near Newark | 5.44 | 33.6 | 0.0003 | Gravel | C4c- |
| 03149500 | Salt Creek near Chandlersville | 6.51 | 15.9 | 0.0015 | Gravel | C4 |
| 03150333 | Keith Fork at Keith | 9.38 | 14.8 | 0.0027 | Gravel | C4 |
| 03157000 | Clear Creek near Rockbridge | 5.24 | 10.4 | 0.0011 | Gravel | E4 |
| 03158100 | Hayden Run near Haydenville | 18.19 | 9.3 | 0.0025 | Gravel | E4 |
| 03159450 | Mill Creek near Chauncey | 4.97 | 12.8 | 0.0067 | Gravel | C4 |
| 03159540 | Shade River near Chester | 5.09 | 12.9 | 0.0012 | Gravel | C4 |
| 03201700 | Big Four Hollow Creek near Lake Hope | 2.48 | 19.5 | 0.0091 | Gravel | C4 |
| 03201800 | Sandy Run near Lake Hope | 10.25 | 11.6 | 0.0014 | Gravel | E4 |
| 03205995 | Sandusky Creek near Burlington | 4.12 | 10.2 | 0.0123 | Gravel | E4 |
| 03235000 | Salt Creek at Tarlton | 6.54 | 19.1 | 0.0065 | Gravel | C4 |
| 03235080 | Bull Creek near Adelphi | 16.94 | 7.8 | 0.0059 | Gravel | E4 |
| 03235500 | Tar Hollow Creek at Tar Hollow State Park | 7.25 | 13.4 | 0.0087 | Gravel | C4 |
| 03237010 | Crooked Creek at Alma | 3.77 | 26.0 | 0.0074 | Gravel | C4 |
| 03237023 | No Name Creek at No Name | 2.48 | 19.5 | 0.0163 | Gravel | C4 |
| 03237500 | Ohio Brush Creek near West Union | 3.64 | 17.3 | 0.0006 | Gravel | C4c- |
| 03238600 | Higgins Run near Higginsport | 1.50 | 19.8 | 0.0504 | Cobble | B3a |
| 03240500 | North Fork Massie Creek at Cedarville | 10.26 | 15.5 | 0.0003 | Gravel | C4c- |
| 03242100 | Wayne Creek at Waynesville | 2.45 | 11.5 | 0.0266 | Gravel | E4b |
| 03260700 | Bokengehalas Creek near De Graff | 4.59 | 24.4 | 0.0021 | Gravel | C4 |
| 03264000 | Greenville Creek near Bradford | 3.74 | 32.0 | 0.0011 | Gravel | C4 |
| 03266500 | Mad River at Zanesfield | 6.50 | 16.3 | 0.0021 | Gravel | C4 |
| 03268500 | Beaver Creek near Springfield | 1.87 | 13.0 | 0.0017 | Gravel | B4c |
| 03271763 | Price Creek near Brennersville | 5.12 | 17.8 | 0.0015 | Gravel | C4 |
| 03274100 | Blake Run near Reily | 3.40 | 15.9 | 0.0147 | Gravel | C4 |
| 04180943 | Gallman Creek near Monticello | 2.69 | 11.2 | 0.0020 | Gravel | E4 |
| 04185000 | Tiffin River at Stryker | 8.26 | 15.0 | 0.0001 | Sand | C5 |
| 04185440 | Unnamed tributary to Lost Creek near Farmer | 6.04 | 10.1 | 0.0018 | Gravel | E4 |
| 04192737 | Big Creek at McClure | 4.95 | 10.2 | 0.0016 | Gravel | E4 |
| 04196000 | Sandusky River near Bucyrus | 4.38 | 22.8 | 0.0015 | Gravel | C4 |
| 04198040 | Walnut Creek near Boughtonville | 8.76 | 15.0 | 0.0057 | Gravel | C4 |
| 04199155 | Old Woman Creek at Berlin Road near Huron | 6.03 | 10.2 | 0.0019 | Gravel | E4 |
| 04199800 | Neff Run near Litchfield | 4.35 | 15.2 | 0.0067 | Gravel | C4 |
| 04206212 | North Fork at Bath Center | 2.50 | 13.8 | 0.0064 | Gravel | C4 |
| 04206220 | Yellow Creek at Botzum | 3.35 | 18.0 | 0.0050 | Cobble | C3 |
| 04208777 | Chagrin River at Fullertown | 5.54 | 21.5 | 0.0075 | Gravel | C4 |
| 04212100 | Grand River near Painesville | 2.49 | 52.2 | 0.0006 | Cobble | C3c- |
The entrenchment ratio is a measure of the degree of channel incision and is computed as the valley width at 2 times the maximum bankfull depth divided by the channel width at bankfull stage. The width/depth ratio is a measure of channel shape and is computed as the average of the individual width/depth (WBF/DBF) ratios computed for each cross section. (It is not equal to WBF presented in table 2 divided by the DBF presented in table 2.) The slope is computed by dividing the difference in channel-centerline elevation at the most upstream bankfull cross section and channel-centerline elevation at the most downstream bankfull cross section (in feet) by the distance between the two points (in feet) along the centerline-adjusted thalweg. (Note: All bankfull cross sections were surveyed at the crests of riffles.) The dominant channel material is based on the percentages by substrate type of the bed- and bank-material data presented in tables 3 and 4. Classification of the 50 study sites did not require computation of sinuosity because all sites have entrenchment ratios greater than 1.4, and sinuosity is only used to differentiate stream types having entrenchment ratios less than 1.4 (types A, G, and F). Use of the Rosgen Level II stream classification does not constitute an endorsement of that system over any other. It is provided for information only. An evaluation of the Rosgen Level II stream classification for its usefulness in assessing stream stability, inferring geomorphic processes, predicting future geomorphic response, and guiding restoration or rehabilitation activities across a range of physical environments is given in Juracek and Fitzpatrick (2003).
The primary reason for selecting sites for this study at streamflow-gaging stations is to facilitate accurate determination of the discharge (streamflow) corresponding to bankfull stage. An accurate estimate of bankfull discharge is often a useful variable for stream-restoration and other geomorphic projects. Bankfull discharge was determined for the 40 gaged study sites as part of an effort to develop a method or methods to estimate bankfull discharge at ungaged sites.
The longitudinal profiles used to determine the left and right bankfull elevations for the geomorphic analyses were also used to determine the bankfull stage at the location of the stage sensor for the gaging station. If well-defined indicators of bankfull stage were not evident at the location of the stage sensor, then well-defined indicators of bankfull stage were identified and surveyed both upstream and downstream from the location of the stage sensor, and estimates of bankfull stage at the stage sensor determined by interpolation from the bankfull-stage profile.
Relations between stage (gage height) and discharge at streamflow-gaging stations are developed from concurrent measurement and plotting of stage and discharge over time (Rantz and others, 1982). This is necessary because the channel changes form over time due to erosion and sedimentation, which cause perturbations in the stage-discharge relation. Ultimately, the stage-discharge relations are used to determine discharge from stage measured at regular intervals by instrumentation at the gaging station.
The current stage-discharge relation was used to determine bankfull discharge at the 16 active streamflow-gaging stations. The most recent stage-discharge relation was used to determine bankfull discharge at the 24 discontinued streamflow-gaging stations. As a check for the bankfull discharge determined from the stage-discharge relation, Manning's equation was used to compute discharge at each cross section used for the geomorphic analyses, and the average of the Manning's equation estimates was compared to the bankfull discharge determined from the stage-discharge relation. In general, the estimates based on Manning's equation compared well; however, in all cases, the bankfull discharge determined from the stage-discharge relation was used with no weight being given to the estimates based on Manning's equation.
The following table shows the simple statistics for the bankfull discharge (QBF) estimates determined from the stage-discharge relation and the bankfull discharge estimates based on Manning's equation.
| Maximum | Minimum | Mean | |
|---|---|---|---|
| QBF estimates based on stage- discharge relation | 14,500 | 36 | 1589 |
| QBF estimates based on Manning's equation | 13,800 | 34 | 1583 |
The Pearson correlation coefficient for QBF estimates based on the stage-discharge relation and QBF estimates based on Manning's equation is 0.973.
Plots of discharge as a function of recurrence interval (flood-frequency curve) based on the log-Pearson Type III flood-frequency estimates reported by Koltun (2003) were prepared for each of the 40 gaged study sites. The bankfull discharge determined from the stage-discharge relation was then plotted on the flood-frequency curve to estimate the recurrence interval of the bankfull discharge.
A wide range of estimates of the recurrence interval of bankfull discharge have been reported. Numerous previous investigators have reported that the recurrence interval of bankfull discharge is somewhere between 1 to 2 years with a mean of around 1.5 years (Leopold and others, 1964). Although this may be true for most streams, the concept of a universally applicable recurrence interval for bankfull discharge has been questioned by several investigators (Knighton, 1998; Richards, 1982; Williams, 1978). Some studies (Emmett and Wolman, 2001; Grant and others, 1990; Kilpatrick and Barnes, 1964; Lisle, 1987) have found that the recurrence interval of bankfull discharge tends to increase with an increase in channel slope; that is, high-gradient streams having coarse bed material tend to overtop their banks less frequently than low-gradient streams do.
The relation between slope and bankfull-discharge recurrence interval may be due to several factors. First, high-gradient streams may tend to be more entrenched than lower gradient streams, thus affording them greater conveyance within the channel and, as a result, less frequent overbank flooding. Second, the coarse bed material generally associated with high-gradient streams will tend to have higher entrainment thresholds and may require less frequent floods of greater discharge and velocity to cause movement of appreciable quantities of bed material. In this study, simple-regression analyses and Pearson correlation coefficients indicated strong positive relations between bankfull-discharge recurrence interval and main-channel slope, local-channel slope, bed-material particle size, and bank-material particle size. A negative relation was found between bankfull-discharge recurrence interval and entrenchment ratio. The bankfull-discharge recurrence intervals of the 40 gaged study sites ranged from about 1.01 to 9.7 years with an average of 1.8 years and a median of 1.4 years. In general, streams having very low bankfull-discharge recurrence intervals (less than 1.1 years) also had lower gradients (LCSL mean of 11.4 ft/mi), smaller bed material (BED50 mean of 16.3 mm), smaller bank material (BNK95 mean of 1.08 mm), and larger entrenchment ratios (mean of 6.3), whereas streams having very high bankfull-discharge recurrence intervals (greater than 2.5 years) also had higher gradients (LCSL mean of 167 ft/mi), larger bed material (BED50 mean of 68.8 mm), larger bank material (BNK95 mean of 20.6 mm), and smaller entrenchment ratios (mean of 2.2). Collection of more data on high-gradient streams is needed to confirm or contradict the interpretations of these analyses. The bankfull discharges determined from the stage-discharge relations for the 40 gaged study sites and their associated recurrence intervals and selected basin and geomorphic characteristics are presented in table 6.
| USGS Station number | Bankfull discharge (cubic feet per second) | Recurrence interval (years) | Local-channel slope (feet per mile) | Bed-material particle size of which 50 percent are finer (millimeters) | Bank-material particle size of which 95 percent are finer (millimeters) | Entrenchment ratio (feet per foot) |
|---|---|---|---|---|---|---|
| 03087000 | 775 | 1.35 | 15.50 | 11.13 | 13.50 | 7.02 |
| 03089500 | 500 | 1.06 | 16.61 | 45.05 | 0.71 | 8.70 |
| 03092090 | 910 | 1.94 | 20.62 | 39.20 | 0.33 | 6.48 |
| 03092099 | 178 | 1.03 | 8.27 | 12.94 | 4.75 | 6.97 |
| 03093000 | 1,220 | 1.03 | 2.90 | 4.16 | 0.49 | 6.50 |
| 03110000 | 2,920 | 1.88 | 17.60 | 54.12 | 1.68 | 3.16 |
| 03114240 | 190 | 9.65 | 209.60 | 51.83 | 6.40 | 1.88 |
| 03115280 | 590 | 1.79 | 27.13 | 18.66 | 0.42 | 7.99 |
| 03139980 | 416 | 1.97 | 25.80 | 28.72 | 0.33 | 9.35 |
| 03139990 | 388 | 1.32 | 31.59 | 29.17 | 0.31 | 6.94 |
| 03144800 | 52 | 1.15 | 41.42 | 15.17 | 0.76 | 6.35 |
| 03146500 | 10,300 | 1.61 | 1.57 | 14.71 | 0.26 | 5.44 |
| 03149500 | 2,090 | 1.10 | 7.71 | 13.83 | 0.26 | 6.51 |
| 03157000 | 2,730 | 2.15 | 5.84 | 31.23 | 0.32 | 5.24 |
| 03158100 | 64 | 1.52 | 13.16 | 10.60 | 0.26 | 18.19 |
| 03159450 | 98 | 1.56 | 35.37 | 14.20 | 0.40 | 4.97 |
| 03159540 | 2,100 | 1.05 | 6.49 | 17.90 | 0.28 | 5.09 |
| 03201700 | 54 | 1.29 | 48.13 | 13.43 | 0.67 | 2.48 |
| 03201800 | 331 | 1.94 | 7.24 | 5.54 | 0.42 | 10.25 |
| 03205995 | 66 | 1.15 | 64.95 | 16.99 | 13.70 | 4.12 |
| 03235000 | 920 | 1.78 | 34.12 | 41.44 | 0.76 | 6.54 |
| 03235080 | 202 | 1.30 | 31.31 | 12.41 | 0.56 | 16.94 |
| 03235500 | 120 | 2.26 | 46.10 | 11.03 | 1.12 | 7.25 |
| 03237500 | 14,500 | 1.26 | 3.37 | 37.93 | 0.13 | 3.64 |
| 03238600 | 710 | 5.55 | 266.21 | 94.86 | 37.70 | 1.50 |
| 03240500 | 139 | 1.04 | 1.39 | 8.40 | 0.24 | 10.26 |
| 03242100 | 280 | 2.26 | 140.40 | 48.98 | 7.50 | 2.45 |
| 03260700 | 542 | 1.45 | 10.84 | 17.73 | 0.82 | 4.59 |
| 03264000 | 2,490 | 1.50 | 5.55 | 27.86 | 0.66 | 3.74 |
| 03266500 | 280 | 1.40 | 10.93 | 11.69 | 0.42 | 6.50 |
| 03268500 | 689 | 1.04 | 9.04 | 15.62 | 0.36 | 1.87 |
| 03274100 | 45 | 1.53 | 77.71 | 38.63 | 0.42 | 3.40 |
| 04185000 | 1,930 | 1.12 | 0.61 | 0.21 | 0.15 | 8.26 |
| 04185440 | 250 | 1.17 | 9.58 | 7.03 | 0.38 | 6.04 |
| 04196000 | 1,610 | 1.18 | 7.85 | 44.30 | 0.46 | 4.38 |
| 04199155 | 630 | 1.14 | 9.93 | 15.17 | 0.42 | 6.03 |
| 04199800 | 36 | 1.01 | 35.31 | 9.78 | 0.74 | 4.35 |
| 04206212 | 320 | 1.52 | 33.84 | 28.23 | 5.35 | 2.50 |
| 04206220 | 1,250 | 2.59 | 26.21 | 59.83 | 17.70 | 3.35 |
| 04212100 | 10,600 | 1.36 | 3.04 | 74.93 | 0.62 | 2.49 |
| Maximum | 14,500 | 9.65 | 266.21 | 94.86 | 37.70 | 18.19 |
| Minimum | 36 | 1.01 | 0.61 | 0.21 | 0.13 | 1.50 |
| Mean | 1589 | 1.77 | 34.27 | 26.37 | 3.07 | 5.99 |
| Median | 521 | 1.38 | 16.05 | 17.36 | 0.48 | 5.74 |
Traditional methods for estimating bankfull characteristics of natural streams are commonly based on scatterplots of bankfull width, bankfull mean depth, bankfull cross-sectional area, and bankfull discharge as a function of drainage area. Such plots are commonly referred to as "regional curves." In recent years, regional curves reported by Dunne and Leopold (1978), which are applicable to the eastern United States, have been commonly used in Ohio for estimating bankfull dimensions of streams in the design of stream channels for stream-restoration projects. The data for the Dunne and Leopold (1978) regional curves are unpublished, so the accuracy of estimates of bankfull dimensions of streams in Ohio based on those curves is unknown. In general, much variability is present in relations between drainage area and bankfull dimensions and discharge. Typically, regional curves may also be accompanied by a simple-regression equation (one explanatory variable) to estimate bankfull width, bankfull mean depth, bankfull cross-sectional area, and bankfull discharge (response variables) as a function of drainage area (explanatory variable). Because simple regression is limited to one explanatory variable, only the variance explained by that variable is accounted for in the equation.
Multiple-regression equations can have more than one explanatory variable; thus, more of the variance can be accounted for in a multiple-regression equation. Although drainage area would likely be the basin characteristic accounting for the largest proportion of the variance in bankfull characteristics, other basin characteristics could account for additional variance in bankfull characteristics (as is true of relations between basin characteristics and flood characteristics). Because moderate discharges at or near bankfull stage do much work in terms of moving sediment and forming the main channel, any basin characteristic that affects (or is related to) discharge magnitudes near bankfull discharge (such as slope) could be statistically significant in a multiple-regression analysis of bankfull characteristics. In previous studies in Ohio in which regression equations are presented to estimate flood-peak-frequency characteristics from basin characteristics (Koltun, 2003; Koltun and Roberts, 1990; Webber and Bartlett, 1977) main-channel slope is the second-most statistically significant explanatory variable after drainage area. Thus, for two streams having the same drainage area but significantly different channel slopes, the stream having the steeper channel slope could have a greater bankfull discharge (and larger bankfull dimensions) than the stream having the flatter slope because of the generally positive relation between channel slope and discharge. Because multiple-regression equations can account for more sources of variance in the response variable than simple-regression equations, they can provide response-variable estimates with lower standard errors of prediction. The multiple-regression technique also yields a measure of the accuracy of the equation, a measure of the statistical significance of each explanatory variable in the equation, and a measure of the proportion of the variance explained by each variable. In the analysis, several combinations of explanatory variables are tested, and the combination that results in a best fit to the observed data is selected—provided that each explanatory variable is plausibly related to the response variable and is statistically significant in the regression.
In this study, both simple-regression (including regional curves) and multiple-regression methods were developed to estimate bankfull characteristics of Ohio streams. The following sections describe the development and application of both methods.
Graphical and statistical analyses were used to develop regional curves and simple-regression equations relating drainage area to bankfull width, bankfull mean depth, bankfull cross-sectional area, and bankfull discharge.
Initially, scatterplots of bankfull width, bankfull mean depth, bankfull cross-sectional area, and bankfull discharge as a function of drainage area indicated linear relations with considerable unexplained variance, as is typical of regional curves. Ordinary least-squares regression was used to quantify these relations and to develop equations to estimate bankfull characteristics from drainage area. As is typical of regression variables in hydrologic studies, the distributions of the logarithmic transformations (base 10) of the variables fit a normal distribution more closely than do the distributions of untransformed variables. The logarithmic transformations also improve the linearity of the relations between response and explanatory variables. In this study, the logarithmic transformations of variables were used in all regression analyses. The analysis resulted in four simple-regression equations to estimate bankfull characteristics (bankfull width, bankfull mean depth, bankfull cross-sectional area, and bankfull discharge) from drainage area.
In an effort to account for some of the variance that might be due to regional differences and to minimize geographical bias of the equations, residuals (differences between observed and predicted values) from the simple-regression analyses of bankfull characteristics against drainage area were plotted on a state map of Ohio to determine whether the drainage-area-only simple-regression equations consistently overpredicted or underpredicted bankfull characteristics in particular areas of the State. These plots indicated overprediction in western Ohio and underprediction in southern Ohio. The residuals also were plotted on maps of five sets of predetermined regions—ecologic regions, geologic regions, physiographic provinces, physiographic sections, and flood regions—to determine whether areas of overprediction and underprediction coincided with any these regions, but no coincidences were apparent.
As an additional check for regional differences in bankfull characteristics, binary indicator variables representing the five predetermined regions were entered into a regression analysis, along with drainage area, as explanatory variables. None of the five predetermined regions were statistically significant for all bankfull characteristics or resulted in an appreciable reduction in average prediction errors.
Further review of the state-map residual plots resulted in delineation of a region of underprediction in southern Ohio. This region (region B) was tested in the regression analysis as a binary indicator variable. Region B was found to be statistically significant for all bankfull characteristics (bankfull width, bankfull mean depth, bankfull cross-sectional area, and bankfull discharge), and it accounted for appreciable reduction in average prediction errors. State-map residual plots for equations with region B included as an explanatory variable indicated that there were no areas in region A or region B that consistently overpredicted or underpredicted bankfull characteristics (the area of overprediction previously identified in western Ohio was no longer apparent). Region B includes five study sites and generally coincides with an unglaciated area of high relief and high precipitation in the Shawnee-Mississippian Allegheny Plateau and Outer Bluegrass physiographic regions (Brockman, 1998). The boundary of the region was defined so as not to cross any 14-digit hydrologic unit code boundaries so that few streams will span multiple regions. Detailed explanations of hydrologic unit codes can be found in Seaber and others (1987) and Stafford (1999). The two bankfull regions for Ohio are depicted in figure 7.
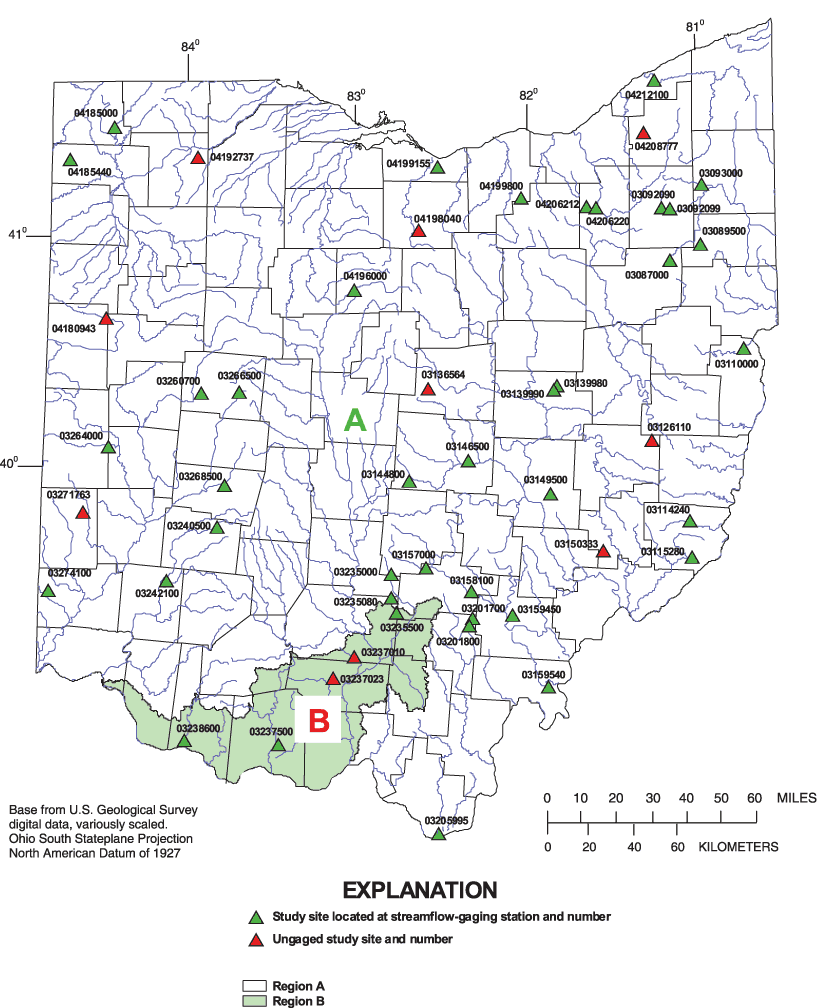
Figure 7. Bankfull regions A and B and locations of the 50 selected study sites in Ohio.
The indicator-variable method was used instead of separate regression analyses for each region because it gives one estimate of the common error variance for the State and provides more residual degrees of freedom than would result from fitting separate regressions. Moreover, separate regressions for each region were not feasible because only five study sites are in region B. The effect of the indicator variable is an adjustment in the intercept term for the logarithmic form of the regression equation. Additional information on the use of indicator variables in regression analyses is given in Montgomery and Peck (1982).
Simple-regression (drainage-area-only) equations for estimating bankfull characteristics of Ohio streams are presented in table 7. For the reader's convenience, the regional intercept term is combined with the equation constant and separate equations are presented for each region. Regional curves of bankfull characteristics of Ohio streams based on drainage area only are shown in figures 8–11. The regional curves are plots of predicted values of the bankfull characteristics from regression equations 1–8 as a function of drainage area.
|
[WBF, bankfull width, in feet; DBF, bankfull mean depth, in feet; ABF, bankfull cross-sectional area, in square feet; QBF, bankfull discharge, in cubic feet per second; DA, drainage area, in square miles] |
|||||||
|---|---|---|---|---|---|---|---|
| Equation number | Equation | Average standard errror of prediction (percent) | Coefficient of determination (adjusted r-square) | ||||
| Region A | |||||||
| 1 | WBFA | = | 18.0 | DA | 0.356 | 24.8 | 0.911 |
| 2 | DBFA | = | 1.52 | DA | 0.265 | 20.6 | 0.881 |
| 3 | ABFA | = | 27.1 | DA | 0.621 | 30.6 | 0.953 |
| 4 | QBFA | = | 93.3 | DA | 0.637 | 78.7 | 0.822 |
| Region B | |||||||
| 5 | WBFB | = | 32.0 | DA | 0.356 | 24.8 | 0.911 |
| 6 | DBFB | = | 2.02 | DA | 0.265 | 20.6 | 0.881 |
| 7 | ABFB | = | 64.5 | DA | 0.621 | 30.6 | 0.953 |
| 8 | QBFB | = | 230 | DA | 0.637 | 78.7 | 0.822 |
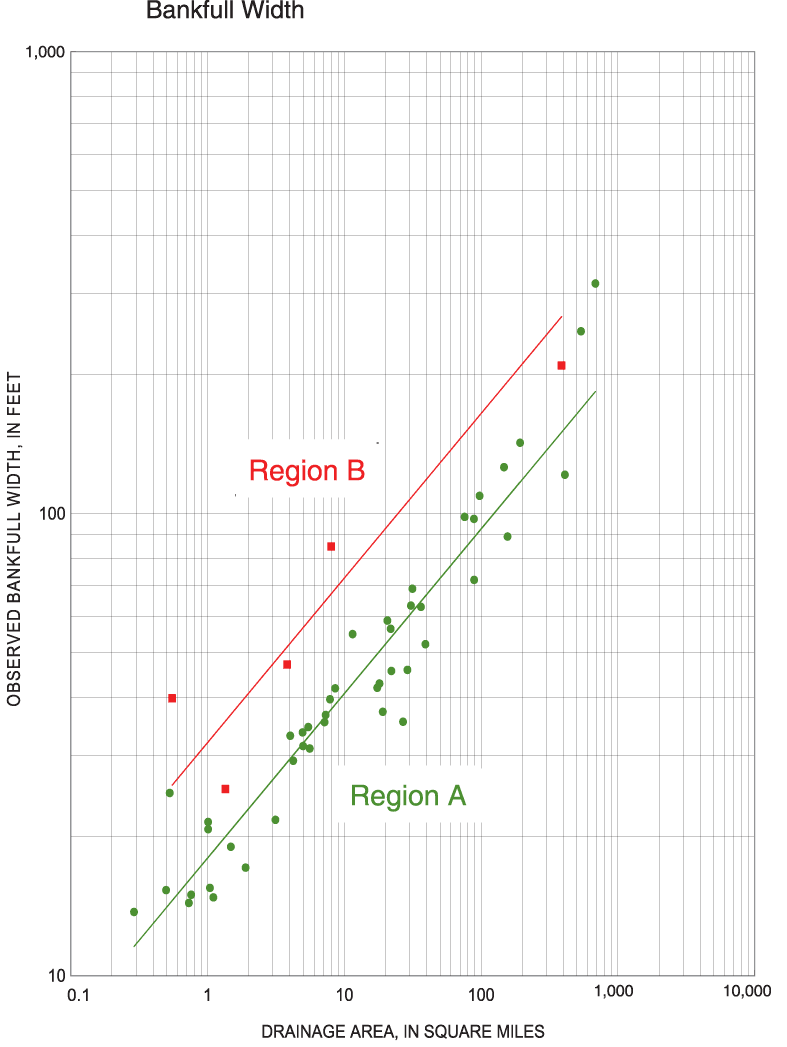
Figure 8. Regional curves for bankfull width for Ohio.
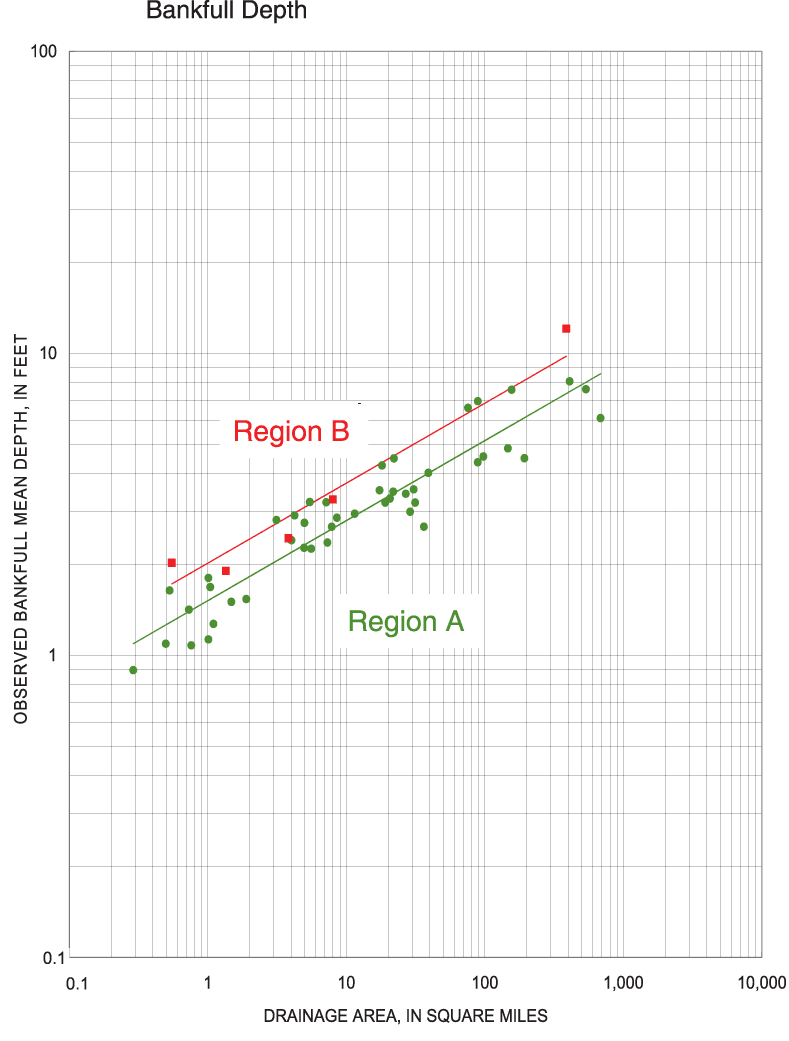
Figure 9. Regional curves for bankfull mean depth for Ohio.
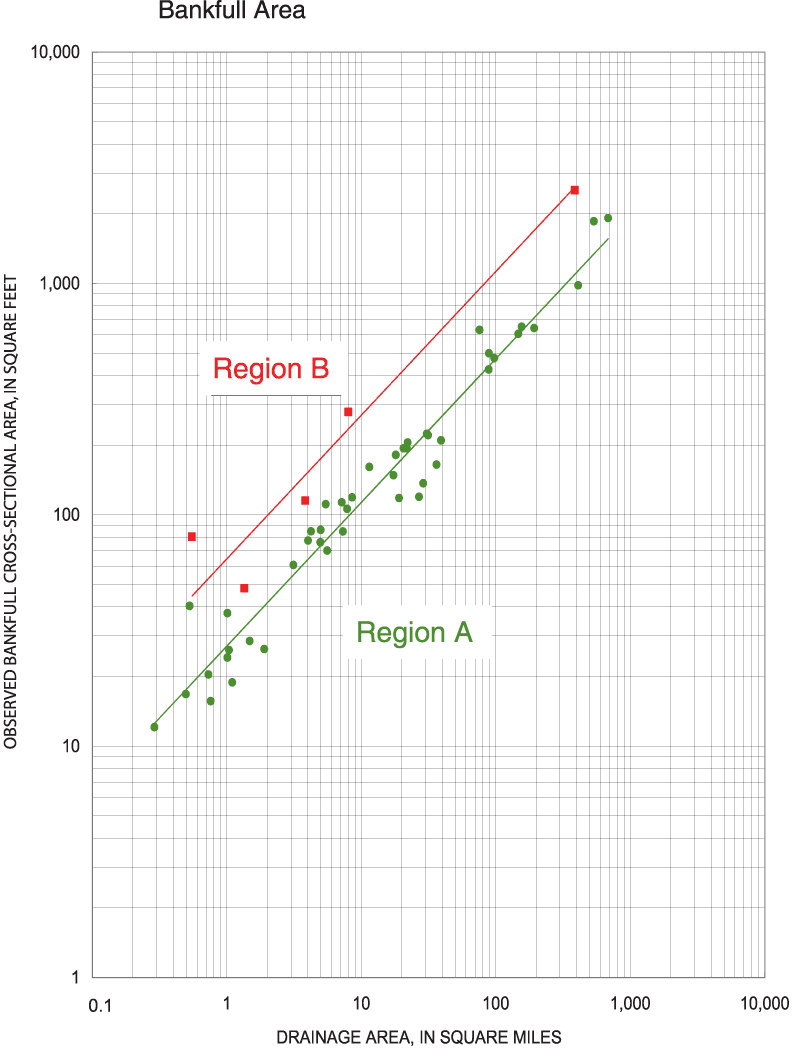
Figure 10. Regional curves for bankfull cross-sectional area for Ohio.
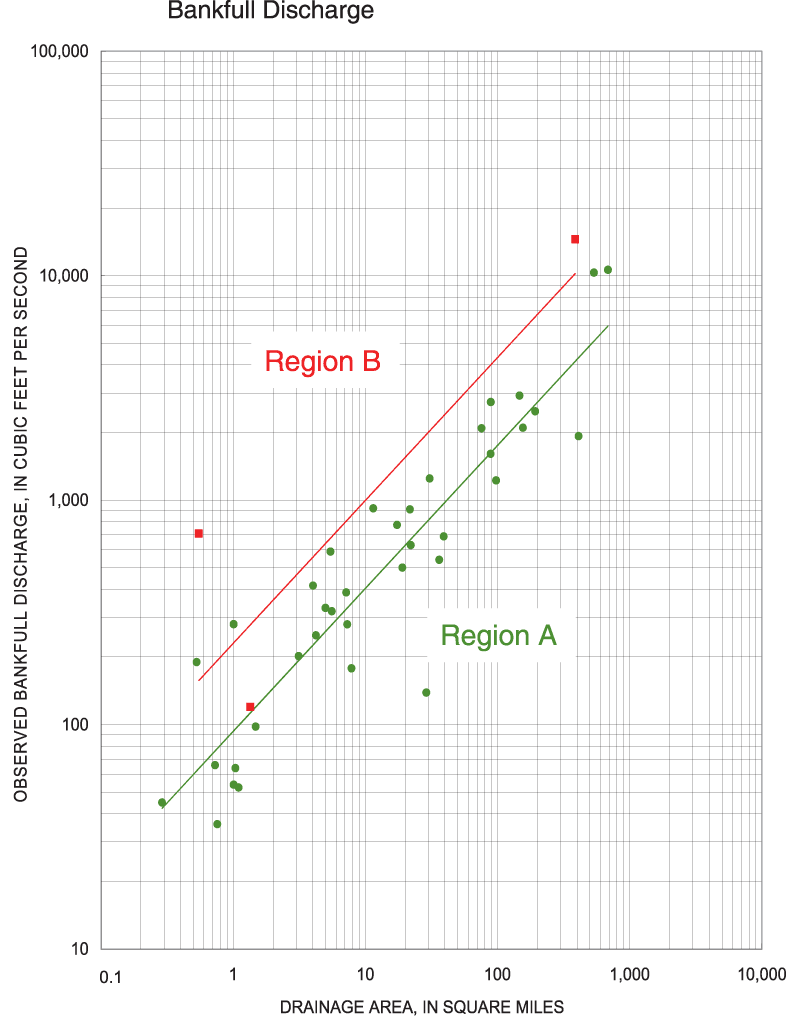
Figure 11. Regional curves for bankfull discharge for Ohio.
Because the binary indicator variable method was used in the regression analyses, the regional curves for both regions A and B are based on the relation between drainage area and geomorphic bankfull characteristics for all 50 study sites and drainage area and bankfull discharge for the 40 gaged study sites (not just the study sites in each region).
Drainage area is statistically significant at the 99.99 percent confidence level for all equations listed in table 6, which means that there is a 0.01 percent chance that drainage area is not related to bankfull characteristics. The average standard errors of prediction reported in table 6 are a measure of the expected prediction errors when estimating bankfull characteristics at sites not included in the regression analysis. They are computed by leaving out one site, developing an equation based on the other 49 sites, and computing the residual for the site left out. The process is repeated for each site, and the 50 residuals are squared and summed. The sum of the squared prediction residuals is called the PRESS statistic (Montgomery and Peck, 1982). The average standard error of prediction is computed by dividing the PRESS statistic by the number of observations (n). Gilroy and Tasker (1990) found that the use of PRESS/n as an estimate of the average mean square error of prediction for a multiple-regression linear model yielded reasonably good predictions when applied to split-sample data. Plots of residuals from the regression analyses as a function of drainage area indicated that prediction errors did not vary as a function of drainage area.
The coefficient of determination (adjusted r-squared) values listed in table 7 are a measure of how well the explanatory variable (in this case, drainage area) explains the variation in the response variable. For example, the r-squared of 0.911 reported in table 7 for bankfull width means that drainage area accounts for about 91.1 percent of the variability in the logarithms of the bankfull-width data.
In an effort to further reduce the prediction errors for bankfull characteristics estimated by use of the drainage-area-only simple-regression equations, multiple-regression analyses were done. Additional explanatory variables were tested for statistical significance and were ultimately included in the multiple-regression equations, provided that their inclusion would reduce parametrical bias and improve estimates of bankfull characteristics. The additional variables also had to be plausibly related to the response variable and statistically significant in the regression. The technique also yields a measure of the accuracy of the equation, a measure of the statistical significance of each explanatory variable in the equation, and a measure of the proportion of the variance explained by each variable.
Initially, bankfull characteristics were plotted (simple linear and base 10 logarithmic transformations) as a function of numerous other basin characteristics (such as main-channel slope, forested area, and storage area) and other geomorphic characteristics (such as bed-material size and local-channel slope). These plots indicated, at best, weak relations. Additionally, residuals (differences between observed and predicted values) from the simple-regression analyses were plotted as a function of numerous other basin characteristics and geomorphic characteristics. These plots indicated that, for some basin and geomorphic characteristics, low values of that characteristic tended to be associated with overprediction or underprediction of a particular bankfull characteristic, whereas high values of that characteristic tended to have the opposite effect. For example, the residuals from the bankfull cross-sectional area drainage-area-only equation plotted as a function of main-channel slope indicated that, for low values of main-channel slope the equation overpredicted bankfull area, whereas for high values of main-channel slope the equation underpredicted bankfull area. Therefore, main-channel slope may be related to bankfull area and, if included as an explanatory variable in a multiple-regression equation, may help to improve estimates of bankfull area. It also seems plausible that, because of the generally positive relation between main-channel slope and peak discharge (Benson, 1962; Jennings and others, 1994), streams having steeper main-channel slopes would have greater magnitudes of bankfull discharge, which might result in larger cross-sectional areas of the main channel.
Multiple-regression analyses were done in which bankfull width, bankfull mean depth, bankfull cross-sectional area, and bankfull discharge were regressed against numerous potential explanatory variables. Some of the basin, geomorphic, and climatic characteristics initially tested included the following (definitions of terms are at the beginning of this report):
| DA |
— |
Drainage area, in square miles |
| MCSL |
— |
Main-channel slope, in feet per mile |
| LCSL |
— |
Local-channel slope, in feet per mile |
| ELEV |
— |
Average main-channel elevation index, in feet |
| LG |
— |
Main-channel length, in miles |
| STOR |
— |
Storage area, in percent |
| FOR |
— |
Forested area, in percent |
| DECLAT |
— |
Decimal latitude, in decimal degrees |
| DECLONG |
— |
Decimal longitude, in decimal degrees |
| PREC |
— |
Average annual precipitation, in inches |
| I24,2 |
— |
24-hour 2-year rainfall intensity, in inches |
| BEDXX |
— |
Bed-material particle size of which XX percent is finer, in millimeters, where XX equals 16, 35, 50, 84, and 95 percent |
| BNKXX |
— |
Bank-material particle size of which XX percent is finer, in millimeters, where XX equals 50, 84, and 95 percent |
As in the simple-regression analyses, all predetermined regions (ecologic regions, geologic regions, physiographic provinces, physiographic sections, and flood regions), as well as the A and B bankfull regions defined in the simple-regression analyses, were also tested in the multiple-regression analyses by use of binary indicator variables.
A combination of step-forward and step-backward regression procedures were used to assist in determining which of the explanatory variables should be included in the multiple-regression equations. Selection of explanatory variables for use in the final model was based on the following criteria:
The analyses resulted in the 15 multiple-regression equations, which are presented in tables 8 and 9. The multiple-regression equations in table 8—in which the explanatory variables are DA, MCSL, and ELEV—will, on average, result in more accurate estimates of bankfull characteristics than the simple-regression equations in table 7, in which DA is the only explanatory variable. Measures of all explanatory variables in equations presented in tables 7 and 8 (DA, MCSL, and ELEV) can be obtained from USGS 7.5-minute topographic quadrangle maps.
| [ WBF, bankfull width, in feet; DBF, bankfull mean depth, in feet; ABF, bankfull cross-sectional area, in square feet; QBF, bankfull discharge, in cubic feet per second; DA, drainage area, in square miles; MCSL, main-channel slope, in feet per mile; ELEV, main-channel elevation index, in feet] |
|||||||||||
| Equation number | Equation | Average standard error of prediction (percent) | Coefficient of determination (adjusted r-square) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Region A | |||||||||||
| 0.424 | 0.147 | ||||||||||
| 9 | WBFA | = | 9.6 | DA | MCSL | 23.5 | 0.921 | ||||
| 0.263 | -0.516 | ||||||||||
| 10 | DBFA | = | 51.8 | DA | ELEV | 18.8 | 0.903 | ||||
| 0.718 | 0.213 | -0.537 | |||||||||
| 11 | ABFA | = | 427 | DA | MCSL | ELEV | 27.4 | 0.963 | |||
| Region B | |||||||||||
| 0.424 | 0.147 | ||||||||||
| 12 | WBFB | = | 15.5 | DA | MCSL | 23.5 | 0.921 | ||||
| 0.263 | -0.516 | ||||||||||
| 13 | DBFB | = | 62.7 | DA | ELEV | 18.8 | 0.903 | ||||
| 0.718 | 0.213 | -0.537 | |||||||||
| 14 | ABFB | = | 806 | DA | MCSL | ELEV | 27.4 | 0.963 | |||
| Statewide | |||||||||||
| 0.951 | 0.684 | -1.154 | |||||||||
| 15 | QBF | = | 12925 | DA | MCSL | ELEV | 66.6 | 0.864 | |||
| [ WBF, bankfull width, in feet; DBF, bankfull mean depth, in feet; ABF, bankfull cross-sectional area, in square feet; QBF, bankfull discharge, in cubic feet per second; DA, drainage area, in square miles; MCSL, main-channel slope, in feet per mile; ELEV, main-channel elevation index, in feet; LCSL, local-channel slope, in feet per mile; BED50, bed-material particle size of which 50 percent is finer, in millimeters] |
|||||||||||||
| Equation number | Equation | Average standard error of prediction (percent) | Coefficient of determination (adjusted r-square) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Region A | |||||||||||||
| 0.405 | 0.100 | 0.130 | |||||||||||
| 16 | WBFA | = | 7.9 | DA | MCSL | BED50 | 20.6 | 0.940 | |||||
| 0.263 | -0.516 | ||||||||||||
| 17 | DBFA | = | 51.8 | DA | ELEV | 18.8 | 0.903 | ||||||
| 0.701 | 0.173 | -0.636 | 0.119 | ||||||||||
| 18 | ABFA | = | 699 | DA | MCSL | ELEV | BED50 | 25.4 | 0.969 | ||||
| Region B | |||||||||||||
| 0.405 | 0.100 | 0.130 | |||||||||||
| 19 | WBFB | = | 11.8 | DA | MCSL | BED50 | 20.6 | 0.940 | |||||
| 0.263 | -0.516 | ||||||||||||
| 20 | DBFB | = | 62.7 | DA | ELEV | 18.8 | 0.903 | ||||||
| 0.701 | 0.173 | -0.636 | 0.119 | ||||||||||
| 21 | ABFB | = | 1202 | DA | MCSL | ELEV | BED50 | 25.4 | 0.969 | ||||
| Statewide | |||||||||||||
| 0.890 | 0.537 | -1.131 | 0.436 | ||||||||||
| 22 | QBF | = | 5584 | DA | MCSL | ELEV | BED50 | 49.7 | 0.919 | ||||
| 1.320 | 0.364 | ||||||||||||
| 23 | QBF | = | 0.280 | ABF | LCSL | 27.0 | 0.972 | ||||||
Similarly, the multiple-regression equations presented in table 9 in which the explanatory variables BED50, ABF (QBF equation only), and LCSL (QBF equation only) are added, will, on average, provide more accurate estimates of bankfull characteristics than the multiple-regression equations presented in table 8 in which DA, MCSL, and ELEV are the explanatory variables. The additional explanatory variables in some of the equations in table 9 (there are no additional explanatory variables in the DBF equation) require data that must be collected in the field. Readers can refer to the definitions of abbreviations at the beginning of this report for explanations of how to determine values for all explanatory variables in tables 7, 8, and 9. Values of all explanatory variables in tables 7, 8, and 9 for the 50 study sites are listed in table 10. Values of all response variables in tables 7, 8, and 9 for the 50 study sites are listed in tables 2 and 6.
Table 10. Values of all explanatory variables in tables 7, 8, and 9 for the 50 study sites.
| [ DA, drainage area, in square miles; MCSL, main-channel slope, in feet per mile; ELEV, main-channel elevation index, in feet; BED50, bed-material particle size of which 50 percent is finer, in millimeters; ABF, bankfull cross-sectional area, in square feet; LCSL, local-channel slope, in feet per mile] |
|||||||
| Station number | Region | DA | MCSL | ELEV | BED50 | ABF | LCSL |
|---|---|---|---|---|---|---|---|
| 03087000 | A | 17.4 | 27.0 | 1150 | 11.13 | 148.3 | 15.50 |
| 03089500 | A | 19.1 | 11.1 | 1100 | 45.05 | 118.2 | 16.61 |
| 03092090 | A | 21.8 | 19.0 | 1108 | 39.20 | 194.0 | 20.62 |
| 03092099 | A | 7.85 | 18.3 | 1110 | 12.94 | 106.0 | 8.27 |
| 03093000 | A | 97.6 | 10.7 | 974 | 4.16 | 475.4 | 2.90 |
| 03110000 | A | 147 | 9.8 | 835 | 54.12 | 605.3 | 17.60 |
| 03114240 | A | 0.53 | 246 | 1010 | 51.83 | 40.4 | 209.60 |
| 03115280 | A | 5.45 | 90.3 | 820 | 18.66 | 111.1 | 27.13 |
| 03126110 | A | 26.9 | 8.7 | 924 | 3.47 | 119.5 | 0.52 |
| 03136564 | A | 0.50 | 81.4 | 1288 | 27.85 | 16.8 | 66.88 |
| 03139980 | A | 4.02 | 77.8 | 969 | 28.72 | 77.5 | 25.80 |
| 03139990 | A | 7.16 | 39.5 | 900 | 29.17 | 113.1 | 31.59 |
| 03144800 | A | 1.10 | 37.0 | 1051 | 15.17 | 18.9 | 41.42 |
| 03146500 | A | 537 | 10.7 | 985 | 14.71 | 1855.0 | 1.57 |
| 03149500 | A | 75.7 | 9.0 | 775 | 13.83 | 629.5 | 7.71 |
| 03150333 | A | 8.56 | 51.2 | 839 | 11.43 | 119.0 | 14.39 |
| 03157000 | A | 89.0 | 9.2 | 852 | 31.23 | 499.1 | 5.84 |
| 03158100 | A | 1.04 | 94.0 | 792 | 10.60 | 26.0 | 13.16 |
| 03159450 | A | 1.48 | 80.4 | 750 | 14.20 | 28.5 | 35.37 |
| 03159540 | A | 156 | 4.0 | 658 | 17.90 | 650.2 | 6.49 |
| 03201700 | A | 1.01 | 103 | 848 | 13.43 | 24.2 | 48.13 |
| 03201800 | A | 4.99 | 22.0 | 805 | 5.54 | 86.1 | 7.24 |
| 03205995 | A | 0.73 | 124 | 630 | 16.99 | 20.4 | 64.95 |
| 03235000 | A | 11.5 | 28.6 | 961 | 41.44 | 160.9 | 34.12 |
| 03235080 | A | 3.13 | 60.4 | 905 | 12.41 | 60.7 | 31.31 |
| 03235500 | B | 1.35 | 140 | 897 | 11.03 | 48.1 | 46.10 |
| 03237010 | B | 8.01 | 51.3 | 756 | 55.27 | 278.5 | 38.82 |
| 03237023 | B | 3.82 | 44.8 | 884 | 71.90 | 115.1 | 86.18 |
| 03237500 | B | 387 | 8.3 | 673 | 37.93 | 2527.4 | 3.37 |
| 03238600 | B | 0.55 | 301 | 696 | 94.86 | 80.4 | 266.21 |
| 03240500 | A | 28.9 | 7.0 | 1073 | 8.40 | 136.7 | 1.39 |
| 03242100 | A | 1.01 | 98.0 | 854 | 48.98 | 37.5 | 140.40 |
| 03260700 | A | 36.3 | 28.6 | 1180 | 17.73 | 164.7 | 10.84 |
| 03264000 | A | 193 | 5.8 | 1042 | 27.86 | 641.4 | 5.55 |
| 03266500 | A | 7.31 | 49.8 | 1304 | 11.69 | 84.6 | 10.93 |
| 03268500 | A | 39.2 | 15.7 | 1088 | 15.62 | 209.8 | 9.04 |
| 03271763 | A | 20.7 | 13.6 | 1068 | 36.57 | 194.0 | 7.73 |
| 03274100 | A | 0.29 | 93.0 | 946 | 38.63 | 12.1 | 77.71 |
| 04180943 | A | 1.90 | 23.0 | 829 | 5.23 | 26.2 | 10.47 |
| 04185000 | A | 410 | 5.3 | 843 | 0.21 | 981.9 | 0.61 |
| 04185440 | A | 4.23 | 16.8 | 796 | 7.03 | 84.9 | 9.58 |
| 04192737 | A | 18.1 | 3.9 | 676 | 4.80 | 181.5 | 8.49 |
| 04196000 | A | 88.8 | 7.4 | 1098 | 44.30 | 424.6 | 7.85 |
| 04198040 | A | 4.96 | 30.6 | 984 | 41.34 | 76.1 | 29.97 |
| 04199155 | A | 22.1 | 34.8 | 734 | 15.17 | 205.3 | 9.93 |
| 04199800 | A | 0.76 | 31.0 | 938 | 9.78 | 15.6 | 35.31 |
| 04206212 | A | 5.58 | 46.7 | 1076 | 28.23 | 70.0 | 33.84 |
| 04206220 | A | 30.7 | 32.0 | 949 | 59.83 | 223.8 | 26.21 |
| 04208777 | A | 31.4 | 13.0 | 1129 | 60.68 | 221.2 | 39.65 |
| 04212100 | A | 685 | 2.5 | 743 | 74.93 | 1916.4 | 3.04 |
| Maximum | 685 | 301 | 1304 | 94.86 | 2527.4 | 266.21 | |
| Minimum | 0.29 | 2.5 | 630 | 0.21 | 12.1 | 0.52 | |
| Mean | 65.6 | 47.5 | 926 | 27.46 | 305.2 | 33.48 | |
| Median | 8.29 | 28.6 | 915 | 17.81 | 118.6 | 16.05 | |
The hydrologic and geomorphic validity for the inclusion of MCSL, as well as the sign and magnitude of the associated regression coefficient for MCSL, is consistent with the generally positive relation between main-channel slope and peak discharge (Benson, 1962; Jennings and others, 1994); that is, on average, streams having steeper main-channel slopes will have greater magnitudes of bankfull discharge and consequently greater bankfull dimensions. Support for the inclusion of ELEV is less obvious. It seems that ELEV may be a surrogate for a combination of several other factors. Pearson correlation coefficients indicate moderate negative correlations between ELEV and drainage area, main-channel slope, average annual precipitation, D50 bed-material particle size, and bankfull discharge. The combination of these five negative correlations may cause ELEV to be statistically significant and may also explain the negative sign of the associated regression coefficient. Without ELEV in the equations, bias is indicated in plots of residuals as a function of ELEV. Further support for the inclusion of MCSL and ELEV is that either or both have been statistically significant in flood-peak equations relating flood characteristics to basin characteristics in Ohio (Koltun, 2003; Koltun and Roberts, 1990; Webber and Bartlett, 1977). The inclusion of MCSL and ELEV is convenient for the user of the equations, in that the elevation points used to determine ELEV are the same as the elevation points used to determine MCSL. The inclusion of and sign of the regression coefficient for BED50 coincides with the inclusion of and sign of the regression coefficient for MCSL, in that streams having steeper slopes often are associated with larger bed-material particle size. The inclusion of additional explanatory variables (MCSL, ELEV, BED50, ABF, and LCSL) in QBF equations 15, 22, and 23 resulted in the binary indicator variable for region B no longer being statistically significant for bankfull discharge, so QBF equations 15, 22, and 23 are applicable statewide.
For the bankfull-discharge regression equations, bankfull cross-sectional area (ABF) alone explains more of the variance in bankfull discharge (coefficient of partial determination equals 0.926) than does drainage area or any combination of drainage area and other explanatory variables. In combination with local-channel slope (LCSL), the coefficient of multiple determination for equation 23 is 0.972. This rather high coefficient of multiple determination indicates that LCSL is a reasonably good surrogate for velocity in the basic hydraulic flow equation Q = VA , where Q equals discharge, V equals mean velocity, and A equals cross-sectional area. Many topographic and meteorologic characteristics and other factors, the nature of which are yet unknown, can affect discharges near bankfull discharge. The high coefficient of multiple determination indicates that many of these factors may be reflected in the bankfull cross-sectional area. Only a few of all the factors that may affect bankfull discharge can be easily measured or quantified for inclusion in a multiple-regression analysis. Factors that may be affecting bankfull cross-sectional area, but that cannot be easily measured or quantified for inclusion in a multiple-regression analysis, may account for bankfull cross-sectional area explaining more of the variance than any other combination of explanatory variables used in this analysis.
The regional curves and regression equations presented provide a means to estimate bankfull characteristics of Ohio streams. Four options are available: a graphical method that employs a set of regional curves relating bankfull characteristics to drainage area, and three sets of regression equations relating bankfull characteristics to basin and geomorphic characteristics. Application and comparison of different and independent methods may be advisable. Table 11 lists information about studies in five areas of Ohio where other geomorphic data have been collected and regional curves have been developed. The amount of data collected in these areas for these five studies may be considerably greater than the amount of data collected in these areas for this study. Also, not well represented in this study were low-gradient channels dominated by herbaceous vegetation in northwest Ohio, particularly headwaters, whereas the geomorphic data and regional curves referenced in table 11 for northwest Ohio are based predominantly on low-gradient channels dominated by herbaceous vegetation.
| Data characteristic | Northwest | Northeast | Southwest | Southeast | Central |
|---|---|---|---|---|---|
| Counties of data collection | Sandusky, Wood | Ashtabula, Cuyahoga, Erie, Geauga, Huron, Lake, Lorain, Summit | Butler, Champaign, Clinton, Greene, Madison, Montgomery, Pickaway, Preble, Warren | Gallia, Hocking, Washington | Crawford, Delaware, Franklin, Madison, Marion, Morrow, Pickaway, Ross |
| Dates of data collection | 2000-04 | 2002 | 1999-2004 | 2003 | 2003-2005 |
| Number of study sites | 19 | 21 | 27 | 35 | 44 |
| Maximum DA | 2430 | 246 | 534 | 166 | 5131 |
| Minimum DA | 0.10 | 0.83 | 0.10 | 0.03 | 0.40 |
| Mean DA | 226 | 39.6 | 35.0 | 24.4 | 283 |
| Median DA | 11.3 | 20.2 | 7.8 | 3.6 | 12.4 |
| Reference | Ward and others, 2004 | Whiting 1 | Mecklenburg 2 |
Chang and others, 2004 | Witter, D'Ambrosio, and Ward 3 |
| Whiting 1 -Written communication with Dr. Peter Whiting, Department of Geological Sciences, Case Western Reserve University, unpublished at time of this writing Mecklenburg 2 -Written communication with Daniel Mecklenburg, Ohio Department of Natural Resources, Division of Soil and Water Conservation, unpublished at time of this writing Witter, D'Ambrosio, and Ward 3 -Written communication with Jon Witter, Jessica D'Ambrosio, and Andy Ward, Ohio State University, Department of Food, Agriculture and Biological Engineering, unpublished at time of this writing |
|||||
Table 12. Summary statistics of explanatory variables by region.
[ DA, drainage area, in square miles; MCSL, main-channel slope, in feet per mile; ELEV, main-channel elevation index, in feet; BED50, bed-material particle size of which 50 percent is finer, in millimeters; ABF, bankfull cross-sectional area, in square feet; LCSL, local-channel slope, in feet per mile]
| Region | Statistic | DA | MCSL | ELEV | BED50 | ABF | LCSL |
|---|---|---|---|---|---|---|---|
| A | Maximum | 685 | 246 | 1304 | 74.93 | 1916.4 | 210 |
| Minimum | 0.29 | 2.5 | 630 | 0.21 | 12.1 | 0.52 | |
| Mean | 63.9 | 40.7 | 942 | 24.49 | 271.4 | 27.4 | |
| Median | 11.5 | 27.0 | 946 | 16.99 | 119.0 | 14.4 | |
| B | Maximum | 387 | 301 | 897 | 94.86 | 2527.4 | 266 |
| Minimum | 0.55 | 8.3 | 673 | 11.03 | 48.1 | 3.4 | |
| Mean | 80.1 | 109 | 781 | 54.20 | 609.9 | 88.1 | |
| Median | 3.82 | 51.3 | 756 | 55.27 | 115.1 | 46.1 | |
The eight regional curves in figures 8–11 and the 23 equations presented in tables 7, 8, and 9 are applicable to sites on rural streams in Ohio that are free of appreciable regulation of flows near bankfull discharge and whose basin characteristics are within the ranges of the basin and geomorphic characteristics of the 50 study sites used in the regression analysis. In general, basins having usable storage of less than 103 acre-ft/mi 2 are considered to be unregulated; however, the flood-peak discharges for an ungaged site directly below a large reservoir could be considered regulated regardless of the usable storage criterion (Benson, 1962). The ranges of the basin and geomorphic characteristics of the 50 study sites used in the regression analysis are listed in table 12. Use of the regional curves and regression equations for basins with characteristics outside of these ranges would be an extrapolation, and the average errors associated with such estimates could be different than those implied by the standard errors of prediction.
Table 5 indicates that the highest percentage of channel material (on riffles) for 45 of the 50 sites is gravel, for three sites it is cobble, for one site sand, and one site silt/clay. Thus, streams in which the highest percentage of channel material is silt/clay, sand, cobble, and boulder are few in the dataset for this study, and caution should be used when applying the equations to streams in which the highest percentage of channel material is not gravel. It should be noted that for four of the five sites in which the highest percentage of channel material (on riffles) is not gravel, there was substantial and consistent improvement in accuracy when the multiple-regression equations were used to estimate bankfull cross-sectional area instead of the simple-regression (drainage-area only) equations. Averages of the absolute values of the errors of the bankfull cross-sectional area estimates for the five sites are 31.0, 29.8, and 21.4 percent, respectively, for the DA-only equations, DA-SL-ELEV equations, and DA-SL-ELEV-BED50 equations. These errors are comparable to the average standard errors of prediction (30.6, 27.4, and 25.4 percent) for those equations, indicating that, for this dataset, prediction errors are not significantly greater for sites in which the highest percentage of channel material (on riffles) is not gravel.
Determination of values of the explanatory variables for application in the regional curves and equations is fairly straightforward, objective, and reproducible; however, although determination of ABF for application in equation 23 is a simple computation, it depends on an accurate assessment of bankfull stage, which is a function of the quality of the bankfull indicators and the skill and experience of the person making the assessment.
Use of the simple-regression equations in table 7 and regional curves in figures 8–11, requires that the bankfull region and drainage area of the stream be determined. Figure 7 can be used to determine whether the stream is in bankfull region A or B. If the stream is near the boundary between regions, a map showing 14-digit hydrologic unit code boundaries may be helpful because the boundary between regions A and B coincides with the 14-digit hydrologic unit code boundaries (Seaber and others, 1987; Stafford, 1999). The drainage area (DA) of the stream may be accurately determined from USGS 7.5-minute topographic quadrangle maps. A geographic information system (GIS) also may be used to determine drainage area provided that the GIS data are of sufficiently high resolution.
The following example demonstrates the procedure for estimating bankfull characteristics for one of the 50 study sites (Salt Creek at Tarlton, Ohio, 03235000).
1. The drainage area (DA) is determined to be 11.5 mi 2 and the stream is in region A (figure 7).
2. From plots in figures 8–11, the bankfull characteristics are estimated to be
| WBFA | = | 42 ft |
| DBFA | = | 2.8 ft |
| ABFA | = | 120 ft2 |
| QBFA | = | 440 ft3/s |
3. From the equations in table 7, the bankfull characteristics are computed to be
| WBFA | = | 18.0 (DA) 0.356 | = | 18.0 (11.5) 0.356 | = | 42.9 ft |
| DBFA | = | 1.52 (DA) 0.265 | = | 1.52 (11.5) 0.265 | = | 2.9 ft |
| ABFA | = | 27.1 (DA) 0.621 | = | 27.1 (11.5) 0.621 | = | 123 ft2 |
| QBFA | = | 93.3 (DA) 0.637 | = | 93.3 (11.5) 0.637 | = | 442 ft3/s |
Use of the plots presented in figures 8–11 results in an estimation of bankfull characteristics based on the equations in table 7; however, calculation of bankfull characteristics by use of the equations in table 7 will likely result in a more precise estimate. Consideration may be given to the use of both methods, as one provides a check on the other. It should be noted that the product of the estimates of WBF and DBF from the DA-only equations for the 50 study are nearly equivalent (average difference is less than 1 percent) to the estimates of ABF from the DA-only equation. Therefore, when applying the DA-only equations to estimate bankfull characteristics, the product of the estimates of WBF and DBF can serve as a check on the estimate of ABF from the ABF equation.
The USGS has periodically published reports for Ohio in which regression equations are presented to estimate flood-peak-frequency characteristics from basin characteristics (Webber and Bartlett, 1977; Koltun and Roberts, 1990; Koltun, 2003). The most recent report (Koltun, 2003) presents simple-regression equations, in which drainage area is the explanatory variable, and multiple-regression equations, in which drainage area, main-channel slope, and the percentage of the basin classified as water or wetland are the explanatory variables. The equations may be used to estimate flood-peak discharges with recurrence intervals of 2, 5, 10, 25, 50, 100, and 500 years and average standard errors of prediction range from about 39 to 49 percent, respectively for the simple-regression equations and about 34 to 41 percent, respectively for the multiple-regression equations. The equations are based on flood-frequency estimates for 305 streamflow-gaging stations in Ohio and neighboring states having a mean drainage area of about 310 mi 2 and a median drainage area of 65.3 mi2.
As an independent alternative method to estimate flood-frequency characteristics, regression equations have been published to estimate flood-frequency characteristics from channel geomorphic characteristics, in which the explanatory variable is width of the active channel and the average standard errors of estimate range from about 42 to 55 percent (Webber and Roberts, 1981). Those equations are based on flood-frequency estimates for 160 streamflow-gaging stations having a mean drainage area of 373 mi 2 and a median drainage area of 97.2 mi 2.
Statistical and graphical analyses were conducted as part of this study to investigate development of methods to estimate flood-peak discharges from geomorphic characteristics based on the 40 study sites at streamflow-gaging stations having a mean drainage area of 78.8 mi 2 and a median drainage area of 9.7 mi 2.
Log-Pearson Type III flood-frequency estimates were related to geomorphic, basin, and climatic variables by multiple-regression analysis. The frequency analyses were performed as recommended by the Interagency Advisory Committee on Water Data (1982). The multiple-regression procedures used were the same as for those previously discussed for the bankfull characteristics multiple-regression analyses. Basin, geomorphic, and climatic characteristics initially tested included the following (definitions of abbreviations are at the beginning of this report):
| WBF |
— |
Bankfull width, in feet |
| DBF |
— |
Bankfull mean depth, in feet |
| ABF |
— |
Bankfull cross-sectional area, in square feet |
| WAC |
— |
Active-channel width, in feet |
| DAC |
— |
Active-channel mean depth, in feet |
| AAC |
— |
Active-channel cross-sectional area, in square feet |
| DA |
— |
Drainage area, in square miles |
| MCSL |
— |
Main-channel slope, in feet per mile |
| LCSL |
— |
Local-channel slope, in feet per mile |
| ELEV |
— |
Average main-channel elevation index, in feet |
| LG |
— |
Main-channel length, in miles |
| STOR |
— |
Storage area, in percent |
| FOR |
— |
Forested area, in percent |
| DECLAT |
— |
Decimal latitude, in decimal degrees |
| DECLONG |
— |
Decimal longitude, in decimal degrees |
| PREC |
— |
Average annual precipitation, in inches |
| 124,2 |
— |
24-hour 2-year rainfall intensity, in inches |
| BEDXX |
— |
Bed-material particle size of which XX percent is finer, in millimeters, where XX equals 16, 35, 50, 84, and 95 percent |
| BNKXX |
— |
Bank-material particle size of which XX percent is finer, in millimeters, where XX equals 50, 84, and 95 percent |
The analyses resulted in the six simple-regression equations presented in table 13 in which ABF is the only explanatory variable. Values of the log-Pearson Type III flood-frequency estimates (of which most were previously reported by Koltun, 2003) and bankfull cross-sectional area used in the regression analysis for the 40 gaged study sites are presented in table 14. In the analyses, ABF consistently (for all six recurrence intervals) resulted in the lowest average standard errors of prediction and highest coefficients of determination. As was noted for bankfull discharge, bankfull cross-sectional area alone explains more of the variance in flood-peak discharges than does drainage area or any combination of drainage area and other explanatory variables. Interestingly, this was true for all recurrence intervals. One might expect bankfull cross-sectional area to explain much less of the variance in flood-peak discharges for high-recurrence-interval floods, owing to a smaller proportion of the total discharge flowing in the main channel and a larger proportion flowing over the flood plain; however, this is not the case. This finding may lend support to the concept that there is no single "channel-forming" discharge but rather that a wide range of discharges that, combined, form the main channel. Residuals from the equations were plotted as a function of entrenchment ratio and main-channel slope to see whether results for streams having wider flood plains and (or) lower gradients might have larger errors. The plots indicated that the signs and magnitudes of the residuals varied randomly throughout the ranges of entrenchment ratio and main-channel slope with no tendency for streams having wider flood plains and (or) lower gradients to have larger errors. As indicated in table 13, the coefficients of determination are appreciably lower for the higher recurrence-interval flood-peak discharges than for the lower recurrence intervals, but they remain higher than the respective coefficients of determination for simple-regression equations in which drainage area is the explanatory variable (not reported).
[ Qt, flood-peak discharge with a t-year recurrence interval, in cubic feet per second; ABF, bankfull cross-sectional area, in square feet]
| Equation number | Equation | Average standard error of prediction (percent) | Coefficient of determination (adjusted r-square) | ||||
|---|---|---|---|---|---|---|---|
| 24 | Q2 | = | 3.58 | ABF | 1.072 | 31.6 | 0.960 |
| 25 | Q5 | = | 7.80 | ABF | 1.011 | 32.6 | 0.953 |
| 26 | Q10 | = | 11.8 | ABF | 0.978 | 35.9 | 0.940 |
| 27 | Q25 | = | 18.6 | ABF | 0.943 | 41.5 | 0.918 |
| 28 | Q50 | = | 25.0 | ABF | 0.919 | 46.2 | 0.898 |
| 29 | Q100 | = | 32.6 | ABF | 0.898 | 51.2 | 0.875 |
| [ Qt, flood-peak discharge with a t-year recurrence interval, in cubic feet per second; ABF, bankfull cross-sectional area, in square feet] |
|||||||
| Station number | Q2 | Q5 | Q10 | Q25 | Q50 | Q100 | ABF |
|---|---|---|---|---|---|---|---|
| 03087000 | 1,080 | 1,580 | 1,910 | 2,310 | 2,600 | 2,890 | 148.3 |
| 03089500 | 972 | 1,360 | 1,620 | 1,940 | 2,180 | 2,420 | 118.2 |
| 03092090 | 922 | 1,310 | 1,590 | 1,960 | 2,250 | 2,550 | 194.0 |
| 03092099a | 534 | 966 | 1,340 | 1,940 | 2,490 | 3,120 | 106.0 |
| 03093000 | 2,680 | 3,780 | 4,500 | 5,400 | 6,050 | 6,700 | 475.4 |
| 03110000 | 3,020 | 4,390 | 5,420 | 6,840 | 8,000 | 9,240 | 605.3 |
| 03114240 | 65 | 133 | 192 | 284 | 365 | 456 | 40.4 |
| 03115280 | 629 | 979 | 1,260 | 1,670 | 2,030 | 2,420 | 111.1 |
| 03139980 | 414 | 810 | 1,140 | 1,620 | 2,020 | 2,470 | 77.5 |
| 03139990 | 701 | 1,420 | 2,080 | 3,180 | 4,210 | 5,440 | 113.1 |
| 03144800 | 108 | 191 | 259 | 359 | 444 | 538 | 18.9 |
| 03146500 | 11,800 | 17,800 | 22,100 | 27,700 | 32,100 | 36,700 | 1,855.0 |
| 03149500 | 3,180 | 4,130 | 4,720 | 5,430 | 5,940 | 6,440 | 629.5 |
| 03157000 | 2,630 | 4,100 | 5,310 | 7,160 | 8,790 | 10,700 | 499.1 |
| 03158100 | 83 | 149 | 207 | 298 | 381 | 477 | 26.0 |
| 03159450 | 120 | 197 | 256 | 340 | 409 | 483 | 28.5 |
| 03159540 | 3,540 | 5,080 | 6,290 | 8,050 | 9,550 | 11,200 | 650.2 |
| 03201700 | 118 | 308 | 528 | 970 | 1,460 | 2,130 | 24.2 |
| 03201800a | 336 | 576 | 755 | 990 | 1,170 | 1,360 | 86.1 |
| 03205995 | 100 | 143 | 175 | 219 | 254 | 291 | 20.4 |
| 03235000 | 996 | 1,600 | 2,070 | 2,770 | 3,350 | 4,000 | 160.9 |
| 03235080 | 348 | 660 | 928 | 1,340 | 1,700 | 2,120 | 60.7 |
| 03235500 | 109 | 213 | 307 | 462 | 607 | 780 | 48.1 |
| 03237500 | 20,700 | 30,600 | 38,100 | 48,600 | 57,200 | 66,500 | 2,527.4 |
| 03238600a | 480 | 690 | 829 | 1,000 | 1,130 | 1,260 | 80.4 |
| 03240500 | 701 | 1,500 | 2,240 | 3,460 | 4,600 | 5,940 | 136.7 |
| 03242100 | 258 | 448 | 596 | 806 | 980 | 1,170 | 37.5 |
| 03260700 | 672 | 951 | 1,140 | 1,380 | 1,560 | 1,750 | 164.7 |
| 03264000 | 3,070 | 4,790 | 6,060 | 7,820 | 9,240 | 10,800 | 641.4 |
| 03266500 | 409 | 725 | 989 | 1,390 | 1,730 | 2,120 | 84.6 |
| 03268500 | 1,850 | 2,870 | 3,590 | 4,540 | 5,280 | 6,030 | 209.8 |
| 03274100 | 61 | 111 | 149 | 202 | 244 | 287 | 12.1 |
| 04185000 | 3,480 | 4,930 | 5,820 | 6,860 | 7,580 | 8,260 | 981.9 |
| 04185440 | 425 | 675 | 868 | 1,140 | 1,370 | 1,610 | 84.9 |
| 04196000 | 2,600 | 3,920 | 4,890 | 6,230 | 7,310 | 8,460 | 424.6 |
| 04199155 | 926 | 1,230 | 1,430 | 1,690 | 1,880 | 2,080 | 205.3 |
| 04199800 | 71 | 97 | 115 | 138 | 156 | 175 | 15.6 |
| 04206212a | 412 | 738 | 1,010 | 1,440 | 1,810 | 2,240 | 70.0 |
| 04206220a | 1,130 | 1,590 | 1,940 | 2,400 | 2,770 | 3,170 | 223.8 |
| 04212100 | 12,700 | 15,700 | 17,300 | 19,100 | 20,200 | 21,300 | 1,916.4 |
| Maximum | 20,700 | 30,600 | 38,100 | 48,600 | 57,200 | 66,500 | 2,527.4 |
| Minimum | 61 | 97 | 115 | 138 | 156 | 175 | 12.1 |
| Mean | 2,111 | 3,086 | 3,801 | 4,786 | 5,585 | 6,452 | 347.8 |
| Median | 687 | 1,104 | 1,386 | 1,815 | 2,105 | 2,445 | 115.7 |
| a Flood-frequency estimate not published in Koltun (2003) |
|||||||
[Qt, flood-peak discharge with a t-year recurrence interval, in cubic feet per second; ABF, bankfull cross-sectional area, in square feet; DA, drainage area, in square miles; WAC, active-channel width, in feet]
| This study | Koltun (2003) | Webber and Roberts (1981) | |
|---|---|---|---|
| Number of study sites | 40 | 305 | 160 |
| Median drainage area | 9.7 | 65.3 | 97.2 |
| Mean drainage area | 78.8 | 310 | 373 |
| Explanatory variable | ABF | DA | WAC |
| Average standard error of prediction | Average standard error of prediction | Average standard error of estimate | |
| Q2 | 31.6 | 39.6 | 42 |
| Q5 | 32.6 | 39.0 | 43 |
| Q10 | 35.9 | 39.5 | 45 |
| Q25 | 41.5 | 41.1 | 49 |
| Q50 | 46.2 | 42.7 | 52 |
| Q100 | 51.2 | 44.4 | 55 |
Active-channel width (WAC), which is the explanatory variable in the equations presented by Webber and Roberts (1981), was also tested in this study and found to be statistically significant; however, the average standard errors of prediction were considerably higher for WAC (59.7, 56.1, 56.4, 58.6, 61.3, and 64.5, respectively for the 2-, 5-, 10-, 25-, 50-, and 100-year recurrence intervals) and the coefficients of determination were considerably lower (0.871, 0.871, 0.863, 0.846, 0.823, and 0.811, respectively for the 2-, 5-, 10-, 25-, 50-, and 100-year recurrence intervals) than for ABF.
As was discussed earlier in this section, the study sites used in this analysis have much smaller drainage areas than those used in the previous studies by Koltun (2003) and Webber and Roberts (1981). The number of study sites used to develop the flood-peak discharge equations presented in table 13 is also much smaller than the number of sites used in the previous studies. These factors—along with the differences in explanatory variables, prediction errors, and coefficients of determination—should be considered when choosing which equations to apply for estimating flood-peak discharges for an ungaged site. Some of this information is presented in table 15 for comparison purposes. For a given equation, the average standard error of prediction will generally be slightly higher than the average standard error of estimate, and therefore the two measures of prediction error are not directly comparable. As indicated in table 15, it appears that the equations developed as part of this study may be especially useful for estimation of relatively low recurrence interval flood-peak discharges (Q2, Q5, and Q10) of streams having relatively small drainage areas. Once again, application and comparison of different and independent methods may be advisable.
The six multiple-regression equations presented in table 13 for estimating peak streamflows of streams in Ohio are applicable to sites on rural streams in Ohio that are free of appreciable flood regulation and whose basin characteristics are within the ranges of the basin characteristics of the 40 study sites used in the regression analysis. In general, basins having usable storage of less than 103 acre-ft/mi 2 are considered to be unregulated; however, the flood-peak discharges for an ungaged site directly below a large reservoir could be considered regulated regardless of the usable storage criterion (Benson, 1962). The minimum and maximum values for bankfull cross-sectional area (ABF) for sites in this study are 12 and 2,527 ft 2 , respectively. Use of the peak-streamflow regression equations for basins having values of ABF outside of this range would be an extrapolation, and the average errors associated with such estimates could be different than those implied by the standard errors of prediction.
Selected geomorphic, basin-characteristic, and peak-streamflow data that are presented in tables 1-6, 10, and 14 for the 50 streams are also contained in a geographic information system (GIS) data set that is available on the World Wide Web (Sherwood, 2005). The data set is in Arc/Info export and shapefile formats. Metadata, which is included in the data sets, must be read and fully comprehended by the user prior to data set use.
The addition of more sites to the computer data set and GIS data set would facilitate the improvement and refinement of methods to estimate bankfull characteristics of Ohio streams. Data collected as part of past and future studies could be added to the database provided that the methods of data collection are consistent with those used in this study.
In this study, a region in southern Ohio (region B) was found to have statistically different bankfull characteristics than region A. These findings are based on data collected at the 50 study sites, of which only 5 (3 gaged and 2 ungaged) are in region B. The collection of additional geomorphic data at sites in and near region B could be used to confirm or revise the regression equations developed for and the boundary delineated in this study for region B.
In cooperation with the Ohio Department of Transportation and the U.S. Department of Transportation, Federal Highway Administration, the USGS developed a database of geomorphic data for a sampling of unregulated natural alluvial streams in Ohio. The database, in turn, was used to develop methods to estimate bankfull characteristics of Ohio streams and to relate geomorphic characteristics of Ohio streams to peak streamflows of selected recurrence intervals. The database and methods developed are intended to improve understanding of the relations between geomorphic, basin, and flood characteristics of streams in Ohio and to aid in the design of hydraulic structures, such as culverts and bridges, where stability of the stream and structure is an important element of the design criteria.
The database developed for this study consists of geomorphic, basin, and flood-frequency characteristics for 50 study sites in Ohio, of which 40 sites are near streamflow-gaging stations. Field surveys were done at each site to collect the geomorphic data. Bankfull indicators were identified and evaluated, cross-section and longitudinal profiles were surveyed, and bed- and bank-material were sampled. Field data were analyzed to determine various geomorphic characteristics such as bankfull width, bankfull mean depth, bankfull cross-sectional area, bankfull discharge, streambed slope, and bed- and bank-material particle-size distribution.
The various geomorphic characteristics were analyzed by means of a combination of graphical and statistical techniques. These techniques resulted in a set of regional curves, simple-regression (drainage-area only) equations, and multiple-regression equations to estimate bankfull width, bankfull mean depth, bankfull cross-sectional area, and bankfull discharge. Explanatory variables included drainage area, main-channel slope, main-channel elevation index, median bed-material particle size, bankfull cross-sectional area, and local-channel slope. Average standard errors of prediction for bankfull width equations ranged from 20.6 to 24.8 percent; for bankfull mean depth, 18.8 to 20.6 percent; for bankfull cross-sectional area, 25.4 to 30.6 percent; and for bankfull discharge, 27.0 to 78.7 percent. The simple-regression (drainage-area only) equations have the highest average standard errors of prediction. The multiple-regression equations—in which the explanatory variables included drainage area, main-channel slope, main-channel elevation index, median bed-material particle size, bankfull cross-sectional area, and local-channel slope—have the lowest average standard errors of prediction.
Statistical and graphical analyses were done to investigate development of methods to estimate flood-peak discharges from geomorphic characteristics based on the 40 study sites at streamflow-gaging stations. The logarithms of the annual peak discharges for each site were fit by a Pearson Type III frequency distribution to develop a flood-peak-frequency relation for each site. The peak-frequency data were related to geomorphic, basin, and climatic variables of the 40 study sites by multiple-regression analysis. The analyses resulted in a set of multiple-regression equations to estimate flood-peak discharges with recurrence intervals of 2, 5, 10, 25, 50, and 100 years from bankfull cross-sectional area, in which the average standard errors of prediction are 31.6, 32.6, 35.9, 41.5, 46.2, and 51.2 percent, respectively.
The authors acknowledge the Ohio Department of Transportation, the U.S. Department of Transportation, and the Federal Highway Administration for their support and cooperation throughout the project.
Special recognition and appreciation are also extended to Timothy Diehl, a USGS research hydrologist, and Daniel Mecklenburg, an Ohio Department of Natural Resources ecological engineer, who assisted with the identification of bankfull indicators at selected sites and provided technical support throughout the project; and to Gregory Koltun, a USGS hydrologist, for his assistance with the statistical analyses.
American Geological Institute, 1982, Grain-size scales used by American geologists, modified Wentworth scale, in Data sheets (2d ed.): Falls Church, Va., American Geological Institute, sheet 17.1.
American Society of Testing Materials, 1998, Standard Methods for Particle-Size Analysis of Soils, in 1998 Annual Book of American Society of Testing Materials Standards, v 4.08, Philadelphia, Penna., p. D422-63.
Andrews, E.D., 1980, Effective and bankfull discharges of streams in the Yampa River Basin, Colorado and Wyoming: Journal of Hydrology, v. 46, p. 311-330.
Annable, W.K., 1995, Morphological relations of rural water courses in southeastern Ontario for use in natural channel design: Guelph, Ontario, Canada, University of Guelph, School of Engineering, Masters thesis, 389 p.
Benson, M.A., 1962, Factors influencing the occurrence of floods in a humid region of diverse terrain: U.S. Geological Survey Water-Supply Paper 1580-B, 64 p.
Borghese, W.D., ca. 1957, The frequency of bankful stage and flow of Ohio streams: U.S. Geological Survey unpublished report, 9 p.
Brockman, S.C., 1998, Physiographic regions of Ohio: Ohio Department of Natural Resources, Division of Geological Survey, map and descriptions, 2 p.
Center for Watershed Protection, Aquafor Beech, Ltd., Barg, L., and Kort, R., 1999, Watershed hydrology protection and flood mitigation project, Phase II—Technical Analysis: Stream Geomorphic Assessment, 10 p.
Chang, T.J., Fang, Y.Y., Wu, H., and Mecklenburg, D.E., 2004, Bankfull channel dimensions in southeast Ohio, in Proceedings of the Self-Sustaining Solutions for Streams, Wetlands, and Watersheds Conference, American Society of Agricultural Engineers, September 2004: 9 p.
Cowan, W.L., 1956, Estimating hydraulic roughness coefficients: Agricultural Engineering, v. 37, p. 437-475.
Dunne, Thomas, and Leopold, L.B., 1978, Water in environmental planning: New York, W.H. Freeman and Company, 818 p.
Emmett, W.W., 2004, A historical perspective on regional channel geometry curves: Fort Collins, Colo., Stream Systems Technology Center, U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station, Stream Notes January 2004, 2 p.
Emmett, W.W. and Hadley, R., 1968, The Vigil Network—Preservation and access of data: U.S. Geological Survey Circular 460-C, 21 p.
Emmett, W.W., and Wolman, M.G., 2001, Effective discharge and gravel-bed rivers: Earth Surface Processes and Landforms, v. 26, p. 1369-1380.
Fitzpatrick, F.A., Waite, I.R., D'Arconte, P.J., Meador, M.R., Maupin, M.A., and Gurtz, M.E., 1998, Revised methods for characterizing stream habitat in the National Water-Quality Assessment Program: U.S. Geological Survey Water-Resources Investigations Report 98-4052, 67 p.
Gilroy, E.J., and Tasker, G.D., l990, Multicollinearity and influential observations in hydrologic model selection, in Berk, K., and Malone, L. (ed.), Computing Science and Statistics—Proceedings of the 2lst Symposium on the Interface: p. 350-354.
Grant, G.E., Swanson, F.J., Wolman, M.G., 1990, Pattern and origin of stepped-bed morphology in high-gradient streams, Western Cascades, Oregon: Geological Society of America Bulletin, v. 102, p. 340–352.
Harrelson, C.C., Rawlins, C.L., and Potyondy, J.P., 1994, Stream channel reference sites—An illustrated guide to field technique: U.S. Department of Agriculture Forest Service General Technical Report RM-245, 61 p.
Harstine, L.J., 1991, Hydrologic atlas for Ohio—Average annual precipitation, temperature, streamflow, and water loss for 50-year period, 1931-1980: Ohio Department of Natural Resources, Division of Water, Water Inventory Report 28, 13 p., 4 pl.
Hershfield, D.M., 1961, Rainfall frequency atlas of the United States: U.S. Weather Bureau Technical Paper 40, 115 p.
Horton, R.E., 1945, Erosional development of streams and their drainage basins—Hydrophysical approach to quantitative morphology: Geological Society of America Bulletin, v. 56, p. 275-370.
Interagency Advisory Committee on Water Data, 1982, Guidelines for determining flood flow frequency: Bulletin 17B of the Hydrology Subcommittee, 183 p.
Jennings, M.E., Thomas, Jr., W.O., Riggs, H.C., 1994, Nationwide summary of U.S. Geological Survey regional regression equations for estimating magnitude and frequency of floods for ungaged sites, 1993: U.S. Geological Survey Water-Resources Investigations Report 94-4002, 196 p.
Johnson, P.A., Gleason, G.L. and Hey, R.D. 1999, Rapid assessment of channel stability in vicinity of road crossings: Journal of Hydraulic Engineering, v. 125, no. 6, p. 645-651.
Juracek, K.E., and Fitzpatrick F.A., 2003, Limitations and implications of stream classification: Journal of the American Water Resources Association, v. 39, p. 659-670.
Kilpatrick, F.A., and Barnes, H.H., Jr., 1964, Channel geometry of Piedmont streams as related to frequency of floods: U.S. Geological Survey Professional Paper 422-E, 10 p.
Koltun, G.F., 2003, Techniques for estimating flood-peak discharges of rural, unregulated streams in Ohio, (2d ed.): U.S. Geological Survey Water-Resources Investigations Report 03-4164, 75 p.
Koltun, G.F., and Roberts, J.W., 1990, Techniques for estimating flood-peak discharges of rural, unregulated streams in Ohio: U.S. Geological Survey Water-Resources Investigations Report 89-4126, 68 p.
Knighton, D., 1998, Fluvial forms and processes, a new perspective: London, Arnold Publishers, 383 p.
Leopold, L.B., and Maddock, T., Jr., 1953, The hydraulic geometry of stream channels and some physiographic implications: U.S. Geological Survey Professional Paper 252, 57 p.
Leopold, L.B., Wolman, W.G., and Miller, J.P., 1964, Fluvial processes in geomorphology: San Francisco, W.H. Freeman, 522 p.
Lisle, T. E., 1987, Overview—Channel morphology and sediment transport in steepland streams, in Beschta, R. L.; Blinn, T.; Grant, G. E.; [and others], eds. Erosion and sedimentation in the Pacific Rim: Oslo, Norway, International Association of Hydrological Sciences, IAHS Pub. 165, p. 287–297
Mecklenburg, D.E., 2003, Reference reach spreadsheet v2-2L (MS-Excel): Ohio Department of Natural Resources, accessed December 10, 2004, at http://www.dnr.state.oh.us/soilandwater/streammorphology.htm
Montgomery, D.C., and Peck, E.A., 1982, Introduction to linear regression analysis: New York, Wiley, 504 p.
Montgomery, D.R., and Buffington, J.M. 1997, Channel-reach morphology in mountain drainage basins: Geological Society of American Bulletin, v. 109, p. 596-611.
Moody, T. and Odem, W., 1999, Regional relationships of bankfull stage in central and southern Arizona, in Olsen, D.S. and Potyondy, J.P., editors, Wildland Hydrology, American Water Resources Association Specialty Conference Proceedings, June 20-July 2, 1999: Bozeman, Mont., TPS-99-3, 536 p.
Natural Resources Conservation Service, 2005, Regional Hydraulic Geometry Curves Glossary, accessed March 8, 2005, at http://wmc.ar.nrcs.usda.gov/technical/HHSWR/Geomorphic/glossary.html
Rantz, S.E., and others, 1982, Measurement and computation of streamflow—Volume 1, Measurement of stage and discharge, and volume 2, Computation of discharge: U. S. Geological Survey Water Supply Paper 2175, 631 p.
Richards, K.S., 1982, Rivers—Form and process in alluvial channels: New York, Methuen and Company, 357 p.
Rosgen, Dave, 1996, Applied river morphology: Pagosa Springs, Colo., Wildland Hydrology, (variously paginated)
Roth, D.K., 1985, Estimation of flood peaks from channel characteristics in Ohio: U.S. Geological Survey Water-Resources Investigations Report 85-4175, 63 p.
Seaber, P.R., Kapinos, F.P., and Knapp, G.L., 1987, Hydrologic unit maps: U.S. Geological Survey Water-Supply Paper 2294, 63 p.
Sherwood, J.M., 2005, Geomorphic, basin-characteristic, and peak-streamflow data for 50 streams in Ohio: U.S. Geological Survey data available on the World Wide Web at http://water.usgs.gov/lookup/getspatial?sir2005-5153_ohio_bankfull_data
Simon, A., 1989, A model of channel response in disturbed alluvial channels: Earth Surface Processes Landforms, v. 14, no. 1, p. 11–26.
Smith, D., and Turrini-Smith, L., 1999, Western Tennessee fluvial geomorphic regional curves: Report to U. S. Environmental Protection Agency, Region IV, Water Management Division, (variously paginated)
Stafford, J.N., 1999, 14-digit hydrologic unit areas for Ohio: Natural Resources Conservation Service data, accessed March 16, 2005, at http://www.oh.nrcs.usda.gov/technical/14-digit/
Thomas, D.M., and Benson, M.A., 1970, Generalization of streamflow characteristics from basin characteristics: U.S. Geological Survey Water-Supply Paper 1975, 55 p.
U.S. Department of Agriculture, 2003, Identifying bankfull stage in forested streams in the eastern United States: Stream Systems Technology Center, Rocky Mountain Research Station, Forest Service videotape, approx. 46 minutes.
U.S. Department of Agriculture, Soil Conservation Service, 1982, Procedures for collecting soil samples and methods of analysis for soil survey: Washington, D.C., Soil Survey Investigations Report 1, Soil Conservation Service, U.S. Department of Agriculture, 68 p.
Ward, A.D., Mecklenburg, D.E., Powell, G.E., Brown, L.C., and Jayakaran, A.C., 2004, Two-stage channel design procedures, in Proceedings of the Self-Sustaining Solutions for Streams, Wetlands, and Watersheds Conference, American Society of Agricultural Engineers, September 2004: 9 p.
Webber, E.E., and Bartlett, W.P., Jr., 1977, Floods in Ohio—magnitude and frequency: Ohio Department of Natural Resources Division of Water Bulletin 45, 74 p.
Webber, E.E. and Roberts, J.W., 1981, Flood flow characteristics related to channel geometry in Ohio: U.S. Geological Survey Open-File Report 81-1105, 28 p.
Williams, G.P., 1978, Bank-full discharge of rivers: Water Resources Research, v. 14, no. 6, p. 1141-1154.
Wolman, M.G., 1954, A method of sampling coarse river-bed material: Transactions of the American Geophysical Union, v. 35, p. 951-956.
Wolman, M.G., and Leopold, L.B., 1957, River flood plains—Some observations on their formation: U.S. Geological Survey Professional Paper 282-C, 107 p.
Wolman, M.G., and Miller, J.P., 1960, Magnitude and frequency of forces in geomorphic processes: Journal of Geology, v. 68, p. 54-74.
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|