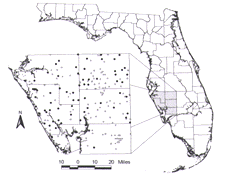
Figure 1. Location map showing borehole control points used for the Southwest Florida subsurface mapping project (black circles). Control data for mapping the top of the Suwannee Limestone are also shown (gray circles). |
Florida Geological Survey
903 W. Tennessee St.
Tallahassee, FL 32304
Telephone: (850) 488-9380
Fax: (850) 488-8086
e-mail: arthur_j@dep.state.fl.us
In March 1997, the Florida Geological Survey (FGS) began a regional subsurface geologic mapping project to identify the thickness and extent of several lithostratigraphic and hydrostratigraphic units in a five-county region of southwest Florida. More than 275 irregularly spaced control points for the maps include data from cores, cuttings, or geophysical logs (Figure 1). In addition to generation of structure contour and isopach maps, project goals include geographic information system (GIS) compatibility and 3-D visualization of the multiple subsurface horizons to be mapped. Application of the maps will include protection, regulation, and assessment of ground water and solid earth resources, rules enforcement, and frameworks for ground-water flow and aquifer vulnerability models.
The suite of Environmental Systems Research Institute (ESRI) software products, including Arc/Info and ArcView, are the standard for the Florida Department of Environmental Protection, the parent agency of the FGS. Recent additions and modifications to ArcView have made it more capable of surfacing, contouring, and 3-D functions that were once available only from within the Arc/Info environment. In ArcView GIS (version 3.0a), add-on software, called extensions, can be attached to an ArcView project. The Spatial Analyst extension provides the ability to generate grids and contours with a variety of data-interpolation methods. Three-dimensional visualization and generation of triangulated irregular networks are available through the 3-D Analyst extension. Functionality, compatibility, cost-effectiveness, relative ease of use, and user support are primary reasons for selection of ArcView GIS and these related extensions as the preferred application software for this mapping project.
This paper provides an introduction to surface modeling options available in ArcView GIS and related extensions in the context of contour map generation for the Southwest Florida Subsurface Mapping Project. The primary focus of this paper is to evaluate data interpolation methods readily available from ArcView GIS, with the Spatial Analyst and the 3-D Analyst extensions loaded. Effects of interpolation methods and related user-definable parameters (grid cell size, weights) on map accuracy and realistic surface representation are discussed.
Since the publication of last year's (1997) Digital Mapping Techniques Workshop Proceedings, our mapping database has only recently evolved to the point where an evaluation of contours from surface modeling methods is feasible. Although the database is not in final form, visualization of the effect of anomalous (or problematic) control points is useful toward evaluating various surface modeling scenarios. The structure contour maps presented herein are for illustrative purposes and are not to be considered finalized maps.
The top of the Oligocene Suwannee Limestone is considered representative and suitable to illustrate and evaluate differences in contours derived from various surface model interpolations. This unit is one of the 11 stratigraphic horizons to be eventually mapped. Elevations (relative to mean sea level) of the top of the unit compose the data set. Control points (i.e., data from wells) are, on average, 7 miles apart and the study area covers approximately 2,800 square miles. The Suwannee Limestone gently dips approximately 0.1 degree to the southwest. The surface of this unit is likely punctuated by karst features and is offset by faults within the southwest part of the study area. Although the maps being generated will include delineated faults, well data are not of sufficient density to accurately map karst features within the Suwannee Limestone surface.
The Southwest Florida Subsurface Mapping Project is a five-year project cooperative agreement between the FGS and the Southwest Florida Water Management District (SWFWMD). Work began in 1995 with the development of an extensive database containing more than 4,800 wells in the southwest Florida region. Funding for this part of the project totaled $15,000. The database contains all available information on the wells pertaining to location, construction, use, and types of geophysical and lithologic data. Once completed, this database was used as a screen to select wells that would be appropriate control points for the subsurface mapping project. The mapping phase is presently funded at $80,000 per year and will continue through 2001. During each of the first three years, one-third of the approximately 10,000 square mile study area will be mapped. The fourth year will be used to add recently acquired well data throughout the region, resolve boundary issues, finalize structural interpretation, and review and publish the maps.
Products to be generated include structure contour and isopach maps for Eocene and younger lithostratigraphic units and all regionally extensive aquifer systems. Further details about the project, including database design, data accuracy issues, units to be mapped, and a related cross section project can be found in Arthur (1997). Of the more than 275 control points in the first mapping phase of the project, 74 are deep enough to penetrate the target stratigraphic unit discussed in this paper (Figure 1). The amount of well control increases for maps of shallower stratigraphic units in the regional mapping study.

Figure 1. Location map showing borehole control points used for the Southwest Florida subsurface mapping project (black circles). Control data for mapping the top of the Suwannee Limestone are also shown (gray circles). |
The GIS hardware resources at the FGS include two Pentium II 266 MHz computers, a Sun Microsystems Ultra2 workstation, two HDS x-terminals and an HP Designjet 750C plotter. The PCs are running Microsoft Windows 95, with 64Mb of RAM, 4Mb VRAM, and 3.5Gb hard drives. The Sun workstation is running Sun OS (release 5.5.1) with Solaris 2.5.1, two 167 MHz processors, 128 Mb RAM, and four 2.1Gb hard drives. All computers are on uninterruptible power supply/surge protection units. Images and analysis for this paper, however, were made using only one of the above-mentioned PCs and the plotter.
The triangulated irregular network (tin) is a surface representation based on randomly or irregularly spaced data points that have x, y, and z coordinates. A typical example of this coordinate system is longitude (x), latitude (y), and an elevation or concentration (z). Non-overlapping, connecting triangles are drawn between all data points where the data points (or control points) are the vertices. In its basic form, tin elevations are calculated based on linear regression between control points; contours are then drawn across the sides of the connected, tilting triangular plates. More advanced algorithms are discussed in Davis (1986) and Houlding (1994).
The tin surface model is available through the 3-D Analyst extension of ArcView GIS. There are very few parameters to set in this extension in order to generate and contour a tin. For the beginner, this is an asset; however, the more advanced user may require more menu-driven control over default values. Through Avenue script, which is a macro language for ArcView, more advanced parameter modification is possible.
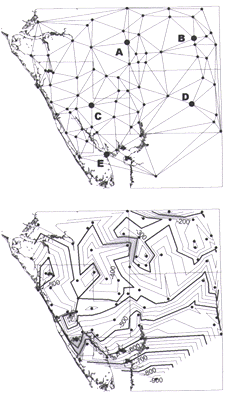
Figure 2A shows a tin surface model representing the top of the Suwannee Limestone using the control points shown in Figure 1. The 3-D Analyst was used to create the model (Figure 2A), which is contoured at 25-foot intervals (Figure 2B). The wide distribution of control-point data yields a coarse, angular surface representation that is not desirable for structure contour and isopach maps; the angular contours do not accurately reflect the natural geologic environment. Two advantages with tin, however, are that it does not interpolate beyond the distribution of the data, and the map is forced to fit the control points. Tin is well suited for the purpose of generating a more highly resolved structure on which to drape or hang feature layers. One example would be to drape a surface geology coverage on a land surface elevation tin model.
|
Figure 2A. Triangulated irregular network model based on control points in Figure 1. See Table
1 for reference to points labeled A through E.
Figure 2B. Contours at 25-foot intervals for the tin model shown in Figure 2A. |
A grid is comprised of a continuous array of discrete, uniform, square cells that are georeferenced (i.e., known location on the Earth's surface) and contain values that characterize the site. The values for each grid cell, for example, can include elevation, land use, geologic formations, population, or remotely sensed data. Grid cell values are calculated from a mathematical function relating the nearby control points. Usually this function is a form of a spatial average, where the closer control points are weighted more heavily than the more distant ones. Variants of this function include fitting a plane or curved surface to the control data in order to estimate grid cell values by means of regression or projection. Contours are then generated based on the regularly spaced grid cell values.
One disadvantage with grid-based contours is that control point data may not exactly fit the contours, because the contours are based on the calculated cell values that are one step removed from the control data. In contrast, contours from a tin surface model are based on the irregularly spaced control data. The advantage of grid interpolations is that complex surface model algorithms are better suited for a continuous array of evenly spaced data rather than an irregular spatial distribution.
Two grid interpolation functions, spline and inverse distance weighted (IDW), are available in pull down menus within the 3-D Analyst and the Spatial Analyst. The Spatial Analyst provides much more user control and spatial analysis tools than the 3-D Analyst. Additional interpolators available through both of these ArcView GIS extensions include kriging and trend. Note, however, that these two techniques are presently available only through Avenue scripts. For purposes herein, only the "menu-driven" options, spline and IDW, are discussed. As the mapping project database becomes more finalized and we become more proficient in writing Avenue scripts, we plan to evaluate kriging and trend interpolation methods for structure contour and isopach mapping within the ArcView GIS environment.
The inset below, slightly modified from the ArcView GIS Help screen (ESRI, 1990-1996), describes IDW and spline functions and variables:
IDW - This interpolator assumes that each input [or control] point has a local influence that diminishes with distance. It weights the points closer to the processing cell greater than those farther away. A specified number of points [i.e., nearest neighbor], or optionally all points within a specified radius [i.e., fixed radius], can be used to determine the output value for each location. ... The power parameter in the IDW interpolation controls the significance of the surrounding points upon the interpolated value. A higher power results in less influence from distant points.
The Spline interpolator is a general purpose interpolation method that fits a minimum-curvature surface to the control points. Conceptually, it is like bending a sheet of rubber to pass through the points, while minimizing the total curvature of the surface. It fits a mathematical function to a specified number of nearest input points, while passing through the sample points. This method is best for gently varying surfaces such as elevation, water table heights, or pollution concentrations. It is not appropriate if there are large changes in the surface within a short horizontal distance, because it can overshoot estimated values. The Regularized method yields a smooth surface. The Tension method adjusts the stiffness of the surface according to the character of the modeled phenomenon. When you choose Regularized, the weight parameter defines the weight of the third derivatives of the surface in the curvature minimization expression. If you choose Tension, the weight parameter defines the weight of tension. The number of points parameter identifies the number of points per region used for local approximation.
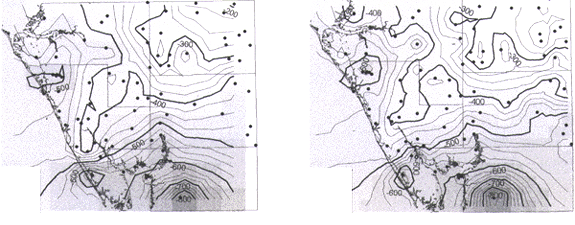
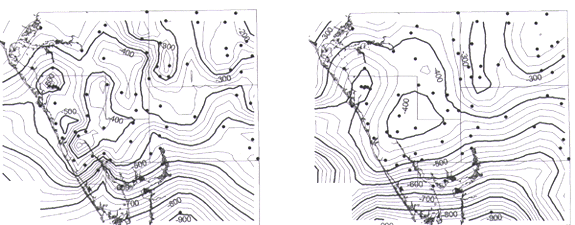
To illustrate the effect of different grid cell sizes on a surface model, the IDW - nearest neighbor method is used. Three cell sizes are selected: a cell size equal to the average spread of control data (7 miles; Figure 3), half of that distance (3.5 miles; Figure 4), and one order of magnitude less than the average spacing (0.7 mile; Figure 5). The gray-shaded blocks provide an indication of grid cell size on which the model is based. Comparison of Figures 3, 4 and 5 reveals that a reduction in cell size causes an increase in surface irregularity whereby the surface is heavily controlled by anomalous data points (see especially Figure 5). Grid surface-model accuracy is qualitatively checked by comparing control point data to grid cell values at the same location (Table 1). Based on the cell size comparison using IDW - nearest neighbor, the model more accurately reflects control point data with decreasing cell size (Table 1).
For purposes of discussion and consistency, a cell size of 3.5x3.5 miles is used for subsequent comparative analysis in this paper. This cell size tends to smooth over local perturbations (e.g., possible karst features), while reflecting accurately the semi-regional and regional trends.
|
| Figure 3. Contours (25-foot intervals) generated from IDW - nearest neighbor grid using a cell size of 7x7 miles; power = 2 (default). The pattern of gray shading shows the grid cell size. | Figure 4. Contours (25-foot intervals) generated from IDW - nearest neighbor grid using a cell size of 3.5x3.5 miles; power = 2 (default). The pattern of gray shading shows the grid cell size. |
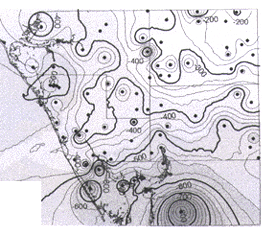
Figure 5. Contours (25-foot intervals) generated from IDW - nearest neighbor grid using a cell size of 0.7x0.7 miles; power = 2 (default). The pattern of gray shading shows the grid cell size. |
Table 1. Comparison of selected control-point values (feet MSL) and interpolated values from surface models contoured in Figures 2B [tin], 3 through 5 [IDW(nn - nearest neighbor)], 6 [IDW(fr - fixed radius)], 7 [Spline (tension)], and 8 [Spline (regularized)].
[Point label (PL) refers to labeled control points shown in Figure 2A; "abs" is absolute difference between actual and model values. PL "A" is an anomalous value included to demonstrate how each model handles abrupt surface changes]
| PL | Actual value | Tin value | IDW (nn) | abs | IDW (nn) | abs | IDW (nn) | abs | IDW (fr) | abs | Spline (tension) | abs | Spline (regularized) | abs |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | -451 | -451 | -353 | 98 | -376 | 75 | -448 | 3 | -375 | 76 | -465 | 14 | -361 | 90 |
| B | -223 | -223 | -247 | 24 | -231 | 8 | -223 | 0 | -229 | 6 | -234 | 11 | -31 | 8 |
| C | -369 | -369 | -426 | 57 | -388 | 19 | -370 | 1 | -388 | 19 | -377 | 8 | -394 | 25 |
| D | -520 | -520 | -432 | 88 | -494 | 26 | -520 | 0 | -509 | 11 | -511 | 9 | -497 | 23 |
| E | -615 | -615 | -585 | 30 | -591 | 24 | -612 | 3 | -597 | 18 | -629 | 14 | -633 | 18 |
| Cell size (miles) | 7.0 | 3.5 | 0.7 | 3.5 | 3.5 | 3.5 |
Figure 6 shows a surface model based on IDW - fixed radius, where the radius is 10.5 miles (i.e., 1.5 times the average control point spread). Figures 4 and 6 allow comparison of nearest neighbor and fixed radius IDW methods using identical cell sizes. The two methods yield similar, "geologically reasonable," and somewhat accurate surfaces; however, preliminary evaluation suggests that the fixed radius method is slightly more accurate (Table 1). Note, however, that the fixed radius method of IDW will not interpolate across the entire map area (Figure 6) because it considers only data within a fixed distance from the grid cell value being calculated, rather than by a fixed number of control points. In other words, depending on the assigned fixed radius value, the method will not calculate a grid (or contour data) across large gaps in data. Both IDW methods yield somewhat pinched, angular contours. Moreover, this interpolation method tends to handle anomalous values as isolated highs and lows. This "bull's-eye" effect, a result of neighboring data influence that diminishes with distance, may be more appropriate for mapping karst features (if one has sufficient data control), or perhaps geophysical- and geochemical-data contouring.
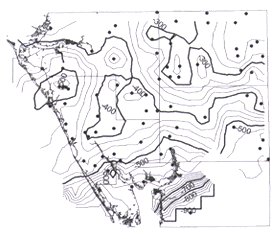
Figure 6. Contours (25-foot intervals) generated from IDW - fixed radius, where radius = 10.5 miles and cell size = 3.5x3.5 miles; power = 2 (default). |
A series of spline surface models using the regularized and tension methods were generated by holding constant the grid cell size and number of points in order to evaluate effects of the weight parameter, which is defined above (see inset). With the regularized interpolator, the weight parameter tends to smooth the model surface when values are increased from the program default value of 0.1. This smoothing effect is observed to a lesser extent when weight values are decreased from the default value as well. Weight values less than 0.1 yield the most geologically reasonable interpretation as well as more accurate results.
As the weight parameter is increased using the tension model, the resulting surface becomes more smooth. In our data set, optimum weight values range from 0.001 to 1.0. In our data set and an ESRI data set, weight values<0.001 yield an unreasonable range of cell values and a very inaccurate, implausible surface.
Figures 7 and 8 show contoured surface models generated from the two spline methods, tension and regularized (respectively). The tension method results in a much more irregular surface than the regularized, however the tension yields a more accurate model when comparing grid cell values to the control points (Table 1). Moreover, the anomalous value (point label "A") is more accurately represented by the tension method. Although the tension method in this example creates overshooting (i.e., closed contours around areas without control point data), this undesirable effect is more pronounced using the regularized method. With the Suwannee Limestone data set, as the weight value is increased to remove the overshooting effect, the spline - regularized method tends to smooth the data beyond acceptable accuracy levels.
|
| Figure 7. Contours (25-foot intervals) generated from spline - tension, using weight = 0.1, number of points = 12. | Figure 8. Contours (25-foot intervals) generated from spline - regularized, using weight = 100, number of points = 12. |
In summary, the contour methods explored in this paper produce results that range from smooth and relatively less accurate to less smooth and more accurate. For purposes of generating a series of structure contour and isopach maps of possibly karstic, faulted stratigraphic units in Florida, selection of a single interpolation method that reflects semi-regional to regional geological trends, yet accurately reflect the control data, becomes problematic. We will continue to explore these methods as our work continues. Based on the present analysis, the spline - tension interpolation method is preferred as it tends to reflect a more accurate, natural geologic surface.
As our database becomes larger and more refined, and we become more proficient at writing Avenue scripts, we will explore the trend and kriging methods as alternative surface models from which contour maps could be generated. Alternatives such as generating contours from tin surfaces that can then be smoothed will be considered as well. The ability to display and interpret multi-layered spatial data in three dimensions will facilitate aspects of the Southwest Florida Subsurface Mapping Project. These aspects include fault interpretation and lateral continuity of permeable zones within aquifer systems. Initial evaluation of the 3-D Analyst extension indicates that the program will be well suited to this task.
Arthur, J.D., 1997, Digital mapping projects at the Florida Geological Survey, in Soller, D.R., ed., Proceedings of a workshop on digital mapping techniques: Methods for geologic map data capture, management and publication: U.S. Geological Survey Open-File Report 97-269, p. 57-59.
Davis, J.C., 1986, Statistics and data analysis in geology: New York, John Wiley and Sons, 646 p.
Environmental Systems Research Institute, Inc., 1990-1996, ArcView GIS On Line Help Documentation (Microsoft Windows Help, version 4.00.950).
Houlding, S.W., 1994, 3-D geoscience modeling -- Computer techniques for geological characterization: Berlin, Springer-Verlag, 309 p.
U.S.Department of the Interior, U.S. Geological Survey
<https://pubs.usgs.gov/openfile/of98-487/arthur.html>
Maintained by Dave Soller
Last updated 10.06.98