USGS Home
Contact USGS
Search USGS

Inferences from Textural Measures of the Aeromagnetic Data

Textural Measures of Potential Field Data

Another objective of this study was to map textural measures (Gettings, 1999) of the aeromagnetic anomaly field that might be related to rock lithologies and thus be of use in elucidating the geologic structure. Common univariate statistical measures do not characterize texture because they describe integrative properties of the function (fig. 3). Several investigators (for example, Pilkington and Todoeschuck, 1993; Gettings and others, 1991) have shown that the distribution of magnetic anomalies and magnetic susceptibility are fractal in nature and thus highly variable. The fractal character comes from the geologic distribution of the sources which is then mirrored in the potential field anomalies. The fractal dimension characterizes a distribution, but measurement of the dimension for potential field data proves to be quite difficult. This is because potential field data are not self-similar but instead are self-affine fractals, and the dimension is not defined uniquely. In fact, these distributions are mutifractal and possess a spectrum of dimensions (Feder, 1988). Gettings (1999) and Gettings and Bultman (1997) have shown that two robust measures of texture are the normalized number of peaks and troughs and the normalized Euclidean length of the data in a window moving over the dataset. The number of peaks and troughs provides a measure of the "roughness" of the data while the Euclidean length measures the amplitude of the data. Thus, for the aeromagnetic data, the Euclidean length is a measure of the intensity of magnetization and the number of peaks and troughs is measure of the number and distribution of sources.

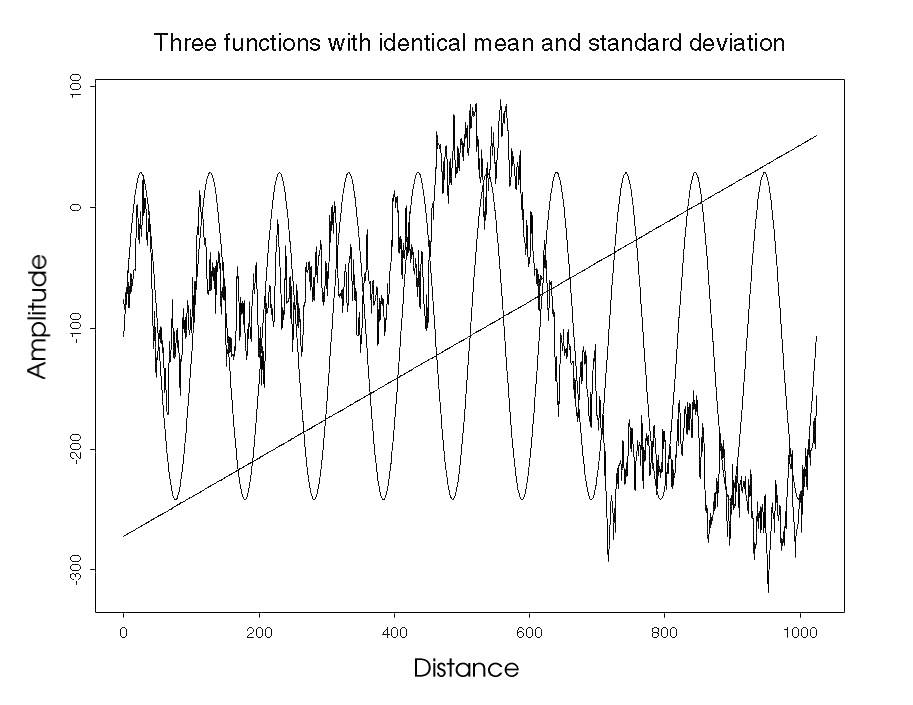Figure 3. Three functions with identical mean and standard deviation: a straight line, a sine function, and fractional Brownian motion (Feder, 1988) with a dimension of 1.70.

All computations are performed on the flight line data, rather than on some filtered derivative product such as a grid, in order to minimize loss of information content from processing. The general strategy is to compute the desired quantities along flight lines and then interpolate the results onto a regular grid for map presentation. In practice, this was accomplished by computing all measures of interest on the data in a single, compute intensive, pass through the data which produced a very large output dataset that was analyzed in multiple ways.

Moving Window Processing

The survey data are organized into concatenated flight lines in a single large file. The processing program processes one flight line at a time by repeatedly passing a moving window over the data and computing the various measures within the window. The sizes of the windows and their movement down the flight line (that is, the amount of overlap of successive windows) can be controlled by the user. For each window width, the window was moved from one end of the line to the other in overlapping increments. Maximum delineation of textural boundaries (resolution) is achieved by moving the window only one data point at a time (maximum overlap); however this becomes very compute intensive and in practice the window is moved some larger fraction of the window width for each calculation, such as 200 m or one half or one quarter of the window width. A version of the software (in FORTRAN language) used to calculate the measures is given in Appendix 2.

Within every window, several statistical, textural and wavelet fit measures are calculated. Output consists of the x and y coordinates of the window center (ordinarily UTM easting and northing), the width of the window in km and in number of data points, and the aeromagnetic field minimum, maximum, mean, and standard deviation. Three textural measures are calculated for the data within the window. These are the number of peaks and troughs, the Euclidean length of the data, and the range of the aeromagnetic data divided by its standard deviation. The Euclidean length is a measure of the amplitude of the data and is the square root of the sum of the squares of the successive differences in distance (Dx) and magnetic anomaly (DT) across the window.

This measure has mixed units of the square root of km squared plus nanoTeslas squared and thus is not a true length. The name "Euclidean length" was given to this measure by Gettings (1999) to avoid confusion with a true length. In order to make measures comparable between different window sizes, the Euclidean length and number of peaks and troughs are normalized by the window width Xw so that they are in units of length per km or peaks and troughs per km. Figure 4 shows an example of the calculation of Euclidean length and number of peaks and troughs for two successive windows.

The ratio of range to standard deviation (often termed R/S, Feder, 1988) is a normalized measure of variability which can be used to estimate the fractal dimension at various scales (window sizes). The Euclidean length divided by the twice the number of peaks and troughs, a measure of mean anomaly amplitude, is also calculated. Finally, a wavelet of a specified shape may also be fit to the data in the window (not done in this study). The window is then moved by the specified increment and calculations repeated. At the end of a line for a given window size, mean and standard deviation of R/S are calculated and the window size changed by the specified amount, and so on. The procedure is repeated for each line. Partial windows at the ends of lines with total number of points not evenly divisible by the window size are calculated as smaller windows of the remaining number of points. This can lead to gaps in the processing in map view if the survey has lines which end in the interior of the survey area and are completed by other lines beginning where the former line left off.

Results for One Line of an Aeromagnetic Survey

To see the properties of these measures, the methods outlined above applied to a single flight line of aeromagnetic survey data will be examined. Figure 5 shows a plot of the magnetic anomaly versus distance for a single flight line. The data show a highly variable and magnetic terrane to the west, a central zone of smooth, smaller amplitude anomalies, and a western zone of larger and "rougher" anomalies. The computational procedure outlined above was applied for windows from 260 (5.2 km) points to 20 (400m) points in width, moving 10 points (200m) at a time.

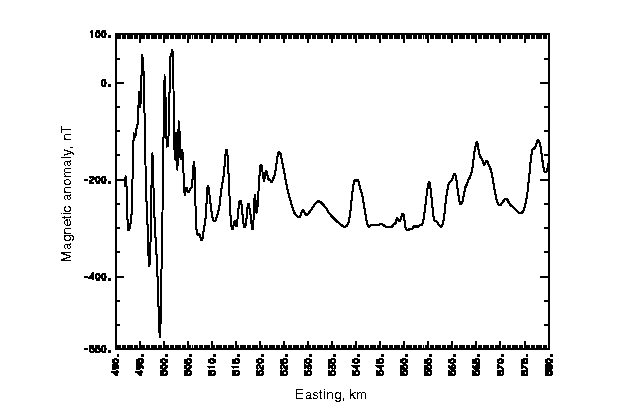Figure 5. Aeromagnetic anomaly data from one line of a high resolution aeromagnetic survey.

Textural measures of the data of figure 5 are shown in figure 6 for the number of peaks and troughs per km and in figure 7 for the Euclidean length per km for four window widths. Study of these figures demonstrates that the window width is not a first order variable and any peak at a larger window width is also present at higher resolution at a smaller window width. For the textural measures, then, it is only necessary to consider the measures at the window width appropriate for the smallest geologic structure of interest.

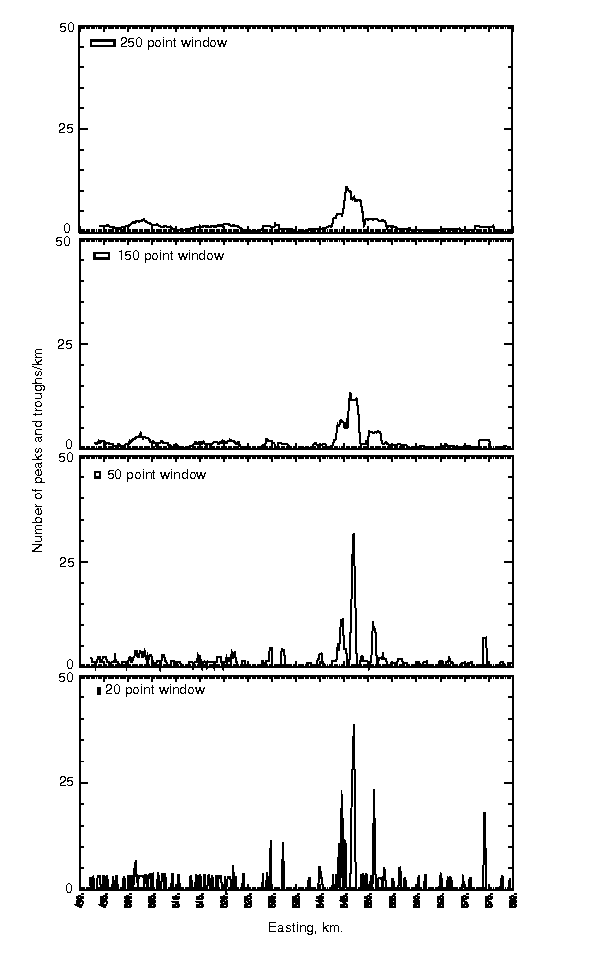Figure 6. Number of peaks and troughs per km for the data of figure 5 for four different window widths. Spacing between data points is about 20 m.

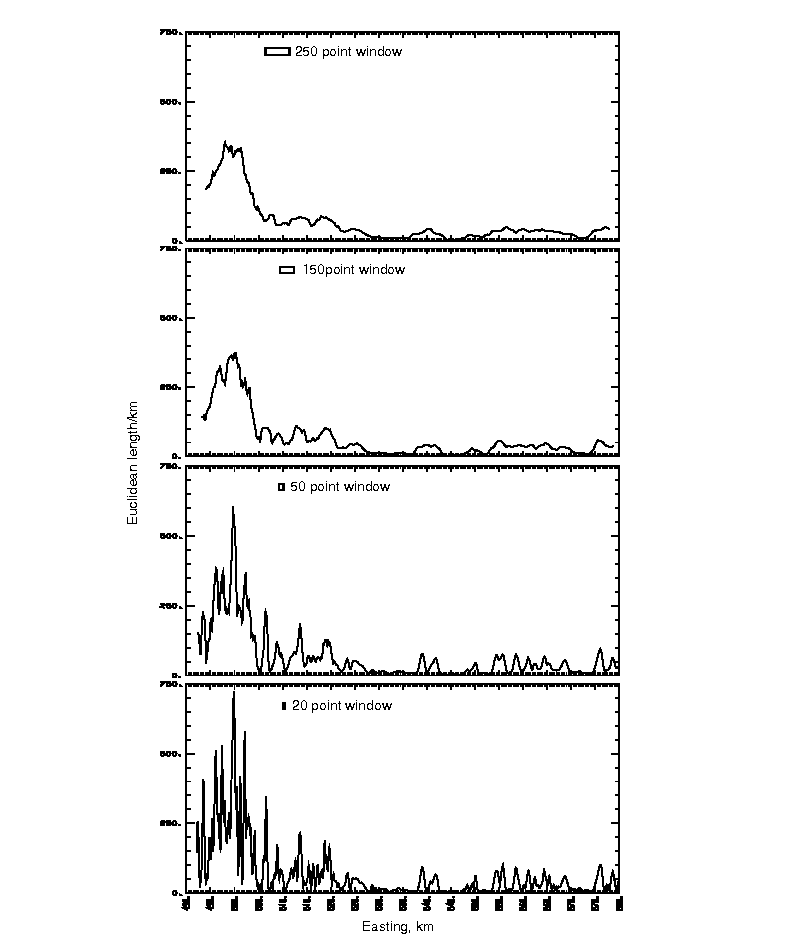Figure 7. Euclidean length per km in units of the square root of km squared plus nanoTeslas squared for the data of figure 5 for four different window widths. Spacing between data points is about 20 m.

In figure 6, the number of peaks and troughs is characterized by about 3/km for the western 40% of the profile, and less than 1/km for the eastern 60% which has clusters of higher values superposed on it. At about 545 km several large peaks are present denoting very "noisy" data even though the amplitudes of the anomalies are very small as shown on figure 7 and on figure 5.

The Euclidean length per km, figure 7, shows a large peak in the western 20% of the profile with a moderate cluster of peaks immediately to the east. These reflect the large amplitude, relatively "noisy" (many peaks and troughs) anomalies in figure 5. Amplitudes are relatively small in the central part of the profile, and there are moderate amplitude anomalies in the eastern third of the data profile.

Number of Peaks and Troughs per Kilometer

The number of peaks and troughs per kilometer computed as described above on the flight line profiles and then converted to a grid using minimum curvature (Webring, 1981) is shown as a colored image in Plate 5. The geologic map line work has been overlain for reference as in previous plates. The average spacing between observations for this dataset is 9 m; a 200 point window was used to define textural differences of about 1.8 km extent or larger. Window overlap was 0.1 the window width or 180 m on average. One result of using such a large window is to remove the effects of shorter spatial wavelength anomalies; in general, these are the effects of near-surface sources.

The area of large amplitude anomalies in the central part of the map is generally an area of relatively few peaks and troughs, and the areas of JTrvs in the northeast part of the map (pl. 1 and pl. 5) are generally the smoothest areas of all. Some areas of Tertiary conglomerate and basin fill also have few peaks and troughs, although some areas of both unconsolidated fill and conglomerate have large numbers of peaks and troughs (no. 1, pl. 5). These areas may be loci of deposition of rocks of igneous (magnetic) provenance within the basin fill. Alternatively, they could be due to volcanic flows within or beneath basin fill. This is less likely, however, because areas of obvious extension of volcanic flows from the Tumacacori Mountains into the basin fill are not characterized by such a large number of peaks and troughs per km (for example, the area about 5 km southwest of "1" on pl. 5). The good correlation with the Santa Cruz younger gravels (basin fill) in plate 5 (no. 1) probably reflects sources of magnetic detritus from tributary canyons from the Tumacacori and Santa Rita Mountains.

The area outlined in the southwest part of the map (no. 2, pl. 5) has a large area of large number of peaks and troughs over an area of both outcropping bedrock and basin fill. Because the boundary of this area crosses several lithologies and does not correlate well with the basin fill, it is here inferred that the portion of the area outlined that is beneath basin fill represents the downfaulted portion of a rhyolite caldera. To the southwest, within the outlined area (no. 2, pl. 5) are exposed rhyolitic rocks (pl. 1) identified as part of a Mesozoic caldera by Lipman and Sawyer (1985).

In the central part of the map area, the high amplitude anomalies of the Grosvenor Hills volcanics (no. 3, pl. 5) and the Laramide intrusives (no. 3, pl. 5) to the northeast have only moderate to few peaks and troughs per km, but they are not distinguished from each other by this measure. The extrusive tuffs of the Salero Formation (Drewes, 1971) do correlate well with areas of large number of peaks and troughs (pl. 1 and pl. 5).

In the extreme northeast, a large area of large number of peaks and troughs (pl. 5) appears to correlate with the drainage pattern and alluvium. To its south however, several northwest trending belts of large number of peaks and troughs occur (no. 5, pl. 5) and cut across the alluvial and drainage pattern onto bedrock. These areas appear to correlate with Laramide and Lower Cretaceous volcanic rocks of andesitic to rhyolitic composition (pl. 1), although the correlation is somewhat ambiguous. The patterns may therefore be caused by magnetic sources beneath those exposed at the surface. It should be noted that these areas occur along steep gradients on the anomaly map (pl. 2) and would not be detected without examining the number of peaks and troughs measure.

Finally, the Tumacacori Mountains volcanics (no. 6, pl. 5) display a distinctive and coherent pattern on plate 5. The pattern clearly extends outside the area of outcrop eastward into the Santa Cruz Valley along much of the mountain front. This suggests the volcanic flows are present in much of the subsurface of the western Santa Cruz Valley.

Euclidean Length per Kilometer

The Euclidean length per kilometer computed as described above on the flight line profiles and then converted to a grid using minimum curvature (Webring, 1981) is shown as a colored image in plate 6. The geologic map line work has been overlain for reference as in previous plates. This parameter essentially measures strength of magnetization for the rocks within the window because the window width stays constant. Thus, large anomalies give large Euclidean lengths and small anomalies give small values.

The areas in plate 5 (no. 1) appear on plate 6 (no. 1) as areas of small Euclidean length per km, adding weight to the interpretation that they are due to magnetic detritus at shallow depths. If they were due to deep sources, they would likely not show up in either measure because of their small amplitude.

Area no. 2 (pl. 6) conforms closely to the area of the same label in plate 5 and confirms that this is an area of homogenous anomaly signature, here believed to be the downfaulted portion of the Cretaceous rocks exposed to the southwest (Kr, pl. 1).

The large amplitude anomalies of plate 2 show up as areas of large Euclidean length per km (no. 3, pl. 6) but the area of Cretaceous Salero Formation tuffs (mostly normally polarized) lying on the reversely polarized Squaw Gulch granite (Drewes, 1971) appear as large Euclidean length per km anomalies. This area is north of the "3" on plate 6 on the north side of the Salero fault zone (also see pl. 1). The Salero fault zone is the long, northwest trending fault just south of the "2" on pl. 2 and north of the "9" on plate 2. The entire area of the Santa Rita-Patagonia Mountains block as outlined in the trend analysis section above (area "A", pl. 3) is delineated as an area of high magnetization.

The Tumacacori Mountains volcanics appear as a fairly distinctive area of larger Euclidean length per km anomalies. Comparison with plate 2 shows that the larger values occur over strongly reversely polarized rocks. Extensions of the volcanic rocks in the subsurface of the Santa Cruz Valley basin fill are obvious.

The two areas marked "5" on plate 6 are both areas interpreted to be areas of shallow depth of basin fill. These areas are westward extensions of exposed bedrock to the east and are important target for mineral exploration because the exposed bedrock areas contain numerous base and precious metal occurrences.

Ranked Euclidean Length and Number of Peaks and Troughs

The number of peaks and troughs grid and the Euclidean length grid can be combined in a number of ways. For this study, a simple ranking scheme was used to produce a rank for each node of the two grids depending on the length value and number of peaks and troughs value at that node. In the matrix below, number of peaks and troughs increases with increasing column number and Euclidean length increases with increasing row number. For these data the distribution of both number of peaks and troughs and Euclidean length were divided into four bins. Ranks were assigned as integers between 1 and 16 as shown in the matrix table below (fig. 8). For the scheme used, relatively many peaks and troughs and large Euclidean length receive a high rank and few peaks and troughs and small length gets a smaller rank.

Figure 8. Matrix diagram showing the ranking scheme used to categorize the number of peaks and troughs grid and the Euclidean length grid into a single grid.

This combination is shown in the ranked color image of plate 7. The geologic map line work has been overlain for reference as in previous plates. The rank values are displayed as a color scale using a default color scheme. Study of the color scale on plate 7 shows that much of the ranking of interest (that is numbers 5 through 16) is compressed into the warm red colors. A better color scheme would probably reveal more information in the image. For example, in plate 7 it is difficult or impossible to tell a value of "8" (many peaks/troughs but intermediate amplitude) from a "13" (few peaks/troughs and largest amplitudes).

On plate 7, a consistent background texture for the whole of the study area has been identified (blue/dark blue on pl. 7) corresponding to the average crustal magnetic signature. Superimposed on this are areas of subsequent igneous activity. Numerous places of extensions of textural measures from on bedrock to beneath basin fill are detected (for example, nos. 1, pl. 7) thus mapping lithology beneath the cover.

The Jurassic granite at the north end of the Tumacacori Mountains is discriminated from the volcanic rocks and appears to extend in the subsurface to the north and west (no. 2, pl. 7).

As on the two component images (pl. 5 and pl. 6) the areas of magnetic detritus deposition in the Santa Cruz Valley are well delineated (no. 3, pl. 7).

In the southwest of the map area (no. 4, pl. 7), the area of uniform textural measure is well delineated, with superimposed small anomalies from sediments in major washes. The "arm" off to the west may not be part of the same lithology as it does not have as uniform a texture as the rest of the outlined area. The Grosvenor Hills intrusion appears as a crude ring of high values surrounding intermediate values over the intrusive body (no. 5, pl. 7).

The upper Salero Formation ash flow tuffs appear as an area of uniform texture with high values, different from the lower member that has intermediate to small values (no. 6, pl. 7).

In the northeast part of the map (no. 7, pl. 7), there is a large area of uniform texture crossing several lithologies. It is not clear what the texture represents, but it is part of the northwest trending major boundary discussed above (pls. 3 and 4) that may be a northeastern boundary for the Triassic-Jurasssic island arc terrane.

Some areas of the Jurassic-Triassic volcanics and overlying Cretaceous volcanic appear magnetically distinct (no. 8 and to the northwest, pl. 7). These are presumably facies and/or compositional variations within the volcanic sequence as the areas of consistent texture follow stratigraphic strike.

The Jurassic granite of Mt. Benedict is similar to the Jurassic granite at the north end of the Tumacacori Mountains except in the eastern fault block (no. 9, pl. 7), supporting the interpretation that the Mt. Benedict block has been intruded by a later magma in times of normal polarity, probably a Laramide age intrusive.

An extensive area of uniform texture consisting of a large number of peaks and troughs and small Euclidean length (no. 10, pl. 7) occurs in the extreme northeast corner of the map. Although the area does not correlate exactly with present day washs (pl. 7, pl. 1), the pattern suggests that the sources are alluvial in origin and perhaps these represent paleochannels filled with detritus that is on the average more magnetic.

| Previous Section | Next Section |