Description of the measurement sites
Glacier motion and surface altitudes
Results of surface mass balance, motion, and surface altitude measurements
9-14. Graphs showing:
| Multiply | By | To obtain |
|---|---|---|
| millimeter (mm) |
0.03937 | inch |
| meter (m) |
3.281 |
foot |
|
kilometer (km) |
0.6214 | mile |
| square meter (m2) | 10.76 | square foot |
| square kilometer (m2) | 0.3861 | square mile |
| kiogram per liter (kg/L) | 62.43 | pounds per cubic foort |
| meter per year (m/yr) | 3.281 | foot per year |
| grad (angle) | 0.9 | degree (angle) |
| metric ton (t) | 1.102 | ton |
| degree Celsius (oC) | 1.8, then add 32 | defree Fahrenheit (oF) |
Specific conductance is given in microsiemens per centimeter at 25 degrees Celsius (µS/cm at 25°C).
In this report "sea level" refers to the National Geodetic Vertical Datum of 1929 (NGVD of 1929)--a geodetic datum derived from a general adjustment of the first-order level nets of both the United States and Canada, formerly called Sea Level Datum of 1929. Altitudes are the same in both the local coordinate system and the Universal Transverse Mercator system.
Symbols and abbreviations used in this report:
| b0(i) | initial ice balance at a site |
| b0(s) | initial snow balance at a site |
| b1(i) | final ice balance at a site |
| b1(ls) | late snow balance at a site |
| b(f) | new firn balance |
| b(k) | internal accumulation at a site |
| b(s) | snow balance at a site |
| b(i) | old firn and ice balance at a site |
| ba | annual snow, firn, and ice balance during a hydrologic year at a site |
| ba(f) | annual new firn balance |
| ba(i) | annual old firn and ice balance at a site |
| bm(s) | measured snow balance at a site |
| bn | yearly net firn and ice balance between times of minimum balance at a site |
| bn(f) | net new firn balance (ice content only) at a site |
| bn(i) | net balance of old firn and ice at a site |
| b' | average stake height of the glacier surface within a 3- to 5-meter radius |
| b'0 | stake height of the glacier surface at the beginning of a measurement period |
| b'1 | stake height of the glacier surface at the end of a measurement period |
| b'(i) | water equivalent of old firn and ice above a stake base |
| b'ss | height of a summer surface above the base of a stake |
| b* | surveyed stake height of the snow, firn, or ice surface |
| b** | stake height, vertical distance between base of a leaning stake and the glacier surface |
| d | snow depth or depth of snow that has become new firn |
| d or |
as a prefix before any symbol means a change in that quantity |
| Dh | horizontal distance projected to a plane at sea level |
| °d | degree-days |
| e | emergence of the glacier surface during a measurement period |
| é | emergence rate of the glacier surface |
| E | estimated snow density, when listed after density data in tables |
| f | Earth curvature and atmospheric refraction coefficient in optical surveying |
| LSnow | abbreviation for late snow, fresh snow on new firn |
| m | partially measured density, when listed after density data in tables |
| m(w) | meters depth of snow or ice in water equivalent |
| M | measured density, when listed after density data in tables |
| n | number of probes, pits, and cores taken at the time of each measurement |
| NFirn | abbreviation for new firn, snow that has survived the summer melt season |
| OFirn | abbreviation for old firn |
| P | precipitation |
| p | density of snow, firn, or ice |
| p(s) | density of snow |
| p(w) | density of water |
| p(i) | density of glacier ice |
| F | dip of glacier motion near surface |
| S | average glacier surface speed |
| Se | average emergence speed |
| SFirn | abbreviation for superimposed ice in old firn |
| SIce | abbreviation for superimposed ice |
| ss0 | initial summer surface, the glacier reference surface for a measurement year |
| ss1 | final summer surface |
| Swi | irreducible water-volume constant, water retained in snow by capillary retention |
| t0 | beginning of hydrologic year |
| t1 | end of hydrologic year |
| Q | horizontal glacier surface motion direction |
| UTM | Universal Transverse Mercator Projection |
| V | glacier motion vector |
| Vm | vertical angle to a geodetic monument |
| X | project grid coordinate, increasing easterly |
| Y | project grid coordinate, increasing northerly |
| Z | altitude above sea level; glacier surface altitude above sea level |
| Z0 | altitude of the glacier surface at the beginning of a measurement period |
| Z1 | altitude of the glacier surface at the end of a measurement period |
| Zi | altitude of a surveying instrument |
| Zm | altitude of a geodetic monument |
| Zss | summer surface altitude |
Scientific measurements at Wolverine Glacier, on the Kenai Peninsula in south-central Alaska, began in April 1966. At three long-term sites in the research basin, the measurements included snow depth, snow density, heights of the glacier surface and stratigraphic summer surfaces on stakes, and identification of the surface materials. Calculations of the mass balance of the surface strata-snow, new firn, superimposed ice, and old firn and ice mass at each site were based on these measurements. Calculations of fixed-date annual mass balances for each hydrologic year (October 1 to September 30), as well as net balances and the dates of minimum net balance measured between time-transgressive summer surfaces on the glacier, were made on the basis of the strata balances augmented by air temperature and precipitation recorded in the basin. From 1966 through 1995, the average annual balance at site A (590 meters altitude) was -4.06 meters water equivalent; at site B (1,070 meters altitude), was -0.90 meters water equivalent; and at site C (1,290 meters altitude), was +1.45 meters water equivalent.
Geodetic determination of displacements of the mass balance stake, and glacier surface altitudes was added to the data set in 1975 to detect the glacier motion responses to variable climate and mass balance conditions. The average surface speed from 1975 to 1996 was 50.0 meters per year at site A, 83.7 meters per year at site B, and 37.2 meters per year at site C. The average surface altitudes were 594 meters at site A, 1,069 meters at site B, and 1,293 meters at site C; the glacier surface altitudes rose and fell over a range of 19.4 meters at site A, 14.1 meters at site B, and 13.2 meters at site C.
Research into mountain climate, glacier responses to climate, and glacier runoff at Wolverine Glacier in the coastal, maritime Kenai Peninsula of southcentral Alaska (fig. 1) began with measurements in April 1966. This study at Wolverine Glacier is the only long-term, continuous monitoring effort investigating climate, glacier processes, and glacier hydrology in the highly glacierized coastal mountains of southcentral Alaska.
Wolverine Glacier, approximately 18 km2 in area and 7 km long, is one "link" in the International Hydrological Decade’s (1964–75) North-South American “chain of glaciers” from the Antarctic Peninsula to Arctic Alaska (UNESCO, 1970). Two other glaciers in this chain are under routine observation by the U.S. Geological Survey (USGS): South Cascade Glacier in the maritime North Cascade Range of Washington (Krimmel, 1999); and Gulkana Glacier in the continental Alaska Range of interior Alaska (March and Trabant, 1998). Kahiltna and Traleika Glaciers near Mt. McKinley in the Alaska range have been observed since 1990 by the U.S. National Park Service using the same methods used at Wolverine and Gulkana Glaciers.
Three sites (fig. 1) were established on Wolverine Glacier for mass balance measurements. In this report, only surface mass balances are reported for these sites; internal freezing and melting processes are known, but not discussed here. In 1975, additional measurements of glacier surface altitude at fixed locations and ice motion began at the three sites. The purpose of establishing these three sites was to make year-round measurements of mass balance, flow, and surface altitude changes continuously over the long periods of time required for climate change research. The complete time-series of measurements of glacier mass balance, motion, and surface-altitude at each of these sites are presented in tables and graphs in this report.
Research began at Wolverine Glacier as a result of the recognition that glaciers can be significant in both local and global water balance equations. Yet, few reliable data exist for glaciers. Many of the research concepts applied at Wolverine Glacier originated with Carl Benson, Herfreid Hoinkes, Mark Meier, Gunnar Østrem, Hans Rothlisberger, and Wendell Tangborn. Their pioneering work was essential.
Figure 1. Location of Wolverine Glacier, Kenai Peninsula, south-central Alaska, showing the principal measurement sites in the basin.
Wolverine Glacier is in a remote area of Alaska where weather and terrain conditions are severe. Even under ideal conditions, the work is not easy and patience is required to accomplish it. The work was interrupted frequently for 2 to 10 days by high winds, blowing snow, and fog that make glacier and helicopter travel impossible.
Stanley Jones devoted two years coping with these conditions—sometimes with no shelter available—to assist in establishing the necessary scientific equipment and other facilities. Later, several other people assisted in the investigation at Wolverine Glacier, both in winter and summer. These individuals include principally Chester Zenone, David Scully, and Gail Mayo, all of whom contributed to the research program. They were resourceful in accomplishing equipment repairs, contributing useful ideas, and made some of the initial calculations in the data sets. About 30 other individuals also assisted at Wolverine Glacier.
During the 30-year period, small teams of glaciologists travelled safely to Wolverine glacier a total of 115 times to maintain the continuous, year-round measurement campaign. The cooperation of all these people helped to ensure the safety and success of the measurements at Wolverine Glacier for three decades. The authors, as well as the science of glaciology, are indebted to the cumulative efforts of these scientists.
Robert Krimmel, William Harrison, Timothy Brabets, Elizabeth Snyder, Sonja Benson, Ben Kennedy, and Dave Meyer reviewed this report and offered useful suggestions that improved its clarity.
The three long-term measurement sites at Wolverine Glacier (fig. 2) are located in relatively flat parts of the glacier to minimize the damaging effects of snow creep on stakes. Site A, at 590 m altitude, is low in the glacier’s ablation area. Site B, at 1,070 m, is normally high in the ablation area, but during years with large positive mass balances, it is low in the glacier’s accumulation area. The glacier surface at site B in late summer is a complex mixture of old firn, superimposed ice, and iced firn (firn permeated with water because it is near the glacier’s equilibrium line). When this slushy mixture refreezes during the subsequent winter, it usually has a density of 0.90 kg/L. Site C, at 1,290 m, is normally in the accumulation area of the glacier except during years with large negative mass balances, when it is very high in the ablation area.
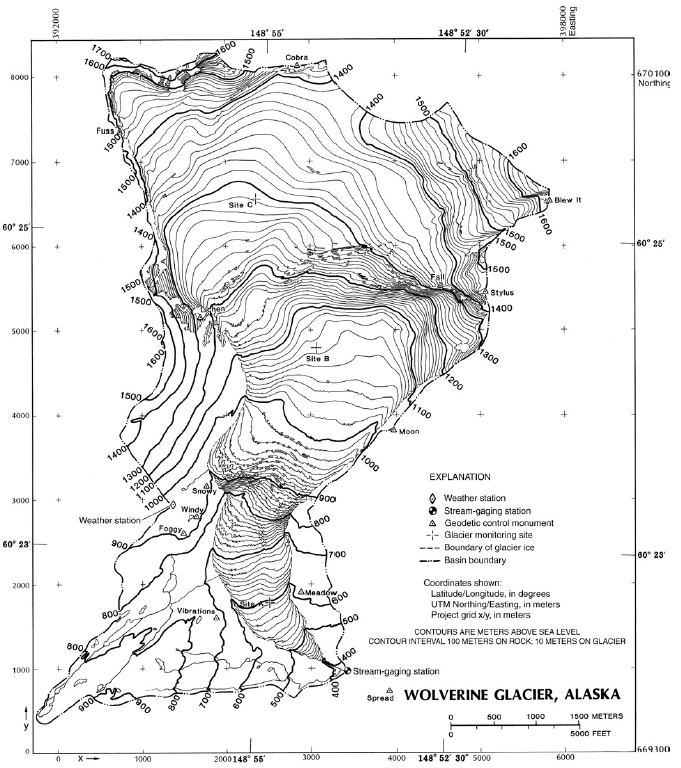
Figure 2. Locations of long-term measurement sites and geodetic control monuments in Wolverine Glacier Basin, Alaska. (Map compiled from August 3, 1979, aerial photography and surveyed control panels)
During the first 2 years of observation, 1966 and 1967, the measurement sites were not at fixed locations; instead, the glacier’s mass balance was mapped (Meier and others, 1971; Tangborn and others, 1977). The data presented in this report for those years are from the mass balance maps and the nearest measurement stake. The fixed measurement sites featured in this report were established in 1968. In 1975, sites A and B were moved about 100 m to the glacier’s centerline, which was defined for glacier-volume-change surveys. In 1978, site C was moved 208.4 m northeastward to the glacier’s centerline.
A weather recording station was established at 990 m elevation near the western boundary of the glacier basin (Mayo and others, 1992; see fig. 2). The station is slightly lower than the glacier’s average equilibrium line altitude and approximately 500 m from the west edge of the glacier. Air temperature and precipitation are recorded at the site since 1967.
The methods of glacier mass balance measurement at Wolverine Glacier evolved from those described in Meier (1960), Meier and Tangborn (1965), Østrem and Stanley (1969), Mayo and others (1979), and Mayo and Trabant (1982); and are similar to the methods used at several Alaska glaciers: Black Rapids Glacier (Heinrichs and others, 1995), and Gulkana Glacier (March and Trabant, 1998), Columbia Glacier (Mayo and others, 1979), and more recently at Wolverine Glacier are described in this report. The internal mass balance, consisting of internal accumulation (Trabant and Mayo, 1985) and internal ablation (Mayo, 1992), is not analyzed here.
Mass balance measurements at the surface of a glacier consist of measuring the changes in snow and ice that result from the cumulative effects of snow precipitation, snow compaction, melting of snow and ice, wind erosion of snow, freezing of water, and sublimation from ice. The measurements are simple in concept, that is, repeated measurements of the height of the glacier surface on stakes installed in the glacier, snow depths, and snow densities, and identification of the mass balance stratum at the surface of the glacier, such as snow, new firn, old firn, superimposed ice, and glacier ice. Making these simple field measurements is often physically demanding and potentially dangerous because of the frequently inclement weather and the remoteness of the site. Maintaining a continuous measurement program also is made difficult because stakes are distorted by glacier movement and snow and wind loading, snow pits require laborious excavation, travel can be dangerous, and snow probing and coring-auger samples do not always produce reliable measurements of the base of the annual snow layer.
Each year’s mass balance measurements at a stake are referenced to the previous year’s summer surface. The data resulting from these measurements are listed in the data files using a combined system, both as the net balance, bn, in the stratigraphic system, and also as the annual balance, ba, in the fixed-date system following the concepts developed by Mayo and others (1972).
The reference plane for each year’s measurement, the summer surface, separates different glacier mass balance stratigraphic units, or strata. The summer surface is a time transgressive feature on a glacier (fig. 3). It forms during the early fall at the top of the glacier, and then progressively later at lower altitudes as winter sets in. The amount of time required for the formation of this summer surface over the entire glacier varies from year to year depending on the local weather, typically taking 2-4 weeks at Wolverine Glacier. Thus, the net new firn and ice balances, bn(f) and bn(i), at the three sites on Wolverine Glacier do not represent the same time period. Annual mass balances, ba, on the other hand, are reported for each fixed-date hydrologic year beginning October 1 and ending the following September 30. The balance data together with air temperature and precipitation data from the basin are used to estimate the small changes in mass balance between the measured balances, the minimum balance, and the balance for the fixed-date year beginning on October 1.
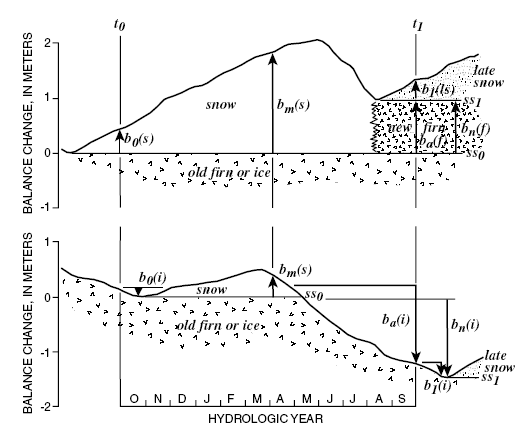
Figure 3. Mass balance quantities measured at two different locations on a glacier. [Measurements made using the stratigraphic system referenced to the summer surface that moves with the glacier (Lagrangian coordinates). Annual balance quantities are obtained from these data by reference to the balance conditions at the beginning and end of the hydrologic year (Mayo and others, 1972). Symbols are: t0 , beginning of hydrologic year; t1, end of hydrologic year; b0(s), initial snow balance; b1(ls), late snow balance; bm(s), measured snow balance; bn(f), net new firn balance; ss0 , initial (reference) summer surface; ss1, final summer surface; b0(i), initial ice balance; b1(i), final ice balance; bn(i), net ice balance; ba(f), annual new firn balance; and ba(i), annual old firn and ice balance]
Each stake set in the glacier is labeled with a unique identification name and installed in a hole drilled with a manual auger or a steam drill. The stakes are 1-inch-(25-mm)-diameter metal electrical conduit cut to lengths of 3 m, and connected with short flanged pipes that fit inside the ends of each stake section. Small holes are drilled in the conduit precisely at 0.5-m intervals to serve as height markers and to let water out. A wood plug is driven into the base of each stake to prevent it from sinking into the ice. In the early years, the need for the wood plugs was not appreciated, so occasionally they were not used and some of these stakes sank into the ice.
At site A, a new stake is usually installed in September of each year to a depth of 10 to 11 m with about 3 m exposed above the ice surface for measurements in winter. No connector is put at the 6-m joint so the stake will come apart at that point during the following summer melt period. The stake is adjusted to be 3 m above the ice surface in the fall. At site B, a new stake is installed about every 2 years to a depth of 9 m. Each fall, stakes at site B that are in good repair are extended 4 to 5 m above the surface for winter measurements. At site C, stakes are installed about 3 m deep into old firn almost every year and extended to 4 to 5 m above the summer surface in the fall. In mid-winter, the stake again is extended to 3 m above the snow surface.
If a stake becomes buried during winter and cannot be found, another stake is installed nearby. If both the old and new stakes are found at a later date, they can be measured and surveyed simultaneously. Assuming that the stakes’ relative positions are constant, the balance and position of the temporarily lost stake can be accurately estimated, thus providing an unbroken measurement series.
At the time a stake is installed, and during each successive visit, the stake name and height of the snow, firn, or ice surface, (b’), on the stake are measured and recorded (fig. 4). Generally, snow and firn surfaces at Wolverine Glacier are smooth, without large wind features such as sastrugi and snow dunes. However, local relief on glacier ice surfaces commonly is 0.2 to 0.5 m.
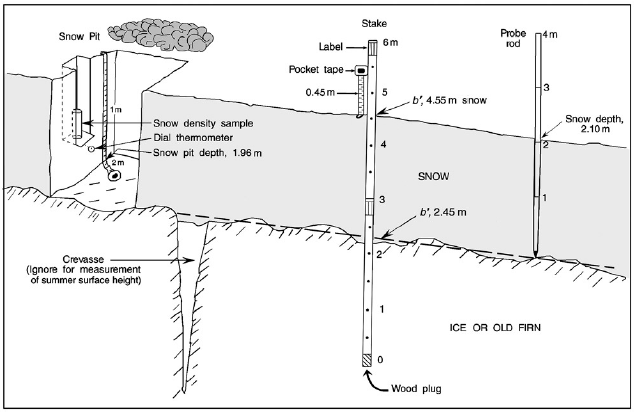
Figure 4. Surface mass balance measurement site showing snow pit, stake, and snow probe measurements. (b’, average stake height of the glacier surface within a 3- to 5-meter radius; b’ss, height of summer surface above the base of the stake; m, meters)
Both snow density and direct measurements to buried summer surfaces are possible when pits are dug in snow and firn. In very deep snow, a pit is dug through part of the snow, and auger core samples are taken from the floor of the pit to the base of the snow. If the snow is less than 3 m deep, coring of the snowpack is possible by simply thrusting a long tube into the snow. Because snow density is difficult to measure, relatively few measurements have been made at Wolverine Glacier, and most of those were made before 1980. Continuous vertical coring of the snow in pit walls using relatively large diameter coring tube (72.3 mm) that is 0.6-m long, produces highly accurate snow density data. However, auger coring is often discontinuous, with gaps in the core where the snow was very soft; in these cases, the density of missing layers was estimated. Pit and auger-coring sites are far enough from stakes so that stake and snow near the stake are not disturbed. As a result snow depths at pits may be slightly different from snow depths at stakes. A total of 107 snow pits and cores at Wolverine Glacier successfully produced snow density and depth measurements for the full depth of the snowpack (table 1—excel file 29KB). [Note: all tables are in a section at the back of this report]. Additional snow density measurements in the upper part of deep snowpacks are listed in the mass balance tables (tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB).
Snow depths in the ablation area of Wolverine Glacier are measured with a probe rod if the snow is less than about 6 m deep, the ice at the summer surface is very hard, and a false summer surface (a very hard layer in the snow) is usually absent. When possible, 5 to 10 probe measurements are made within a 3- to 5-m radius of the stake to obtain the average snow depth. In this way, errors caused by local variations of snow depth and surface roughness near the stake are reduced. Sometimes the summer surface, especially in the accumulation area, is difficult or impossible to identify when probing. All probing data are listed in the mass balance tables in this report; however, some data were disregarded because subsequent measurements indicated that the probing did not produce the correct snow depth. Probing, while relatively easy, is the least reliable measure of snow depth at Wolverine Glacier.
Summer surfaces (ss0 and ss1, fig. 3) at Wolverine Glacier are usually easily identifiable, but in some instances, can be difficult to identify if they are very clean. Care is taken with all measurements to ensure that the reference summer surface is identified correctly. Several problems can arise with identification of a summer surface. (1) A false summer surface can be created by a fall storm with mixed rain and snow, which forms a slush layer. When the slush freezes, a solid false summer surface is formed. Even though it feels like glacier ice with a probe, careful observation in a pit can reveal that the hard layer does not have a concentration of dirt at its surface, and that it overlies an identifiable dirty summer surface. (2) Occasionally, no dirt accumulates on the snow surface during the summer. (3) Thick ice layers may form in the snow during severe winter ice storms or during spring when meltwater percolates into cold snow. These can stop a probe rod and give the appearance of a solid ice surface at the floor of a snow pit. (4) Even in the ablation area, summer surfaces may be misidentified because a layer of ice usually forms at the base of the snow overlying cold glacier ice in spring when meltwater refreezes. At Wolverine Glacier, layers of transient, superimposed ice are commonly 0.01 to 0.05 m thick.
In the glacier’s accumulation area at site C, a 1-m2 piece of plywood with a hole in the center is placed over the stake and lowered to the surface each fall. During subsequent measurements, the plywood is used to positively identify the previous summer surface. However, even this technique is not foolproof because investigators have believed several times that they were probing to the plywood, whereas other measurements indicated that they had been probing to an ice layer in the snow above the plywood. The best method to ensure accuracy of snow depth data with a plywood marker is to use a steam drill to penetrate to the plywood. Additionally, sawdust and wire meshes can be placed on the surface during late summer to identify it, but plywood is the easiest and most effective. Plywood markers can also be used for glacier motion analysis when a stake is buried by snow.
The glacier surface mass balance tables for Wolverine Glacier (tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB)) present the measurements, necessary interim calculations, and mass balance results for each site in meters of water equivalent, m(w), for each surface stratum of the glacier: snow, new firn, old firn, superimposed ice, and old firn and ice. For clarity, all measurements that were needed to calculate the mass balance at a site are included with each measurement year, even though some duplication results from year to year. Each stake is identified by its name, and unusual features of the stake. Explanations of each column in the tables are given in the following paragraphs.
Field Notes: This column references the original field notes on file at the Fairbanks office of the USGS. This reference is included to expedite further research that might require access to related observations.
Date: Measurement dates are in month/day/year format. Specific dates relating to the beginning and end of each measurement year are also listed. These include the date of minimum balance at the beginning of the net-balance year, the date of the beginning of each fixed-date hydrologic year (October 1), the date of the minimum balance at the end of the net-balance year, and the date of the end of the fixed-date hydrologic year (September 30).
Stake Heights: Tape: Each stake measurement, b’, is the height in meters on the stake from the base of the stake to the glacier surface. The measurement incorporates a visually estimated average surface height within a 3- to 5-m radius of the stake. Standard practice is to mark this height on the stake and then measure to the point with a pocket tape from the nearest height mark (hole) in the stake. If measurements of more than one stratum are made, the entries are recorded; for example, both the snow surface and superimposed ice surface are recorded for stake 66-3 on 4/23/66 ( Table 2—excel file 152KB).
Survey: Beginning in 1978, each stake was surveyed at two points—one well above the glacier surface, and the other at the glacier surface. The glacier surface point as viewed with a theodolite, b*, may not be precisely the same point as the b’ measurement, so both are listed. Another stake height, b**, is a calculated value that has been corrected for stake lean or other distortions. Stake heights are corrected for lean by first calculating the lean of the stake top using the surveyed position data, then calculating the stake bow if in snow, and finally calculating the coordinates of the stake base using any lean previously measured for the lower sections of the stake. This method was developed by Hodge (1972) for use at Nisqually Glacier, Washington. The calculated vertical distance from the stake base to the sloping glacier surface directly above it is listed as b**. This value would have been the stake height had the stake been vertical. In calculations of mass balance involving stake heights, b** values are used instead of b’ values when available, because mass balance quantities are always considered to be vertical measurements.
Stratum: Identification of the stratum at a glacier surface is essential to interpretation of mass balance. Surface strata include snow, superimposed ice, new firn, old firn, glacier ice, and “superfirn,” a mixture of old firn and superimposed ice. To save space in the data tables, these are listed, respectively, as Snow, SIce, NFirn, OFirn, Ice, and SFirn. New snow from a recent storm and old snow are distinguished in some places.
Snow Depth: Snow depth is calculated from the field measurements. First, the stake height of each summer surface (“Obsvd. b'ss”, tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB)) is calculated as either b**, b*, or b’ minus the average snow depth. Next, the average summer surface height, Average b’ss, for the entire winter is calculated by weighting the measurements by the number (n) of probes, pits, and cores made at the time of each measurement. This is the most reliable measure of the height of the reference summer surface at a stake. Finally, the snow depth, d, is the difference between the stake heights, b**, b*, or b' and the average summer surface height, average b’ss. This system utilizes all relevant information at each stake to produce the most representative snow depth at a stake.
The very deep spring snowpack at site C in 1981 was difficult to measure and required detailed notation than normal in the mass balance data set (table 4—excel file 176KB). The 1980 reference summer surface at site C was difficult to document because all of the stakes were buried and digging a snow pit deeper than 10 m was not feasible. Probing through cold winter snow on January 26, 1981, defined a hard layer at a depth of 6.7 m, and hard surfaces that felt like firn at depths of 10.25 and 10.42 m. Four corings on January 27, 1981, exposed a grain size increase from 0.5-mm diameter to 1.5-mm diameter at a depth of 12.00 m. On June 7, 1981 core samples were taken from the site (surveyed and assuming average glacier motion) where sawdust was spread on the snow surface in August 1980. These samples were melted to search for debris that might indicate a summer surface. One sawdust particle and numerous small vegetation fragments were found in the sample that came from the depth interval from 13.4 to 13.7 m; the coring auger flights held two more sawdust particles. Checks of field notes from earlier years show that sawdust had not been put at this site previously. Stake 81-C2 was placed on a small wooden base in this core hole. On September 2, 1981, a core sample from the sawdust site contained an abrupt change in snow grain size at a depth of 9.65 m, which was about the same level relative to the stake as the sawdust found earlier. Coring on September 25, 1981, did not identify a summer surface nor did it go deep enough to encounter the previously identified grain size changes or sawdust layer. Analysis of the reference summer surface (table 4—excel file 176KB) determined that the grain size change found at 12.00-m depth found on January 27, 1981; the sawdust at an average depth of 13.55 m on June 7, 1981, and the abrupt grain size increase found at 9.65-m depth on September 2, 1981, are the 1980 summer surface. Therefore, the snowpack was concluded to have reached a depth of 13.6 m by June 5 or 6, 1981, and to have been 9.4-m deep on September 11, 1981, the end of the summer. Although this is not the record snow depth for Wolverine Glacier (15.2 m was measured on June 7, 1977, at 1,530-m altitude), the snow depth at site C in 1981 was greater than expected, judging from the snow depths at sites A and B.
Pit: Snow depth measured at a pit in which the summer surface can be identified visually is the most reliable method. However, it is a measurement at only one point and the observation is laborious, so pit studies are made much less frequently than other types of snow depth measurements.
Probe: Snow depths measured by probing become
more reliable when done in conjunction with pit measurements, because false
summer surfaces that are exposed in the pit can be identified when probing.
Probing can be done quickly at a number of points, so probing is useful in establishing
the average snow depth, especially in the ablation area, which has a rough ice
surface. If a snow pit was not made to confirm the probing horizon, depth measured
by snow probing was verified by previous evaluations of the stake height of
the summer
surface whenever possible.
Average, standard error, and number of snow depth measurements: Snow depth measurements use all of the pit and probe data on a given date. However, because the snow depth, d, at a stake is the difference between the stake height of the glacier surface (b**, b*, or b') and the average summer surface height (b'ss), it is not an independent evaluation of snow depth and is, therefore, not included in the calculation of standard error (s.e.) or counted in the number (n) of measurements. The average of the direct snow depth measurements is used when no measurements at a stake are available.
Summer Surface: Observed: Stake heights of reference summer surfaces, b'ss (fig. 4), are listed as “Obsvd.” in the mass balance data tables (2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB)) for each combination of stake and snow-depth measurement.
Average: When the summer surface heights cluster about a central value, the b'ss on the stake is assigned the average value. A series of summer surface heights that continuously rise relative to the stake indicate that the stake is sinking into the glacier and the average stake height is not used for mass balance calculations.
Old Firn and Ice: Density is mass per unit volume. Snow and ice densities are used to convert linear measurements of depth and stake height to water equivalent values. The “stake-reference” old firn and ice balance, b’(i), in meters water equivalent, m(w), is the product of summer surface average height, b’ss, on the stake and the density of the stratum. This interim value, b’(i), is the basis for calculating the amount of old firn and glacier ice that melts during the summer and is posted in tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB). The annual ice balance,ba(i), is the difference between the amount of old firn and ice, b’(i), at the beginning of the measurement year and the amount remaining at the end of the year.
Accurate snow and firn density data are essential for mass balance measurements. A total of 107 full-depth snow and firn density measurements were made at Wolverine Glacier (table 1—excel file 29KB) for this study. Numerous other partial-depth measurements were made also and are reported with the stake data (tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB)).
Samples of snow and firn for density measurements are continuous vertical cores rather than horizontal cores. Vertical core sampling produces accurate average density data for each depth interval cored (Østrem and Stanley, 1969). Horizontal cores produce accurate information about internal layering for identifying snow and firn strata (Benson, 1959), but the data can be difficult to interpret to obtain the average density of a stratum. At Wolverine Glacier, vertical coring was chosen for its accuracy and speed, and summer surfaces were identified as by searching for dirty layers. Although this method works in most years, the dirt marking summer surfaces at Wolverine Glacier is not distributed uniformly, so it can be missed by a coring auger. Occasionally, there is no dirt on the summer surface at Wolverine Glacier.
The accuracy of measuring snow density has not been studied at Wolverine Glacier. Some investigators, for example, George Claggett, U.S. Department of Agriculture Snow Surveyor,oral communication, 1984, have estimated that small samplers, such as the McCall (11.61 cm2 cross-section area) push-type sampler, may under-sample loose snow by about 6 percent. Larger samplers, such as the Norwegian tube (41.05 cm2) are estimated to be accurate to within 2 percent in firm snow.
Density measurements of deep snow tend to be more accurate than measurements of shallow snow because more samples of deep snow are collected, and random errors tend to cancel when the average density is calculated. Snow density measurements in this report are posted to three digits and the sampling method is identified (table 1—excel file 29KB). Reporting values is probably more precise than can realistically be obtained but was done so that precise corrections can be applied in the future for each method, thus avoiding additional errors associated with rounding. This is consistent with the standard practices followed for performing all calculations with more significant digits than can be measured absolutely and rounding the final result.
Snow and New Firn: The snow balance, b(s), for any date is the snow depth, d, at the stake multiplied by the density of snow, p(s). The product has the dimension of depth in meters of water equivalent, m(w), after the density has been converted to a relative density with respect to water, p(s)/p(w).
Snow Density: Snow density, p(s), can be measured (M), partially measured (m), or estimated (E) from generalized knowledge of snow density as a function of snow depth and date. Density can be measured by one or a combination of methods—various core sampling devices, vertical coring in a pit wall, and occasionally extended in depth by vertical coring from a pit floor to the base of the snow.
Two methods have been used for estimating snow density when snow depth is the only measurement. In one method, the snow density is measured in the upper part of the snowpack and an estimate of the unmeasured lower part of the snowpack is made. To do this, reliable snow density measurements are plotted so that the average density above any specified depth in a snowpack is shown (fig. 5). When the density measured in the upper part of the snowpack is plotted, the density for the entire snowpack can be estimated by assuming that the increase in snow density with depth is a reasonable estimate of the density of the unmeasured part of the snowpack. Snow density entries based on partial measurements are given the notation “m” in the mass balance data tables (tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB)).
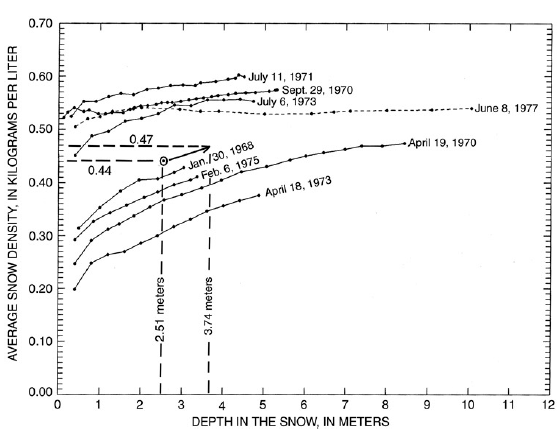
Figure 5. Average snow density above specified depths in the snow for different dates, Wolverine Glacier, Alaska. (The circled dot shows a measurement of snow density at site B on May 13, 1992 of 0.44 kilograms per liter average density to a partial depth of 2.51 meters. The average density for the entire snowpack of 3.74 meters depth is estimated from this graph to be 0.47 kilograms per liter)
If no snow density is measured, the average density of the entire snowpack must be estimated. Snow depth and density data for Wolverine Glacier (table 1—excel file 29KB) show that snow and new firn densities increase both with depth and with age, where age is defined in terms of the date of measurement (fig. 6). The generalized contours of density on figure 6 are used to obtain the density estimates listed in the mass balance data tables (tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB)); these estimates are indicated by the notation “E.”
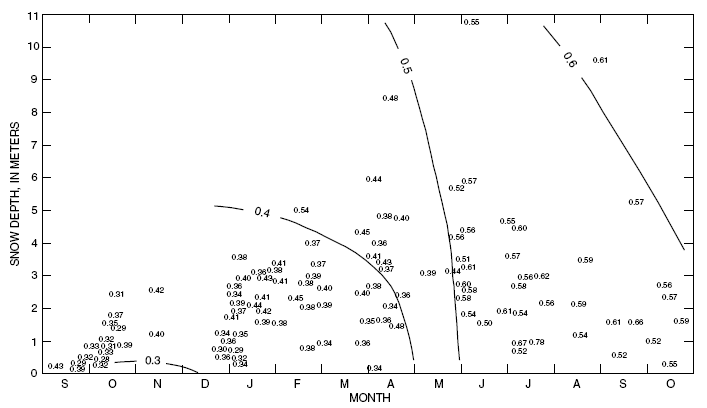
Figure 6. Average snow and new firn densities (numerals) at Wolverine Glacier, Alaska, as a function of snow depth and age, on the date of measurement. (Contours are a generalization from the data and are used for estimating snow density when only snow depth and date are known. Density values are kilograms per liter)
NFirn: New firn, bn(f), is the seasonal snow remaining at the time of minimum balance at the end of the summer in the accumulation area of a glacier. Snow that becomes new firn is a mixture of ice crystals, liquid water, and air. However, only the ice component of the snow becomes a relatively permanent addition to the glacier. The liquid component is in temporary storage. Some of it is converted into internal accumulation, b(k), by freezing during the next winter (Trabant and Mayo, 1985); the rest drains from the glacier as the firn compresses gradually into glacier ice. The liquid component of new firn creates a potential problem in glacier mass balance accounting, because the same material could be counted twice, once in the new firn, and a second time when it freezes. At Wolverine Glacier, the liquid component is subtracted from the snow balance when snow becomes new firn.
The liquid component is analyzed separately for determining the amount of internal accumulation that will be included in the new firn. The rest of the liquid is assumed to become part of the glacier’s runoff. The amount of ice (without water) contained in new firn, bn(f), at Wolverine Glacier, is calculated by subtracting the water volume retained by capillary retention, 0.07 of the void space of the old snow, from the snow balance, b(s):
![]()
where
Swi is the irreducible water volume constant, the water retained in snow by capillary retention (Colbeck, 1974);
d is the depth of snow that becomes new firn;
p(s) is the snow density that is measured (bulk density including water); and
p(i) is the density of ice, assumed to be 0.9 kg/L.
Yearly Results: The last two columns of the mass balance tables are the total surface mass balances summed for the two periods defined in the combined glacier mass balance system (Mayo and others, 1972). The net balance, bn, is the snow, firn, and ice balance accumulated since the previous minimum balance at the beginning of the net-balance year when the initial summer surface formed. The annual balance, ba, is the sum of the snow, firn, and ice balance accumulated since October 1, the beginning of the fixed-date hydrologic year.
Both the stratigraphic system (net) and the fixed-date system (annual) mass balances are derived from the same field measurements. The initial snow and ice balance at each site are listed for the dates of minimum balance and the beginning of the hydrologic year. During a year, several stakes may be measured at a single site. Frequently only one stake is judged to be reliable, so that stake is used to compute the mass balance for the site. For other years, measurements from several stakes are averaged for determining the mass balance of the site. Balance measurements made during the year result in “year-to-date” values listed under the “Yearly Results” heading (tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB). The net balance of old firn and ice, bn(i), is zero during the winter. For this reason, only the annual old firn and ice balances, ba(i), are tabulated separately (tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB).
Other mass balance quantities can be identified or calculated from the measurements. For example, the initial snow balance, b0(s), is the new snowpack on the glacier at the beginning of a hydrologic year. This value is listed in tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB as the snow balance, b(s), on October 1. Similarly, the initial ice balance, b0(i), is the loss of ice after October 1 and before winter accumulation begins. The quantity is the difference between the ice balance at the stake, b’(i), on October 1 and the b’(i) listed for the date of the minimum balance, when the minimum balance occurs after October 1. In other words, this is the part of a year’s net balance that occurs after the beginning of the next fixed-date year.
For field safety reasons, the last visit of the summer usually is made before the time of the minimum balance and seldom precisely at the beginning of the fixed-date mass balance year, on October 1. The field safety concerns are that shortly after the time of minimum mass balance, thin new snow bridges form over crevasses and intense winter storms prevail at Wolverine Glacier; both increase the dangers of surface access to and movement in the vicinity of the measurement sites.
The net balance minima and balance values for the end of the fixed-date (hydrologic) year are measured or estimated using late summer measurements of air temperature and precipitation and the mass balances measured before and after the end of summer. Minimum values for the net mass balance are actually measured during subsequent winter field visits, before the next spring melting begins. However, the time of occurrence of the net mass balance minima and the mass balance at the end of the hydrologic year must be estimated.
A simple mass balance model is used to estimate the date of the net balance minimum and the adjustment values needed to evaluate the mass balance at the end of the hydrologic year. The model is applied to the period between the measured mass balances that bound the end of summer and uses the average lapse rate of air temperature between the nearby coastal city of Seward, 17 m altitude (fig. 1), and Wolverine Glacier, 990 m altitude, of -5.8°C/1,000 m (calculated from data in Mayo and others (1992), Kennedy (1995), and tables 5—excel file 26KB and 6—excel file 27KB in this report). Daily precipitation at each site is estimated by using the ratio of snow accumulation at each site and the precipitation-gage catch (tables 7—excel file 18KB and 8—excel file 25KB) for periods when there is no snowmelt. Snow and rain are differentiated by assuming that wet snow falls when the daily average air temperature is between 0°C and +1.7°C, as documented elsewhere (U.S. Army, 1956, p. 55). During periods when temperatures are within that range, snow accumulation and snowmelt occur simultaneously. Dry snow is assumed to accumulate when the daily average temperature is below 0°C, and rain is assumed to be falling when the daily average temperature is above +1.7°C at each site. The model estimates ablation on the basis of the daily average air temperature and the rate of icemelt expressed in meters of water equivalent per degree-day, m(w)/°d (9—excel file 22KB). A melting rate of -0.0045 m/°C-day is used to estimate the melting of wet snow and glacier ice.
The date of the net mass balance minimum at each site is estimated by using the model to evaluate daily snow and ice balances for the period after the late-summer field trip. After the date of the net mass balance minimum is determined, the mass balance at the end of the hydrologic year is evaluated.
If the net mass balance minimum occurs before the end of the hydrologic year, the amount of accumulation between the two dates must be estimated. This estimated quantity is termed the late snow balance, b1(ls). The late snow balance is evaluated for the period between the net balance minimum and the end of the hydrologic year as the cumulative value of the modeled daily precipitation as snow.
If the net mass balance minimum occurs after the end of the hydrologic year, the amount of melting of snow and ice between the two dates is estimated. This estimated quantity is termed the final ice balance, b1(i). The final ice balance is evaluated for the period between the end of the hydrologic year and the time of the net balance minimum by accumulating the number of degree-days warmer than 0°C at each measurement site and multiplying by the average melt rate.
The estimated quantities are small increments of mass balance that are added to or subtracted from the field measurements to determine the annual mass balance for the hydrologic year. The estimated quantities are different for each site and each year. However, the estimated quantities introduce no cumulative errors in mass balance because the final ice balance increments, b1(i), and late snow balance, b1(ls), of one year become the initial balances, bo(i) and bo(s), of the next year.
All the mass balance measurements from April 1966 through January 1996, the estimated balance-minimum dates, and end-of-year balances are listed in tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB for each measurement stake. The net and annual mass balances from 1966 through 1995 at three sites on Wolverine Glacier are summarized in table 10—excel file 23KB and in figure 7.
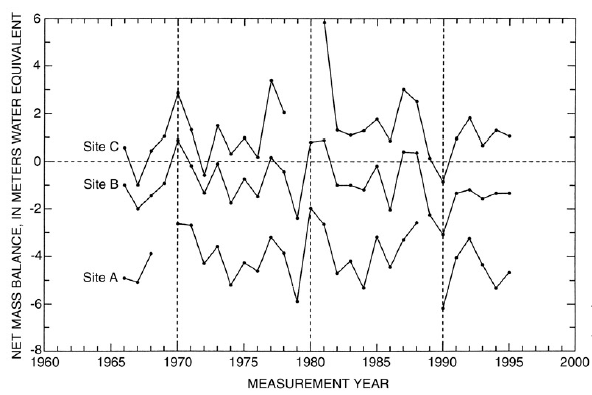
Figure 7. Yearly net mass balance measurements at sites A, B, and C on Wolverine Glacier, Alaska. (Lines connecting measurements are discontinuous where data are missing)
Permanent geodetic monuments are installed at Wolverine Glacier at strategic locations (fig. 2) where the snow usually is blown away. The monuments are visible from the glacier because the reference points are the tops of cementfilled pipes that extend above the rock, except the monument Stylus, which is a sharp, rocky peak, and Precip, which is the precipitation gage orifice at the weather station. These monuments provide year-round reference marks for all motion and glacier surface altitude measurements. The coordinates assigned to the monuments are based on the Universal Transverse Mercator Projection (UTM Zone 6). A local, rectilinear coordinate system at Wolverine Glacier has its origin at UTM Easting = 392,000 m and Northing = 6,693,000 m; NAD 27; its linear scale is located at sea level.
The coordinates of the monuments (table 11—excel file 35KB) evolved from 1976 to 1979 for several reasons. First, the altitude of the surface where the horizontal scale is calculated in the local system changed, initially at 1,000 m altitude, and finally at sea level. Second, eventually all angles and all sides of adjacent triangles were measured, which improved the accuracy. Third, the coordinates were based, at first, to geodetic monuments having coordinates that pre-dated the 1964 Good Friday earthquake (9.2 Richter magnitude) in south-central Alaska. Before 1979, the horizontal coordinates represented pre-earthquake positions. The altitude control at Wolverine Glacier, however, was based on the pre-earthquake positions of control monuments but corrected for the lowering of 0.9 m measured in nearby coastal areas (Plafker, 1969).
In 1979, the USGS established post-earthquake coordinates in the southern region of Alaska to correct for the considerable crustal movement that accompanied the 1964 earthquake. The 1979 coordinates at Wolverine Glacier (Net79, table 11—excel file 35KB) are based on surveys to the glacier from control monuments having post-1964 earthquake positions. The horizontal coordinates of Net79 are at sea level.
Project grid coordinates (Net79) at Wolverine Glacier can be converted to UTM (Zone 6) coordinates with the following equations:
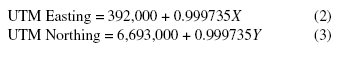
Great care was taken at Wolverine Glacier to establish accurate monument coordinates. All sides and angles of each adjacent triangle were measured. Then the angles and side lengths were adjusted within the measurement uncertainty to form mathematically correct figures. Accurate vertical angles were measured simultaneously between two survey theodolites located over each of two monuments so that the effects of Earth curvature and atmospheric refraction could be determined and eliminated in the process of defining the precise altitude differences between monuments. As a result, adjacent monuments have relative position accuracies on the order of 0.01 to 0.02 m in X, Y, and Z coordinates, and the cumulative uncertainty over the entire geodetic network is on the order of 0.10 m. High relative precision of monument coordinates enables the analysis of variable atmospheric refraction conditions that result from variable weather conditions during each glacier survey. Thus, variable atmospheric conditions do not introduce vertical errors in stake positions and glacier surface altitudes at Wolverine Glacier.
Geodetic surveys before 1979 either were shifted by the amounts indicated in table 11—excel file 35KB or recalculated using Net79 coordinates. In either case, accuracy is maintained within about ±0.05 m. Final values are rounded to 0.1 m because glacier surface roughness and stake deformation produce larger uncertainties in the glacier motion results than do the surveys.
Accurate measurements of stake positions and glacier surface altitudes are made routinely at sites A, B, and C at Wolverine Glacier at the same time that mass balance measurements are made. A description of the survey methods used at Wolverine Glacier is given here because some of the methods are very useful for glacier research but are not described in standard surveying texts.
To reduce the time required for the measurements, any of four survey methods can be used: resection, foresight, and intersection (see Mayo and Trabant, 1982, for details). The method selected is the one that requires the least travel. Surveys are made most frequently with a theodolite set up on the glacier surface. Its precise location is determined by the resection method. The local targets then are surveyed by short foresights. At site A, intersection from two easily accessible monuments sometimes is used if the stake does not need attention, thus avoiding a hike to the site. Occasionally, when crevasses block access to the stakes or when many stakes are visible, intersection surveys are made to the stakes from two accessible resection sites.
To set up a theodolite on the glacier, three small plywood boards are placed in holes chopped in the ice or stamped firmly into the snow to serve as supports for the tripod legs. A period of 5 to 10 minutes is sometimes required between the initial setup and the beginning of the survey to allow the supports and the instrument to stabilize. If the temperature is above 0oC, snow or ice is placed on the tripod feet to shield them from the effects of sunlight and warm air.
After the theodolite is stable, measurements are made to three monuments to determine the coordinates of the instrument by resection. The closest monument typically is used as the principal reference, and then a second monument is observed. The principal monument is surveyed a second time to detect any instrument motion. Immediately, the third monument is measured, and a final closing measurement of the principal monument is made. This produces eight independently measured horizontal angles between the monuments, six vertical angles to the principal reference monument, and two vertical angles to the other two monuments.
The horizontal angle data are used to calculate the instrument’s horizontal location by the resection method that is explained in standard surveying texts (for example, Moffitt and Bouchard, 1987).
To reduce the effect of variable meteorological conditions, the measured vertical angles are used to solve for two unknowns: the Earth curvature/atmospheric refraction coefficient, f, and the altitude of the surveying instrument, Zi, using a technique developed by the authors for surveying at large mountain glaciers (Mayo and others, 1979). The method requires using two equations to solve for the two unknowns. The equation used to calculate the instrument altitude is:
![]()
where
Zm is the monument altitude,
Dh is the horizontal distance between the instrument and the monument, and
Vm is the vertical angle to the monument.
The second equation is the same as the first (equation 4) but uses a second monument, its altitude, and the measured vertical angle to it. In the general case, the subscript, m, is replaced by A, B, or C to identify the monuments. Because Zi must have a single value, the right sides of the two equations can be equated. Then, assuming that the combined Earth curvature and refraction coefficient, f, has a unique value:
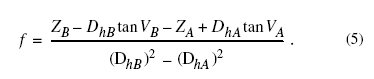
Once the curvature and refraction coefficient, f, is known, the instrument altitude, Zi , can be calculated using equation 4.
In practice, the measurements to the three monuments are paired in three combinations, AB, BC, and CA. This results in three independent determinations of Zi and f. Some care must be exercised in interpreting these results. For example, as the horizontal distances to the two monuments approach the same value, the denominator of equation 5 approaches zero and the ability of this technique to determine Earth curvature/ atmospheric refraction diminishes. The strongest solution for f is where the difference in the distances to two monuments is relatively large. Knowing this, the surveyor can select an optimal group of monuments for a resection. The coefficient f normally ranges from about 0 to 70 x10-9. If f is 0, light travels along a curve that is the same as Earth curvature; the Earth appears to be flat and there is no correction. This can be caused by temperature inversion conditions. If f is 70 x10-9, then the vertical correction is 0.28 m at a horizontal distance, Dh , of 2,000 m. Values outside these limits are rejected if there is a reason to suspect they are weak. For example, sometimes the exact top of a monument is not clear in the telescope view. If that is noted, calculations of f using that monument are also suspect.
The final instrument altitude, Zi, is determined using only the reliable vertical measurements and strong solutions for f. The result of this altitude determination process is that variable atmospheric refraction conditions do not contaminate the data. Thus, resection location data are relatively accurate despite the fact that instruments are set up on snow and ice and that they are calculated on the basis of monuments located at some distance away at the margin of the glacier.
After the theodolite location is established by resection, care is taken not to disturb the instrument when foresight surveys to the stake and glacier surface are made. Local survey targets include two points on each stake: one above the glacier surface and a second at the glacier surface. These two surveys enable calculation of stake lean and the position of the base of the stake.
The glacier surface altitude at a fixed location is measured during each visit by surveying three points on the glacier surface. The points form a triangle surrounding a horizontally fixed measurement site, enabling calculation of the surface altitude at the fixed location (the horizontally fixed sites are listed later in the “Surface Altitudes” section). In some cases, the glacier surface beneath the surveying instrument serves as one of these points and the glacier surface at the stake often serves as a second point, so only one additional surface point is needed. To help select the three surface points, the field crew carries a map showing the expected location of the stake relative to the horizontally fixed surface altitude measurement site.
The base of a stake is the most reliable point to follow for glacier ice motion determination because the stake base is affected least by stake lean. Stake positions listed in table 12—excel file 43KB, 13—excel file 43KB, and 14—excel file 46KB are the coordinates of the bases of the stakes. The average ice speed between surveys is calculated from the stake displacement in three dimensions and the number of days between surveys divided by 365.25 days per year. This results in speed expressed as meters per year. Stake locations are calculated initially to 0.01-m accuracy, then rounded to 0.1 m because of uncertainties about the stake lean and the location of the stake base. The uncertainties of stake position surveys are on the order of 0.1 to 0.2 m in the horizontal and 0.05 to 0.10 m in the vertical.
Glacier motion directions, both horizontal and vertical, are reported using the grad angular unit, in which 100 grads is a right angle. Horizontal motion direction is reported using standard rectangular to polar coordinate conversions where zero is east and the positive direction is counter clockwise from east. Vertical motion direction also is reported in grad units where horizontal is zero and positive is upward.
Sometimes stakes are temporarily lost because they are buried by deep snow. Nevertheless, the glacier motion record can be maintained without interruption. A buried stake sometimes can be found by predicting where glacier motion has moved it, then finding that location by surveying and digging a wide pit at the site. In one case, the stake was not found in the initial pit, but a compass indicated its presence in the snow behind the pit wall, where it was, indeed, found.
The method used for recovering glacier motion data from a temporarily lost stake is to install another stake near the buried stake and survey it. Later, when both stakes become visible, both are surveyed to determine their relative positions. Assuming that the two stakes have maintained their relative positions, the coordinates of the buried stake can be calculated for the dates when only the replacement stake was surveyed. This procedure sustains a continuous glacier motion record, even when deep snow interrupts sequential measurements. When this Procedure is used, the mass balance data tables (tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB) list a stake as buried, but the ice motion tables (tables 12—excel file 43KB, 13—excel file 43KB, and 14—excel file 46KB) indicate estimated coordinates for the buried stake and a calculated stake height, b'.
Glacier surface altitudes at horizontally fixed locations are calculated for the following three sites on Wolverine Glacier (Mayo and Trabant, 1982):
| Site | X(meters) | Y(meters) |
|---|---|---|
| A | 2502.6 | 1773.0 |
| B | 3075.8 | 4796.9 |
| C | 2160.5 | 6473.6 |
| (before 2/28/78 | ||
| C | 2353.1 | 6553.2 |
| (before 2/28/78 | ||
Snow depths reported in the mass balance tables (tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB) are transferred to the ice motion tables (tables table 12—excel file 43KB, 13—excel file 43KB, and 14—excel file 46KB) to calculate the altitudes of buried summer surfaces. Surface altitude and snow depth values are rounded to 0.1 m for calculations of summer surface altitudes and the emergence component of motion because that is the general precision of determining glacier surface altitudes.
Emergence (fig. 8) is the vertical component of glacier motion measured near the surface of a glacier (Meier and Tangborn, 1965). In other words, emergence is a measure of how much glacier motion would change the thickness of the glacier at a location that is fixed in space if the mass balance were zero. The motion is emergent if the vector is directed upward; that is, the glacier would become thicker at this location if the mass balance were zero. The motion is submergent (negative emergence) if the vector is directed downward; the glacier would become thinner at this location if the mass balance were zero. The emergence for a period can be determined as the difference between the change in altitude of the glacier surface at a fixed location and the altitude effect of the mass balance change during the period (eq. 6 and fig. 8).
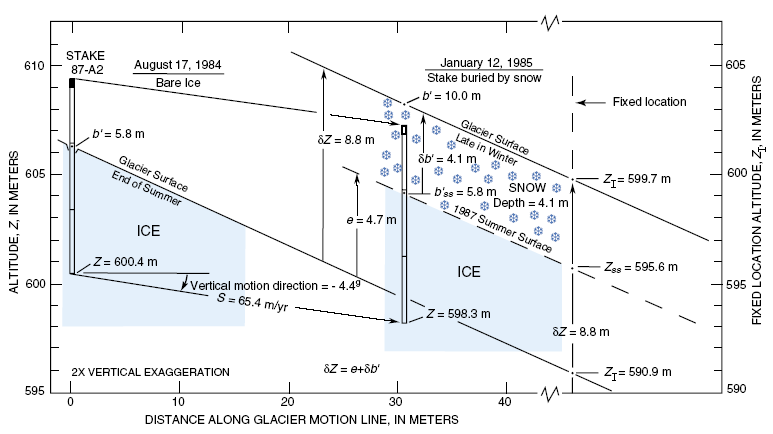
Figure 8. Vertical section along the glacier flow
line at Site A on Wolverine Glacier, Alaska, showing the relations among mass
balance measurements, stake positions, components of glacier motion, and surface
heights from August 17, 1984, to January 12, 1985. (The diagram shows a single
stake at two different times and the fixed location. Stake heights of the glacier
surface (b’) are listed in tables 2 and 12. The method used to
evaluate the position of a temporarily buried stake using a second, nearby stake,
is defined in text section "Glacier Motion." Consecutive positions
of stake 87-A2 (X, Y, and Z), glacier speed vector (S),
stake readings (b’), altitudes of the glacier surface at the
fixed-location measurement site (ZI each date), and emergence (e) are
listed in table 12. The upward emergence (e) caused by the vertical
angle of motion being less steep downward than the glacier’s surface slope
indicates that the glacier would have become 4.7 meters (m) thicker at this
site during the measurement period if the mass balance had been zero. However,
4.1 m of snow accumulated between the two dates and, as a result, the glacier
altitude increase, ![]() Z,
was the total of 4.7 m (emergence) + 4.1 m (mass balance) = 8.8 m. Other abbreviations:
b’ss, height of summer surface above base of stake; Zss,
summer surface altitude; g, grad angular units; m/yr, meters per year)
Z,
was the total of 4.7 m (emergence) + 4.1 m (mass balance) = 8.8 m. Other abbreviations:
b’ss, height of summer surface above base of stake; Zss,
summer surface altitude; g, grad angular units; m/yr, meters per year)
The emergence, e, for the period between surveys is:
![]()
where
Z1 is the altitude of the glacier surface at the fixed site at the end of the period,
Z0 is the altitude of the glacier surface at the fixed site at the beginning of the period,
b’1 is the stake height of the glacier surface at the end of the period, and
b’0 is the stake height of the glacier surface at the beginning of the period.
The emergence rate, e, in meters per year, is the emergence, e, divided by the time period, in years. Emergence and emergence rate are tabulated on tables table 12—excel file 43KB, 13—excel file 43KB, and 14—excel file 46KB).
Thirty years of net and annual mass balances from April 1966 through the 1995 measurement year at three sites on Wolverine Glacier are summarized in table 10 and in figure 7. The estimated balance-minimum dates, end-of-year balances, and all the field measurements are listed in tables 2—excel file 152KB, 3—excel file 184KB, and 4—excel file 176KB for each measurement stake. The average annual balance at site A (590 meters altitude) was -4.06 meters water equivalent; at site B (1,070 meters altitude), -0.90 meters water equivalent; and at site C (1,290 meters altitude), +1.45 meters water equivalent.
Glacier ice motion measurements began in February 1975; the data are listed through January 1996. The measurements provide a 21-year record of seasonal glacier surface speeds (figs. 9, 10, and 11) and glacier surface altitude fluctuations (figs. 12, 13, and 14). A small number of breaks in the record are caused by extreme conditions, such as the burial of stakes by snow, snow depths too great for reliable probing, or summers with large amounts of melt that caused stakes to fall before they could be reset. The average surface speed at the three sites from 1975 to 1996 was 50.0 m/yr at site A, 83.7 m/yr at site B, and 37.2 m/yr at site C. Surface speeds ranged from a minimum of 34.1 m/yr to a maximum of 74.0 m/yr at site A; from 67.4 to 100.3 m/yr at site B; and from 27.3 to 50.3 m/yr at site C. In response to mass balance and glacier motion variations, glacier surface altitudes rose and fell over a range of 19.4 m at site A, 14.1 m at site B, and 13.2 m at site C. The average surface altitudes were 594 m at site A, 1,069 m at site B, and 1,293 m at site C.
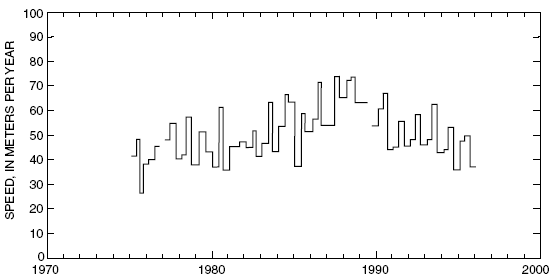
Figure 9. Glacier surface speed at site A on Wolverine Glacier, Alaska. (When more than one stake was measured during a period, the average speed is plotted. Lines are discontinuous where data are missing)
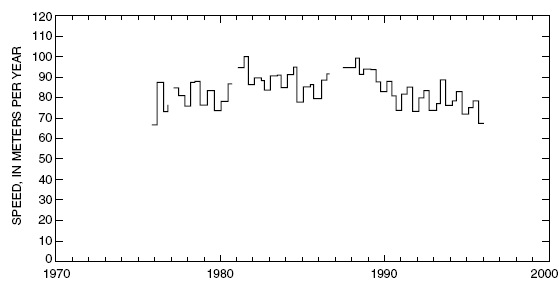
Figure 10. Glacier surface speed at site B on Wolverine Glacier, Alaska. (When more than one stake was measured during a period, the average speed is plotted. Data for stakes located more than 100 meters from the flow line though the measurement site are not shown. Lines are discontinuous where data are missing)
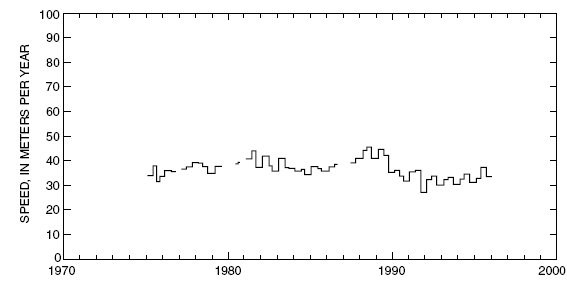
Figure 11. Glacier surface speed at site C on Wolverine Glacier, Alaska. (When more than one stake was measured during a period, the average speed is plotted. Lines are discontinuous where data are missing
Figure 12. Glacier surface altitude at site A on Wolverine Glacier, Alaska. (The line connecting the surface altitude measurements also is drawn through estimates of the seasonal maxima and minima. Dots below the line representing the glacier surface indicate altitudes of summer surfaces buried under the snow)
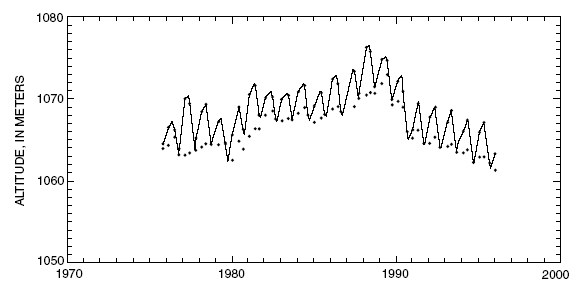
Figure 13. Glacier surface altitude at site B on Wolverine
Glacier, Alaska. (The line connecting the surface altitude measurements also
is drawn through estimates of the seasonal maxima and minima. Dots below the
line representing the glacier surface indicate altitudes of summer surfaces
buried under the snow)
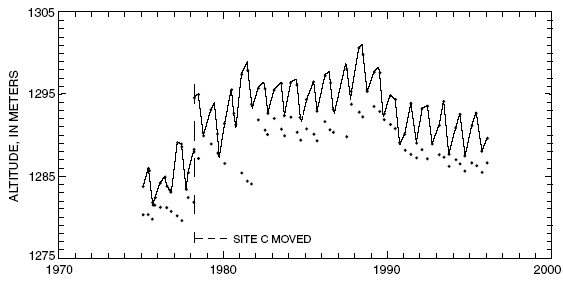
Figure 14. Glacier surface altitude at site C on Wolverine
Glacier, Alaska. (The line connecting the surface altitude measurements also
is drawn through estimates of the seasonal maxima and minima. Dots below the
line representing the glacier surface indicate altitudes of summer surfaces
buried under the snow)
Benson, C.S., 1959, Physical investigations of the snow and firn of northwest Greenland, 1952, 1953, and 1954: U.S. Army Corps of Engineers, Snow Ice and Permafrost Research Establishment Research Report 26, 62 p.
Colbeck, S.C., 1974, The capillary effects on water percolation in homogeneous snow: Journal of Glaciology, v. 13, no. 67, p. 85-98.
Heinrichs, T.A., Mayo, L.R., Trabant, D.C., and March, R.S., 1995, Observations of the surge-type Black Rapids Glacier, Alaska, during a quiescent period, 1970-92: U.S. Geological Survey Open-File Report 94-512, 95 p., appendixes.
Hodge, S.M., 1972, The movement and basal sliding of the Nisqually Glacier, Mt. Rainier: University of Washington, Department of Atmospheric Sciences, Science Report, 409 p. (Ph.D. dissertation.)
Kennedy, B.W., 1995, Air temperature and precipitation data, Wolverine Glacier Basin, Alaska, 1967-94: U.S. Geological Survey Open-File Report 95-444, 79 p.
Krimmel, R.M., 1999, Water, ice, meteorological, and speed measurements at South Cascade Glacier, Washington, 1998 balance year: U.S. Geological Survey Water-Resources Investigations Report 99-4049, 36 p.
March, R.S., and Trabant, D.C., 1998, Mass balance, meteorological, ice motion, surface altitude, and runoff data at Gulkana Glacier, Alaska, 1994 balance year: U.S. Geological Survey Water-Resources Investigations Report 97-4251, 31 p.
Mayo, L.R., 1992, Internal ablation—An overlooked component of glacier mass balance: Eos, Transactions American Geophysical Union, v. 73, no. 43, p. 180.
Mayo, L.R., March, R.S., and Trabant, D.C., 1992, Air temperature and precipitation data, 1967-88, Wolverine Glacier Basin, Alaska: U.S. Geological Survey Open-File Report 91-246, 80 p.
Mayo, L.R., Trabant, D.C., March, Rod, and Haeberli, Wilfried, 1979, Columbia Glacier stake location, mass balance, glacier surface altitude, and ice radar data, 1978 measurement year: U.S. Geological Survey Open-File Report 79- 1168, 72 p.
Mayo, L.R., Meier, M.F., and Tangborn, W.V., 1972, A system to combine stratigraphic and annual mass balance systems: A contribution to the International Hydrological Decade: Journal of Glaciology, v. 11, no. 61, p. 3-14.
Mayo, L.R., and Trabant, D.C., 1982, Geodetic trisection, altitude, and ice-radar techniques used at Knik Glacier, Alaska, and summary of 1979, 1980, and 1981 data: U.S. Geological Survey Open-File Report 82-685, 26 p.
Mayo, L.R., Trabant, D.C., March, Rod, and Haeberli, Wilfried, 1979, Columbia Glacier stake location, mass balance, glacier surface altitude, and ice radar data, 1978 measurement year: U.S. Geological Survey Open-File Report 79- 1168, 79 p.
Meier, M.F., 1960, Mode of flow of Saskatchewan Glacier, Alberta, Canada: U.S. Geological Survey Professional Paper 351, 70 p.
Meier, M.F., and Tangborn, W.V., 1965, Net budget and flow of South Cascade Glacier, Washington: Journal of Glaciology, v. 5, no. 41, p. 547-566.
Meier, M.F., Tangborn, W.V., Mayo, L.R., and Post, Austin, 1971, Combined ice and water balances of Gulkana and Wolverine Glaciers, Alaska, and South Cascade Glacier, Washington, 1965 and 1966 hydrologic years: U.S. Geological Survey Professional Paper 715-A, 23 p.
Moffitt, F.H., and Bouchard, H., 1987, Surveying (8th edition):
New York, Harper Collins Publishers, 876 p.
Østrem, Gunnar, and Stanley, Alan, 1969, Glacier mass balance measurements—A
manual for field and office work, revised edition: Canadian Department of Energy,
Mines and Resources, and The Norwegian Water Resources and Electricity Board,
107 p.
Plafker, George, 1969, Tectonics of the March 27, 1964, Alaska Earthquake: U.S. Geological Survey Professional Paper 543-I, 74 p.
Tangborn, W.V., Mayo, L.R., Scully, D.R., and Krimmel, R.M., 1977, Combined ice and water balances of Maclure Glacier, California, South Cascade Glacier, Washington, and Wolverine and Gulkana Glaciers, Alaska, 1967 hydrologic year: U.S. Geological Survey Professional Paper 715-B, 20 p.
Trabant, D.C., and Mayo, L.R., 1985, Estimation and effects of internal accumulation on five glaciers in Alaska: Annals of Glaciology, v. 6, p. 113-117.
UNESCO, 1970, Combined heat, ice and water balances at selected glacier basins: United Nations Educational, Scientific, and Cultural Organization, International Association of Scientific Hydrology, Technical Papers in Hydrology, no. 5, 20 p.
U.S. Army, 1956, Snow hydrology; summary report of snow investigations: U.S. Army Corps of Engineers, North Pacific Division, Portland, Oregon, 435 p.
This report is available in Portable Document Format (PDF) 2.1MB
If you do not have the Adobe Acrobat PDF Reader, it is available for free download from Adobe Systems Incorporated.
Document Accessibility: Adobe Systems Incorporated has information about PDFs and the visually impaired. This information provides tools to help make PDF files accessible. These tools convert Adobe PDF documents into HTML or ASCII text, which then can be read by a number of common screen-reading programs that synthesize text as audible speech. In addition, an accessible version of Acrobat Reader 5.0 for Windows (English only), which contains support for screen readers, is available. These tools and the accessible reader may be obtained free from Adobe at Adobe Access.
For more information about USGS activities in Alaska, visit the USGS Alaska District home page.
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|