

Prepared in cooperation with Holloman Air Force Base and the City of Alamogordo
Simulation of Ground-Water Flow
Appendix 1. Computation of Ground-Water-Flow Directions
Figure 1. Location of the Tularosa geologic basin and study area.
Figure 2. Generalized section across the Tularosa Basin. Line of section shown in figure 1.
Figure 3. Location of subbasins on the margin of the Tularosa hydrologic ba...
Figure 4. Location of ground-water flow-model grid.
Figure 5. Location of active ground-water flow-model layers.
Figure 6. Location of cells in which recharge is implemented in the ground-...
Figure 7. Areas of municipal ground-water withdrawals.
Figure 8. Areas of agricultural ground-water withdrawals and agricultural s...
Figure 9. Location of model cells representing steady-state and transient-m...
Figure 10. Water-level contours representing measured 1911-12 water levels ...
Figure 11. Zones of hydrologic properties.
Figure 12. Test for nonnormality of steady-state residual errors.
Figure 13. Values of steady-state residual errors, simulated steady-state w...
Figure 14. Distribution of steady-state residual errors.
Figure 15A. Simulated and measured water levels from 1948 to 1995 at transi...
Figure 15B. Simulated and measured water levels from 1948 to 1995 at transi...
Figure 15C. Simulated and measured water levels from 1948 to 1995 at transi...
Figure 15D. Simulated and measured water levels from 1948 to 1995 at transi...
Figure 15E. Simulated and measured water levels from 1948 to 1995 at transi...
Figure 15F. Simulated and measured water levels from 1948 to 1995 at transi...
Figure 16. Sensitivity of steady-state model to changes in selected hydrolo...
Figure 17. Sensitivity of transient model to changes in selected hydrologic...
Figure 18. Locations of model cells representing water levels measured in 1...
Figure 19. Areas of simulated evapotranspiration under steady-state conditi...
Figure 20. Areas of simulated evapotranspiration under 1995 zero return-flo...
Figure 21. Contours of simulated water levels in the uppermost active model...
Figure 22. Contours of simulated water levels in the uppermost active model...
Figure 23. Contours of simulated water levels in the uppermost active model...
Figure 24. Contours of simulated water levels in the uppermost active model...
Figure 25. Contours of projected water levels in the uppermost active model...
Figure 26. Contours of projected water levels in the uppermost active model...
Figure 27A. Measured water levels and water levels simulated or projected u...
Figure 27B. Measured water levels and water levels simulated or projected u...
Figure 27C. Measured water levels and water levels simulated or projected u...
Figure 28. Simulated water-level changes within the well-calibrated area of...
Figure 29. Projected water-level changes within the well-calibrated area of...
Figure 30. Generalized simulated directions of horizontal and vertical grou...
Figure 31. Generalized simulated directions of vertical ground-water flow i...
Figure 32. Generalized simulated directions of horizontal ground-water flow...
Figure 33. Generalized simulated directions of horizontal and vertical grou...
Figure 34. Generalized simulated directions of horizontal and vertical grou...
Figure 35. Generalized simulated directions of horizontal ground-water flow...
Figure 36. Generalized projected directions of horizontal and vertical grou...
Figure 37. Generalized projected directions of horizontal and vertical grou...
Figure 38. Generalized projected directions of horizontal ground-water flow...
Figure 39. Generalized simulated directions of horizontal and vertical grou...
Figure 40. Generalized simulated directions of horizontal and vertical grou...
Figure 41. Generalized simulated directions of horizontal ground-water flow...
Figure 42. Generalized simulated directions of horizontal and vertical grou...
Figure 43. Generalized simulated directions of horizontal and vertical grou...
Figure 44. Generalized simulated directions of horizontal ground-water flow...
Figure 45. Generalized projected directions of horizontal and vertical grou...
Figure 46. Generalized projected directions of horizontal and vertical grou...
Figure 47. Generalized projected directions of horizontal ground-water flow...
Table 1. Rates of selected ground- and surface-water usage in the Tularosa ...
Table 2. Sources, durations, and locations of ground-water withdrawal stres...
Table 3. Location of transient-model calibration points, selected informati...
Table 4. Ground-water levels measured in the Tularosa Basin from Meinzer an...
Table 5. Horizontal hydraulic conductivity and vertical conductance estimat...
Table 6. Apparent ages and calculated travel times of ground water at selec...
Table 7. Measured and simulated water levels using the zero and maximum ret...
Table 8. Subbasin number and characteristics, fraction of precipitation in ...
Table 9. Simulated flows into and out of the basin-fill aquifer, 1948-2040.
| Multiply | By | To obtain |
|---|---|---|
| Length | ||
| inch (in.) | 2.54 | centimeter (cm) |
| foot (ft) | 0.3048 | meter (m) |
| mile (mi) | 1.609 | kilometer (km) |
| Area | ||
| acre | 0.004047 | square kilometer (km2) |
| square mile (mi2) | 2.590 | square kilometer (km2) |
| Volume | ||
| cubic foot (ft3) | 0.02832 | cubic meter (m3) |
| acre-foot (acre-ft) | 1,233 | cubic meter (m3) |
| gallon | 3.785 | liter |
| Flow rate | ||
| gallon per minute (gal/min) | 0.06309 | liter per second (L/s) |
| foot squared per day (ft2/d) | 0.09290 | meter squared per day |
| acre-foot per acre (acre-ft/acre) | 0.003048 | cubic hectometer per hectare |
Horizontal coordinate information is referenced to the North American Datum of 1983 (NAD 83).
Vertical coordinate information is referenced to the North American Vertical Datum of 1988 (NAVD 88).
The hydrology of the basin-fill aquifer in the Tularosa Basin was evaluated through construction and calibration of steady-state and transient three-dimensional ground-water-flow simulations. Simulations were made using the U.S. Geological Survey finite-difference modular ground-water-flow computer software MODFLOW-96. The transient simulation covered 1948-2040. Both steady-state and transient simulations were calibrated by matching simulation output to available ground-water-level measurements. The root-mean-square error of the steady-state calibration in the well-calibrated area of the ground-water-flow simulation was 6.3 meters, and root-mean-square errors of individual transient-calibration points ranged from 0.8 to 17.0 meters. The areal distribution of water-level measurements used in the steady-state and transient calibrations restricts the well-calibrated area of the model to the eastern side of the Tularosa Basin. Water levels in the La Luz Creek subbasin area were underestimated by both the steady-state and transient models, suggesting that the hydrology of this area is not well represented in the model.
About 143,000 cubic meters per day of recharge is estimated to enter the basin-fill aquifer from subbasins that rim the Tularosa Basin. The estimated recharge is about 4-5 percent of total precipitation in most subbasins. Approximately 88 percent of total recharge left the basin-fill aquifer as evapotranspiration under predevelopment conditions.
Water levels were simulated for 1948, 1995, and 2040 under scenarios of zero and maximum return flows. Estimated return flows from municipalities were calculated on the basis of data in the Tularosa Basin Regional Water Plan for 2000-2040. Agricultural return flows were estimated primarily on the basis of ground-water-withdrawal, ground-water-depletion, surface-water-withdrawal, and surface-water-depletion data for the Tularosa Basin. The ground-water-flow simulation was sensitive to the return-flow scenario in the agricultural area near Tularosa and decreasingly sensitive to the south. Declines in simulated water levels near Tularosa between 1948 and 1995 were as large as 30 meters under the zero return-flow scenario and 15 meters under the maximum return-flow scenario. Declines in simulated water levels between 1995 and 2040 were as large as 25 meters under the zero return-flow scenario and 15 meters under the maximum return-flow scenario. Comparison of water levels measured near Tularosa in 1991 and water levels simulated under the maximum return-flow scenario for 1991 suggests that declines in simulated water levels near Tularosa may be overestimated under the zero return-flow scenario. Declines in simulated water levels near the City of Alamogordo well field between 1948 and 1995 were as large as 15 meters under the zero return-flow scenario and 10 meters under the maximum return-flow scenario. Simulated declines in water levels between 1995 and 2040 were nearly 15 meters under both return-flow scenarios assuming that all projected increases in withdrawal came from existing City of Alamogordo public-supply wells and all withdrawal from the wells came from the basin-fill aquifer. Declines in simulated water levels near the Holloman Air Force Base well fields between 1948 and 1995 and between 1995 and 2040 were less than 5 meters under both the zero and maximum return-flow scenarios. In 1995 under the zero return-flow scenario, an estimated 56,000 cubic meters of water per day was removed from aquifer storage. Of the approximately 199,000 cubic meters of water per day that left the aquifer under 1995 conditions, 40 percent left the basin-fill aquifer as ground-water withdrawal, 51 percent as evapotranspiration, 7 percent by interbasin ground-water flow into the Hueco Bolson, and 2 percent by flow into creeks and springs.
Generalized directions of ground-water flow were simulated for 1948, 1995, and 2040 for much of the eastern part of the Tularosa Basin. Localized areas of change between simulated 1948 and 1995 flow directions and between simulated 1995 and 2040 flow directions are present near the City of Alamogordo well field and the Holloman Air Force Base well fields.
Scientific hydrologic study of the Tularosa Basin began in 1911 with the work of Meinzer and Hare (1915). In 1911, railroad and agricultural activity had already begun in the Tularosa Basin; however, development was minimal. Population growth and concurrent development in the intervening years have stressed water resources in the Tularosa Basin. In October 1996, the U.S. Geological Survey (USGS) in cooperation with Holloman Air Force Base and the City of Alamogordo, New Mexico, began a study to evaluate the hydrology of the Tularosa Basin to estimate rates of ground-water recharge and to determine the effects of current and anticipated water use. To accomplish these goals, steady-state and transient ground-water-flow models of the non-saline part of the basin-fill aquifer in the Tularosa Basin were constructed and calibrated.
This report documents the construction and calibration of three-dimensional finite-difference basinwide steady-state and transient ground-water-flow models of the Tularosa Basin and describes simulated ground-water flow in the non-saline part of the basin-fill aquifer. For the purpose of this report, the non-saline part of the basin-fill aquifer is that which contains water having dissolved-solids concentrations of 10,000 milligrams per liter (mg/L) or less. The model simulates steady-state initial conditions represented by water levels measured mostly in 1911-12, historical responses of water levels to hydrologic stresses for 1948-95, and simulated responses of water levels to projected future stresses to 2040.
The Tularosa Basin is a downfaulted, arid to semiarid area covering about 17,000 square kilometers of south-central New Mexico (fig. 1). Median annual precipitation in Alamogordo is 28.3 centimeters (11.2 inches) per year based on 96 complete years of annual precipitation data collected between 1900 and 1999 by the National Oceanic and Atmospheric Administration and tabulated by Barud-Zubillaga (2000, p. 11). Lake evaporation near Alamogordo is approximately 75 inches per year (0.0052 meter per day) (U.S. Bureau of Reclamation and the State of New Mexico, 1976). The basin is bounded on the east by the Sacramento Mountains; on the west by the Organ, San Augustin, San Andres, and Franklin Mountains; on the north by Chupadera Mesa; and on the south by a low topographic rise near the New Mexico-Texas State line that separates the Tularosa Basin from the Hueco Bolson. Large parts of the Tularosa Basin are occupied by White Sands Missile Range, White Sands National Monument, and Holloman Air Force Base. The principal city in the Tularosa Basin is Alamogordo; smaller communities include Carrizozo and Tularosa. The area of the current study is that part of the Tularosa Basin that contains the basin-fill aquifer. The southern boundary of the study area coincides with the northern boundary of the Hueco Bolson, in which ground-water flow was described by Heywood and Yager (2003).
This study benefited from information provided by Holloman Air Force Base, the City of Alamogordo, White Sands Missile Range, and the Village of Tularosa. The individuals contributing to this study are gratefully acknowledged: Bob Creel and John Kennedy (New Mexico Water Resources Research Institute); Fred Fisher, Albert Mendez, Hiram Muse, Roberto Tovar, Mark Urey, and Coy Webb (Holloman Air Force Base); Kevin Heberle, Paul Light, and Jose Miramontes (City of Alamogordo); James Harris (White Sands Missile Range); Brian Wilson (New Mexico Office of the State Engineer); and Charles Heywood, John Lovelace, Mike Kernodle, and Nathan Myers (U.S. Geological Survey).
A representative ground-water-flow simulation needs to be based on known geologic and hydrologic properties of the simulated aquifer. Geologic and hydrologic properties and processes in the Tularosa Basin are discussed in the following sections.
The Tularosa Basin is a downfaulted intermountain closed basin formed by faulting along the southern Rio Grande Rift. The basin may represent the easternmost faulting associated with the Rio Grande Rift in New Mexico (Seager and Morgan, 1979; Keller and others, 1990; Adams and Keller, 1994). Formation of the Tularosa Basin likely began about 35 million years ago (Chapin and Seager, 1975; Seager and others, 1984; Morgan and others, 1986; Keller and others, 1990) with movement along faults adjacent to the Sacramento Mountains. Recent faulting occurred about 10,000 years ago (Koning, 1999; Koning and Pazzaglia, 2002). The result of faulting was the exposure of rocks of Precambrian to Tertiary age in escarpments surrounding the basin floor. These same rocks form the bedrock that underlies the basin fill. The basin fill is derived by erosion of the uplifted terrain surrounding the basin and fluvial deposits of the ancestral Rio Grande. Unconsolidated coarse- to fine-grained coalescing alluvial-fan deposits rim the basin and grade basinward into finer grained alluvial, fluvial, and lacustrine deposits. Evaporite minerals, principally selenite, occur near Lake Lucero (fig. 1).
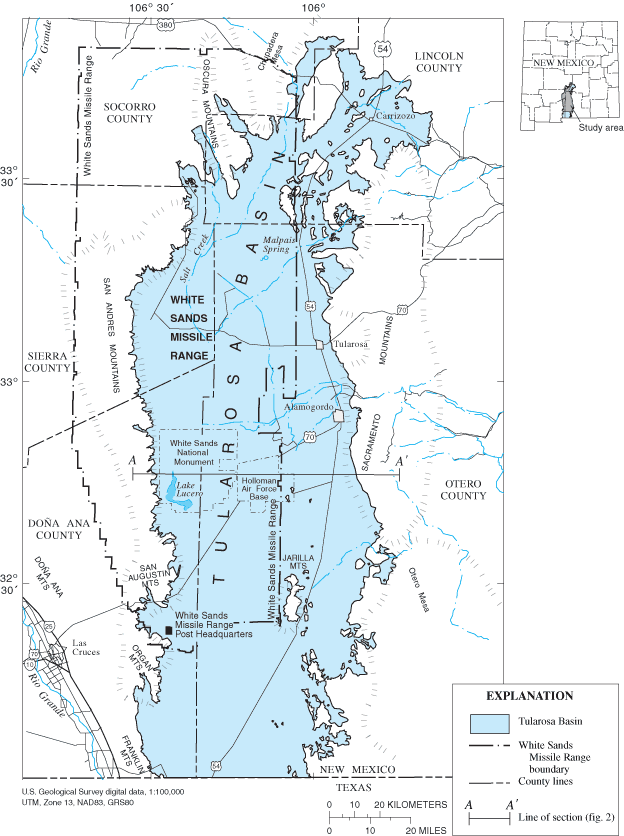
Figure 1. Location of the Tularosa geologic basin and study area.
McLean (1970) and Orr and Myers (1986) provided extensive discussions of the hydrogeology of the Tularosa Basin. The various lithologies of the basin-fill deposits collectively form the basin-fill aquifer. The thickness of the basin-fill aquifer ranges from less than 30 meters over areas of uplifted bedrock to greater than 1,200 meters. Structurally, the Tularosa Basin is divided longitudinally by a bedrock high with north-trending eastern and western grabens (fig. 2) (McLean, 1970; Healy and others, 1978; Seager and Morgan, 1979; King and Harder, 1985; Adams and Keller, 1994). Water-level maps of Meinzer and Hare (1915), McLean (1970), and Livingston Associates and John Shomaker and Associates (2002) indicate that the bedrock high apparently does not inhibit movement of ground water in the basin-fill aquifer. No areally extensive confining unit is recognized in the basin-fill aquifer.
Values of transmissivity and storativity estimated from aquifer-test results were tabulated by Garza and McLean (1977, table 10), Orr and Myers (1986, tables 1 and 2), and Morrison (1989, table 1). Reported estimated transmissivities for the basin-fill aquifer range from approximately 1,370 to 2,700 feet (127 to 251 meters) squared per day near the eastern margin of the basin to approximately 1,000 to 5,000 feet (93 to 465 meters) squared per day near the western margin of the basin. Outlier values of transmissivity as large as 20,000 feet (1,858 meters) squared per day and 79,000 feet (7,339 meters) squared per day have been reported for the basin-fill aquifer near the eastern and western margins of the basin, respectively. Values of transmissivity on the eastern side of the basin obtained from ground-water-flow model calibrations range from approximately 2,000 to 6,000 feet (186 to 557 meters) squared per day for aquifers in alluvial-fan materials to approximately 500 to 1,000 feet (46 to 93 meters) squared per day for aquifers in more basinward deposits (Burns and Hart, 1988; Morrison, 1989, table 1). Values of hydraulic conductivity estimated from aquifer tests in the Holloman Air Force Base well fields range from 6 to 23 feet (1.8 to 7.0 meters) per day (Orr and Myers, 1986). Estimates of hydraulic conductivity range from 1.0 to 15 meters per day (with an outlier value of 71.5 meters per day) for the basin-fill aquifer in alluvial deposits near the western margin of the basin to 0.05 to 0.2 meter per day in more basinward fine-grained lacustrine deposits (Orr and Myers, 1986). Storativity of the basin-fill aquifer on the eastern side of the Tularosa Basin ranges from 0.001 to 0.04 based on aquifer tests and from 0.01 to 0.12 based on numerical simulation (Morrison, 1989, table 1). Reported values of specific yield for the basin-fill aquifer are 0.15 near the White Sands Missile Range Post Headquarters (Kelly and Hearne, 1976) and 0.08 to 0.12 for the basin-fill aquifer in the Holloman Air Force Base well fields (McLean, 1970; Ballance, 1976; Garza and McLean, 1977). Frequent clay intervals in the basin-fill aquifer cause a "very small ratio of vertical to horizontal hydraulic conductivity of basin-fill deposits" (Orr and Myers, 1986, p. 7).
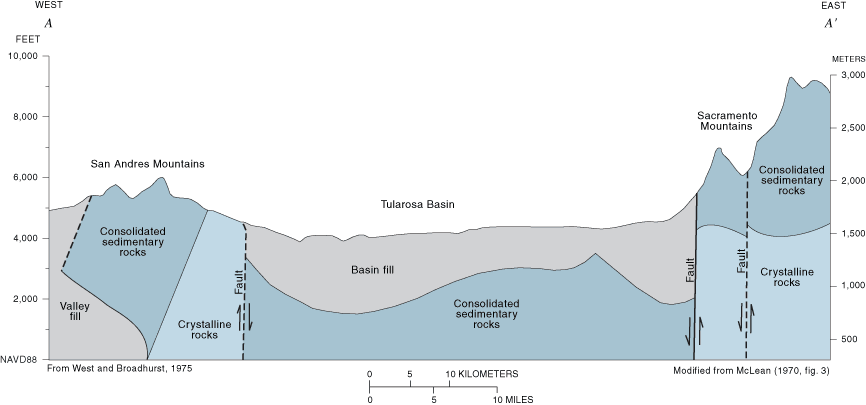
Figure 2. Generalized section across the Tularosa Basin. Line of section shown in figure 1.
The Tularosa Basin is a closed basin with no through-flowing surface-water features. Streams sustained by ground-water discharge within the basin include Salt Creek and Malpais Spring (fig. 1). Perennial streams in the surrounding elevated terrain exist only in a few areas within the higher elevations of the Sacramento Mountains (U.S. Bureau of Reclamation and the State of New Mexico, 1976). The location of subbasins in the elevated terrain surrounding the Tularosa Basin that potentially contribute recharge to the basin-fill aquifer is shown in figure 3. Recharge enters the basin-fill aquifer by infiltration of intermittent surface-water flows into coarse sediment near the proximal end of alluvial fans and as underflow along stream channels associated with larger subbasins (McLean, 1970; Burns and Hart, 1988; Risser, 1988; Morrison, 1989, p. 31-35). Recharge in the Tularosa Basin has been estimated to be 4 to 7 percent of total precipitation in subbasins near Holloman Air Force Base well fields (Hood, 1958; Ballance, 1976), 1 percent of total precipitation (not including surface-water infiltration) in the Tularosa Creek drainage (Garza and McLean, 1977), approximately 1 percent in the northern part of the Tularosa Basin (Bedinger and others, 1989), and about 7.5 percent near Carrizozo (Rao, 1986). Morrison (1989, p. 34-35) concluded that 3 percent of total precipitation generally constitutes mountain-front recharge between Tularosa and Alamogordo. Anderholm (2001) estimated mountain-front recharge in the Albuquerque Basin to range between approximately 1 and 9 percent of total precipitation. Data for subbasin areas and precipitation rates from Waltemeyer (2001) indicate that the basin-fill aquifer could receive between 35,000 and 320,000 cubic meters per day of recharge, which corresponds to 1 and 9 percent, respectively, of the sum of precipitation in all subbasins. Recharge to the Tularosa Basin was estimated to be approximately 86,390 acre-feet per year (approximately 292,000 cubic meters per day) by Livingston Associates and John Shomaker and Associates (2002, table 6.6). It is unlikely that precipitation falling on the basin floor contributes meaningful amounts to ground-water recharge because of the small precipitation rates and large evaporation rates in the Tularosa Basin.
Natural discharges of ground water in the basin-fill aquifer include evapotranspiration (ET), interbasin ground-water flow into the Hueco Bolson, and flow in streams on the basin floor supported by ground-water discharge. Burns and Hart (1988) estimated a maximum ET rate of 4 feet per year (0.0033 meter per day) and an ET extinction depth (maximum depth at which ET occurs) of 15 feet (4.5 meters) near Holloman Air Force Base. Flow in Salt Creek ranges from 250 to 450 gallons per minute (1,365 and 2,457 cubic meters per day) (McLean, 1970). Flow measured in Malpais Spring has been as small as 220 gallons per minute (1,201 cubic meters per day) and estimated to be as large as 1,500 gallons per minute (8,190 cubic meters per day) (McLean, 1970). Flows in Salt Creek and Malpais Spring vary seasonally and with precipitation. Heywood and Yager (2003) estimated interbasin ground-water flow of 20,000 cubic meters per day from the Tularosa Basin into the Hueco Bolson.

As of 1995, water used for agricultural irrigation and public supply accounted for approximately 87 percent of total ground water withdrawn from the basin-fill aquifer; agricultural irrigation accounted for approximately 58 percent of total ground-water withdrawal. Approximately 8 percent of total ground-water withdrawal was used to replenish evaporative losses from livestock watering ponds. The remaining 5 percent was withdrawn for domestic, commercial, and other agricultural uses (Livingston Associates and John Shomaker and Associates, 2002, table 7.9). Morrison (1989) cited an annual ground-water withdrawal rate of 3.3 acre-feet per irrigated acre.
Historical ground-water use in the Tularosa Basin was estimated using published information on current and historical agricultural and public-supply requirements, published information on current and historical land usage, and unpublished water-use information from the files of major users of water for public supply, including Holloman Air Force Base, the City of Alamogordo, and White Sands Missile Range. Monthly data on volumes and areal distribution of ground water withdrawn for public supply are available in Holloman Air Force Base files for 1972-95. Volume and areal-distribution data on ground water withdrawn for public supply of differing periodicities for Holloman Air Force Base, City of Alamogordo, and White Sands Missile Range are available in respective files for 1948-95. The available data range from yearly to 5-year composite information. Ground-water withdrawal for public supply estimated for 1948-95 and projected for 1996-2040 is listed in table 1. Total demand by the City of Alamogordo for public supply is projected to increase by 2,975 acre-feet per year (10,056 cubic meters per day) over the 2000 amount by 2040, whereas demand by White Sands Missile Range and Holloman Air Force Base for public supply is expected to remain relatively unchanged (Livingston Associates and John Shomaker and Associates, 2002, table 7.24). Sparse information available for the Village of Tularosa (fig. 1) shows annual ground-water withdrawals to be less than 1 percent of total public-supply withdrawals from the basin-fill aquifer.
Agricultural ground-water withdrawal in the Tularosa Basin for 1975-95 was estimated using information in a series of reports from the New Mexico Office of the State Engineer that summarize ground-water withdrawals, ground-water depletions, surface-water diversions, and surface-water depletions at 5-year intervals (Sorensen, 1977; 1982; Wilson, 1986; 1992; Wilson and Lucero, 1997). Depletion of water is that part of a withdrawal or diversion that has evaporated, transpired, been incorporated into plants or other products, or otherwise consumed and therefore is not available for ground-water recharge. Ground-water-withdrawal data combined with irrigated-acreage and water-use data in a series of reports from the New Mexico Cooperative Extension Service (Lansford and others, 1982, 1984-88, 1990-93, 1995-97) were used to calculate an average rate of 4.0 acre-feet of withdrawal per acre irrigated with ground water from 1976 to 1995. Ground-water withdrawal from 1955 to 1968 was estimated assuming a withdrawal rate of 4.0 acre-feet per acre of irrigated water and using the irrigated-acreage estimates from Garza and McLean (1977). Ground-water withdrawal for 1969-74 was interpolated between 1968 and 1975 estimates and for 1948-54 was assumed to be the same as in 1955. Ground-water withdrawal for agricultural irrigation estimated from 1948 to 1995 and projected for 1996 to 2040 is listed in table 1. For comparison, total demand of ground water for agricultural irrigation is projected to increase by 8,000 acre-feet per year (27,000 cubic meters per day) over the 2000 amount by 2040 (Livingston Associates and John Shomaker and Associates, 2002, table 7.26).
Agricultural ground-water depletion rates were calculated in the same manner and from the same sources as agricultural ground-water withdrawals. The average rate of ground-water depletion was 3.1 acre-feet per acre irrigated for 1985-95 and 2.2 acre-feet per acre irrigated for 1975-80. Ground-water depletions for 1948-74 were calculated assuming a depletion rate of 2.2 acre-feet per acre irrigated. Ground-water depletions for agricultural irrigation estimated for 1948-95 and projected for 1996-2040 are listed in table 1.
Agricultural surface-water diversion and depletion rates were calculated in the same manner and from the same sources as agricultural ground-water withdrawals and depletions. Surface-water diversion rates ranged from 3.2 to 4.9 acre-feet per acre irrigated and surface-water depletion rates ranged from 1.5 to 2.3 acre-feet per acre irrigated for 1975-95. Average rates of diversion (4.5 acre-feet per acre) and depletion (2.1 acre-feet per acre) using surface water for irrigation for 1975-95 were used to estimate surface-water diversions and depletions for 1948-74. Surface-water diversions and depletions associated with agricultural irrigation estimated for 1948-95 and projected for 1996-2040 are listed in table 1.
The City of Alamogordo and smaller municipalities divert surface water for public supply. In 1995, the City of Alamogordo accounted for approximately 80 percent of the 5,874 acre-feet per year (19,840 cubic meters per day) of surface water diverted for public supply in the Tularosa Basin (Livingston Associates and John Shomaker and Associates, 2002, table 7.20). Morrison (1989, table 5) estimated losses of 17,000 cubic feet per day (approximately 480 cubic meters per day) and 98,000 cubic feet per day (approximately 2,800 cubic meters per day) of ground-water recharge to the basin-fill aquifer from the La Luz Creek and Alamo Canyon drainages, respectively, between 1980 and 1984 from surface-water diversions.
Return flow is that part of a ground-water withdrawal or surface-water diversion that is available for ground-water recharge. Maximum possible return flow is calculated as ground-water withdrawal minus ground-water depletion plus surface-water diversion minus surface-water depletion. Return flow from public-supply systems in the Tularosa Basin ranges from approximately 45 to 60 percent of the water entering the public-supply system (Livingston Associates and John Shomaker and Associates, 2002, p. 7-10). Municipal return flows for 1948-95 were estimated assuming that a 55-percent depletion rate is representative of precipitation in the Tularosa Basin.
Ground water having dissolved-solids concentrations less than 1,000 mg/L occurs principally in the coalescing alluvial-fan deposits along the basin margin. The deepest fresh ground water is located along the basin margins. Dissolved-solids concentrations in ground water increase basinward (McLean, 1970; Orr and Myers, 1986; Risser, 1988). Approximately 2 percent of the saturated deposits of the basin-fill aquifer contain water having dissolved-solids concentrations less than 35 mg/L (McLean, 1970).
Numerical simulations are inherent oversimplifications of geohydrologic systems and, as such, can only approximate the behavior of those systems. Numerical simulations can be valuable, however, for calculating approximate responses of a ground-water system to stresses, including ground-water withdrawal and recharge.
The following sections describe each component of the ground-water-flow model constructed for the Tularosa Basin.
Numerical simulations in this study were made using the USGS finite-difference ground-water-simulation software MODFLOW-96 (Harbaugh and McDonald, 1996). McDonald and Harbaugh (1988) provided an extensive discussion of the internal algorithms and procedures used in the MODFLOW series. Ground-water flow paths and travel times of particles in ground water were simulated using MODPATH (Pollock, 1994). MODTOOLS (Orzol, 1997) was used for generating GIS files containing model results including contouring of simulated water levels and water-level changes. Techniques used to simulated ground-water-flow directions are discussed in Appendix 1. Input files for simulations were created using GIS, thereby enhancing the flexibility of the model to accommodate future updates and refinements.
The model is horizontally discretized into cells ranging from 562,500 to 16,000,000 square meters in area. Model cells are arranged in a grid of up to 81 rows and up to 50 columns (fig. 4). Model cell areas become smaller as the principal areas of municipal ground-water withdrawal are approached along the eastern margin of the basin. The model is vertically discretized into a maximum of six horizontal layers. Not all layers are active over the entire simulated area. The upper two layers are active over the entire simulated area to minimize numerical convergence problems experienced with earlier versions of the model in which only the uppermost model layer was active throughout the entire model. Each layer is of uniform thickness throughout the model. The upper four layers are each 100 meters thick, layer 5 is 250 meters thick, and layer 6 is 450 meters thick. The vertical model discretization, although somewhat arbitrary, is designed to provide an adequate degree of vertical control in ground-water-flow simulations. All ground-water-withdrawal stresses occur within one or more of the upper three model layers. The uppermost active cells were simulated as an unconfined aquifer, and all underlying cells were simulated as a confined aquifer. Stress periods in the transient ground-water-flow simulation were set at 1-year intervals with one time step per stress period. This means that all simulated water levels correspond in time to the end of a particular year.
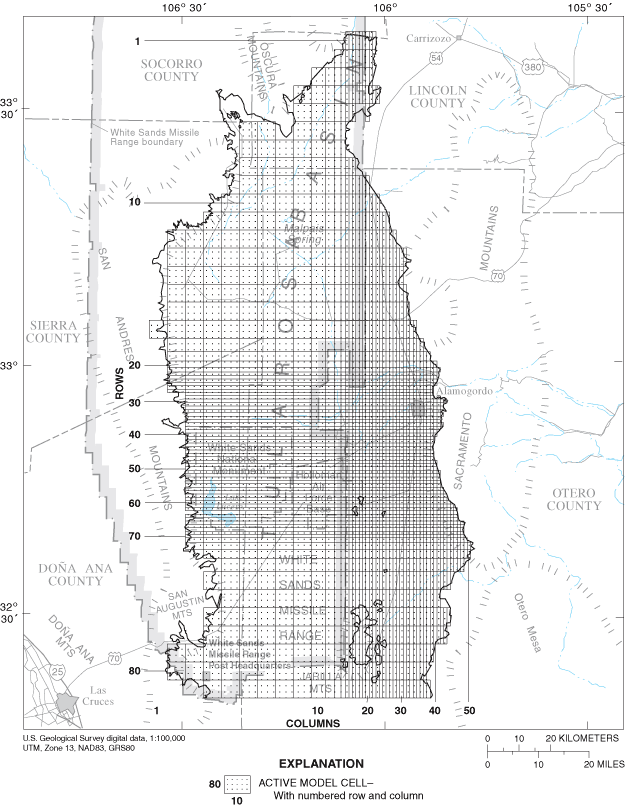
Figure 4. Location of ground-water flow-model grid.
The ground-water-flow model is confined laterally by a no-flow boundary corresponding to the contact between the basin-fill aquifer and the surrounding uplifted terrain, following the assumption that the basin-fill aquifer has a substantially larger hydraulic conductivity. The basal no-flow boundary of the model approximates the depth of ground water with dissolved-solids concentrations of 10,000 mg/L or more or the contact between the basin-fill aquifer and underlying bedrock as given by McLean (1970). This assumes no flow across the 10,000-mg/L salinity surface or across the boundary between bedrock and the basin-fill aquifer. The permeability of rocks of Mesozoic and older ages in the Basin and Range Province of New Mexico is generally low (Boegly and others, 1969). The assumption of no flow across the salinity surface may or may not be correct. However, locations of recharge and withdrawal of freshwater in the model are sufficiently removed from the 10,000-mg/L surface to allow this surface to be a reasonable representation of a model boundary. Active model layers are shown in figure 5. A specified-flow boundary forms the southern limit of the ground-water-flow model.
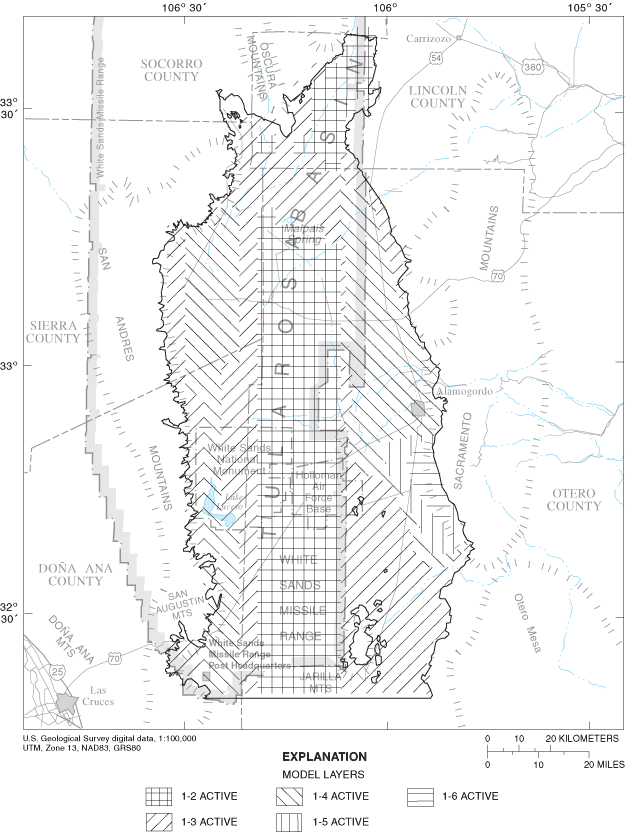
Figure 5. Location of active ground-water flow-model layers.
Model stresses include those processes that add water to or remove water from an aquifer. Stresses can be either natural or anthropogenic.
Ground-water recharge is assumed to enter the model through cells corresponding to the location of the mouths of canyons associated with the subbasins that rim the Tularosa Basin (figs. 3 and 6). Between 1 and 9 percent of annual subbasin precipitation was applied to the model in the uppermost active cells at recharge locations. This recharge is within the range of values previously discussed in the "Ground- and surface-water flows" section of this report. Basinwide recharge from infiltration of precipitation through surficial deposits is assumed to be negligible because of small precipitation and large evaporation rates. Recharge to the model was selectively allowed as return flow from agricultural irrigation. The distribution and volume of return flow associated with agricultural irrigation are discussed in detail in the "Return flow" section of this report.
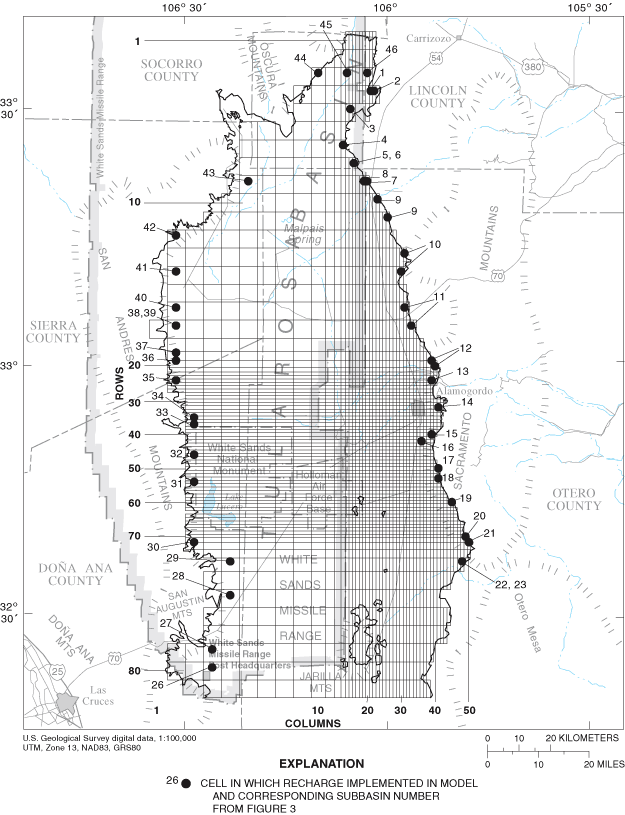
Figure 6. Location of cells in which recharge is implemented in the ground-water-flow model.
The temporal distribution of available municipal ground-water-withdrawal data is described in the "Model discretization" section of this report. The sources and estimation of annual ground-water withdrawals are described in the "Water use" section of this report. Given the small amount of and large uncertainty in ground-water withdrawals by the Village of Tularosa, these withdrawals were not included in the model. The approximately 5 percent of ground water withdrawn for domestic, commercial, and other agricultural uses was not included in the model because of the lack of data on its specific distribution and the small part of total withdrawal it represents. The locations of model cells containing municipal withdrawals are shown in figures 7A and B. All public-supply withdrawals simulated in the model are from the basin-fill aquifer with the exception of the City of Alamogordo public-supply wells, some of which withdraw water from underlying fractured-bedrock aquifers. Information on the fraction of water produced from the basin-fill aquifer in these wells was unavailable for use in this study. Therefore, all withdrawals attributed to the City of Alamogordo public-supply wells are assumed to come from the basin-fill aquifer.
The areal distribution of agricultural ground-water withdrawal in Otero County was based on data from Morrison (1989, app. 2) with additional information from Garza and McLean (1977). The areal distribution of agricultural ground-water withdrawals in Lincoln County was based on data from the U.S. Bureau of Reclamation and the State of New Mexico (1976). The locations of model cells containing agricultural ground-water withdrawals are shown in figure 8 and listed in table 2.
The effects of projected ground-water withdrawal were simulated to 2040 as part of this study. All 1996-2000 withdrawals were assumed to be equal to 1995 withdrawals (table 1). The spatial distribution of ground-water withdrawals for agricultural irrigation and public supply was assumed to be unchanged from that used for 1948-2000 simulations. To maintain withdrawal and diversion values within historical limits (table 1), 50 percent of the projected increases in agricultural withdrawal were assumed to be met by increased ground-water withdrawal and the remaining 50 percent by increased surface-water diversion. These assumptions result in about 86,000 cubic meters per day of ground-water withdrawal and about 33,000 cubic meters per day of surface-water diversion by 2040. Withdrawal from the current (1995) City of Alamogordo well field was assumed to increase by 50 percent (approximately 2,600 cubic meters per day) over 1995 rates by 2040. This amount of increase in withdrawal from the City of Alamogordo well field may not be possible. The remaining water needed to meet City of Alamogordo projected demands was assumed to come from increased surface-water flows through improved watershed management and desalination of brackish ground water (Livingston Associates and John Shomaker and Associates, 2002, p. 8-16 - 8-22). Ground-water withdrawals by Holloman Air Force Base and White Sands Missile Range were assumed constant at 1995 values for 2000-40 (Livingston Associates and John Shomaker and Associates, 2002, table 7.24).

Figure 7. Areas of municipal ground-water withdrawals.

Figure 8. Areas of agricultural ground-water withdrawals and agricultural surface-water diversions.
Uncertainties in the volume of ground water depleted from the basin-fill aquifer by agricultural and municipal withdrawals and diversions are addressed in the model by simulation of zero and maximum return-flow scenarios. Zero return flow represents maximum ground-water depletion, whereas maximum return flow represents minimum ground-water depletion. Return flows from agricultural ground-water withdrawal were implemented in the model as reduced withdrawal rates. Agricultural ground-water depletion was assumed to follow the same areal distribution as agricultural ground-water withdrawal (fig. 8). Return flows from agricultural surface-water diversions were implemented in the model as specified fluxes to the uppermost active model layer. Agricultural surface-water depletion was assumed to follow the same areal distribution as agricultural surface-water diversion (fig. 8). The areal distribution of ground-water withdrawals and surface-water diversions for agricultural irrigation was based on data from Morrison (1989, app. 2).
The locations of return flows associated with municipal water use were assumed to coincide with the corresponding municipality or military installation. Return flow associated with White Sands Missile Range Post Headquarters is implemented as reduced ground-water withdrawal (fig. 7A). Return flows associated with Holloman Air Force Base and the City of Alamogordo are implemented in the model as specified flows because areas of return flow are spatially removed from areas of withdrawal. Return flows associated with the City of Alamogordo (fig. 7B) were calculated using total ground-water withdrawals plus surface-water diversions from reservoirs in the Sacramento Mountains. Incorporating surface-water diversions from La Luz Creek and Alamo Canyon into return-flow calculations for the City of Alamogordo would have required assessing the effect of surface-water diversion on ground-water recharge in these areas to balance the basin water budget. Such an assessment was beyond the scope of this study.
[All water-related units in cubic meters per day. Sources of data in this table are discussed in the "Water use" section of the report]
| Year | Ground water withdrawn for agricultural irrigation | Ground water depleted by agricultural irrigation | Ground water withdrawn for public supply | Surface water diverted for agricultural irrigation | Surface water depleted by agricultural irrigation |
|---|---|---|---|---|---|
| 1948 | 26,000 | 14,000 | 2,000 | 18,000 | 8,000 |
| 1949 | 26,000 | 14,000 | 2,000 | 18,000 | 8,000 |
| 1950 | 26,000 | 14,000 | 1,000 | 18,000 | 8,000 |
| 1951 | 26,000 | 14,000 | 3,000 | 18,000 | 8,000 |
| 1952 | 26,000 | 14,000 | 4,000 | 18,000 | 9,000 |
| 1953 | 26,000 | 14,000 | 5,000 | 18,000 | 8,000 |
| 1954 | 26,000 | 14,000 | 5,000 | 18,000 | 9,000 |
| 1955 | 26,000 | 14,000 | 7,000 | 18,000 | 8,000 |
| 1956 | 36,000 | 20,000 | 8,000 | 18,000 | 9,000 |
| 1957 | 36,000 | 20,000 | 6,000 | 18,000 | 8,000 |
| 1958 | 36,000 | 20,000 | 6,000 | 17,000 | 8,000 |
| 1959 | 36,000 | 20,000 | 7,000 | 18,000 | 8,000 |
| 1960 | 36,000 | 20,000 | 9,000 | 18,000 | 8,000 |
| 1961 | 36,000 | 20,000 | 13,000 | 18,000 | 8,000 |
| 1962 | 36,000 | 20,000 | 12,000 | 18,000 | 8,000 |
| 1963 | 36,000 | 20,000 | 13,000 | 18,000 | 8,000 |
| 1964 | 52,000 | 29,000 | 19,000 | 18,000 | 8,000 |
| 1965 | 52,000 | 29,000 | 15,000 | 18,000 | 8,000 |
| 1966 | 52,000 | 29,000 | 15,000 | 18,000 | 8,000 |
| 1967 | 55,000 | 30,000 | 20,000 | 18,000 | 8,000 |
| 1968 | 55,000 | 30,000 | 18,000 | 21,000 | 10,000 |
| 1969 | 59,000 | 33,000 | 21,000 | 22,000 | 10,000 |
| 1970 | 64,000 | 35,000 | 22,000 | 24,000 | 11,000 |
| 1971 | 69,000 | 38,000 | 24,000 | 26,000 | 12,000 |
| 1972 | 75,000 | 41,000 | 23,000 | 27,000 | 12,000 |
| 1973 | 80,000 | 44,000 | 22,000 | 29,000 | 10,000 |
| 1974 | 86,000 | 47,000 | 22,000 | 30,000 | 14,000 |
| 1975 | 92,000 | 50,000 | 20,000 | 34,000 | 16,000 |
| 1976 | 91,000 | 51,000 | 22,000 | 33,000 | 16,000 |
| 1977 | 90,000 | 52,000 | 20,000 | 34,000 | 16,000 |
| 1978 | 90,000 | 53,000 | 18,000 | 33,000 | 16,000 |
| 1979 | 89,000 | 54,000 | 20,000 | 34,000 | 16,000 |
| 1980 | 88,000 | 55,000 | 19,000 | 34,000 | 16,000 |
| 1981 | 82,000 | 51,000 | 19,000 | 33,000 | 15,000 |
| 1982 | 75,000 | 47,000 | 20,000 | 32,000 | 14,000 |
| 1983 | 68,000 | 44,000 | 18,000 | 31,000 | 14,000 |
| 1984 | 61,000 | 40,000 | 15,000 | 30,000 | 13,000 |
| 1985 | 54,000 | 36,000 | 20,000 | 29,000 | 12,000 |
| 1986 | 53,000 | 36,000 | 12,000 | 26,000 | 11,000 |
| 1987 | 52,000 | 37,000 | 14,000 | 23,000 | 10,000 |
| 1988 | 50,000 | 37,000 | 14,000 | 20,000 | 9,000 |
| 1989 | 49,000 | 38,000 | 17,000 | 17,000 | 8,000 |
| 1990 | 48,000 | 38,000 | 14,000 | 14,000 | 6,000 |
| 1991 | 51,000 | 41,000 | 14,000 | 14,000 | 7,000 |
| 1992 | 54,000 | 44,000 | 14,000 | 15,000 | 7,000 |
| 1993 | 57,000 | 46,000 | 16,000 | 16,000 | 8,000 |
| 1994 | 61,000 | 49,000 | 20,000 | 17,000 | 8,000 |
| 1995 | 64,000 | 52,000 | 19,000 | 17,000 | 8,000 |
| 1996 | 64,000 | 52,000 | 19,000 | 17,000 | 8,000 |
| 1997 | 64,000 | 52,000 | 19,000 | 17,000 | 8,000 |
| 1998 | 64,000 | 52,000 | 19,000 | 17,000 | 8,000 |
| 1999 | 64,000 | 52,000 | 19,000 | 17,000 | 8,000 |
| 2000 | 64,000 | 52,000 | 19,000 | 17,000 | 8,000 |
| 2001 | 65,000 | 53,000 | 19,000 | 17,000 | 8,000 |
| 2002 | 65,000 | 53,000 | 19,000 | 18,000 | 8,000 |
| 2003 | 66,000 | 53,000 | 19,000 | 18,000 | 8,000 |
| 2004 | 66,000 | 53,000 | 19,000 | 19,000 | 9,000 |
| 2005 | 67,000 | 54,000 | 19,000 | 19,000 | 9,000 |
| 2006 | 67,000 | 54,000 | 19,000 | 19,000 | 9,000 |
| 2007 | 68,000 | 55,000 | 20,000 | 20,000 | 9,000 |
| 2008 | 69,000 | 56,000 | 20,000 | 20,000 | 9,000 |
| 2009 | 69,000 | 56,000 | 20,000 | 21,000 | 10,000 |
| 2010 | 70,000 | 57,000 | 20,000 | 21,000 | 10,000 |
| 2011 | 70,000 | 57,000 | 20,000 | 21,000 | 10,000 |
| 2012 | 71,000 | 58,000 | 20,000 | 22,000 | 10,000 |
| 2013 | 71,000 | 58,000 | 20,000 | 22,000 | 10,000 |
| 2014 | 72,000 | 58,000 | 20,000 | 23,000 | 11,000 |
| 2015 | 73,000 | 59,000 | 20,000 | 23,000 | 11,000 |
| 2016 | 73,000 | 59,000 | 20,000 | 23,000 | 11,000 |
| 2017 | 74,000 | 60,000 | 20,000 | 24,000 | 11,000 |
| 2018 | 74,000 | 60,000 | 20,000 | 24,000 | 11,000 |
| 2019 | 75,000 | 61,000 | 20,000 | 25,000 | 12,000 |
| 2020 | 76,000 | 62,000 | 21,000 | 25,000 | 12,000 |
| 2021 | 76,000 | 62,000 | 21,000 | 25,000 | 12,000 |
| 2022 | 77,000 | 62,000 | 21,000 | 26,000 | 12,000 |
| 2023 | 77,000 | 62,000 | 21,000 | 26,000 | 12,000 |
| 2024 | 78,000 | 63,000 | 21,000 | 27,000 | 13,000 |
| 2025 | 78,000 | 63,000 | 21,000 | 27,000 | 13,000 |
| 2026 | 79,000 | 64,000 | 21,000 | 27,000 | 13,000 |
| 2027 | 80,000 | 65,000 | 21,000 | 28,000 | 13,000 |
| 2028 | 80,000 | 65,000 | 21,000 | 28,000 | 13,000 |
| 2029 | 81,000 | 66,000 | 21,000 | 29,000 | 14,000 |
| 2030 | 81,000 | 66,000 | 21,000 | 29,000 | 14,000 |
| 2031 | 82,000 | 66,000 | 21,000 | 29,000 | 14,000 |
| 2032 | 82,000 | 66,000 | 21,000 | 30,000 | 14,000 |
| 2033 | 83,000 | 67,000 | 21,000 | 30,000 | 14,000 |
| 2034 | 84,000 | 68,000 | 22,000 | 31,000 | 15,000 |
| 2035 | 84,000 | 68,000 | 22,000 | 31,000 | 15,000 |
| 2036 | 85,000 | 69,000 | 22,000 | 31,000 | 15,000 |
| 2037 | 85,000 | 69,000 | 22,000 | 32,000 | 15,000 |
| 2038 | 86,000 | 70,000 | 22,000 | 32,000 | 15,000 |
| 2039 | 86,000 | 70,000 | 22,000 | 33,000 | 16,000 |
| 2040 | 86,000 | 70,000 | 22,000 | 33,000 | 16,000 |
| Model location | ||||
|---|---|---|---|---|
| Ground-water withdrawal stress | Period of time stress applied, in years | Row | Column | Layer |
| City of Alamogordo public supply | 1965-95 | 22 | 39 | 2 |
| City of Alamogordo public supply | 1955-95 | 22 | 40 | 2 |
| City of Alamogordo public supply | 1965-95 | 24 | 40 | 2 |
| City of Alamogordo public supply | 1955-95 | 25 | 39 | 2 |
| City of Alamogordo public supply | 1965-95 | 26 | 39 | 2 |
| Holloman Air Force Base public supply | 1948-95 | 44 | 37 | 1 |
| Holloman Air Force Base public supply | 1948-95 | 44 | 38 | 1 |
| Holloman Air Force Base public supply | 1948-83 | 45 | 35 | 1 |
| Holloman Air Force Base public supply | 1948-95 | 45 | 37 | 1 |
| Holloman Air Force Base public supply | 1948-95 | 47 | 35 | 1 |
| Holloman Air Force Base public supply | 1961-95 | 49 | 38 | 1 |
| Holloman Air Force Base public supply | 1963-95 | 49 | 39 | 1 |
| Holloman Air Force Base public supply | 1963-80 | 49 | 39 | 2 |
| Holloman Air Force Base public supply | 1963-89 | 49 | 39 | 4 |
| Holloman Air Force Base public supply | 1963-95 | 49 | 40 | 3 |
| Holloman Air Force Base public supply | 1961-80 | 50 | 38 | 1 |
| Holloman Air Force Base public supply | 1961-81 | 50 | 39 | 1 |
| Holloman Air Force Base public supply | 1961-80 | 50 | 39 | 2 |
| Holloman Air Force Base public supply | 1964-86 | 50 | 39 | 3 |
| Holloman Air Force Base public supply | 1986-95 | 54 | 41 | 3 |
| Holloman Air Force Base public supply | 1987-96 | 56 | 42 | 3 |
| Holloman Air Force Base public supply | 1987-96 | 61 | 44 | 3 |
| White Sands Missile Range public supply | 1948-95 | 69 | 4 | 2 |
| White Sands Missile Range public supply | 1948-95 | 70 | 4 | 2 |
| White Sands Missile Range public supply | 1948-95 | 77 | 4 | 2 |
| White Sands Missile Range public supply | 1948-95 | 78 | 4 | 2 |
| White Sands Missile Range public supply | 1948-95 | 79 | 3 | 3 |
| White Sands Missile Range public supply | 1948-95 | 80 | 3 | 2 |
| White Sands Missile Range public supply | 1948-95 | 80 | 3 | 3 |
| White Sands Missile Range public supply | 1948-95 | 80 | 4 | 3 |
| Discharge to Salt Creek | 1948-95 | 12 | 5 | 1 |
| Discharge to Malpais Spring | 1948-95 | 11 | 8 | 1 |
| Agricultural irrigation | 1948-95 | 5 | 14 | 1 |
| Agricultural irrigation | 1948-95 | 5 | 15 | 1 |
| Agricultural irrigation | 1948-95 | 5 | 16 | 2 |
| Agricultural irrigation | 1948-95 | 10 | 23 | 1 |
| Agricultural irrigation | 1948-95 | 11 | 23 | 1 |
| Agricultural irrigation | 1948-95 | 11 | 25 | 1 |
| Agricultural irrigation | 1948-95 | 14 | 25 | 1 |
| Agricultural irrigation | 1948-95 | 14 | 26 | 1 |
| Agricultural irrigation | 1948-95 | 14 | 27 | 1 |
| Agricultural irrigation | 1948-95 | 14 | 28 | 1 |
| Agricultural irrigation | 1948-95 | 15 | 25 | 1 |
| Agricultural irrigation | 1948-95 | 15 | 27 | 2 |
| Agricultural irrigation | 1948-95 | 15 | 28 | 2 |
| Agricultural irrigation | 1948-95 | 16 | 21 | 1 |
| Agricultural irrigation | 1948-95 | 16 | 23 | 1 |
| Agricultural irrigation | 1948-95 | 16 | 25 | 1 |
| Agricultural irrigation | 1948-95 | 16 | 27 | 1 |
| Agricultural irrigation | 1948-95 | 16 | 27 | 2 |
| Agricultural irrigation | 1948-95 | 16 | 29 | 1 |
| Agricultural irrigation | 1948-95 | 16 | 30 | 1 |
| Agricultural irrigation | 1948-95 | 16 | 31 | 1 |
| Agricultural irrigation | 1948-95 | 16 | 32 | 1 |
| Agricultural irrigation | 1948-95 | 17 | 23 | 1 |
| Agricultural irrigation | 1948-95 | 17 | 25 | 1 |
| Agricultural irrigation | 1948-95 | 17 | 27 | 1 |
| Agricultural irrigation | 1948-95 | 17 | 29 | 1 |
| Agricultural irrigation | 1948-95 | 17 | 30 | 1 |
| Agricultural irrigation | 1948-95 | 17 | 31 | 1 |
| Agricultural irrigation | 1948-95 | 17 | 32 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 25 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 27 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 28 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 29 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 30 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 31 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 32 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 34 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 35 | 1 |
| Agricultural irrigation | 1948-95 | 18 | 36 | 1 |
| Agricultural irrigation | 1948-95 | 19 | 27 | 1 |
| Agricultural irrigation | 1948-95 | 19 | 28 | 1 |
| Agricultural irrigation | 1948-95 | 19 | 34 | 1 |
| Agricultural irrigation | 1948-95 | 20 | 27 | 1 |
| Agricultural irrigation | 1948-95 | 20 | 28 | 1 |
| Agricultural irrigation | 1948-95 | 20 | 31 | 1 |
| Agricultural irrigation | 1948-95 | 20 | 32 | 1 |
| Agricultural irrigation | 1948-95 | 20 | 34 | 1 |
| Agricultural irrigation | 1948-95 | 20 | 36 | 1 |
| Agricultural irrigation | 1948-95 | 20 | 38 | 3 |
| Agricultural irrigation | 1948-95 | 21 | 32 | 1 |
| Agricultural irrigation | 1948-95 | 21 | 34 | 1 |
| Agricultural irrigation | 1948-95 | 21 | 38 | 3 |
| Agricultural irrigation | 1948-95 | 23 | 32 | 1 |
| Agricultural irrigation | 1948-95 | 23 | 34 | 1 |
| Agricultural irrigation | 1948-95 | 25 | 31 | 1 |
| Agricultural irrigation | 1948-95 | 29 | 35 | 1 |
| Agricultural irrigation | 1948-95 | 29 | 36 | 1 |
| Agricultural irrigation | 1948-95 | 31 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 32 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 33 | 31 | 1 |
| Agricultural irrigation | 1948-95 | 33 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 33 | 35 | 1 |
| Agricultural irrigation | 1948-95 | 33 | 36 | 1 |
| Agricultural irrigation | 1948-95 | 34 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 34 | 35 | 1 |
| Agricultural irrigation | 1948-95 | 34 | 36 | 1 |
| Agricultural irrigation | 1948-95 | 35 | 31 | 1 |
| Agricultural irrigation | 1948-95 | 35 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 36 | 31 | 1 |
| Agricultural irrigation | 1948-95 | 36 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 44 | 35 | 1 |
| Agricultural irrigation | 1948-95 | 44 | 36 | 1 |
| Agricultural irrigation | 1948-95 | 46 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 47 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 53 | 33 | 1 |
| Agricultural irrigation | 1948-95 | 53 | 34 | 1 |
| Agricultural irrigation | 1948-95 | 53 | 40 | 1 |
| Agricultural irrigation | 1948-95 | 55 | 36 | 1 |
| Agricultural irrigation | 1948-95 | 55 | 38 | 1 |
| Agricultural irrigation | 1948-95 | 56 | 35 | 1 |
| Southern specified-flow boundary | 1948-95 | 81 | 4 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 4 | 4 |
| Southern specified-flow boundary | 1948-95 | 81 | 5 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 5 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 5 | 4 |
| Southern specified-flow boundary | 1948-95 | 81 | 6 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 7 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 8 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 9 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 10 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 11 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 12 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 13 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 13 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 14 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 14 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 15 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 16 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 17 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 18 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 19 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 20 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 21 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 22 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 22 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 23 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 23 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 24 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 24 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 25 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 25 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 26 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 26 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 27 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 27 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 28 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 28 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 29 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 29 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 30 | 2 |
| Southern specified-flow boundary | 1948-95 | 81 | 30 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 31 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 32 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 33 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 34 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 35 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 36 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 37 | 3 |
| Southern specified-flow boundary | 1948-95 | 81 | 38 | 3 |
The model was allowed to calculate ET fluxes from all active cells in the uppermost model layer using a maximum ET rate of 0.0033 meter per day and a maximum depth from which ET could occur (ET extinction depth) of 4.5 meters after Burns and Hart (1988). No attempt was made to separate the effects of pond or stream evaporation from those of ET in the model.
Salt Creek is implemented in the model as specified outflows of 1,600 cubic meters per day. These flows are within the range of measured values previously discussed in the "Ground- and surface-water flows" section. All spring water, once on the basin floor, is assumed to be lost to ET. Interbasin ground-water flow was specified across the southern model boundary into the Hueco Bolson. Simulated rates of interbasin flow were estimated during model calibration.
The initial disribution of aquifer properties in the ground-water-flow model were based on the surface geology of the Tularosa Basin as shown in Green and Jones (1997). Initial estimates of horizontal hydraulic conductivity ranged from approximately 15 meters per day for coarse-grained alluvial-fan deposits to approximately 0.5 meter per day for basinward finer grained deposits. Initial estimates of the ratio of vertical to horizontal hydraulic conductivity were allowed to range from 1:10 to as low as 1:1,000 given the frequent occurrence of clay intervals in the basin-fill aquifer. Initial values of 0.004 for storativity and 0.08 for specified yield were assigned to each model layer. No inherent horizontal anisotropy was assumed in the construction of the ground-water-flow model. Recharge to the basin-fill aquifer was restricted to between 1 and 9 percent of total precipitation in the subbasins surrounding the Tularosa Basin. Interbasin ground-water flow across the southern model boundary was initially estimated to be 20,000 cubic meters per day. The ranges of values for hydrologic properties, with the exception of the ratio of vertical to horizontal hydraulic conductivity, are within the ranges discussed in the "Aquifer properties" section. The relatively wide range of values assigned to the ratio of vertical to horizontal hydraulic conductivity reflects the range of uncertainty and possible spatial variability in this ratio. The initial values of selected hydrologic properties were varied within reasonable limits during model calibration as described in the "Model calibration" section of this report.
The ground-water-flow model was calibrated by minimizing the difference between measured and simulated ground-water levels in steady-state and transient simulations. Additionally, an attempt was made to improve the steady-state model calibration by adjusting values of horizontal hydraulic conductivity and vertical conductance to better match simulated ground-water travel times to available carbon-14 (14C) apparent ages of ground water.
Differences between measured and simulated ground-water levels in the steady-state simulation were quantified through calculation of the root-mean-square error (RMSE). RMSE is defined as:
i=n
 (1)
(1)
i=1
where:
Wm = measured water level best representing a selected model cell;
Ws = simulated water level in the selected model cell; and
n = number of model cells for which the calculation is made.
Differences between measured and simulated ground-water levels for each selected model cell in the transient simulation were quantified through calculation of RMSE values using equation 1 above but where: Wm = value of measured water levels best representing a selected model cell during a given stress period; Ws = simulated water level in the selected model cell during the given stress period; and n = number of stress periods for which values of Wm in the selected model cell are available.
The minimum value of RMSE represents the greatest degree of agreement between simulated and measured water levels.
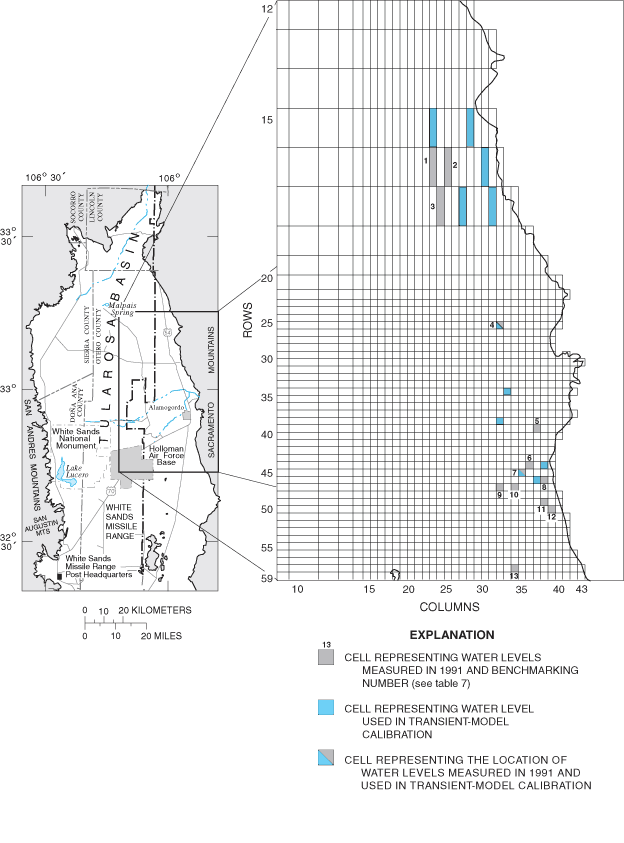
A steady-state model calibration assumes that natural hydrologic stresses on an aquifer will result in ground-water levels and ground- and surface-water flows that vary little over time. These long-term stresses and corresponding responses are known as steady-state conditions. Steady-state hydrologic conditions prevail predominantly in predevelopment periods during which anthropogenic influences, such as ground-water withdrawal and surface-water diversion, are minimal or nonexistent. Ground-water levels measured in the Tularosa Basin during 1911-12 by Meinzer and Hare (1915) are assumed to represent steady-state conditions. Model cells assigned values of measured water levels from data in Meinzer and Hare (1915) and used as steady-state calibration points are shown in figure 9 and are listed in table 3.
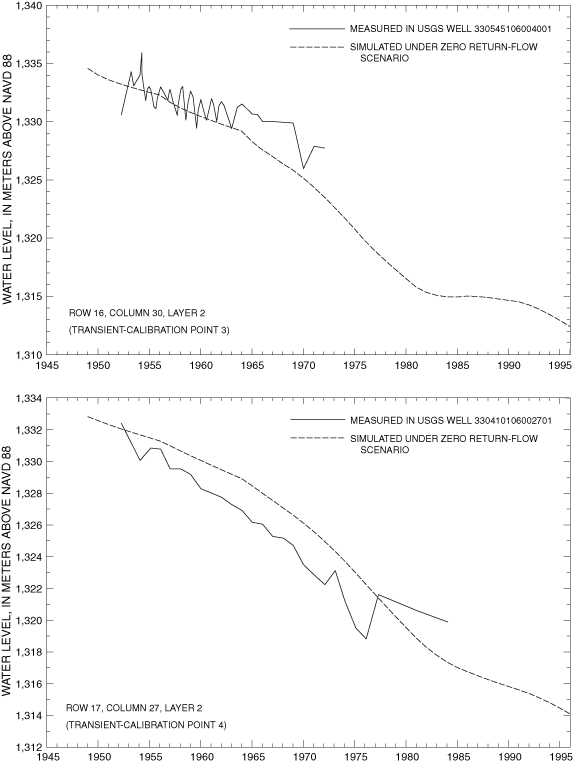
| Transient-model calibration point number | Model location | U.S. Geological Survey well identification number | Well depth, in meters below land surface | Range of years for which measured water-level data are available | RMSE from transient-model calibration, in meters | Number of points compared in calculation of transient RMSE | ||
|---|---|---|---|---|---|---|---|---|
| Row | Colunm | Layer | ||||||
| 1 | 15 | 23 | 2 | 330817106040501 | 107 | 1953-76 | 15.7 | 22 |
| 2 | 15 | 28 | 1 | 330658106015801 | 91 | 1952-86 | 6.7 | 30 |
| 3 | 16 | 30 | 2 | 330545106004001 | 100 | 1952-72 | 2.5 | 20 |
| 4 | 17 | 31 | 2 | 330410106002701 | 107 | 1952-84 | 1.6 | 27 |
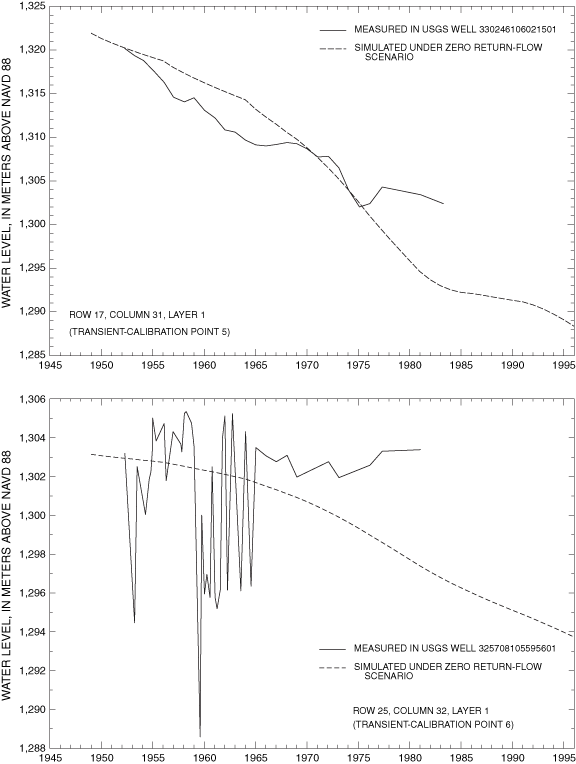
| 5 | 17 | 27 | 1 | 330246106021501 | 46 | 1952-83 | 3.5 | 28 |
| 6 | 25 | 32 | 1 | 325708105595601 | 73 | 1952-81 | 3.2 | 23 |
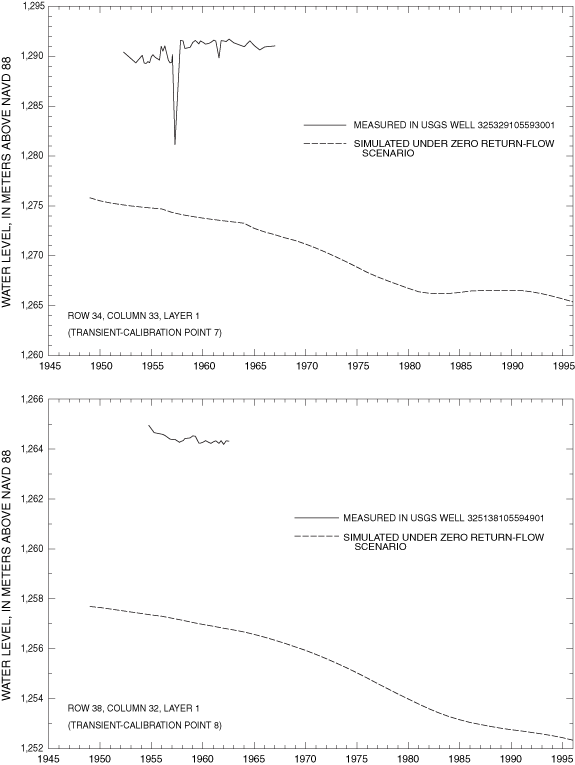
| 7 | 34 | 33 | 1 | 325329105593001 | 26 | 1952-67 | 17.0 | 16 |
| 8 | 38 | 32 | 1 | 325138105594901 | 43 | 1954-62 | 7.4 | 9 |
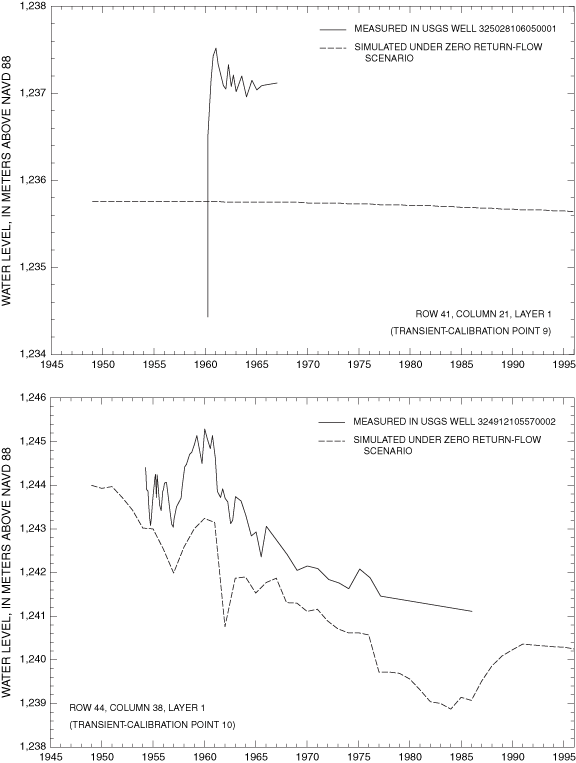
| 9 | 41 | 21 | 1 | 325028106050001 | 6 | 1960-67 | 1.3 | 8 |
| 10 | 44 | 38 | 1 | 324912105570002 | 79 | 1954-86 | 1.5 | 24 |
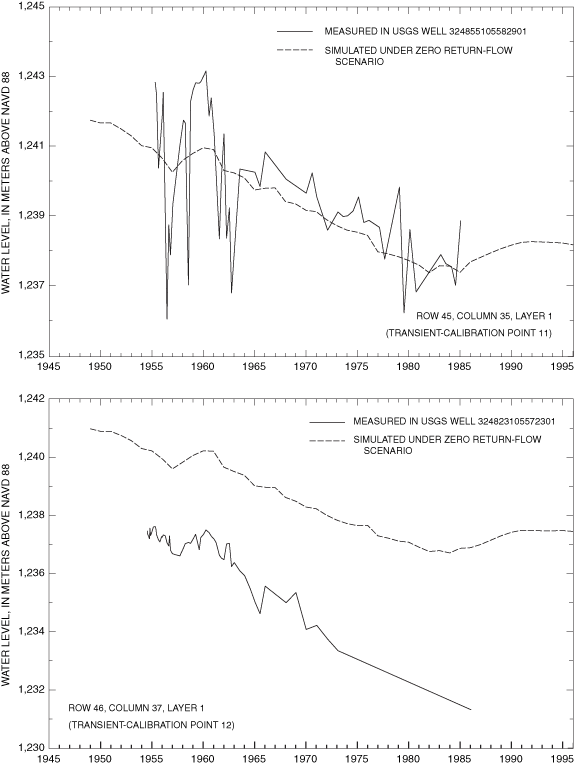
| 11 | 45 | 35 | 1 | 324855105582901 | 77 | 1955-85 | 0.8 | 25 |
| 12 | 46 | 37 | 1 | 324823105572301 | 75 | 1954-86 | 3.5 | 20 |
Selected hydrologic parameters were systematically varied within a range of reasonable values to achieve the minimum value of RMSE. Hydrologic parameters modified during calibration of the steady-state model include horizontal hydraulic conductivity, vertical conductance between model layers, specified flow across the southern model boundary, and recharge. Values of maximum ET flux and ET extinction depth were held constant at 0.0033 meter per day and 4.5 meters, respectively, during all simulations.
Horizontal hydraulic conductivity was allowed to range from 0.5 to 15 meters per day. Vertical conductance was calculated as a function of horizontal hydraulic conductivity, vertical hydraulic conductivity expressed as a ratio of vertical to horizontal hydraulic conductivity, and layer thickness using the relations from McDonald and Harbaugh (1988, p. 5-12). The ratio of vertical to horizontal hydraulic conductivity was allowed to range between 1:10 and 1:1,000. Interbasin ground-water flow across the southern boundary was allowed to range from 12,000 to 20,000 cubic meters per day. In individual subbasins surrounding the Tularosa Basin, recharge to the basin-fill aquifer was allowed to range from 1 to 9 percent of total precipitation based on prior estimates of recharge to the Tularosa and Albuquerque Basins.
A transient ground-water flow-model calibration attempts to account for the effects of time-variant stresses, such as ground-water withdrawal or anthropogenically induced ground-water recharge, on ground-water systems. The transient simulation is from 1948 to 1995, corresponding to the period of available municipal ground-water-withdrawal data (table 1). Water-level measurements are available for variable spans of time between 1952 and 1986 (table 3) for model cells representing transient-calibration points (fig. 9). Transient ground-water-flow simulations were done for zero and maximum return-flow scenarios to determine the sensitivity of the model to assumptions regarding return flow. Zero return flow was assumed for transient calibration because this represents the maximum potential effect of ground-water withdrawal. Hydrologic properties in the transient model include storativity and specific yield in addition to those described for the steady-state model. Values of storativity and specific yield were fixed at 0.004 and 0.008, respectively. The simulated steady-state water-level distribution served as the initial condition for all transient simulations.
Initial attempts at model calibration consisted of matching simulated steady-state water-level contours with measured water-level contours from Meinzer and Hare (1915) by systematically varying selected hydrologic parameters within reasonable ranges. The steady-state calibration was refined for the eastern side of the basin by comparison of simulated water levels with water levels in 40 model cells for which 1911-12 water-level measurements are available (fig. 9). The RMSE of the steady-state calibration was 6.3 meters within the well-calibrated area. The area containing these 40 cells defines the well-calibrated area of the model. Model calibration proceeded with a series of iterative steady-state and transient simulations in which hydrologic parameters were varied within reasonable ranges in an attempt to preserve the minimum RMSE value for the steady-state calibration while minimizing individual RMSE values for each transient-calibration point.
The final value of RMSE for the steady-state model within the well-calibrated area is 6.3 meters. Ground-water-level measurements by Meinzer and Hare (1915) and final steady-state simulated ground-water levels are listed in table 4. Visual representations of the agreement between final simulated steady-state water levels and measured 1911-12 water levels are shown in figure 10. The final distribution of zones of hydrologic properties is shown in figure 11. Numerical values of selected hydrologic properties are listed in table 5. The final simulated flow across the southern model boundary was adjusted to 13,000 cubic meters per day to better match head contours in the area shown in McLean (1970). Residual error is defined as Wm minus Ws for each model cell for which a value of Wm is available. Application of the statistical test of Looney and Gulledge (1985) failed to disprove the null hypothesis of normality of residual errors at the 95-percent confidence level (fig. 12). Accordingly, a normal distribution of residual errors is assumed, and standard deviation is considered a meaningful parameter. The standard deviation of residual error in the final steady-state model is 6.3 meters. The standard deviation and mean value of residual error in the steady-state simulation are presented in figure 13. The final steady-state model includes an area near La Luz Creek and surrounding subbasins in which the model systematically simulates water levels that are lower than measured water levels (fig. 14).
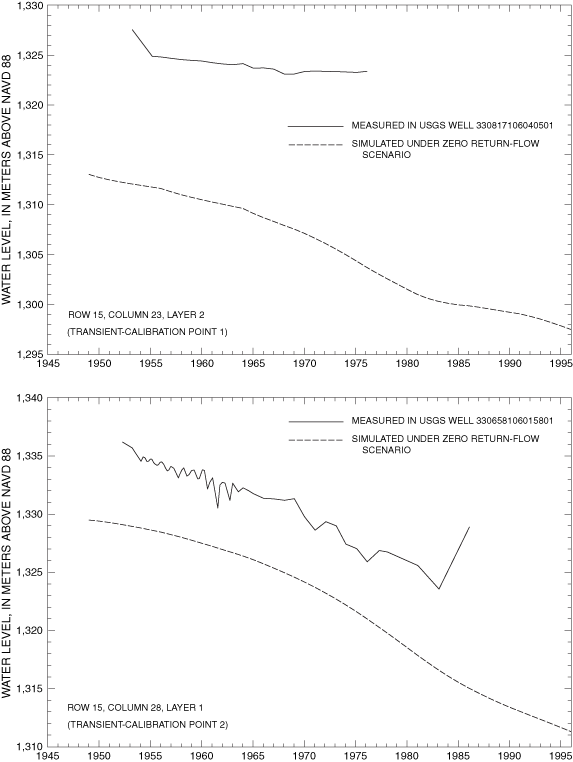
Final values of RMSE for transient-calibration points are listed in table 3. Visual representations of the agreement between final simulated and measured transient water levels for the zero return-flow scenario are shown in figure 15A-F. Values of transient RMSE range from 0.8 to 17.0 meters (table 3). Underestimations associated with transient-model calibration points 7 and 8 cluster in the same area as the grouping of underestimations in the steady-state model. This indicates that the hydrology of the La Luz Creek subbasin area and the corresponding basin-fill aquifer is not well represented in this model. The distributions of horizontal hydraulic conductivity and ratio of vertical to horizontal hydraulic conductivity by property zone and model layer as derived from model calibration are listed in table 5. The horizontal hydraulic-conductivity values derived from model calibration fall within the range of reasonable values based on aquifer-test data. Only part of the model on the eastern side of the Tularosa Basin (fig. 9) can be considered well calibrated because of the distribution of water-level data available for steady-state and transient calibrations.
MODPATH (Pollock, 1994) was used to estimate the travel time of ground water through the basin-fill aquifer between selected model cells and the corresponding points of ground-water recharge under steady-state conditions. Points of recharge were identified by extrapolating the paths of simulated particles from selected cells backward in time until they exited the model of the basin-fill aquifer. An effective porosity of 30 percent for the basin-fill aquifer was assumed in calculating travel times. The results of travel-time simulations plus apparent 14C ages of water from the location of these selected cells (Huff, 2002) are listed in table 6. The range in simulated travel times listed in table 6 reflects the differences in path lengths and flow velocities along all simulated flow paths within the model between recharge cells and the cell representing the termination of a given flow path. Apparent ages are systematically greater than simulated travel times. The discrepancy between apparent ages of water and simulated travel times may be caused by a number of factors, including residence time of water in the subbasin prior to entering the basin-fill aquifer, an increase in the 14C apparent age of water through geochemical processes not accounted for by Huff (2002), simulated rates of water movement through the model that are greater than actual rates of movement, or extrapolation to recharge points closer to the selected cells than are the actual recharge points.
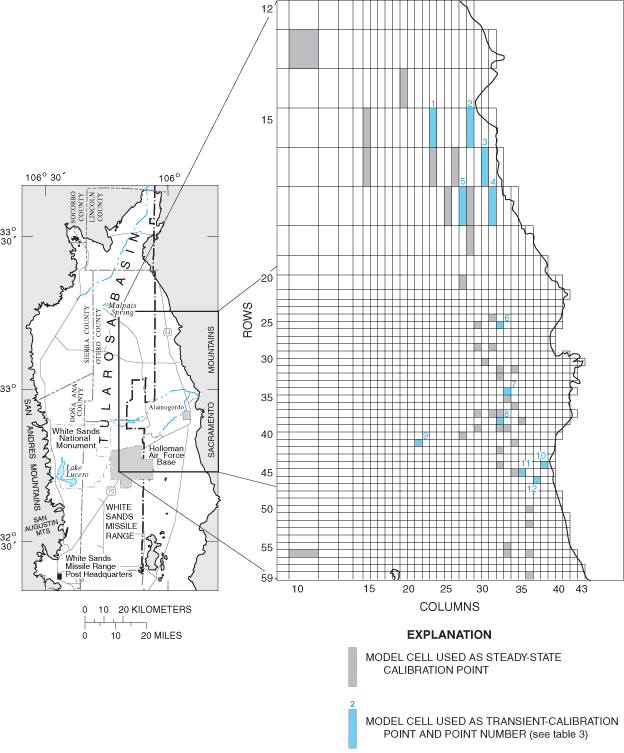
Figure 9. Location of model cells representing steady-state and transient-model calibration points.
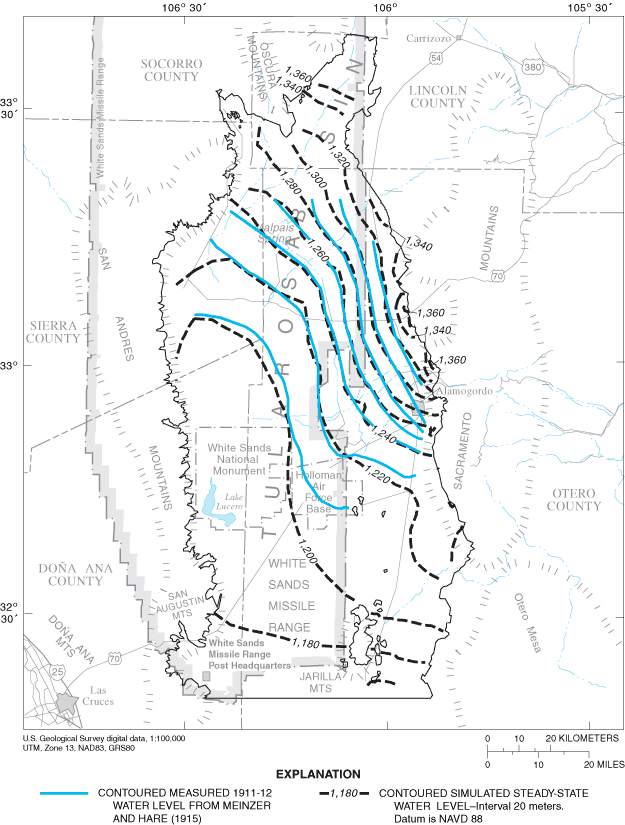
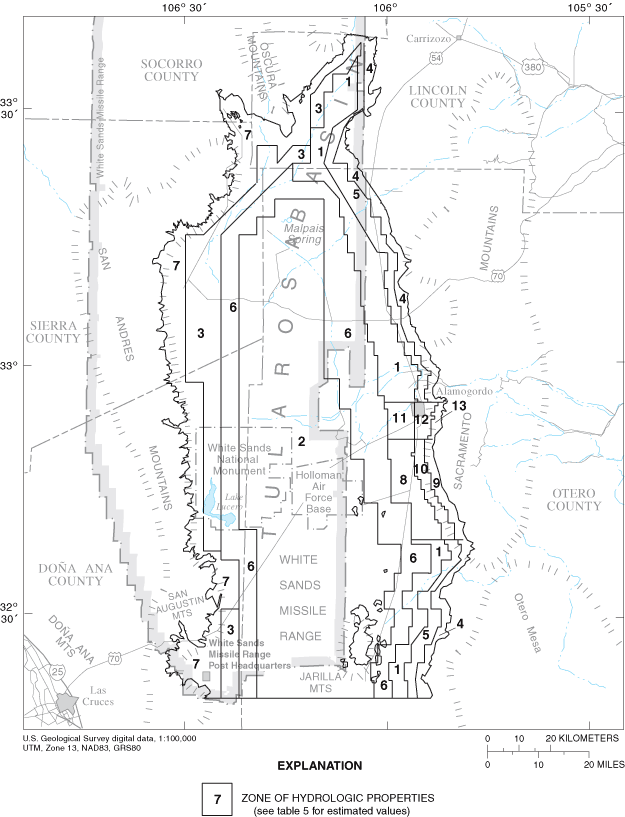
Figure 11. Zones of hydrologic properties.
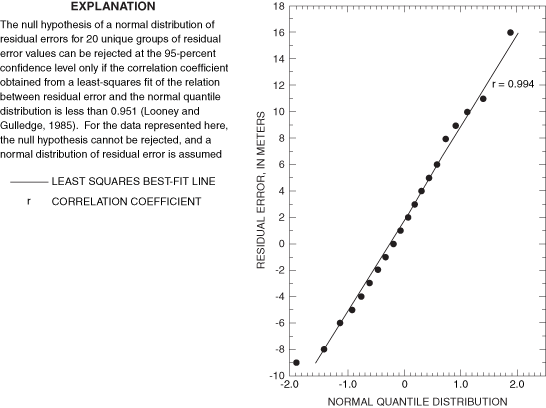
Figure 12. Test for nonnormality of steady-state residual errors.
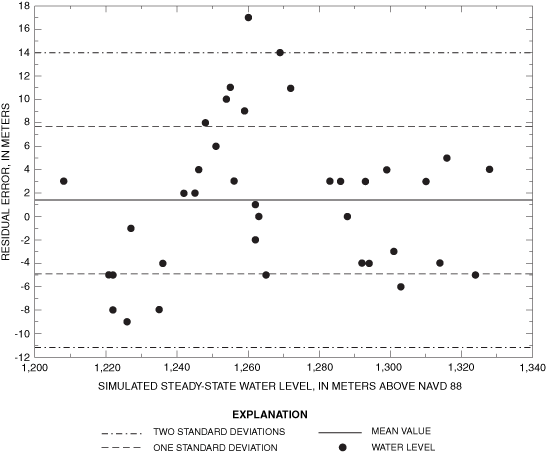
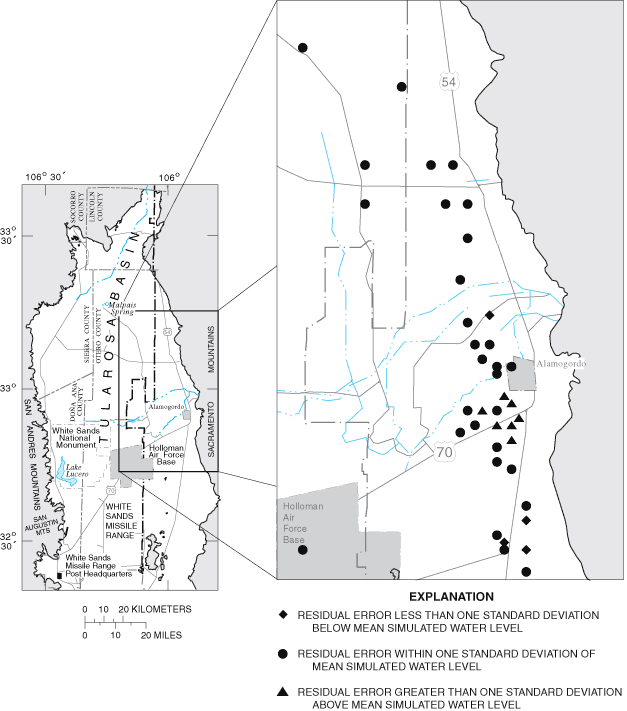
Figure 14. Distribution of steady-state residual errors.
| Model location | Well identification number in table 1 of Meinzer and Hare (1915) | Measured water level, calculated in meters above sea level | Steady-state simulation water level, in meters above sea level | |
|---|---|---|---|---|
| Row | Column | |||
| 13 | 10 | 1,304 | 1,260 | 1,262 |
| 14 | 19 | 1,307 | 1,303 | 1,299 |
| 16 | 14 | 1,406 | 1,260 | 1,265 |
| 16 | 23 | 1,416 | 1,313 | 1,310 |
| 16 | 26 | 1,415 | 1,319 | 1,324 |
| 17 | 14 | 1,409 | 1,263 | 1,263 |
| 17 | 25 | 1,506 | 1,310 | 1,314 |
| 17 | 28 | 1,504 | 1,332 | 1,328 |
| 18 | 28 | 1,509 | 1,321 | 1,316 |
| 20 | 27 | 1,512 | 1,298 | 1,301 |
| 24 | 31 | 1,604 | 1,297 | 1,303 |
| 25 | 28 | 1,605 | 1,288 | 1,292 |
| 28 | 29 | 1,611 | 1,288 | 1,288 |
| 28 | 31 | 1,612 | 1,290 | 1,294 |
| 30 | 30 | 1,617 | 1,289 | 1,286 |
| 31 | 32 | 1,620 | 1,288 | 1,288 |
| 31 | 34 | 1,622 | 1,296 | 1,293 |
| 32 | 32 | 1,619 | 1,286 | 1,283 |
| 35 | 33 | 1,639 | 1,283 | 1,272 |
| 36 | 34 | 1,641 | 1,283 | 1,269 |
| 37 | 28 | 1,712 | 1,259 | 1,256 |
| 37 | 30 | 1,710 | 1,268 | 1,259 |
| 37 | 32 | 1,705 | 1,263 | 1,262 |
| 38 | 35 | 1,703 | 1,277 | 1,260 |
| 39 | 29 | 1,714 | 1,257 | 1,251 |
| 39 | 32 | 1,718 | 1,264 | 1,254 |
| 39 | 34 | 1,717 | 1,266 | 1,255 |
| 40 | 27 | 1,713 | 1,250 | 1,246 |
| 41 | 34 | 1,719 | 1,256 | 1,248 |
| 44 | 32 | 1,722 | 1,244 | 1,242 |
| 45 | 34 | 1,727 | 1,244 | 1,242 |
| 50 | 36 | 1,803 | 1,232 | 1,236 |
| 52 | 36 | 1,804 | 1,227 | 1,235 |
| 54 | 32 | 1,805 | 1,217 | 1,222 |
| 55 | 33 | 1,810 | 1,214 | 1,222 |
| 56 | 10 | 1,802 | 1,211 | 1,208 |
| 56 | 33 | 1,811 | 1,216 | 1,221 |
| 56 | 36 | 1,809 | 1,217 | 1,226 |
| 59 | 36 | 1,812 | 1,226 | 1,227 |
| Vertical conductance, in inverse days | ||||||
|---|---|---|---|---|---|---|
| Zone of hydrologic properties (fig. 11) | Horizontal hydraulic conductivity, in meters per day | Between model layers 1 and 2 | Between model layers 2 and 3 | Between model layers 3 and 4 | Between model layers 4 and 5 | Between model layers 5 and 6 |
| 1 | 1.0 | 1.0X10-5 | 1.0X10-5 | 1.0X10-4 | 1.0X10-4 | 1.0X10-4 |
| 2 | 0.60 | 6.0X10-6 | 6.0X10-6 | 6.0X10-6 | 6.0X10-6 | 6.0X10-6 |
| 3 | 1.0 | 1.0X10-5 | 1.0X10-5 | 1.0X10-4 | 1.0X10-4 | 1.0X10-4 |
| 4 | 5.0 | 5.0X10-5 | 5.0X10-5 | 5.0X10-3 | 5.0X10-3 | 5.0X10-3 |
| 5 | 1.0 | 1.0X10-5 | 1.0X10-3 | 1.0X10-3 | 1.0X10-3 | 1.0X10-3 |
| 6 | 0.75 | 7.5X10-6 | 7.5X10-6 | 7.5X10-6 | 7.5X10-3 | 7.5X10-3 |
| 7 | 3.0 | 3.0X10-5 | 3.0X10-3 | 3.0X10-3 | 3.0X10-3 | 3.0X10-3 |
| 8 | 1.0 | 1.0X10-5 | 1.0X10-5 | 1.0X10-3 | 1.0X10-3 | 1.0X10-3 |
| 9 | 5.0 | 5.0X10-5 | 5.0X10-3 | 5.0X10-3 | 5.0X10-3 | 5.0X10-3 |
| 10 | 5.0 | 5.0X10-5 | 5.0X10-3 | 5.0X10-3 | 5.0X10-3 | 5.0X10-3 |
| 11 | 0.75 | 1.0X10-3 | 1.0X10-3 | 1.0X10-3 | 1.0X10-3 | 1.0X10-3 |
| 12 | 1.0 | 1.0X10-5 | 1.0X10-5 | 1.0X10-3 | 1.0X10-3 | 1.0X10-3 |
| 13 | 3.0 | 3.0X10-5 | 3.0X10-5 | 3.0X10-3 | 3.0X10-3 | 3.0X10-3 |
Table 6. Apparent ages and calculated travel times of ground water at selected model locations.
| Model location | Apparent age of ground water, in years (Huff, 2002) | Range of simulated travel times between the specified model location and the extrapolated model-recharge cell, in years | Subbasin associated with the extrapolated model-recharge cell (fig. 3) | ||||
|---|---|---|---|---|---|---|---|
| Row | Column | Layer | Minimum | Mean | Maximum | ||
| 49 | 38 | 1 | 8,019 | 500 | 600 | 1,100 | 15 |
| 49 | 39 | 2 | 5,777 | 1,100 | 1,400 | 1,800 | 15 |
| 50 | 39 | 3 | 9,188 | 1,900 | 2,200 | 3,000 | 15 |
| 44 | 37 | 1 | 1,534 | 80 | 200 | 400 | 15 |
| 44 | 37 | 2 | 3,372 | 600 | 1,100 | 2,700 | 15 |
| 47 | 35 | 1 | 2,283 | 200 | 300 | 350 | 16 |
Sensitivity of the steady-state and transient ground-water-flow simulations to changes in selected hydraulic properties were evaluated by the magnitude of corresponding changes in calculated values of RMSE. Calculation of RMSE for the steady-state model was previously defined in the "Model calibration" section. A composite RMSE was calculated for the transient model for sensitivity analysis. The composite transient RMSE was calculated using all available values of Wm at each calibration point and the corresponding values of Ws and assigning n the value of the total number of Wm available.
The steady-state model showed the most sensitivity in the upper two model layers to changes in recharge and horizontal hydraulic conductivity (fig. 16). The apparent sensitivity to changes in specified flow across the southern boundary is deceptive. Increasing specified flow across the southern boundary to three times the assigned value causes a large increase in water-level gradient within the model. This increase, in turn, causes lowering of simulated water levels along the southern model boundary to altitudes below the base of the active model cells. Simulated water levels below the base of model cells cause simulated flow in these cells to become zero. The corresponding loss of flow across the southern boundary forces additional simulated water to leave the system by ET. Because the ET rate is simulated in MODFLOW as a function of water level, the required increase in ET rate to compensate for lost flow across the southern boundary requires a large increase in simulated water levels throughout much of the model. This large increase in water levels causes a large change in steady-state RMSE. The transient ground-water-flow simulation shows sensitivities similar to those in the steady-state simulation but with slightly more sensitivity to horizontal hydraulic conductivity in model layers 3 and 4 (fig. 17). The apparent sensitivity to specified flows is caused by the same mechanism as that in the steady-state simulation.
The lack of sensitivity of the steady-state and transient models to reasonable changes in specified flows and ET parameters justifies the use of a southern specified flow boundary, characterization of Salt Creek and Malpais Spring as specified flow, and constant preselected ET parameters. The lack of sensitivity of the transient ground-water-flow simulation to changes in storativity and specific yield justifies the use of constant preselected values of these hydrologic parameters.
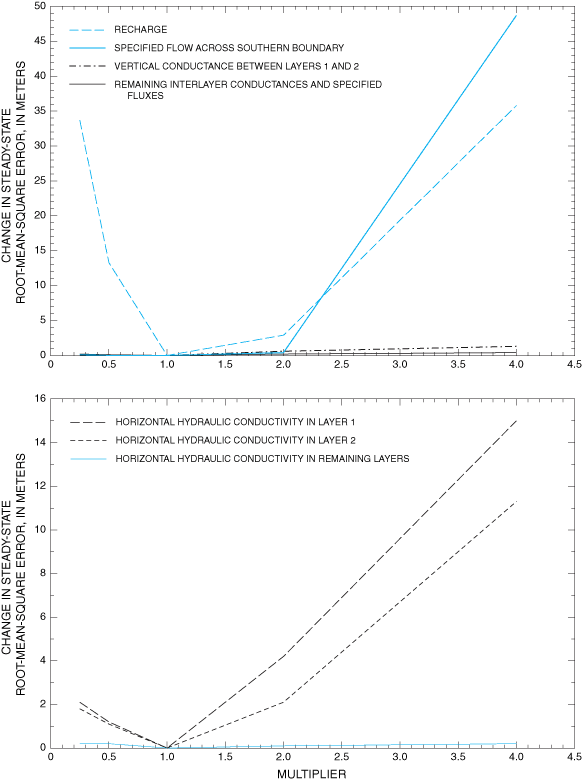
Figure 16. Sensitivity of steady-state model to changes in selected hydrologic properties.
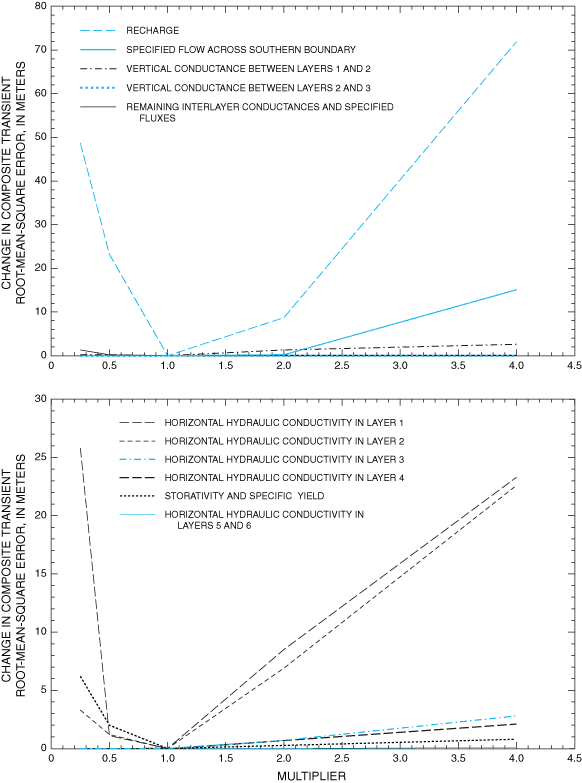
Figure 17. Sensitivity of transient model to changes in selected hydrologic properties.
Thirteen cells within the well-calibrated area of the ground-water-flow model represent the locations of water levels measured in 1991 (fig. 18). The 1991 water-level measurements plus 1991 water levels simulated under the zero and maximum return-flow scenarios are shown in table 7. The overall RMSE calculated under the zero return-flow scenario is 13.4 meters in contrast to 6.4 meters if transient-model verification points 1-3, located in the area of largest agricultural ground-water withdrawal near Tularosa, are excluded. Approximately 83 percent of the total squared error present under the zero return-flow scenario simulation for 1991 is accounted for by the data in transient-model verification points 1-3.
The choice of return-flow scenario has relatively little apparent effect on simulated water levels other than near Tularosa. Comparison of measured and simulated water levels shown in table 7 indicates that the maximum return-flow scenario, for some stress periods, may more accurately simulate conditions near Tularosa. In particular, simulated and projected water-level declines near Tularosa may be overestimated under the zero return-flow scenario. Uncertainties in hydrologic parameters that describe the basin-fill aquifer or errors in the volume of ground-water withdrawal assigned to the Tularosa area also could contribute to the lack of agreement between measured and simulated water levels for 1991.
Model results include simulated flows of water into and out of the model; water levels simulated for 1948, 1995, and 2040 for the zero and maximum return-flow scenarios; calculated water-level changes between 1948 and 1995 and between 1995 and 2040 for the zero and maximum return-flow scenarios; and water levels simulated for 1948-2040 at selected transient-calibration points. Generalized simulated directions of ground-water flow for 1948, 1995, and 2040 in areas near the City of Alamogordo and Holloman Air Force Base well fields are shown for the zero return-flow scenario. The zero return-flow scenario is used in calculating generalized ground-water-flow directions because this scenario represents the maximum potential effect of ground-water withdrawal.
The location and rates of estimated recharge to the basin-fill aquifer derived from the steady-state model calibration are listed in table 8. Recharge amounts typically range from 4 to 5 percent of total subbasin precipitation. Exceptions to this range include subbasins 44-46 (fig. 3) along the northern boundary of the Tularosa Basin, where estimated recharge is 1 percent of total precipitation, and subbasins 12-14 near La Luz Creek, where estimated recharge is 9 percent of total precipitation. Annualized average recharge to the basin-fill aquifer is estimated to be approximately 143,000 cubic meters per day from the steady-state model calibration. An estimated 88 percent of this total recharge leaves the basin by ET, 9 percent by interbasin ground-water flow into the Hueco Bolson, and 3 percent by flow into creeks and springs in the steady-state simulation. Results of the steady-state simulation approximate predevelopment conditions. Under 1995 zero return-flow conditions, total inflow to the simulated system was estimated to be approximately 199,000 cubic meters per day, of which approximately 143,000 cubic meters per day was from recharge and approximately 56,000 cubic meters per day was from aquifer storage. An estimated 40 percent of this total inflow left the system by ground-water withdrawal, 51 percent by ET, 7 percent by interbasin ground-water flow into the Hueco Bolson, and 2 percent by flow into creeks and springs. Areas of active ET in the steady-state and 1995 simulations are shown in figures 19 and 20, respectively. Simulated flows for 1948-2040 are listed in table 9.
Differences between water levels simulated for 1948 under the zero return-flow and maximum return-flow (figs. 21 and 22) scenarios are minimal. Differences between both 1948 scenarios and the steady-state simulation (fig. 10) also are minimal. Differences between water levels simulated for 1995 under the zero return-flow and maximum return-flow scenarios (figs. 23 and 24) lie mainly in a more pronounced lowering of simulated water levels near Tularosa under the zero return-flow scenario. The pattern of differences is the same for water levels simulated for 2040 under the zero return-flow and maximum return-flow scenarios (figs. 25 and 26).
Measured and simulated water levels for 1948-2040 for both the zero and maximum return-flow scenarios for selected transient-model calibration points are shown in figure 27. These points were chosen on the basis of relatively small values of RMSE (table 3) and a relatively large number of comparisons between measured and simulated water levels. The effects of changes in return-flow scenarios are far greater for transient-model calibration points 3 and 5 near the agricultural area west of Tularosa than for points 10 and 11 near the Holloman Air Force Base well fields. This is consistent with the areal distribution of the apparent effects of return flow on simulated 1991 water levels (table 7). The relative lack of sensitivity of the ground-water-flow model near the Holloman Air Force Base well fields to the return-flow scenario may be caused by a lack of nearby areas of return-flow applications (figs. 7B and 8). Water levels simulated under maximum return-flow conditions were below the ET extinction depth in more than 95 percent of the model cells in the area of agricultural ground-water withdrawals in 1948, 1995, and 2040. Therefore, any overestimation of ET values associated with basing maximum return-flow ground-water withdrawals on calculated depletion rates would be minimal.
Declines in simulated water levels under the zero and maximum return-flow scenarios between 1948 and 1995 within the well-calibrated area of the ground-water-flow model are shown in figure 28. Simulated water-level declines were as large as 30 meters under the zero return-flow scenario and as large as 15 meters under the maximum return-flow scenario near the agricultural area west of Tularosa. Water-level declines of 15 and 10 meters are simulated near the City of Alamogordo well field under the zero and maximum return-flow scenarios, respectively. Less than 5 meters of water-level decline is simulated under both return-flow scenarios near the Holloman Air Force Base well fields. The increase in simulated water levels near Alamogordo under the maximum return-flow scenario results from the application of return flow.
Declines in water levels simulated under the zero and maximum return-flow scenarios between 1995 and 2040 within the calibrated area of the ground-water-flow model are shown in figure 29. Simulated water-level declines were as large as 25 meters under the zero return-flow scenario and as large as 15 meters under the maximum return-flow scenario near the agricultural area west of Tularosa. Both scenarios result in approximately 15 meters of water-level decline near the City of Alamogordo well field and less than 5 meters of water-level decline near the Holloman Air Force Base well fields.
Uncertainties in the spatial distribution of ground-water withdrawals near the agricultural area west of Tularosa and in the City of Alamogordo well field cause uncertainty in the degree of declines in simulated water levels. The spatial distribution of agricultural ground-water withdrawals near Tularosa is assumed to be unchanged from that of Morrison (1989). All ground-water withdrawal in the City of Alamogordo well field is assumed to come from the basin-fill aquifer. In actuality, some part of the withdrawal comes from an aquifer or aquifers in fractured rock underlying the basin-fill aquifer. Information was unavailable regarding the fraction of total withdrawal produced from the fractured-rock aquifer(s) and the degree of interconnectedness between the basin-fill and any underlying aquifer. Assuming that all withdrawal comes from the basin-fill aquifer may result in overestimated declines in simulated water levels. Assuming larger values of storativity may lessen declines in simulated water levels near Tularosa and the City of Alamogordo well fields. Sensitivity analysis indicates that the effect of increasing storativity at the basin scale is not large.
Generalized simulated directions of horizontal ground-water flow were calculated by performing a vector summation of horizontal outflows from each model cell. Vectors were computed using outflow per unit width to correct for variable cell sizes. Vertical ground-water flows were calculated using interlayer differences in simulated water levels between individual model cells. The procedure used to calculate ground-water flow directions are discussed in Appendix 1.
Generalized simulated directions of horizontal and vertical ground-water flow in model layers 1 and 2 for 1948 near the City of Alamogordo well field are shown in figures 30 and 31, respectively. Generalized simulated directions of horizontal ground-water flow for 1948 in model layer 3 near the City of Alamogordo well field are shown in figure 32. The direction of simulated horizontal ground-water flow is predominantly west to southwest in all three model layers with a southward component near the mountain front in model layers 2 and 3. Simulated vertical ground-water flow is largely upward into the active cells of model layer 1. Simulated vertical ground-water flow is largely downward from model layer 2 into model layer 3 near the mountain front and largely upward from model layer 3 into model layer 2 near the western part of the area shown in figure 31.
The generalized simulated directions of horizontal ground-water flow for 1995 and 2040 in model layers 1-3 (figs. 33-38) differ little from 1948 simulations. Conditions of downward to near zero simulated vertical ground-water flow in model cells in columns 38-39 and rows 26-27 of model layer 2 in 1948 (fig. 31) are reversed to upward simulated potential for ground-water flow by 2040 (fig. 37). Ground-water withdrawal is the only model variable changed between the 1948, 1995, and 2040 simulations. This reversal represents a small and localized change in overall simulated flow patterns near the City of Alamogordo well field. The geohydrologic cross section J-J' of Orr and Myers (1986, figs. 5 and 6) (figs. 30-38) shows increasing ground-water salinity with depth in the basin-fill aquifer. Movement of water from depth of the quality described by Orr and Myers (1986) along cross section J-J' could diminish shallower water quality in the basin-fill aquifer. Any corresponding deterioration in water quality in City of Alamogordo public-supply wells would be difficult to anticipate because these wells withdraw water from both the basin-fill aquifer and the underlying consolidated-rock aquifer.
Generalized simulated directions of horizontal and vertical ground-water flow for 1948 in model layers 1 and 2 near the Holloman Air Force Base well fields are shown in figures 39 and 40, respectively. Generalized simulated directions of horizontal ground-water flow for 1948 in model layer 3 near the Holloman Air Force Base well fields are shown in figure 41. The direction of simulated horizontal ground-water flow is predominantly southward in all three model layers in approximately the northern half of the area near the Holloman Air Force Base well fields and predominantly westward to southwestward in the southern half. The direction of simulated vertical ground-water flow is predominantly downward from model layer 1 into model layer 2 in approximately the northern third of the area near the Holloman Air Force Base well fields and predominantly upward from model layer 2 into model layer 1 in the southern two-thirds of the area. The simulated vertical flow is near zero between model layers 2 and 3 in approximately the eastern half of the area near the Holloman Air Force Base well fields and follows much the same pattern as simulated flow does between model layers 1 and 2 over the western half of the area.
Generalized simulated directions of horizontal ground-water flow for 1995 and 2040 in model layers 1-3 (figs. 42-47) near the Holloman Air Force Base well fields show localized differences from 1948 simulations (figs. 39-41). Differences exist primarily along the mountain front south of model row 47 and generally represent localized changes in flow directions in and near model cells containing the Holloman Air Force Base public-supply wells. The changes in horizontal ground-water-flow direction do not generally extend west of model column 38. Geohydrologic cross sections E-E' and F-F' of Orr and Myers (1986, fig. 5) (figs. 39-47) show ground water with dissolved-solids concentrations predominantly smaller than 1,000 mg/L in and east of model column 38 at depths corresponding to model layers 1-3. Horizontal inflow of water of the quality described by Orr and Myers along geohydrologic cross sections E-E' and F-F' east of model column 38 should not greatly affect the quality of water in mountain-front areas. The overall simulated directions of vertical ground-water flow in model layers 1 and 2 for 1995 and 2040 differ little from 1948 simulations. Locally, the simulated upward flow into model layer 1 in model cells in columns 41 and 42 and rows 57-59 in 1948 changes to near zero simulated potential for flow between model layers 1 and 2 by 1995 and remains so in 2040.
| Transient- model verification point number (fig. 18) | Model location | U.S. Geological Survey well identification number | Measured water level, in meters above NAVD 88 | Water level simulated using the zero return-flow scenario, in meters above NAVD 88 | Water level simulated using the maximum return-flow scenario, in meters above NAVD 88 | ||
|---|---|---|---|---|---|---|---|
| Row | Column | Layer | |||||
| 1 | 16 | 23 | 1 | 330529106042901 | 1,306 | 1,275 | 1,296 |
| 2 | 16 | 25 | 1 | 330526106033201 | 1,311 | 1,287 | 1,310 |
| 3 | 17 | 24 | 1 | 330355106034301 | 1,300 | 1,280 | 1,305 |
| 4 | 25 | 32 | 1 | 325655105594201 | 1,298 | 1,295 | 1,299 |
| 5 | 39 | 37 | 1 | 325135105571901 | 1,259 | 1,253 | 1,258 |
| 6 | 44 | 36 | 1 | 324930105575401 | 1,247 | 1,240 | 1,241 |
| 7 | 45 | 35 | 1 | 324905105583901 | 1,237 | 1,238 | 1,239 |
| 8 | 46 | 38 | 1 | 324844105570801 | 1,246 | 1,238 | 1,239 |
| 9 | 47 | 32 | 1 | 324813105594001 | 1,225 | 1,233 | 1,234 |
| 10 | 47 | 34 | 1 | 324800105585501 | 1,231 | 1,235 | 1,236 |
| 11 | 49 | 38 | 1 | 324713105571201 | 1,226 | 1,235 | 1,236 |
| 12 | 50 | 39 | 1 | 324648105564201 | 1,229 | 1,234 | 1,235 |
| 13 | 58 | 34 | 1 | 324343105585001 | 1,214 | 1,222 | 1,222 |
| Subbasin number (fig. 3) | Name of stream or canyon associated with subbasin | Subbasin drainage area, in square miles (Waltemeyer, 2001) | Mean annual precipitation in subbasin, in inches (Waltemeyer, 2001) | Fraction of precipitation in subbasin that becomes ground-water recharge as estimated from model calibration, in percent | Ground-water recharge as estimated from model calibration, in cubic meters per day | Model cell(s) in which ground-water recharge is implemented (fig. 6) | |
|---|---|---|---|---|---|---|---|
| Row(s) | Column(s) | ||||||
| 1 | Bear Canyon | 1.39 | 24.27 | 4 | 243 | 4 | 22 |
| 2 | Water Canyon | 2.50 | 24.89 | 4 | 448 | 4 | 21 |
| 3 | Sanders Canyon | 0.87 | 24.67 | 4 | 156 | 5 | 15 |
| 4 | Elder Canyon | 1.73 | 24.46 | 4 | 305 | 7 | 13 |
| 5 | Unnamed arroyo | 0.97 | 22.82 | 4 | 159 | 8 | 16 |
| 6 | Unnamed arroyo | 3.60 | 24.42 | 4 | 633 | 8 | 16 |
| 7 | Unnamed arroyo | 3.77 | 23.63 | 4 | 642 | 9 | 19 |
| 8 | Unnamed arroyo | 4.76 | 21.17 | 4 | 726 | 9 | 20 |
| 9 | Three Rivers | 86.5 | 22.01 | 4 | 13,700 | 10 11 | 23 26 |
| 10 | Rinconada Canyon | 97.5 | 21.16 | 4 | 14,900 | 13 14 | 31 30 |
| 11 | Tularosa River | 157 | 21.23 | 4 | 24,000 | 16 17 | 31 33 |
| 12 | La Luz Creek | 65.2 | 21.07 | 9 | 22,300 | 20 21 | 39 40 |
| 13 | Dry Canyon | 8.98 | 19.35 | 9 | 2,820 | 25 | 39 |
| 14 | Marble Canyon | 3.45 | 17.08 | 9 | 955 | 33 | 41 |
| 15 | Alamo Canyon | 24.9 | 20.99 | 5 | 4,710 | 41 | 39 |
| 16 | Mule Canyon | 6.70 | 16.22 | 5 | 978 | 43 | 36 |
| 18 | Dog Canyon | 10.5 | 20.82 | 5 | 1,970 | 54 | 41 |
| 19 | Escondido Canyon | 11.0 | 19.95 | 5 | 1,980 | 61 | 45 |
| 20 | Bug Scuffle Canyon | 12.3 | 19.50 | 5 | 2,160 | 71 | 49 |
| 21 | Grapevine Canyon | 33.5 | 19.37 | 5 | 5,840 | 72 | 50 |
| 22 | Pipeline Canyon | 6.11 | 14.26 | 5 | 785 | 74 | 48 |
| 23 | Culp Canyon | 23.2 | 14.29 | 5 | 2,990 | 74 | 48 |
| 24 | Oak Canyon | 8.94 | 14.85 | Not within simulated area | |||
| 25 | Soledad Canyon | 15.6 | 15.88 | Not within simulated area | |||
| 26 | Sotol Creek | 13.1 | 14.32 | 4 | 1,350 | 80 | 4 |
| 27 | Unnamed arroyo | 12.2 | 11.91 | 4 | 1,050 | 79 | 4 |
| 28 | Bear Canyon | 15.4 | 11.80 | 4 | 1,310 | 76 | 5 |
| 29 | Little San Nicolas Canyon | 7.35 | 12.00 | 4 | 635 | 74 | 5 |
| 30 | Ash Canyon | 7.60 | 13.81 | 4 | 756 | 72 | 3 |
| 31 | San Andres Canyon | 8.90 | 15.63 | 4 | 1,000 | 55 | 3 |
| 32 | Mayberry Canyon | 11.5 | 15.49 | 4 | 1,280 | 47 | 3 |
| 33 | Deadman Canyon | 16.1 | 14.33 | 4 | 1,660 | 38 | 3 |
| 35 | Hembrillo Canyon | 17.2 | 12.00 | 4 | 1,490 | 25 | 2 |
| 36 | Grandview Canyon | 2.82 | 12.00 | 4 | 244 | 20 | 2 |
| 37 | Sulfur Canyon | 30.3 | 12.04 | 4 | 2,630 | 19 | 2 |
| 38 | Ash Canyon | 4.30 | 12.08 | 4 | 374 | 17 | 2 |
| 39 | Workman Canyon | 5.99 | 12.66 | 4 | 546 | 17 | 2 |
| 40 | Cottonwood Canyon | 45.3 | 13.73 | 4 | 4,480 | 16 | 2 |
| 41 | Rhoades Canyon | 39.7 | 14.57 | 4 | 4,170 | 14 | 2 |
| 42 | Good Fortune Canyon | 24.0 | 15.34 | 4 | 2,650 | 12 | 2 |
| 43 | Thurgood Canyon | 37.2 | 13.80 | 4 | 3,700 | 9 | 6 |
| 44 | Unnamed arroyo | 73.8 | 15.61 | 1 | 2,070 | 3 | 10 |
| 45 | Red Canyon | 55.6 | 14.31 | 1 | 1,430 | 3 | 14 |
| 46 | Wagon Canyon | 120 | 12.95 | 1 | 2,800 | 3 | 20 |
Table 9. Simulated flows into and out of the basin-fill aquifer, 1948-2040.
[All values in cubic meters per day]
| Year | Simulated ground-water recharge | Simulated ground-water flow across the southern model boundary | Simulated ground-water flow to springs | Simulated evapotrans-piration using the zero return-flow scenario | Simulated evapotrans-piration using the maximum return-flow scenario | Simulated decrease in aquifer storage using the zero return-flow scenario | Simulated decrease in aquifer storage using the maximum return-flow scenario |
|---|---|---|---|---|---|---|---|
| 1948 | 143,000 | 13,000 | 4,600 | 124,000 | 124,000 | 23,000 | 5,000 |
| 1949 | 143,000 | 13,000 | 4,600 | 124,000 | 124,000 | 23,000 | 5,000 |
| 1950 | 143,000 | 13,000 | 4,600 | 124,000 | 124,000 | 23,000 | 3,000 |
| 1951 | 143,000 | 13,000 | 4,600 | 124,000 | 124,000 | 24,000 | 4,000 |
| 1952 | 143,000 | 13,000 | 4,600 | 124,000 | 124,000 | 24,000 | 5,000 |
| 1953 | 143,000 | 13,000 | 4,600 | 123,000 | 124,000 | 25,000 | 5,000 |
| 1954 | 143,000 | 13,000 | 4,600 | 123,000 | 124,000 | 25,000 | 4,000 |
| 1955 | 143,000 | 13,000 | 4,600 | 123,000 | 125,000 | 27,000 | 5,000 |
| 1956 | 143,000 | 13,000 | 4,600 | 122,000 | 125,000 | 37,000 | 12,000 |
| 1957 | 143,000 | 13,000 | 4,600 | 122,000 | 125,000 | 36,000 | 9,000 |
| 1958 | 143,000 | 13,000 | 4,600 | 122,000 | 124,000 | 34,000 | 6,000 |
| 1959 | 143,000 | 13,000 | 4,600 | 122,000 | 124,000 | 35,000 | 6,000 |
| 1960 | 143,000 | 13,000 | 4,600 | 121,000 | 125,000 | 37,000 | 7,000 |
| 1961 | 143,000 | 13,000 | 4,600 | 121,000 | 125,000 | 39,000 | 12,000 |
| 1962 | 143,000 | 13,000 | 4,600 | 121,000 | 125,000 | 38,000 | 9,000 |
| 1963 | 143,000 | 13,000 | 4,600 | 120,000 | 125,000 | 39,000 | 10,000 |
| 1964 | 143,000 | 13,000 | 4,600 | 119,000 | 126,000 | 58,000 | 24,000 |
| 1965 | 143,000 | 13,000 | 4,600 | 119,000 | 125,000 | 55,000 | 21,000 |
| 1966 | 143,000 | 13,000 | 4,600 | 118,000 | 125,000 | 54,000 | 18,000 |
| 1967 | 143,000 | 13,000 | 4,600 | 118,000 | 125,000 | 61,000 | 25,000 |
| 1968 | 143,000 | 13,000 | 4,600 | 117,000 | 125,000 | 59,000 | 21,000 |
| 1969 | 143,000 | 13,000 | 4,600 | 116,000 | 125,000 | 65,000 | 25,000 |
| 1970 | 143,000 | 13,000 | 4,600 | 116,000 | 125,000 | 69,000 | 26,000 |
| 1971 | 143,000 | 13,000 | 4,600 | 115,000 | 124,000 | 75,000 | 32,000 |
| 1972 | 143,000 | 13,000 | 4,600 | 114,000 | 124,000 | 77,000 | 30,000 |
| 1973 | 143,000 | 13,000 | 4,600 | 113,000 | 124,000 | 79,000 | 30,000 |
| 1974 | 143,000 | 13,000 | 4,600 | 112,000 | 123,000 | 83,000 | 33,000 |
| 1975 | 143,000 | 13,000 | 4,600 | 112,000 | 122,000 | 84,000 | 31,000 |
| 1976 | 143,000 | 13,000 | 4,600 | 111,000 | 122,000 | 86,000 | 34,000 |
| 1977 | 143,000 | 13,000 | 4,600 | 110,000 | 121,000 | 84,000 | 33,000 |
| 1978 | 143,000 | 13,000 | 4,600 | 110,000 | 120,000 | 83,000 | 33,000 |
| 1979 | 143,000 | 13,000 | 4,600 | 109,000 | 121,000 | 84,000 | 35,000 |
| 1980 | 143,000 | 13,000 | 4,600 | 108,000 | 120,000 | 82,000 | 34,000 |
| 1981 | 143,000 | 13,000 | 4,600 | 108,000 | 120,000 | 77,000 | 33,000 |
| 1982 | 143,000 | 13,000 | 4,600 | 107,000 | 120,000 | 71,000 | 27,000 |
| 1983 | 143,000 | 13,000 | 4,600 | 107,000 | 119,000 | 62,000 | 23,000 |
| 1984 | 143,000 | 13,000 | 4,600 | 106,000 | 118,000 | 53,000 | 18,000 |
| 1985 | 143,000 | 13,000 | 4,600 | 106,000 | 118,000 | 52,000 | 18,000 |
| 1986 | 143,000 | 13,000 | 4,600 | 105,000 | 118,000 | 42,000 | 15,000 |
| 1987 | 143,000 | 13,000 | 4,600 | 105,000 | 118,000 | 42,000 | 20,000 |
| 1988 | 143,000 | 13,000 | 4,600 | 104,000 | 117,000 | 41,000 | 21,000 |
| 1989 | 143,000 | 13,000 | 4,600 | 104,000 | 117,000 | 42,000 | 25,000 |
| 1990 | 143,000 | 13,000 | 4,600 | 104,000 | 117,000 | 39,000 | 27,000 |
| 1991 | 143,000 | 13,000 | 4,600 | 103,000 | 116,000 | 41,000 | 29,000 |
| 1992 | 143,000 | 13,000 | 4,600 | 103,000 | 116,000 | 43,000 | 31,000 |
| 1993 | 143,000 | 13,000 | 4,600 | 102,000 | 116,000 | 46,000 | 33,000 |
| 1994 | 143,000 | 13,000 | 4,600 | 102,000 | 116,000 | 54,000 | 39,000 |
| 1995 | 143,000 | 13,000 | 4,600 | 101,000 | 115,000 | 56,000 | 41,000 |
| 1996 | 143,000 | 13,000 | 4,600 | 101,000 | 115,000 | 56,000 | 41,000 |
| 1997 | 143,000 | 13,000 | 4,600 | 101,000 | 115,000 | 56,000 | 39,000 |
| 1998 | 143,000 | 13,000 | 4,600 | 100,000 | 114,000 | 55,000 | 39,000 |
| 1999 | 143,000 | 13,000 | 4,600 | 100,000 | 114,000 | 55,000 | 39,000 |
| 2000 | 143,000 | 13,000 | 4,600 | 99,000 | 114,000 | 55,000 | 38,000 |
| 2001 | 143,000 | 13,000 | 4,600 | 99,000 | 113,000 | 55,000 | 38,000 |
| 2002 | 143,000 | 13,000 | 4,600 | 99,000 | 113,000 | 55,000 | 38,000 |
| 2003 | 143,000 | 13,000 | 4,600 | 98,000 | 113,000 | 55,000 | 38,000 |
| 2004 | 143,000 | 13,000 | 4,600 | 98,000 | 112,000 | 55,000 | 38,000 |
| 2005 | 143,000 | 13,000 | 4,600 | 98,000 | 112,000 | 55,000 | 38,000 |
| 2006 | 143,000 | 13,000 | 4,600 | 97,000 | 112,000 | 55,000 | 38,000 |
| 2007 | 143,000 | 13,000 | 4,600 | 100,000 | 111,000 | 54,000 | 38,000 |
| 2008 | 143,000 | 13,000 | 4,600 | 97,000 | 111,000 | 54,000 | 38,000 |
| 2009 | 143,000 | 13,000 | 4,600 | 96,000 | 111,000 | 54,000 | 37,000 |
| 2010 | 143,000 | 13,000 | 4,600 | 96,000 | 110,000 | 54,000 | 37,000 |
| 2011 | 143,000 | 13,000 | 4,600 | 95,000 | 110,000 | 54,000 | 37,000 |
| 2012 | 143,000 | 13,000 | 4,600 | 95,000 | 110,000 | 54,000 | 37,000 |
| 2013 | 143,000 | 13,000 | 4,600 | 95,000 | 109,000 | 54,000 | 37,000 |
| 2014 | 143,000 | 13,000 | 4,600 | 94,000 | 109,000 | 54,000 | 37,000 |
| 2015 | 143,000 | 13,000 | 4,600 | 94,000 | 109,000 | 54,000 | 37,000 |
| 2016 | 143,000 | 13,000 | 4,600 | 94,000 | 109,000 | 54,000 | 37,000 |
| 2017 | 143,000 | 13,000 | 4,600 | 93,000 | 108,000 | 54,000 | 37,000 |
| 2018 | 143,000 | 13,000 | 4,600 | 93,000 | 108,000 | 54,000 | 37,000 |
| 2019 | 143,000 | 13,000 | 4,600 | 93,000 | 108,000 | 54,000 | 37,000 |
| 2020 | 143,000 | 13,000 | 4,600 | 92,000 | 107,000 | 54,000 | 37,000 |
| 2021 | 143,000 | 13,000 | 4,600 | 92,000 | 107,000 | 54,000 | 37,000 |
| 2022 | 143,000 | 13,000 | 4,600 | 92,000 | 107,000 | 54,000 | 36,000 |
| 2023 | 143,000 | 13,000 | 4,600 | 91,000 | 106,000 | 52,000 | 36,000 |
| 2024 | 143,000 | 13,000 | 4,600 | 91,000 | 106,000 | 52,000 | 36,000 |
| 2025 | 143,000 | 13,000 | 4,600 | 91,000 | 106,000 | 52,000 | 36,000 |
| 2026 | 143,000 | 13,000 | 4,600 | 90,000 | 106,000 | 52,000 | 36,000 |
| 2027 | 143,000 | 13,000 | 4,600 | 90,000 | 105,000 | 52,000 | 36,000 |
| 2028 | 143,000 | 13,000 | 4,600 | 90,000 | 105,000 | 51,000 | 36,000 |
| 2029 | 143,000 | 13,000 | 4,600 | 89,000 | 105,000 | 52,000 | 36,000 |
| 2030 | 143,000 | 13,000 | 4,600 | 89,000 | 104,000 | 52,000 | 36,000 |
| 2031 | 143,000 | 13,000 | 4,600 | 89,000 | 104,000 | 52,000 | 36,000 |
| 2032 | 143,000 | 13,000 | 4,600 | 88,000 | 104,000 | 52,000 | 36,000 |
| 2033 | 143,000 | 13,000 | 4,600 | 88,000 | 104,000 | 52,000 | 36,000 |
| 2034 | 143,000 | 13,000 | 4,600 | 88,000 | 103,000 | 52,000 | 36,000 |
| 2035 | 143,000 | 13,000 | 4,600 | 88,000 | 103,000 | 52,000 | 36,000 |
| 2036 | 143,000 | 13,000 | 4,600 | 87,000 | 103,000 | 52,000 | 36,000 |
| 2037 | 143,000 | 13,000 | 4,600 | 87,000 | 103,000 | 52,000 | 36,000 |
| 2038 | 143,000 | 13,000 | 4,600 | 87,000 | 102,000 | 52,000 | 36,000 |
| 2039 | 143,000 | 13,000 | 4,600 | 86,000 | 102,000 | 52,000 | 36,000 |
| 2040 | 143,000 | 13,000 | 4,600 | 86,000 | 102,000 | 52,000 | 36,000 |
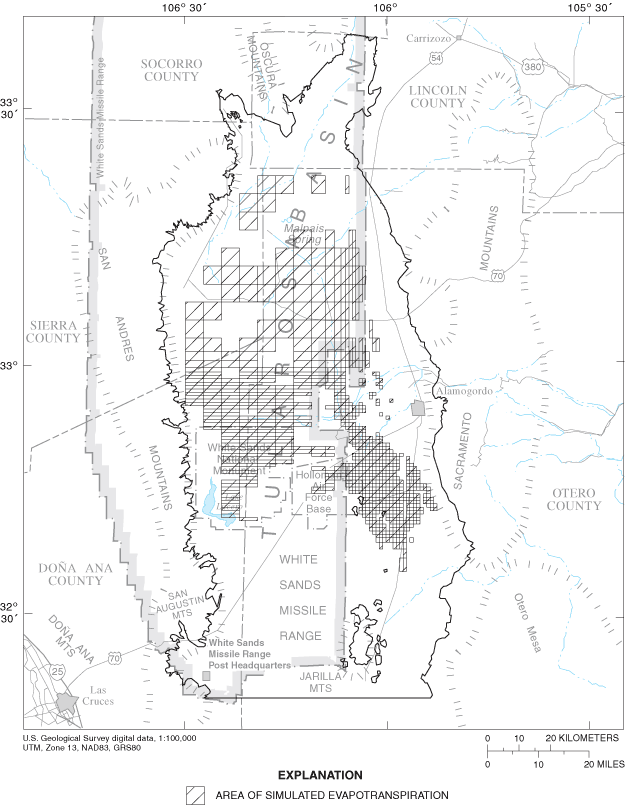
Figure 19. Areas of simulated evapotranspiration under steady-state conditions.
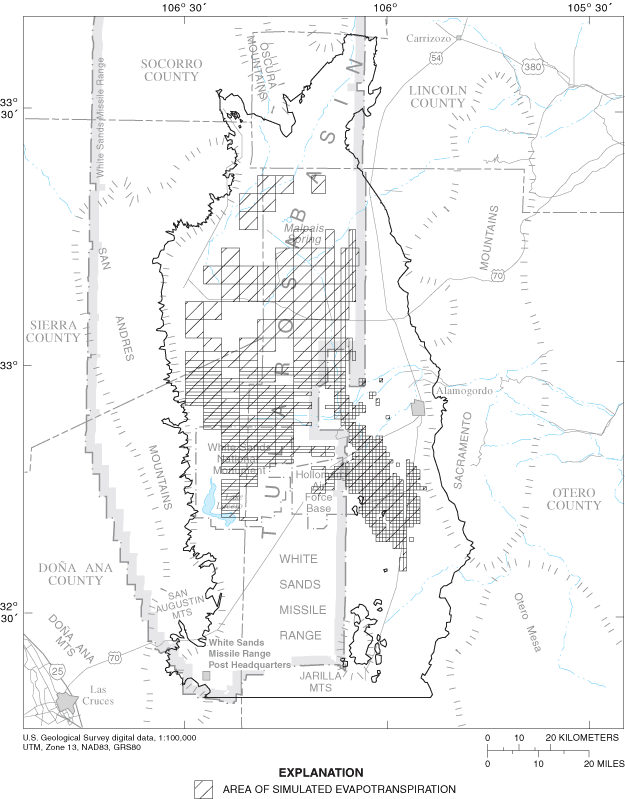
Figure 20. Areas of simulated evapotranspiration under 1995 zero return-flow conditions.
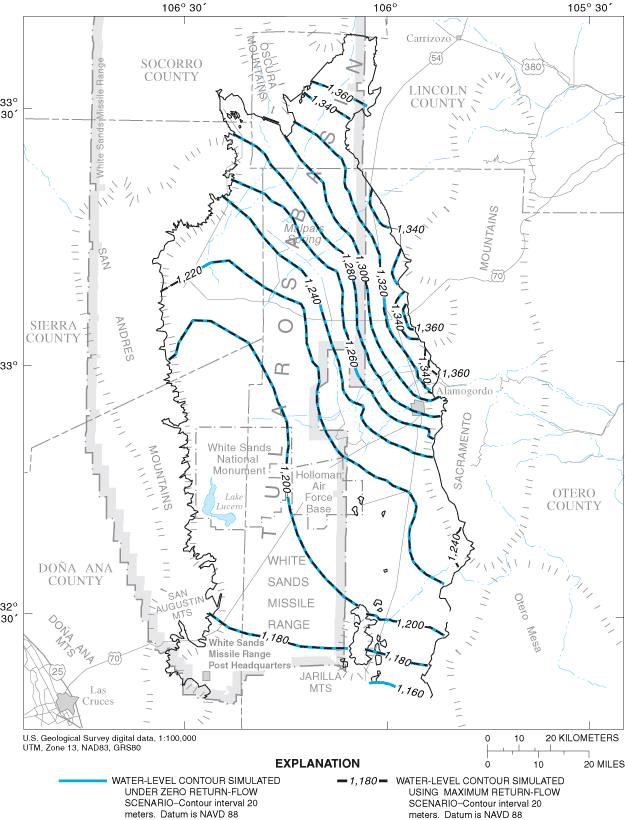
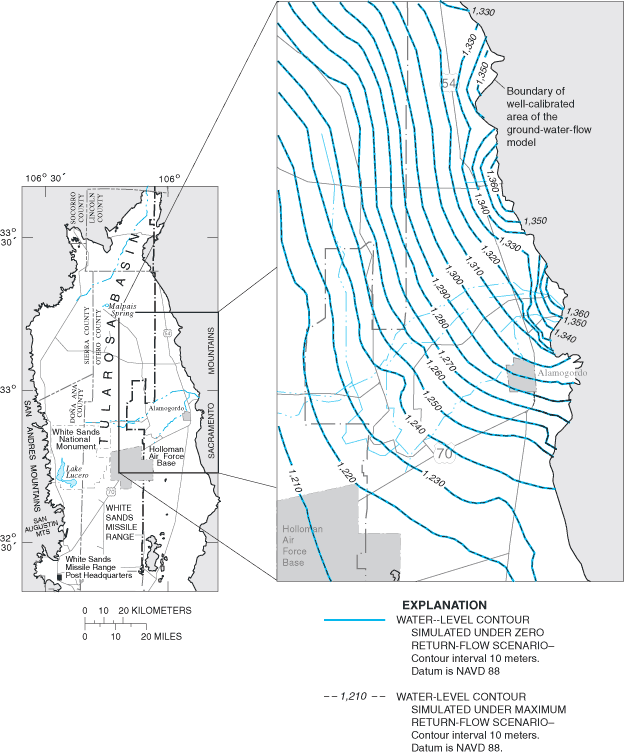

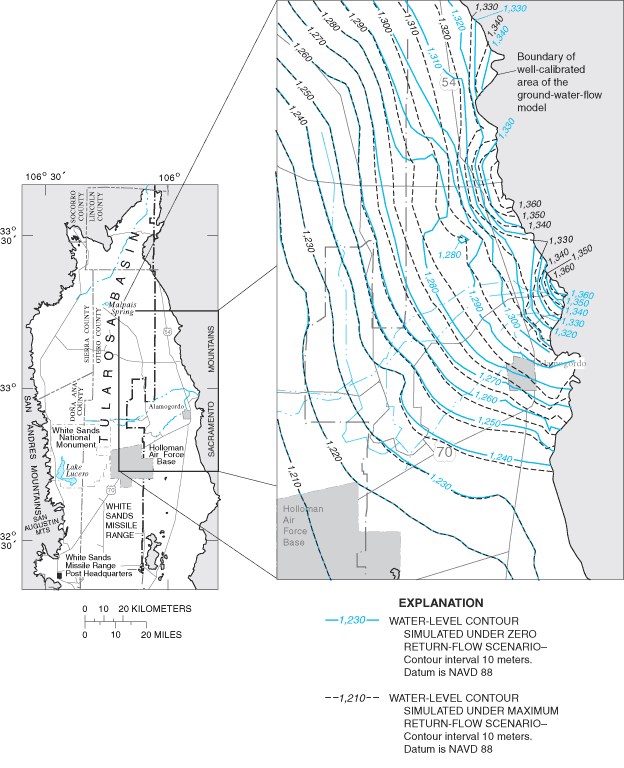
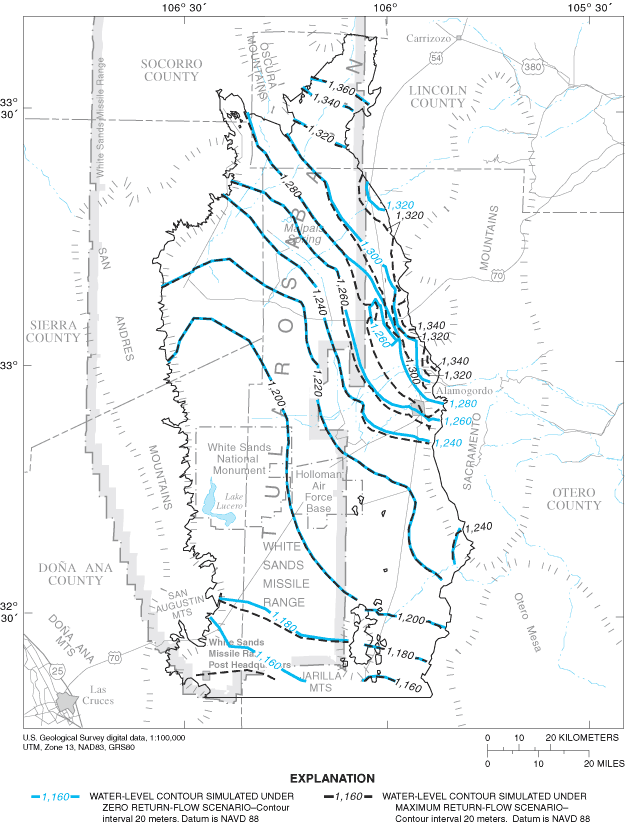
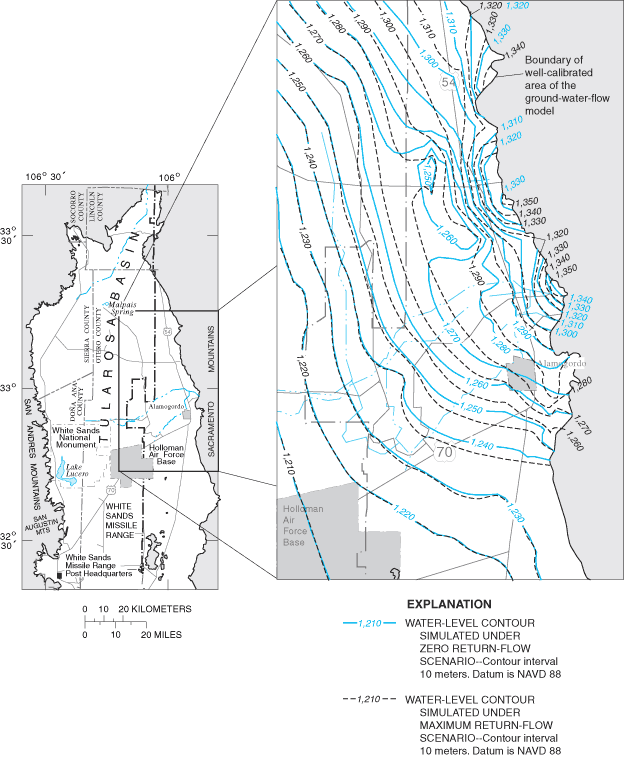
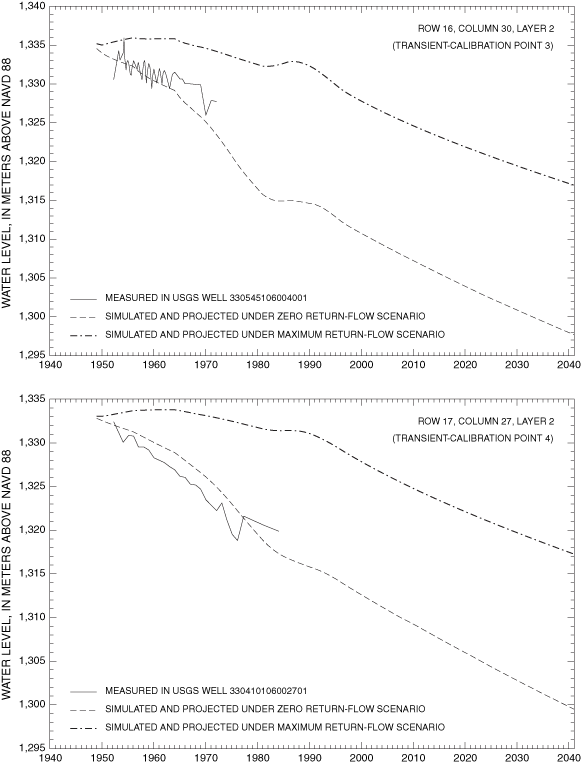
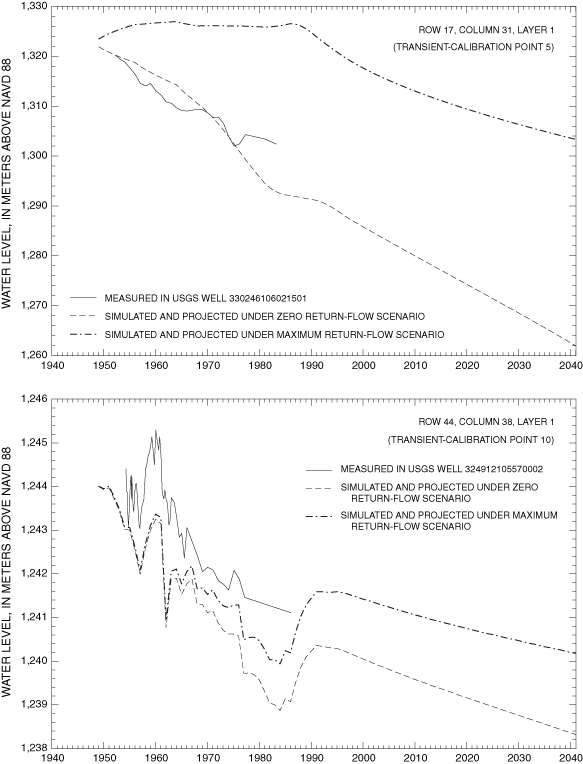
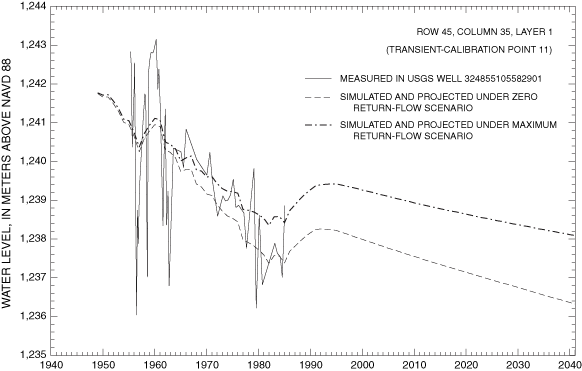
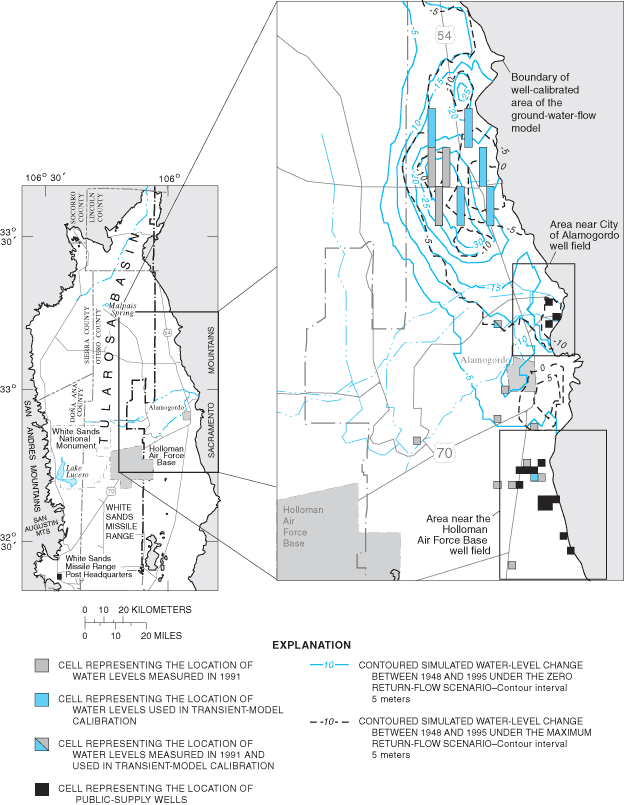


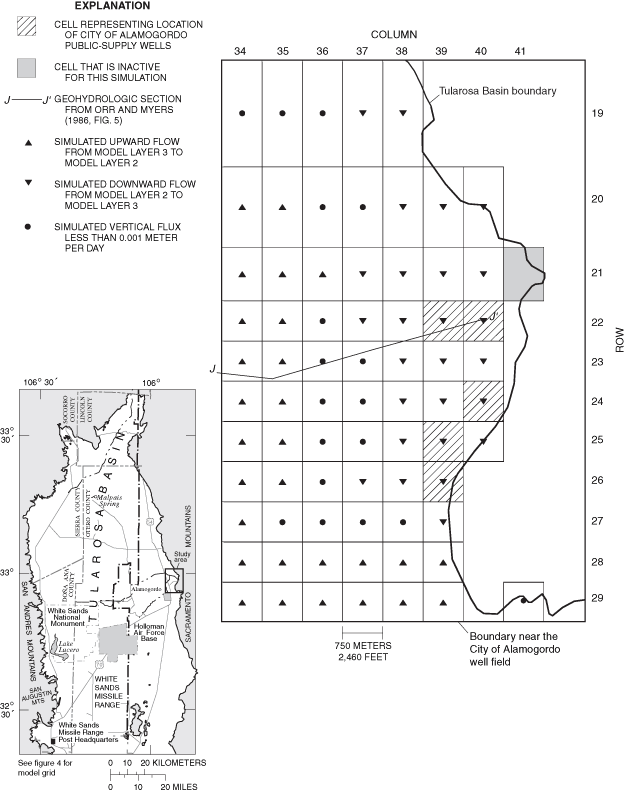

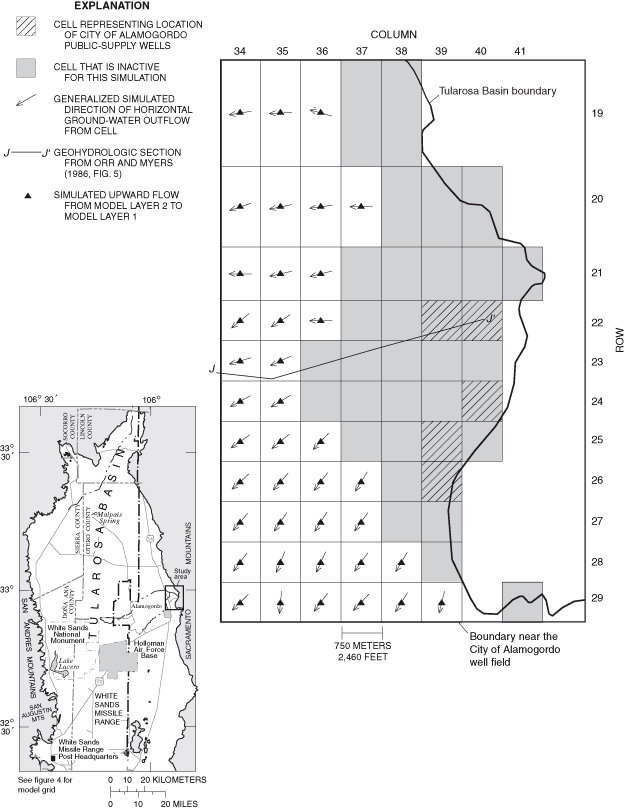
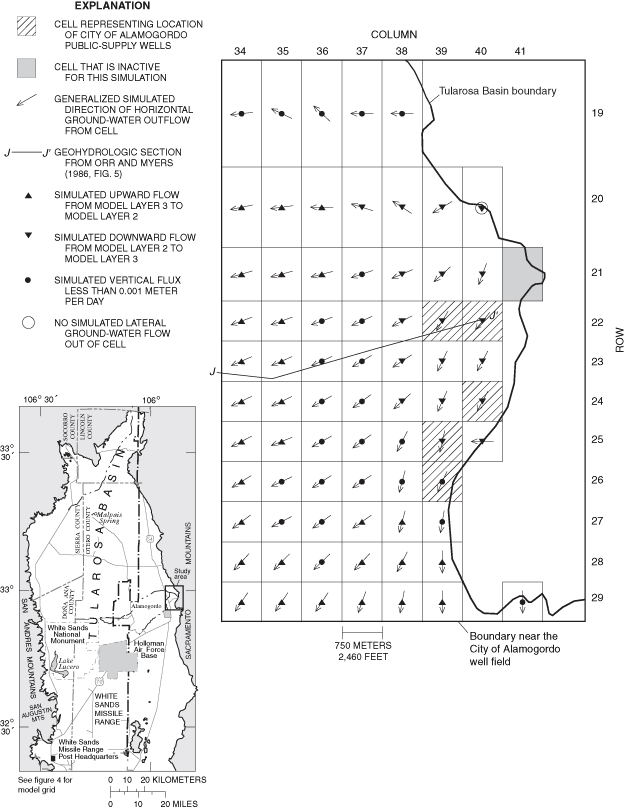
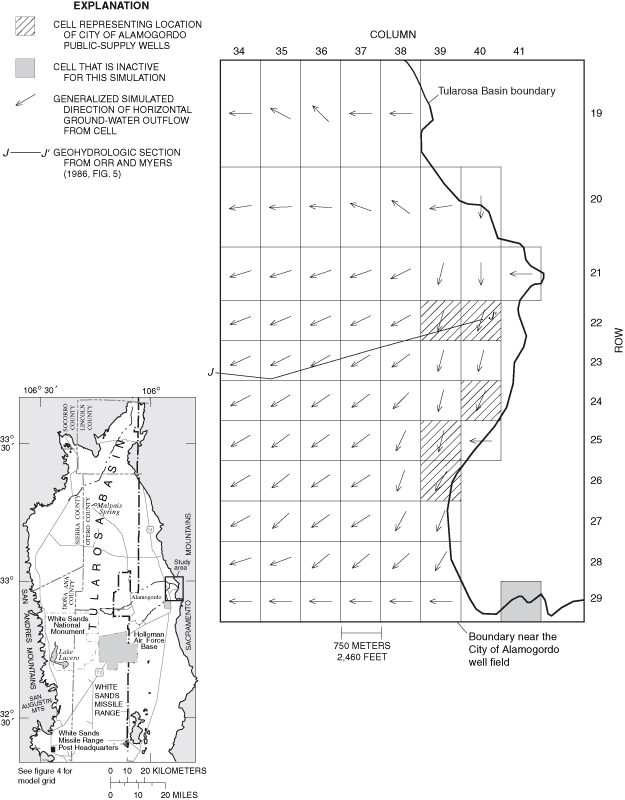
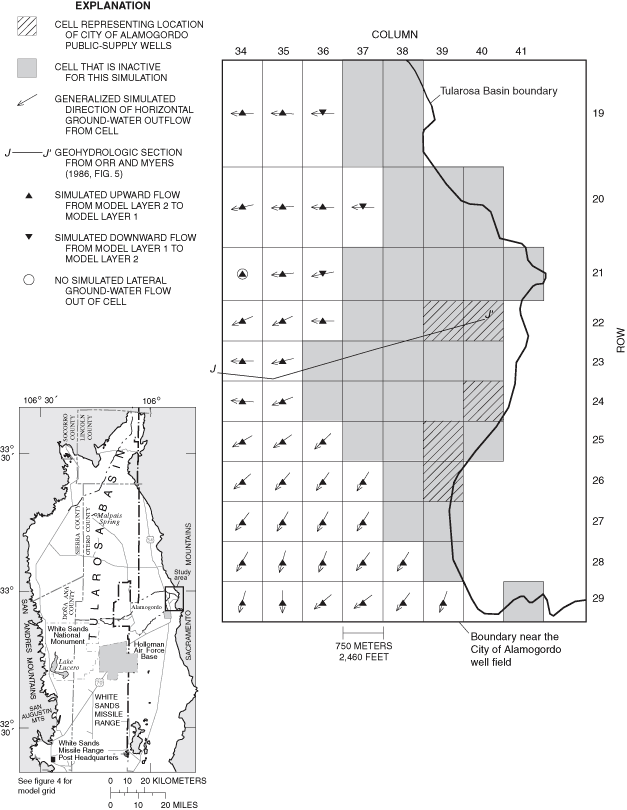
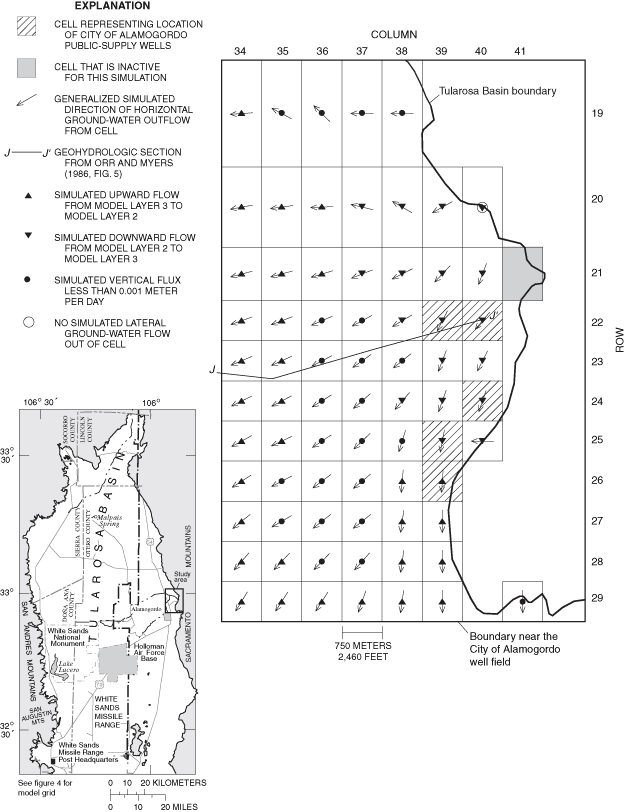
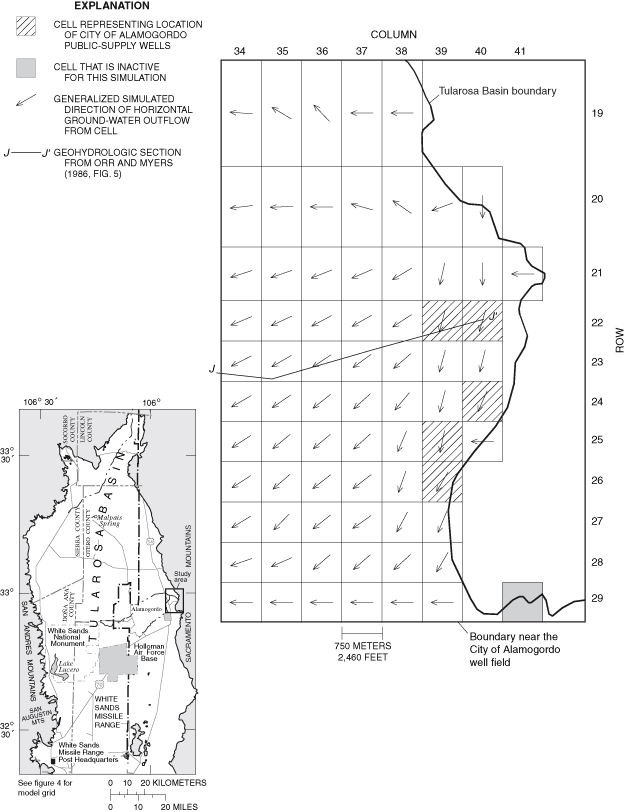
The basal no-flow boundary in this model is assigned to the contact between the basin-fill aquifer and bedrock or the approximate location of the first occurrence of ground-water with dissolved-solids concentrations of 10,000 mg/L. This assumes that little or no water flows through bedrock into the basin-fill aquifer or across the 10,000-mg/L salinity surface within the basin-fill aquifer. Neither of these assumptions can be demonstrated to be accurate using existing field data. The Tularosa Basin is geologically complex, particularly near the basin margin. The basin margin is the area of the basin-fill aquifer under the most stress from ground-water recharge and withdrawal and the area for which accurate information on future water levels is of greatest interest. The ability of the model to simulate water levels in the basin-fill aquifer near the basin margins is limited by the lack of detailed representation of this geological complexity.
Hydrologic properties used in the model were assigned to achieve a trial-and-error best fit between simulated and measured water-level data. Little data were available for measured flows into or out of the modeled system other than for ground-water withdrawal. For example, ET accounts for 88 percent of simulated flow out of the basin under steady-state conditions. However, no direct measurements of ET were available for use in this study. Ground-water recharge was estimated on the basis of the steady-state simulation calibration and does not take into account the possible effects on ground-water recharge by present (1995) surface-water diversions by the City of Alamogordo. Fit between measured and simulated fluxes is an important element in model calibration (Hill, 1998), and uncertainty in recharge, ET, and return-flow fluxes limits confidence in the model calibration.
The spatial and temporal distribution of water-level measurements limits the area of the ground-water-flow model that can be considered to be well calibrated. Selected hydrologic properties, such as horizontal and vertical hydraulic conductivity and hydrologic stresses, including recharge, were allowed to vary within reasonable ranges during model calibration. Reasonable quantitative ranges are fairly well established for recharge, based on areally limited data for hydraulic conductivity, and almost nonexistent for vertical hydraulic conductivity. This lack of quantitative knowledge regarding hydrologic properties limits confidence in the model calibration.
There is considerable uncertainty in the present (1995) and future distribution and volume of agricultural ground-water withdrawals and in the amounts and effects of agricultural return flow, limiting confidence in model performance particularly in the area near Tularosa. Assuming that all withdrawals in the City of Alamogordo well field are from the basin-fill aquifer may result in overestimated declines in simulated water levels. Additionally, all projected increases in ground-water withdrawal for agricultural irrigation and public supply are uncertain.
Simulated results are reasonable only for projections used in this model. Systematic errors between simulated and measured water levels exist near La Luz Creek and show that this area is poorly represented in the model. Lack of agreement between simulated ground-water travel times and 14C apparent ages in selected Holloman Air Force Base public-supply wells suggests that parts of the geochemistry and hydrology of the basin-fill aquifer near the Holloman Air Force Base well fields are poorly understood. Temporal changes in simulated water levels and simulated directions of ground-water flow are sensitive to values of and assumptions regarding aquifer properties and hydrologic stress. Temporal changes in simulated water levels and simulated ground-water-flow directions presented in this report should be considered valid only for the set of properties and stresses used in this model.
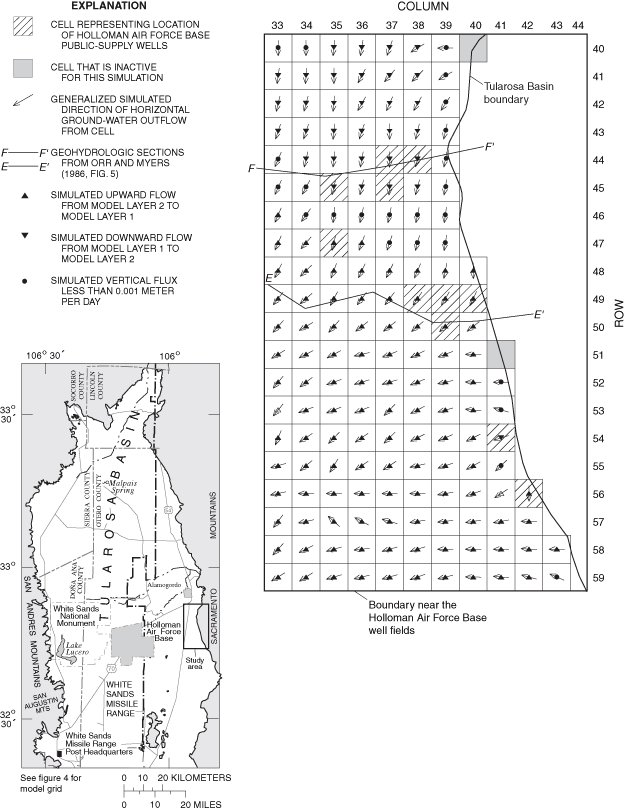
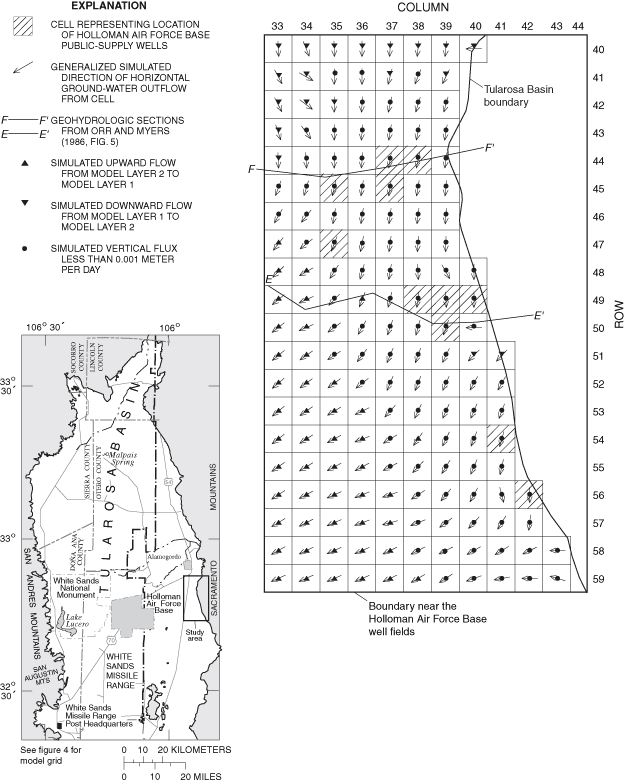
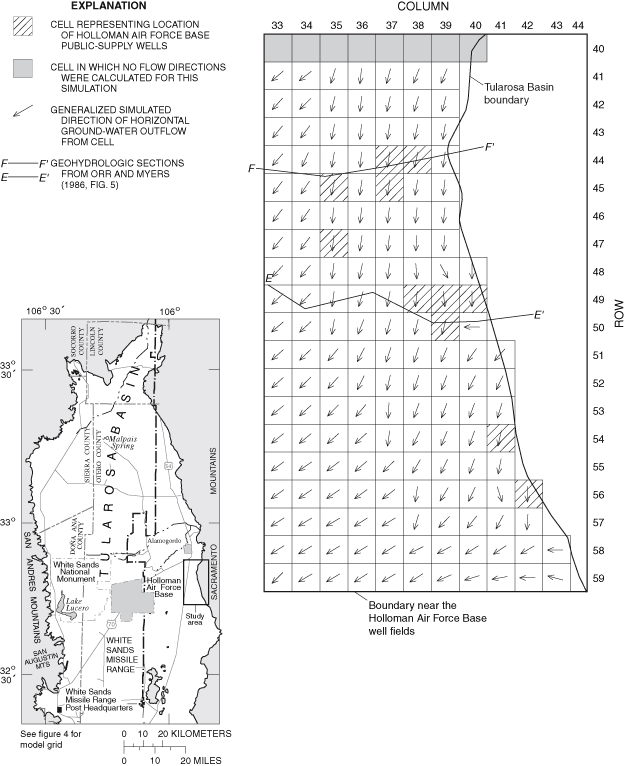
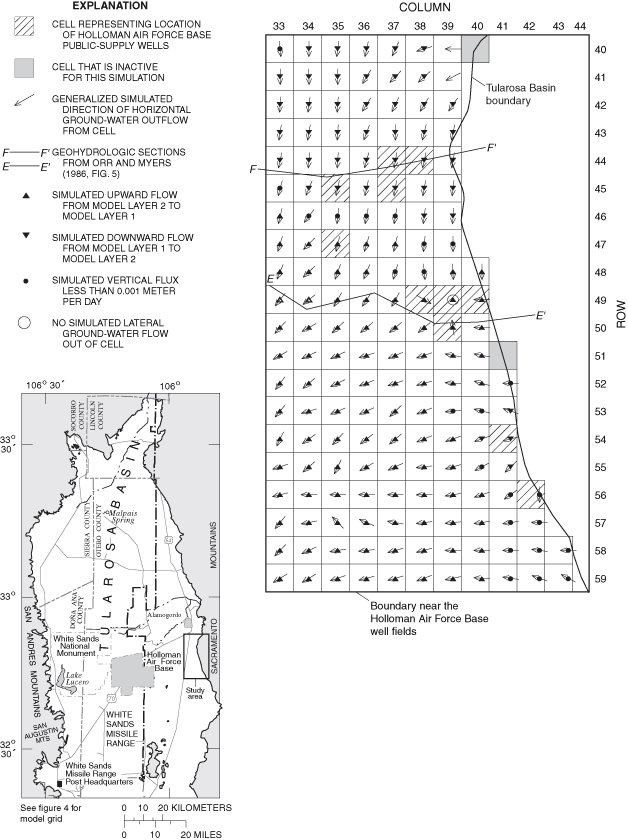
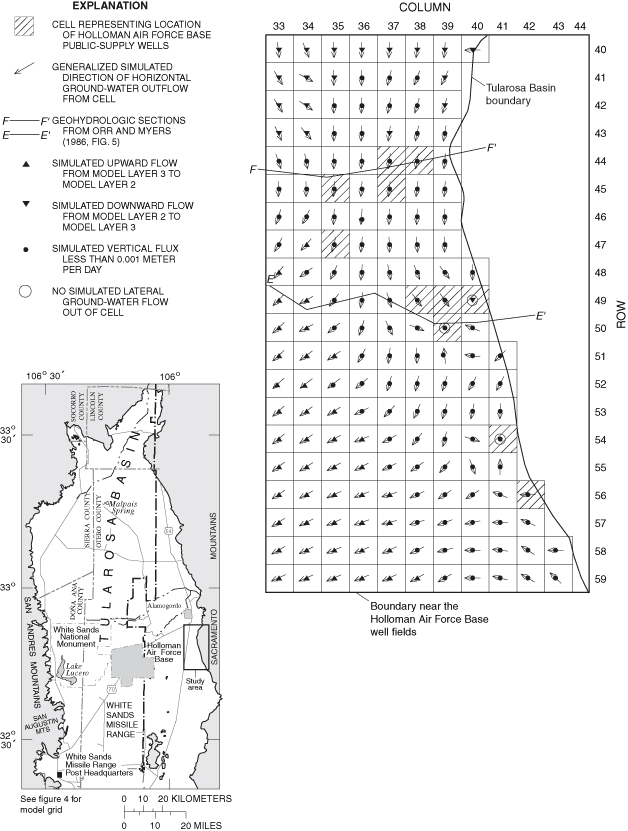
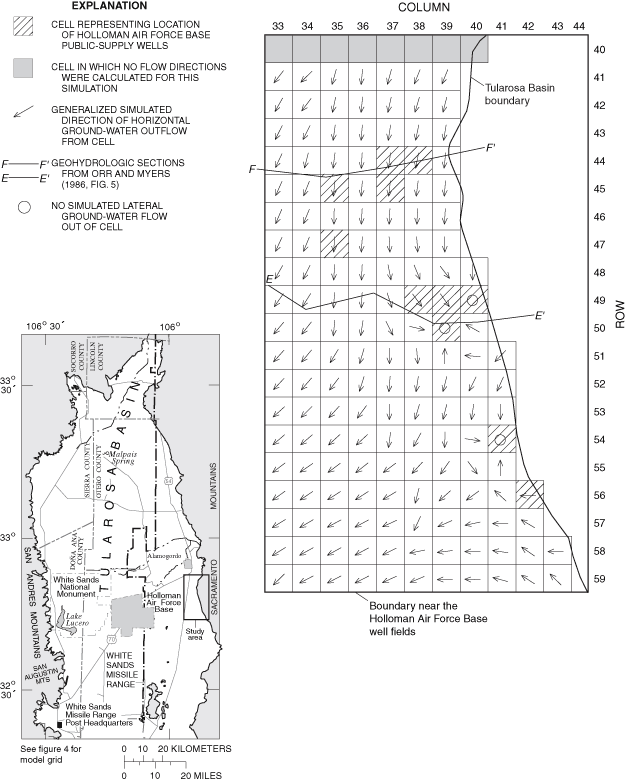
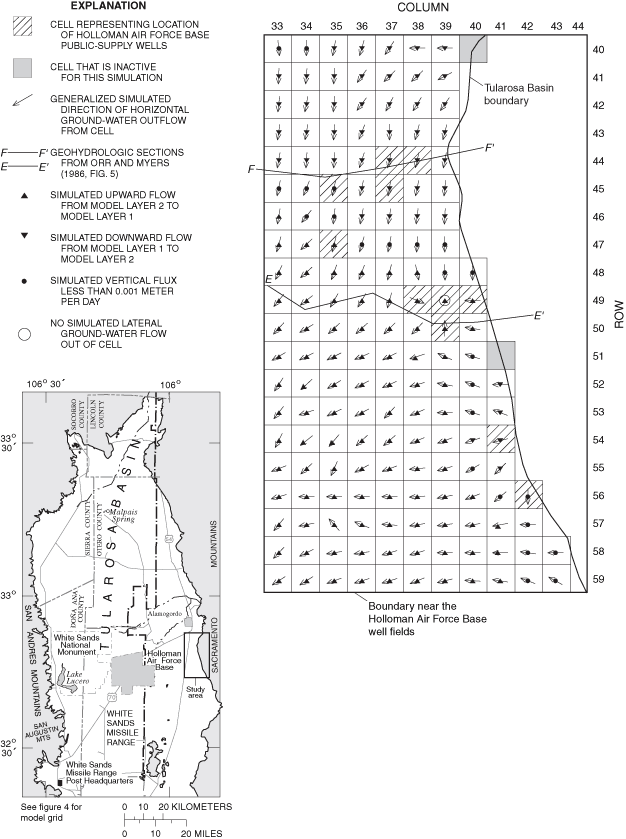
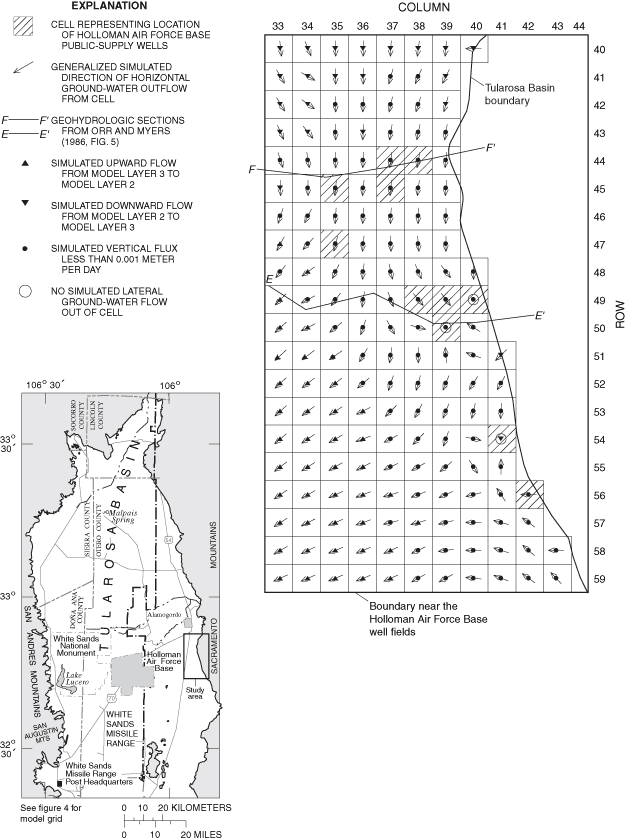
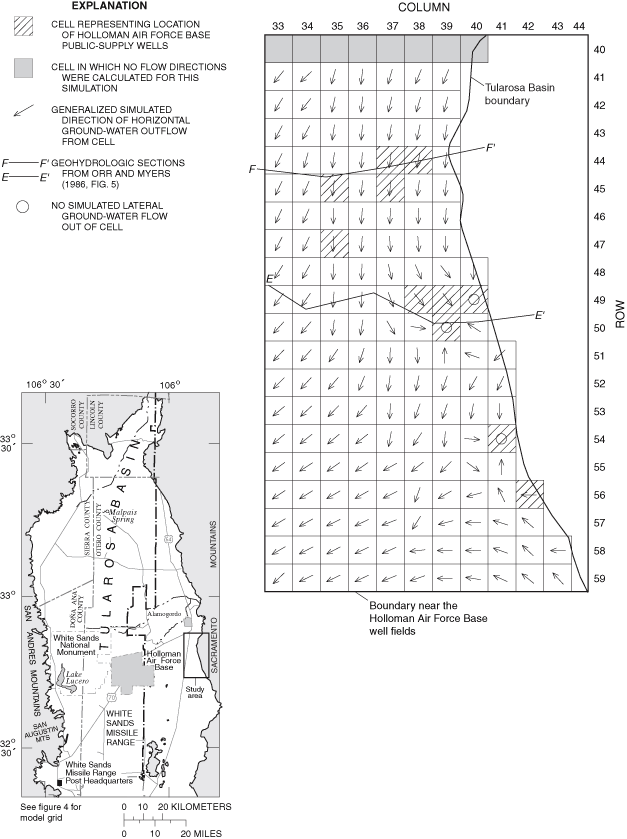
The USGS in cooperation with Holloman Air Force Base and the City of Alamogordo, New Mexico, has completed a study to evaluate the hydrology of the Tularosa Basin to estimate rates of ground-water recharge and to determine the effects of current and anticipated water use. These goals were accomplished by construction and calibration of steady-state and transient ground-water-flow models of the non-saline part of the basin-fill aquifer in the Tularosa Basin. This report documents the construction and calibration of these ground-water-flow models and describes simulated ground-water flow in the non-saline part of the basin-fill aquifer. Numerical simulations were made using the USGS finite-difference ground-water-flow software MODFLOW-96. Hydrologic investigation of the basin-fill aquifer included both a steady-state ground-water-flow simulation and a transient ground-water-flow simulation between 1948 and 2040. The steady-state simulation was calibrated by comparing contours of simulated water levels with contours of water levels measured in 1911-12. The steady-state calibration was refined for the eastern side of the basin by comparison of simulated water levels with water levels in 40 model cells for which 1911-12 water-level measurements are available. The area containing these 40 model cells defines the well-calibrated area of the model. The RMSE of the steady-state calibration was 6.3 meters within the well-calibrated area of the model. MODPATH was used to estimate travel time for ground water between selected wells having 14C apparent ages for ground water and the associated model-recharge cell. Simulated travel times were systematically smaller than the corresponding 14C apparent ages, indicating an error in simulated ground-water-flow rates, in 14C apparent ages, or in assumed flow paths used to estimate ground-water travel times. The transient ground-water-flow simulation was calibrated by comparing a time series of simulated water levels in 12 model cells within the well-calibrated area of the model with available water levels measured at various intervals between 1952 and 1986. Values of RMSE at these model cells ranged from 0.8 to 17.0 meters. Results of the transient simulation were benchmarked by comparing simulated 1991 water levels at 13 model cells within the well-calibrated area of the model with water levels measured in wells within these cells in 1991. The overall RMSE of the transient ground-water flow-model benchmarking was 13.4 meters. If benchmarking points in the area of the largest agricultural ground-water withdrawal near Tularosa are excluded, the RMSE of the transient ground-water-flow benchmarking is 6.4 meters. An area of underestimated water levels in the steady-state and transient-model calibrations occurs in the La Luz Creek subbasin area, indicating that this area is not well represented in the model.
About 143,000 cubic meters per day of annualized average recharge is estimated to enter the basin-fill aquifer from subbasins that rim the Tularosa Basin. This recharge equates to approximately 4-5 percent of total precipitation in most of the subbasins. Approximately 88 percent of this recharge left the basin by ET prior to development. In 1995, under the zero return-flow scenario, an estimated 56,000 cubic meters of water per day entered the hydrologic system from aquifer storage in addition to that available from recharge. Of this 1995 total amount, an estimated 40 percent left the basin-fill aquifer by ground-water withdrawal, 51 percent by ET, 7 percent by interbasin ground-water flow into the Hueco Bolson, and 2 percent by flow into creeks and springs.
Water levels were simulated for 1948, 1995, and 2040 under scenarios of zero and maximum return flow from agricultural and municipal water use. Changes in simulated water levels were calculated between 1948 and 1995 and between 1995 and 2040. The ground-water-flow simulation was relatively sensitive to the choice of the return-flow scenario in the agricultural area near Tularosa and decreasingly sensitive to the choice of the return-flow scenario to the south. The ground-water-flow simulation showed little sensitivity to the choice of the return-flow scenario near the Holloman Air Force Base well fields. Declines in simulated water levels in the agricultural area near Tularosa between 1948 and 1995 were as large as 30 meters under the zero return-flow scenario and 15 meters under the maximum return-flow scenario. Declines in simulated water levels in the agricultural area near Tularosa between 1995 and 2040 were as large as 25 meters under the zero return-flow scenario and 15 meters under the maximum return-flow scenario. Comparison of water levels measured near Tularosa in 1991 and water levels simulated under the maximum return-flow scenario for 1991 indicates that declines in simulated water levels near Tularosa may be overestimated under the zero return-flow scenario. Declines in simulated water levels near the City of Alamogordo well field between 1948 and 1995 were as large as 15 meters under the zero return-flow scenario and 10 meters under the maximum return-flow scenario. Declines in simulated water levels near the City of Alamogordo well field between 1995 and 2040 are nearly 15 meters under both return-flow scenarios. Simulated declines in water levels near the City of Alamogordo well fields may be overestimated based on the assumption of ground-water withdrawal solely from the basin-fill aquifer. Simulated declines in water levels near the Holloman Air Force Base well fields between 1948 and 1995 and projected declines between 1995 and 2040 are less than 5 meters under both the zero and maximum return-flow scenarios. Generalized simulated directions of ground-water flow for 1948, 1995, and 2040 in the area containing the City of Alamogordo and Holloman Air Force Base well fields show only localized changes between 1948 and 1995 and between 1995 and 2040.
Adams, D.C., and Keller, G.R., 1994, Crustal structure and basin geometry in south-central New Mexico, in Keller, G.R., and Cather, S.M., eds., Basins of the Rio Grande Rift—Structure, stratigraphy, and tectonic setting: Geological Society of America Special Paper 291, p. 241-255.
Anderholm, S.K., 2001, Mountain-front recharge along the eastern side of the Middle Rio Grande Basin, central New Mexico: U.S. Geological Survey Water-Resources Investigations Report 00-4010, 36 p.
Ballance, W.C., 1976, Ground-water resources of the Holloman Air Force Base well-field area, 1967, with a section on Geophysical exploration, by Robert Mattick: U.S. Geological Survey Open-File Report 76-807, 128 p.
Barud-Zubillaga, Alberto, 2000, A conceptual model of the hydrogeology of White Sands National Monument, south-central New Mexico: University of Texas at El Paso, master's thesis, 138 p.
Bedinger, M.S., Langer, W.H., and Reed, J.E., 1989, Ground-water hydrology, in Bedinger, M.S., Sargent, K.A., and Langer, W.H., eds., Studies of geology and hydrology in the Basin and Range Province, southwestern United States, for isolation of high-level radioactive waste—Characterization of the Rio Grande region, New Mexico and Texas: U.S. Geological Survey Professional Paper 1370-C, p. C27-C34.
Boegly, W.J., Jr., Jacobs, D.G., Lomenick, T.F., and Sealand, O.M., 1969, The feasibility of deep-well injection of waste brine from inland desalting plants: Office of Saline Water Research and Development Progress Report No. 432, 76 p.
Burns, A.W., and Hart, D.L., Jr., 1988, Simulated water-level declines caused by ground-water withdrawals near Holloman Air Force Base, Otero County, New Mexico: U.S. Geological Survey Water-Resources Investigations Report 86-4324, 44 p.
Chapin, C.E., and Seager, W.R., 1975, Evolution of the Rio Grande Rift in the Socorro and Las Cruces areas, in Seager, W.R., Clemons, R.E., and Callender, J.F., eds., Las Cruces Country: Socorro, New Mexico Geological Society Guidebook 26, p. 297-321.
Garza, Sergio, and McLean, J.S., 1977, Freshwater resources in the southeastern part of the Tularosa Basin: New Mexico State Engineer Technical Report 40, 67 p.
Green, G.N., and Jones, G.E., 1997, The digital geologic map of New Mexico in ARC/INFO format: U.S. Geological Survey Open-File Report 97-52, 9 p.
Harbaugh, A.W., 1990, A computer program for calculating subregional water budgets using results from the U.S. Geological Survey modular three-dimensional ground-water flow model: U.S. Geological Survey Open-File Report 90-392, 46 p.
Harbaugh, A.W., and McDonald, M.G., 1996, User's documentation for MODFLOW-96, an update to the U.S. Geological Survey modular finite-difference ground-water flow model: U.S. Geological Survey Open-File Report 96-485, 56 p.
Healy, D.L., Wahl, R.R., and Currey, F.E., 1978, Gravity survey of the Tularosa Valley and adjacent areas, New Mexico: U.S. Geological Survey Open-File Report 78-309, 56 p.
Heywood, C.E., and Yager, R.M., 2003, Simulated ground-water flow in the Hueco Bolson, an alluvial-basin aquifer near El Paso, Texas: U.S. Geological Survey Water-Resources Investigations Report 02-4108, 73 p.
Hill, M.C., 1998, Methods and guidelines for effective model calibration: U.S. Geological Survey Water-Resources Investigations Report 98-4005, 90 p.
Hood, J.W., 1958, Ground-water resources and related geology in the vicinity of Holloman Air Force Base, Otero County, New Mexico: U.S. Geological Survey Open-File Report, 261 p.
Huff, G.F., 2002, Apparent age of ground water near the southeastern margin of the Tularosa Basin, Otero County, New Mexico, in Lueth, V.W., Giles, K.A., Lucas, S.G., Kues, B.S., Myers, Robert, and Ulmer-Scholle, D.S., eds., Geology of White Sands: Socorro, New Mexico Geological Society Guidebook 53, p. 303-307.
Keller, G.R., Morgan, Paul, and Seager, W.R., 1990, Crustal structure, gravity anomalies, and heat flow in the southern Rio Grande Rift and their relationship to extensional tectonics: Tectonophysics, v. 174, p. 21-37.
Kelly, T.E., and Hearne, G.A., 1976, The effects of ground-water development on the water supply of the Post Headquarters area, White Sands Missile Range, New Mexico: U.S. Geological Survey Open-File Report 76-277, 97 p.
King, W.E., and Harder, V.M., 1985, Oil and gas potential of the Tularosa Basin-Otero Platform-Salt Basin graben area, New Mexico and Texas: Socorro, New Mexico Bureau of Mines and Mineral Resources Circular 198, 36 p.
Koning, D.J., 1999, Fault segmentation and paleoseismicity of the southern Alamogordo Fault, southern Rio Grande Rift, New Mexico: Albuquerque, University of New Mexico, master's thesis, 286 p.
Koning, D.J., and Pazzaglia, F.J., 2002, Paleoseismiscity of the Alamogordo Fault along the Sacramento Mountains, Southern Rio Grande Rift, New Mexico, in Lueth, V.W., Giles, K.A., Lucas, S.G., Kues, B.S., Myers, Robert, and Ulmer-Scholle, D.S., eds., Geology of White Sands: Socorro, New Mexico Geological Society Guidebook 53, p. 107-119.
Lansford, R.R., Creel, B.J., Mapel, C.L., Gerhardt, Donald, West, F.G., and Wilson, Brian, 1987, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1984-86: Las Cruces, New Mexico State University Agricultural Experiment Station Research Report 620, 50 p.
Lansford, R.R., Creel, B.J., Mapel, C.L., West, F.G., Peacock, Bruce, Vanderberry, Herb, and Gerhardt, Donald, 1985, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1980-84: Las Cruces, New Mexico State University Agricultural Experiment Station Research Report 571, 51 p.
Lansford, R.R., Creel, B.J., Mapel, C.L., West, F.G., Peacock, Bruce, Vanderberry, Herb, and Gerhardt, Donald, 1986, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1980-85: Las Cruces, New Mexico State University Agricultural Experiment Station Research Report 596, 48 p.
Lansford, R.R., Creel, B.J., Mapel, C.L., Wilson, B.C., Roark, Robin, and Gerhardt, Donald, 1984, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1977-82: Las Cruces, New Mexico State University Agricultural Experiment Station Research Report 514, 44 p.
Lansford, R.R., Dominguez, Larry, Gore, Charles, Hand, James, West, F.G., Wilson, Brian, and Cohen, T.M., 1991, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1988-90: Las Cruces, New Mexico State University Agricultural Experiment Station Technical Report 4, 52 p.
Lansford, R.R., Dominguez, Larry, Gore, Charles, Wilken, W.W., West, F.G., Wilson, Brian, and Runyun, S.L., 1992, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1989-91: Las Cruces, New Mexico State University Agricultural Experiment Station Technical Report 13, 50 p.
Lansford, R.R., Dominguez, Larry, Gore, Charles, Wilken, W.W., Wilson, Brian, and Franz, T.L., 1993, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1990-92: Las Cruces, New Mexico State University Agricultural Experiment Station Technical Report 16, 79 p.
Lansford, R.R., Franz, T.L., Gore, Charles, Wilken, W.W., and Lucero, A.A., 1996, Irrigation water sources and cropland acreages in New Mexico, 1993-1995: Las Cruces, New Mexico State University Agricultural Experiment Station Technical Report 27, 86 p.
Lansford, R.R., Franz, T.L., Gore, Charles, Wilken, W.W., Wilson, Brian, and Coburn, C.S., 1995, Sources of irrigation water and cropland acreages in New Mexico, 1992-1994: Las Cruces, New Mexico State University Agricultural Experiment Station Technical Report 22, 88 p.
Lansford, R.R., Lucero, David, Gore, Charles, Wilken, W.W., Nedom, Robert, Lucero, A.A., and Schultz, Jane, 1997, Irrigation water sources and cropland acreages in New Mexico, 1994-1996: Las Cruces, New Mexico State University Agricultural Experiment Station Technical Report 29, 87 p.
Lansford, R.R., Mapel, C.L., Gerhardt, Donald, West, F.G., and Wilson, Brian, 1988, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1985-87: Las Cruces, New Mexico State University Agricultural Experiment Station Research Report 630, 49 p.
Lansford, R.R., Mapel, C.L., Gore, Charles, Hand, James, West, F.G., and Wilson, Brian, 1990, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1987-89: Las Cruces, New Mexico State University Agricultural Experiment Station Research Report 650, 52 p.
Lansford, R.R., Sorensen, E.F., Creel, B.J., Gollehan, N.R., Wilson, B.C., Roark, Robin, and Benger, Gene, 1982, Sources of irrigation water and irrigated and dry cropland acreages in New Mexico, by county, 1976-81: Las Cruces, New Mexico State University Agricultural Experiment Station Research Report 495, 41 p.
Livingston Associates and John Shomaker and Associates, 2002, Tularosa Basin and Salt Basin regional water plan 2000-2040: Carrizozo, N. Mex., South Central Mountain RD&C Council, Inc., v. 1, variously paged.
Looney, S.W., and Gulledge, T.R., 1985, Use of the correlation coefficient with normal probability plots: The American Statistician, v. 39, p. 75-79.
McDonald, M.G., and Harbaugh, A.W., 1988, A modular three-dimensional finite-difference ground-water flow model: U.S. Geological Survey Techniques of Water-Resources Investigations, book 6, chap. A1, 586 p.
McLean, J.S., 1970, Saline ground-water resources of the Tularosa Basin, New Mexico: U.S. Department of the Interior Office of Saline Water Research and Development Progress Report 561, 128 p.
Meinzer, O.E., and Hare, R.F., 1915, Geology and water resources of Tularosa Basin, New Mexico: U.S. Geological Survey Water-Supply Paper 343, 317 p., 19 pls.
Morgan, Paul, Seager, W.R., and Golombek, M.P., 1986, Cenozoic thermal, mechanical, and tectonic evolution of the Rio Grande Rift: Journal of Geophysical Research, v. 91, p. 6263-6276.
Morrison, T.D., 1989, A regional model of the basin-fill aquifer near Tularosa and Alamogordo, New Mexico: New Mexico State Engineer Office Technical Division Hydrology Report 89-3, 71 p. plus app.
Orr, B.R., and Myers, R.G., 1986, Water resources in basin-fill deposits in the Tularosa Basin, New Mexico: U.S. Geological Survey Water-Resources Investigations Report 85-4219, 94 p.
Orzol, L.L., 1997, User's guide for MODTOOLS—Computer programs for translating data of MODFLOW and MODPATH into geographic information system files: U.S. Geological Survey Open-File Report 97-240, 86 p.
Pollock, D.W., 1994, User's guide for MODPATH/MODPATH-PLOT, version 3—A particle tracking post-processing package for MODFLOW, the U.S. Geological Survey finite-difference ground-water flow model: U.S. Geological Survey Open-File Report 94-646, variously paged, plus app.
Rao, B.K., 1986, Ground-water resources in the Carrizozo area, New Mexico, in Clemons, R.E., King, W.E., and Mack, G.H., eds., Truth or Consequences Region: Socorro, New Mexico Geological Society Guidebook 37, p. 315-317.
Risser, D.W., 1988, Simulated water-level and water-quality changes in the bolson-fill aquifer, Post Headquarters area, White Sands Missile Range, New Mexico: U.S. Geological Survey Water-Resources Investigations Report 87-4152, 71 p.
Seager, W.R., and Morgan, Paul, 1979, Rio Grande Rift in southern New Mexico, west Texas, and northern Chihuahua, in Riecker, R.E., ed., Rio Grande Rift—Tectonics and magmatism: Washington, D.C., American Geophysical Union, p. 87-106.
Seager, W.R., Shafiqullah, M., Hawley, J.W., and Marvin, R.F., 1984, New K-Ar dates from basalts and the evolution of the southern Rio Grande Rift: Geological Society of America Bulletin 95, p. 87-99.
Sorensen, E.F., 1977, Water use by categories in New Mexico counties and river basins, and irrigated and dry cropland acreage in 1975: New Mexico State Engineer Technical Report 41, 34 p.
Sorensen, E.F., 1982, Water use by categories in New Mexico counties and river basins, and irrigated acreage in 1980: New Mexico State Engineer Technical Report 44, 51 p.
U.S. Bureau of Reclamation and the State of New Mexico, 1976, New Mexico water resources assessment for planning purposes: U.S. Bureau of Reclamation and the State of New Mexico, 218 p., 3 v. supporting data, 23 maps.
Waltemeyer, S.D., 2001, Estimates of mountain-front streamflow available for potential recharge to the Tularosa Basin, New Mexico: U.S. Geological Survey Water-Resources Investigations Report 01-4013, 8 p.
West, S.W., and Broadhurst, W.L., 1975, Summary appraisals of the Nation's ground-water resources—Rio Grande: U.S. Geological Survey Professional Paper 813-D, p. 39.
Wilson, B.C., 1992, Water use by categories in New Mexico counties and river basins, and irrigated acreage in 1990: New Mexico State Engineer Technical Report 47, 141 p.
Wilson, B.C., and Lucero, A.A., 1997, Water use by categories in New Mexico counties and river basins, and irrigated acreage in 1995: New Mexico State Engineer Technical Report 49, 149 p.
Wilson, Brian, 1986, Water use in New Mexico in 1985: New Mexico State Engineer Technical Report 46, 84 p.
Changes in simulated ground-water-flow directions that correspond to changes in stresses applied to an aquifer can give insight into the nature of a simulated flow system. Generalized simulated horizontal ground-water-flow directions were calculated in this study using cell-by-cell flow rates output by the MODFLOW-96 program (Harbaugh and McDonald, 1996). Only flows exiting across the horizontal cell faces were used in the calculations. The arrows, such as those shown in figure 30, represent the simulated ground-water-flow per unit width exiting each model cell. An explanation of how the flow arrows presented in this report were computed (written commun., Douglas McAda, U.S. Geological Survey) follows:
The locations and directions of the arrows were calculated using two ARC/Info (version 8.0.1) AML (Arc Macro Language) programs and two FORTRAN 77 programs. A third AML, arrows.aml, was used to execute the AMLs and programs in the proper sequence. Execution of the programs in sequence extracts model-cell flow data from the MODFLOW-96 cell-by-cell budget file, creates six ARC/Info line coverages (one for each layer of the model) which contain lines oriented in the direction of flow and passing through the center of each model cell, and six ARC/Info point coverages with point locations where there is no flow out of model cells. Flow arrows and no-flow points are calculated for the user-specified stress period and time step extracted from the MODFLOW-96 cell-by-cell budget file.
The programs used to compute the flow arrows presented in this report are documented below:
arrows.amlThe FORTRAN program, READ_CBC, is modified from the ZONEBUDGET program for MODFLOW-96 (Harbaugh, 1990).
This program reads the MODFLOW cell-by-cell budget output file and creates temporary ASCII files containing
the simulated flows for cell faces and a file listing the contents of the cell-by-cell budget file. As in
ZONEBUDGET, the user must enter file names, pumping period, and time steps in response to the prompts.
The program READ_CBC is listed below:
READ_CBC
The AML, gen_flow_info.aml reads the temporary files created by READ_CBC and writes the data into Info files. These Info files subsequently are used in the gen_flow_arrows.aml. The AML, gen_flow_info.aml is listed below:
gen_flow_info.aml
The AML, gen_flow_arrows.aml uses horizontal fluxes (from the Info files
created by gen_flow_info.aml) to calculate the relative flux of water per unit
width across cell faces and the flow-direction arrows. This AML creates six ARC/Info
line coverages (one for each model layer) of the arrows and six ARC/Info point
coverages (one for each model layer) of cells with no flux exiting the cell. The
FORTRAN program GEN_FLOW_ARROWS is executed from within gen_flow_arrows.aml. The
AML, gen_flow_info.aml is listed below:
gen_flow_arrows.aml
The FORTRAN program, GEN_FLOW_ARROWS, executed from within gen_flow_arrows.aml, calculates the beginning and ending coordinates of the arrows for each model cell. The program GEN_FLOW_ARROWS is listed below:
GEN_FLOW_ARROWS
Document Accessibility: Adobe Systems Incorporated has information about PDFs and the visually impaired. This information provides tools to help make PDF files accessible. These tools convert Adobe PDF documents into HTML or ASCII text, which then can be read by a number of common screen-reading programs that synthesize text as audible speech. In addition, an accessible version of Acrobat Reader 6.0, which contains support for screen readers, is available. These tools and the accessible reader may be obtained free from Adobe at Adobe Access.
| AccessibilityFOIAPrivacyPolicies and Notices | |
 |
|