

Many studies of local and regional ground-water systems (Hubbert, 1940; Toth, 1962; Faye and Mayer, 1990; and Robinson and others, 1997) have assumed that surface-water and ground-water divides coincide, especially for small drainage basins. The primary utility of this assumption for the model analysis is in the location and assignment of types of model boundaries. Specifically, surface-water and ground-water divides are simulated as no-flow boundaries.
The shallow aquifer system at NSA Memphis was assumed to be in a steady-state condition. Data that support this assumption include continuous water-level measurements in three wells completed in the loess, alluvial-fluvial deposits aquifer, and in a clayey unit of the upper Cockfield Formation (fig. 6) and two synoptic water-level measurement surveys made in April and October 1996 (table 4). Within the study area, ground-water levels in the shallow aquifers changed seasonally about 1 to 5 feet, which is small relative to the saturated thickness of the shallow aquifers (10 to 60 feet) and to the difference between the water levels of the shallow aquifer system and the Memphis aquifer (about 40 feet). Horizontal ground-water gradients across the site also were relatively constant. Therefore, a steady-state ground-water-flow model was considered adequate to address most of the questions raised by site assessments and remediation plans.
The assumption that the sediments which comprise the shallow aquifers transmit water as uniform porous media is reasonable for coarse-grained, clastic, unconsolidated sediments such as the lower part of the alluvium and the fluvial deposits. Darcy's Law can be assumed to apply to ground-water flow in these sediments, and the use of the finite-difference model MODFLOW to simulate ground-water flow in these sediments is appropriate.
The final assumption, that the aquifers at NSA Memphis are homogeneous and isotropic, may not necessarily be true, but data are insufficient to determine the variability of the hydraulic characteristics of the aquifers. However, even conduit-flow aquifers can be modeled as homogeneous as long as the scale of investigation is large enough (Glenn and others, 1989; Nelson, 1989). For the model of the shallow aquifer system at NSA Memphis, the relatively coarse grid size used should compensate for small-scale heterogeneities in the aquifers. The assumption of homogeneity of the aquifers on a gross scale can be partially tested by inspection of the aquifer-test data from the site.
The best estimate of the representative horizontal hydraulic conductivity of the alluvial-fluvial deposits aquifer (about 5 ft/d) was assumed to have been determined by the constant-withdrawal aquifer test performed by the USGS at the location of the continuous water-level observation wells (fig. 2). This test utilized observation wells to measure a response in the aquifer at 76 and 555 feet away from the pumped well (Sh:U-103) and to monitor water levels in an area as far as 6,600 feet away from the pumped well. A ground-water-flow model, VS2DT (Lappala and others, 1987; Healy, 1990), was used to simulate the response of the shallow aquifer system to pumping a well completed in the alluvial-fluvial deposits aquifer. A significant finding from this analysis was that the VS2DT model adequately simulated the response of the shallow aquifer system to pumping using a single representative value of hydraulic conductivity for each of the aquifers included in the model. The shallow aquifers at NSA Memphis were further assumed to be isotropic with respect to horizontal hydraulic conductivity. This assumption is not unreasonable for coarse-grained unconsolidated sediments such as those in the lower part of the alluvium and the fluvial deposits.
Proper representation of model boundary conditions is one of the most important aspects in the simulation of ground-water flow. Model boundaries are assigned to correspond to actual hydrologic boundaries as accurately as possible. If model boundaries necessarily are highly generalized, they are placed far enough away from the influence of hydrologic stresses in the model area to minimize their effects on simulation results. The upper boundary of this model is a specified-flux boundary formed by using the recharge package of MODFLOW to simulate the infiltration of water from the alluvium-loess confining unit to the A1 aquifer. The lower boundary of the model is formed by the specified heads of model layer 3 based on the potentiometric surface of the Memphis aquifer (Kingsbury, 1996). Seasonal changes in water levels in the shallow aquifer system (1 to 5 feet) were not considered because they were small relative to the saturated thickness of the shallow aquifers (10 to 60 feet) and to the difference between the water levels of the shallow aquifer system and the Memphis aquifer (about 40 feet). Because ground-water levels in the Memphis aquifer are lower than in the shallow aquifer system, layer 3 functions as a sink and removes water from the model. The lateral model boundaries in each layer are simulated either as no-flow boundaries assumed to be ground-water divides that coincide with surface-water divides, or general head boundaries where flow into and out of the model varies depending upon the head difference between the model cell and some external source (fig. 17).
Recharge to the A1 aquifer occurs as leakage across the loess and alluvium. Initial estimates of 1 inch per year (in/yr) proved too large. A tentative estimate of about 0.3 in/yr produced better results, and final estimates provided by the parameter-estimation program (table 7) were similar to the tentative estimate. During calibration, about 0.67 to 1.8 in/yr of additional recharge to the A1 aquifer were determined necessary to generate the high potentiometric levels centered on the NSA Memphis facility. Inspection of the April 1996 potentiometric map of the alluvialfluvial deposits aquifer (fig. 10) and cultural features at NSA Memphis shows that the ground-water mound is located beneath base housing developments, parks, and areas where the alluvium-loess confining unit has been disturbed (SWMU 2, Southside Landfill, fig. 2). Water leaks from the base water distribution and sewerage systems, watering of lawns and green areas at parks, and reduced confinement in the SWMU 2 area where the alluvium-loess confining unit was excavated during solid-waste disposal operations possibly result in recharge rates greater than the "background" rates (Carmichael and others, 1997). For simplicity and to separate the anthropogenic or "human induced" recharge rates from the background or natural recharge rate, the MODFLOW well package was used to allocate the additional anthropogenic recharge to the model.
The initial vertical conductance arrays used to represent confining units in the model were calculated based on the vertical hydraulic conductivities determined for samples of the confining units (table 2), confining unit thickness, and equation 53 of McDonald and Harbaugh (1988). Increased vertical conductance values used to simulate features such as faults and windows in the confining units were determined during calibration using the parameter-estimation program.
The transmissivity array for model layer 1 (fig. 19) was calculated by multiplying the horizontal hydraulic conductivity determined for either the alluvial-fluvial deposits aquifer (about 5 ft/d) or the sand unit representing the upper part of the Cockfield aquifer (about 1 ft/d) by the estimated thickness of the appropriate unit for each model cell of layer 1. The locations of suspected buried river valleys (fig. 19) are indicated by areas of increased transmissivity simulating thicker sand and gravel sequences. The thickness values available for the sand and gravel of the lower part of the alluvium or fluvial deposits from Carmichael and others (1997) were accepted as a known value and held constant during the calibration process. However, substantial parts of the modeled area were not within the study area of Carmichael and others (1997), and the values representing the thickness of the alluvial-fluvial deposits aquifer or the sand unit of the Cockfield aquifer in those model cells were adjusted as necessary to match observed ground-water levels. Thicknesses of the units were not adjusted beyond the upper or lower limits reported by Carmichael and others (1997).
During the calibration process, ground-water levels generated by the model were determined to be too low for the section of layer 1 representing the A1 aquifer northeast of the erosional scarp. Possible causes for this result include higher actual recharge rates or a lower hydraulic conductivity for the A1 aquifer than was input to the model. Additional recharge in that part of the model was not justified, and no data existed that would suggest that the hydraulic conductivity of the A1 aquifer was significantly less than elsewhere. Ground-water levels northeast of the erosional scarp were eventually simulated by reducing the hydraulic conductivity of the model cells in layer 1 at and proximate to the erosional scarp at NSA Memphis. The relatively low hydraulic conductivity at the scarp produces a "hydraulic dam" causing higher ground-water levels in the upgradient area. A relatively low hydraulic conductivity for the alluvialfluvial deposits in the area of the erosional scarp could be the result of a large fraction of fine sediments eroded off the tread and deposited in the scarp.
The transmissivity array for model layer 2 (fig. 20) was calculated by multiplying an assumed horizontal hydraulic conductivity of 2.8 ft/d for the Cockfield aquifer by the corresponding thickness for that unit in each model cell of layer 2. The values representing the thickness of the Cockfield aquifer were adjusted during calibration because both the horizontal hydraulic conductivity and the thickness of the sand units were estimated from comparatively few data. Within the NSA Memphis boundary, final values for the transmissivity array of layer 2 were determined with the parameter-estimation program. Some additional modifications to the values generated by the parameter-estimation program were made to more closely match observed ground-water levels in areas not within the NSA Memphis boundary.
The major surface-water drains within the modeled area (fig. 3) were simulated with the MODFLOW river package (fig. 17). Surface-water stage was fixed at 1 foot above the elevation of the creek bottoms. Elevations of creek bottoms were taken from survey data presented in an urban flood-control study performed by the U.S. Army Corps of Engineers (1989a, b). Riverbed hydraulic conductance was estimated using the vertical hydraulic conductivity of the upper part of the alluvium (table 2) and the dimensions of the model cell for the river node (fig. 34, McDonald and Harbaugh, 1988).
Some stresses must be known to calibrate a model if both recharge rates and hydraulic conductivity are being adjusted. The shallow ground-water system at NSA Memphis is believed to have only limited connection to the surface-water system; therefore, discharge measurements of streams could not be used to estimate ground-water discharge to the surface-water system. Such data would have provided an independent estimate of recharge rates. To constrain the simulation, the USGS aquifer test was assumed to provide a representative hydraulic conductivity for the A1 aquifer and this value was held constant during calibration. The model was calibrated by adjusting recharge rates to layer 1 and the vertical conductance arrays used to control vertical flow between model layers. Calibration improvement was determined by decreases in sum-of-squares error (SSE) that is defined by:
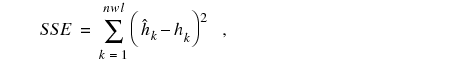 (1)
(1)The root mean square error (RMSE) is reported instead because the RMSE is more directly comparable to actual values and serves as a composite of the average and the standard deviation of a set. RMSE is related to the SSE by:
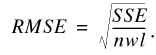 (2)
(2)Logs of the parameters, log(x), were estimated because the hydraulic conductivities are usually log-normally distributed (Domenico and Schwartz, 1990). Log parameters are better behaved from a numerical perspective because estimates are restricted to positive values and are scaled to some degree. Consequently, all sensitivities, covariances, and correlation coefficients are based on
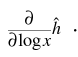
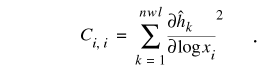
Normalization is achieved by computing correlation coefficients (Hill, 1992),
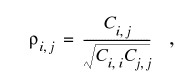
Seven parameters (table 8) were used as multipliers that changed the value of either hydraulic conductivity, vertical conductance, or recharge by a fixed amount for specified zones within the model grid. The initial values of horizontal hydraulic conductivity came from the results of the aquifer and specific-capacity tests (table 3), and initial values for the vertical hydraulic conductivity of confining units were estimated from analyses of sediment-core samples (table 2). Water levels at 38 wells within the NSA Memphis boundary were selected as control points for the parameter-estimation program. The RMSE of the model after the parameter-estimation program had run was 2.25 feet. Many of the parameters were highly correlated, but not to a degree that prevented independent estimation (table 8).
The distribution of water simulated by the flow model is consistent with the proposed concept of flow in the shallow aquifer system at NSA Memphis. The hydraulic connection between the ground-water and surface-water systems probably is limited; therefore, the volume of water passing between the two systems should be relatively small. The hydraulic conductivities of the A1 and Cockfield aquifers are relatively low, and a downward hydraulic gradient exists between the shallow aquifer system and the Memphis aquifer. Under such conditions, ground-water-flow directions should be predominantly downward, and the flow path of water moving laterally through the shallow aquifer system would be relatively short prior to drainage to the Memphis aquifer.
The horizontal ground-water gradient in a confined porous media is depicted graphically in two dimensions by potentiometric maps (figs. 9 and 10 for the A1 aquifer). Comparison of figures 9 and 10 to figure 22 and inspection of figure 21 and table 6 show that the model adequately simulates the ground-water gradient in the A1 aquifer at NSA Memphis. However, no water-level measurements were available for the Cockfield aquifer within the modeled area at NSA Memphis because no wells exist in this zone; therefore, determination of whether or not the model accurately simulates the potentiometric surface of the Cockfield aquifer is not possible.
The results of model sensitivity analyses indicate that the model is relatively insensitive to the lateral boundary conditions (table 10). Most of the water moving through the model enters and exits a vertical boundary (table 9). For this reason only moderate confidence can be placed in the accuracy of the lateral boundaries. The model also is insensitive to changes in the conductance values of the river nodes. The volume of water moving between the surface-water and ground-water systems at NSA Memphis is probably relatively small because the two systems are generally not in direct hydraulic connection. Under these conditions, the model may not accurately quantify the volume of water exchanged between the surface-water and ground-water systems.
The most serious limitation of the model analysis is the lack of an independent check of the simulated water budget. A brief discussion of Darcy's Law can be used to illustrate the problems that result from this situation. Darcy's Law (3) is expressed here as:
Q = -KA dh/ds, (3)
where
Q is the volumetric flow, in cubic feet
per day;
K is the hydraulic conductivity of the porous
flow medium, in feet per day;
A is the cross-sectional area of flow, in
square feet;
ds is the horizontal distance of flow, in feet; and
dh is the difference in fluid potential, in feet over ds.
A rearrangement of Darcy's Law shows that the ground-water gradient
(dh/ds) for any defined flow section is proportional to the ratio of Q/-KA:
Q/-KA = dh/ds. (4)
The model closely simulates the ground-water gradient in the A1 aquifer at NSA Memphis. However, because no measurement of Q is available as an independent check, Q or K cannot be independently quantified. Thus, the model could generate the same potentiometric surface for layer 1, simulating the potentiometric surface of the A1 aquifer using a variety of flow rates (Q) and lateral hydraulic conductivities (K), as long as the ratio of Q/K in the model remained the same. The model solution is not unique because many combinations of parameters exist that will result in the same solution.
The significance of the above limitation is illustrated when the equation for the average linear velocity of ground-water flow in a porous flow medium is examined (modified from eq. 2.82, p. 71, Freeze and Cherry, 1979):
v = Q/nA = K/n (dh/ds), (5)
where
v is the average linear velocity, in feet per day;
Q is the volumetric flow, in cubic feet per day;
n is the effective porosity of the flow
media, in percent;
A is the cross-sectional area of flow, in
square feet;
K is the hydraulic conductivity of the porous
flow medium, in feet per day;
ds is the horizontal distance of flow, in
feet; and
dh is the difference in fluid potential,
in feet.
Inspection of equation 5 shows that the average linear velocity is
directly proportional to Q and K, and inversely proportional to n and A.
Doubling or halving Q and K would double or halve the average linear velocity.
This relation between ground-water-flow velocity, Q, and K reduces the
confidence that can be placed in the estimated time-of-travel for ground
water simulated by the particle-tracking analyses; however, the simulated
direction of ground-water flow is not affected.