Open-File Report 96-532
Recurrence Models for FaultsNow we add the hazard from specific faults. This is the right side of Figure 17. We divided the faults into types A and B, roughly following the nomenclature of WGCEP (1995). We classify a fault as A-type if there have been sufficient studies of it to produce models of fault segmentation. In California the A-type faults are: San Andreas, San Jacinto, Elsinore, Hayward, Rodgers Creek, and Imperial (M. Petersen, C. Cramer, and W. Bryant, written comm., 1996). The only fault outside of California that we classified as A-type is the Wasatch Fault. We assumed single-segment ruptures on the Wasatch Fault (see below). Note that we have not included uncertainty in segment boundaries for these hazard maps. For California, we followed the rupture scenarios specified by Petersen, Cramer and Bryant of CDMG, with input from Lienkaemper of USGS for northern California. We assumed single-segment, characteristic rupture for the San Jacinto and Elsinore faults. For the San Andreas fault, multiple-segment ruptures were included in the hazard calculation, including repeats of the 1906 and 1857 rupture zones, and a scenario with the southern San Andreas fault rupturing from San Bernardino through the Coachella segment. Both single-segment and double-segment ruptures of the Hayward Fault were included. For California faults, we used characteristic magnitudes derived by CDMG from the fault area using the relations in Wells and Coppersmith (1994). For the remainder of the WUS, we determined characteristic magnitude from the fault length using the relations of Wells and Coppersmith (1994) appropriate for that fault type. For the B-type faults, we felt there were insufficient studies to warrant specific segmentation boundaries. For these faults, we followed the scheme of Petersen et al. (1996) and used both characteristic and Gutenberg-Richter (GR; exponential) models of earthquake occurrence. These recurrence models were weighted equally. The G-R model basically accounts for the possibility that a fault is segmented and may rupture only part of its length. We assume that the G-R distribution applies from a minimum moment magnitude of 6.5 up to a moment magnitude corresponding to rupture of the entire fault length. In the Pasadena workshop, we showed that without the M6.5 minimum, southern California faults would produce far too many M4-5 events compared to the historic record. For this comparison we determined the predicted rates of M4-5 events using fault slip rates and the equation for a-value given next. Given a geologic slip rate  (1) (1)
where µ is shear modulus, N(M) is the annual number of events in a magnitude bin from M-0.05 to M+0.05, L is fault length and W is fault width. Equation (1) is re-arranged to determine the a-value for each fault. We used a b-value of 0.8 for all of the faults (except for California faults where we used b=0.9), based on the b-value derived from the regional seismicity (see above). Equation (1) is a discrete version of similar equations to find a-values by Anderson (1979). The procedure for calculating hazard using the G-R model involves looping through magnitude increments. For each magnitude we calculate a rupture length using Wells and Coppersmith (1994). Then a rupture zone of this length is floated along the fault trace. For each site, we find the appropriate distance to the floating ruptures and calculate the frequency of exceedance (FE). The FE's are then added for all the floating rupture zones. Of course we normalize the rate of occurrence of the floating rupture zones to maintain the proper overall rate. As we apply it, the characteristic earthquake model (Schwartz and Coppersmith, 1984) is actually the maximum magnitude model of Wesnousky (1986) Here we assume that the fault only generates earthquakes that rupture the entire fault. Smaller events along the fault would be incorporated by models 1 and 2 with the distributed seismicity or by the G-R model described above. Following Wesnousky (1986) we find a recurrence rate for the characteristic event with moment M0c as 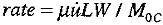 (2) (2)
It should be noted that using the G-R model generally produces higher probabilistic ground motions than the characteristic earthquake model, because of the more frequent occurrence of earthquakes with magnitudes of about 6.5. Fault widths (except for California)were determined by assuming a seismogenic depth of 15 km and then using the dip, so that the width equaled 15 km divided by the sine of the dip. For most normal faults we assumed a dip of 60 degrees. Dip directions were taken from the literature. For the Wasatch, Lost River, Beaverhead, Lemhi, and Hebgen Lake faults, the dip angles were taken from the literature (see fault parameter table on Website). Strike-slip faults were assigned a dip of 90 degrees. For California faults, widths were often defined using the depth of seismicity (J. Lienkaemper, written comm., 1996; M. Petersen, C. Cramer, and W. Bryant, written comm., 1996). Fault length was calculated from the total length of the digitized fault trace.
|
Part or all of this report is presented in Portable Document Format (PDF); the latest version of Adobe Reader or similar software is required to view it. Download the latest version of Adobe Reader, free of charge. |