CHAPTER 10

MODELING DEFORMATION AT THE ACTIVE TOE OF THE SLUMGULLION LANDSLIDE

by William Z. Savage, David J. Varnes, William K. Smith, and Philip S. Powers

Introduction

Precise leveling in front of the active toe of the Slumgullion landslide has been carried out annually since 1991 (Varnes and others, 1993). The leveling observation points near the active toe are shown in figure 1A. These leveling surveys establish a general pattern of downward displacement of older slide material in response to the advance of the younger, overriding active toe. Because we do not know how far ahead of the advancing active front the effects of the surcharge may eventually be felt, or at what rate deformation over large areas, if any, is occurring, a theoretical model to supplement intermittent field measurements and to predict this deformation was developed. This model is described in this chapter.

The Deformation Model

The measured downward deflections are consistent with the predicted response of an elastic half-space to surface loading applied as shown in figure 2. The load, which consists of a thick strip with beveled edges, extends infinitely in the direction normal to the x-y plane, and is symmetric about the y-axis. Because of this symmetry, only the right half of the load is shown in the figure. The details of the elastic solution, which is based on Muskhelishvili's (1953) complex variable method, will not be presented, because of their complexity.

The vertical loading for the elastic solution is given by

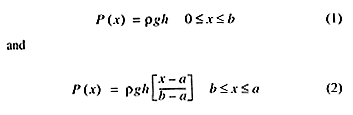
where

where

E is Young's modulus and

v is Poisson's ratio.

Figure 3C shows predicted nondimensional deflections given by the two normalized displacements are normalized by dividing both sides of equation 3 by 4gh (1 - v² )/E. The change in normal loading and the consequent change in deflections shown in figures 3C and 3D are taken to be analogous to the deformational response caused by the forward advance of the toe of an actual landslide. Note in figure 3D that the greatest change in the predicted deflections occurs in the vicinity of x/a = 1, that is, near the active toe.

Measured and predicted deflections for an annual advance of the toe of 1 m are shown in figure 4. The measured and predicted deflections show that greatest displacements are near the active toe with diminishing deformation away from the toe.

Annual deflections measured during the period 1991-93 are summarized in table 1. The distance from the toe given in table 1 is the shortest distance from a leveling station to the edge of the active toe. Note that all leveling-station elevations, and hence their changes, are measured relative to BM H169, which itself is on the old slide (fig. 1A). With the exception of deflections measured at TP7 and TP14 for 1991-92, all annual deflections shown in table 1 are downward. Linear regression of ln V against distance yields the exponential expression V = - 0.015 exp ( -0.011d), where d is the distance in front of the edge of the active toe for the measured downward annual deflections shown on figure 4. This exponential expression is fit to the measured data because it gives a reasonable approximation to the theoretical curve and provides a simpler form for least-squares analysis. The correlation coefficient, r, for this exponential fit is 0.53. This correlation coefficient is significant at the 99.9 percent confidence level (Volk, 1958, p. 231); that is, there is only one chance in a thousand of obtaining a correlation coefficient this large if there is no correlation between downward displacement and distance from the front of the landslide toe.

The parameters used for the predicted deflection for the advance of the Slumgullion landslide are a = 175 m, b = 0 m, a' = 176 m, b' = 1 m, and 4gh ( 1 - v² )/E = 0.02. Here, a and b are the geometric parameters describing the initial shape of the toe of the landslide, and a' and b' are the geometric parameters describing the shape of the toe of the landslide after an advance of 1 m. The values for the geometric parameters, a , b , a' , and b' give the triangular loading shown by the long dashed line in figure 5. Only the line for the geometric parameters, a and b is shown because of the short 1-m annual displacement of the toe of the landslide. Note that the loading shown in figure 5 is approximately 75 m shorter than the triangular loading that one might infer from figure 1B. This suggests that slide material to the left of b and perhaps the upper part of the triangular loading between b and a in figure 2 will have little or no effect on measured deflections. This inference must also be tested against further leveling measurements. If the average height of the slide, h, is taken to be 40 m, the density, , to be 2,000 kg/m³, and Poisson's ratio, v, to be 0.5, then the Young's modulus, E, of the overridden slide material is predicted to be 2.35x10⁶ N/m².

Conclusions

Although this theoretical model can provide some basis for predicting how far ahead of the advancing front the effects of the surcharge may be felt, it has two principal shortcomings. The first is the assumed symmetry of the loading about the y-axis. This symmetry does not exist in the landslide. The second is the assumption of vertical loading only. Shear tractions will be produced where the active slide overrides the inactive slide. An improved model will be developed to address these problems.

References Cited

Muskhelishvili, N.I., 1953, Some basic problems of the mathematical theory of elasticity: Groningen, Netherlands, P. Noordhoof, 704 p.

Varnes, D.J., Smith, W.K., Savage, W.Z., and Varnes, K.L., 1993, Control and deformation surveys at the Slumgullion Slide, Hinsdale County, Colorado--A progress report: U.S. Geological Survey Open-File Report 93-877, 15 p.

Volk, W., 1958, Applied statistics for engineers: New York, McGraw-Hill, 354 p.