Peak-Flow and Low-Flow Magnitude Estimates at Defined Frequencies and Durations for Nontidal Streams in Delaware
Links
- Document: Report (8.12 MB pdf) , HTML , XML
- Data Releases:
- USGS data release - Magnitude and frequency of peak flows and low flows on nontidal streams in Delaware—Peak and low flow estimates and basin characteristics
- USGS data release - PeakFQ inputs and selected outputs for selected gages in or near Delaware
- USGS data release - Basin characteristics rasters for Delaware StreamStats 2020
- USGS data release - Fundamental dataset rasters for Delaware StreamStats 2020
- Download citation as: RIS | Dublin Core
Abstract
Reliable estimates of the magnitude of peak flows in streams are required for the economical and safe design of transportation and water conveyance structures. In addition, reliable estimates of the magnitude of low flows at defined frequencies and durations are needed for meeting regulatory requirements, quantifying base flows in streams and rivers, and evaluating time of travel and dilution of toxic spills. This report, in cooperation with the Delaware Department of Transportation and the Delaware Geological Survey, presents methods for estimating the magnitude of peak flows and low flows at defined frequencies and durations on nontidal streams in Delaware, at locations both monitored by streamflow-gage sites and ungaged. Methods are presented for estimating (1) the magnitude of peak flows for return periods ranging from 2 to 500 years (50-percent to 0.2-percent annual-exceedance probability), and (2) the magnitude of low flows as applied to 7-, 14-, and 30-consecutive day low-flow periods with recurrence intervals of 2, 10, and 20 years (50-, 10-, and 5-percent annual non-exceedance probabilities). These methods are applicable to watersheds that exhibit a full range of development conditions in Delaware. The report also describes StreamStats, a web application that allows users to easily obtain peak-flow and low-flow magnitude estimates for user-selected locations in Delaware.
Peak-flow and low-flow magnitude estimates for ungaged sites are obtained using statistical regression analysis through a process known as regionalization, where information from a group of streamflow-gage sites within a region forms the basis for estimates for ungaged sites within the same region. Ninety-four streamflow-gage sites in and near Delaware with at least 10 years of nonregulated annual peak-flow data were used for the peak-flow regression analysis, a subset of the 121 sites for which peak-flow estimates were computed. These sites included both continuous-record streamflow-gage sites as well as partial record sites. Forty-five streamflow-gage sites with at least 10 years of nonregulated low-flow data available were used for the low-flow regression analyses, a subset of the 68 sites for which low-flow estimates were computed. Estimates for gaged sites are obtained by combining (1) the station peak-flow statistics (mean, standard deviation, and skew) and peak-flow estimates using the recent Bulletin 17C guidelines that incorporate the Expected Moments Algorithm with (2) regional estimates of peak-flow magnitude derived from regional regression equations and regional skew derived from sites with records greater than or equal to 35 years. Example peak-flow estimate calculations using the methods presented in the report are given for (1) ungaged sites, (2) gaged sites, (3) sites upstream or downstream from a gaged location, and (4) sites between gaged locations. Estimates for low-flow gaged sites are obtained by combining (1) the station low-flow statistics (mean, standard deviation, and skew) and low-flow estimates with (2) regional estimates of low-flow magnitude derived from regional regression equations. Example low-flow estimate calculations using the methods presented in the report are given for (1) ungaged sites, (2) gaged sites, (3) sites upstream or downstream from a gaged location, and (4) sites between gaged locations. A total of 54 sites in the Coastal Plain region were used to develop peak-flow regressions for the region and 40 sites were used for the Piedmont region. Similarly, 24 sites were used for low-flow regression equation development in the Coastal Plain, with 21 in the Piedmont. Peak and low-flow site inclusion in the Coastal Plain tended to be more restricted with tidal influence and ranges of basin characteristics, including drainage area, limiting regression equation development and application.
Regional regression equations for peak flows and low flows, as applicable to ungaged sites in the Piedmont and Coastal Plain Physiographic Provinces in Delaware, are presented. Peak-flow regression equations used variables that quantified drainage area, basin slope, percent area with well-drained soils, percent area with poorly drained soils, impervious area, and percent area of surface water storage in estimating peak-flow estimates, whereas low-flow regression equations used only drainage area and percent poorly drained soils in the estimation of low flows. Average standard errors for peak-flow regressions tended to be lower than those for low- flow regressions, with lower errors in the Piedmont region for both peak- and low-flow regressions. For peak-flow estimates, a sensitivity analysis of Piedmont regression equation estimates to changes in impervious area is also presented.
Additional topics associated with the analyses performed during the study are discussed, including (1) the availability and description of 32 basin and climatic characteristics considered during the development of the regional regression equations; (2) the treatment of increasing trends in the annual peak-flow series identified at 18 gaged sites and inclusion in or exclusion from the regional analysis; (3) regional skew analysis and determination of regression regions; (4) sample adjustments and removal of sites owing to regulation and redundancy; and (5) a brief comparison of peak- and low-flow estimates at gages used in previous studies.
Introduction
Reliable estimates of the magnitude of peak flows in streams at defined frequencies are required for the economical design of transportation and water-conveyance structures such as roads, bridges, culverts, storm sewers, dams, and levees (Ries and Dillow, 2006). These estimates are also needed for the effective planning and management of land use and water resources to protect lives and property in flood-prone areas and to determine flood-insurance rates (Ries and Dillow, 2006).
In addition, reliable estimates of the magnitude of low flows are needed by engineers, scientists, natural resource managers, and many others for (1) establishment of regulatory minimum flow-by requirements for streams and rivers, (2) quantifying base flow in streams and rivers, (3) wastewater discharge permitting, (4) water-supply planning and management, (5) protection of stream biota, and (6) evaluation of time of travel and dilution of toxic spills (Carpenter and Hayes, 1996; Ries, 2006; Doheny and Banks, 2010).
Estimates of peak-flow magnitude at defined frequencies and low-flow magnitude at defined frequencies and durations are needed, both at locations monitored by streamflow-gages and at ungaged sites where no streamflow information is available for determining estimates (Ries and Dillow, 2006). Estimates for ungaged sites are usually achieved through a process known as regionalization, where peak-flow and low-flow information for groups of streamflow-gage sites within a region are used to calculate estimates for ungaged sites (Ries and Dillow, 2006).
Because peak-flow and low-flow statistics that are computed at individual streamflow-gage sites can represent different record lengths and different periods of time, they should be considered estimates when used for predicting long-term and future extreme peak-flow or low-flow conditions (Ries, 2006; Doheny and Banks, 2010). Statistics also change over time as more streamflow data are recorded at individual streamflow-gage sites and with the addition of extreme hydrologic conditions (Ries, 2006; Doheny and Banks, 2010). As a result, both peak-flow and low-flow statistics at individual streamflow-gage sites should be updated periodically to reflect the longer periods of data collection, and for use in the regionalization process to produce updated estimates at ungaged sites (Ries, 2006; Doheny and Banks, 2010).
Purpose and Scope
The purpose of this report is to present methods for estimating the magnitude of peak flows and low flows at defined frequencies and durations on nontidal streams in Delaware. This report (1) describes methods used to estimate the magnitudes of both peak flows and low flows at sites monitored by streamflow-gage sites; (2) presents estimates of peak-flow magnitude at the 50-percent (2 year [yr]), 20-percent (5 yr), 10-percent (10 yr), 4-percent (25 yr), 2-percent (50 yr), 1-percent (100 yr), 0.5-percent (200 yr), and 0.2-percent (500 yr) annual-exceedance probability (AEP) for 94 streamflow-gage sites in and near Delaware; (3) presents estimates of low-flow magnitudes at selected frequencies (7Q2, 7Q10, 7Q20, 14Q2, 14Q10, 14Q20, 30Q2, 30Q10, and 30Q20) describing 7-, 14-, and 30-consecutive-day low-flow periods with annual nonrecurrence intervals of 2, 10, and 20 years (annual non-exceedance probabilities of 50 percent, 10 percent, and 5 percent, respectively) for 45 streamflow-gage sites in and near Delaware; (4) describes methods used to develop regression equations to estimate the magnitude of peak flows and low flows for defined frequencies and durations at ungaged sites in Delaware; (5) describes the accuracy and limitations of the peak-flow and low-flow equations; (6) presents example applications of the peak-flow and low-flow methods; and (7) describes the U.S. Geological Survey (USGS) StreamStats web application from which basin characteristics, streamflow statistics, and estimates can be obtained.
Previous Investigations
Methods for determining peak-flow magnitude estimates for nontidal streams in Delaware were published in previous reports by Tice (1968), Cushing and others (1973), Simmons and Carpenter (1978), Dillow (1996), and most recently by Ries and Dillow (2006). The regionalization methods described in the earlier reports relied on fewer monitored sites and shorter periods of recorded data than those used in Ries and Dillow (2006). Since Ries and Dillow (2006) was published, an additional 13 water years of streamflow data and computationally improved regionalization techniques have become available.
Methods for determining low-flow statistics for nontidal streams in Delaware were published previously in Carpenter and Hayes (1996). Regionalization methods used in that report relied on data through March 1987 (the end of the 1986 climatic year). An additional 31 years of streamflow data and computationally improved regionalization techniques for low-flow statistics have become available since the analyses described by Carpenter and Hayes (1996).
Doheny and Banks (2010) also presented selected low-flow statistics for 114 continuous-record streamflow-gage sites in Maryland based on available data through the 2009 climatic year. Low-flow statistics at several streamflow-gage sites from the Coastal Plain area of Maryland and the Piedmont area of northeastern Maryland included in that investigation were updated using an additional 8 years of continuous streamflow data and used for regionalization in this investigation.
Description of Study Area
The study area, composed of the State of Delaware, is in the Mid-Atlantic region of the United States. Delaware lies between lat 38°27' and 39°51' N. and long 75°04' and 75°48' W. and is bordered on the north by Pennsylvania, on the west and south by Maryland, on the east by Delaware Bay, and the Atlantic Ocean in the southeast section of the State (fig. 1). The State of New Jersey is on the eastern shore of the Delaware River and Delaware Bay. Delaware has a land area of 1,954 square miles (mi2) and a 2020 population of 986,809, an increase of 1.04 percent from 2019 (Macrotrends, 2021).
The climate in the study area is generally temperate (Ries and Dillow, 2006). The mean annual temperature across Delaware ranges from about 54 degrees Fahrenheit (° F) in northern New Castle County to 58.1° F along the Atlantic coast of southern Delaware. Mean annual precipitation is about 45 inches statewide (Delaware State Climatologist, 2021). The precipitation is distributed fairly evenly throughout the year, though with greater precipitation surplus (precipitation minus potential evapotranspiration) during the winter and spring months. Annual peak flows in the State are triggered by a mix of frontal storms with rain and melting snow in the spring, thunderstorms in the summer, and tropical storms and hurricanes in the summer and fall (Ries and Dillow, 2006). Annual low-flow periods are the result of extended periods with minimal rainfall that occur periodically, generally between July and October.
The study area is in two major physiographic provinces, the Coastal Plain and the Piedmont (fig. 1; Fenneman, 1938). The Fall Line, which crosses the northeast corner of Delaware about 5 miles (mi) south of the northwest corner of the State, forms the divide between the two provinces. The Piedmont Physiographic Province, northwest of the Fall Line, consists of gently rolling landscape with maximum elevations generally less than 400 feet (ft) above sea level. Delaware streams in this province have steep gradients and drain to either the Delaware River or to Delaware Bay (Dillow, 1996; Ries and Dillow, 2006). The Coastal Plain Physiographic Province, southeast of the Fall Line, consists of an area of low relief adjacent to the Chesapeake Bay and Delaware Bay, with elevations ranging from sea level to less than 100 ft. Streams in the Coastal Plain are often affected by tides for substantial distances above their mouths. The Fall Line is named as such because numerous waterfalls occur where rivers and streams drop in elevation from the Piedmont onto the Coastal Plain (Ries and Dillow, 2006).
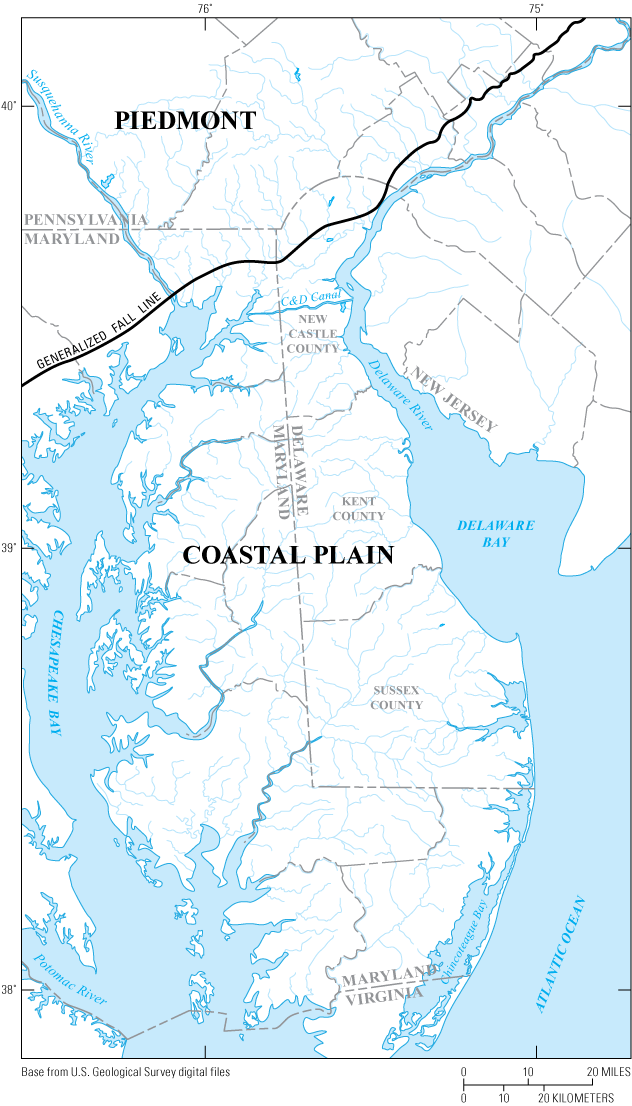
Map showing the study area and physiographic provinces in Delaware and surrounding states.
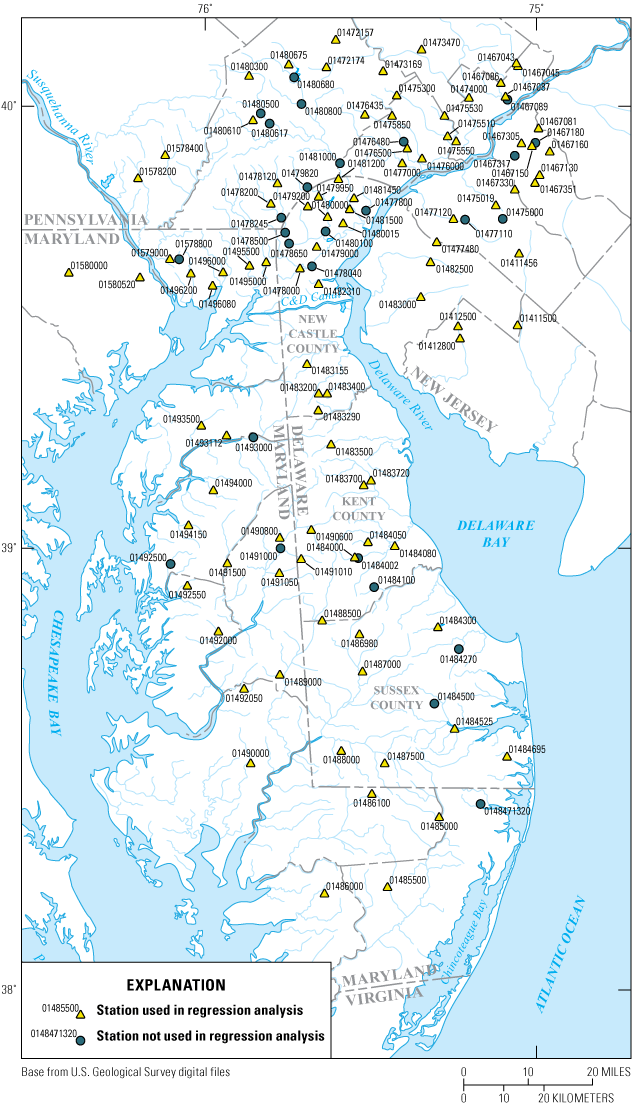
Map showing the location of streamflow-gage sites in Delaware and surrounding states for which peak-flow magnitude estimates were computed.
Table 1.
Summary of streamflow-gage sites in and near Delaware used in peak-flow regional regression equations.[mi2, square mile; N, number of annual peaks; CP, Coastal Plain; DE, Delaware; MD, Maryland; NJ, New Jersey; PA, Pennsylvania; Ave., Avenue; Br, branch; Cr, creek; Phila., Philadelphia; SB, South Branch; NB, North Branch]
Methods for Estimating the Magnitude of Peak Flows at Defined Frequencies
This report describes methods for estimating the magnitude of peak flows associated with defined frequencies for sites monitored by streamflow-gage sites and for ungaged sites in and around Delaware. The process followed for determining peak-flow magnitude estimates for ungaged sites in a given region usually includes (1) selecting a group of streamflow-gage sites in and around the region with at least 10 years of annual peak-flow data and streamflow conditions that generally represent the whole area; (2) computing initial peak-flow magnitude estimates and at-site skew values as determined by use of “Guidelines for Determining Flood Flow Frequency—Bulletin 17C” (England and others, 2019); (3) computing physical and climatic characteristics (hereafter referred to as “basin characteristics”) that have a conceptual relation to the generation of peak flows for the drainage basins associated with the monitored sites; (4) analyzing the initial at-site skew coefficients to compute regional skew values; (5) recomputing the peak-flow magnitude estimates for the sites monitored by streamflow-gages by weighting the at-site skew coefficients and the new regional skew values that correspond to their respective record lengths; (6) analyzing relations between peak-flow magnitude estimates and basin characteristics to determine homogeneity throughout the region or whether to divide the region into subregions; (7) using regression analysis to develop equations to estimate peak-flow magnitudes at ungaged sites in the region or subregions; and (8) assessing and describing the accuracy associated with estimation of peak-flow magnitudes for ungaged sites (Ries and Dillow, 2006).
Streamflow-gage sites within Delaware and in adjacent states having basin centroids within 25 mi of the Delaware border were investigated for possible use in the regional analysis. Gaged sites in this region were not used in the analysis if less than 10 years of annual peak-flow data were available, or if peak flows at the stations were substantially affected by dam regulation or storage of storm flows by reservoirs. Use of these criteria resulted in the initial selection of 121 gaged sites for use in the regional analysis (Hammond, 2021a) (fig. 2, table 1). The number of gaged sites that describe basins with an appreciable amount of urban development within the region was insufficient to develop separate regression equations based solely on urban drainage basins; however, the Delaware Department of Transportation is interested in understanding how development can affect peak-flow magnitude estimates, so gaged sites that monitor basins with appreciable development were not excluded from the analysis.
Determination of Basin Characteristics
Basin characteristics that were initially considered for use in the regression analyses included data variables related to drainage area, basin slope, impervious area, soil types, basin storage, developed land, mean basin elevation, basin relief, forest cover, mean-annual and maximum precipitation totals, hydraulic conductivity, development density, outlet-point elevation, flowpath lengths, housing units and housing density, and basin population. A list of specific basin characteristics considered for use in both the peak-flow and low-flow regression analyses is shown in table 2.
Table 2.
Basin characteristics considered for use in the peak-flow and low-flow regression analyses.| Name | Units | Description |
|---|---|---|
| DRNAREA | Square miles | Drainage area |
| BSLDEM3M | Percent | Mean basin slope |
| IMPERV | Percent | Percent impervious surface area from 2016 National Land Cover Database (Homer and others, 2012) |
| SOILA | Percent | Percent soil type A, well drained (SSURGO) |
| SOILD | Percent | Percent soil type D, poorly drained (SSURGO) |
| STORNHD | Percent | Percent area of surface water storage from National Hydrography Dataset |
| LC16STOR | Percent | Percent area of surface water storage from 2016 National Land Cover Database (Class 10, 90, 95) (Homer and others, 2012) |
| LC16DEV | Percent | Percent of developed land use categories from 2016 National Land Cover Database (Class 21–24) (Homer and others, 2012) |
| ELEV | Feet | Mean basin elevation |
| RELIEF | Feet | Maximum minus minimum basin elevation |
| FOREST | Percent | Percent of forested land use from 2016 National Land Cover Database (Class 41–43) (Homer and others, 2012) |
| PRECIP | Inches | Mean annual precipitation |
| I24HXY | Inches | 24-hour, 2-, 5-, 10-, 25-, 50-, 100-, 200-, 500-, 1,000-year maximum precipitation where X is the recurrence interval in years (recurrence intervals correspond to the 50-, 20-, 10-, 4-, 2-, 1-, 0.5-, 0.2-, and 0.1-percent chance annual-exceedance probabilities) |
| SSURGOKSAT | Inches per hour | Mean surface layer vertical hydraulic conductivity (SSURGO) |
| DINTNLCD16A | NA | Development intensity (categories 21, 22, 23, 24; weighted 0.1, 0.25, 0.65, 0.9, respectively) from 2016 National Land Cover Database (Homer and others, 2012) |
| OUTLETELEV | Feet | Outlet point elevation |
| LFPLENGTH | Miles | Longest flow-path length |
| BSHAPELFP | Unitless | Longest flow-path length squared divided by drainage area |
| LFPSLPFM | Feet per mile | Longest flow-path slope |
| LFPSLP1085FM | Feet per mile | Longest flow-path slope from the U.S. Geological Survey 10–85 slope method |
| HOUSINGTOT2010 | Number of housing units | Total housing units from 2010 census block groups (U.S. Census Bureau, 2010) |
| HOUSINGDEN2010 | Housing units per acre | Housing density from 2010 census block groups (U.S. Census Bureau, 2010) |
| POPTOTAL10 | Population | Total population in basin from 2010 census block groups (U.S. Census Bureau, 2010) |
| POPDENS10 | Population per acre | Basin population density from 2010 census block groups (U.S. Census Bureau, 2010) |
Flow Statistics for Streamflow-Gage Sites
There were 121 streamflow-gage sites identified either within the State of Delaware or within a 25-mi buffer of the State of Delaware border and located within Maryland, New Jersey, or Pennsylvania, each of which is associated with 10 or more years of annual peak-flow data. Of these sites, 94 were subsequently used for the development of peak-flow regression equations following analyses of trend, redundancy, and regulation as described in the sections below. Following Wagner and others (2016), record lengths from individual gaged sites were not combined following the analysis of contributing-area redundancy and flow regulation. Record combination would only have been possible for two sets of gage sites, and instead of introducing potential error, the longer record was chosen for each set of redundant gages (01467087 and 01467089, 01476480 and 01476500) providing a dataset composed solely of individual streamflow-gage-site data records.
For each of the 121 streamflow-gage sites, peak-flow magnitudes at the 50-, 20-, 10-, 4-, 2-, 1-, 0.5-, and 0.2-percent AEPs (2-year to 500-year recurrence intervals) were determined using the PeakFQ program version 7.3 (Veilleux and others, 2014) and guidance from Bulletin 17C Guidelines for determining flood-flow frequency (England and others, 2019). Bulletin 17C is implemented in PeakFQ version 7.3 using the Expected Moments Algorithm (EMA) (Cohn and others, 1997) and a generalized version of the Grubbs-Beck test for low outliers (Cohn and others, 2013). Flow statistics are provided for sites included in regression analyses as well as those not suitable for inclusion in regression equations owing to regulation, redundancy, or the presence of trend as detailed below. At-site, regression-based, and weighted flow statistics are provided for sites included in regression equation development. At-site, regression-based, and weighted peak-flow estimates along with basin characteristics can be found in Hammond (2021a).
Procedures for Implementing the Bulletin 17C Guidelines
Procedures for implementing the Bulletin 17C guidelines include (1) EMA analysis for fitting the log-Pearson Type III (LP3) distribution, incorporating historical information where applicable; (2) the use of weighted skew coefficients (based on weighting at-site skew coefficients, fig. 3, with regional skew coefficients from the section “Regional Skew Analysis and Determination of Streamflow Analysis Regions” below); and (3) the use of the Multiple Grubbs-Beck Test (MGBT) for identifying potentially influential low flows (PILFs) (England and others, 2019; Sando and McCarthy, 2018).
The standard procedures for incorporating historical information with the EMA methodology involve defining and applying the best-available flow intervals and perception thresholds for peak-flow magnitude analyses that include recorded streamflow data, historical peak flows, and ungaged historical periods. The EMA method improves upon the standard LP3 method in Bulletin 17B by integrating censored and interval peak-flow data into the analysis (Cohn and others, 1997). There are two types of censored peak-flow data in this report: (1) annual peak flows at crest-stage gages for which the flow is less than a minimum recordable value, and (2) historical annual peak flows that have not exceeded a recorded historical peak (Eash and others, 2013). In EMA, interval discharges were used to characterize peak flows known to be greater or less than a specific value, peak flows that could only be reliably estimated within a certain range, or to characterize missing data in periods of recorded data. The MGBT is used by EMA to identify not just low outliers but also other PILFs (Cohn and others, 2013). Although low outliers are typically one or two homogeneous values in a dataset that do not conform to the trend of the other observations, PILFs have a magnitude that is much smaller than the flood quantile of interest, occur below a statistically significant break in the flood magnitude-frequency plot, and have excessive influence on the estimated magnitude of large floods at defined frequencies. An example implementation of Bulletin 17C methods is shown in figure 4 for USGS gage 01480000 (Red Clay Creek at Wooddale, Delaware).
For crest stage gage locations, which differ from continuous record sites in that measurements are only available for the maximum stage of an individual event, it was also necessary to determine the minimum recordable flow as part of implementing perception thresholds. The minimum recordable flow threshold primarily affects treatment of peak flows near the extreme lower tail of the frequency distribution. Generally, the handling of peak flows near the extreme lower tail of the frequency distribution has limited effect on magnitude-frequency analyses, with very low peak flows either censored by PILF thresholds or exerting small influence in determining the distributional parameters of the LP3 distribution.
For some streamflow-gage sites, the peak-flow records are not well represented by the standard procedures and require informed user adjustments. For this study, adjustments were made to account for atypical lower-tail peak-flow data at seven sites (01412500, 01467086, 01467317, 01467351, 01473470, 01475019, and 01488500) by implementing the Single Grubbs-Beck Test instead of the recommended MGBT, resulting in an improved EMA fit of the LP3 distribution. The PeakFQ models for all 121 sites used in this study are provided in Hammond (2021b).
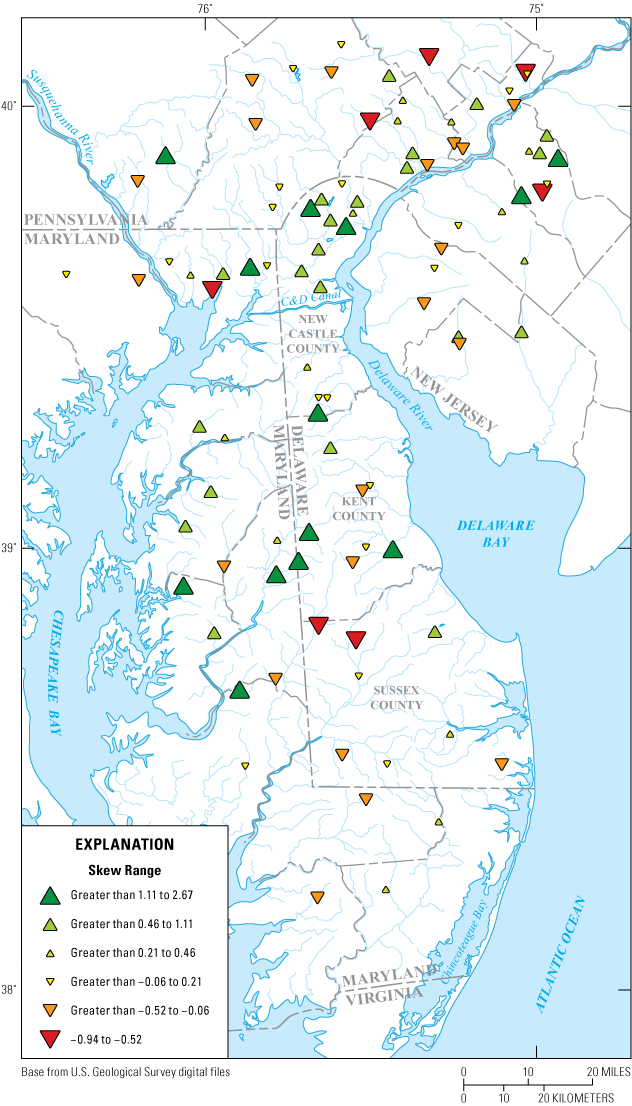
Map showing at-site skew values for streamflow-gage sites in Delaware and surrounding states for which peak-flow magnitude estimates were computed.
Analysis of Trends in Annual Peak-Flow Time Series
PeakFQ implements the nonparametric Mann-Kendall test for the identification of monotonic trends in annual peak-flow data. The results from this test show that peak-flow data from 18 of the original 121 sites had significant trends, where significance is defined by p-values less than 0.05. Similar to Wagner and others (2016), if sites displayed a significant trend, the Mann-Kendall trend test was implemented on variations of the original annual peak-flow series by removing 5 percent of the annual peak-flow data from the beginning or end of the dataset, or a combination of the two. This practice assumes that if a significant trend is not identified using 90 or 95 percent of the data, then the trend was likely not present and not impactful on the peak-flow magnitude analysis (Eash and others, 2013). If a trend remained after removing data as described, the site was not included in the development of regional regression equations. Nine of the 18 sites were kept for further analysis, although some not included were possibly eliminated owing to redundancy or regulation as described in the sections below. The nine sites that were not used for regression equation development owing to trends were 01467317, 01475000, 01477800, 01484100, 01484270, 01484500, 01491000, 01492500, and 01493000.
Regional Skew Analysis and Determination of Regression Regions
To assess whether separate regions with different regional skew values were present within our study area, we implemented the nonparametric Wilcoxon rank sum test for significant differences between the Coastal Plain and Piedmont physiographic regions used in the prior peak-flow frequency study (Ries and Dillow, 2006). For this analysis, we only considered sites with more than 35 years of peak-flow record, following Bulletin 17B (Interagency Advisory Committee on Water Data, 1982) and Wagner and others (2016). The Wilcoxon rank-sum test showed no significant difference between the long-term skew values in the Coastal Plain and Piedmont physiographic regions; thus, the average of all Coastal Plain and Piedmont at-site skews were used to calculate a regional skew value (0.264) applicable to the entire study region. This value was used along with the at-site skew coefficients to produce the weighted-skew PeakFQ models. Though only one regional skew value was used across the study area, when regression equations were constructed, separate regression equations were built for the Coastal Plain and Piedmont physiographic regions owing to improved model performance for individual regions as compared to using one model for the entire study area. Sites were assigned to physiographic regions based on the region containing the majority of their contributing drainage area. For one site, we deviated from this rule. USGS 01479000 White Clay Creek near Newark, DE, has 55 percent of the contributing area in the Coastal Plain and 45 percent from the Piedmont. The 45 percent located in the Piedmont is in the headwater of the basin where much of the flood generating urban influence is likely located, and this was the justification for assigning it to the Piedmont region in the prior study (Ries and Dillow, 2006).
Sample Adjustments and Removal of Sites Owing to Redundancy
Streamflow-gage sites with significant degrees of regulation were not included in the original dataset if there were regulation qualifiers applied to the annual peak flows in the USGS National Water Information System (NWIS) database. Adjustments to the dataset were also made based on any redundancy among sites that could influence the relations determined by regression analysis. The process used to justify removal of streamflow-gage sites as a result of redundancy is discussed below.
Statistical redundancy occurs when data from one streamflow-gage site can be partly or completely deduced from the data associated with another nearby gage on the same stream or river, or nearby in the same watershed. Inclusion of redundant data in a peak-flow analysis can influence the resulting regression-derived relation. The peak-flow dataset for this investigation was evaluated for redundancy in order to remove any potential influence or bias on the peak-flow magnitude regression analyses. Sites were flagged for possible redundancy if the drainage area ratio between two sites was less than 5.0 and the standardized distance between the two sites was less than 0.5 (Wagner and others, 2016).
There were 25 potential instances of redundancy identified in the peak-flow dataset, involving a total of 30 sites. Decisions regarding site redundancy for peak flows were made based primarily on record length and drainage-area size. Consideration was also given to the length of the data record, any breaks in the continuous record or annual peak-flow record, and how well the peak-flow record represents the current watershed conditions.
Of the 30 sites potentially affected by redundancy issues and questions, 18 were removed from the peak-flow analysis. For this study, no site records for peak flow were combined following removal of regulated or trend-affected sites, as a minimum of 10 years of concurrent data were not available (following Bulletin 17C guidelines and Wagner and others [2016]). The final number of streamflow-gage sites used for peak regression equation development in each state and region is provided in table 3, and a summary of the drainage areas for these streamflow-gage sites is provided in table 4. The ranges of basin characteristics used to develop the equations for each subregion are provided in table 5.
Development of Regression Equations
In developing regional regression equations, basin characteristics for candidate regression models were evaluated based on multicollinearity with other basin characteristics and statistical significance using ordinary least-squares regression. Subsequently, generalized least-squares regression was used to develop the final regression models for each region.
Explanatory Variable Selection for Peak-Flow Estimation
Each of the 32 basin characteristics in table 2 were considered for inclusion as explanatory variables in the peak-flow magnitude estimating equations. Prior to identifying the strongest peak-flow magnitude predictor variables, a multicollinearity matrix was calculated for all candidate variables and used to identify variables that were strongly correlated with each other. Multicollinearity was evaluated using the variance inflation factor (VIF), which provides an index of the magnitude of variance increase for an estimated regression coefficient owing to multicollinearity (Helsel and others, 2020). For this study, it was desirable to keep the VIF for all explanatory variables below 2.5 with statistical significance determined at the 95-percent confidence level (p≤0.05). In each case of multicollinearity between two variables, the simpler variable with more direct causal connection to peak-flow magnitude was retained for further consideration. Following the multicollinearity analysis, a subset of 20 basin characteristics remained for consideration using an iterative ordinary least-squares (OLS) regression approach to determine the best set of basin-characteristic variables to include in the peak-flow magnitude estimation equations.
Ordinary Least-Squares Regression for Peak-Flow Estimation
OLS regression techniques were used to select basin characteristics to use as explanatory variables for each AEP and to assess whether developing separate peak-flow estimation equations for study subregions based on physiographic provinces (as was done in prior reports) remained a justifiable approach. The mathematical objective of least-squares regression is to minimize the sum of the squared residuals (the differences between the actual and predicted value of a response variable) for all observations included in the regression (Farmer and others, 2019). The technique provides a consistent, reproducible way to estimate the linear best fit for a given set of data. OLS is a specific form of least-squares regression that is characterized by an underlying assumption of homoscedasticity, meaning that the uncertainty associated with each response-variable observation in a dataset is approximately equal. As detailed by Southard and Veilleux (2014), other assumptions inherent in the use of OLS regression include (1) a linear relation between the independent explanatory variable (basin characteristic) and the dependent response variable (the P-percent AEP), and (2) normality of residuals. All variables were transformed using base-10 logarithm to meet the first assumption. Variables expressed in percent, such as land-cover characteristics, were transformed by the addition of a value of 1 prior to log base-10 transformation to avoid the potential for computing an undefined quantity (the logarithm of zero). The normality of residuals resulting from various regression-based relations was assessed to assure that the final assumption was valid before considering inclusion of those relations in the results of this study.
Initial OLS regression equations were developed for the 1-percent AEP using 20 explanatory variables for 94 streamflow-gage sites in the study area. The Q1 percent, which is the 1-percent AEP, was chosen for optimizing the selection of explanatory variables because it is the AEP most often used by water managers, engineers, and planners (Eash and others, 2013). An iterative OLS regression approach using the allReg function from the USGS smwrStats R package (R Core Team, 2020; Lorenz, 2020) was utilized to examine the best subsets of explanatory variables for each AEP following the methodology suggested by Helsel and others (2020). A maximum of five concurrent variables for each AEP were considered for use in peak-flow estimation. Separate OLS models for the entire study area, as well as for each potential subregion (Coastal Plain, Piedmont), were developed using this method. Candidate regression models in each case were evaluated with respect to several metrics, including (1) maximizing the coefficient of determination (R2) and adjusted coefficient of determination (R2 adj), (2) minimizing residual standard error, (3) minimizing Mallow’s Cp, and (4) minimizing the predicted residual sum of squares (PRESS).
Additionally, peak-flow magnitude data for each streamflow-gage site and each AEP were analyzed to determine whether they exerted undue leverage and influence during variable selection using the iterative OLS approach. Although data from several sites displayed either influence or leverage that exceeded recommended values, no sites were removed as the watershed properties and peak-flow characteristics for the sites identified were not unrepresentative of those common in the study area, and no other disqualifying rationale was identified. Finally, sites representing basins that straddle the boundary between Piedmont and Coastal Plain physiographic regions were examined to determine if any displayed undue influence or leverage on the results of the selected OLS regressions. Only one site (01467087) exceeded the statistical threshold for undue influence (for the 0.02 AEP only), with no straddle sites exerting undue leverage for any of the AEP relations.
Generalized Least-Squares Regression for Peak Flow Estimation
Generalized least-squares (GLS) multiple-linear regression was used to compute the final regression coefficients and measures of accuracy for the regression equations to estimate peak flows at defined frequencies. The GLS method weights data from streamflow-gage sites in the regression analysis according to differences in streamflow reliability (record length), variability (record variance), and spatial cross correlations of concurrent streamflow among streamflow-gage sites (Farmer and others, 2019). Compared to OLS regression, the GLS regression approach provides improved estimates of streamflow statistics and increases the predictive accuracy of the regression equations (Stedinger and Tasker, 1985). The weighted-multiple-linear regression (WREG) program (Eng and others, 2009) updated to run in R (Farmer, 2017) was used to perform the GLS regressions. A correlation smoothing function is used by WREG to compute a weighting matrix for the streamflow-gage sites in each subregion. The smoothing function relates the correlation between annual peak discharges from each pair of streamflow-gage sites to the geographic distance between the sites. Smoothing functions were developed iteratively and generated separately for the Coastal Plain and Piedmont subregions. The statistical parameters needed to perform prediction-interval computations for peak-flow magnitude estimates can be found in table 6 of this report. The resulting GLS-derived regression equations follow the general structure shown below:
whereQp
is the dependent variable, the P-percent AEP, in cubic feet per second (ft3/s);
A and B
are independent (explanatory) variables; and
a,b, and c
are regression coefficients.
If the dependent variable, Qp, and the independent variables, A and B, are logarithmically transformed, the model takes the following form:
GLS-derived regression equations for Coastal Plain and Piedmont subregions:Coastal Plain
PiedmontTable 3.
Number of streamflow-gage sites included in the peak-flow regression analyses by subregion and state.[POR, period of record; ≥, greater than or equal to; DE, Delaware; MD, Maryland; NJ, New Jersey; PA, Pennsylvania]
Table 4.
Summary of drainage area, number of streamflow-gage sites, and average years of record used in the peak-flow regression analyses for Delaware.[--, not applicable]
Table 5.
Ranges of basin characteristics used to develop the peak-flow regression equations.[--, data not used in equations; NHD, National Hydrography Dataset]
Table 6.
Values needed to determine 90-percent prediction intervals for the best peak-flow regression equations by subregion in Delaware.[t, critical value from Student’s t-distribution for the 90-percent probability; MEV, regression model-error variance; U, covariance matrix of model coefficients; Intercept, y-axis intercept of regression equation; --, not applicable]
Table 7.
Mean and median percent differences between peak-flow magnitudes at defined frequencies computed from the annual peak-flow data for streamflow-gage sites included in both the current study and previous studies.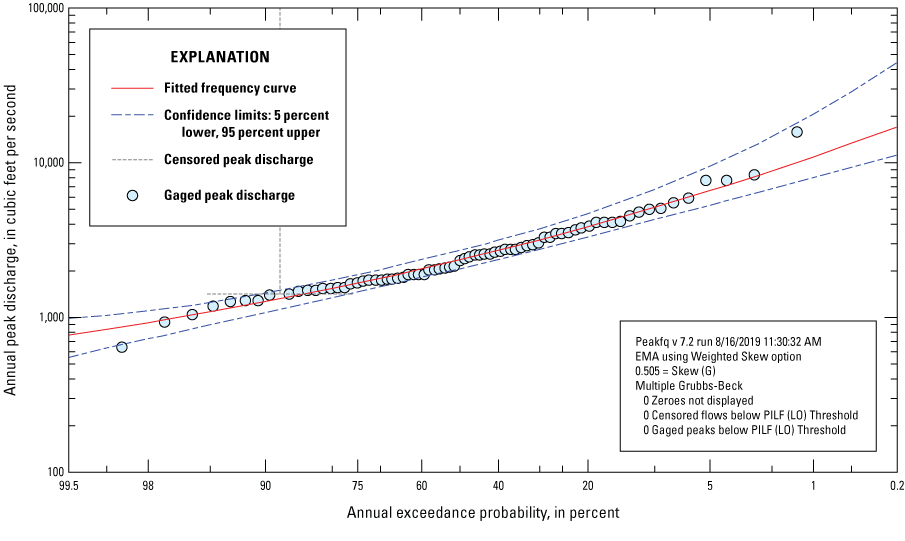
Example peak-flow magnitude-frequency curve produced by the PeakFQ program for USGS gage 01480000 (Red Clay Creek at Wooddale, Delaware) with weighted skew using at-site and regional skew values.
Comparison of Results with Previous Study
Median percent differences in peak-flow magnitudes computed from the annual peak-flow data from streamflow-gage sites included in this study show that flow estimates were generally within 10 percent of those from Ries and Dillow (2006), with slightly higher estimates for the sites and years included in this report (table 7). Sites in the Coastal Plain appeared to have higher median percent differences, particularly sites with additional recorded data since the prior study.
In Ries and Dillow (2006), variables to predict peak-flow magnitudes for the Piedmont region included drainage area, the percent area forested, the percent area with well drained soils (soil A), the percent area with impervious cover, and the percent area of surface water storage. For the Coastal Plain, variables used included drainage area, mean basin slope, and percent area with well drained soils (soil A). Similarly, in this report, for the Piedmont drainage area, mean basin slope, percent area of surface water storage, and percent area with impervious cover were chosen, but percent area poorly drained soils (soil D) was selected instead of well drained soils (soil A) and percent area forested. Variables chosen for the Coastal Plain were identical to the prior report. The model errors for the equations generated in this report (table 8) were generally within 5 percent of those from the prior report, with slightly higher model error in the Piedmont subregion and slightly lower error for the Coastal Plain subregion.
Accuracy and Limitations of Peak-Flow Regression Equations
The accuracy of a regression equation depends on the model error and the sampling error associated with the data used in its development. Model error measures the ability of a set of explanatory variables to estimate the values of peak-flow characteristics calculated from the recorded streamflow-gage data used to develop the equation (Ries and Dillow, 2006). Sampling error measures the ability of a finite number of sites with a finite number of recorded annual peak flows to describe the true peak-flow characteristics of a site. Model error depends on the number and predictive power of the explanatory variables in a regression equation. Sampling error depends on the number of sites and the amount of peak-flow data at each site used in the analysis. Sampling error decreases as the number of sites and amount of data increase (Ries and Dillow, 2006). By definition, approximately two-thirds of the flow estimates derived using a given equation will contain errors within the standard error (estimate or prediction) associated with that equation.
Traditional measures of the accuracy of peak-flow regression equations are the standard error of estimate and the standard error of prediction. The standard error of estimate is derived from the model error, and is a measure of how well the estimated peak discharges generated using a regression equation agree with the peak-flow statistics generated from the at-site annual peak-flow data used to create the equation (Ries and Dillow, 2006). The standard error of prediction is derived from the sum of the model error and sampling error and is a measure of how accurately the estimated peak discharges generated using an equation will be able to predict the true value of peak discharge at the selected AEP (Ries and Dillow, 2006). Average standard errors of estimate and prediction associated with equations 3 through 18 are shown in table 8.
For the Coastal Plain region, Thomas and Sanchez-Claros (2019) similarly developed regional regression equations for 50- to 0.2-percent annual-exceedance probabilities using Bulletin 17B guidance and data through 2017 (Interagency Advisory Committee on Water Data, 1982). The study area overlapped well with sites used in the present study, including only sites in the Coastal Plain. Their equations included drainage area, watershed slope, and percent area in soil class A, which were the same variables used by Coastal Plain equations in the present study, and had similar values of standard error as equations used in this report. For the Piedmont region, Thomas and Moglen (2016) similarly developed regional regression equations for 50- to 0.2-percent annual-exceedance probabilities using Bulletin 17B guidance and data through 2012 (Interagency Advisory Committee on Water Data, 1982). The study area only partly overlapped with the sites in the present study including sites in the Appalachian Plateau, Allegheny Ridge, Blue Ridge, and Great Valley regions in addition to the Piedmont. Drainage area, limestone as a percent of watershed area, impervious area, and forest as percent of watershed areas were included in the regional regression equations—and though the present report used drainage area, watershed slope, percent watershed in soil class D, impervious area and storage along the NHD network—standard error for both sets of regional regression equations were similar.
Table 8.
Average standard errors of estimate and prediction for selected peak-flow regression equations by subregion in Delaware.Table 9.
Sensitivity analysis of Piedmont regression equation estimates to changes in impervious area. Table values are the median percent change in flow estimates with corresponding changes in impervious area. Impervious area increase columns—for example, 5 percent—report the percent change in flow estimate for each annual-exceedance probability with a 5-percent increase in the 2016 National Land Cover Database impervious percent for each watershed.A measure of uncertainty that can provide information about the range of error associated with an estimate is the prediction interval. The prediction interval states the minimum and maximum values within which there is a defined probability that the true value of an estimated variable exists. For instance, defining the 90-percent prediction interval for the 1-percent-chance AEP at an ungaged site would allow the user to know the minimum and maximum flow magnitudes that have a 90-percent chance of bounding the range in which the true flow value exists. A full explanation, including example computations, of the prediction interval can be found in Ries and Dillow (2006; p. 24–28).
The regression equations can be used to estimate peak-flow magnitudes for ungaged sites with natural flow conditions in Delaware. The equations should not be applied to streams with substantial flood-retention storage upstream from sites of interest (Ries and Dillow, 2006).
Additionally, in this report, static impervious area from the National Land Cover Database [NLCD] (2016) dataset was used to represent the role of urban effects in the Piedmont regression equations (Homer and others, 2012). Although the NLCD dataset has temporal coverage back to the early 2000s, impervious percent estimates at high spatial resolution are more uncertain before that time. In an effort to assess the sensitivity of peak flow estimates to changes in impervious area through time, we artificially increased the impervious percent of each watershed in each Piedmont regression equation to examine the changes in peak-flow estimates. Doubling the impervious area of a watershed on average resulted in a 7–14 percent increase in the flow estimate depending on the AEP used (table 9). Future studies may utilize alternate datasets with proxy information on impervious area going back many decades (for example, Uhl and others, 2021) to provide an estimate of urban effects on peak flows through time.
The accuracy of the regression equations is known only within the range of basin characteristics that were used to develop the equations. The equations can be applied to ungaged sites with basin characteristics that are not within the range of applicability, but the accuracy of the resulting estimates will be unknown (Ries and Dillow, 2006).
Procedures for Estimating Peak-Flow Magnitudes
At ungaged sites on ungaged streams with no current or historical recorded at-site data, the best estimates of peak-flow characteristics can be obtained from regression equations 3 through 18 presented in this report. At gaged sites, and ungaged sites near gaged sites on the same stream, the best estimates of peak-flow characteristics can be obtained by using the results of those equations in conjunction with recorded data from a streamflow-gage site as described below.
The best magnitude estimates for peak flows are often obtained through a weighted combination of estimates produced from more than one method (Ries and Dillow, 2006). Tasker (1975) demonstrated that if two independent estimates of a streamflow statistic are available, a properly weighted average of the independent estimates will provide an estimate that is more accurate than either of the two independent estimates. Improved magnitude estimates for peak flows can be determined for Delaware streamflow-gage sites by weighting estimates from the at-site annual peak-flow data from each site with estimates obtained from the regression equations provided in this report. Improved estimates can be determined for ungaged sites in Delaware by weighting the estimates obtained from the regression equations with estimates determined based on the flow per unit area of an upstream or downstream streamflow-gage site, when available (Ries and Dillow, 2006).
In this section, step-by-step examples are provided that demonstrate how to compute magnitude estimates for peak flows. The examples are based on the methods described previously in the section “Estimating Peak-Flow Magnitudes for Ungaged Sites.” Basin characteristics that are needed for use in the estimation equations can be determined as described in table 2.
Estimation for a Gaged Site
The Interagency Advisory Committee on Water Data (1982) recommends that the best estimates of flood-magnitude statistics for a streamflow-gaging site can be obtained by combining the estimates determined from LP3 analysis of the at-site annual peak data with estimates obtained for the site using regression equations. Weighted estimates were computed for sites used in regression analyses by considering at-site estimates and regression estimates using the methodology first developed and reported by Sando and McCarthy (2018). This method includes adjustment of confidence intervals to include EMA uncertainty (England and others, 2019).
Procedures for Weighting with Regional Regression Equations
The uncertainty of peak-flow magnitude estimates can be reduced by combining the at-site magnitude estimates with other independent estimates, such as from regression equations, to obtain a weighted magnitude estimate at the streamflow-gage site. As indicated in Bulletin 17C (England and others, 2019), the weighted-magnitude method assumes that the two magnitude estimates are independent and unbiased and the variances are reliable and consistent. The weighted-magnitude method, presented in appendix 9 of Bulletin 17C, uses the log-transformed magnitude estimates and variances from two separate estimates (s, at-site and r, regression) to compute a weighted-magnitude estimate (wtd) and confidence intervals using the following equations:
whereQ
is the magnitude estimate for estimation method s, r, or wtd, in cubic feet per second;
X
is the log-transformed magnitude estimate for estimation method s, r, or wtd;
V
is the variance for estimation method s, r, or wtd;
and
are the upper and lower log-transformed confidence limits for the two-tailed 90-percent confidence interval;
1.64
is the one-tailed Student’s t-value for the 95-percent (upper) and 5-percent (lower) confidence limits assuming infinite degrees of freedom; and
and are the upper and lower limits of the two-tailed 90-percent confidence interval for the weighted-magnitude estimate
in cubic feet per second.
The weighted-magnitude method using equations 19 through 27 calculates confidence intervals for the weighted estimate using the weighted variance; however, this method does not consider the confidence intervals for an at-site magnitude analysis computed using EMA. Thus, the USGS developed a method for weighting an at-site magnitude estimate with another independent estimate that preserves the characteristics of the confidence intervals computed using EMA (Sando and McCarthy, 2018). This method uses the effective variances of the upper and lower confidence intervals (Veff,U and Veff,L) from the at-site analysis to compute confidence intervals for the weighted estimates as shown in equations 28 through 35:
whereand
are the upper and lower limits of the two-tailed 90-percent confidence interval from the at-site magnitude analysis, in cubic feet per second;
and
are the upper and lower log-transformed confidence limits for the two-tailed 90-percent confidence interval from the at-site magnitude analysis;
and
are the computed effective variances for the upper and lower confidence limits;
is the variance of the second method, such as regression equations; and
and
are the weighted variances of the upper and lower confidence limits, which are computed using the effective variances from the magnitude analysis.
Estimation for a Site Upstream or Downstream from a Gaged Site
Guimaraes and Bohman (1992) and Stamey and Hess (1993) presented the following method to improve flood-magnitude estimates for an ungaged site with a drainage area that is between 0.5 and 1.5 times the drainage area of a streamflow-gaging site that is on the same stream. As in the previous section, the symbols used to explain this method in the source publications have been preserved in the discussion below, and the equivalent expressions used in this report are identified in the variable definitions that accompany each equation (Ries and Dillow, 2006).
To obtain a weighted peak-flow estimate (QT(U)w) for recurrence interval T (where AEP is equivalent to 1/T) at the ungaged site, the weighted flow estimate for an upstream or downstream streamflow-gaging site (QT(G)w) must first be determined from the “Peak flow estimates” table in Hammond (2021a). The weighted streamflow-gaging site estimate is then used to obtain an estimate for the ungaged site that is based on the flow per unit area at the streamflow-gaging site (QT(U)g) by use of the equation
whereAu
is the drainage area (DRNAREAu) for the ungaged site,
Ag
is the drainage area (DRNAREAg) for the upstream or downstream streamflow-gaging site
b
is 0.68 in the Piedmont and 0.70 in the Coastal Plain, as determined by computing the mean of the drainage-area exponents for all AEPs from regressions of peak-flow magnitudes against drainage area as the only explanatory variable, and where the equation constant is forced to be zero.
ΔA
is the absolute value of the difference between the drainage areas of the streamflow-gaging site and the ungaged site, |DRNAREAg - DRNAREAu|, and
QT(U)r
is the peak-flow estimate for AEP (Q50%, Q20%,…,Q0.2%) at the ungaged site derived from the applicable regional equation given above.
Use of the equations above gives full weight to the regression estimates when the drainage area for the ungaged site is less than 0.5 or greater than 1.5 times the drainage area for the streamflow-gaging site and increasing weight to the streamflow-gaging-site-based estimates as the drainage area ratio approaches 1. The weighting procedure should not be applied when the drainage area ratio for the ungaged site and streamflow-gaging site is less than 0.5 or greater than 1.5. In theory, the standard errors for these estimates should be at least as small as those for the estimates derived from the regression equations alone (Ries and Dillow, 2006).
Estimation for a Site Between Gaged Sites
In the case where a peak-flow magnitude estimate is needed for a site that is located between two gaged sites on a stream, the estimate may be obtained by use of the procedure presented earlier for calculating weighted estimates for a gaged site, with the following procedural alteration. For consistency, the symbology used below is the same as that used in the previous section, and the equivalent expressions used elsewhere in this report are identified in the variable definitions that accompany each equation.
Because the site is ungaged, a direct determination of the flow at the site for the selected AEP is not possible. An interpolated value can be obtained by use of the equation
whereAu
is the drainage area (DRNAREAu) for the ungaged site,
Agu
is the drainage area (DRNAREAgu) for the upstream gaged site,
Agd
is the drainage area (DRNAREAgd) for the downstream gaged site,
QTu
is the discharge at the T-percent AEP (Q50%, Q20%,…, Q0.2%) for the ungaged site,
QTgu
is the discharge at the T-percent AEP (Q50%, Q20%,…, Q0.2%) for the upstream gaged site, and
QTgd
is the discharge at the T-percent AEP (Q50%, Q20%,…, Q0.2%) for the downstream gaged site.
Estimation Examples
Ungaged Site on Ungaged Stream
Problem: Estimate the 1-percent AEP discharge for Horsepen Arm at Fox Hunters Road (lat 38.94339° N., long 75.64637° W.) in Kent County, Delaware. This location is in the Coastal Plain subregion.
DRNAREA = 5.21 mi2, BSLDEM3M = 1.64 percent, SOILA = 0.43 percent-
2. Calculate the 1-percent AEP using equation 8:
Q1% =(102.616)(5.210.693)(1.640.483)((0.43+1)-0.356)
Q1% =1,450 ft3/s
Gaged Site
Problem: Estimate the 1-percent AEP discharge for USGS 01488500. This site is in the Coastal Plain subregion.
-
1. Obtain the 1-percent AEP discharge and variance in cubic feet per second for USGS 01488500 for the at-site (s) and regression (r) methods in the “Peak flow estimates” table in Hammond (2021a):
-
2. Calculate Xs and Xr using equations 19 and 20:
Xs = log10(4,945); Xr = log10(4,097)
Xs = 3.694; Xr = 3.612
-
3. Calculate Xwtd using equation 21:
Xwtd = ((3.694*0.06384)+(3.612*0.0056))/(0.0056+0.06384)
Xwtd = 3.688
Qwtd = 103.688 = 4,871 ft3/s
Site Between Gaged Sites
Problem: Estimate the 20-percent AEP discharge for the ungaged location (lat 39.73897° N., 75.63439° W.) at the State Route 41 bridge near Elsmere, Delaware between USGS 01480000 and USGS 01480015. This site is in the Piedmont subregion.
-
1. Obtain the 20-percent AEP weighted discharge estimate and drainage areas for USGS 01480000 and USGS 01480015 from the “Peak flow estimates” and “Peak basin stats” tables in Hammond (2021a). Also obtain the drainage area for the ungaged site using the StreamStats application:
Au = 51.1 mi2
Agu = 47.4 mi2
Agd = 52.3 mi2
QTgu = 3,761 ft3/s
QTgd = 5,113 ft3/s
[(51.1–47.4)/(52.3–47.4)*((5,113/52.3)–(3,761/47.4))+(3,761/47.4)]*51.1
QTu = 4,765 ft3/s
Site Upstream from a Gaged Site
Problem: Estimate the 1-percent AEP discharge for ungaged location (lat 39.69087° N., long 75.70685° W.) White Clay Creek at Red Mill Road, upstream of USGS 01479000. This location is in the Piedmont subregion.
-
1. Obtain the 1-percent AEP weighted discharge estimate and drainage areas for USGS 01479000 from the “Peak flow estimates” and “Peak basin stats” tables in Hammond (2021a). Also obtain the drainage area and relevant basin characteristics for the 1-percent AEP regression equation for the ungaged site using the StreamStats application:
Au = 79.2 mi2
Ag = 88.9 mi2
b is 0.68 in the Piedmont, as determined by computing the mean of the drainage-area exponents for all AEPs.
QT(G)w= 18,705 ft3/s
SOILD = 14.31
IMPERV = 6.42
STORNHD = 0.52
-
2. Calculate using equation 36:
-
3. Calculate using equation 16:
-
4. Calculate using equation 37:
Methods for Estimating the Magnitude of Low Flows at Defined Frequencies and Durations
This report also presents methods for estimating the magnitude of low flows at defined frequencies and durations both for streamflow-gage sites and for ungaged sites in Delaware. The process followed for determining low-flow magnitude estimates for ungaged sites in a given region usually includes (1) selecting a group of streamflow-gage sites in and around the region with at least 10 years of annual 7-day low-flow data based on climatic years, and streamflow conditions that are generally representative of the area as a whole, (2) computing initial low-flow magnitude estimates for the streamflow-gage sites using analytical techniques automated within the USGS SWToolbox program (Kiang and others, 2018); (3) computing basin characteristics that have a conceptual relation to the generation of low flows for the drainage basins associated with the gaged sites; (4) recomputing the low-flow magnitude estimates for the streamflow-gage sites by weighting the at-site skew coefficients with the new regional skew values; (5) determining if relations between low-flow magnitude estimates and basin characteristics are homogeneous throughout the region or if the region should be divided into subregions; (6) using regression analysis to develop equations to estimate low-flow magnitudes at ungaged sites in the region or subegions; and (8) assessing and describing the accuracy associated with estimation of low-flow magnitudes for ungaged sites (Ries and Dillow, 2006; Carpenter and Hayes, 1996).
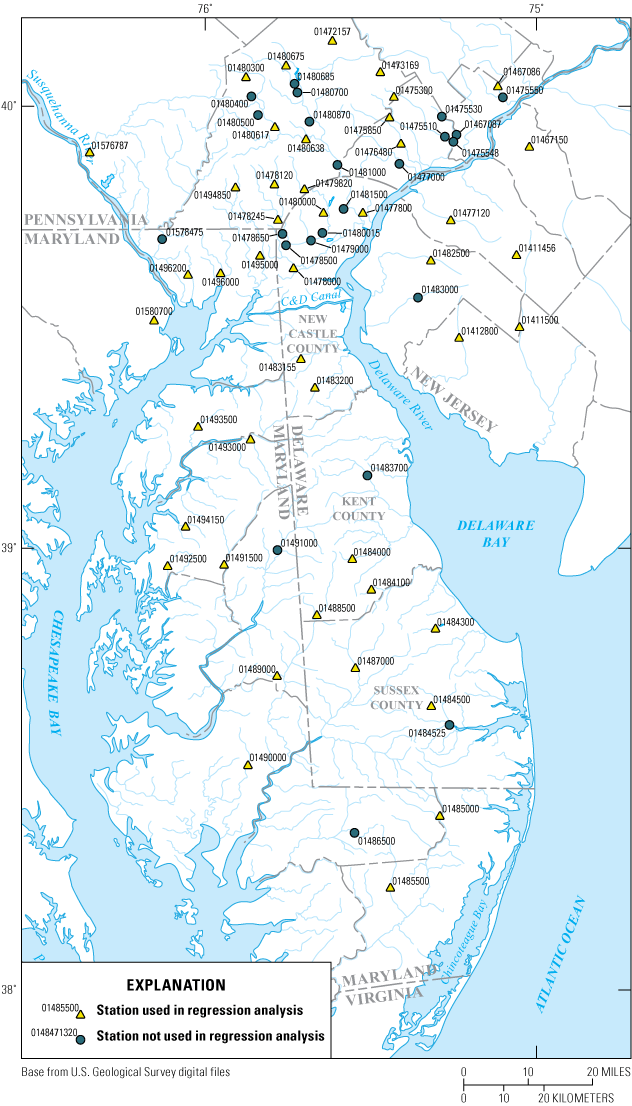
Map showing location of streamflow-gage sites in Delaware and surrounding states for which low-flow magnitude estimates were computed.
Table 10.
Summary of streamflow-gage sites in and near Delaware used in low-flow regional regression equations.[mi2, square mile; N, number of years of recorded data; CP, Coastal Plain; DE, Delaware; MD, Maryland; NJ, New Jersey, PA, Pennsylvania; Ave, Avenue; Hwy, highway, No., number; Ave., Avenue; Phila., Philadelphia; Cr, Creek]
Determination of Streamflow Analysis Regions
Similar to the peak-flow analysis, prior reports (Carpenter and Hayes, 1996; Doheny and Banks, 2010) demonstrated that separating low-flow sites into Coastal Plain and Piedmont physiographic regions resulted in improved regression equation performance. In this study, we implement the same separation and note improved regression performance when data are separated by physiographic region as described in the regression equation development section below.
Flow Statistics for Streamflow-Gage Sites
Sixty-eight streamflow-gage sites were identified within the State of Delaware, or within a 25-mi buffer of the Delaware border (located within Maryland, New Jersey, or Pennsylvania) that each had 10 or more complete climatic years (April 1 to March 30) of recorded daily flow data (fig. 5, table 10). Climatic years were used in line with common practice in prior low-flow studies (Carpenter and Hayes, 1996; Dudley and others, 2020) as this period better brackets the occurrence and duration of low-flow periods than the calendar year or water year. No partial-record streamflow-gage sites were used owing to the uncertainty associated with implementing correlations in flow between sites, and no sites containing minimum flows of zero were included in the analysis. The 7-, 14-, and 30-consecutive-day low-flow discharges for annual non-exceedance probabilities (ANPs) of 50, 10, and 5 percent (corresponding to the 2-, 10-, and 20-year recurrence intervals, respectively) were calculated using the USGS SW Toolbox (Kiang and others, 2018). Forty-five of these streamflow-gage sites were subsequently used to develop low-flow regression equations following analyses of redundancy and regulation as described in the sections below. Note that although several sites included in the analyses exhibit infrequent and intermittent periods of recorded stage data that are affected by tidal influences, the published daily discharge data associated with those sites (and used in the analyses) describe computed flows (and flow statistics) that are not affected by the tidally influenced stage data. Flow statistics are provided for sites included in the regression analyses as well as those not suitable for inclusion as a result of regulation or redundancy. At-site, regression-based and weighted flow statistics are provided for sites included in regression equation development, whereas only at-site statistics are provided for sites not included in regression equation development. Weighted flow statistics were calculated as in the section “Procedures for Weighting with Regional Regression Equations.” At-site, regression-based and weighted estimates of low-flow statistics, along with basin characteristics, can be found in “Low flow estimates” and “Low basin stats” in Hammond (2021a).
Sample Adjustments
Adjustments to the dataset were made based on analysis of the degree of watershed regulation or any redundancy among sites that could influence the relations determined from the regression analysis. The process used for removal of streamflow-gage sites as a result of regulation and redundancy are discussed below.
Removal of Streamflow-Gage Sites Owing to Regulation
Sixty-eight streamflow-gage sites were evaluated for possible regulation that could affect the analysis of low-flow characteristics and frequency. The data from 27 of these sites showed possible effects on flow that required further investigation and verification.
Basins were evaluated for flow regulation using the USGS GAGES II dataset (Falcone, 2017) and other datasets that represent flow-accumulated attributes. After assessment of basin characteristics including (1) drainage area; (2) stream density; (3) percent of watershed area covered by lakes, ponds, and reservoirs; (4) base-flow index; (5) power generation capacity; (6) basin storage; and (7) high-density development, the GAGES II attributes for freshwater withdrawal and National Inventory of Dam storage accumulated to NHDPlus version 2.1 (Wieczorek and others, 2018) were chosen to broadly characterize basin regulation. Streamflow-gage sites with more than 1,000 acre-feet of reservoir storage volume and more than 1,200 megaliters per square kilometer per year of freshwater withdrawal were identified and marked as locations with potentially significant regulation effects. Individual state records of permitted effluent were not used to screen sites in this study.
Published site data in the USGS NWIS database were also consulted. Consideration was given to effects from irrigation and diversions, streamflow augmentation, tidal influences, proximity of sites to impoundments or reservoirs, or if sites were located on lake outlets where streamflow is controlled by gates or valves. Reports from other low-flow investigations for this study area and adjacent areas were also consulted to aid in determining suitability of sites for the analysis (Carpenter and Hayes, 1996; Stuckey and Roland, 2011; Watson and McHugh, 2014). Twenty-one of the 27 streamflow-gage sites were eliminated from the low-flow analysis owing to various regulation effects, based on evaluation of the GAGES II variables and analysis of data from the sites.
Removal of Streamflow-Gage Sites Owing to Redundancy
Twenty possible instances of redundancy were identified in the recorded low-flow data from 19 sites. Of the 19 sites identified, 13 had already been eliminated from the low-flow analysis based on watershed regulation. Decisions regarding redundancy for the remaining six sites were made based on length of data record and drainage-area size, period of the data record, any breaks in the continuous record period, and how well the low-flow data record represented current watershed conditions at each site. Based on these considerations, two of the remaining six sites being evaluated were eliminated from the low-flow analysis owing to redundancy. The final number of streamflow-gage sites used for low regression equation development in each state and region is provided in table 11, and a summary of the drainage areas for these streamflow-gage sites is provided in table 12. The ranges of basin characteristics used to develop the equations for each subregion are provided in table 13.
Development of Regression Equations
Explanatory Variable Selection for Low-Flow Estimation
Each of the 32 basin characteristics in table 2 were considered for inclusion as explanatory variables in the low-flow magnitude estimating equations. Prior to identifying the strongest low-flow magnitude predictor variables, a multicollinearity matrix was calculated for all candidate variables to identify strong correlations between variables. The process and parameters used in the investigation of multicollinearity between potential explanatory variables was described previously in the section “Explanatory Variable Selection for Peak-Flow Estimation.” In each case of multicollinearity between two variables, the simpler variable with more direct causal connection to low-flow magnitude was retained for further consideration. Following the multicollinearity analysis, a subset of 20 basin characteristics remained for consideration using an iterative ordinary least-squares regression approach to determine the best set of basin-characteristic variables to include in the low-flow magnitude estimation equations.
Ordinary Least-Squares Regression for Low-Flow Estimation
OLS regression was used to select basin characteristics as explanatory variables for estimating low flows associated with each selected combination of duration and ANP, and to assess whether developing separate low-flow estimation equations in each study subregion based on physiographic provinces (as was done in prior reports) remains a justifiable approach. The mathematical basis of OLS, along with the accompanying assumptions and constraints, can be reviewed in the previous section titled “Ordinary Least-Squares Regression for Peak-Flow Estimation.”
Initial OLS regression equations were developed for the 7-day duration, 10-percent ANP (7Q10) using 20 explanatory variables for 45 streamflow-gage sites in the study area. The 7Q10 was selected for optimizing the selection of explanatory variables because it is the duration and ANP discharge combination most often used by water managers, engineers, and planners (Pryce, 2004). An iterative OLS regression approach using the allReg function from the USGS “smwrStats” R package (R Core Team, 2020; Lorenz, 2020) was utilized to examine the best subsets of explanatory variables for each duration-ANP combination following the methodology suggested by Helsel and others (2020). A maximum of five concurrent variables for each duration-ANP combination were considered for use in low-flow estimation. Separate OLS models for the entire study area, as well as for each potential subregion (Coastal Plain, Piedmont), were developed using this method. Candidate regression models in each case were evaluated with respect to several metrics, including (1) maximizing the coefficient of determination (R2) and adjusted coefficient of determination (R2 adj), (2) minimizing residual standard error, (3) minimizing Mallow’s Cp, and (4) minimizing the predicted residual sum of squares (PRESS).
Additionally, low-flow magnitude data for each streamflow-gage site and each combination of duration and ANP were analyzed to determine whether they exerted undue leverage and influence during variable selection using the iterative OLS approach. Although data from several sites displayed either influence or leverage that exceeded recommended values, no sites were removed, as the watershed properties and low-flow characteristics for the sites identified were not unrepresentative of those common in the study area, and no other disqualifying rationale was identified.
Weighted Least-Squares Regression for Low-Flow Estimation
Weighted least-squares (WLS) multiple-linear regression was used to compute the final regression coefficients and measures of accuracy for the low-flow regression equations. Unlike OLS, WLS can account for the heterogeneous uncertainties associated with the computed at-site low-flow statistics used to develop the estimation equations (Farmer and others, 2019). The method weights observations in proportion to the variance of the time-series data used to compute at-site statistics or some surrogate of the variance such as the length of the at-site data record. Giving additional weight to data with less uncertainty produces more accurate estimation equations than would be the case using OLS regression. Although drainage area and percent of the watershed with soil D are chosen for both Piedmont and Coastal Plain equations, the variable exponents and equation coefficient differ, suggesting somewhat different relations between the variables and low flow in the two regions.
WLS regression equations for Coastal Plain and Piedmont subregions are as follows:Coastal Plain
PiedmontTable 11.
Number of streamflow-gage sites included in the low-flow regression analyses by subregion and state.[POR, period of record; ≥, greater than or equal to; DE, Delaware; MD, Maryland; NJ, New Jersey; PA, Pennsylvania]
Table 12.
Summary of drainage area, number of streamflow-gage sites, and average years of record used in the low-flow regression analyses for Delaware.[mi2, square miles; --, no data]
Table 14.
Average standard errors of estimate and prediction for the best low-flow regression equations, by subregion in Delaware.[N, the averaging period of the low flow statistic in days]
Table 15.
Values needed to determine 90-percent prediction intervals for the best low-flow regression equations, by subregion in Delaware.[t, the critical value from Student’s t-distribution for the 90-percent probability; MEV, regression model error variance; U, covariance matrix of model coefficients; Intercept, y-axis intercept of regression equation; N, the averaging period of the low flow statistic in days; --, not applicable]
Table 16.
Mean and median percent differences between low-flow magnitude statistics computed from recorded at-site data for streamflow-gage sites included in this study and in Carpenter and Hayes (1996).[N, the averaging period of the low flow statistic in days; --, no data]
Accuracy and Limitations of Low-Flow Regression Equations
As with peak flows, the traditional measures of the accuracy of low-flow regression equations are the standard error of estimate and the standard error of prediction. Average standard errors of estimate and prediction associated with equations 39 through 56 are shown in table 14. The statistical parameters needed to perform prediction-interval computations for low-flow magnitude estimates can be found in table 15, and the mean and median percent differences between low-flow magnitude statistics computed from recorded at-site data for streamflow-gage sites included in this study and the previous study can be found in table 16.
The regression equations can be used to estimate low-flow magnitudes for ungaged sites with natural flow conditions in Delaware. The equations should not be applied to streams in tidal areas, or to streams with substantial basin storage or flow regulation upstream from sites of interest. Applicable drainage areas in the Coastal Plain region will be particularly limited by tidal influence.
The accuracy of the regression equations is known only within the range of basin characteristics that were used to develop the equations. The equations can be applied to ungaged sites with basin characteristics that are not within the range of applicability, but the accuracy of the resulting estimates will be unknown (Ries and Dillow, 2006).
Note that the potential effects of basin development, trends, and regionalized skews on low-flow estimates obtained using the methods described in this report were not evaluated as a part of the study described herein. Further research to understand and define such potential effects may be warranted.
Procedures for Estimating Low-Flow Statistics at Gaged and Ungaged Sites
For gaged streams, the magnitude analysis developed from at-site data records generally provides the best estimates of low-flow characteristics at the streamflow-gage sites (see “Low flow estimates” in Hammond [2021a]). For ungaged sites on ungaged streams with no current or historical at-site data record, the best estimates of low-flow characteristics can be obtained from the new low-flow estimation equations presented in this report.
Procedures for estimating low-flow characteristics at ungaged sites upstream and downstream from streamflow-gage sites were previously presented in Carpenter and Hayes (1996). The method is based on three basic assumptions: (1) if two independent estimates of a streamflow statistic are available, a properly weighted average of the independent estimates will provide an estimate that is more accurate than either of the two independent estimates (Tasker, 1975; Carpenter and Hayes, 1996; Ries and Dillow, 2006); (2) the best estimate of a low-flow statistic can be obtained by first estimating the discharge from the appropriate regional estimation equation and then adjusting the result to reflect available data and information at a streamflow-gage site located nearby on the same stream, and on the basis of a drainage-area ratio between the two sites; and (3) the at-site value based on the magnitude analysis of site records is the best estimate of a low-flow characteristic at a streamflow-gage site. The different weighting techniques for estimation of low flows at ungaged sites upstream and downstream from a streamflow-gage site were previously described and demonstrated by Carpenter and Hayes (1996) and are briefly summarized below.
Sites Upstream from Streamflow-Gage Sites
The transfer equation for estimating low flows upstream from streamflow-gage sites is based on an additional assumption that the difference between an at-site flow characteristic (based on the at-site data record) and the corresponding estimated flow characteristic (based on the regional estimation equation) at a streamflow-gage site is affected equally by all parts of the upstream drainage basin (Carpenter and Hayes, 1996).
The drainage-area ratio (RA) is defined as follows:
whereAu
is the drainage area at the selected ungaged site; and
Ag
is the drainage area at the streamflow-gage site.
The discharge for a selected site upstream from a streamflow-gage site, where the RA value is between 0 and 1.0, is computed by the equation
whereQf
is the final weighted estimate of discharge at the selected ungaged site on the gaged stream;
Qu
is the discharge at the selected ungaged site as determined from the appropriate regional estimation equation;
Qo
is the discharge at the streamflow-gage site as determined from the streamflow-gage data (see “Low flow estimates” in Hammond [2021a]);
Qe
is the discharge at the streamflow-gage site as determined from the appropriate regional estimation equation; and
ΔQg
is the discharge at the streamflow-gage site as determined from the streamflow-gage site data, minus discharge at the streamflow-gage site as determined from the regional estimation equation; and
Qo and Qe
are as defined in equation 58.
Sites Downstream from Streamflow-Gage Sites
The transfer equations for estimating low flows downstream from a streamflow-gage site are based on additional assumptions that (1) the difference between the at-site flow characteristics (based on at-site data records) and the estimated flow characteristics (based on the regional estimation equation) at the streamflow-gage site reflects the effect of upstream conditions that is expected to persist to some extent downstream, though gradually diminishing, and (2) that the increment of upstream flow (Qo –Qe, variables as defined above) apparent at the streamflow-gage site, continues downstream essentially undiminished to the mouth of the stream and is not arbitrarily removed from the system at any point (Carpenter and Hayes, 1996).
The assumed persistent effect of upstream flow conditions on the downstream low-flow characteristics is based on the probability that drainage basin and geologic characteristics will be similar nearby upstream and downstream from any given point (Carpenter and Hayes, 1996). The incremental rate, which reflects the upstream conditions, is assumed to diminish linearly from [(Qo – Qe)/Ag] at the streamflow-gage site to zero at some point downstream. The total incremental flow accumulated at the point Ag downstream is then assumed to stay in the stream and continue to flow downstream to the mouth, but without any further accretion (Carpenter and Hayes, 1996).
The discharge for a selected site downstream from a streamflow-gage site (where RA > 1.0) is then computed as follows:for 1.0 < RA < 2.0
and for RA > 2.0These equations are mathematical representations of the low-flow response-pattern assumptions listed above (Carpenter and Hayes, 1996). In the absence of any additional information about a selected drainage basin, the assumptions for development and use of the equations were found to be reasonable, based on verification tests that were conducted by Carpenter and Hayes (1996).
Estimation Examples
In this section, step-by-step examples are provided that demonstrate how to compute estimated values for low-flow characteristics. The three examples are based on the methods described in the previous section. Basin characteristics that are needed for use in the estimation equations can be determined from StreamStats for ungaged sites, or as described in table 2 for streamflow-gage sites.
Ungaged Site on Ungaged Stream
Problem: Estimate the 7-day, 2-year low-flow discharge of Rocky Run at US-202 (Concord Pike) in Wilmington, New Castle County, Delaware. This site is in the Piedmont subregion.
-
1. Obtain the DRNAREA in square miles and SOILD percentage for the selected site by use of StreamStats:
Using equation 48 (Piedmont region),
7Q2 = (10-0.052)(DRNAREA1.077)((SOILD + 1)-0.439)
By substitution,
7Q2 = (0.887)(0.86)1.077(40.5 + 1)-0.439
7Q2 = (0.887)(0.850)(0.195)
7Q2 = 0.15 ft3/s
Ungaged Site Upstream from a Streamflow-Gage Site
Problem: Estimate the 7-day, 10-year low-flow discharge of Nanticoke River at Reddon Road, near Bridgeville, Delaware, about 1.7 mi upstream from streamflow-gage site 01487000. This site is in the Coastal Plain subregion.
-
1. Obtain the DRNAREA in square miles and SOILD percentage for Nanticoke River at Reddon Road (ungaged site) by use of StreamStats:
drainage area = Au = 33.5 mi2, soil type D percentage = 49.5 percent
-
2. Obtain the DRNAREA in square miles and SOILD percentage for the streamflow-gage site on Nanticoke River near Bridgeville (station 01487000) from table “Low basin stats” in Hammond (2021a):
drainage area = Ag = 73.1 mi2, soil type D percentage = 42.7 percent
-
3. Obtain the 7-day, 10-year low-flow discharge for Nanticoke River at the streamflow-gage site from table “Low flow estimates” in Hammond (2021a):
Qo = 14.9 ft3/s
-
4. Calculate the estimated 7-day, 10-year discharge for Nanticoke River at the streamflow-gage site by use of the regional estimation equation. Using equation 40 (Coastal Plain region):
Qe = 7Q10 = (10-0.342)(DRNAREA1.357)((SOILD + 1)-0.745)
By substitution,
Qe = 7Q10 = (0.455)(73.1)1.357(42.7 + 1)-0.745
Qe = 7Q10 = (0.455)(338.3)(0.060)
Qe = 7Q10 = 9.2 ft3/s
-
5. Calculate the estimated 7-day, 10-year discharge for Nanticoke River at the selected ungaged site by use of the regional estimation equation. Using equation 40 (Coastal Plain region):
Qu = 7Q10 = (10-0.342)(DRNAREA1.357)((SOILD + 1)-0.745)
By substitution,
Qu = 7Q10 = (0.455)(33.5)1.357(49.5 + 1)-0.745
Qu = 7Q10 = (0.455)(117.4)(0.054)
Qu = 7Q10 = 2.88 ft3/s
-
6. Determine the difference between the at-site and the estimated discharge for Nanticoke River at the streamflow-gage site. Using equation 59:
ΔQg = Qo – Qe
By substitution,
ΔQg = 14.9 - 9.2
ΔQg = 5.7 ft3/s
-
7. Determine the ratio of the drainage area at the ungaged site to the drainage area at the streamflow-gage site. Using equation 57:
RA = Au/Ag
By substitution,
RA = (33.5/73.1)
RA = 0.46
-
8. Based on the RA value being between 0 and 1.0, the final adjusted 7-day, 10-year low-flow discharge is determined by equation 58:
Qf = Qu(Qo/Qe)
By substitution,
Qf = (2.88)(14.9/9.2)
Qf = 4.66 ft3/s
Ungaged Site Downstream from a Streamflow-Gage Site
Problem: Estimate the 30-day, 20-year low-flow discharge of Silver Lake Tributary at Delaware State Route 71, approximately 0.7 mi downstream from streamflow-gage site 01483155. This site is in the Coastal Plain subregion.
-
1. Obtain the DRNAREA in square miles and SOILD percentage for Silver Lake Tributary at Delaware State Route 71 (ungaged site) by use of StreamStats:
drainage area = Au = 3.25 mi2, soil type D percentage = 5.5 percent
-
2. Obtain the DRNAREA in square miles and SOILD percentage for the streamflow-gage site on Silver Lake Tributary at Middletown (01483155) from table “Low basin stats” in Hammond (2021a):
drainage area = Ag = 2.00 mi2, soil type D percentage = 1.5 percent
-
3. Obtain the 30-day, 20-year low-flow discharge for Silver Lake Tributary at the streamflow-gage site from table “Low flow estimates” in Hammond (2021a):
-
4. Calculate the estimated 30-day, 20-year low-flow discharge for Silver Lake Tributary at the streamflow-gage site by use of the regional estimation equation. Using equation 56 (Coastal Plain region):
Qe = 30Q20 = (10-0.288)(DRNAREA1.301)((SOILD + 1)-0.698)
By substitution,
Qe = 30Q20 = (0.515)(2.0)1.301(1.5 + 1)-0.698
Qe = 30Q20 = (0.515)(2.464)(0.528)
Qe = 30Q20 = 0.67 ft3/s
-
5. Calculate the estimated 30-day, 20-year low-flow discharge for Silver Lake Tributary at the selected ungaged site by use of the regional estimation equation. Using equation 56 (Coastal Plain subregion):
Qu = 30Q20 = (10-0.288)(DRNAREA1.301)((SOILD + 1)-0.698)
By substitution,
Qu = 30Q20 = (0.515)(3.25)1.301(5.5 + 1)-0.698
Qu = 30Q20 = (0.515)(4.634)(0.271)
Qu = 30Q20 = 0.65 ft3/s
-
6. Determine the difference between the at-site and the estimated discharge for Silver Lake Tributary at the streamflow-gage site. Using equation 59:
ΔQg = Qo – Qe
By substitution,
ΔQg = 0.90 - 0.67
ΔQg = 0.23 ft3/s
-
7. Determine the ratio of the drainage area at the ungaged site to the drainage area at the streamflow-gage site. Using equation 57:
RA = Au/Ag
By substitution,
RA = (3.25/2.00)
RA = 1.63
-
8. Based on the RA value being between 1.0 and 2.0, the final adjusted 30-day, 20-year low-flow discharge at the ungaged site is determined by equation 60:
Qf = Qu +RA(ΔQg)(1.25 - 0.25RA)
By substitution,
Qf = 0.65 + 1.63(0.23)(1.25 - 0.25 x 1.63)
Qf = 0.65 + 0.375(1.25 - 0.41)
Qf = 0.65 + 0.375(0.84)
Qf = 0.65 + 0.32
Qf = 0.97 ft3/s
StreamStats
StreamStats is a map-based USGS web application that makes it easy for users to obtain streamflow statistics and basin characteristics for USGS streamflow-gage sites and ungaged sites of interest (Ries and Dillow, 2006). It uses digital map data and a geographic information system (GIS) to automatically determine the basin characteristics for ungaged sites. Ries and others (2004) provided a detailed description of the application. StreamStats is typically developed as a state-by-state application using data, statistics, and regression equations developed regionally or locally, but it is implemented in the national application.
StreamStats was originally implemented for Delaware in 2006 and has been updated for this investigation. Updated basin characteristics for the study area were prepared collaboratively between staff from the Delaware Geological Survey and USGS (Warner and others, 2021a,b). Users can access all of the flow-magnitude statistics and basin characteristics published in this report for the streamflow-gage sites used in this study by selecting the streamflow-gage site on the map shown in the StreamStats user interface. Users can also obtain estimates for ungaged sites in Delaware by selecting a site of interest on the map (Ries and Dillow, 2006).
The USGS StreamStats web page provides information on the StreamStats application, documentation, news and status on the current version, and frequently asked questions. Complete instructions for using StreamStats are also provided through links on the StreamStats application site at https://streamstats.usgs.gov/ss/. The application site provides a help link with tabs to (1) the online StreamStats user manual, (2) frequently asked questions, and (3) an online form for submitting a support request to the USGS StreamStats team. The application site also provides a link with tabs that inform users about (1) the current version of the StreamStats application (version 4.4.0, March 2021); (2) state and regional information available as part of the latest version; (3) news that lists recently implemented updates as part of different state efforts; and (4) USGS data, software, and product name disclaimers.
Summary
This study was conducted by the U.S. Geological Survey (USGS) in cooperation with the Delaware Geological Survey and the Delaware Department of Transportation. The report presents (1) estimates of peak-flow magnitude statistics and basin characteristics for 121 sites in and within 25 miles (mi) of Delaware, and (2) estimates of low-flow magnitude statistics and basin characteristics for 68 sites in and within 25 mi of Delaware. Ninety-four of the peak-flow sites and 45 of the low-flow sites were used to generate regional regression equations. It also describes methods for estimating peak-flow and low-flow magnitudes at both streamflow-gage sites and ungaged sites in Delaware.
Statistically significant upward trends were found in the annual time series of peak flows for 18 of the 121 streamflow-gage sites analyzed for this study, with 9 sites ultimately removed owing to trends that were robust to adjustments to the start and end of the period used for trend analysis. An analysis of station skews resulted in a new generalized-skew value defined for the entire study region, 0.264, owing to a lack of significant difference between station skews at long record sites using the nonparametric Wilcoxon rank sum test. This new generalized-skew value was used to determine the peak flow magnitude values from the systematic records for the streamflow-gage sites presented in this report. Discharge estimates determined from the systematic record for this study were, on average, larger than those from the previous study, especially for the Coastal Plain region. The changes are due partly to the longer periods of record and partly the updated methods from Bulletin 17C using the Expected Moments Algorithm (England and others, 2019).
Two sets of regression equations are presented for estimating peak flows for return periods ranging from 2 to 500 years (50- to 0.2-percent annual-exceedance probability) at ungaged sites in Delaware. Separate sets of equations were developed for the Coastal Plain and the Piedmont hydrologic regions. The explanatory variables in the equations for the Coastal Plain include drainage area, percent of drainage basin covered by soil type A, and mean basin slope. The explanatory variables in the equations for the Piedmont include drainage area, percent of basin covered by soil type D, percent of basin covered by impervious surfaces, and percent storage (areas of wetlands and waterbodies) determined from the National Hydrography Dataset.
Peak flow average standard errors of prediction for the regression equations ranged from 27 to 44 percent for the Piedmont, and from 61 to 74 percent for the Coastal Plain. Although they are not directly comparable because of differences in the stations used and their lengths of record, the errors associated with the new equations are lower than those presented in the previous report for the Piedmont and higher for the Coastal Plain. The differences in error cannot be fully explained, but it is likely that the new average standard errors of prediction give a more precise indication of the true errors associated with estimates from the regression equations than the average standard errors of prediction given for the previous equations. Discharge estimates determined from the systematic record for this study were, on average, smaller than those from the previous study for the Piedmont and larger than those from the prior report in the Coastal Plain, especially for gages with additional years of record since the prior report. The changes are a result of the longer periods of record available for analysis in this report.
Similar to the peak flow analysis, two sets of regression equations are presented for estimating low flows separately for the Coastal Plain and Piedmont hydrologic regions, with return periods ranging from 2 to 20 years and for 7-, 14-, and 30-day periods at ungaged sites in Delaware. The explanatory variables in the equations for the Coastal Plain and Piedmont include drainage area and the percent of drainage basin covered by soil type D. Average standard errors of prediction for the best regression equations ranged from 34 to 74 percent for the Piedmont, and from 58 to 131 percent for the Coastal Plain. These standard errors are larger than those for the peak flow regressions, but comparable to errors for regression equations developed by the USGS in other states.
The report describes methods for obtaining improved peak-flow and low-flow magnitude estimates for streamflow-gage sites and ungaged sites at defined frequencies and durations. Improved estimates for streamflow-gage sites are obtained by computing the weighted average of the estimates computed using recorded at-site data and the estimates obtained from the regression equations. Improved estimates for ungaged sites on a gaged stream can be obtained by combining the estimates from the regression equations with estimates determined by applying a flow-per-unit-area adjustment to at-site flow statistics from an upstream or downstream streamflow-gage site based on the drainage area for the ungaged site, and weighting the two estimates according to the difference in drainage area between the ungaged site and the streamflow-gage site.
The equations developed during this study have been incorporated into the USGS StreamStats program. The StreamStats program is a web application that can provide the streamflow statistics and basin characteristics for streamflow-gage sites when users select a site location in the user interface. StreamStats can also compute basin characteristics and provide estimates of streamflow statistics for ungaged sites when users select the location of a site along any stream in Delaware.
Acknowledgments
The authors would like to thank Daniel M. Wagner, Andrea G. Veilleux, and Michelle P. Katoski of the U.S. Geological Survey for assistance, advice, and support with technical issues and data interpretation.
The U.S. Geological Survey SWToolbox Team is acknowledged for technical assistance in applying a new workflow for computation of low-flow statistics at streamflow-gage sites based on at-site data, with special thanks to Julie E. Kiang and Amy R. McHugh. Thank you to Toby Feaster and Thomas Suro for providing detailed reviews of this report.
References Cited
Carpenter, D.H., and Hayes, D.C., 1996, Low-flow characteristics of streams in Maryland and Delaware: U.S. Geological Survey Water-Resources Investigations Report 94–4020, 113 p., accessed September 2020 at https://pubs.er.usgs.gov/publication/wri944020.
Cohn, T.A., England, J.F., Berenbrock, C.E., Mason, R.R., Stedinger, J.R., and Lamontagne, J.R., 2013, A generalized Grubbs-Beck test statistic for detecting multiple potentially influential low outliers in flood series: Water Resources Research, v. 49, no. 8, p. 5047–5058, accessed September 2020 at https://doi.org/10.1002/wrcr.20392.
Cohn, T.A., Lane, W.L., and Baier, W.G., 1997, An algorithm for computing moments-based flood quantile estimates when historical flood information is available: Water Resources Research, v. 33, no. 9, p. 2089–2096, accessed September 2020 at https://doi.org/10.1029/97WR01640.
Delaware State Climatologist, 2021, Delaware’s Climate: Delaware Climate Office web page, accessed March 9, 2021, at https://climate.udel.edu/delawares-climate/.
Doheny, E.J., and Banks, W.S.L., 2010, Selected low-flow frequency statistics for continuous-record streamgage locations in Maryland, 2010: U.S. Geological Survey Open-File Report 2010–1310, 22 p., accessed September 2020 at https://doi.org/10.3133/ofr20101310.
Dudley, R.W., Hirsch, R.M., Archfield, S.A., Blum, A.G., and Renard, B., 2020, Low streamflow trends at human-impacted and reference basins in the United States: Journal of Hydrology (Amsterdam), v. 580, p. 124254, accessed September 2020 at https://doi.org/10.1016/j.jhydrol.2019.124254.
England, J.F., Jr., Cohn, T.A., Faber, B.A., Stedinger, J.R., Thomas, W.O., Jr., Veilleux, A.G., Kiang, J.E., and Mason, R.R., Jr., 2019, Guidelines for determining flood flow frequency—Bulletin 17C (ver. 1.1, May 2019): U.S. Geological Survey Techniques and Methods, book 4, chap. B5, 148 p., accessed September 2020 at https://doi.org/10.3133/tm4B5.
Falcone, J.A., 2017, U.S. Geological Survey GAGES II time series data from consistent sources of land use, water use, agriculture, timber activities, dam removals, and other historical anthropogenic influences: U.S. Geological Survey data release, accessed September 2020 at https://doi.org/10.5066/F7HQ3XS4.
Farmer, W.H., 2017, WREG: USGS WREG (v. 2.02): U.S. Geological Survey R package web page, accessed September 2020 at https://rdrr.io/github/USGS-R/WREG/
Hammond, J.C., 2021a, Magnitude and frequency of peak flows and low flows on nontidal streams in Delaware—Peak and low flow estimates and basin characteristics: U.S. Geological Survey data release, https://doi.org/10.5066/P9B7CUVO.
Hammond, J.C., 2021b, PeakFQ inputs and selected outputs for selected gages in or near Delaware: U.S. Geological Survey data release, https://doi.org/10.5066/P9S3LNSH.
Helsel, D.R., Hirsch, R.M., Ryberg, K.R., Archfield, S.A., and Gilroy, E.J., 2020, Statistical methods in water resources: U.S. Geological Survey Techniques and Methods, book 4, chapter A3, 458 p., accessed September 2020 at https://doi.org/10.3133/tm4A3. [Supersedes USGS Techniques of Water-Resources Investigations, book 4, chapter A3, version 1.1.]
Kiang, J.E., Flynn, K.M., Zhai, T., Hummel, P., and Granato, G., 2018, SWToolbox—A surface-water toolbox for statistical analysis of streamflow time series: U.S. Geological Survey Techniques and Methods, book 4, chap. A–11, 33 p., accessed September 2020 at https://doi.org/10.3133/tm4A11.
Lorenz, D.L., 2020, smwrStats—An R package for the analysis of hydrologic data (ver. 0.7.5): U.S. Geological Survey R package web page, accessed September 2020 at https://github.com/USGS-R/smwrStats/blob/master/R/smwrStats-package.R.
Macrotrends, 2021, Delaware population 1900–2020: Macrotrends web page, accessed March 9, 2021, at https://macrotrends.net/states/delaware/population.
R Core Team, 2020, R—A language and environment for statistical computing: R Foundation for Statistical Computing web page, accessed September 2020 at https://www.R-project.org/.
Ries, K.G., III, 2006, Selected streamflow statistics for streamgaging stations in Northeastern Maryland, 2006: U.S. Geological Survey Open-File Report 2006–1335, 16 p., accessed September 2020 at https://pubs.usgs.gov/of/2006/1335/.
Ries, K.G., III, and Dillow, J.J.A., 2006, Magnitude and frequency of floods on nontidal streams in Delaware: U.S. Geological Survey Scientific Investigations Report 2006–5146, 59 p., accessed September 2020 at https://pubs.usgs.gov/sir/2006/5146/.
Ries, K.G., III, Steeves, P.A., Coles, J.D., Rea, A.H., and Stewart, D.W., 2004, StreamStats—A U.S. Geological Survey web application for stream information: U.S. Geological Survey Fact Sheet 2004–3115, 4 p., accessed September 2020 at https://doi.org/10.3133/fs20043115.
Sando, S.K., and McCarthy, P.M., 2018, Methods for peak-flow frequency analysis and reporting for streamgages in or near Montana based on data through water year 2015: U.S. Geological Survey Scientific Investigations Report 2018–5046, 39 p., accessed September 2020 at https://doi.org/10.3133/sir20185046.
Southard, R.E., and Veilleux, A.G., 2014, Methods for estimating annual exceedance-probability discharges and largest recorded floods for unregulated streams in rural Missouri: U.S. Geological Survey Scientific Investigations Report 2014–5165, 39 p., accessed September 2020 at http://dx.doi.org/10.3133/sir20145165.
Stuckey, M.H., and Roland, M.A., 2011, Selected streamflow statistics for streamgage locations in and near Pennsylvania: U.S. Geological Survey Open-File Report 2011–1070, 88 p., accessed September 2020 at https://pubs.er.usgs.gov/publication/ofr20111070.
Uhl, J.H., Leyk, S., McShane, C.M., Braswell, A.E., Connor, D.S., and Balk, D., 2021, Fine-grained, spatiotemporal datasets measuring 200 years of land development in the United States: Earth System Science Data, v. 13, no. 1, p. 119–153, accessed September 2020 at https://doi.org/10.5194/essd-13-119-2021.
U.S. Census Bureau, 2010, 2010 Census: U.S. Census Bureau web page, accessed January 1, 2013, at https://www.census.gov/2010census/data/.
Veilleux, A.G., Cohn, T.A., Flynn, K.M., Mason, R.R., Jr., and Hummel, P.R., 2014, Estimating magnitude and frequency of floods using the PeakFQ 7.0 program: U.S. Geological Survey Fact Sheet 2013–3108, 2 p., accessed September 2020 at https://doi.org/10.3133/fs20133108.
Wagner, D.M., Krieger, J.D., and Veilleux, A.G., 2016, Methods for estimating annual-exceedance probability discharges for streams in Arkansas, based on data through water year 2013: U.S. Geological Survey Scientific Investigations Report 2016–5081, 136 p., accessed September 2020 at https://doi.org/10.3133/sir20165081.
Warner, D.L., O’Hara, B., Callahan, J.A., Kolb, K.R., Steeves, P.A., and Nardi, M.R., 2021a, Basin characteristics rasters for Delaware StreamStats 2020: U.S. Geological Survey data release, https://doi.org/10.5066/P99602LW.
Warner, D.L., O’Hara, B., Callahan, J.A., Kolb, K.R., Steeves, P.A., and Nardi, M.R., 2021b, Fundamental dataset rasters for Delaware StreamStats 2020: U.S. Geological Survey data release, https://doi.org/10.5066/P935LVAD.
Watson, K.M., and McHugh, A.R., 2014, Regional regression equations for the estimation of selected monthly low-flow duration and frequency statistics at ungagged sites on streams in New Jersey: U.S. Geological Survey Scientific Investigations Report 2014–5004, 59 p., accessed September 2020 at https://pubs.usgs.gov/sir/2014/5004/.
Wieczorek, M.E., Jackson, S.E., and Schwarz, G.E., 2018, Selected attributes for NHDPlus version 2.1 reach catchments and modified network routed upstream watersheds for the conterminous United States (ver. 2.0, November 2019): U.S. Geological Survey data release, accessed September 2020 at https://doi.org/10.5066/F7765D7V.
Glossary
- Base flow
The contribution of flow in a stream from groundwater or spring effluent.
- Climatic year
The climatic year is the 12-month period from April 1 through March 31. The climatic year is designated by the calendar year in which it begins. For example, the 12-month period starting on April 1, 1986, and ending on March 31, 1987, is the 1986 climatic year.
- Fall Line
The line marking the point on each stream where the streamflow descends from the eastern section of the Piedmont Physiographic Province to the western Coastal Plain in Maryland, Delaware, and Pennsylvania. The Fall Line is characterized by an abrupt decrease in channel slope in transition between the Piedmont and Coastal Plain Physiographic Provinces.
- Hydraulic conductivity
A measure of how easily water can permeate through soil or through fractures in rock. For this study, hydraulic conductivity was analyzed in units of inches per hour. High values indicate permeable material through which water can pass more easily, and low values indicate material that is less permeable.
- Recurrence interval
As applied to low-flow statistics, the recurrence interval is the average number of years within which the streamflow will be equal to or less than the given statistic on one occasion. As applied to peak-flow statistics, the recurrence interval is the average number of years within which the streamflow will be equal to or exceed the given statistic on one occasion.
- Standardized distance
Standardized distance is defined as the distance between basin centroids in miles divided by the square root of one half the sum of the drainage areas of the two basins in square miles.
- Streamflow-gage site
A particular site on a stream where systematic observations of gage height or discharge are made.
- Water year(s)
Water year is defined as the 12-month period beginning October 1 and ending on September 30. The water year is designated by the calendar year in which it ends. For example, the year beginning October 1, 2016, and ending September 30, 2017, is called water year 2017.
- 7Q2
The lowest 7-day average streamflow that occurs, on average, once every 2 years (having a 50-percent annual non-exceedance probability). All 7-day low-flow streamflow statistics are computed based on the annual 7-day minimum daily streamflow that occurs during each climatic year of the site’s period of continuous record.
- 7Q10
The lowest 7-day average streamflow that occurs, on average, once every 10 years (having a 10-percent annual non-exceedance probability).
- 7Q20
The lowest 7-day average streamflow that occurs, on average, once every 20 years (having a 5-percent annual non-exceedance probability).
- 14Q2
The lowest 14-day average streamflow that occurs, on average, once every 2 years (having a 50-percent annual non-exceedance probability). All 14-day low-flow streamflow statistics are computed based on the annual 14-day minimum daily streamflow that occurs during each climatic year of the site’s period of continuous record.
- 14Q10
The lowest 14-day average streamflow that occurs, on average, once every 10 years (having a 10-percent annual non-exceedance probability).
- 14Q20
The lowest 14-day average streamflow that occurs, on average, once every 20 years (having a 5-percent annual non-exceedance probability).
- 30Q2
The lowest 30-day average streamflow that occurs, on average, once every 2 years (having a 50-percent annual non-exceedance probability). All 30-day low-flow streamflow statistics are computed based on the annual 30-day minimum daily streamflow that occurs during each climatic year of the site’s period of continuous record.
- 30Q10
The lowest 30-day average streamflow that occurs, on average, once every 10 years (having a 10-percent annual non-exceedance probability).
- 30Q20
The lowest 30-day average streamflow that occurs, on average, once every 20 years (having a 5-percent annual non-exceedance probability).
- 50-percent annual-exceedance probability (AEP) flood
A flood peak with a magnitude that, on average, has a 50-percent chance of being equaled or exceeded in any given year. A 50-percent AEP flood has previously been referred to as a 2-year flood. All peak streamflow statistics are computed based on the annual instantaneous peak streamflow that occurs during each water year of the site’s period of continuous record.
- 20-percent annual-exceedance probability (AEP) flood
A flood peak with a magnitude that, on average, has a 20-percent chance of being equaled or exceeded in any given year. A 20-percent AEP flood has previously been referred to as a 5-year flood.
- 10-percent annual-exceedance probability (AEP) flood
A flood peak with a magnitude that, on average, has a 10-percent chance of being equaled or exceeded in any given year. A 10-percent AEP flood has previously been referred to as a 10-year flood.
- 4-percent annual-exceedance probability (AEP) flood
A flood peak with a magnitude that, on average, has a 4-percent chance of being equaled or exceeded in any given year. A 4-percent AEP flood has previously been referred to as a 25-year flood.
- 2-percent annual-exceedance probability (AEP) flood
A flood peak with a magnitude that, on average, has a 2-percent chance of being equaled or exceeded in any given year. A 2-percent AEP flood has previously been referred to as a 50-year flood.
- 1-percent annual-exceedance probability (AEP) flood
A flood peak with a magnitude that, on average, has a 1-percent chance of being equaled or exceeded in any given year. A 1-percent AEP flood has previously been referred to as a 100-year flood.
- 0.5-percent annual-exceedance probability (AEP) flood
A flood peak with a magnitude that, on average, has a 0.5-percent chance of being equaled or exceeded in any given year. A 0.5-percent AEP flood has previously been referred to as a 200-year flood.
- 0.2-percent annual-exceedance probability (AEP) flood
A flood peak with a magnitude that, on average, has a 0.2-percent chance of being equaled or exceeded in any given year. A 0.2-percent AEP flood has previously been referred to as a 500-year flood.
Conversion Factors
U.S. customary units to International System of Units
Datum
Vertical coordinate information is referenced to the North American Vertical Datum of 1988 (NAVD 88).
Horizontal coordinate information is referenced to the North American Datum of 1983 (NAD 83).
Altitude, as used in this report, refers to distance above the vertical datum.
Abbreviations
AEP
annual exceedance probability
ANP
annual non-exceedance probability
EMA
Expected Moments Algorithm
GLS
generalized least-squares
LP3
log-Pearson Type III
MGBT
Multiple Grubbs-Beck Test
NAD 83
North American Datum of 1983
NAVD 88
North American Vertical Datum of 1988
NLCD
National Land Cover Database
NWIS
National Water Information System
OLS
ordinary least-squares
PILF
potentially influential low flow
PRESS
predicted residual sum of squares
USGS
U.S. Geological Survey
VIF
variance inflation factor
WLS
weighted least-squares
WREG
weighted-multiple-linear regression
For additional information, contact:
Director, Maryland-Delaware-D.C. Water Science Center
U.S. Geological Survey
5522 Research Park Drive
Catonsville, MD 21228
or visit our website at https://www.usgs.gov/centers/md-de-dc-water/
Publishing support provided by the West Trenton Publishing Service Center
Disclaimers
Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Although this information product, for the most part, is in the public domain, it also may contain copyrighted materials as noted in the text. Permission to reproduce copyrighted items must be secured from the copyright owner.
Suggested Citation
Hammond, J.C., Doheny, E.J., Dillow, J.J.A., Nardi, M.R., Steeves, P.A., and Warner, D.L., 2022, Peak-flow and low-flow magnitude estimates at defined frequencies and durations for nontidal streams in Delaware: U.S. Geological Survey Scientific Investigations Report 2022–5005, 46 p., https://doi.org/10.3133/sir20225005.
ISSN: 2328-0328 (online)
Study Area
| Publication type | Report |
|---|---|
| Publication Subtype | USGS Numbered Series |
| Title | Peak-flow and low-flow magnitude estimates at defined frequencies and durations for nontidal streams in Delaware |
| Series title | Scientific Investigations Report |
| Series number | 2022-5005 |
| DOI | 10.3133/sir20225005 |
| Publication Date | February 18, 2022 |
| Year Published | 2022 |
| Language | English |
| Publisher | U.S. Geological Survey |
| Publisher location | Reston, VA |
| Contributing office(s) | Maryland-Delaware-District of Columbia Water Science Center |
| Description | Report: vi, 46 p.; 4 Data Releases |
| Country | United States |
| State | Delaware |
| Online Only (Y/N) | Y |
| Additional Online Files (Y/N) | N |


