Development of Projected Depth-Duration-Frequency Curves (2050–89) for South Florida
Links
- Document: Report (23.3 MB pdf) , HTML , XML
- Tables:
- Data Releases:
- USGS data release - Change factors to derive projected future precipitation depth-duration-frequency (DDF) curves at 174 National Oceanic and Atmospheric Administration (NOAA) Atlas 14 stations in central and south Florida
- USGS data release - Change factors to derive projected future precipitation depth-duration-frequency (DDF) curves at 242 National Oceanic and Atmospheric Administration (NOAA) Atlas 14 stations in Florida (ver 2.0, May 2024)
- Download citation as: RIS | Dublin Core
Acknowledgments
The authors gratefully acknowledge the South Florida Water Management District for its cooperation, technical input, and for providing data and funding for this project. We also thank the Sea Level Solutions Center in the Institute of Environment at Florida International University for collaborating on this project and assembling a technical review panel of experts to review and advise the project team on technical aspects of this project. We thank the review panel members for their input and guidance including Dr. Wendy Graham from the University of Florida, Sandra Pavlovic from the National Oceanic and Atmospheric Administration, and Dr. Stacey Archfield from the U.S. Geological Survey (USGS).
We acknowledge the World Climate Research Programme's Working Group on Coupled Modelling, which is responsible for the Coupled Model Intercomparison Project, and we thank the climate modeling groups (listed in table 3 and table 7 of this report) for producing and making available their model output. For the Coupled Model Intercomparison Project, the U.S. Department of Energy's Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. The Multivariate Adaptive Constructed Analogs dataset MACAv2-LIVNEH was produced under the Northwest Climate Adaptation Science Center USGS Grant Number G12AC20495. The dataset MACAv2-METDATA was produced with funding from the Regional Approaches to Climate Change project and the Southeast Climate Science Center. We acknowledge the U.S. Department of Defense Environmental Security Technology Certification Program for its support of the North America Coordinated Regional Downscaling Experiment data archive. We are also grateful to Jupiter Intelligence for providing the files and methodology necessary for implementing their analog resampling and statistical scaling method. We are grateful to the University of California at San Diego for providing data from the Localized Constructed Analogs downscaled climate dataset. We are thankful to Dr. Francesco Serinaldi from Newcastle University in the United Kingdom for providing R code to perform bootstrapping of p-values for goodness-of-fit tests for the generalized extreme value distribution, which we adapted to the generalized Pareto distribution and the constrained maximum likelihood approach used in this project.
We are grateful to the USGS Advanced Research Computing team for providing access to the Yeti supercomputer, which was used for running most of the R code used in this project. Finally, many thanks to USGS colleagues Jory S. Hecht and Stacey Archfield for providing useful comments and suggestions when reviewing this manuscript.
Abstract
Planning stormwater projects requires estimates of current and future extreme precipitation depths for events with specified return periods and durations. In this study, precipitation data from four downscaled climate datasets are used to determine changes in precipitation depth-duration-frequency curves from the period 1966–2005 to the period 2050–89 primarily on the basis of Representative Concentration Pathways 4.5 and 8.5 emission scenarios from the Coupled Model Intercomparison Project Phase 5. The four downscaled climate datasets are (1) the Coordinated Regional Downscaling Experiment (CORDEX) dataset, (2) the Localized Constructed Analogs (LOCA) dataset, (3) the Multivariate Adaptive Constructed Analogs (MACA) dataset, and (4) the Jupiter Intelligence Weather Research and Forecasting Model (JupiterWRF) dataset. Change factors—multiplicative changes in expected extreme precipitation magnitude from current to future period—were computed for grid cells from the downscaled climate datasets containing National Oceanic and Atmospheric Administration Atlas 14 stations in central and south Florida. Change factors for specific durations and return periods may be used to scale the National Oceanic and Atmospheric Administration Atlas 14 historical depth-duration-frequency values to the period 2050–89 on the basis of changes in extreme precipitation derived from downscaled climate datasets. Model culling was implemented to select downscaled climate models that best captured observed historical patterns of precipitation extremes in central and south Florida.
Overall, a large variation in change factors across downscaled climate datasets was found, with change factors generally greater than one and increasing with return period. In general, median change factors were higher for the south-central Florida climate region (1.05–1.55 depending on downscaled climate dataset, duration, and return period) than for the south Florida climate region (1–1.4 depending on downscaled climate dataset, duration, and return period) when considering best performing models for both areas, indicating a projected overall increase in future extreme precipitation events.
Introduction
The planning, permitting, and design of stormwater management projects requires estimates of current and future precipitation amounts, expressed as depths, for specified return periods and durations. The South Florida Water Management District’s (SFWMD’s) permitting manual (SFWMD, 2016) has specific descriptions of precipitation-depth estimates for several return periods and durations, which are used for planning and permitting. Precipitation-depth estimates are used to quantify extreme events, such as an event that has a 1-percent chance of being equaled or exceeded in a given year, alternatively referred to as a “100-year return period.” Precipitation events are also defined by the time period over which the event is measured, such as the total precipitation accrued over a 1-, or 3-, or 7-day window, alternatively referred to as the “duration” of the event. In particular, 1- and 3-day design storms of various return periods are specified in the SFWMD permitting manual and are based on weather-station data prior to 1990 (Trimble, 1990). Through the Flood Protection Level of Service (FPLOS) Program, the SFWMD is evaluating basins in the SFWMD’s 16-county region to determine the current and future level-of-service for flood protection the water management system provides. The flood protection level-of-service is typically defined as the degree of flood protection afforded to an area or community and is often stated in terms of the return period of a precipitation event sufficient to avoid an unacceptable level of flooding. The FPLOS Program, through the application of advanced and integrated hydrologic and hydraulic models, measures the performance of the existing flood control system under current and projected future climate and land development scenarios. In addition to sea-level rise scenarios, the FPLOS Program assessments at the SFWMD require an evaluation of the SFWMD adopted design precipitation-depth estimates to determine if changes are necessary to account for changes in future precipitation patterns. This definition is not consistently applied across the jurisdictions within the region, and the return periods differ on the basis of land use and similar considerations. The FPLOS Program, therefore, uses a suite of six quantitative measures to relate precipitation to (1) depth and duration of overland flooding, (2) discharge capacity and flow containment in canals, and (3) discharge capacity at coastal structures subject to the effects of tide and storm surge.
The U.S. Geological Survey (USGS) has experience working in various areas of climate science, notably in both downscaling and using general circulation model (GCM) output that has been downscaled by other groups for making regional and local climate projections, and in working with the management community to assist with adaptation planning (Terando and others, 2020). To help address the needs of the FPLOS program, the USGS and SFWMD have cooperated on a study to develop depth-duration-frequency (DDF) curves for the basins in the SFWMD that incorporate projections of future climate change across relevant greenhouse-gas (GHG) emission scenarios. The study area is shown in figure 1.
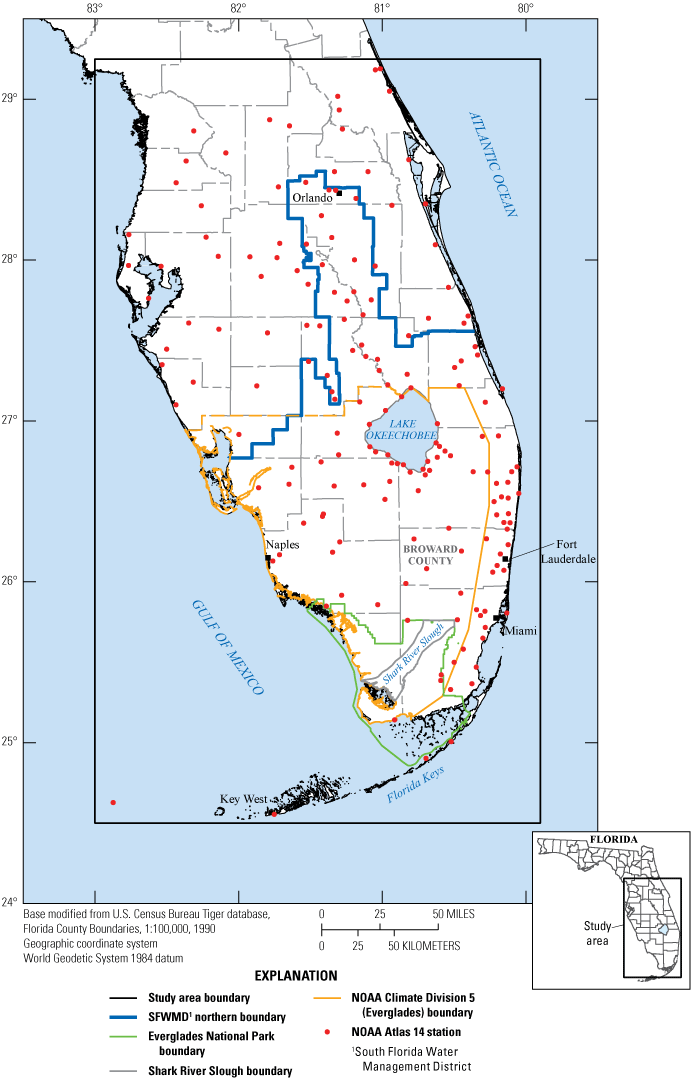
Study area, National Oceanic and Atmospheric Administration (NOAA) Atlas 14 stations, and administrative and geographic features mentioned in this report.
Purpose and Scope
This report documents the development of projected DDF curves (2050–89) for the SFWMD. As part of this study, an ensemble method was used to determine median change factors for precipitation depths as well as inter-model variability at locations throughout central and south Florida. Change factors were determined for durations of 1, 3, and 7 days, and return periods of 5, 10, 25, 50, 100, and 200 years. The 1- and 3-day durations are required for the design and permitting of stormwater systems in the State of Florida. The 7-day duration was included to capture potential future changes in precipitation at the multiday timescale, in particular the possibility of high precipitation caused by stalling storms. Change factors were computed from DDF curves fit to precipitation data from downscaled climate datasets for 40-year periods representing future projected climate for the period 2050–89 (centered on 2070) and historical (retrospective) climate for 1966–2005 for the study area. The start of the historical period coincides with the approximate start of the global warming trend from the 1970s onward (Rahmstorf and others, 2017), and the end was selected to coincide with the end of the Coupled Model Intercomparison Project Phase 5 (CMIP5) historical simulations (2005). The downscaled climate datasets used to derive the change factors as part of this study include the Coordinated Regional Downscaling Experiment (CORDEX), Localized Constructed Analogs (LOCA), Multivariate Adaptive Constructed Analogs (MACA), and JupiterWRF.
Terando and others (2020) recommend that, whenever feasible, the entire range of representative concentration pathway (RCP)-based scenarios be considered when assessing potential future impacts. As part of the FPLOS Program, and with the purposes of planning for future stormwater infrastructure projects with a long design lifetime, the SFWMD is interested in the medium-low (RCP4.5) and high (RCP8.5) emission scenarios that are widely available in downscaled climate datasets. Other climate scenarios such as RCP2.6 are generally not available in downscaled climate datasets and are, therefore, not considered as part of this study. These scenarios are described in more detail in the “Datasets" section.
Perica and others (2013) derived historical DDF curves based on historical observations at meteorological stations in central and south Florida, which are published in National Oceanic and Atmospheric Administration (NOAA) Atlas 14. The DDF curves based on partial-duration series (PDS) from NOAA can be multiplied by the change factors derived in this study to determine potential future extreme precipitation depths for events of a given duration and return period.
Background
The climate of Florida and its relation to remote climate oscillations via atmospheric teleconnections have been studied extensively. In the next sections, factors influencing precipitation extremes in the State as well as projected changes in these extremes, will be discussed.
Factors Influencing Precipitation Extremes in Florida
Kirtman and others (2017) discuss global and local sources and mechanisms for climate variability in Florida across timescales and how they are used to make weather and climate predictions across various timescales. Precipitation in Florida, which is predominantly in the form of rainfall, is influenced by teleconnections to remote climate oscillations, such as the El Niño Southern Oscillation (ENSO) and the Atlantic Multidecadal Oscillation (AMO), and their interactions. The persistence of these oscillations, in particular, the lower frequency decadal modes of variability, allows for seasonal forecasting of temperature and precipitation at various lead times using statistical and dynamical modeling techniques (Kirtman and others, 2017). Modeling tools are also used to simulate the evolution of higher frequency modes of variability such as ENSO. The resulting forecasts are used by water managers to guide operational decisions (Cadavid and others, 1999). For example, ENSO influences dry-season precipitation patterns in Florida by means of changes to the midlatitude subtropical jet streams. During El Niño winters, the subtropical jet stream is displaced toward the Equator and becomes more zonally oriented, which increases the frequency of frontal and cyclone activity along the southeastern United States (Misra and others, 2017). The increased dry-season total and extreme precipitation in Florida during El Niño conditions compared to La Niña conditions (Piechota and Dracup, 1996; Goly and Teegavarapu, 2014) affects water-resource management in south Florida, for example, by increasing net inflows into Lake Okeechobee during El Niño conditions (Obeysekera and others, 2000).
The AMO is thought to be driven by the ocean's thermohaline circulation, also called the “Atlantic Meridional Overturning Circulation,” which includes the Gulf Stream and the Florida Current. During warm AMO phases, it is thought that the thermohaline circulation becomes faster, transporting more warm water from the Equator to high latitudes of the North Atlantic than during cool AMO phases (Enfield and others, 2001). Whether the AMO is internally driven, externally forced by natural and anthropogenic sources of aerosols, or both has been debated (Enfield and Cid-Serrano, 2010; Mann and others, 2020; Mann and others, 2021) with implications for the future predictability of seasonal and extreme precipitation for the State of Florida.
The AMO phase is related to the size of the Atlantic Warm Pool (AWP; Enfield and Cid-Serrano, 2010), which is an area of warm water within the Gulf of Mexico, the Caribbean Sea, and the western tropical North Atlantic. Warm (cool) phases of the AMO are generally associated with large (small) AWPs. It is known that anomalously large AWPs result in weak tropospheric vertical shear in the main development region for hurricanes, increase the moist static instability of the troposphere, and, coupled with a deep warm upper ocean, result in increased hurricane activity in the Atlantic (Wang and others, 2006, 2008a). As described by Donders and others (2011), the size and northward extent of the AWP during the summer determines the summer position of the Intertropical Convergence Zone. As this zone moves north, the North Atlantic High will move northeast, affecting the easterly winds on the southern side of the high and directing moisture to Florida, affecting precipitation in the State. Teegavarapu and others (2013) found an overall increase in the magnitude of precipitation extremes in the warm phase of the AMO for durations longer than 1 day throughout Florida with exceptions in the inland, west coast, and panhandle areas of the State. They found that in northwest, southeast, and central Florida north of Lake Okeechobee (fig. 1), the AMO warm phase influences extreme-precipitation depths for all temporal durations, whereas the AMO cool phase dominates extreme precipitation in the panhandle region of Florida and Key West. In northern Florida, the cool phase of the AMO influences frontal precipitation events during the dry season, causing more extreme events. Teegavarapu and others (2013) show that for durations longer than 6 hours during both phases of the AMO, northwest and southeast Florida consistently exhibit the greatest extreme-precipitation depths within the State. These are regions that tend to experience precipitation events of long duration from tropical storms and hurricanes that are passing through. Teegavarapu and others (2013) also found a general shift in the occurrence of extremes from the latter part of the year in the warm phase of the AMO to the first half of the year during the cool phase. In particular, they found that as the duration increases, extreme events become more frequent from August through October during the AMO warm phase and from June through August during the AMO cool phase. Extreme precipitation events greater than 1 day in duration in their study were associated with increased hurricane landfalls during AMO warm phases (Goldenberg and others, 2001; Poore and others, 2007). Irizarry-Ortiz and others (2013) also found a strong correspondence between the warm phase of the AMO and increased regional precipitation in central and south Florida. Teegavarapu and González-Ramírez (2010) found that approximately 20–50 percent of the extreme precipitation events greater than 2 days in duration in south Florida were associated with hurricane landfalls. Lastly, Goly and Teegavarapu (2014) found that wetter antecedent conditions precede daily extremes during the AMO warm phase compared to the cool phase, with implications for flooding and stormwater design in the State.
Other factors influencing precipitation extremes in Florida include the Pacific Decadal Oscillation (PDO), the North Atlantic Oscillation, the Arctic Oscillation, local sea-surface and land-temperature contrasts, and land use changes. Misra and Mishra (2016) show that sea-surface temperature changes resulting from changes in the Loop and Florida Currents influence summer precipitation over peninsular Florida. As described in Shepherd (2005), various studies have found that the urban heat-island effect enhances warm-season precipitation over and downwind from urban centers, increasing the frequency of occurrence and intensity of heavy precipitation events. A modeling study by Marshall and others (2004) indicates that increased sea-breeze convergence and small increases in convective precipitation over urban areas along the eastern coastal ridge of south Florida are caused by increased sensible heat flux, which appears to be related to urbanization during the period 1900–93.
Projected Changes in Precipitation Extremes: Characteristics and Causes
As discussed by Giorgi (2010), precipitation exhibits a much more complex spatiotemporal variability than temperature, and its changes in response to global warming are highly dependent on how regional circulations change under increased GHG emissions. Regional and local forcings such as land use changes can also affect the precipitation change signal, as demonstrated by Bukovsky and others (2021). For this reason, precipitation projections are much more uncertain than temperature projections at regional and local scales, as evidenced by relatively low consensus in the sign of future precipitation changes across climate models. Projected changes in extreme precipitation tend to be even more uncertain. The response of mean sea levels to global warming is slower than the atmospheric response; therefore, sea-level rise projections over the short-term (on the order of a few decades) tend to have a relatively small range. For example, the Southeast Florida Regional Climate Compact’s (2020) Unified Sea Level Rise Projections for Southeast Florida indicates that local sea-level rise will range between 10–17 inches (in.) by 2040 and 21–54 in. by 2100 compared to year 2000 mean sea level at Key West, Florida. However, in the long-term, sea-level rise projections range between 40 and 136 in. by 2120. The much larger projected range of sea-level rise, especially beyond 2070, stems from uncertainties in future GHG emissions and resulting geophysical effects, most notably the response of the Antarctic and Greenland ice sheets to increased levels of warming.
Seneviratne and others (2012) report that global and regional studies indicate it is likely that the frequency of heavy precipitation or the proportion of total precipitation from heavy precipitation events will increase in the 21st century over many global areas as a result of climate change. They also state that changes in extreme precipitation cannot easily be related to changes in total precipitation because changes can be of opposite sign in some cases. This finding was documented in the Intergovernmental Panel on Climate Change’s (IPCC’s) Fifth Assessment Report (Collins and others, 2013) and further validated in their Sixth Assessment Report (IPCC, 2021, p. 15), which states, “There will be an increasing occurrence of some extreme events unprecedented in the observational record with additional global warming, even at 1.5 degrees Celsius [°C] of global warming. Projected percentage changes in frequency are higher for rarer events (high confidence).”
Using data from observing stations worldwide, Pendergrass and Knutti (2018) show that the median number of the wettest days in a year over which half of annual precipitation falls is 12 days, and that this asymmetric distribution of precipitation will become even more asymmetric because of climate change, with one fifth of the projected increase in rainfall occurring during the wettest 2 days of the year. Collins and others (2013) summarize the science of extreme precipitation events and state that changes in extreme precipitation will be driven by two major mechanisms: (1) a thermodynamic mechanism based on the Clausius-Clapeyron (CC) relation (Wallace and Hobbs, 2006), which specifies that as the air temperature increases, the amount of water vapor in the air at saturation also increases (approximately 7-percent increase per degree Celsius of warming); and (2) a dynamic mechanism that states that extreme precipitation events are controlled by variations in horizontal moisture convergence and associated convection, which would change in a more complicated way as a result of global warming. The conjecture under the thermodynamic mechanism is that, as the climate warms and in the absence of moisture limitation, specific humidity increases according to the CC relation, whereas relative humidity remains constant on a global scale (Koutsoyiannis, 2020). Precipitation intensity is believed to be proportional to surface atmospheric moisture content. In particular, the intensity of precipitation extremes, which tend to occur when the atmosphere is close to saturation, is often proportional to the moisture holding capacity of surface air, which increases with temperature according to the CC relation (Wang and others, 2017). However, Wang and others (2008b) found that air temperature and water vapor trends do not support the assumption of unchanging relative humidity over North America. Koutsoyiannis (2020) analyzed monthly data from two global reanalysis datasets and found a decrease in relative humidity with an increase in temperature. On the basis of global observations, reanalysis data, and climate model output, Wang and others (2017) found a peak-shaped relation between daily temperature and daily precipitation extremes, with precipitation extremes increasing at the CC rate for the low-medium range of local temperatures but decreasing at higher local temperatures. After the peak of the temperature-precipitation relation, specific humidity increases more slowly with temperature and as a result, the relative humidity decreases. Wang and others (2017) discuss how this can be the result of moisture limitations (that is, a dynamic mechanism) and temperature responses to precipitation (as opposed to precipitation responses to temperature).
Martinkova and Kysely (2020) reviewed observational studies on the CC relation scaling for middle latitudes. They discuss how several studies have identified super-CC scaling (that is, scaling above the CC relation) for temperatures above 10–15 °C with some studies showing a 2CC relation above this range of temperatures (that is, approximately 14-percent increase per degree Celsius of warming). This range of temperatures is above normal daily high temperatures during the wet season in south Florida and central Florida when most extreme precipitation events tend to occur because of convection and tropical systems. Therefore, a super-CC scaling relation is likely to dominate in the region. Some studies have also identified a higher temperature threshold above which sub-CC scaling (that is, scaling below the CC relation) or even negative scaling (that is, a decrease in precipitation with increasing temperature) can occur; however, this threshold varies with location. According to Martinkova and Kysely (2020), although sub-CC scaling at very high temperatures can result from a lack of moisture, it may instead be caused by smaller sample sizes resulting in underestimation of high quantiles. In their paper, Martinkova and Kysely (2020) summarize the factors for which super-CC scaling regime has been attributed, which include (1) dynamical feedbacks resulting from additional latent heat being released during condensation and increased near-surface humidity resulting in enhanced convection, (2) microphysical processes, (3) the size of cloud cells and their merging, (4) quasi-stationary convective storms, (5) convective events versus large-scale stratiform precipitation events, among others. More recently, Ali and others (2022) found that using quality-controlled hourly precipitation and daily dewpoint temperature data for the continental United States results in higher median scaling that is closer to the CC rate than when using raw data. They also found higher scaling for higher measurement precision of hourly precipitation. A method that removes seasonality in the precipitation and the dewpoint temperature also gives higher scaling. This highlights the importance of using high-quality observations and robust methods in estimating the temperature-humidity scaling relation.
The thermodynamic mechanism is believed to dominate in high latitudes, whereas the dynamic mechanism is believed to dominate at low latitudes such as in the tropics. Collins and others (2013) also state that projections of relative changes in future extreme precipitation may exceed projections of relative changes in future mean precipitation at the regional scales; however, natural variability in extremes is also larger than in the mean, resulting in decreased signal-to-noise ratios, especially for the most extreme events. Large-scale changes in global and regional circulations (for example, storm tracks) of both natural and anthropogenic origin may also dominate over the thermodynamic and dynamic effects for certain regions and events (Collins and others, 2013). For example, Hall and Kossin (2019) have found evidence of increased hurricane stalling along the North American coast since the mid-20th century but do not attribute these changes to anthropogenic climate forcing, stating that these trends could be due to low-frequency natural variability. Bhatia and others (2019) identified recent increases in tropical cyclone intensification rates in the Atlantic basin over the period 1982–2009 with a positive contribution from anthropogenic forcing.
Dougherty and Rasmussen (2019) evaluated the frequency of various flood types by season during the period 2002–13 across the continental United States. They classified flood events as flash floods, slow-rise floods, and hybrid floods that exhibit characteristics of both flash and slow-rise floods. For the State of Florida as a whole, they found that all three types of flood events can occur at various times of the year, predominantly in the summer and fall. However, a larger number of events that could be classified as slow-rise floods were identified as having occurred in the fall (September–November) and a larger number of hybrid floods were identified as having occurred during the summer (June–August) for the State of Florida. Events classified as flash floods in Florida had a mean precipitation duration of 10–20 hours and durations as long as 2 days in south-central Florida, whereas events classified as slow-rise floods had durations of about 7 days in south Florida and durations as long as 10 days in central Florida.
Kharin and others (2013) found that across future emission scenarios, the multimodel median return value for the 20-year daily precipitation event increases by a global mean of 5.3 percent per degree Celsius of warming. Collins and others (2013) show a multimodel ensemble median percent increase in 20-year return values of daily precipitation for the Florida region ranging from about 2.5 to 5 percent per degree Celsius for 2081–2100 with respect to 1986–2005. Over land areas, Kharin and others (2018) found that the probability of an annual maximum 1-day precipitation extreme with a 20-year return period for the current climate is projected to increase by 17 and 36 percent at 1.5 and 2.0 °C of warming, respectively. Kharin and others (2018) also found that the probability of the 50-year return period daily event in the current climate is projected to increase by 20 and 43 percent over land at 1.5 and 2.0 °C of warming, respectively.
The GCMs that the IPCC reports rely on have spatial resolutions that are generally too coarse to be able to provide projections of climate changes at scales that are relevant for impact studies and planning. In particular, regional and local changes in extremes cannot be adequately captured by GCMs, because they are not only affected by teleconnections to global phenomena but are also highly dependent on local microclimatic conditions. To overcome some of these limitations, GCM output can be downscaled to regional and local scales. Trend analysis of historical observations of relevant meteorological and hydrologic variables also provides important information on the local response to climate change. General increases in extreme precipitation are already being observed in the southeastern United States (DeGaetano, 2009), but trends over Florida are mixed in terms of their sign or significance.
Irizarry-Ortiz and others (2013) evaluated historical changes in precipitation at 32 weather stations over the State of Florida with the longest records ranging from 50 to more than 100 years. They only found upward trends in precipitation maxima in the dry season when considering the entire period of record at these stations, although most of these upward trends were found to be insignificant at the 0.05 significance level. For the period after 1950, most stations, except for those in south Florida, exhibited increases in November–January maxima. They highlighted how the multidecadal variability in precipitation related to changes in the AMO complicates the determination of secular trends and their attribution. Mahjabin and Abdul-Aziz (2020) evaluated precipitation data at 24 Florida stations using the Mann-Kendall nonparametric trend test with prewhitening. They found locally significant (p < 0.1) upward trends in the magnitude of 1- to 12-hour extreme precipitation events for the period 1950–2010 and in 6-hour to 7-day extreme precipitation for the period 1980–2010. Trends in precipitation of 2- to 12-hour duration, specifically 0.26 millimeter per year on average for 2-hour duration increasing to 0.53 millimeter per year on average for 12-hour duration, were found to also be globally significant (that is, trends had field significance, where the number of trends found exceeded the number of trends that could occur by chance) for the period 1950–2010 when accounting for cross-correlations across stations using bootstrap resampling. Mahjabin and Abdul-Aziz (2020) also found globally significant downward trends in the annual number of 1- to 3-hour, 1- to 6-hour, and 3- to 6-hour extreme precipitation events for the periods 1950–2010, 1960–2010, and 1980–2010, respectively. Trends in the number of 1- to 7-day extreme precipitation events were found to be mixed and lacked global significance. The Fourth National Climate Assessment (Carter and others, 2018) found an overall increase in the number of heavy precipitation days (defined as precipitation greater than 3 inches per day) interspersed with interdecadal variability for the southeastern United States for the period 1900–2016. For Florida specifically, the study found a mix of upward and downward trends in the number of heavy precipitation days for the period 1950–2016.
The SFWMD (2021) recently evaluated water and climate resiliency metrics districtwide including long-term trends in hydrologic and meteorological observations. A daily peaks-over-threshold (POT) analysis for occurrences above the 1-in-10 and 1-in-25 return frequency event magnitude was performed for six stations with more than 50 years of available precipitation data. The results showed statistically significant upward trends at the 5-percent significance level at two stations but no significant trends at the other four stations. The SFWMD (2021) also performed regional trend analysis using gridded daily precipitation data from the SFWMD’s precipitation “Super-grid” at 2- × 2-mile (mi) resolution (fig. 2B), grouped by SFWMD ArcHydro Enhanced Database (AHED) rain area (as of November 2020; fig. 3). Contact the SFWMD for more information about the November 2020 AHED rain areas. The results from this analysis showed (1) significant upward trends in daily annual maxima for the Eastern Everglades Agricultural Area, Martin-St. Lucie, and Upper Kissimmee AHED rain areas for a 5-year return period; (2) no significant trends in 3-day, 5-year annual maxima; and (3) a significant downward trend in the 5-day, 5-year annual maxima in the Broward AHED rain area. Results of a POT analysis on AHED rain areas is also included in SFWMD (2021).
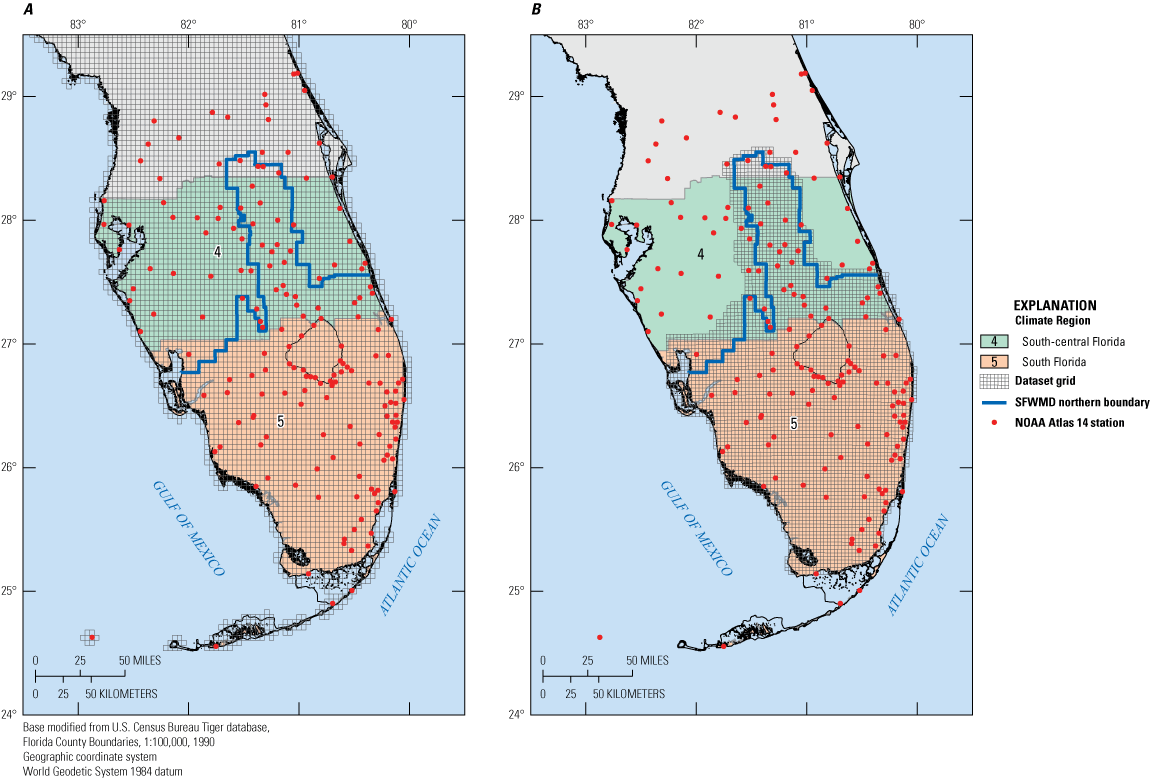
Grids for the, A, Parameter-elevation Regressions on Independent Slopes Model (PRISM) and, B, South Florida Water Management District (SFWMD) “Super-grid” datasets.
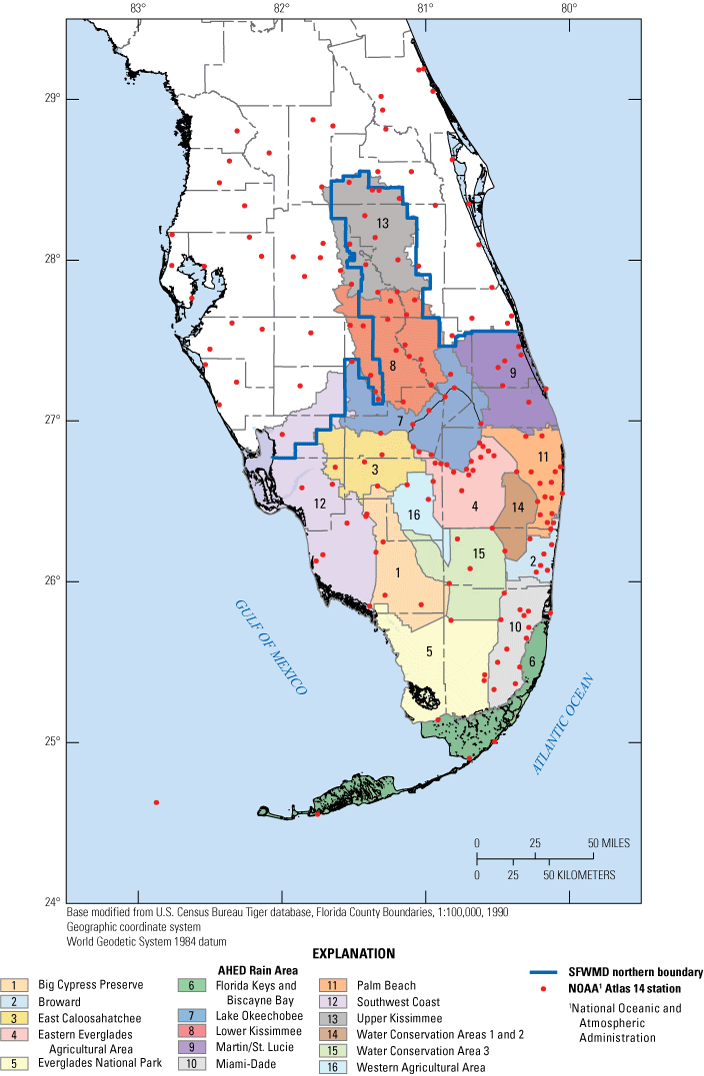
Rain areas defined in the South Florida Water Management District (SFWMD)'s ArcHydro Enhanced Database (AHED).
DDF Curve Development Efforts for Florida
Driven by the need for evaluating future changes in precipitation patterns, the SFWMD previously reviewed existing methods for DDF curve fitting, including comparisons with the NOAA Atlas 14 DDF curves (the “NOAA Atlas 14” section describes this dataset) at stations throughout the State of Florida (Irizarry and others, 2016). The method selected by Irizarry and others (2016), called “At-site Regional Frequency Analysis” (Ayuso-Muñoz and others, 2015), fits a probability distribution to normalized annual maxima for all durations simultaneously at a particular station and was used to develop DDF curves at NOAA Atlas 14 stations (fig. 1) for periods centered on the years 1970, 2030, and 2060. For this purpose, time series of annual maxima of precipitation for durations and periods of interest were obtained from bias-corrected and statistically downscaled climate projections from the World Climate Research Programme’s CMIP5 (https://pcmdi.llnl.gov/mips/cmip5) based on (1) the Bureau of Reclamation’s Bias-Corrected Constructed Analog (BCCA) dataset (Maurer and others, 2007; Bureau of Reclamation, 2013), and (2) the University of California San Diego’s LOCA dataset (Pierce and others, 2014). Biases in simulated historical and future projections of fitted precipitation extremes were corrected using a multiplicative quantile delta mapping (MQDM) technique (Li and others, 2010; Cannon and others, 2015). A concern with the results of this effort was that biases in the historical period (−30 to −60 percent) were larger than the estimated magnitude of the change from historical simulations to future projection period (−5 to +30 percent) for both datasets, especially for BCCA. These findings are consistent with those of NOAA (2022a), which found that both LOCA and BCCA version 2 datasets show a dry bias, and BCCA version 2 shows lower skill than other available downscaling datasets.
Various local governments in south Florida have used similar approaches to develop future DDF curves. For example, as part of the Broward County Future Conditions Map Series, an approach similar to the one developed by SFWMD was extended to evaluate precipitation data from dynamically downscaled climate projections, including the CORDEX project (Giorgi and others, 2009) and Jupiter Intelligence’s Weather Research and Forecasting model dataset (JupiterWRF; Madaus, 2019). The CORDEX project uses regional climate models (RCMs) to dynamically downscale CMIP5 model scenarios for different regions worldwide, including North America. Despite the relatively coarse spatial resolution of the CORDEX output (25–50 kilometers [km]), analysis of CORDEX data showed smaller historical biases for Broward County in some models than the statistical-downscaling products (Geosyntec Consultants, 2020), which prompts consideration of this dataset for deriving future DDF curves for other areas across the State. The JupiterWRF dataset uses a hybrid statistical- and dynamical-downscaling approach consisting of an analog and a scaling method to produce downscaled future climate projections, but specifically focused on extreme events. The JupiterWRF analysis also showed smaller historical biases for Broward County than previously analyzed products, which also prompts consideration of this dataset for deriving DDF curves in other areas across the State (Geosyntec Consultants, 2020). It is worth noting that in Broward County’s effort, the traditional “Spatial Regional Frequency Analysis” technique for DDF fitting was used and the problem of crossing curves described in Irizarry and others (2016) was handled by applying fixed offsets to precipitation values for durations after the intersection. This guarantees that precipitation depths monotonically increase across all durations and return periods but introduces uncertainties in the tails of the distribution, where the problem of crossing occurs most often. Finally, an ensemble method was used to determine median changes in DDF curves as well as the variability in the estimates across models, scenarios, and downscaling products. The overall ensemble results show median values of spatially aggregated DDF change factors under RCP8.5, for the future projection period 2041–90 compared to the historical period 1956–2005 across urban portions of Broward County, ranging between a 9- and 20-percent increase for 1- and 3-day durations and 10- through 500-year return periods.
Terminology Used in This Report
In describing our processing and analysis, the definitions of several terms are important to clarify. In this report, the term “reanalysis” will be used to refer to dynamical climate model simulations that are based on observed boundary conditions and are meant to match observed weather as precisely as possible. The term “historical observations” will be used to refer to weather observations used in statistical downscaling. The term “historical simulations” will be used to refer to GCM and associated downscaled models that are tuned to preindustrial conditions (around 1850 or 1750 depending on reference; see Schurer and others, 2017 for a discussion) and possibly to more recent historical conditions (Mauritsen and others, 2012; and Hourdin and others, 2017), but are otherwise not constrained to precisely match daily weather conditions from 1850 to the present. The term “future projections” refers to GCM and associated downscaled models of future climate that assume a specific GHG emission scenario or concentration trajectory.
Datasets Used in This Study
The datasets used in this study include precipitation datasets based on observations, and historical and future projected precipitation data based on statistical, dynamical, and hybrid downscaling methods applied to coarse spatial-scale output from GCMs developed as part of the World Climate Research Programme (https://www.wcrp-climate.org/) CMIP5 and the Coupled Model Intercomparison Project Phase 6 (CMIP6). These datasets will be discussed in more detail in the following sections.
Observational Datasets
Three observational precipitation datasets were used in this study to define base historical conditions for comparing DDF curves fitted to precipitation output from downscaled climate datasets for the historical period and for evaluating the performance of climate models in reproducing historical climate extreme indices. The observational datasets include NOAA Atlas 14, volume 9 (Perica and others, 2013), the Parameter-elevation Regressions on Independent Slopes Model (PRISM; Daly and others, 2008, 2021) and the South Florida Water Management District’s Precipitation “Super-grid” (SFWMD, 2005).
NOAA Atlas 14
The NOAA Atlas 14 dataset contains estimates of precipitation DDF and intensity-duration-frequency curves along with associated 90-percent confidence intervals for the United States and its territories at weather stations and as a gridded product with a 30-arc-second spatial resolution (approximately 0.5 mi). Supplementary information available as part of this product includes the annual maximum series data used in developing the DDF curves, analysis of the annual maximum series seasonality and trends, and temporal distributions for extreme precipitation events of 6- to 96-hour duration. Volume 9 of NOAA Atlas 14 covers the southeastern States, including Florida (Perica and others, 2013). Two types of DDF curves and their confidence intervals are provided in NOAA Atlas 14. The first type is based on the annual maximum series or block-maxima approach. The second type is based on partial-duration series (PDS) and is derived by means of Langbein’s formula (Langbein, 1949), which converts PDS-based average recurrence intervals to an annual exceedance probability (AEP). Selected average recurrence intervals are first converted to AEPs using Langbein’s formula and then precipitation frequency estimates are calculated for those AEPs using the same approach used in the annual maximum series analysis. Return levels from annual maximum series and PDS are about the same for return periods longer than 10 years.
For the southeastern United States, Perica and others (2013) found the generalized extreme value (GEV) distribution to be the best among 5 three-parameter distributions to model annual maxima across the range of frequencies and durations evaluated. NOAA used the regional frequency analysis method for GEV fitting at each weather station based on the L-moments fitting method implemented one duration at a time. L-moments are a sequence of statistics that define the shape of a distribution (such as mean, skewness, and kurtosis; Hosking, 1990). The L-moments method is briefly described in the “Goodness of Fit” section of this report. Regional frequency analysis fits a GEV distribution to normalized annual maximum series data at various stations around the station of interest (region of influence approach). This method results in more robust estimates of the GEV parameters and derived return levels. The derived return levels, which were calculated independently for each duration, were found to not always vary smoothly with duration. Therefore, NOAA used cubic splines to smooth out the DDF curves. In addition, 5- and 95-percent confidence limits were constructed by NOAA by means of a Monte Carlo simulation procedure and smoothed across durations using cubic splines.
For this study, DDF curves based on annual maximum series and PDS along with 90-percent confidence intervals and the associated constrained annual maximum series (inches) were downloaded from NOAA’s Precipitation Frequency Data Server (National Weather Service, 2020) for 174 weather stations in central and south Florida (fig. 1). Sources of weather station data for the State of Florida used in Atlas 14 include the NOAA-National Climatic Data Center, National Interagency Fire Center-Western Region Climate Center-Remote Automatic Weather Stations, SFWMD, St. Johns River Water Management District, National Aeronautics and Space Administration-Tropical Rainfall Measuring Mission Satellite Validation Office-Melbourne, Florida gage network, and University of Florida’s Institute for Food and Agricultural Studies-Florida Automated Weather Network (FAWN; Perica and others, 2013, table 4.2.1). The period of record for these Florida stations extends as far back as 1840 and ends in 2012 (appendix 1, table 1.1 of this report; Perica and others, 2013, appendix A.1).
Precipitation traditionally has been recorded at clock-based (constrained) intervals of 15 minutes, 1 hour, or 1 day at these weather stations. The recording interval is also called the “base duration.” Data at the base duration were accumulated over durations of interest from 5 minutes to 60 days by NOAA to develop constrained annual maximum series for each duration. Owing to the use of clock-based precipitation measurements, the constrained annual maximum series underestimates actual maxima. In order to convert the constrained annual maximum series to unconstrained annual maximum series values to be used in DDF development, NOAA Atlas 14 estimated correction factors. The unconstrained annual maximum series values would approximate the actual maxima for the given duration. The correction factors applied to durations of 1 to 7 days are shown in table 1 (Perica and others, 2013) and are quite similar to the theoretical correction factors determined by Weiss (1964) and to empirical values determined in other studies (Hershfield, 1961; Asquith, 1998; Overeem and others, 2008). These correction factors affect only the location and scale parameters of a dataset and do not affect the shape (skew) parameter (Schaefer, 1990). Application of these correction factors to obtain unconstrainted annual maximum series can result in inconsistencies across durations, where the precipitation depth for a shorter duration may exceed the precipitation depth for a longer duration. In these cases, some authors have used ad hoc methods for adjusting the calculated depth for a longer duration by adding a small number to the depth for the shorter duration (Perica and others, 2013), DDF smoothing techniques (Asquith and Roussel, 2004; Veneziano and others, 2007; Perica and others, 2013), or constrained scaling approaches (Xu and Tung, 2009).
Parameter-Elevation Regressions on Independent Slopes Model (PRISM)
PRISM provides monthly and daily climate data based on interpolation of weather station data (Daly and others, 2008, 2021). The PRISM dataset has a spatial resolution of 1/24th of a degree (approximately 4.4 km) and covers the conterminous United States. PRISM calculates a climate-elevation regression for each model grid cell, and stations included in the regression are assigned weights based on the similarity of each station to the corresponding grid cell. The similarity is defined on the basis of physiographic factors such as elevation, location, distance to the coast, topographic facet orientation, among others (Daly and others, 2008). Daily PRISM precipitation for Florida was downloaded for the period 1981–2019 using the prism R package (Hart and Bell, 2015).
As part of this study, daily PRISM precipitation data were used to develop areal reduction factors (ARFs), which convert point precipitation extremes to areal precipitation extremes. PRISM was also used to evaluate models for culling, which is the process by which the most reliable climate models are selected to inform future change factors. The PRISM precipitation grid is shown in figure 2A.
South Florida Water Management District’s Precipitation “Super-Grid”
The SFWMD’s precipitation “Super-grid” is a gridded dataset of daily precipitation with a spatial resolution of 2 mi (3.2 km), which covers the AHED rain areas in the SFWMD with the exception of the Florida Keys and Biscayne Bay (figs. 2B and 3). The SFWMD “Super-grid” dataset was developed using the TIN–10 method (SFWMD, 2005) to interpolate gage precipitation data from 1914 to 2002. Gage-corrected Next Generation Weather Radar precipitation data are used from 2002 to 2016. This dataset is considered by the SFWMD to be the most complete gridded precipitation dataset for south Florida. In this study, the SFWMD “Super-grid” precipitation dataset was used for model culling in addition to PRISM. The "Super-grid" data were provided to the USGS by SFWMD, who can be contacted directly for more details on the acquisition of these data.
Downscaled Climate Datasets
Various efforts to downscale global-climate predictions to local and regional scales have been initiated by climate research groups in the United States and abroad; however, it is notable that most of these downscaled datasets have not been tuned specifically to Florida climatic conditions. In this report, historical and future projections of precipitation based on statistical, dynamical, and hybrid downscaling of GCMs were used to develop future DDF curves for central and south Florida. The GCMs were developed as part of the World Climate Research Programme’s CMIP5 and CMIP6. The CMIP5 model data are a concatenation of historical (retrospective) GCM simulations covering the period 1850–2005 and future projections for the period 2006–2100 (https://pcmdi.llnl.gov/mips/cmip5/data-access-getting-started.html). The CMIP6 historical simulation period is 1950–2014 and future projections are for the period 2015–2100 (https://pcmdi.llnl.gov/CMIP6/Guide/index.html). CMIP6 data are only used by the JupiterWRF downscaled climate dataset that will be discussed in the next sections. See Taylor and others (2012) for an overview of the CMIP5 experimental design and Eyring and others (2016) for CMIP6. It is important to note that the historical CMIP5 and CMIP6 model simulations are not intended to reproduce the precise sequence of historical climate variability. GCMs are often run starting with different initial conditions to create an ensemble of possible trajectories for the historical and future climates that may result because of changes in natural variability (unforced or internal variability, also called “climate noise” in Taylor and others, 2012). This helps separate the climate change “signal” from the “climate noise.” However, often only one ensemble member is used for downscaling, which limits the range of events that are downscaled.
The global performance of the CMIP5 GCMs is summarized in the IPCC’s Fifth Assessment Report (Flato and others, 2013, p. 741–866). The overall model performance for the CMIP5 models in terms of the features of the 20th century climate most relevant to this study is summarized in table 2. For example, the Fifth Assessment Report (Flato and others, 2013, fig. 9.44) states that there is high confidence that the CMIP5 model performance in simulating ENSO is medium. Confidence in the validity of a finding is expressed qualitatively (see Mastrandrea and others, 2010).
Table 2.
Summary of how well the Coupled Model Intercomparison Project Phase 5 models simulate relevant features of the 20th century climate as documented in the Intergovernmental Panel on Climate Change’s Fifth Assessment Report.[Source: Flato and others, 2013, fig. 9.44; AGCM, atmospheric general circulation model]
See Mastrandrea and others (2010) for a detailed explanation.
The CMIP5 future projections are based on four different RCPs corresponding to low (RCP2.6), medium-low (RCP4.5), medium high (RCP6.0), and high (RCP8.5) year 2100 total radiative forcing values with respect to the preindustrial period (circa 1750; IPCC, 2013). The number next to the RCP label indicates the approximate increase in total radiative forcing, in watts per meter squared, caused by GHG emissions. RCP2.6 represents scenarios in which global mitigation of GHG emissions is significant, and the radiative forcing increase at 2100 from GHG emissions is 2.6 watts per meter squared. RCPs with higher numbers are the result of higher emissions and result in larger changes in global temperatures. RCP8.5 represents future conditions that could result from limited or no climate change mitigation, whereas the two middle scenarios are roughly equally spaced between the low and high scenarios (Terando and others, 2020). It is important to note that RCP8.5 is not necessarily a business-as-usual nor a worst-case scenario, but representative of a plausibly higher level of GHG concentrations. These RCP scenarios are developed using a risk-based framework and are highly uncertain. For this reason, individual RCP scenarios have not been formally assigned a likelihood of occurrence but represent plausible outcomes. Similar to the historical simulations, the CMIP5 future projections are also not intended to simulate the precise sequence of actual future variations in climate and may not capture the timing of future shifts in natural cycles.
Terando and others (2020) recommend that, whenever feasible, the entire range of RCP-based scenarios be considered when assessing potential future impacts. As part of the FPLOS Program, and with the purposes of planning for future stormwater infrastructure projects with long design lifetime, the SFWMD is interested in the evaluation of the middle-low and high emission scenarios RCP4.5 and RCP8.5. The choice of scenarios is also limited by their availability in downscaled climate datasets. The inherent assumption here is that RCP4.5 and RCP8.5 may result in higher extreme precipitation amounts for durations and return periods of interest compared to RCP2.6 because of increased atmospheric warming and higher atmospheric water-holding capacity resulting from these selected emission scenarios. This general assumption does not account for potential modulating factors that could affect precipitation variability and extremes in Florida, such as future changes or shifts in large-scale atmospheric circulations, teleconnection effects, or changes in tropical cyclone intensity. For example, Infanti and others (2020) analyzed precipitation from the Bias-Corrected Spatially Disaggregated (Maurer and others, 2007; Bureau of Reclamation, 2013) dataset for central and south Florida. After subsetting for the best performing models in terms of their ability to capture large-scale sea surface temperature anomalies and regional 2-meter temperature, they found that areas south of Lake Okeechobee may receive less wet-season precipitation in the future under both RCP4.5 and RCP8.5 scenarios. In particular, wet events (those with a Standardized Precipitation Index, SPI, above 0.5) during the wet season would become less wet in the middle-term (2046–72) under RCP4.5 and in the long-term (2073–99) under RCP8.5. The Sea Level Solutions Center at Florida International University (2021) evaluated output from the BCCA downscaled climate dataset (Maurer and others, 2007; Bureau of Reclamation, 2013), for changes in the seasonality of precipitation in Florida and found a decrease in wet-season precipitation and an increase in early dry-season precipitation over the NOAA Climate Division 5 (Everglades; fig. 1). Whether these findings hold for precipitation extremes of interest in this study remains to be seen.
The Coupled Model Intercomparison Project Phase 3 (CMIP3) defined emission scenarios as based on the following notation: economic (A) versus environmental (B) focus, and global (1) versus regional (2) responses (IPCC, 2000). Technological emphasis is added by means of an additional set of letters: fossil-fuel intensive (FI), nonfossil-fuel energy sources (T), or balance across all energy sources (B). The A1B scenario is considered similar to “medium” emissions scenario RCP6.0 from CMIP5 (Walsh and others, 2014). Based on the A1B intermediate emissions scenario simulated with the previous generation of climate models as part of CMIP3, Misra and others (2011) found that a decrease in June–August precipitation and an increase in September–November precipitation is projected in south Florida for the period 2080–2100 with respect to 2000–20. They attribute this decrease in June–August precipitation to the broad summer drying expected for the Caribbean region in CMIP3 models as well as a potential decrease in sea-breeze frontogenesis because of the potential future inundation of the Shark River Slough in Everglades National Park (fig. 1). Potential drying of the Caribbean region is also observed in CMIP5 models with a simulated global warming of 2.0–2.5 °C (Taylor and others, 2018) and is likely by the end of the 21st century under the RCP8.5 scenario (Collins and others, 2013). The simulated drying is associated with a narrowing of the Intertropical Convergence Zone resulting in more intense convection organized over narrower regions and a drier subtropical atmosphere caused by an enhanced and widened subsidence region (Byrne and others, 2018). On the basis of the ensemble mean of six perturbed physics dynamical downscaling simulations of the HadCM3 CMIP3 model under the A1B scenario, Campbell and others (2021) show that the Caribbean drying extends into south Florida during February–April at 1.5 °C global warming, during November–January at 2.0 °C, and during May–July at 2.5 °C. However, these prior studies did not examine whether extreme events might follow the same trends as changes in the mean and in the less extreme quantiles analyzed in these studies.
Most of the downscaled climate datasets used in this study rely on CMIP5 climate data except for the analog resampling and statistical scaling method developed by Jupiter Intelligence (2021), which also uses CMIP6 data. The CMIP6 projection scenarios are described by Eyring and others (2016) and are based on the concept of “shared socioeconomic pathways” (SSPs), which have been developed by the energy modeling community. Updated versions of the four CMIP5 RCP scenarios are available in CMIP6 and called “SSP1-2.6,” “SSP2-4.5,” “SSP4-6.0,” and “SSP5-8.5,” with each of these having a similar change in 2100 radiative forcing levels as their CMIP5 RCP counterpart. However, even though the 2100 radiative forcing is similar, the pathways of emissions, GHG mix, and land uses vary over time between the RCP and corresponding SSP scenario. For this reason, results from CMIP5 and CMIP6 may not be directly comparable. The use of different GCMs or different versions of GCM models in the two projects also precludes a direct comparison. CMIP6 also includes four additional SSPs representing intermediate levels of forcing between the four original scenarios. The CMIP6 model data are a concatenation of historical (retrospective) GCM simulations covering the period 1850–2014 and future projections for the period from 2015 to at least 2100. A description of the GCMs downscaled by the different downscaled climate datasets evaluated in this study can be found in table 3.
Table 3.
General circulation models downscaled by the different downscaled climate datasets used in this study.[CMIP, Coupled Model Intercomparison Project; GCM, general circulation model; AGCM, atmospheric general circulation model; RCM, regional climate model; MACA, Multivariate Adaptive Constructed Analogs]
The GEMatm AGCM is a global version of the CRCM5 RCM that uses sea ice and sea-surface temperatures (SSTs) from a separate GCM simulation as lower boundary conditions over the ocean for a one-degree global atmosphere-only simulation. The SSTs are bias-corrected on the basis of historical data. Further details are provided at https://na-cordex.org/agcm-simulations.html. GEMatm-Can uses SSTs from the CanESM2 GCM. GEMatm-MPI uses SSTs from the MPI-ESM-MR GCM.
Many GCMs have poor skill in simulating extremes because of their coarse spatial resolution and because of the difficulties in capturing subgrid scale physics (Misra and others, 2011). Statistical and dynamical downscaling are two methods used to generate high-resolution climate projections based on large-scale fields simulated by GCMs.
Statistical Downscaling
In statistical downscaling, large-scale fields simulated by GCMs are used as predictors of fine-scale meteorological variables. Historical observations are used to train the statistical downscaling methods and the results are, therefore, highly dependent on the quality of the observational data in capturing the fine-scale patterns in the meteorological variable(s) of interest (see, for example, Wang and others, 2020; Wootten and others, 2021). Wilby and Wigley (1997) and Wilby and others (1998) describe statistical downscaling methods. Such methods are largely empirical, and there is an inherent assumption that the methods will perform equally well in the future as in the historical training period. The assumption is that historical spatial relations between GCM output and local climate conditions such as bias will remain the same in the future (Nover and others, 2016). Dixon and others (2016) demonstrate how this assumption can break down under higher degrees of projected warming. Lanzante and others (2021) compared various quantile mapping (QM) approaches for statistical downscaling of precipitation using a “perfect model” experimental design to test the stationarity assumption inherent to all statistical downscaling methods. They found that compared to temperature, the statistical downscaling of precipitation has more complex configuration choices that affect the results more than the choice of QM method. This can be attributed to the intermittent occurrence of precipitation and how its distribution is conditional on occurrence. For their entire study region, which includes the continental United States and portions of Canada and Mexico, they found that a mean-absolute-error metric applied to assess day-to-day variability results in a future downscaling skill of only 20–25 percent, which is close to half of that observed for daily maximum temperature. The same mean-absolute-error metric applied to assess the agreement of the downscaled precipitation distribution indicates a greater skill of 50–60 percent overall and about half of that in the right tail of the distribution. For the southeastern United States, specifically, they found that absolute daily errors in the tails of the distribution can be large (approximately 20 mm or more) with implications for future projections of extremes. Wootten (2018) shows how subtle decisions performed in the process of statistical downscaling, such as tail adjustment, trace adjustment, and interpolation, can affect the skill of the prediction and increase the uncertainty in future projections, especially for extremes and event occurrence (defined as the number of events exceeding a threshold). These findings are likely to affect the output from the downscaled climate datasets evaluated as part of this study, although some of the methods used in developing these datasets rely on analog finders in addition to QM techniques for statistical downscaling and bias correction, respectively. For example, the MACA statistical-downscaling method uses an epoch adjustment in which seasonal and yearly trends in precipitation are removed prior to the analog search and bias correction. This reduces the need for tail adjustments as novel extremes appear in the distribution.
Dynamical Downscaling
In dynamical downscaling, an RCM is forced by large-scale boundary and initial conditions from a coarse resolution GCM. The RCM solves the physical equations just like those a GCM solves, but over a limited area and discretized at finer temporal and spatial resolutions than the source GCM. This method results in more physically based downscaling than that of statistical methods. However, dynamical downscaling is more time- and computer-resource-intensive than statistical downscaling. Owing to computational constraints, RCM resolutions on the order of tens of kilometers are typically used to downscale long-term simulations. Without proper boundary conditions, physics parameterizations, and tuning of these coarse-scale RCMs for the spatial region where they are applied, key features of the local climate, such as the annual cycle of precipitation and extremes, may not be adequately captured (Srivastava and others, 2022, provides an example for Florida), and model output may need to be bias-corrected. These scales fall within what is called the “gray zone” between hydrostatic and nonhydrostatic (convection-resolving) regimes (Jeevanjee, 2017). The gray zone encompasses resolutions between approximately 100 km and 100 meters, below which convection is considered to be fully resolvable (Gibbon and Holm, 2011; Jeevanjee, 2017). Convective precipitation is associated with nonhydrostatic forcings on vertical pressure that result in acceleration of air in the vertical direction. Terms describing acceleration can be incorporated into the momentum equation when applied at finer scales, typically grid scales less than 5 km. However, a hydrostatic approximation is often assumed for computing equations of motion in the vertical direction at grid resolutions of tens of kilometers. In the hydrostatic approximation, vertical accelerations caused by vertical changes in pressure are neglected and a balance exists between the gravity and vertical pressure gradient force (White and others, 2005). In this case, a cumulus convective parameterization scheme is used to estimate convective precipitation in the model.
Advancements in computing power, cloud computing, and distributed computing are allowing for models with a few-kilometer resolution to be run in shorter times. In these cases, the models can be run in convective-permitting mode, where convection can be partially resolved, and where the hydrostatic equation is replaced by the vertical momentum equation with the vertical acceleration term included. This is especially important for the State of Florida, where most warm-season precipitation events are generated by local convection enhanced by the convergence of sea breezes from both coasts. Higher-resolution convection-permitting models have been shown to improve the representation of extreme precipitation, especially on subdaily timescales and for summer high-precipitation intensity events compared to coarser-scale regional models with parameterized convection (Prein and others, 2015), which tend to produce rainfall that is too light and widespread. In addition, the simulation of tropical cyclones has been shown to be improved when using convection-permitting models (Prein and others, 2015).
It is important to note that any biases in the boundary conditions as well as uncertainties in the RCM model parameterization will influence the downscaled results. Potential microclimatic changes resulting from future land use changes, such as urbanization and the potential future inundation of the Shark River Slough in Everglades National Park, are uncertain and may not be captured in the RCM. For example, according to Bukovsky and others (2021), the existing North America CORDEX simulations of the future climate keep the land surface conditions constant at present-day. In order to assess the combined effects of GHG-forced climate change and land use for the end of the 21st century, Bukovsky and others (2021) used the WRF RCM forced by the MPI-ESM GCM under the RCP8.5 scenario. They evaluated two land use change scenarios consistent with SSP3 (under which the United States sees an increase in domestic cropland and low urban-land expansion) and SSP5 (under which the United States has a large expansion of urban land but a minimal increase in domestic cropland). For the five urbanized areas examined (located over the eastern half of the United States including the central Florida megaregion centered on Tampa), Bukovsky and others (2021) found enhanced precipitation in the form of both higher intensity storms and longer-lasting storms during June–August in the SSP5 land use scenario compared to the original land use. For less-urbanized areas to the east of the urbanized areas, they found that conditions were made less favorable for precipitation, as indicated by the stronger divergence of near-surface winds and large areas of increased convective inhibition that lead to fewer and shorter precipitation events in the SSP5 land use scenario compared to the original land use. For Florida specifically, they found that the more intense heat island effect from increasing urbanization in SSP5 enhances the sea-breeze and makes it more persistent throughout the day, which increases precipitation frequency and intensity.
In addition to the issues identified above, the RCM simulation has no feedback to the global climate due to the use of GCM boundary conditions. For all the reasons mentioned above, it often becomes necessary to bias-correct the dynamically downscaled fields. Lastly, hybrid approaches that combine features of statistical and dynamic downscaling have been developed. These approaches combine the ability of dynamical techniques to capture the physics of the precipitation process with a reduction in computational requirements for downscaling a single or multiple GCMs (see, for example, Walton and others, 2015; Madaus and others, 2020).
Localized Constructed Analogs (LOCA)
The University of California at San Diego has developed the LOCA statistical-downscaling technique (http://loca.ucsd.edu) to downscale 32 GCMs from the CMIP5 archive at 1/16th degree (approximately 6.6 km) spatial resolution, covering North America from central Mexico through southern Canada. The historical period for this dataset is 1950–2005, and two future projected scenarios are available: RCP4.5 and RCP8.5 over the period 2006–2100, although data are only available through 2099 for some models. Only one ensemble member from each GCM is downscaled by the LOCA method. This means that potential alternative trajectories for the historical and future climates that may result from changes in natural variability are not considered. The interaction of natural variability and secular trends caused by climate change and their effects on precipitation at various scales, including extremes, is therefore incompletely sampled. The Fourth National Climate Assessment (Avery and others, 2018) relied on the LOCA dataset as a source of downscaled climate information. For this study, daily precipitation data for the State of Florida were downloaded from the USGS Center for Integrated Data Analytics THREDDS data server (USGS, 2020a, b). The CMIP5 models downscaled by using the LOCA method and used in this study are listed in table 4. The LOCA grid in central and south Florida is shown in figure 4A.
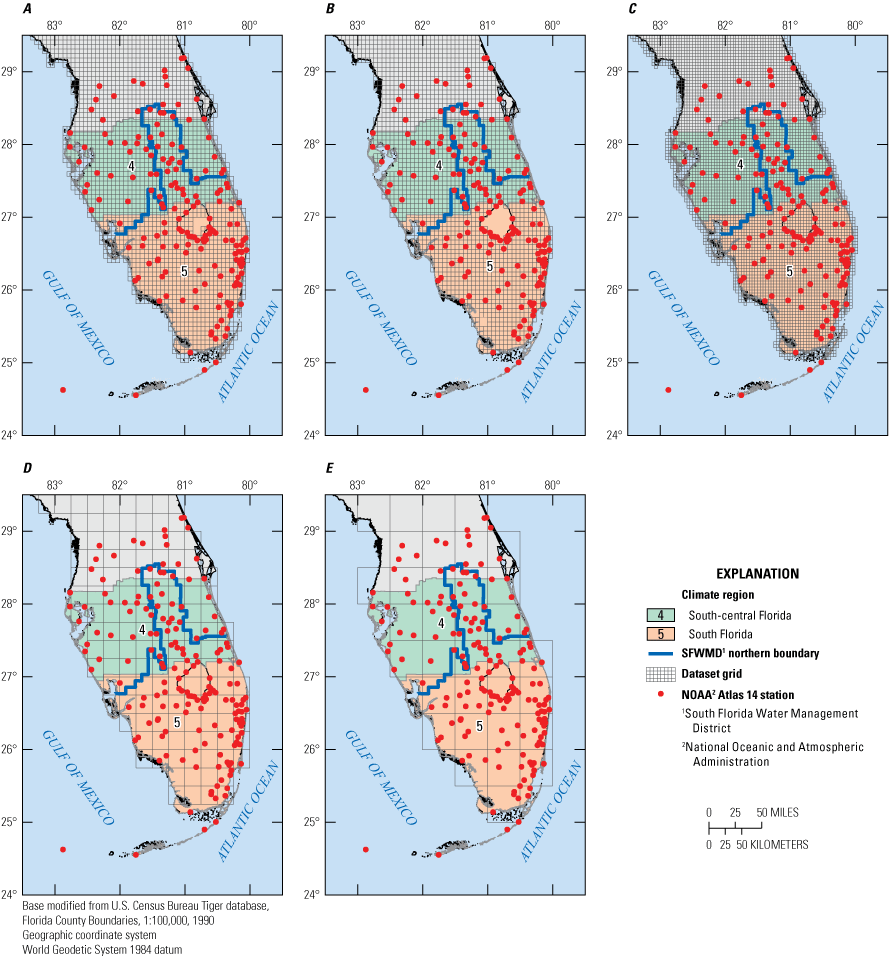

Grids for the, A, Localized Constructed Analogs (LOCA), B, Multivariate Adaptive Constructed Analogs (MACA) Livneh, C, MACA gridMET, D, Coordinated Regional Downscaling Experiment (CORDEX) NAM-22i, E, CORDEX NAM-44i, F, Jupiter Weather Research and Forecasting (WRF) model, and G, North America WRF model datasets.
Table 4.
General circulation models downscaled by the Localized Constructed Analogs (LOCA) statistical-downscaling method and evaluated in this study.[HIST, historical; RCP, representative concentration pathway; ensemble member r1i1p1 used for each model for both RCP4.5 and RCP8.5 with the exception of CCSM4_r6i1p1 for RCP4.5, CCSM4_r6i1p1 for RCP8.5, EC-EARTH_r8i1p1for RCP4.5, EC-EARTH_r2i1p1for RCP8.5, GISS-E2-H_r6i1p3, GISS-E2-R_r6i1p1, GISS-E2-H_r2i1p1for RCP8.5, and GISS-E2-R_r2i1p1for RCP8.5]
The LOCA method is a statistical downscaling technique that uses past historical observations to add improved fine-scale detail to global climate models (Pierce and others, 2014). The historical observational gridded precipitation dataset used for LOCA is the Livneh and others (2015) dataset over the period 1950–2005. Pierce and others (2021) found that daily precipitation extremes are muted by about 30 percent in the Livneh and others (2015) dataset over most areas of the continental United States, including Florida, and attribute this to the way Livneh and others (2015) split daily precipitation measurements across 2 days, depending on time of observation. A new gridded daily precipitation dataset over the continental United States that preserves extremes has been developed by Pierce and others (2021); however, the LOCA dataset has not been updated on the basis of this new dataset.
Figure 5, which is adapted from Lopez-Cantu and others (2020), shows an overview of the statistical downscaling methodology used for LOCA and described by Pierce and others (2014), which is summarized below. Before downscaling, LOCA performs bias correction on the daily precipitation data. First, LOCA uses a preconditioning approach to correct the annual cycle of daily values. Then, LOCA applies the Preserves Ratio (PresRat) bias-correction scheme to daily precipitation data, as described by Pierce and others (2015). The PresRat scheme consists of applying a multiplicative quantile delta mapping (MQDM) technique to the daily precipitation (described in the “Multiplicative Quantile Delta Mapping” section herein), special treatment of zero-precipitation days, followed by a final correction factor that tries to preserve the mean precipitation change predicted by the GCM as a percentage of the GCM’s historical climatology. As shown in Pierce and others (2015), the final corrections required to maintain the GCM-predicted mean precipitation change tend to be small and between 0.95 and 1.05 for most of Florida during the months of January, April, July, and October. After PresRat bias correction, LOCA also applies a frequency-dependent bias-correction scheme to reduce inaccuracies in the GCMs’ spectra. The spectrum of a time series describes the strength of the variation of a time series over different frequencies, such as daily, annual, and decadal timescales. The frequency-dependent bias-correction method is implemented as a digital filter in the frequency domain to make the model spectrum better match that of the observations.
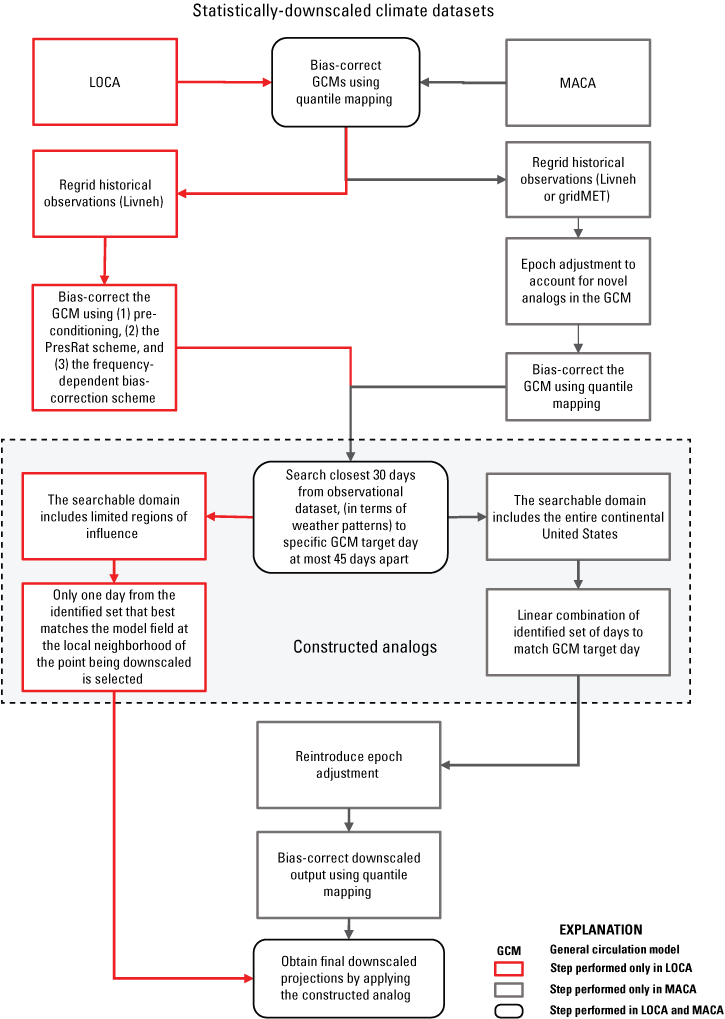
Overview of statistical downscaling methodology used in Localized Constructed Analogs (LOCA), and Multivariate Adaptive Constructed Analogs (MACA) downscaled climate datasets. Adapted from Lopez-Cantu and others (2020).
Implementing the LOCA downscaling method involves the following process. The continental United States is split into regions, and a point near the center of each region is selected and designated as an analog pool point. A spatial weighting mask around each analog pool point is then developed that includes all areas having a positive temporal correlation with the data at the analog pool point. The weighting mask is computed from coarsened observations and extends beyond the region that is represented by the analog pool point. The weighting mask varies by season and is used to limit the region over which the model field for the variable being downscaled is compared to coarsened observations of the variable. Analog days are then selected at the regional scale. For each day that is to be downscaled, a pool of 30 candidate observed analog days is chosen at each analog pool point by matching the model field for the variable being downscaled to days from coarsened observations that have the lowest root-mean-square difference (RMSD). This is done over the masked region corresponding to the analog pool point. This method contrasts with other analog downscaling methods in which the same analog days are chosen for the entire domain that is being downscaled. Only analog days within 45 days of the day of the year being downscaled are allowed. Then the single candidate analog day representing the best match within the local area around the fine-scale grid cell being downscaled is chosen as the single analog day to use for that location. This local matching is done by comparing the modeled field to the coarsened observations for the analog days after interpolating them to the fine-scale grid by using bicubic interpolation. The analog day with the lowest RMSD over a region of 21 fine-scale grid cells around the fine-scale grid cell being downscaled is then selected as the analog day for that point. In the case of precipitation, the selected analog day is scaled by the ratio of the interpolated model field to the interpolated analog day. For most grid cells, only the single locally selected analog day is used in downscaling. However, to reduce discontinuities, locations for which neighboring cells have a different analog day use a weighted combination of the center and adjacent analog days. In contrast to LOCA, other constructed analog methods typically use a weighted mean of the same 30 analog days for the entire domain. LOCA reduces this averaging and is therefore expected to (1) produce better estimates of extreme days, (2) more realistically depict the spatial coherence of the downscaled field (which other analog methods tend to overestimate), and (3) reduce the problem of producing drizzle (light-precipitation) days resulting from other analog downscaling methods. It is worth noting that GCMs themselves have a tendency for drizzle, as documented by Stephens and others (2010) and Pendergrass and Hartmann (2014b), and it is possible that some of this drizzle tendency may be persistent in downscaled datasets.
Deficiencies in the Livneh and others (2015) historical observational dataset used in LOCA have recently been documented by Wootten and others (2021), and Pierce and others (2021). These deficiencies arise because of the way the Livneh and others (2015) split observations of daily precipitation on the basis of their time of observation, where the precipitation total is prorated by the number of hours overlapping the date of the observation. For example, if the observations are made at 8 a.m., one-third (8/24) of the observed precipitation for a given day is assigned to the current day, whereas two-thirds (16/24) of the observed precipitation is assigned to the previous day. This method differs from other gridded datasets such as Daymet and PRISM, which use daily precipitation amounts recorded at any time during a day as the daily total for the 24-hour period from 12 a.m. to 12 a.m. and 7 a.m. to 7 a.m. local time, respectively. The apportioning process in Livneh increases the frequency of wet events, increases the wet spell length, and reduces the intensity of events (Oyler and Nicholas, 2018). Pierce and others (2021) found that daily precipitation extremes are muted by about 30 percent in Livneh over most areas of the continental United States, including Florida. This affects single-day events more than multiday events in both Livneh (Wootten and others, 2021) and the derived LOCA dataset. Previous analyses of DDF curves fit to annual maximum series of precipitation from LOCA’s historical period by Irizarry and others (2016), indicate that return levels for daily maximum precipitation are underestimated by about 40 percent in LOCA and that the underestimation is reduced to about 10 percent for 7-day duration return levels. These findings are generally consistent with those of Pierce and others (2021) and Wang and others (2020), which indicate that a large portion of the bias in daily extremes in LOCA may be due to the deficiencies in the Livneh observational dataset. For Florida in particular, Behnke and others (2016) found that out of the seven gridded datasets evaluated, Livneh performed the worst in capturing extreme precipitation climate indices at meteorological stations that are part of the Florida Automated Weather Network (FAWN, http://fawn.ifas.ufl.edu).
Multivariate Adaptive Constructed Analogs (MACA)
The University of California Merced has developed the MACA statistical-downscaling technique (https://climate.northwestknowledge.net/MACA/index.php) to downscale 20 GCMs from the CMIP5 archive to spatial resolutions of 1/24th degree (approximately 4.4 km) to 1/16th degree (approximately 6.6 km) for the continental United States. The historical period for this dataset is 1950–2005, and two future projected scenarios are available: RCP4.5 and RCP8.5 over the period 2006–99. The MACA dataset is described in more detail by Abatzoglou and Brown (2012).
MACA version 2 utilizes two observational gridded “training” datasets for bias correction and analog construction: Livneh 2013 (1950–2011; Livneh and others, 2013) and gridMET (1979–2012; Abatzoglou, 2013). GridMET is also known as Metdata. Hereafter, the MACA data based on these two training datasets will be called “MACA-Livneh” and “MACA-gridMET.” Deficiencies in the Livneh and others (2015) observational dataset related to how observations of daily precipitation are split across consecutive days as previously described for LOCA also apply to the Livneh and others (2013) dataset used in MACA (see the “Localized Constructed Analogs (LOCA)” section herein). For this study, daily precipitation data for the State of Florida for MACA-gridMET were downloaded from the USGS Center for Integrated Data Analytics THREDDS data server (USGS, 2021a, b) Daily precipitation data for the State of Florida for MACA-Livneh were downloaded from the Northwest Knowledge Network THREDSS data server (NKN, 2021). The CMIP5 models downscaled by MACA and used in this study are listed in table 5. The MACA-Livneh and MACA-gridMET grids in central and south Florida are shown in figure 4B and figure 4C, respectively.
Table 5.
General circulation models downscaled by the Multivariate Adaptive Constructed Analogs (MACA) statistical-downscaling method and evaluated in this study.[HIST, historical; RCP, representative concentration pathway; ensemble member r1i1p1 used for each model for both RCP4.5 and RCP8.5 with the exception of CCSM4_r6i1p1 for RCP4.5 and RCP8.5]
The MACA technique is a statistical downscaling technique that directly incorporates synoptic daily weather fields from GCMs using a “weather-typing” approach to resolve subsynoptic or mesoscale features. The overall procedure for downscaling precipitation is summarized in figure 5, which is adapted from Lopez-Cantu and others (2020), and consists of (1) aggregating both the GCM and observational data to a common 1-degree grid in latitude and longitude, (2) adaptively accounting for disappearing and novel analogs by performing an initial epoch adjustment (removing seasonal and yearly trends in precipitation multiplicatively using a 21-day 31-year moving window) prior to the analog search, (3) bias-correcting the GCM precipitation field using the MQDM approach, (4) searching the best historically observed analog days at the GCM scale and weighing them to obtain weather fields at the training-dataset scale, (5) reintroducing epoch adjustments to ensure consistency with GCM data, and (6) performing a post-processing bias correction at the training-dataset scale using the MQDM approach. In step 4, the 30 best analog days are identified on the basis of pattern root-mean-square error (RMSE) of the absolute values taken from a library of observed patterns that fall within 45 days of the target date. The MACA method was validated across the western United States by Abatzoglou and Brown (2012) using daily data from the European Centre for Medium-Range Weather Forecasts ERA-Interim reanalysis (Simmons and others, 2007) dataset in place of a GCM for the period 1989–2008.
Coordinated Regional Downscaling Experiment (CORDEX)
The North American Coordinated Regional Downscaling Experiment (NA-CORDEX) is part of the global CORDEX program sponsored by the World Climate Research Program to provide global coordination of regional climate downscaling (Giorgi and others, 2009; Mearns and others, 2017). NA-CORDEX consists of output from RCMs over a domain covering the majority of North America and using boundary conditions from CMIP5 GCMs (tables 6 and 7). According to Bukovsky and others (2021), the existing NA-CORDEX simulations for both the historical and future climates keep the land surface conditions constant at present-day conditions. The historical period for most models is 1950–2005, whereas the future projection period is from 2006 to 2100. Future projections are available for RCP4.5 and RCP8.5 scenarios. The RCMs have a spatial resolution of 0.22° (approximately 25 km) or 0.44° (approximately 50 km) and produce data for critical climate variables, including daily precipitation. Because the grids from the various RCMs are not all coincident, the data are also made available on two common grids of 0.25° or 0.50° resolution (called “NAM-22i” and “NAM-44i,” respectively) based on interpolation of the native RCM grid. Bias-corrected simulated meteorological data are also provided by NA-CORDEX. The bias correction of the RCM output is performed using the multivariate quantile-mapping method MBCn (Cannon, 2018) using the gridMET (1979–2016; Abatzoglou, 2013) or Daymet (1980–2017; Thornton and others, 2016) gridded observational datasets. Bias correction is done for the central calendar month of a 3-month sliding window at each grid point (Cannon, 2018).
Table 6.
General circulation models downscaled by the Coordinated Regional Downscaling Experiment (CORDEX) using various regional climate models and their native resolutions.[ECS, equilibrium climate sensitivity; °C, degrees Celsius; WRF, Weather Research and Forecasting model; RCP, representative concentration pathway; GCM, general circulation model; AGCM, atmospheric general circulation model; RCM, regional climate model; --, GCM/RCM combination not available; ~, approximate value. Values in RCM columns indicate the spatial resolution of the RCMs, in degrees (°) or kilometers (km)]
All available combinations of the general circulation model and regional climate model are also available for a historical period.
The GEMatm AGCM is a global version of the CRCM5 RCM. It uses sea ice and sea-surface temperatures (SSTs) from a separate GCM simulation as lower boundary conditions over the ocean for a one-degree global atmosphere-only simulation. The SSTs are bias-corrected on the basis of historical data. Further details provided at https://na-cordex.org/agcm-simulations.html.
Table 7.
Regional climate models used for dynamical downscaling in the Coordinated Regional Downscaling Experiment (CORDEX).[RCM, regional climate model]
The NA-CORDEX experiment downscaled GCMs having a wide range of equilibrium climate sensitivity (ECS) from 2.4 to 4.6 °C (table 6) to encompass a large range of possible changes in climate. For this study, bias-corrected daily precipitation data on the common NAM-22i and NAM-44i grids were obtained from the National Center for Atmospheric Research Climate Data Gateway portal (https://www.earthsystemgrid.org/search/cordexsearch.html) for the State of Florida (tables 6 and 7) in January 2022. An error was previously found in the bias-corrected CORDEX data used in this study and is described by Mearns and others (2017). However, the NA-CORDEX bias-corrected data were corrected and republished by the National Center for Atmospheric Research in January 2022 (NCAR, 2021, 2022), and this updated dataset was used for this study. The CORDEX NAM-22i and NAM-44i grids in central and south Florida are shown in figure 4D and figure 4E, respectively. It is evident, especially for the CORDEX NAM-44i grid, that many NOAA Atlas 14 stations are located within a single grid cell. This is more pronounced in areas of high station density such as the southeast coast of south Florida, Lake Okeechobee, and the Upper and Lower Kissimmee AHED rain areas northwest of the lake (figs. 1 and 3).
Analog Resampling and Statistical Scaling Method Using the Weather Research and Forecasting Model (JupiterWRF)
Jupiter Intelligence (https://jupiterintel.com) has developed a Weather Research and Forecasting (WRF, Skamarock and others, 2019) model for central and south Florida at 4-km resolution that can be used to downscale historical observations of extreme precipitation events in the region (fig. 4F). They provided the USGS with simulated precipitation fields at 15-minute temporal resolution and 4-km spatial resolution for 1,044 historical precipitation events between 1979 and 2017. The output from this model is used by Jupiter Intelligence together with an analog resampling and statistical scaling method they developed, to produce downscaled future climate projections of extreme precipitation events. Because this method uses high-resolution output from climate models as well as statistical techniques, it is considered a hybrid downscaling approach.
An analog resampling technique is used by Jupiter Intelligence to project future changes in event frequency due to changes in large-scale meteorological fields that are conducive to extreme precipitation over central and south Florida. For analog resampling, Jupiter Intelligence uses future projections from various CMIP5 and CMIP6 GCMs (table 8). To provide a wider range of potential future extreme events, many ensemble members are used for each GCM when available. The GCMs and projections used for analog resampling were chosen by Jupiter Intelligence primarily on the basis of a subjective evaluation of their relative quality compared to other GCMs and on the availability of the daily meteorological data needed to define analogs. To project future changes in event magnitude, Jupiter Intelligence uses a statistical scaling technique that intends to capture increases in extreme precipitation resulting from increases in the atmosphere’s water holding capacity under global warming. The statistical scaling technique uses output from a WRF model of North America by Liu and others (2017), which is also described by Rasmussen and others (2020). The portion of the North America WRF model grid in central and south Florida is shown in figure 4G. The statistical scaling data were provided to the USGS by Jupiter Intelligence, who can be contacted directly for more details on the acquisition of these data.
Table 8.
General circulation models downscaled by the analog resampling and statistical scaling method developed by Jupiter Intelligence using the Weather Research and Forecasting model (JupiterWRF) and used in this study.| General circulation model |
Scenarios available |
Number of ensemble members |
|---|---|---|
| CESM-LENS1 | RCP8.5 | 40 |
| ACCESS-ESM1-5 | SSP2-4.5, SSP5-8.5 | 3 |
| GFDL-ESM4 | SSP2-4.5, SSP5-8.5 | 1 |
| MPI-ESM1-2-LR | SSP2-4.5, SSP5-8.5 | 10 |
The CESM-LENS (Large ENSemble Project) dataset from the National Center for Atmospheric Research includes a 40-member ensemble of climate simulations, where each run begins with slightly different initial conditions. The simulations are performed using the Community Earth System Model version 1 (CESM1) with CAM5.2 for the atmospheric component. For more information, see https://www.cesm.ucar.edu/projects/community-projects/LENS/.
Additional details about how to implement this method are included in appendix 2 and were provided by Jupiter Intelligence. Madaus and others (2020) apply similar analog resampling and statistical scaling methods to the prediction of hyper-local temperatures in New York City; however, some details are different from the methodology recently proposed by Jupiter Intelligence for downscaling precipitation extremes. The method was programmed in R language to provide estimates of future DDF curves for daily duration only.
Methods
The methodology used to derive change factors based on CORDEX, LOCA, and MACA downscaled climate datasets is illustrated in figure 6. Change factors were computed for these three downscaled climate datasets for durations of 1, 3, and 7 days, and return periods of 5, 10, 25, 50, 100, and 200 years. The historical period was chosen as the 40-year period 1966–2005, which is centered around 1985. The beginning of this period matches the approximate beginning of the global warming trend from the 1970s onward (Rahmstorf and others, 2017), and the end was selected to match the end of the CMIP5 historical simulations (2005). The future (projected) period of interest is a 40-year period centered around 2070 that spans 2050–89. These two 40-year periods were used to develop change factors for application of the MQDM bias-correction method described in the “Multiplicative Quantile Delta Mapping” section.
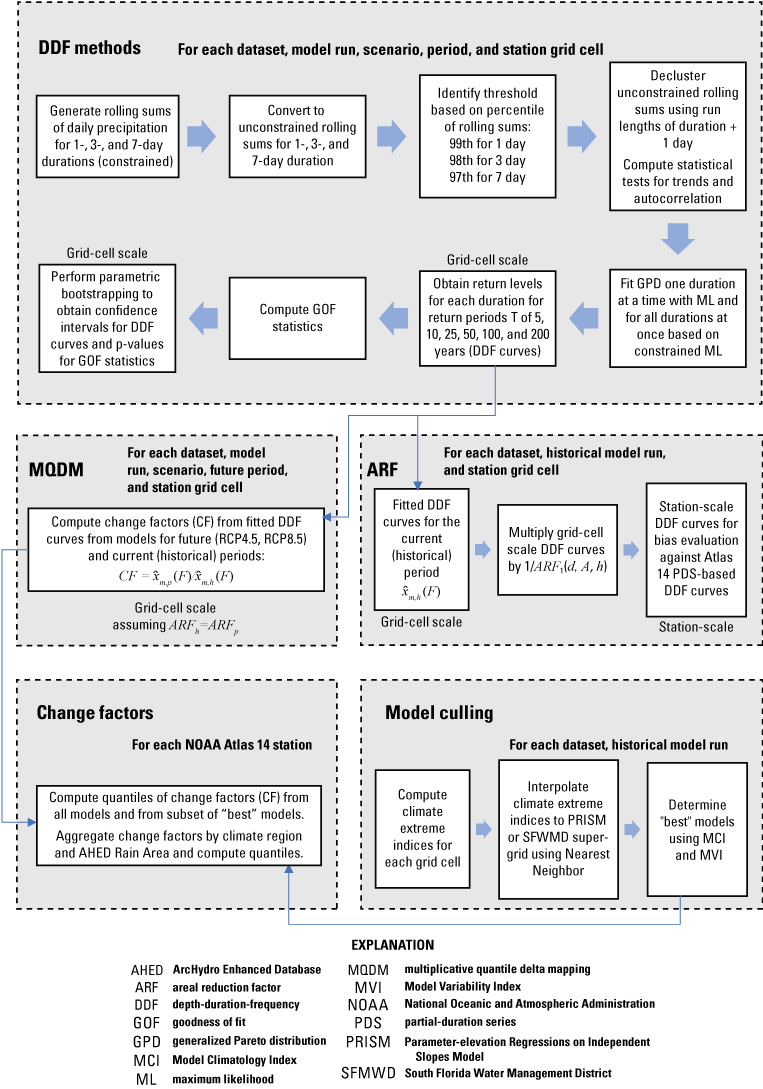
Methodology for deriving change factors for the Coordinated Regional Downscaling Experiment (CORDEX), the Localized Constructure Analogs (LOCA), and the Multivariate Adaptive Constructed Analogs (MACA) downscaled climate datasets.
Stationarity was assumed within the 40-year historical and future projection periods of interest, which means that a quasi-stationary approach was used. This might seem contradictory to the expectation of nonstationarity since the 1970s on a global scale as described in Rahmstorf and others (2017); however, natural variability in precipitation extremes is larger than in the mean, resulting in decreased signal-to-noise ratios, especially for the most extreme events. The appropriateness of the use of a quasi-stationary approach was tested, as will be described later. Although the DDF curves fit as part of this study are based on a stationary framework within the selected 40-year historical and future projection periods, they are only considered applicable around the central year for each of the two 40-year periods. DDF curves for periods centered on different historical and future years are expected to be different from the ones developed here. As one moves away from the central years analyzed here, the differences in DDF curves may become more pronounced and may become significant.
Other studies have used the quasi-stationary approach for DDF fitting during specific time windows identified using trend tests. For example, Ren and others (2019) found that DDF curves based on the quasi-stationary approach generally match DDF curves developed on the basis of the nonstationarity assumption of a long-term trend within a longer time period. NOAA (2022a) compared the quasi-stationary approach applied to time windows against the nonstationary approach over a longer period based on annual maxima from LOCA over the northeastern United States, one of the regions where the percentage of precipitation falling in the heaviest 1 percent of all daily precipitation events has been found to have increased the most within the United States during 1958–2012 (Walsh and others, 2014). NOAA (2022a) found that overall, future changes in precipitation frequency estimates match reasonably well between the quasi-stationary approach and the nonstationary approach with the location, scale, and shape parameters varying with covariates of time or radiative forcing. However, the quasi-stationary approach results in more spatial variability and inter-model spread for the 100-year event than the nonstationary approach because of the use of a smaller sample size (time window) in the quasi-stationary approach, which results in more uncertain shape parameter estimates. A quasi-stationary approach was used in this study because of the high degree of subjectivity in defining how the parameters of the extreme value distribution may vary in time, which increases uncertainty in return levels. Other limitations in using a nonstationary approach include the assumption that these parameter variations will hold for the entire future design-life period and the difficulty in parsing out multidecadal natural variability influences from trends induced by climate change. First-order stationarity was tested using the Mann-Kendall nonparametric trend test. For an in-depth discussion of these and other issues related to the assumption of nonstationarity in extreme value analysis, see Coles (2001) and Serinaldi and Kilsby (2015).
The analysis was performed using R programming software (R Core Team, 2020) and various common statistical and extreme value analyses packages on both a local Windows personal computer and the USGS Yeti supercomputer (Falgout and Gordon, 2020). Several key R packages will be described in later sections. The next sections describe the theory behind the methods used to compute change factors based on the CORDEX, LOCA, and MACA datasets, followed by details on the implementation of the methodology. The methods used for deriving change factors from JupiterWRF output for daily duration are described in appendix 2.
Extreme Value Theory
Extreme value theory is a branch of statistics that deals with the stochastic behavior of extreme and rare events found in the tails of probability distributions and includes events larger or smaller than usual. The probability of occurrence of a climate or weather variable can be described by a probability distribution function. Under global climate change, small changes in the mean of a distribution may result in changes in the frequency of extremes at both ends of a distribution (Cubasch and others, 2013). Furthermore, changes in the variance and skewness or shape of the distribution may also result in substantial changes in the frequency and magnitude of extremes. For stormwater planning in particular, the concern is how the upper tail of the probability distribution, representing the larger values of extreme precipitation, will change under future conditions. Extreme value theory provides a class of models that make it possible to extrapolate from observed or modeled extremes to unobserved or unmodeled extremes (Coles, 2001).
Extreme value theory has developed under two main approaches. In the classical block maxima (or minima) approach, the probability distribution of maxima (minima) over a given block of time, typically a year, is modeled. This is herein referred to as the “annual maxima approach.” The peaks-over-threshold (POT) approach consists of extracting, from a continuous record, the peak values that exceed (or fall below) a particular threshold and modeling their distribution. Both approaches can be implemented under stationary and nonstationary frameworks. Stationarity implies that, given any subset of variables, their joint distribution stays the same through time, which is the approach taken here. First-order stationarity was validated using the Mann-Kendall nonparametric trend test with a significance level (alpha) of 0.05. In contrast, nonstationary processes have characteristics that change systematically through time, for example, as seasonal effects or in the form of trends (Coles, 2001). These changes are reflected as changes in their probability distribution through time. Both extreme value approaches will be discussed hereafter in the context of the stationary framework.
Annual Maxima
According to extreme value theory, if under suitable normalization, the cumulative distribution function (CDF) of the maxima
whereMn
is the maxima over n observations of variable X;
max()
is the maximum value function, that is, the largest value from the values inside the parentheses;
Xi
is the ith observation of random variable X;
i
is an index for the observation number that ranges from 1 to n; and
n
is the number of independent and identically distributed realizations of random variable X;
F(x)
is the CDF of the GEV distribution, that is, the annual nonexceedance probability function;
Pr (X ≤ x)
is the probability that random variable X is less than or equal than x within a year or the number of nonexceedances of x per year;
X
is the random variable X, which here is the precipitation depth, in inches;
x
is the value for the precipitation depth, in inches;
exp{}
is the exponential function of the expression in braces (e{});
ξ
is the shape parameter or extreme value index;
μ
is the location parameter; and
σ
is the scale parameter.
The GEV distribution models the annual maxima of a series of independent and identically distributed observations and is an appropriate distribution for analyzing extreme values. The distribution encapsulates the following three distinct extreme value distributions by means of the shape parameter, which changes the skewness of the distribution and the heaviness of the right tail or the rate of increase of the upper quantiles as the nonexceedance probability approaches one: (1) Gumbel (ξ = 0), which is light-tailed and unbounded (Type I exponential upper tail); (2) Fréchet (ξ > 0), which has a lower limit at and is heavy-tailed (Type II power-law upper tail); and (3) the reverse Weibull (ξ < 0), which has an upper limit at and is short-tailed (Type III). These limits derive from the constraint . The parent distribution dictates which GEV subtype the annual maxima converge to.
The corresponding quantile function for the GEV is given by
wherex(F)
is the quantile function of the GEV distribution;
F
is the annual nonexceedance probability, that is, the CDF value or the Pr (X ≤ x); and
ln
is the natural logarithm function.
Other frequency distributions to model extreme values are described in the literature; however, the GEV distribution has been found to provide the best fit to annual maxima of precipitation in the State of Florida (Perica and others, 2013; Teegavarapu and others, 2013). The parameters of the GEV distribution can be fitted by the following methods, among others: maximum likelihood (ML), penalized ML, method of moments, and L-moments. Martins and Stedinger (2000) describe the behavior of different GEV fitting methods in terms of their stability and bias and show how their performance varies as a function of the population’s true shape parameter. They show that unreasonable values of the GEV shape parameter can be estimated from small samples when using the ML approach and suggest using a Bayesian prior distribution to restrict its values to a reasonable range. Hosking and others (1985) recommend the probability-weighted moment estimators, which are equivalent to the L-moments estimators (Hosking, 1990; and Hosking and Wallis, 1997) and are robust against random outliers and gross observational errors (Gubareva and Gartsman, 2010). The L-moments method is briefly described in the “Goodness of Fit” section herein. The estimation of the shape parameter has been found to be quite sensitive to sample size in these and other studies, and it is this parameter that dictates the rate of increase of extreme upper quantiles, which are the most relevant in hydrologic applications. In particular, the probability of observing more rare extreme events in the upper tail of the distribution increases with increasing sample size. Thus, estimated shape parameters based on short record lengths tend to be negatively biased.
In developing DDF curves for a location, the GEV distribution is often fit to annual maximum series for various durations, d, independently. It is possible for the fitted CDFs for consecutive durations to cross, which is reflected in the DDF curves as decreasing quantiles with increasing duration. This violates the physical constraint that precipitation-depth quantiles at longer durations must exceed quantiles at shorter durations for a given return period. An objective in fitting GEV curves to the annual maximum series (as opposed to just using empirical quantiles) is to extrapolate to large return periods (small exceedance frequencies) beyond the length of the annual maximum series record. It has been shown that these extreme quantiles are very sensitive to the fitted parameters, especially to the shape parameter, ξ. The estimated shape parameter can have large errors and can be very noisy, especially when estimated from short datasets and when using methods such as ML. The large variation in estimated shape parameter across durations increases the chance of crossing CDFs.
In developing DDF curves, many studies have traditionally assumed a constant shape parameter across duration and (or) space because of the difficulty in robustly estimating this parameter from small sample sizes. This facilitates the fitting of DDF curves across durations. One common assumption is that extremes follow a Gumbel distribution (ξ = 0). Lu and Stedinger (1992) have shown that for sample sizes less than 50 and when fitting by probability weighted moments, using the Gumbel distribution results in smaller mean squared error in the 100-year flood estimate than the three-parameter GEV distribution, even if the shape parameter is misrepresented. Koutsoyiannis (2004a, b) showed that most time series of hydrologic extremes follow a type II GEV distribution (Fréchet, ξ > 0), which has a lower limit (μ – σ/ξ) and is heavy tailed. Koutsoyiannis (2004a) showed how small sample sizes (usually less than 50 annual maxima values) tend to hide the heavy-tail behavior, leading to selection of the Gumbel distribution even though the real distribution is Fréchet. This is problematic when DDF curves are used in critical-infrastructure design because quantiles for long return periods tend to be underestimated under a Gumbel assumption, which may lead to unconservative design. Koutsoyiannis (2004b) hypothesized that the shape parameter is constant across locations and is about 0.15 for a daily duration, whereas Overeem and others (2008) found that the shape parameter tends to be constant across a region and across durations with a value of about 0.114 and a standard deviation of about 0.021. Papalexiou and Koutsoyiannis (2013) later found that the shape parameter follows approximately a normal distribution with a mean of about 0.114 and a standard deviation of about 0.045 for all durations as sample size tends to infinity. Courty and others (2019) fitted GEV distributions to annual maxima precipitation intensities from the European Centre for Medium-Range Weather Forecasts ERA5 reanalysis dataset (0.25° spatial resolution) for a range of durations from 1 to 360 hours assuming a constant shape parameter of 0.114. The null hypothesis that the annual maxima follow a GEV distribution with a shape parameter of 0.114 was tested by Courty and others (2019) using the Filliben goodness-of-fit (GOF) test; they found that at the 5-percent significance level, the null hypothesis could only be rejected in 5.7 percent of the fitted cells. Serinaldi and Kilsby (2014) analyzed a subset of the daily data evaluated by Papalexiou and Koutsoyiannis (2013) to investigate the behavior of the shape parameter using a POT approach (see the “Peaks-Over-Threshold” section). They found that the asymptotic mean value of the shape parameter tends to be within the range 0.061–0.097, depending on season.
Nadarajah and others (1998) evaluated constraints on the GEV parameters resulting from the constraint on precipitation quantiles for consecutive durations given by
wherex(F, d)
is the quantile function for duration d;
d
is the duration of an event; and
dʹ
is the next longer duration to d, where dʹ is greater than d.
Nadarajah and others (1998) showed theoretically that equation 4 imposes the following restrictions on the marginal GEV distribution parameters: (1) For ξ greater than 0, ξ is constant across durations; and (2)
whereNadarajah (2005) fitted GEV distributions to daily annual maximum precipitation data at 14 stations in west-central Florida for the period 1901–2003 and found the shape parameter to be positive at all stations. For daily durations, Cavanaugh and others (2015) found that the thickness of the GEV tail is related to the variability in precipitation causing events. Florida extreme precipitation is generated by convective storms, tropical storms, and cold fronts in northern parts of the State (Winsberg, 2020); therefore, a larger shape parameter is expected relative to those for areas having less diverse precipitation-generating mechanisms. Furthermore, for floods in particular, Dawdy and Gupta (1995) show that at sites with mixed populations, true skewness may be more underestimated than expected based on simulation from various common flood frequency distributions.
Veneziano and others (2007) and other studies have found that the shape parameter peaks at about 1–3 hours and decreases for shorter and longer durations. According to Veneziano and others (2007), a decreasing shape parameter with increasing duration agrees closely with the decay observed in multifractal precipitation models (that is, under multiple/dissipative scaling; see Veneziano and others, 2009); however, declines in the shape parameter observed for very short durations at many locations around the world show a lack of multifractality for the shortest durations. (Multifractal theory indicates that the shape parameter would be nearly constant for short durations.) Furthermore, on the basis of multifractal theory, the shape parameter would always be in the type II GEV distribution range (ξ > 0, that is, a Fréchet distribution), and the parameter is significantly higher than estimated from short records. (Hence, high quantiles of the GEV would tend to be underestimated as well.) Veneziano and others (2009) proposed a near-universal relation to estimate the shape parameter as a function of duration and found a value close to that of Koutsoyiannis (2004b) for daily accumulations. Although negative shape parameters are generally thought to be unlikely to occur in climatology, Ribereau and others (2011) provides examples where negative shape parameters have been observed. On the basis of the analysis of annual maxima data from NOAA Atlas 14 for the State of Florida, Irizarry and others (2016) found that the shape parameter peaks for daily durations and decreases for shorter and longer durations with negative shape parameters obtained at a substantial number of stations for the shorter and longer durations. Goly (2013) found an increase in the frequency of negative shape parameters for durations shorter and longer than 1 day during the warm phase of the AMO in Florida, with most stations having negative shape parameters located in the interior of the Florida peninsula. It is expected that, in general, high precipitation intensities will not be sustainable for long periods of time (Dougherty and Rasmussen, 2019) and the GEV parameters should reflect this. Carney (2016) evaluated observed annual maxima from NOAA Atlas 14 and found that for the southeastern United States, the shape parameter tends to decrease with duration for durations greater than or equal to 2 days. They attributed this decrease, at least in part, to precipitation being more intermittent as the duration increases, with precipitation totals for these longer durations reflecting multiple storms and dry periods between the storms. On the basis of the various studies that found a decrease in the shape parameter for longer durations, we expect the shape parameter (skewness of the distribution) to generally decrease with increasing duration beyond 1 day.
As discussed previously, estimating return levels for very long return periods by the annual maxima approach is prone to large sampling errors and potentially large biases because of uncertainty in the shape parameter. According to the World Meteorological Organization (2009) and discussed by Kao and others (2020), confidence in a return level decreases rapidly when the return period is more than about two times the period of record of the original dataset. NOAA (2022a) indicates that, for return periods greater than 100 years, one may need to rely on an extension or adjustment of the percent change for lower return periods to higher return periods. To address the negative biasing of the shape parameters for short records, Papalexiou and Koutsoyiannis (2013) evaluated global daily precipitation data and developed a bias-correction equation for the shape parameter estimated from L-moments. They found that the L-moment-based shape parameter for daily annual maximum series is underestimated and converges slowly toward asymptotic values with increasing record lengths. The L-moments method is briefly described in the “Goodness of Fit” section herein. Serinaldi and Kilsby (2014) extended the work of Papalexiou and Koutsoyiannis to develop an unbiased estimator for the shape parameter based on the POT concept with 98th-percentile exceedances fitted by ML. After they applied their bias-correction equation, overall shape parameter values shifted toward positive and variance was reduced. Serinaldi and Kilsby (2014) found that most remaining cases of negative shape parameter after bias correction were not statistically significant. Carney (2016) extended the work of Papalexiou and Koutsoyiannis (2013) to all durations on the basis of NOAA Atlas 14 data and the relation between the true shape parameter and the product of its bias times the record length previously developed by Hosking and others (1985). These methods for bias correction depend on the fitting method and may not fully resolve the problem of crossing CDF curves across durations.
Several approaches exist in the literature to increase the sample size and improve the robustness of the estimated parameters. One such approach to increase the sample size is to extract the r largest values per year (for example, the 2 largest values per year) instead of a single annual maximum (Weissman, 1978; Smith, 1986), which leads to a limiting distribution that is an extension of equation 2. Another approach is the regional frequency analysis approach used by NOAA Atlas 14 (Perica and others, 2013), which uses additional annual maxima data from nearby stations. In the next sections, the POT approach is described, which uses more data in the tail of the distribution at a site to obtain more robust parameter estimates than based on the annual maxima approach.
Peaks-Over-Threshold
In the POT approach, a high threshold value of precipitation is chosen and a probability distribution is fit to precipitation data exceeding the chosen threshold. Contrary to the annual maxima approach, where only the largest precipitation value during every year in the selected period is used in probability distribution fitting, the threshold in the POT approach can be chosen so that it results in a larger sample size, and only the truly larger precipitation values in the time series are selected.
The conditional CDF of excesses, Y, of random variable X above threshold u is given by
whereFY
is the CDF for random variable Y;
Pr (Y ≤ y)
is the probability that random variable Y is less than or equal than y;
Y
is a random variable representing the excess of random variable X above u (that is, X – u given that X is greater than u);
y
is a realization of random variable Y, in inches;
is the conditional CDF for random variable X given that X is greater than u;
X
is a random variable consisting of the precipitation depth, in inches;
x
is a realization of random variable X, the precipitation depth, in inches;
FX
is the CDF for random variable X; and
u
is a threshold, in inches.
G(y)
is the conditional CDF of the GP distribution, that is, the conditional nonexceedance probability function;
is the probability that X – u is less than or equal to y given that X is greater than u; and
is the scale parameter of the GP.
The corresponding quantile function for X based on the GP conditional CDF is given by
wherex(Gʹ)
is the quantile function for X;
Gʹ
is the nonexceedance probability, that is, the CDF value or the Pr(X ≤ x) in units of the number of non-exceedances of x per observation; and
ζu
is the Poisson intensity parameter, that is, the rate of exceedance of the threshold u.
The rate of exceedance of threshold u is given by the following expression:
and is estimated from the data as the number of exceedances of threshold u in the record, Nu, divided by the number of observations in the record, n.Equation 8 can be modified to obtain annual return levels for annual return period T (years) using the following expression:
wherePʹ
is the annual exceedance probability (AEP) for POT, that is, Pr(X > x) within a year or the number of exceedances of x per year, which is equal to 1/T; and
ny
is the number of observations in a block (for example, 365.25 for daily data in an annual block).
Comparing equations 8 and 10 shows that Pʹ = (1 − Gʹ)ny The parameters of the GP distribution can be fitted by the methods of ML, penalized ML, method of moments, and L-moments among others (Hosking and Wallis, 1987). The L-moments method is generally preferred for small sample sizes because it is less sensitive to outliers. The R programming software (R Core Team, 2020) has various packages such as extRemes (Gilleland and Katz, 2016), lmom (Hosking, 2019), ismev (Heffernan and Stephenson, 2018), and POT (Ribatet and Dutang, 2019) that implement various methods for stationary and nonstationary GP fitting. Various methods are documented in the literature to obtain confidence intervals for the GP quantiles. According to Claps and Laio (2003), asymptotic formulas for the variance of the GP quantiles usually provide a poor approximation of the actual variance because of the probability distribution of the quantiles generally being skewed. The variance of the quantiles tends to be proportional to the inverse of the sample size (1/Nu).
The GP and GEV distribution families are theoretically interconnected in that they share a common shape parameter. The location and scale parameters of both distributions are linked by the following expression (Coles, 2001):
This equation contains two variables that must be solved for and thus cannot be solved for individual GEV parameters unless an additional equation is found.The probability that the annual maximum of the excesses is less than some value y is given by
wherePr(N = 0)
is the probability of no exceedances in a year,
N
is the number of exceedances of the threshold u in a year;
ne
is one possible value for the number of exceedances of threshold u in a year; and
is the sum of the joint probabilities of n exceedance events in a year and that all excesses Y1... are less than the value y.
Shane and Lynn (1964) proposed that the arrivals of POT occur according to a homogeneous Poisson process, that is, the peaks occur randomly and independent of one another. Under this assumption, the number of exceedances of the threshold u in a year, N, has a Poisson distribution with mean λ, where λ is the mean number of threshold exceedances in a year (N~Poisson[λ]). It is also assumed that the occurrence process is independent of the excesses. The mean time between exceedances (in years) is therefore the reciprocal of the mean number of exceedances per year (1/λ). Under these assumptions, equation 12 becomes
Recalling that y represents an excess (y = x – u), equation 13 would be identical to the form of the GEV if equation 11 holds and if
The mean number of threshold exceedances in a year, λ, can be estimated from the data and is equal to the product of ny and ζu. Knowing λ, the equivalent GEV parameters can be obtained from the GP parameters on the basis of the following expressions:
Therefore, Poisson occurrences with identically distributed GP exceedances lead to an annual maxima distribution given by the GEV distribution (Davison and Smith, 1990). If occurrences are Poisson and threshold excesses belong to the GP family, then the annual maxima follow a GEV distribution. The POT and annual maxima approaches are expected to lead to the same results asymptotically.A more elegant approach is the Poisson point process (PP) model, whose log-likelihood function considers the joint distribution of the number and size of the excesses over threshold u. The solution to the PP model fits the GEV parameters directly from excesses above the threshold u. Fitting the GP and GEV by using the PP approach to exceedances one duration at a time was also tested, and the problem of CDF crossing and inconsistent DDF curves across durations persists, even with longer POT sample sizes compared to the annual maxima approach (GEV fits). As previously mentioned, this problem is likely exacerbated by the use of correction factors to obtain unconstrained rolling sums and occurs regardless of which method is used to fit the GP parameters one duration at a time.
Various methods exist in the literature to determine a reasonable threshold u that balances (1) the potential for large parameter bias from too low a threshold, invalidating the model asymptotics and biasing results, and (2) the potential for a large parameter (and quantile) variance caused by the use of too high a threshold that reduces the available data for fitting. For example, the mean residual life plot, the parameter stability plots, and the dispersion index plot are defined in Coles (2001). Despite the existence of these methods, the selection of a threshold tends to be subjective and is difficult to automate to fit thousands of GP models without user intervention. Therefore, thresholds are often defined on the basis of high percentiles of precipitation depths for each duration of interest and some criteria such as the desired number of exceedances per year (λ) for each duration. For example, Langbein (1949) recommends 3–4 annual floods per year be included in the analysis of PDS for floods. On the basis of theoretical considerations, Cunnane (1973) showed that for return periods above 10 years, the PDS estimate of the return levels for floods has a smaller sampling variance than the annual maxima only if there are at least 1.65 exceedances per year, on average. This condition holds for the POT model with exponentially distributed peaks. However, Madsen and others (1997) showed that the minimum number of average exceedances per year recommended to minimize the sampling variance of the PDS estimate depends on the value of the shape parameter, the record length, and the fitting method. For a return period of 100 years, a 50-year record length, a shape parameter ranging from −0.3 to +0.3, and using the ML method, at least 1.1–1.4 exceedances per year, on average, are required for the sampling variance of the return level based on PDS to be comparable to that based on the annual maximum series. In the case of ML estimation, for a 30-year record length and a return period of 100 years, they found that the PDS model should always be preferred (that is, PDS is better than annual maximum series when there are more than 0.4 exceedances per year on average).
Threshold exceedances often tend to occur in clusters, which violates the assumption that threshold exceedances are independent. A declustering technique therefore must be implemented prior to GP fitting. The extremal index, θ, is a measure of the degree of dependence between exceedances in a stationary sequence, with values less than one implying some dependence (clustering) with increasing dependence as the value decreases (Leadbetter, 1983). Dependence affects the limiting distribution that is reached. The extremal index has been interpreted as the limit of the reciprocal of the mean cluster length as the threshold increases. Two methods are frequently used to calculate the extremal index: the runs method (Coles, 2001) and the intervals method (Ferro and Segers, 2003). The runs method consists in choosing a run length, r, and any extreme observations separated by fewer than r nonextreme observations belong to the same cluster. Only the maximum exceedance within the cluster is chosen for fitting. In this case, the extremal index is estimated as the ratio of the number of clusters found to the total number of exceedances in the sequence (Ferro, 2003). A problem with this method is that the selection of r is mostly arbitrary and can have a major influence on the estimation of θ (Hsing, 1991).
The intervals method first estimates the extremal index θ. The distribution of the Poisson intensity parameter, ζu, integrated between consecutive inter-exceedance times in the general case of dependence and in the limit as the threshold increases is a mixed distribution with mass of (1 – θ) at zero (in practice, for small inter-exceedance times) and an exponential function with mean of 1/θ that is weighted by θ (Ferro, 2003). In this case, θ has a dual role of being the proportion of nonzero inter-exceedance times and the reciprocal of the mean of the nonzero inter-exceedance times. The value of θ is obtained by equating raw theoretical moments of the mixed distribution to empirical moments and is interpreted as the proportion of inter-exceedance times that can be regarded as inter-cluster times. The nc-largest inter-exceedance times (where nc = θ* Nu is the number of clusters in the sample) can be assumed to be approximately independent inter-cluster times that divide the remainder into approximately independent sets of intra-cluster times. Then, the nc-largest inter-exceedance time, Tc, is taken as the optimal run length, r, that is subsequently used for runs declustering. Again, only the maximum exceedance within each cluster is chosen for fitting the GP.
The traditional ML method for fitting the GP distribution is described hereafter. Assuming that the excesses, yi, above threshold u for a given duration are independent and identically distributed, the log-likelihood function for the GP for a given duration is given by
whereis the log-likelihood function for the GP,
θ
is the set of parameters for the GP (,
L(θ)
is the likelihood function for the GP,
n
is the number of excesses, yi, for a given duration, and
g
is the probability distribution function for the GP.
When implementing an optimization technique to determine the set of parameters that maximize the log-likelihood (eq. 17), several constraints are added. The first constraint is that the scale parameter, , must be positive, and the second constraint is that the quantity must be positive. These constraints can be incorporated into an optimization scheme that minimizes the negative log-likelihood function (which is the negative of equation 17) by returning infinite values when any of these constraints are not met, or by using an augmented Lagrange multiplier technique (Müller, 2018).
Rather than applying a fixed ad hoc offset to quantiles for a duration and assigning this value to quantiles for a longer duration or employing DDF smoothing techniques, here the traditional ML approach is modified, and a constrained maximum likelihood (CML) method is developed to obtain consistent DDF curves. This approach was motivated by the approach used by Polarski (1989) to fit a three-parameter Weibull distribution to annual minimum flows of different durations while assuring noncrossing CDFs. In the CML approach, the GP parameters are fit for all durations at once by assuming that exceedances are independent between durations. First, a functional form is assigned for the variation of the GP scale and shape parameters with duration. From exploratory GP fits performed one duration at a time, both parameters were found to vary linearly with duration for the durations of interest (1, 3, and 7 days). The scale parameter tends to increase with duration whereas the shape parameter tends to decrease with duration and even become negative in a large number of cases for the 7-day duration. The decrease in the shape parameter with duration is consistent with the expectation that high precipitation intensities may not be sustainable for long time periods. Although negative shape parameters are thought unlikely to occur in climatology, Ribereau and others (2011) provides examples in which negative shape parameters have been observed. Here, a linear functional form for the GP parameters is assumed, which is given by
wherea0, b0
are the intercept and slope for the GP scale parameter, respectively; and
a1, b1
are the intercept and slope for the GP shape parameter, respectively.
Next, the joint log-likelihood is defined for all durations of interest (1, 3, and 7 days) at once as
whereis the joint log-likelihood function for the GP for all durations;
θ
is the set of parameters defining the variation of the GP parameters with duration (a0, b0, a1, b1) according to equations 18 and 19;
dmax
is the maximum duration of interest (here 7 days);
nd
is the number of excesses, yi,d, for a given duration, d; and
yi,d
is the ith excess for a given duration, d.
The minimization of the negative of is implemented by using the optim function in the R programming software package stats (R Core Team, 2020). In addition to the constraints in the traditional ML approach, constraints are added to ensure that return levels for a given duration are larger than for a shorter duration. The constraints are added by making sure that the negative log-likelihood function, which the optim function tries to minimize, returns a positive infinite value whenever the quantile for a duration minus the corresponding quantile for a shorter duration is less than or equal to zero. This CML method results in consistent DDF curves by design and is a pragmatic approach that slightly compromises the GOF within individual durations in exchange for consistency between durations. In addition, the CML method avoids potential overfitting to noisy data for a given duration by reducing the number of parameters to be fit from six (one scale and one shape parameter per duration) to four (intercept and slope for the variation of each parameter with duration). The degradation in the GOF is quantified by comparing the sum of the log-likelihoods for the case when each duration is fit independently (traditional ML) to the joint log-likelihood for the CML approach. The Akaike Information Criterion (AIC) is then employed (Akaike, 1973) for model selection to determine the best model. The AIC penalizes extra model complexity, meaning that the addition of parameters must improve the model sufficiently to justify their inclusion. It balances the degradation in the log-likelihood with preventing overfitting. The AIC is given by
whereIn computing the AIC for the traditional ML approach of fitting the GP one duration at a time, the sum of the log-likelihoods for each individual duration is used for , and df equals six. For the CML approach, is used, and df equals four. The model with the lowest AIC is selected as the best model, but models with similar AICs are considered to be similarly good. The delta AIC (ΔAIC) is the relative difference between the AIC for the best model and each other model and it is given by
whereAICm
is the AIC for the suboptimal model m; and
AICmin
is the AIC for the best model (the one with the lowest AIC, here the traditional ML model).
Interpretation of the ΔAIC is subjective. However, Burnham and Anderson (2002) have provided the following criteria for interpreting the ΔAIC scores:
-
• ΔAIC < 2; indicates substantial evidence for the suboptimal model m.
-
• 3 < ΔAIC < 7; indicates less support for the suboptimal model m.
-
• ΔAIC > 10; indicates the suboptimal model m is unlikely.
Burnham and others (2011) later revised their guidance as follows:
Goodness-of-Fit Methods
Serinaldi and Kilsby (2014) used various statistical tests to determine whether precipitation excesses above a given threshold meet the basic statistical assumptions for POT. The significance of the lag-1 Kendall auto-correlation coefficient (KACF) for two consecutive excess values was used to test whether the precipitation excesses for a particular duration are independent. The Mann-Kendall trend test (MK) was used to detect possible monotonic trends in the time series of excesses. The existence of dependence and monotonic trends would bias the outcome of GOF tests for GP, which assume that observations are independent and identically distributed. These tests are available in the R programming software packages stats (R Core Team, 2020) and Kendall (McLeod, 2011).
The suitability of the GP distribution for modeling the excesses above a threshold for each individual duration can be assessed by using GOF tests. The Kolmogorov-Smirnov (KS), Anderson-Darling (AD), Cramér-von Mises (CVM), the Pearson product moment correlation coefficient on probability-probability plots (PPCCPP), and the Pearson product moment correlation coefficient on quantile-quantile plots (PPCCQQ) are used as GOF tests. Serinaldi and Kilsby (2014) implemented the first four of these GOF tests. These GOF tests are also discussed by Chowdhury and others (1991), Stephens (1993), and Kottegoda and Rosso (2008). These five statistical tests can be used to determine—for a preselected significance level—whether a sample belongs to a hypothesized distribution. These tests are based on the null hypothesis that two samples belong the same empirical distribution function (EDF) and are available in the R programming software packages stats (R Core Team, 2020) and goftest (Faraway and others, 2019).
The KS test is an exact test that does not depend on an adequate sample size to be applied. The KS test statistic measures the maximum distance between the hypothesized CDF and the EDF. Using the Weibull plotting position to define the EDF, the KS test statistic is given by
whereis the KS statistic,
i
is the index for the sample value and goes from 1 through ns;
zi
is the CDF value for the hypothesized distribution at the sample value xi [zi = F(xi)] and
ns
is the sample size.
The CVM test is similar to the KS test, but is a measure of the mean-squared difference between the hypothesized CDF and the EDF and is given by
whereThe AD test statistic is given by
whereThe KS test is more sensitive to differences near the center of the distribution than on the tails (NIST/SEMATECH, 2022a), whereas the CVM test looks at differences along the entire range of xi values (as shown in equation 24), and therefore the CVM test tends to be more powerful than the KS test under certain scenarios (D’Agostino and Stephens, 1986). In contrast, the AD test weighs the tails more than the central part of the distribution (NIST/SEMATECH, 2022b), given that the discrepancies between the hypothesized CDF and the EDF tend to generally be smaller in the tails than in the center (that is, because the EDF and CDF converge to 0 or 1 at the ends). For this reason, Stephens (1993) recommends the AD test more than the other two when the main objective is testing for outliers. However, preliminary analyses by Claps and Laio (2003) showed that the CVM test is more stable and has greater power than the AD test when evaluating the null hypothesis of the GP distribution, because the AD test gives too much weight to the left tail of the distribution.
The probability-plot correlation coefficient tests, PPCCPP and PPCCQQ, measure the linearity by means of the correlation coefficient of the probability-probability (P–P) and quantile-quantile (Q–Q) plots, respectively, which are generated from the hypothesized CDF and EDF and their quantile functions. Lower values of these two test statistics indicate more evidence against the null hypothesis that the data follow a GP distribution in this case. The PPCCQQ test was first introduced by Filliben (1975) as a test statistic for normality, but its use has been extended to other distributions with distribution-specific critical values derived by Monte Carlo methods (Vogel, 1986; Vogel and Kroll, 1989; Chowdhury and others, 1991). The PPCCQQ statistic is unaffected by either scaling or translation, and therefore, it tests whether the shape parameter of the sample distribution equals that of the hypothesized distribution. Heo and others (2008) have developed regression equations for the PPCCQQ test for several probability distributions in the case where the distribution’s shape parameter is prespecified. The PPCCPP test used in Serinaldi and Kilsby (2014) is less commonly used and is less sensitive to extreme and outlier values in the data because it relies on P–P values rather than Q–Q values. Tables of critical values for these tests for the case of the GP fit by ML for different sample sizes, and shape parameter values have not been located. The test statistics based on the Weibull plotting position are given as
whereis the PPCCPP statistic,
is the PPCCQQ statistic,
cor
is the Pearson product moment correlation function,
xi
are sample values, and
are quantiles of the hypothesized distribution, F, at the EDF values ().
One-sided versions of these GOF tests are used when one is concerned with deviations between the hypothesized CDF and the EDF regardless of their direction. The KS, AD, and CVM GOF tests are distribution-free only in the simple null hypothesis case when the distribution hypothesized is predetermined (that is, parameters are prespecified and not computed from the sample, called “Case 0” in the literature), the distribution function is continuous, the data are uncensored, and there are no ties in the empirical quantiles. The critical values for the simple case of prespecified distribution and parameters are generic and easily obtained from R functions on the basis of the sample size. Asymptotic critical values can generally be used for sample sizes greater than 25 or 30 samples, which is the case here. However, when these statistical tests are used as GOF statistics in the composite hypothesis case where the sample is compared to a distribution having unknown parameters, standard critical values do not apply. This case in which the parameters of the hypothesized distribution are derived from the sample itself is called “Case p,” where “p” is the number of parameters estimated from the sample itself. In this case, one must use modified critical values that depend on the type of distribution one is testing against, the parameter values (shape parameter in the case of the GP), the sample size, and the method of parameter estimation (for example, ML, L-moments, among others).
Choulakian and Stephens (2001) provide asymptotic critical values for the GP fit by ML for the AD and CVM GOF statistics and state that these apply for ns > 25, consistent with Stephens (1993), which states that the percentage points (quantiles) for finite samples converge very quickly to the asymptotic points. The asymptotic percentage points depend on the shape parameter but not on the scale parameter of the distribution (Stephens, 1993). However, these are applicable to the case when one duration is fit at a time using ML. When using CML, one compromises the GOF slightly for consistency across durations. Therefore, the critical values derived by Choulakian and Stephens (2001) would tend to reject the null hypothesis that the sample comes from a GP distribution more often than in the ML case.
Stephens (1993) indicates that for the KS statistic, the percentage points will not depend on the true value of the scale parameter, but even asymptotic points are very difficult to calculate in “Case p.” Existing critical value tables have been developed by Monte Carlo methods. In the case of KS statistic, percentage points for finite samples do not converge rapidly to the asymptotic points and must therefore be determined by Monte Carlo methods for different sample sizes. Tables of KS critical values for the GP fit by ML for different sample sizes and shape parameter values were not located after an exhaustive literature search.
For all the reasons outlined above, a parametric bootstrapping approach is used to determine p-values for each of these GOF statistics when using the CML approach. The bootstrapping methodology is described in appendix 3. A significance level of 0.05 is used to test the null hypothesis that the sample comes from the GP distribution. Another advantage of the bootstrapping approach is that it can provide confidence intervals for the GP parameters as well as for the return levels of interest.
In addition to the GOF statistics described above, two other methods are used to determine whether the GP distribution is a reasonable distribution to model exceedances above a high threshold. First, the gamlss R package (Rigby and Stasinopoulos, 2005) is used to fit all the available probability distributions in the package that can model real positive values. Second, an L-moment ratio diagram is used to determine whether the excesses above the selected threshold at each location follow a GP distribution. Sample estimators of L-moments are linear combinations of probability weighted moments that use ranked observations and as such are less sensitive to outliers than conventional moments and ML estimators. Sample L-moments (denoted as Ln) can be used to estimate parameters of various frequency distributions by equating them to the true population L-moments for the distribution (λn). The first- and second-order sample L-moments are L-location (L1) and L-scale (L2). L-location is simply the mean of the sample. L-scale is related to the spread of the data. L-moment ratios of importance include L-CV (τ), L-skewness (τ3), and L-kurtosis (τ4). L-CV is the “coefficient of L-variation” and is calculated as the ratio of L-scale to L-location (L2/L1). Because L-skewness (L3/L2) and L-kurtosis (L4/L2) are normalized by L-scale, both are independent of scale. L-skewness quantifies the asymmetry of the sample, whereas L-kurtosis quantifies whether the samples are peaked or flat relative to the normal distribution. L-moment ratio estimators have been found to be nearly unbiased for all underlying distributions and are therefore preferred to product-moment-ratio estimators, which can be highly biased even for large samples from highly-skewed distributions (Vogel and Fennessey, 1993). The L-moment ratio diagram used here plots the relation between L-skewness and L-kurtosis, which can be compared to the theoretical relation for different probability distributions to determine the best-fitting distribution to the data. Probability distributions having no shape parameter are represented as a point in the L-moment ratio diagram, whereas probability distributions with a shape parameter are represented as a curve. More complex distributions having two shape parameters can be represented as areas or regions in the L-moment ratio diagram. The more the sample L-moments cluster around the point or curve, the better the specific distribution fits the sample data. The L-moment ratio diagram point and curve data for the distributions included in R package lmomco (Asquith, 2020) were accessed through the lmrdia function.
Areal Reduction Factors (ARFs)
ARFs are used in stormwater infrastructure design to convert point precipitation for a given duration and return period into areal precipitation over an area for the same duration and return period. Typically, the area of interest is a watershed. ARFs are also useful when comparing simulated precipitation between datasets with different resolutions. As demonstrated by Chen and Knutson (2008), precipitation output from climate models should be interpreted as areal means rather than as point values, and their use and analysis should remain consistent with that interpretation. Otherwise, large differences in precipitation fields among datasets with different resolutions may be misinterpreted as bias. If the comparison is performed at consistent spatial scales, the true bias may be smaller or even of a different sign. In the computation of DDF change factors, described in the “Multiplicative Quantile Delta Mapping” section, current and future ARFs are assumed to be constant so that they would cancel out. However, ARFs are still useful when assessing model performance by comparing modeled extremes against observed extremes.
The most commonly known ARF curves were developed by the U.S. Weather Bureau (now the National Weather Service) and are documented in Technical Paper No. 29 (U.S. Weather Bureau, 1958). The Weather Bureau’s ARF curves can be used to transform point precipitation to areal precipitation for durations from 1 to 24 hours and areas covering as much as 1,000 km2. The curves are based on annual maximum series data at gages in various networks throughout the United States. The gages used in computing ARF had relatively short record lengths (less than or equal to 16 years), which were averaged to obtain areal means of annual maximum series. The Weather Bureau ARFs consist of ratios of mean areal annual maximum series to station-based mean annual maximum series and represent ARFs for an approximately 2-year return period. In some of these earliest studies, ARFs were found to not exhibit systematic regional variations and to be independent of storm magnitude. Since then, ARFs have been studied in more detail and derived on the basis of longer and more spatially complete precipitation datasets for many regions of the United States and the world. ARFs have been found to vary according to the precipitation characteristics of the region under study. Svensson and Jones (2010) document some of these factors. For example, convective storms tend to be more localized than storms associated with frontal systems, resulting in smaller ARFs. In Florida, the seasonal pattern of these precipitation-generating mechanisms results in seasonal variations in ARFs. In some areas, ARFs have been found to decrease with increasing return period (Svensson and Jones, 2010; Kao and others, 2020), because the least frequent (most intense) storms tend to be convective and more localized in these areas. Studies have shown that ARFs decrease with decreasing duration (Olivera and others, 2006; Kao and others, 2020), because short-duration events tend to be more localized. For this reason, ARFs also tend to decrease with area more steeply for shorter durations than for longer durations. ARFs have also been found to vary depending on catchment characteristics, such as shape, topography, and urbanization, although this factor seems to be small (Svensson and Jones, 2010). Proximity to the coast and large water bodies may also affect ARFs.
The characteristics of the data used in developing ARFs, such as period of record, station density, interpolation method, and the methodology used in ARF estimation, will result in varying ARF estimates. Two main approaches for ARF computation are typically used: geographically fixed area ARFs, and storm-centered ARFs. Svensson and Jones (2010) present a review of these different ARF approaches. Storm-centered approaches define the point precipitation as the precipitation at the point having the maximum precipitation in a storm, which varies from storm to storm (Omolayo, 1993). Because of the complexity of this approach in view of storms with multiple centers and the fact that extreme point precipitation and extreme areal precipitation may not be produced by the same storm (Omolayo, 1993), fixed-area methods are most widely utilized and will be used here. In addition, storm-centered ARFs tend to be smaller than fixed-area ARFs and are, therefore, less conservative (Svensson and Jones, 2010).
To evaluate the performance of modeled precipitation extremes from datasets of various resolutions by comparison against observational datasets for a chosen historical period, grid-cell (areal) scale DDF curves were divided by ARFs to approximate station-scale (point-scale) DDF curves. The model-derived station-scale DDF curves for the historical period can then be compared to station-scale DDF curves from NOAA Atlas 14 volume 9 (Perica and others, 2013) or other sources. Because the station data used in developing the NOAA Atlas 14 DDF curves may include data for the period 1840–2008, depending on the station, all the precipitation data available from the historical period (1950–2005) of the downscaled climate datasets were used for this comparison. The two sets of historical DDF curves may not be completely comparable due to the differences inherent in the data and methods used to develop them, which include (1) different periods of record, and (2) different methods for DDF curve fitting (regional frequency analysis on annual maximum series for NOAA Atlas 14 versus CML for the downscaled climate model datasets). Therefore, differences between the two are to be expected.
Pavlovic and others (2016) describe four fixed-area methods that are commonly used in deriving ARFs. For this study, methods M1 and M4 from Pavlovic and others (2016) were tested. Method M1 is similar to that developed by the U.S. Weather Bureau, and results in ARFs that are a function of duration and spatial aggregation scale. Method M4 uses a frequency analysis approach whereby ARFs are estimated as the ratio of quantiles of GEV fits to areal and point annual maximum series for a given return period. Functional forms relating GEV parameters to area and (or) duration can be fitted for smoothing the resulting GEV fits, as done by Overeem and others (2009, 2010) and Pavlovic and others (2016), and ARFs can be derived from these fits. These ARFs will be a function of duration, spatial aggregation scale, and return period. In their review of various ARF methods, Svensson and Jones (2010) describe the advantages of using the Bell (1976) empirical ARF method, which is similar to method M4. The Bell method involves fitting a frequency distribution to areal and point annual maximum series and taking their ratio for the same return period.
The ARF approaches used in this study use the PRISM precipitation dataset discussed in the “Parameter-elevation Regressions on Independent Slopes Model (PRISM)” section. On the basis of the PRISM daily precipitation data from 1981 to 2019, annual maximum series were computed at various durations and spatial scales, which are required for most ARF methods. The procedure for computing the annual maximum series is similar to that of Pavlovic and others (2016); however, the spatial and temporal aggregation steps were reversed, which results in equivalent time series in the end. For PRISM grid cells in central and south Florida, spatial aggregation of the gridded data was performed first. This step consisted in first identifying areas of 1 × 1, 3 × 3, 5 × 5, 7 × 7, 9 × 9, 11 × 11, and 13 × 13 grid cells centered at each grid cell of interest and computing the spatial mean of the daily precipitation. These correspond to areas of approximately 18.9; 170.2; 472.8; 926.7; 1,531.9; 2,288.4; and 3,196.1 km2, respectively. If any of the n × n cells in an area had no precipitation data (for example, ocean cells in the PRISM dataset), then that area was excluded from subsequent computations. Therefore, areal means were obtained for a smaller and smaller number of cells as the spatial aggregation scale increased. The second step consisted of temporal aggregation of the areal mean precipitation to the durations of interest (1, 3, and 7 days). For durations of 3 and 7 days, rolling sums of the areal mean daily precipitation at each spatial scale were computed. The rolling sum time series can be used in implementing a CML approach to fitting the GP to develop ARF curves by a variation of method M4. Finally, the annual maximum value was extracted for each duration and spatial aggregation scale for each year in the period 1981–2019. Because of the order of operations, the annual maximum series for a given aggregation scale is the mean of concurrent precipitation values; however, annual maximum series at different aggregation scales may not be concurrent. Corrections from constrained to unconstrained annual maximum series were not applied, because these are assumed to cancel out in the computations.
In method M1, ARFs were computed from the temporal mean of the annual maximum series for each duration and spatial aggregation scale at each central grid cell according to
whereARF(d, A, c)
is the local areal reduction factor for a given central grid cell;
d
is the duration of interest;
A
is the spatial aggregation level (area, in square kilometers);
c
is the index for the central grid cell;
is the mean of the annual maxima series of precipitation for duration, d, and area, A, centered at grid cell c;
Ao
is the area of a grid cell (in square kilometers); and
is the mean of the annual maxima series of precipitation for duration, d, and area, Ao, centered at grid cell c.
In theory, ARF values should be less than one; however, occasionally, the ARF computed by equation 28 ends up slightly greater than one, in which case, that cell is eliminated for further analysis for the duration and spatial aggregation level where it occurs. This is a result of the mean annual maximum series at a grid cell being smaller than the mean annual maximum series for the n × n area centered at the grid cell because of the fact that the annual maximum series at different spatial scales may not be concurrent. Once the ARF is computed at each central grid cell based on equation 28, the mean of the ARF values for the aggregation scales and durations of interest are computed for climate regions defined in the State of Florida:
whereARF(d, A, h)
is the mean areal reduction factor by method M1,
h
is a climate region,
Nc,h
is the number of central grid cells within the climate region h, and
c
is the index for a central grid cell located within the climate region ().
Climatologically homogeneous precipitation areas determined by Pathak and others (2009) on the basis of rain-gage adjusted Next-Generation Radar (NEXRAD) data were initially used to define climate regions for ARF averaging. These homogeneous precipitation areas were defined on the basis of their mean precipitation and the spatial correlation of precipitation during the wet season in south Florida (June–October). One limitation of these homogeneous precipitation areas is that their spatial extent does not include areas outside the SFWMD boundary in central Florida. In addition, Welch’s t-tests for the null hypothesis of equal means of ARF across homogeneous precipitation areas showed that the mean ARF for some of these homogenous precipitation areas was very similar for the durations and spatial aggregation scales evaluated. Lumley and others (2002) state that in the case of large samples, the t-test is valid for any distribution, not just for normal distributions. They show that the test is valid for sample sizes as low as 65, even in the case of very skewed distributions. All of the homogeneous precipitation areas evaluated here contain between 97 and 315 PRISM grid cells at which ARF is calculated; therefore, the sample size is considered adequate for use of the Welch’s t-test for equality of means.
According to Pathak and others (2009), convection in the center of the southern Florida peninsula results either from local daytime heating or from the collision of thunderstorm outflow boundaries propagated away from storms associated with the east and west sea breezes and the Lake Okeechobee lake breeze. These mechanisms likely result in more consistent and less variable precipitation in these interior areas, relative to other areas, and similar ARFs. On the basis of the t-test results, some of these homogeneous precipitation areas were merged into larger climate regions. For areas outside the SFWMD, the NOAA National Centers for Environmental Information (NCEI) Florida climate divisions (Guttman and Quayle, 1996) were used to define climate regions for ARF averaging in central Florida (fig. 7). Shapefiles of the boundaries of the NOAA NCEI U.S. Climate Divisions in the State of Florida are available from NOAA (2011).
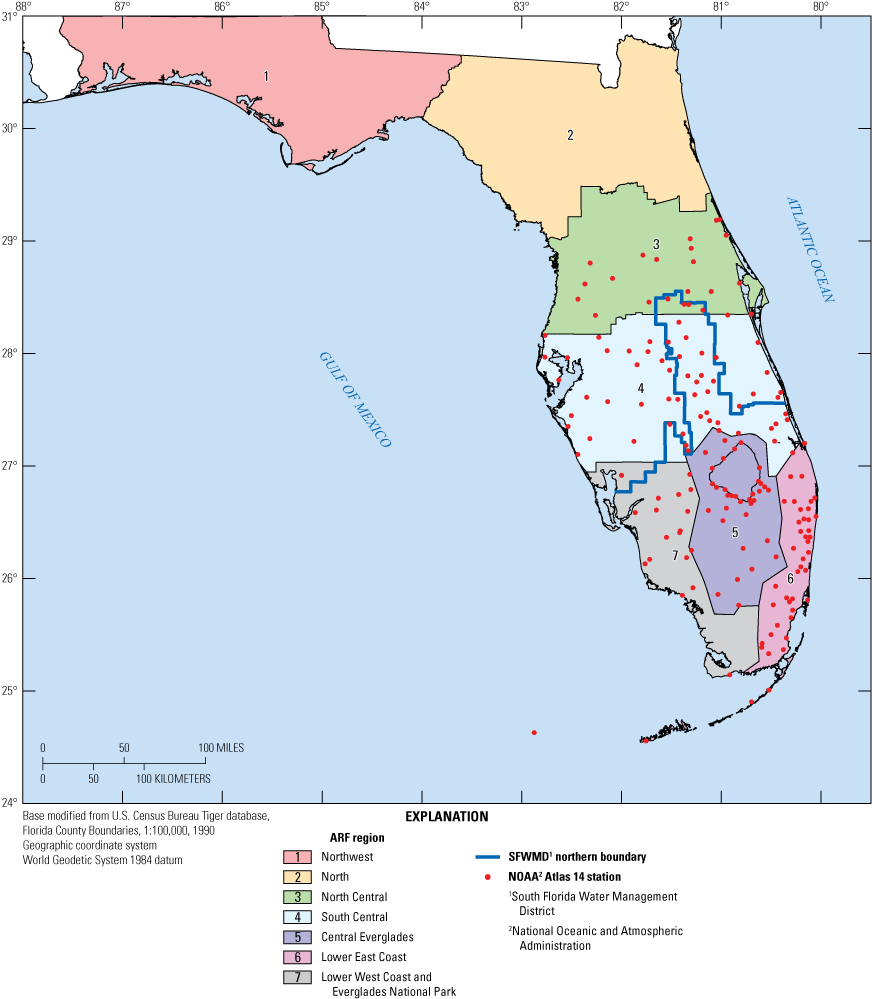
Areal reduction factor (ARF) regions for the State of Florida.
A modified version of ARF method M4 in Pavlovic and others (2016) was also tested by fitting the GP to rolling sums of durations 1, 3, and 7 days at once using the CML approach for each spatial aggregation level of interest. The ARFs for this method consist of ratios of DDF curves at a spatial aggregation level of interest to the 1 × 1 aggregation level and are a function of duration, return period, and spatial aggregation level.
Multiplicative Quantile Delta Mapping
Quantile mapping (QM), a CDF-matching method (Panofsky and Brier, 1968), is typically applied to bias-correct precipitation time series from climate model simulations, but the method can similarly be used to bias-correct annual maximum series of precipitation or DDF curves. It can also be used on its own as a form of statistical downscaling that attempts to bridge the scale mismatch between the model grid-cell estimates and the point observations. However, this can result in misrepresentation of the spatiotemporal structure of the corrected time series and overestimation of area-mean extremes (Maraun, 2013). The expression for QM is given by
whereis the adjusted quantile for the model, m, projections for the future projection period, p;
is the inverse of the CDF (that is, the quantile function) of the observations, o, in the historical baseline period, h;
is the CDF of the model, m, in the historical baseline period, h; and
is the quantile for the model, m, projections in the future projection period, p.
The CDFs are typically developed from data spanning decades and centered around some year of interest. QM only uses information from the historical period to correct for future biases; therefore, it assumes that biases are stationary and that they will persist into the future (Cannon and others, 2015). In other words, QM assumes that Fo,p (the CDF of the observations in the future projection period) is approximated by Fo,h so that as the mean changes, the variance and skew do not, which may not be the case under climate change (Zhang and Zwiers, 2013; Pendergrass and Hartmann, 2014a; Pendergrass and others, 2017). Furthermore, if a future projected value is outside the historical range, then some sort of extrapolation is required and that affects extremes (Wootten, 2018).
To avoid the limitations of traditional QM, other methods have been developed such as quantile delta mapping (QDM). As shown in Cannon and others (2015), QM tends to inflate trends in precipitation extreme indices projected by GCMs, whereas QDM is not as prone to this problem. QDM preserves model-projected changes in quantiles, while simultaneously correcting for systematic biases across quantiles (Cannon and others, 2015). QDM also attempts to bridge the gap between point estimates for the observations versus grid cell estimates in the model. However, it is important to note that changes in the mean may not be adequately preserved by QDM.
QDM can be applied in an additive form, which corresponds to the Equidistant Quantile Mapping algorithm of Li and others (2010), or a multiplicative form, which corresponds to the Maximum Intensity Percentile Based Method of Wang and others (2013). Additive QDM is better suited to correcting biases in air-temperature variables, whereas multiplicative quantile delta mapping (MQDM) is better suited to correcting variables such as precipitation where preserving relative changes is important in order to respect the Clausius-Clapeyron (CC) relation (Wallace and Hobbs, 2006), which relates the amount of atmospheric moisture to temperature changes. Lanzante and others (2021) confirmed the superiority of MQDM over additive QDM by means of a “perfect model” experiment.
In this study, the MQDM version of QM was chosen to bias-correct projected future DDF curves (fig. 8). Multiplicative QDM is given by the following alternative equations and is applied to each duration of interest independently:
whereis the inverse CDF (that is, the quantile function) of the adjusted, adj., model, m, projections for the future projection period, p;
F
is equal to , the annual nonexceedance probability for the model, m, projections in the future projection period, p, and is equal to 1 – P = 1 – 1/T;
T
is the annual return period, in years;
P
is the annual exceedance probability (AEP), which is equal to 1/T; and
Fm,p
is the CDF for the model, m, projections for the future projection period, p.
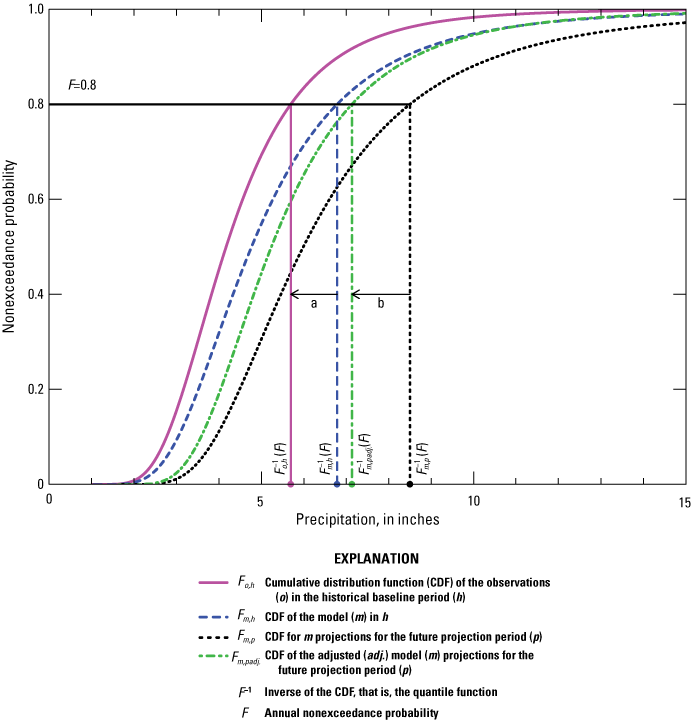
Multiplicative quantile delta mapping (MQDM) method for hypothetical data. The distances a and b are different in MQDM because of the use of a ratio in the bias-correction equation. The distances a and b would be equal in additive quantile delta mapping method.
The term in equation 32 is the bias-correction factor and the term in equation 33 is the change factor for the particular nonexceedance probability (or return period), and duration. The inherent assumption is that the relative change between historical and future projected conditions can be indicative of future changes in DDF curves even if the models are biased. The ultimate goal of this study is to obtain change factors from the historical period (1966–2005) to the future projection period (2050–89) across the locations of NOAA Atlas 14 stations in the SFWMD. These change factors could then be applied to the PDS-based DDF curves from NOAA Atlas 14 to obtain future projected DDF curves.
NOAA Atlas 14 stations in the Florida Keys (08-2418, 08-4570, 08-5035, and 08-8841 in appendix 1, table 1.1) are inactive in most downscaled model grids (fig. 4A–E). Data from the closest mainland grid cells to these four stations were used in developing DDF curves at these four locations. Therefore, change factors developed for these four locations are highly uncertain and should be used with caution.
Derivation of Change Factors
The following is a description of the analytical steps used to derive change factors based on CORDEX, LOCA, and MACA downscaled climate datasets (fig. 6). For each dataset, the closest grid cells to each of the 174 NOAA Atlas 14 stations in central and south Florida were identified for each of its models. For each of these grid cells, rolling sums of daily precipitation were computed using R package RcppRoll (Ushey, 2018) to obtain the cumulative 3- and 7-day precipitation totals. This process was repeated for each climate model run for historical and future projection periods for each RCP scenario in each dataset. Similar to the annual maxima approach used in developing NOAA Atlas 14 volume 9 by Perica and others (2013), it is expected that all extreme values might be downward-biased because of being constrained to a clock-based interval (that is, a consistent daily timestep). Therefore, rolling sums for the durations of interest were multiplied by correction factors (table 1; Perica and others, 2013) to convert constrained precipitation totals to unconstrained precipitation totals for each duration, that is, to the maximum precipitation for any time period of the given duration. In the annual maxima case, once constrained annual maxima are computed, a consistency check is typically made to ensure that constrained annual maxima for a given duration are larger than for a smaller duration. When that is not the case, an ad hoc small offset (usually on the order of 0.1 in.) is applied to the shorter duration annual maxima to obtain the annual maxima for a longer duration. However, the same process was not followed for the unconstrained rolling precipitation time series from which exceedances were computed because durations of interest (1, 3, and 7 days) are not a multiple of each other and, therefore, longer duration events do not contain a discrete number of shorter duration events. For example, a 7-day event overlaps two 3-day events and a 1-day event (or part of a 3-day event) at the beginning or end of the 7-day event. Despite this, checks were made to ensure that the selected exceedances for each duration are larger than for shorter durations overall by comparing their CDFs.
A POT approach was used to fit the GP probability distribution to exceedances above a high threshold as described in the “Peaks-Over-Threshold” section. This requires the selection of a high threshold of precipitation, which tends to be subjective and is difficult to automate to fit thousands of GP models without user intervention. Therefore, thresholds were defined for every location (grid cell) on the basis of a high percentile of the precipitation totals for each duration that would result in 2–3 exceedances per year (λ) for each duration after declustering. The chosen percentiles were 99th, 98th, and 97th for 1-, 3-, and 7-day durations, respectively. Because of the use of rolling sums of precipitation for various durations (d), there is a high degree of dependence between the d-day precipitation values and their exceedances over a threshold. This is in addition to the inherent temporal correlation in precipitation totals within a region. That is, the exceedances above a given threshold tend to cluster, especially as the threshold is reduced. Therefore, a declustering technique was implemented, and the goal was for the declustered time series to have 2–3 exceedances per year on average. The intervals method of Ferro and Segers (2003) was attempted to determine the ideal run lengths for declustering. However, the run lengths obtained from this method varied substantially across stations, ranging from about 1 to 30 or more days depending on duration. Because a physically based reason for the large variation in run lengths could not be identified, the runs declustering method in the extRemes package from R (Gilleland and Katz, 2016) was used with run lengths equal to the duration in days, plus 1 day. In other words, run lengths of 2, 4, and 8 days were chosen for 1-, 3-, and 7-day durations, respectively. Our choice of run length for the 1-day event is similar to that of NOAA (2022a), which found that dependent events in the time series of exceedances do not affect the precipitation frequency estimates significantly and that declustering the daily exceedances using a 1-day separation period between exceedance events would be adequate. The run length is the number of threshold deficits to be considered as starting a new cluster. These run lengths were chosen to exclude neighboring (clustering) rolling sum precipitation values that include the same high precipitation days. The GP is then fit to cluster maxima, hence the POT approach.
The extRemes package from R (Gilleland and Katz, 2016) was used to compute the interval-based extremal index of the exceedances declustered by the runs declustering method with prespecified run lengths. The objective of this exercise is to confirm that the exceedances declustered on the basis of prespecified run lengths are reasonably independent. A cutoff value of 0.7 for the interval-based extremal index, θ, was assumed to be indicative of adequate tail independence.
Subsequently, the GP was fitted one duration at a time using the traditional maximum likelihood (ML) approach and for all durations at once using the CML approach at each model grid cell. The resulting GP fits based on the CML approach are used to derive DDF curves by using the quantile function of the GP for each duration and converting the return periods of interest into nonexceedance probabilities. The CML approach results in consistent DDF curves across durations at each model grid cell but slightly compromises GOF compared to the traditional ML approach of fitting one duration at a time; however, the CML approach also reduces the number of parameters that are being fit. This tradeoff between model fit and parameter parsimony is quantified by means of the AIC. In addition, a bootstrapping approach was used to determine GOF for the GP.
The resulting DDF curves apply at the grid-cell scale and must be divided by appropriate ARFs to obtain station-scale values for both historical and future projection periods. Assuming the historical ARF applies to the future projection period, the ARF would cancel out in the computation of change factors. However, the ARF allows for comparison of the station-scale DDF curves fitted to simulated historical precipitation data as part of this study against the NOAA Atlas 14 PDS-based DDF curves that were fitted to historical observations of precipitation. Finally, the MQDM method was used to compute change factors as the ratio of the future projected DDF precipitation depth to the historical DDF precipitation depth for each station grid cell in each downscaled climate dataset.
Model Culling
Model culling refers to the process by which some models are eliminated from further analysis, and the remaining subset of climate models (called “best” models, hereafter) are selected to inform future changes in impact-relevant climate variables. The “best” models are defined on the basis of a series of performance measures of relevance to the region and variables of interest. The performance measures are typically based on how well the models reproduce historical observations at weather stations or in comparison to observational gridded products in the region of interest. For this study, precipitation extremes and their return periods in central and south Florida are of the utmost importance. The use of the word “best” within double quotes is to emphasize that these models are the ones that best reproduce historical observations, but we do not imply that these models would necessarily perform best in simulating the future climate or result in the most accurate change factors.
The Expert Team on Climate Change Detection and Indices (ETCCDI; http://etccdi.pacificclimate.org/list_27_indices.shtml) has defined climate extremes indices based on daily precipitation data. The original ETCCDI indices and variations thereof (Zhang and others, 2011) have been used by many researchers worldwide to assess the performance of GCMs and downscaled climate products (see, for example, Donat and others, 2013; Sillmann and others, 2013a, b; and Srivastava and others, 2020). Several ETCCDI precipitation extreme indices were selected to quantify model performance, as documented in table 9. The ETCCDI precipitation extreme indices were supplemented with additional indices of relevance to this study listed in table 9. Preliminary evaluation of precipitation extreme indices for the various downscaled climate datasets used in this study showed correlation between some of the indices and that only a very small number of models remained when model culling was based on all the indices listed in table 9. Based on the desire to include as many models as possible to inform the potential range of future change factors, a decision was made to only use four precipitation extremes indices in selecting the best models. These selected indices consist of annual maxima of consecutive precipitation for durations of 1, 3, 5, and 7 days, and are the most relevant to the estimation of precipitation extremes.
Table 9.
Extreme precipitation indices evaluated in this study.[All indices are recommended by the Expert Team on Climate Change Detection and Indices except those indicated as supplemental indices. Italicized indices were used in selecting best models. ID, identifier; mm, millimeter; ≥, greater than or equal to; <, less than]
Two different reference observational datasets were used to evaluate historical precipitation extremes indices in this study: the SFWMD “Super-grid” and PRISM. Various studies have found that the model performance in capturing climate extremes indices varies depending on the reference dataset chosen (Gleckler and others, 2008; Sillmann and others, 2013a, b; Donat and others, 2014; Wang and others, 2020). The SFWMD “Super-grid” and PRISM observational datasets were chosen for validation of precipitation extreme indices over the gridded observational precipitation datasets used in bias correction of the downscaled data used in this study (Livneh, Daymet, and gridMET). This choice was made for several reasons. PRISM was chosen as a reference dataset on the basis of Behnke and others (2016), who found that out of the seven gridded datasets evaluated (including Daymet and Livneh), PRISM best captured daily precipitation statistics and climate extremes indices at meteorological stations from the Florida Automated Weather Network (FAWN). The R95p and R99p indices (table 9), which are defined as the annual total precipitation from days with precipitation above the 95th and 99th percentiles of precipitation in the base period, respectively, are exceptions where PRISM performed more poorly than the other gridded datasets. Zhang and others (2018) also evaluated five gridded precipitation products for the State of Florida including PRISM, Real-Time Mesoscale Analysis, and three interpolation methods for FAWN data. They found that PRISM resulted in better fit with the daily FAWN precipitation dataset when evaluated at stations. The SFWMD “Super-grid” dataset is considered by the SFWMD to be the most complete gridded precipitation dataset for south Florida. Here, the common 25-year historical period between PRISM and the downscaled datasets (1981–2005) was chosen as the base period for computation of percentiles in the percentile-based indices and for calculation and performance evaluation of the precipitation extremes indices.
The precipitation extremes indices are calculated using Python code developed by Gibson (2021). The Python code relies on Python bindings (Max Planck Institute for Meteorology, 2022a) to the Climate Data Operators (CDO; Max Planck Institute for Meteorology, 2022b). The Python code was evaluated to make sure it followed the ETCCDI climate extreme index definitions in table 9 and cross-validated against the CDO ECA climate indices package. All precipitation extremes indices were calculated at the native resolution of the downscaled climate model and observational datasets.
The CDO utility remapnn was used to remap the climate indices computed for the CORDEX, LOCA, and MACA downscaled climate datasets to the grids of the PRISM and SFWMD ”Super-grid” datasets using nearest-neighbor interpolation. Nearest-neighbor interpolation was used so as not to add information to the downscaled climate datasets that was not already there to begin with. In essence, the assumption was made that the node values from CORDEX, LOCA, and MACA models represent mean grid cell values, and the node value was assigned to all PRISM and SFWMD “Super-grid” locations having their centroid within a model grid cell. It is important to note that although the resolution of the indices may be the same for the reference and downscaled datasets after remapping, differences in climate indices are to be expected because of differences in the native scale of each dataset and the order of steps followed in remapping (that is, climate index computation first, followed by remapping, or vice versa). For example, climate indices are calculated on the basis of the approximately 4-km spatial mean of daily station precipitation that was used for each PRISM grid cell. In contrast, climate indices are calculated from the 25- to 50-km daily precipitation simulated for each CORDEX grid cell (which is representative of the mean daily precipitation at those scales as described by Chen and Knutson, 2008) and then assigned to all PRISM cells or SFWMD ”Super-grid” cells located within the area of the CORDEX grid cell.
To summarize the spatial pattern match of each climate index in the downscaled datasets to the reference dataset, various performance measures from Gleckler and others (2008), Sillmann and others (2013a), and Srivastava and others (2020) were used. These performance measures were evaluated separately for two distinct climate regions in central and south Florida (fig. 2). The climate regions were defined as the NOAA (2011) U.S. Climate Divisions for the State of Florida with Florida climate divisions 5, 6, and 7 merged into a single region named “south Florida” and called “climate region 5” hereafter.
The root-mean-square error (RMSE) statistic is used to summarize the performance of each model in capturing the climatology (long-term mean for 1981–2005) of each index calculated from the reference dataset at the model resolution:
whereRMSEm,I
is the RMSE statistic for climate index I in model m,
c
is the index for a grid cell in model m,
C
is the number of grid cells in model m,
is the climatological mean of index I at grid cell c for model m after remapping to the scale of the observational dataset, and
is the climatological mean of index I at grid cell c for the reference observational dataset o.
The best models will have a small RMSEm,I. The relative performance of a model in simulating the climatological mean of the reference observational dataset can be computing by normalizing the RMSEm,I as follows:
whereNRMSEm,I
is the normalized RMSE statistic for climate index I in model m, and
RMSEmed,I
is the median of the RMSE statistic across all models in a particular downscaled climate dataset for climate index I.
The median is used for normalization to avoid undue influence by outlier models having unusually large errors. The best models will have a large negative NRMSEm,I, indicating that the model performs better than most models. A large positive NRMSEm,I indicates that the model performs worse than most models. To quantify the overall performance of a model in simulating the climatological mean of all indices, the Model Climatology Index (MCI) from Srivastava and others (2020) was used, but it was modified to use the mean of the NRMSEm,I values over all indices for a particular model as opposed to the median.
In addition to the spatial pattern in the climatological mean, it is important to quantify how different models capture the spatial pattern of the inter-annual variability of each climate index from gridded observations. For this purpose, the inter-annual variability skill score (Chen and others, 2011; Jiang and others, 2015) was used, which is defined as
whereIVSSm,I
is the inter-annual variability skill score statistic for climate index I in model m,
σI,m,c
is the interquartile range (difference between 75th and 25th percentile) of index I at grid cell c for model m after remapping to the scale of the observational dataset, and
σI,o,c
is the interquantile range (difference between 75th and 25th percentile) of index I at grid cell c for the reference observational dataset o.
The best models will have a small IVSSm,I. The relative performance of a model in simulating the interquartile range of the reference observational dataset can be computed by normalizing the IVSSm,I as follows:
whereNIVSSm,I
is the normalized inter-annual variability skill score for climate index I in model m, and
IVSSmed,I
is the median of the inter-annual variability skill score across all models in a particular downscaled climate dataset for climate index I.
The best models will have a large negative NIVSSm,I, indicating that the model performs better than most models. A large positive NIVSSm,I indicates that the model performs worse than most models. To quantify the overall performance of a model in simulating the inter-annual variability of all indices, the Model Variability Index (MVI) from Srivastava and others (2020) was used but was modified to use the mean of the NIVSSm,I values over all indices for a particular model as opposed to the median. Finally, the MCI and MVI for each model can be plotted as a scatterplot, and the best performing models will have the largest negative MCI and MVIs.
Results
The methods described in previous sections were applied to derive change factors for extreme precipitation events at model grid cells closest to 174 NOAA Atlas 14 stations in central and south Florida. Future changes in the timing of extreme events may or may not correlate directly with changes in the annual cycle of precipitation. However, changes to the seasonality of precipitation combined with sea-level rise will affect the mean antecedent groundwater conditions prior to extreme precipitation events, which will, in turn, influence flood peaks and flood timing. Figure 9 shows the mean annual cycle of precipitation for the historical period (1966–2005) and the future period (2050–89) as simulated in each downscaled climate dataset for the two main climate regions of interest in the SFWMD (fig. 2), south-central Florida (climate region 4) and south Florida (climate region 5). The range of the mean annual cycle of precipitation in historical simulations from different climate models in each downscaled climate dataset tend to match the annual cycle of precipitation from PRISM, the SFWMD “Super-grid,” and the datasets used in bias correction reasonably well. Each downscaled climate dataset was bias-corrected to different gridded observational datasets; therefore, as expected, they match the bias-correction datasets better than they match PRISM and the SFWMD “Super-grid” in the historical period. The variability shown in the historical simulations is likely due, at least in part, to the longer period used in bias-correcting each downscaled climate dataset than the 40-year historical period chosen here for DDF calculation. CORDEX and MACA use more than one bias-correction dataset and also exhibit more variation in the historical annual cycle, especially during the wet season when there are larger differences between bias-correction datasets. CORDEX exhibits more variability in the historical simulations than the other two datasets, with a general overestimation of precipitation during the wet-dry season transition months of May and October, and an underestimation in June. This finding may be explained by the use of a 3-month sliding window in bias correction of each central month in CORDEX as described by Cannon (2018). For those transition months, the 3-month sliding window increases the sample size by mixing data from drier and wetter months in developing the cumulative density functions used in the MBCn quantile-mapping algorithm and might alter the annual cycle of precipitation, as described by Lanzante and others (2021).
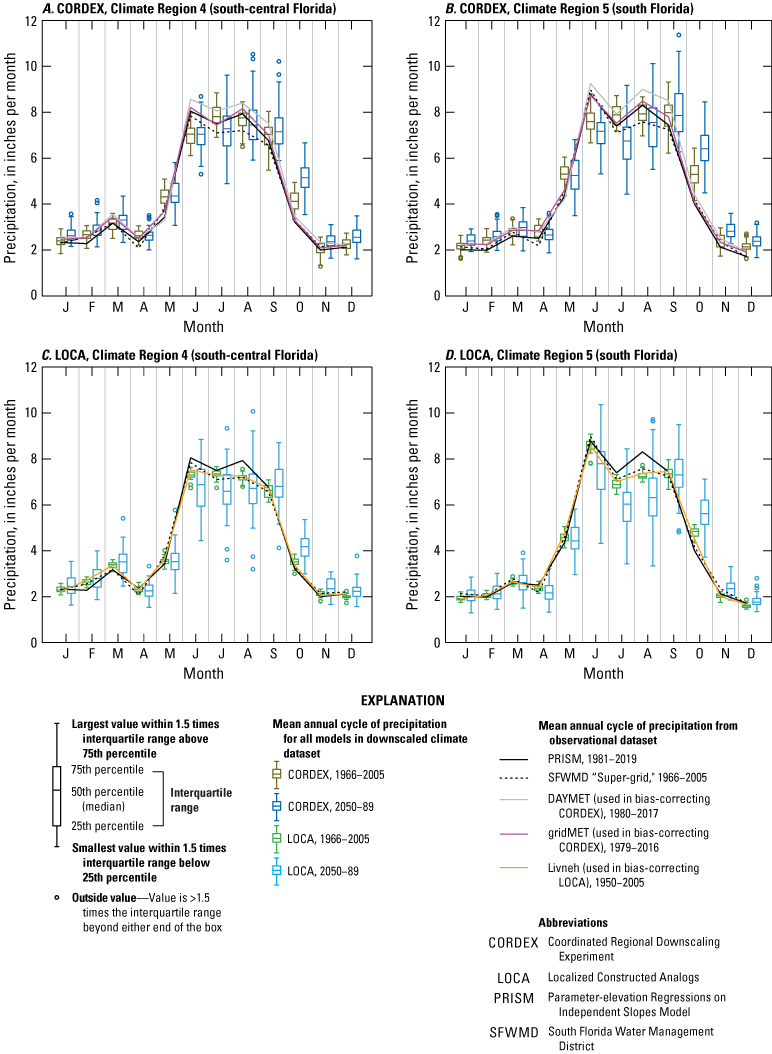
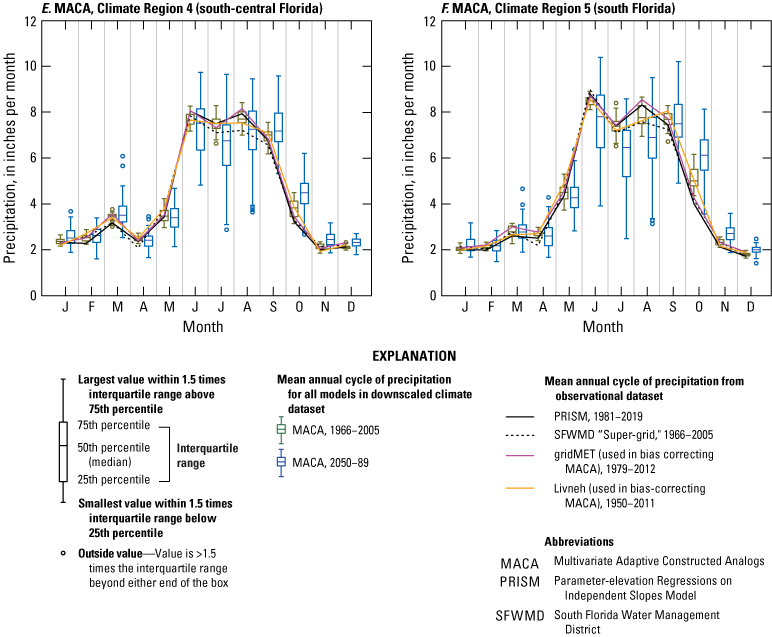
Mean annual cycle of precipitation for the historical period (1966–2005) and the future period (2050–89) as simulated in each downscaled climate dataset for south-central Florida (climate region 4) and south Florida (climate region 5). The green and blue boxplots are the mean annual cycle of precipitation for the historical (1966–2005) and future projection (2050–89) periods, respectively, for all models in a downscaled climate dataset. On the graph, the historical observations are aligned with the corresponding historical boxes on the x axis.
Using raw output from the CORDEX models prior to bias correction, Srivastava and others (2022) show that some CORDEX models are not able to capture the annual cycle of precipitation in Florida, with some models completely out of phase or not able to capture the cycle’s amplitude. The inability of some CORDEX models to capture the annual cycle of precipitation in Florida may be a result of the GCM boundary conditions used to drive the RCMs; however, this does not appear to be the sole factor because some RCMs used to downscale the same GCM perform better than others. Spot checks of the annual cycle for some GCMs showed mixed results. For example, the MPI-ESM-LR GCM shows a similar annual cycle to the raw CORDEX downscaled output with maximum precipitation in September. The CanESM2 GCM shows a similar annual cycle to observations although with a dry bias, but its annual cycle is different from the raw CORDEX downscaled output. Most RCMs evaluated by Srivastava and others (2022) underestimate precipitation from June through August and overestimate it during the rest of the year. The bias-correction algorithm used by CORDEX generally fixes the seasonality problem as shown in figure 9.
Future projections for different climate models in each downscaled climate dataset (fig. 9) have a large range of variation in wet-season precipitation for both climate regions 4 and 5. The median projected change in the mean annual cycle of precipitation from the historical period (1966–2005) to the future period (2050–89) in all datasets (fig. 10) indicates a shift in the seasonality of wet-season precipitation with a reduction in June–August precipitation followed by an increase in September–November precipitation and smaller increases in other dry-season months. Larger changes are expected for climate region 5 in south Florida, consistent with predictions of drying of the Caribbean region extending into south Florida, as shown in some climate models during summer (Misra and others 2011; Taylor and others, 2018).
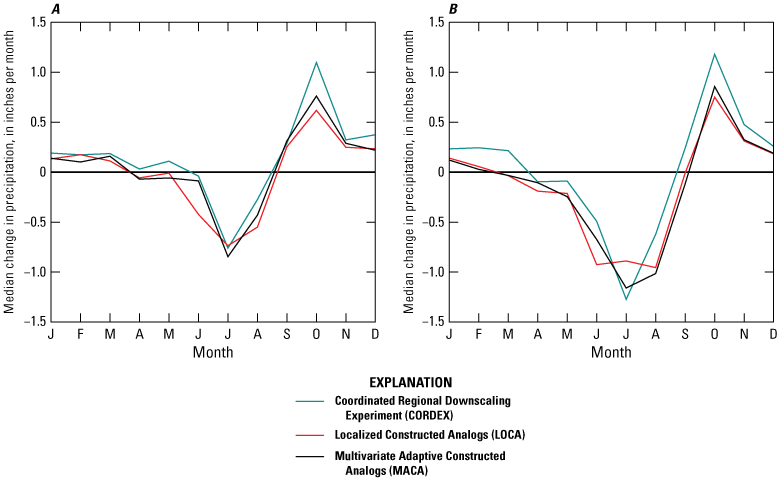
Median change in the mean annual cycle of precipitation from the historical period (1966–2005) to the future period (2050–89) as simulated in each downscaled climate dataset for, A, south-central Florida (climate region 4) and, B, south Florida (climate region 5).
Constrained Maximum Likelihood
The CML approach was used to fit the GP distribution to declustered precipitation excesses for durations of 1, 3, and 7 days, for the periods 2050–89 and 1966–2005 at every grid cell closest to each of the 174 NOAA Atlas 14 stations in central and south Florida. Overall, after declustering the precipitation excesses using run lengths equal to the duration plus 1 day, it was determined that more than 95 percent of grid cells had an extremal index (as calculated from the intervals method of Ferro and Segers, 2003) of 0.8 or greater in both periods and for all models in all downscaled climate datasets. This increases confidence that the declustering was adequate for the vast majority of cells. This approach was applied to the CORDEX, LOCA, and MACA downscaled climate datasets. Figure 11 is an example of the declustering of precipitation excesses above the 99th percentile threshold (1.49 in.) for a LOCA grid cell centered at lat. 25°5ʹ37.5ʺ N, long. 80°5ʹ37.5ʺ W. The figure shows the threshold corresponding to the 99th percentile of the daily precipitation at this grid cell (1.49 in.) as well as the daily precipitation data. The original data above the threshold line were eliminated from the GP fitting by the declustering method because they are considered to be part of the same event. The declustered exceedances correspond to the maximum values for each cluster and were used for GP fitting.
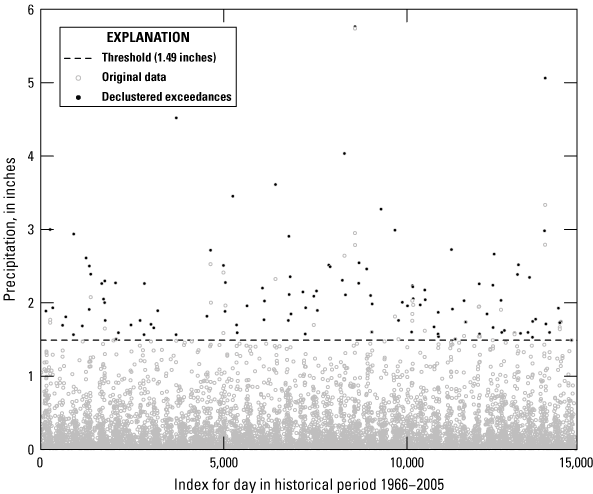
Example of declustering of daily precipitation time series for a Localized Constructed Analogs (LOCA) dataset grid cell for the period 1966–2005 for a precipitation duration of 1 day and a run length of 2. Grid-cell center location is lat. 25°5ʹ37.5ʺ N, long. 80°5ʹ37.5ʺ W.
Figure 12 shows the mean annual cycle of the number of 1-day declustered threshold exceedances for the historical period (1966–2005) and the future period (2050–89) as simulated in each downscaled climate dataset for the two main climate regions of interest in the SFWMD (fig. 2), south-central Florida (climate region 4) and south Florida (climate region 5). The 1-day threshold exceedance events were selected on the basis of the 99th percentile of the daily precipitation time series for each period and location independently; therefore, the actual threshold value used in defining the events varies between periods. The range of the mean annual cycle of the number of 1-day threshold exceedances in the historical simulations from different climate models in each downscaled climate dataset tends to match the annual cycle from PRISM, the SFWMD “Super-grid,” and the datasets used in bias correction reasonably well, with the exception of CORDEX. Each downscaled climate dataset was bias-corrected to different gridded observational datasets; therefore, as expected, they match the bias-correction datasets better than they match PRISM and the SFWMD “Super-grid” in the historical period. The exceptions are some CORDEX models that show a more uniform annual distribution of the number of 1-day threshold exceedance events than the observational and the other downscaled climate datasets. An investigation into CORDEX RCM runs driven by ERA-Interim reanalysis (Simmons and others, 2007) boundary conditions showed that the annual distribution of the number of 1-day threshold exceedances was also quite uniform in those runs, especially in south-central Florida. This indicates a problem with the way some RCMs simulate the timing of extremes, and this issue does not appear to be completely corrected by the bias-correction procedure. This may be a consequence of the inability of many raw CORDEX models to capture the annual cycle of precipitation discussed in the “Results” section and the bias-correction algorithm amplifying large simulated events during months when the observational datasets tend to show fewer extreme events. Of the RCMs driven by ERA-Interim reanalysis that were evaluated, the WRF model at 25-km and 50-km resolutions best captures the seasonality of 1-day threshold exceedances. However, other models such as CanRCM4 are better at capturing the mean annual cycle of precipitation than WRF.
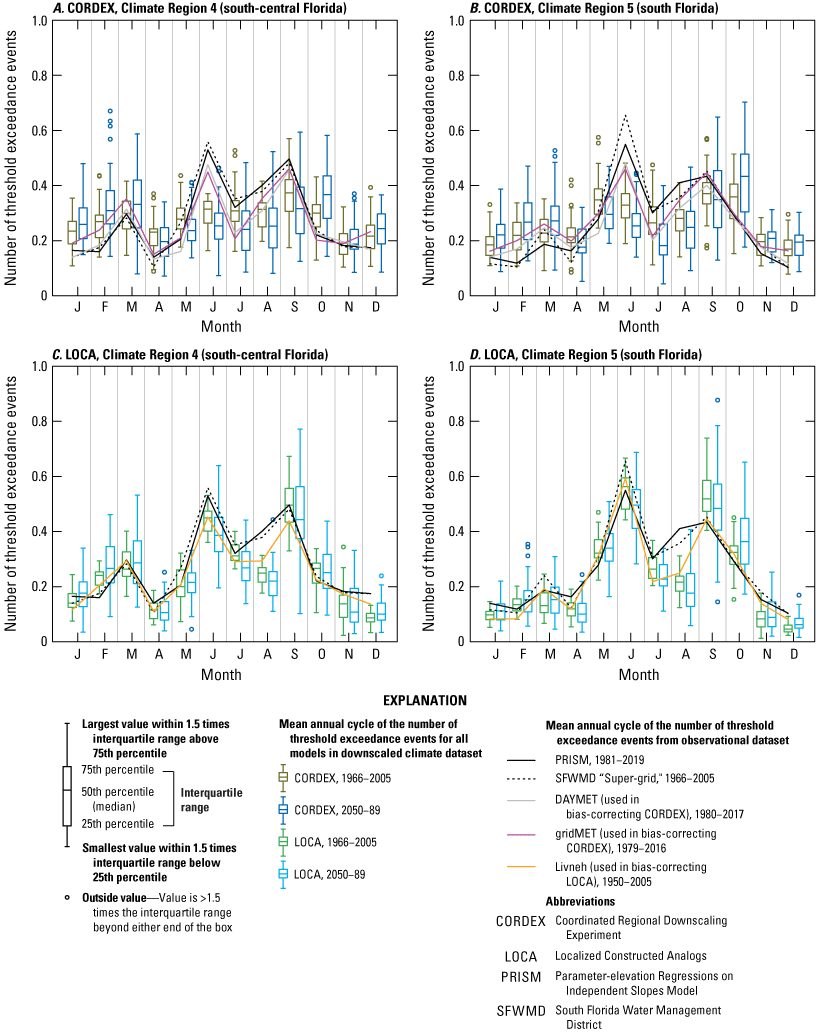
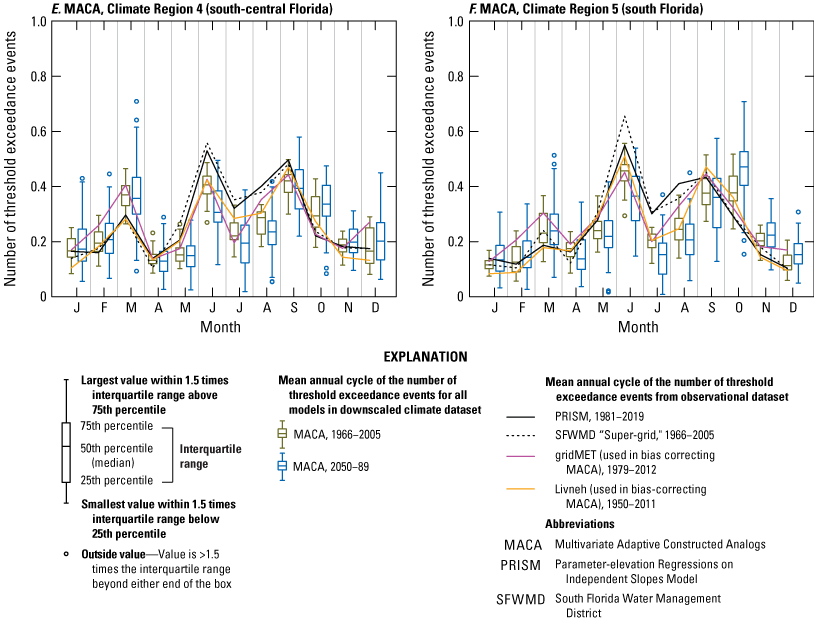
Mean annual cycle of the number of 1-day declustered threshold exceedance events for the historical period (1966–2005) and the future period (2050–89) as simulated in each downscaled climate dataset for south-central Florida (climate region 4) and south Florida (climate region 5). The green and blue boxplots are the mean annual cycle of threshold exceedance events for the historical (1966–2005) and future projection (2050–89) periods, respectively, for all models in a downscaled climate dataset. On the graph, the historical observations are aligned with the corresponding historical boxes on the x axis.
Comparison of figures 9 and 12 shows a similar seasonality in the mean annual cycle of precipitation and the mean annual cycle of 1-day threshold exceedance events. However, the amplitude of the annual cycle of 1-day threshold exceedance events is smaller than that of precipitation. A decline in the mean precipitation and an even more pronounced decline in the number of 1-day threshold exceedance events is observed for July compared to June and August. This pattern is likely due to precipitation during July being more driven by local convection as opposed to tropical storms. This explanation is consistent with Winsberg (2020), who found that for most of the State, the monthly frequency distribution of torrential precipitation is bimodal, peaking in June and September. Winsberg (2020) explained the June peak as resulting from the Intertropical Convergence Zone moving north and having more of an influence on the local weather and the September peak as being caused by the greater frequency of tropical storms reaching the State during that month, which corresponds to the peak of the Atlantic hurricane season.
Figure 13 shows the median change in the mean annual cycle of the number of declustered threshold exceedance events from the historical period (1966–2005) to the future period (2050–89) for durations of 1, 3, and 7 days, as simulated in each downscaled climate dataset for south-central Florida (climate region 4) and south Florida (climate region 5). In the case where the percentile-based threshold is allowed to vary between the historical and future periods, the median projected change in the mean annual cycle of the number of declustered threshold exceedance events in all datasets (fig. 13, solid lines) indicates a future decrease in the number of 1-day threshold exceedances from April to September in CORDEX, and from June to September in LOCA and MACA in both climate regions. MACA also shows a decrease in May for climate region 5 in south Florida (fig. 13B). A future increase in the number of 1-day threshold exceedances is predicted by all datasets in October and to a lesser extent, in some dry-season months. These future changes are consistent with those of the mean annual cycle of precipitation, although more months are affected. However, these conclusions are based on the threshold changing from the historical to the future period based on predefined percentiles, consistent with the way the threshold is defined in fitting the GP distribution in each individual period. When the percentile-based historical threshold is used consistently to define exceedance events for the historical and future periods, the median change in the number of threshold exceedance events (fig. 13, dashed lines) is generally higher than in the case where the threshold varies between periods (fig. 13, solid lines). This means that the percentile-based historical threshold will be exceeded more often in the future period than in the historical period according to the models; viewed another way, it means that the threshold defined on the basis of percentiles within a period increases from the historical to the future period. The main exception to this is LOCA in climate region 5 (south Florida) for all three durations, where on an annual basis, the median change in the number of threshold exceedance events is slightly higher in the case when the threshold varies between periods (fig. 13B, D, F, “LOCA varying threshold”) than in the case where the historical threshold is used in both periods (fig. 13B, D, F, “LOCA historical threshold”). This indicates that the percentile-based thresholds decrease slightly from the historical to future periods for all three durations in LOCA. Another exception is the 7-day duration from MACA in climate region 5 (south Florida), where on an annual basis, the median change in the number of threshold exceedance events is slightly higher in the case when the threshold varies between periods (fig. 13F, “MACA varying threshold”) than in the case where the historical threshold is used in both periods (fig. 13F, “MACA historical threshold”). Overall, the median change in the number of future exceedance events for all durations (fig. 13) follows a similar seasonal pattern as the projected median changes to the mean annual cycle of precipitation (fig. 10), regardless of whether the future events are defined on the basis of the historical threshold or using the future data to define the percentile-based future threshold. In both cases, the number of future exceedance events is generally projected to increase during the dry season (particularly in October) and decrease during the wet season.
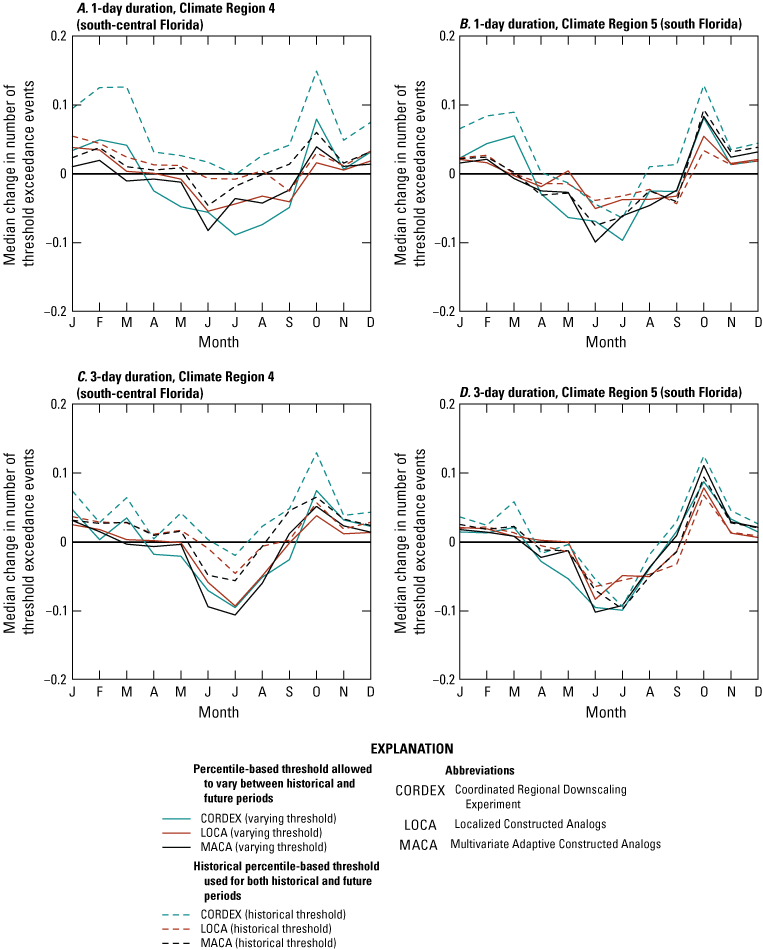
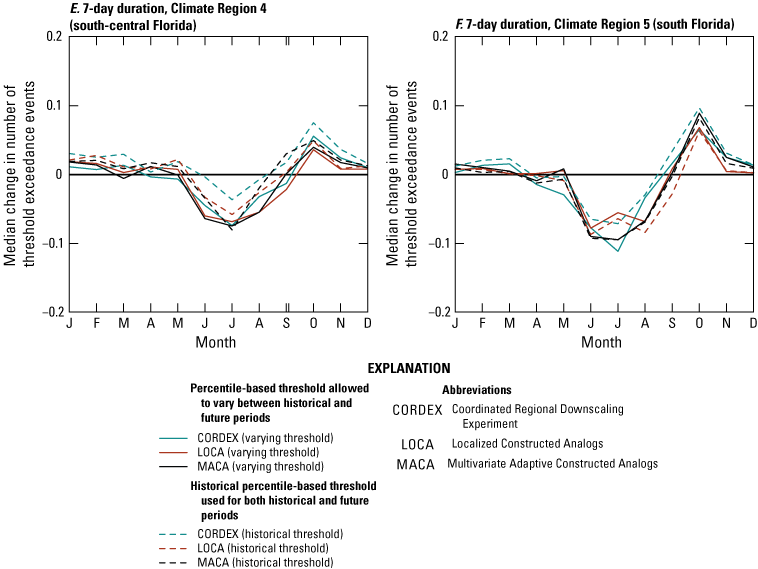
Median change in the mean annual cycle of the number of declustered threshold exceedance events from the historical period (1966–2005) to the future period (2050–89) for durations of 1, 3, and 7 days, as simulated in each downscaled climate dataset for south-central Florida (climate region 4) and south Florida (climate region 5).
Lastly, figure 14 shows the GP fits obtained from the CML method at the LOCA grid cell centered at lat. 25°5ʹ37.5ʺ N, long. 80°5ʹ37.5ʺ W. The corresponding DDF and intensity-duration-frequency curves are shown in figure 15.
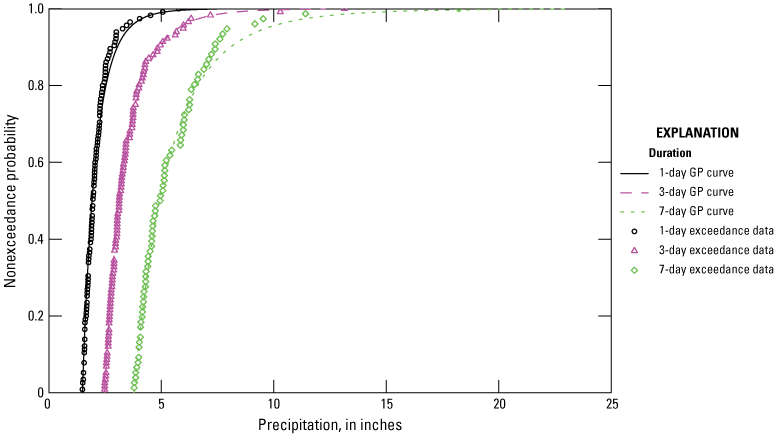
Example of generalized Pareto (GP) distribution fits for 1-, 3-, and 7-day duration for a Localized Constructed Analogs (LOCA) dataset grid cell for the period 1966–2005. Grid-cell center location is lat. 25°5ʹ37.5ʺ N, long. 80°5ʹ37.5ʺ W.
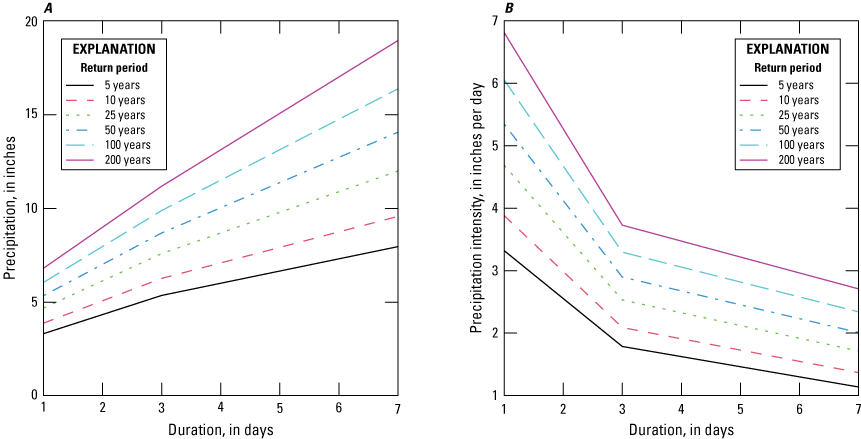
Example of, A, depth-duration-frequency (DDF) and, B, intensity-duration-frequency (IDF) curves for 1-, 3-, and 7-day duration for a Localized Constructed Analogs (LOCA) dataset grid cell for the period 1966–2005. Grid-cell center location is lat. 25°5ʹ37.5ʺ N, long. 80°5ʹ37.5ʺ W.
Figure 16 shows boxplots of the distribution of the delta AIC (ΔAIC) for all grid cells in all models for each downscaled climate dataset in the historical (1966–2005) and future projection (2050–89) periods. The ΔAIC is being calculated with respect to the traditional ML model (that is, in equation 22 is the AIC of the traditional ML model). In this case, a ΔAIC value of −4 (−2 × 2, where 2 is the number of fewer parameters in the CML model) indicates that the negative log-likelihood of the CML and traditional ML models are the same and that GP fits have no degradation when using the CML model as opposed to the ML model. Values of ΔAIC greater than −4 indicate some degradation in the CML model compared to the traditional ML model, as reflected in larger negative log-likelihood values. Overall, median values of ΔAIC range from −3 to −2 for all downscaled climate datasets and periods. It is evident that more than 95 percent of grid cells have values below the ΔAIC thresholds of 2 and 7 for which the (simpler) CML model has substantial evidence and support compared to the traditional ML model, according to Burnham and Anderson (2002) and Burnham and others (2011), respectively. Very few cells exceed the threshold of 7 units. The tradeoff between a slightly higher negative log-likelihood and a simpler model that results in consistent DDF curves automatically seems justifiable on the basis of these results.
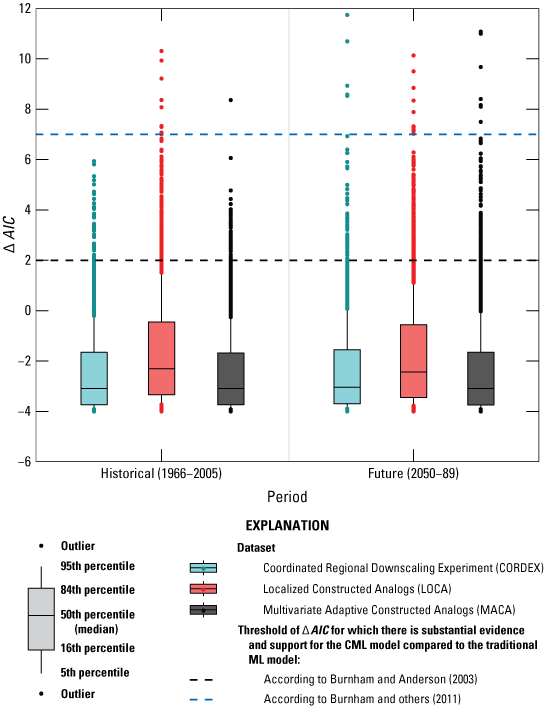
Boxplots showing the distribution of the delta Akaike Information Criterion (ΔAIC) by downscaled climate dataset in the historical (1966–2005) and future projection (2050–89) periods, and thresholds of ΔAIC for which there is substantial evidence and support for the constrained maximum likelihood (CML) model compared to the traditional maximum likelihood (ML) model.
Goodness of Fit
Figure 17 shows bar graphs indicating the percentage of model grid cells with p-values less than 0.05 for the lag-1 KACF and the MK trend test on excess values in the historical (1966–2005) and future projection (2050–89) periods. The null hypothesis that precipitation excess data are not autocorrelated is measured by the KACF, whereas the null hypothesis that it does not exhibit monotonic trends is quantified by the MK test. The nominal rate line in figure 17 represents the expected percentage of rejections of the null hypothesis when it is true, which is the significance level or expected nominal value of 5 percent. Also shown in this figure is the 95-percent prediction interval for the significance level under multiple comparison testing and under the assumptions that the data are uncorrelated and that the number of false rejections of the null hypotheses follows a binomial distribution as in Serinaldi and Kilsby (2014). The prediction interval is slightly wider for CORDEX than for LOCA and MACA, reflecting the smaller number of grid cells with NOAA Atlas 14 stations in them because of its lower resolution compared to LOCA and MACA. The percentage of rejections of the null hypothesis of no autocorrelation and no trend are close to the nominal value for most periods and durations. The main exception is CORDEX for which the null hypothesis is rejected more often than the nominal rate for the 1- and 7-day MK tests in the historical period. The 1- and 3-day MK tests for CORDEX in the future period also show slightly larger rejection rates than the nominal rate. Another exception is MACA for which the null hypothesis rejection rate is slightly larger than the nominal rate for the 3-day MK test in the historical period, for the 1- and 3-day MK test in the future projection period. The 1- and 7-day MK tests for LOCA in the future projection period also have rejection rates slightly larger than the nominal rate. The 7-day KACF test for MACA in the historical period also shows a rejection rate that is slightly larger than expected. It should be noted that the maximum rejection rate obtained for the MK tests is 8.2 percent, which is comparable to the 7–8-percent rejection rates corresponding to the 98th percentile-based threshold chosen by Serinaldi and Kilsby (2014) in fitting the GP to rainfall observations for the period 1970–2011. On the basis of these results, we conclude that it is acceptable to use a stationary approach in fitting the GP for these two 40-year periods.
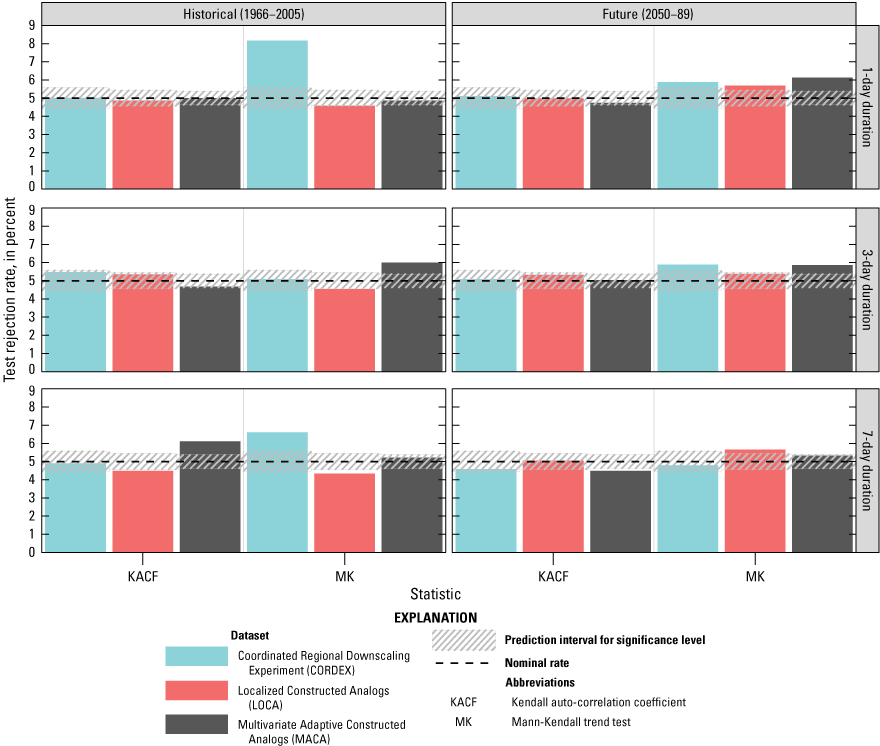
Percentage of model grid cells with a p-value less than 0.05 for peaks-over-threshold (POT) statistics in the historical (1966–2005) and future projection (2050–89) periods by downscaled climate dataset for durations of 1, 3, and 7 days.
Individual MACA models show more variability, with higher percentages of grid cells (as much as about 50 percent) for which the null hypothesis is rejected in a sizeable number of models, especially for the MK test. This result implies that the excesses in MACA are showing significant monotonic trends, most notably in the future projection period. This result is consistent with findings that MACA amplifies the change signal in the native GCMs (Lopez-Cantu and others, 2020; Wang and others, 2020), which would invalidate the assumption of stationarity within historical and future projection periods in a subset of MACA models, in which case a nonstationary model may be more appropriate. It is also possible that the presence of positive autocorrelation in the excess time series may be causing an overestimation of the significance of the computed trend, resulting in rejecting the null hypothesis of no trend more often than according to the chosen significance level of 0.05 (von Storch and Navarra, 1995). As discussed by Serinaldi and Kilsby (2015), when using nonstationary models, there is a high degree of subjectivity in defining how the parameters of the extreme value distribution might vary in time which increases uncertainty in return levels. There is also an inherent assumption that these parameter variations will hold for the entire future design life period. It is also difficult to parse out multidecadal natural variability influences from trends induced by climate change in nonstationary models. Therefore, for simplicity, the stationarity assumption is assumed to be valid.
Figure 18 shows bar graphs indicating the percentage of model grid cells for which the null hypothesis that the historical (1966–2005) and the future projected (2050–89) precipitation excess data follow a GP distribution is rejected at the 0.05 significance level for each duration in each downscaled climate dataset. The p-values are bootstrapped on the basis of the CML assumption, as discussed in the “Peaks-Over-Threshold” section and appendix 3. Results are only shown for the model grid cells closest to the 174 NOAA Atlas 14 stations used in this study. The figure shows a nominal rate of 5 percent and a 95-percent prediction interval for the significance level. Overall, CORDEX tends to perform worse for the 1-day duration compared to the other datasets, especially in the future period, with rejection rates that are much higher than the nominal rate of 5 percent that is expected by chance if, in fact, all data follow a GP distribution. For the 1-day duration, only MACA in the historical period frequently shows rejection rates below 5 percent. LOCA tends to perform worse than the other datasets for 3- and 7-day durations. Limited GOF testing based on the traditional ML approach with bootstrapping shows a similar percentage of rejections indicating that the performance deterioration when using CML does not have a large influence on the large test rejection rates for the GOF statistics and that, in fact, the raw excess data do not always seem to follow a GP distribution.
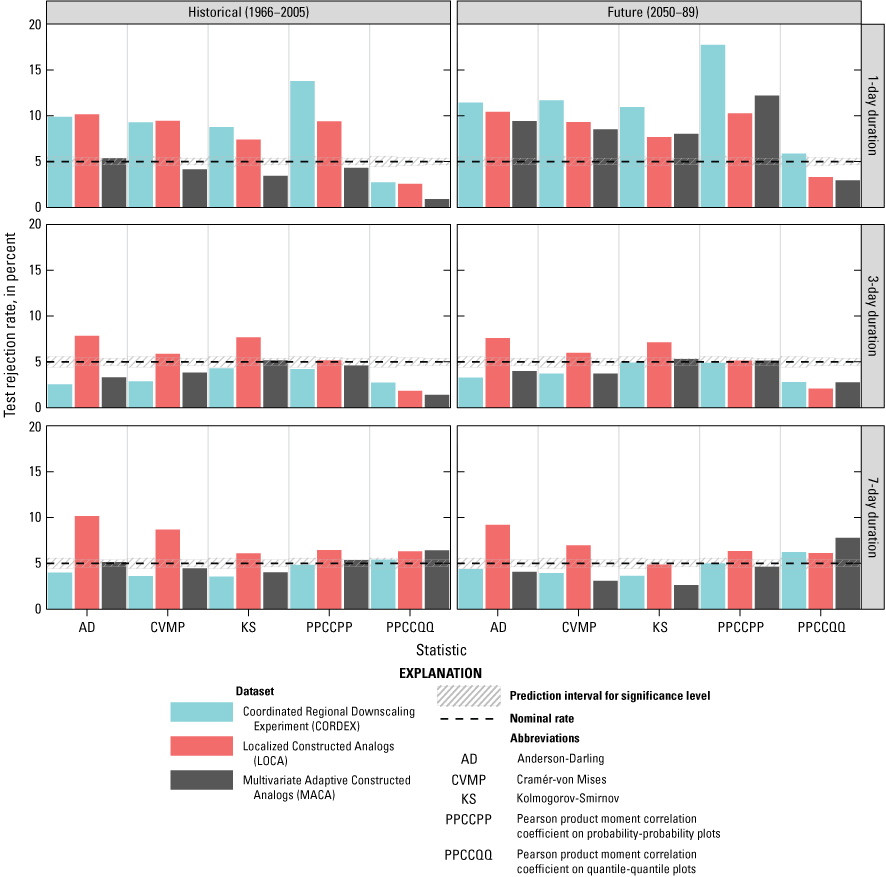
Percentage of model grid cells with p-value less than 0.05 for goodness-of-fit (GOF) statistics in the historical (1966–2005) and future projection (2050–89) periods by downscaled climate dataset for durations of 1, 3, and 7 days.
Figure 19 shows L-moment ratio diagrams for precipitation excesses in the historical (1966–2005) and future projection (2050–89) periods for each downscaled climate dataset. JupiterWRF is only included in the 1-day panel because 3- and 7-day durations were not evaluated for this dataset. The empirical L-moment ratios for all datasets shown in figure 19 tend to follow the generalized Pareto (GP) line shown in the figure. Although not shown, the centroid of the empirical L-moments for each individual model in a downscaled climate dataset and the overall centroid for each dataset and time period are located along the GP line. Also, as the duration increases the cloud of points shifts from the portion of the GP curve to the right of the exponential (“EXP”) point shown in the figure, which corresponds to positive shape parameters, to the portion of the GP curve on the left of the exponential point, which corresponds to negative shape parameters. This shift reflects a general decline in shape parameters with duration. Some LOCA points show lower L-skew and L-kurtosis especially for the 1-day duration, indicating a tendency for lower GP shape parameters and lower extremes in both periods. There is also a tendency for higher L-kurtosis in the future projection period (fig. 19B) than in the historical period (fig. 19A), indicating a tendency for higher GP shape parameters and higher extremes in the future. A portion of the cloud of points to the left of the exponential point tends to be located somewhat below the GP curve. The fact that the cloud of data seems to define an area of the L-moment ratio diagram indicates that three- or four-parameter distributions may be more flexible in fitting the data than the GP distribution. The generalized Beta Type 2 (4 parameters; Papalexiou and Koutsoyiannis, 2012; Chen and Singh, 2017) is an alternative distribution for modeling extremes, of which Burr Type III, generalized Gamma, Log-logistic, Burr Type XII, GP, and GEV are special cases. The log-Pearson Type 3 distribution (three parameters) is another commonly used distribution in modeling extremes (Griffis and Stedinger, 2007). These more complex distributions, which have more than one shape parameter and cover an area of the L-moment ratio diagram as opposed to a curve, may be useful in modeling the points in the L-moment ratio diagram that diverge most from the GP curve. However, a more complex distribution will not necessarily give more accurate results because the same amount of data will be used in fitting more parameters, which may result in overfitting. It is also possible that the scatter in the L-moment ratio diagram may be due to the use of a constant percentile to define the threshold for each duration at all locations as opposed to determining an optimal threshold for each specific location.
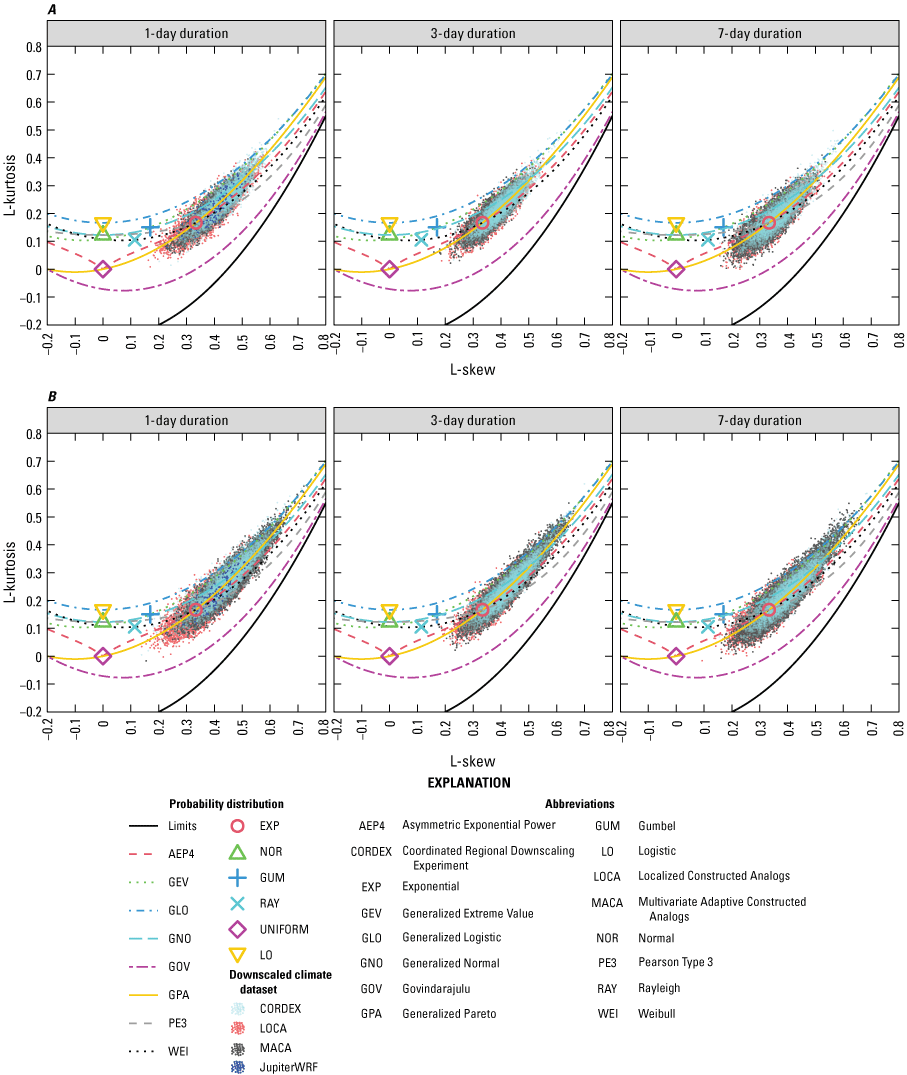
L-moment ratio diagrams for threshold exceedances in, A, the historical period (1966–2005) and, B, the future projection period (2050–89) by downscaled climate dataset. The large points correspond to probability distributions with no shape parameter and the curves correspond to probability distributions with a shape parameter.
Figure 19 also shows more points farther to the right of the GP curve in the future projection period compared to the historical period, which reflects an overall tendency for larger shape parameters and larger extremes in the future. Figure 20 shows L-moment ratio diagrams for annual maxima data obtained from each downscaled climate dataset. The results for annual maxima show substantially more scatter of the points around the GEV curve than the peaks-over-threshold (POT) data around the GP curve (fig. 19). This difference may be at least partly due to the smaller sample sizes used to determine L-moments in the annual maxima case compared to the POT case. This interpretation is supported by the fact that the L-moment ratios for POT based on the longer historical period 1950–2005 (not shown here) were located even more compactly around the GP curve than in the shorter historical period 1966–2005. Therefore, it appears that the POT approach is an overall improvement over the annual maxima approach, even when a single percentile value per duration is used in defining the threshold for all grid cells.
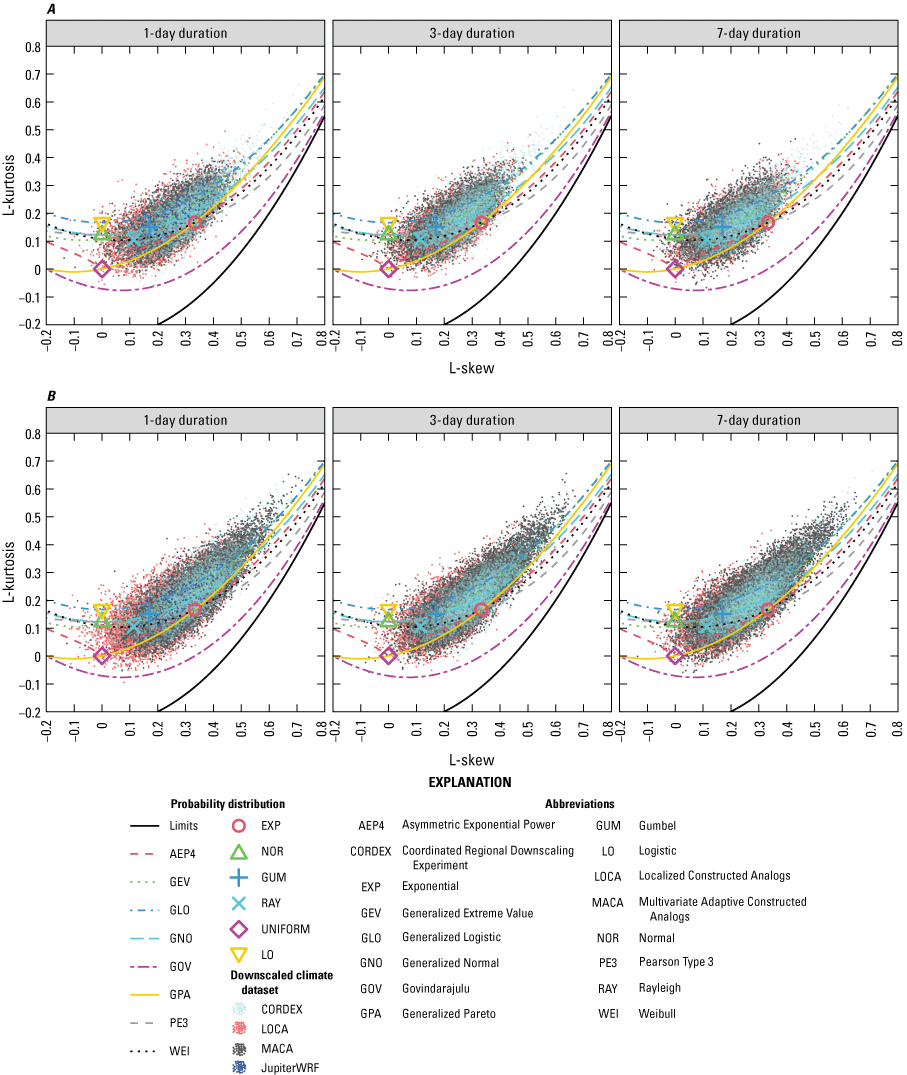
L-moment ratio diagrams for annual maxima in, A, the historical period (1966–2005) and, B, the future projection period (2050–89) by downscaled climate dataset. The large points correspond to probability distributions with no shape parameter and the curves correspond to probability distributions with a shape parameter.
Figure 21 bar charts show the percentage of model grid cells for which one of the five best fitting probability distributions is one of the available functions on the positive real line in the gamlss R package. The selection of the best fitting probability distributions was performed using the fitDist function in gamlss, which uses the AIC to balance GOF with distribution parsimony. In this figure, the first four bars (EXP, PARETO2, PARETO2o, and GP) correspond to different parameterizations of the GP and the exponential distribution, which is the special case of the GP having a shape parameter of zero. The bars for the remaining distributions are ordered from higher to lower percentage. It is evident that the GP is an adequate distribution for most locations; however, various parameterizations of the Weibull distribution also show up as some of the best. Using global precipitation data, Serinaldi and Kilsby (2014) show that positive precipitation (that is, equivalent to a POT approach with a threshold of zero) tends to follow a Weibull distribution and reference studies that show that as the threshold is decreased there is a progressive shift from GP to Weibull. This indicates that it is possible that the selected constant percentile-based threshold for each duration may be too low at some locations (that is, that the asymptotic conditions for the GP are not being met) resulting in more rejections of the null hypothesis of a GP distribution than the expected nominal value of 5 percent (significance level). However, figure 19 shows that the empirical L-moment ratios are in better alignment with the GP curve than with the Weibull curve. In fact, the deviation of the cloud of points from the GP curve in the region below the exponential point is away from the Weibull distribution rather than toward it. Therefore, the GP distribution has more support than the Weibull distribution. Note also that although the generalized Gamma and generalized Beta Type 2 distributions have more parameters, they do not feature among the top best distributions according to the AIC. In other words, the improvement in fit is not sufficient to justify the higher number of parameters in these distributions.
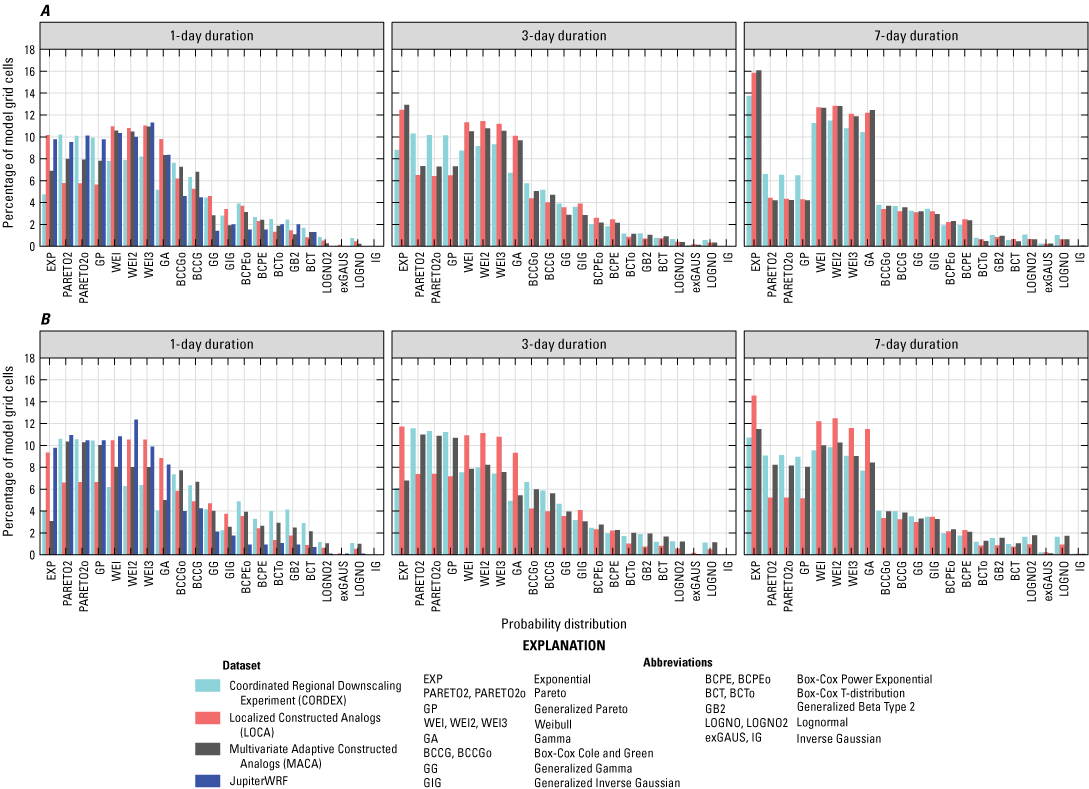
Best fitting distributions to threshold exceedances by duration and downscaled climate dataset from options available in the gamlss R package for, A, the historical period (1966–2005) and, B, the future projection period (2050–89). Distribution names that end with a number are different parameterizations of the distribution. For more details, see the gamlss R package documentation (https://cran.r-project.org/web/packages/gamlss/index.html).
Areal Reduction Factors
Figure 22 shows the mean ARFs from method M1 of Pavlovic and others (2016) for 1-, 3-, and 7-day durations by ARF region (fig. 7). Also shown are error bars representing the mean ARF for each ARF region plus and minus one standard deviation of the grid cell values within each ARF region. As expected, the mean ARF increases with increasing duration and its variability decreases. Overall, ARF values decrease from north to south Florida, and ARF values tend to be lower on the west coast of south Florida than the east coast. According to Winsberg (2020), mid-latitude low-pressure systems can bring heavy rain over north Florida in the winter and, as a result, that part of the State has no seasonal concentration of heavy precipitation. The precipitation associated with these low-pressure frontal systems tends to be more spatially uniform than in convective systems. Baigorria and others (2007) found a more widely spread spatial correlation pattern in the northeast-southwest direction around weather stations during the frontal rainy season in the southeastern United States (perpendicular to the path of weather fronts), whereas the convective rainy season is characterized by correlations that decrease rapidly over short distances from each weather station. The influence of winter frontal systems in characterizing some of the annual maximum precipitation events likely explains the higher ARF values obtained for northern Florida. Winsberg (2020) found that, for most of the State, the monthly frequency distribution of torrential precipitation is bimodal, with a peak in June and another peak in September. He explained the June peak as being the result of the Intertropical Convergence Zone moving north and having more of an influence on the local weather, and the September peak as being due to the greater frequency of tropical storms reaching the State during that month.
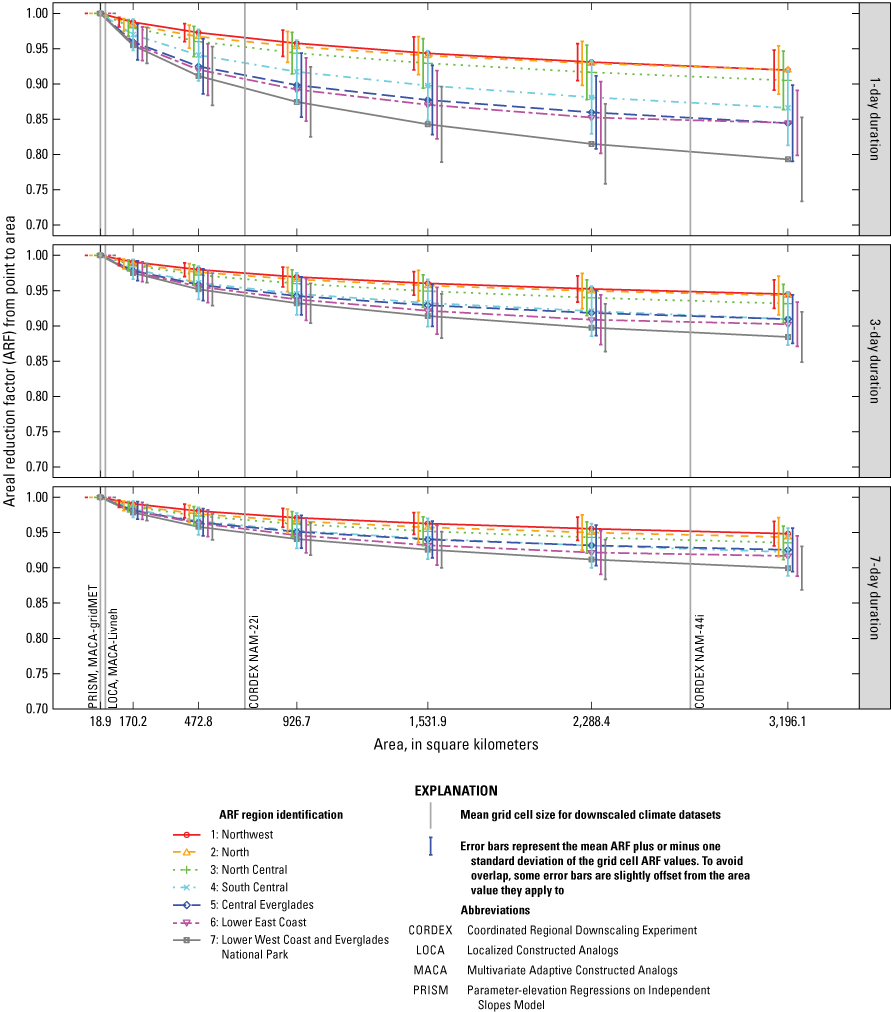
Mean areal reduction factors (ARFs), and associated standard deviation bars, by precipitation duration and ARF region.
Marshall and others (2004) explain how the west coast sea-breeze front typically does not penetrate as far inland as the one on the east coast because of its interaction with the large-scale easterly flow. However, this results in stronger convergence and greater precipitation along the west coast sea-breeze front. As shown by numerical simulations by Pielke (1974) and Baker and others (2001), the largest maximum vertical motion forms over the southwestern corner of the Florida peninsula in areas where the convex curvature of the coastline accentuates the horizontal convergence in the thermally driven sea breeze. Paxton and others (2009) have shown that the convergent pattern leads to a more localized circulation that appears to be associated with tornado development in southwest Florida. This more localized convection likely results in higher spatial variability in precipitation and may explain the lower ARFs obtained for the west coast of south Florida than in other regions of the State. Although ARFs vary across ARF regions, the error bars have a large degree of overlap and the differences among ARFs tend to be small. T-tests for the null hypothesis of equal means across ARF regions were also performed. In most cases, the null hypothesis of equal means of ARFs across ARF regions was rejected with the exception of the 1-day mean ARFs across the Central Everglades and Lower East Coast ARF regions.
For method M4 from Pavlovic and others (2016), where ARFs are a function of duration, return period, and spatial aggregation scale, ARFs for the longer return periods were found to be quite uncertain because of the extrapolation of the right tail of the GP distribution. This results in a large number of cases where the ARF, computed as the ratio of DDF precipitation depths at a given spatial aggregation level (1 × 1, 3 × 3, 5 × 5, 7 × 7, 9 × 9, 11 × 11, or 13 × 13 grid cells) to the 1 × 1 grid-cell aggregation level, was larger than one. The frequency of local ARF values exceeding one increased with return level and occurs more than 50 percent of the time for the 200-year return period. ARF values greater than one were set to one before evaluating trends in ARFs across duration and return period. For central and south Florida as a whole, ARFs were found to increase with increasing duration for return periods of 5 and 10 years. For return periods longer than 10 years, ARFs for 7-day duration move progressively closer to the ARFs for the 1-day duration, both of which are smaller than the ARFs for the 3-day duration. The ARFs do not vary much with return period for return periods of 5, 10, and 25 years, and decrease with increasing return period for return periods of 50, 100, and 200 years. Possible physical explanations for the behavior of the ARF curves derived from method M4 are beyond the scope of this study and are complicated by the larger number of ARF values that were set to one for the longest return periods. Because of the uncertainties associated with extrapolation of the more extreme quantiles, method M1 was chosen as the preferred method for obtaining ARFs. The reciprocal of the M1 ARFs were used to convert grid-cell (areal-) scale DDF curves to station- (point-) scale DDF curves for comparison against the NOAA Atlas 14 PDS-based historical DDF curves. As shown in figure 22, the ARF correction is close to 1 for most datasets, except for the CORDEX models and in particular for the coarser NAM-44i models.
Historical Bias and Spatial Pattern
Figure 23 shows the overall percentage difference of the model-derived station-scale DDF depths for the entire historical period available in the downscaled climate datasets (1950–2005) compared to the PDS-based DDF depths from NOAA Atlas 14 volume 9 (Perica and others, 2013). The percentage differences are calculated from the mean DDF depths at all 174 NOAA Atlas 14 stations in central and south Florida. The DDF depths from NOAA Atlas 14 volume 9 are based on statistical fits to precipitation observations within the period 1840–2008 depending on the station. Although the two datasets use different methods for DDF fitting and different periods of record, it is still informative to evaluate their overall differences. From this figure, it is evident that the JupiterWRF dataset shows the lowest absolute difference from observed DDF depths for the 1-day duration, on the order of less than 5 percent, followed by CORDEX-Daymet with median differences of about −15 to −23 percent, and CORDEX-gridMET with median differences of about −22 and −27 percent. LOCA seems to perform more poorly than the other datasets for the 1-day duration, with median differences in the range of −36 to −40 percent. This is likely a result (at least in part) of deficiencies in its training dataset (Livneh and others, 2015) mentioned earlier in this report. However, the MACA-Livneh dataset did not show differences as large as those for LOCA, with differences in the range of −28 to −29 percent for the 1-day duration, indicating that the differences in LOCA may also be due to the downscaling method. Two different versions of the Livneh dataset (Livneh and others, 2013, 2015) and two different periods are used in bias correcting LOCA and MACA, which may also explain some of the differences. MACA-gridMET shows larger negative differences than those for MACA-Livneh. MACA-gridMET models always show negative differences, whereas some MACA-Livneh models show positive differences for the 7-day duration. Overall, the longer return periods show more negative differences (with the exception of CORDEX for the 1-day duration) and the differences are more variable across models than for the shorter return periods. The negative differences generally decrease with duration for most datasets. For the 7-day duration, some MACA-Livneh and CORDEX-Daymet models even exhibit positive differences. Overall, the range of negative differences increases with duration. Although CORDEX starts with the smallest 1-day negative difference with respect to observations, its percent difference does not improve with duration quite as much as those for the other two datasets, indicating that the RCMs and (or) the bias-correction scheme may be inadequate in simulating multiday extreme events. Although not shown in this figure, lower-resolution CORDEX models (NAM-44i) tend to have slightly smaller negative differences than the higher-resolution CORDEX models (NAM-22i); however, the difference in median percentage difference is less than 2.3 percent. Overall, the CORDEX-Daymet negative differences are smaller than in CORDEX-gridMET by 3.9–9.2 percent, depending on duration and return period, and the improvement in CORDEX-Daymet compared to CORDEX-gridMET is more pronounced for longer durations and longer return periods.

Boxplots showing the overall percentage difference in precipitation depths from depth-duration-frequency (DDF) curves fitted for the model historical period (1950–2005) compared to observations from National Oceanic and Atmospheric Administration (NOAA) Atlas 14 stations (1840–2008) for all models in each downscaled climate dataset. Only one historical simulation is available for JupiterWRF, hence its percent difference is displayed as a horizontal marker.
The differences between extremes fitted to observations and those derived from the downscaled climate datasets likely result from a combination of factors, some of which have been mentioned previously. These factors include the following, among others:
-
1. Biases in the observational datasets used in “training” (analog construction and bias correction of downscaled climate datasets).
-
2. The downscaling and bias-correction methods used.
-
3. The observational datasets not capturing extremes at specific NOAA Atlas 14 stations (for example, because of the observational dataset not including the stations used in NOAA Atlas 14 or averaging more than one station to obtain a grid cell mean).
-
4. Differing methods and periods of record for DDF fitting used to derive the observational and downscaled climate models.
-
5. Biases arising from the parent GCMs. For example, the inability of CMIP5 GCMs to capture increases in extreme precipitation from the latter part of the 20th century to early 21st century has been observed by Wuebbles and others (2014) and Asadieh and Krakauer (2015) for the entire continental United States and North America, respectively.
-
6. Natural variability in the rarest extremes, which results in a lower signal-to-noise ratio, decreasing their predictability especially when estimated from short and in this case, different periods of record.
-
7. Random differences in internal variability between the observations and the bias-corrected downscaled climate data that may be present even if data for the same multidecadal periods were being compared (that is, even after bias correction, observations and climate data may represent different portions of multidecadal cycles).
To evaluate the effect of the different periods of record used in comparing the official NOAA Atlas 14 PDS-based DDF curves and model-derived station-scale DDF depths for the historical period 1950–2005, DDF curves were developed by fitting the GEV distribution to annual maxima data provided by NOAA Atlas 14 at 97 (out of 174) stations (fig. 1) having at least 40 years of data within the period 1950–2005. For simplicity, the method of L-moments was used to fit the GEV distribution to annual maxima one duration at a time without corrections for CDF crossing. It was verified that, on average, data from the 97 stations are representative of data from the larger set of 174 stations. This was accomplished by comparing the median of the official NOAA Atlas 14 PDS-based DDF curves for all 174 stations against the median of the official NOAA Atlas 14 PDS-based DDF curves for the subset of 97 stations for each duration and return period. Then the difference between the model-derived station-scale DDF depths for the 1950–2005 historical period and the DDF curves that were fit to observed annual maxima for 1950–2005 was computed for the 97 stations. It was found that the median percent differences between these two sets of DDF depths were reduced by a mean absolute value of 3.9 percent, with a maximum absolute value of about 7.5 percent, from those shown in figure 23 indicating potential nonstationarity in the observed extremes, some of which may date back to the year 1840 at some stations. However, differences between the method used to develop DDF curves for this exercise and the method used to develop the official NOAA Atlas 14 PDS-based DDF curves may also explain the differences, at least in part. To address this question, we fitted a GEV distribution using the method of L-moments to all the available annual maxima data at each of the 174 stations in the region for the period 1840–2008; data availability within the period 1840–2008 varies among these stations. The DDF depths fitted using the GEV distribution and the method of L-moments for 1840–2008 were slightly smaller than the official NOAA Atlas 14 PDS-based DDF depths for the same period. As a result, the absolute median difference between the model-derived 1950–2005 DDF curves and these newly-fitted 1840–2008 DDF curves had a slight decline of 1.1 percent, on average, and a maximum decline of 3.3 percent compared to the difference between the model-derived 1950–2005 DDF curves and the official NOAA Atlas 14 PDS-based DDF curves. Therefore, it appears that the difference in period of record explains a larger portion of the difference between the official NOAA Atlas 14 PDS-based DDF curves and model-derived station-scale DDF depths for the historical period 1950–2005 than the difference in DDF-fitting methodology. Regardless of these findings, the model-derived station-scale DDF depths still appear to be highly negatively biased when compared to DDF curves developed from observations.
Figure 24 shows the overall percentage difference in station-scale precipitation depths obtained by fitting the GP distribution using CML to precipitation data from the datasets used to bias-correct each downscaled climate dataset compared to observations from NOAA Atlas 14 (1840–2008). The periods of record for each bias-correction dataset vary by downscaled climate dataset as described under the applicable subsection in the “Downscaled Climate Datasets” section. The precipitation data were obtained for the closest grid cell to each of the 174 NOAA Atlas 14 stations at the native resolution of each bias-correction dataset. The native resolution was calculated to be approximately 1 km for Daymet, 6.6 km for Livneh and others (2013 and 2015), and 4.4 km for gridMET in central and south Florida. The ARF values corresponding to these resolutions are very close to one (fig. 22). Comparison of figure 24 with the median percentage difference in precipitation depths across models for each downscaled climate dataset in figure 23 shows similar magnitudes and patterns of change with respect to changes in duration and often with respect to changes in return period. These similarities indicate that the overall percent difference of the model-derived station-scale DDF depths for the entire historical period available in the downscaled climate datasets (1950–2005) compared to the PDS-based DDF depths from NOAA Atlas 14 volume 9 is largely a result of the bias-correction datasets not being able to capture the DDF depths from NOAA Atlas 14. A similar exercise was performed for figure 24 as for figure 23. When comparing to the DDF curves developed by fitting the GEV distribution to annual maxima data provided by NOAA Atlas 14 at the 97 stations having at least 40 years of data within the period 1950–2005, the median percent differences shown in figure 24 were reduced by a mean absolute value of 4.5 percent, with a maximum reduction of about 7.4 percent. When comparing to the DDF curves developed by fitting the GEV distribution to annual maxima at all 174 NOAA Atlas 14 stations, the median percent differences shown in figure 24 declined by an absolute value of 1.2 percent, on average, with a maximum decline of 3.2 percent. Again, it appears that the difference in period of record explains a larger portion of the difference between the official NOAA Atlas 14 PDS-based DDF curves and station-scale DDF depths fitted to the bias-correction datasets than the difference in DDF-fitting methodology. Large negative biases remain, however, indicating that the gridded observational datasets used in the training and bias-correction steps of downscaling do not adequately capture the localized station-based extremes used in developing the NOAA Atlas 14 DDF curves. The biases were found to be the lowest for Daymet, which has the highest resolution of the four bias-correction datasets.
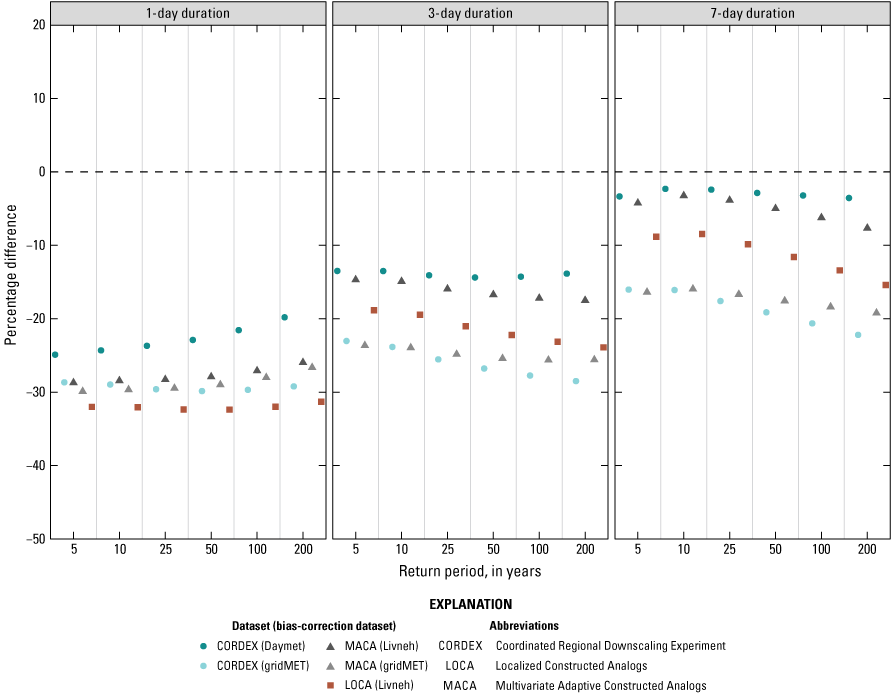
Overall percentage difference in precipitation depths from depth-duration-frequency (DDF) fitted for the bias-correction datasets used for each downscaled climate dataset compared to observations from National Oceanic and Atmospheric Administration (NOAA) Atlas 14 stations (1840–2008).
Figure 25 shows the overall percentage change in DDF depths for the future projection period (2050–89) compared to the historical period (1966–2005) for all models in each downscaled climate dataset. Comparing this figure with figure 23 indicates that the absolute value of the percent differences from observations for LOCA is much larger than the predicted percentage change from the historical to future period. The negative percent differences from observations for LOCA correspond to bias-correction factors for multiplicative quantile delta mapping (MQDM) that are greater than one, whereas the positive percent changes from present to future in LOCA corresponds to change factors that are greater than one. In the case of LOCA, the bias-correction factor would be much larger than the predicted change factors, especially for the 1-day duration, reducing the confidence in those change factors. The median percentage change for CORDEX is more comparable in magnitude to the median percentage difference than for LOCA. The median percentage change for CORDEX is smaller than the absolute value of the percentage difference with respect to observations for the shorter return periods, and equal to or larger than the absolute value of the percentage difference with respect to observations for the longer return periods. In the case of MACA, the median percentage change is smaller than the absolute value of the percentage difference from observations only for the shorter return periods for the 1-day duration and larger otherwise. Overall, the 5th, 16th, 50th, 84th percentiles and low outliers of percent change from the historical period to the future period are similar for MACA-Livneh and MACA-gridMET however, MACA-Livneh has much higher 95th percentiles and high outliers of percent change, especially for the longer return periods. In general, the median percentage change is similar between the two CORDEX bias-corrected datasets with CORDEX-gridMET only as much as 3.7 percent higher than CORDEX-Daymet. The median percentage change for JupiterWRF is larger than the absolute of the percentage difference from observations for all return periods for the 1-day duration. Figure 26 shows that, in general, the higher-resolution CORDEX models (NAM-22i) predict smaller median percentage changes in DDF depths compared to lower-resolution CORDEX models (NAM-44i). For the 5- and 10-year, 1-day event, CORDEX NAM-22i models predict slightly higher median percentage changes in DDF depths compared to CORDEX NAM-44i models.

Boxplots showing the overall percentage change in precipitation depths from depth-duration-frequency (DDF) curves fitted for the model future projection period (2050–89) compared to the model historical period (1966–2005) for all models in each downscaled climate dataset.
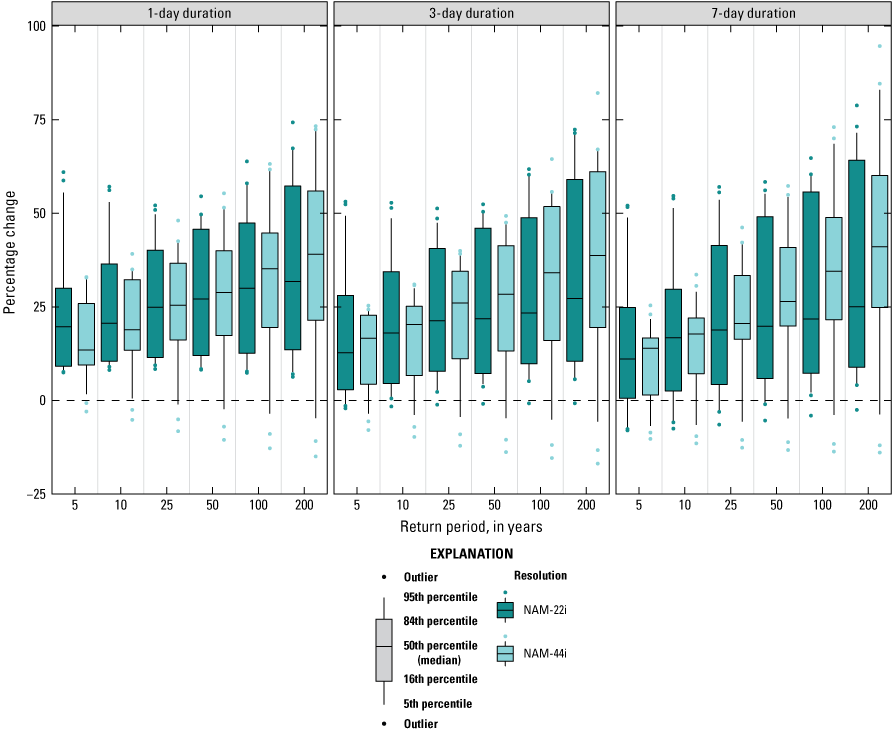
Boxplots showing the overall percentage change in precipitation depths from depth-duration-frequency (DDF) curves fitted for the model future projection period (2050–89) compared to the model historical period (1966–2005) for all models available in the Coordinated Regional Downscaling Experiment (CORDEX) at both model resolutions.
Figure 27 shows Taylor diagrams comparing the model-derived station-scale DDF curves to the NOAA Atlas 14 PDS-based DDF curves for 1-day events. According to Taylor (2001), the Taylor diagram characterizes the statistical relation between two fields, a “test” field (often representing a field simulated by a model) and a “reference” field (usually representing “truth,” on the basis of observations). Note that the means of the fields are subtracted out before computing their second-order statistics, so the diagram does not provide information about overall differences, but solely characterizes the “centered pattern error.” For the 5-year event, the LOCA dataset has a much lower pattern correlation (0.3–0.5) than the other datasets. The pattern correlation is the Pearson product-moment coefficient of the linear correlation between two variables that are respectively the values of the same variables at corresponding locations on two different maps. For the 5-year event, the MACA models cluster in two regions, with the points close to the red line having a standard deviation ratio close to one corresponding to MACA-Livneh and the points having a lower standard deviation ratio corresponding to MACA-gridMET. Also, for the 5-year event, most of the CORDEX models cluster close to JupiterWRF and in between the two MACA clusters. The points having the lowest centered RMSD in the diagrams indicate the best performance, which in the case of the 1-day, 5-year event corresponds to some CORDEX models and MACA-gridMET models, even when the standard deviation of MACA-Livneh is closer to the observed standard deviation. As the return period increases for events of 1-day duration, CORDEX and JupiterWRF seem to deteriorate the most of all four datasets. The spatial standard deviation increases beyond that of the observations in JupiterWRF as the return period increases for events of 1-day duration, and its pattern correlation decreases. The spatial standard deviation for CORDEX gets closer to that of the observations as the return period increases; however, the pattern correlation decreases and even becomes negative for some CORDEX models for the 50- to 200-year events. This result is likely due a combination of the coarse model resolution in CORDEX not being able to capture local variations in extremes (despite the use of mean ARFs for particular regions) and the increased uncertainty associated with the estimation of the rarer extremes. In contrast, LOCA and MACA-Livneh’s performance does not deteriorate as much as the return period increases. Overall, MACA-Livneh performs best among the datasets when all return periods are considered. It is worth noting how the standard deviations tend to increase with increasing return period for all downscaled climate datasets. This is likely because the NOAA Atlas 14 DDF curves are derived by means of regional frequency analysis, which reduces the spatial variation of the shape parameter and the return levels as opposed to the CML method, which is applied more locally. Similar conclusions can be made from the Taylor diagrams for 3- and 7-day durations (figs. 28 and 29); however, for those longer durations, the standard deviation ratios are even higher than for the 1-day duration, especially for the long return periods.
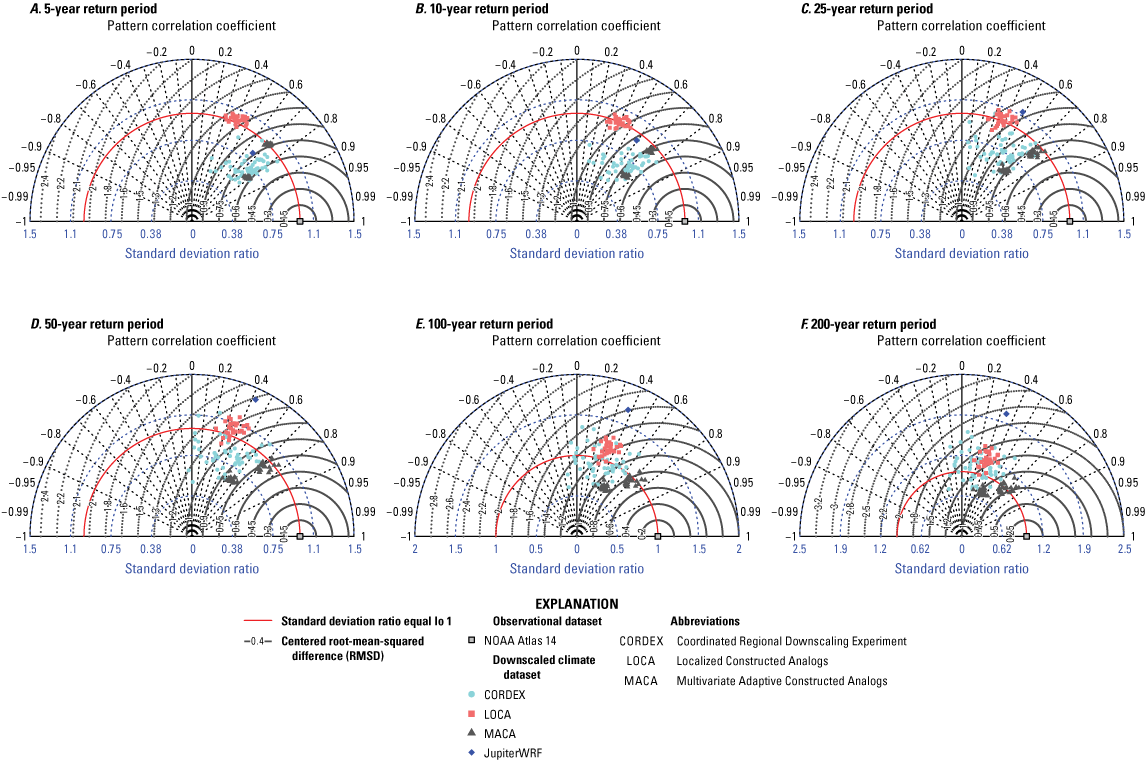
Normalized Taylor diagrams comparing depth-duration-frequency (DDF) curve fits to modeled precipitation for the historical period (1950–2005) against National Oceanic and Atmospheric Administration (NOAA) Atlas 14 partial-duration-series (PDS)-based DDF curves by return period for 1-day duration. The radial distance indicates the ratio of the spatial standard deviation of the model data to that of the observational dataset, whereas the angle indicates the pattern correlation coefficient between the two datasets. The closer a model point is to the observational data point, the better the model performance.
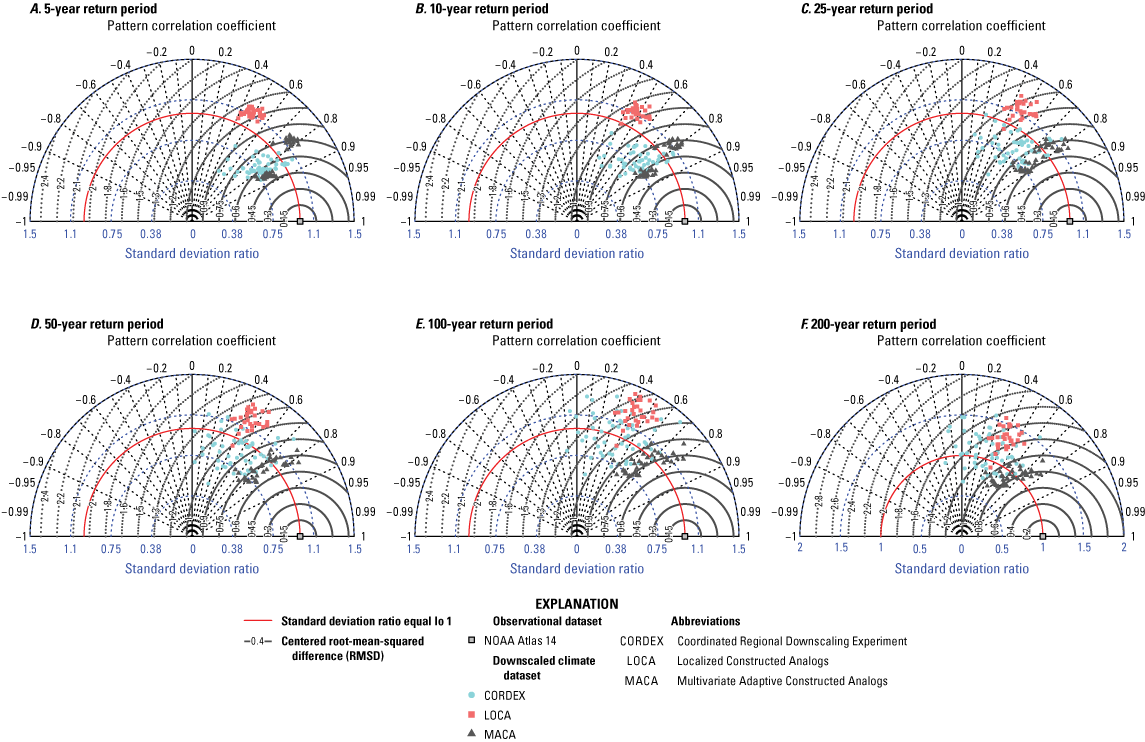
Normalized Taylor diagrams comparing depth-duration-frequency (DDF) curve fits to modeled precipitation for the historical period (1950–2005) against National Oceanic and Atmospheric Administration (NOAA) Atlas 14 partial-duration-series (PDS)-based DDF curves by return period for 3-day duration. The radial distance indicates the ratio of the spatial standard deviation of the model data to that of the observational dataset, whereas the angle indicates the pattern correlation coefficient between the two datasets. The closer a model point is to the observational data point, the better the model performance.
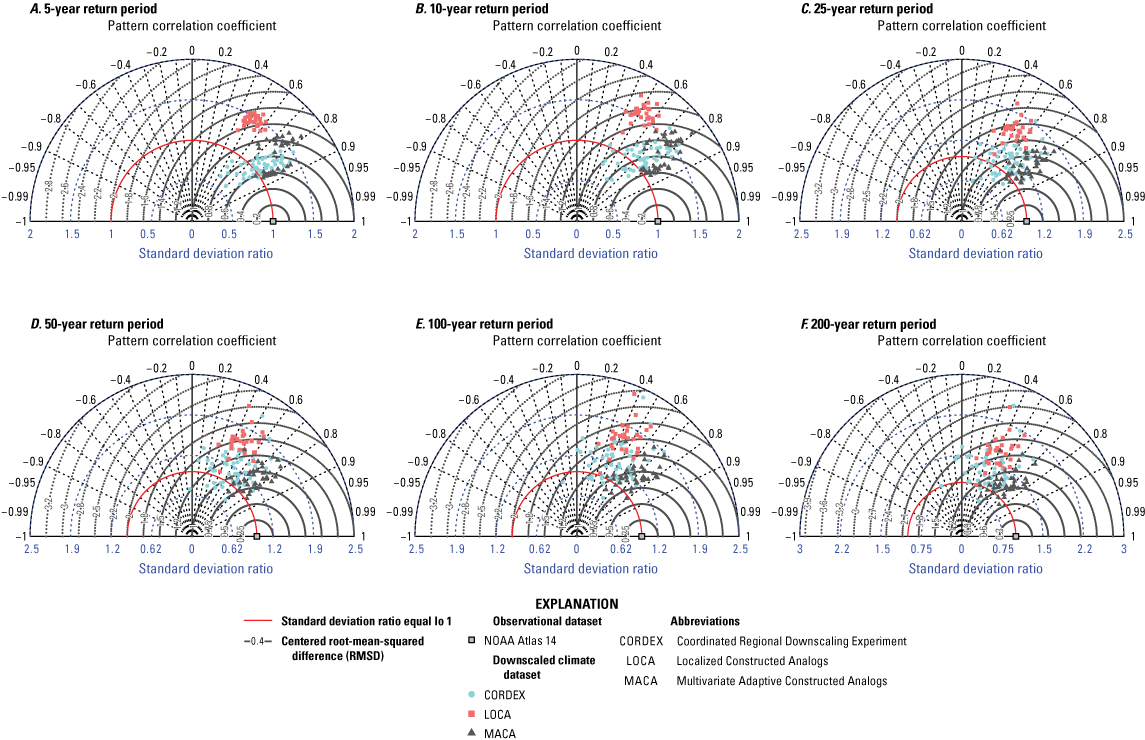
Normalized Taylor diagrams comparing depth-duration-frequency (DDF) curve fits to modeled precipitation for the historical period (1950–2005) against National Oceanic and Atmospheric Administration (NOAA) Atlas 14 partial-duration-series (PDS)-based DDF curves by return period for 7-day duration. The radial distance indicates the ratio of the spatial standard deviation of the model data to that of the observational dataset, whereas the angle indicates the pattern correlation coefficient between the two datasets. The closer a model point is to the observational data point, the better the model performance.
Model Culling
Initially, the best models were selected by evaluating the MCI and MVI criteria from Srivastava and others (2020) and considering all the precipitation extremes indices listed in table 9. This process resulted in a very small subset of best models. On the basis of the desire to include as many models as possible to inform the potential range of future change factors, a decision was made to only use four precipitation extremes indices in selecting best models, namely the annual maxima of precipitation for durations of 1, 3, 5, and 7 consecutive days. Tables 10–12 list the best models for each climate region according to the MCI and MVI when each downscaled climate dataset (CORDEX, LOCA, and MACA) is evaluated on its own for the four precipitation extremes indices chosen. Table 13 lists the best models when all datasets are evaluated together. In this case, the median RMSE and IVSS are defined on the basis of all the models in all the downscaled climate datasets. A model was considered to be among the best if it had a negative MCI and a negative MVI when compared to either the PRISM or SFWMD “Super-grid” observational datasets. Because of the small sample size, all models were considered the best models for the JupiterWRF dataset.
Table 10.
Best models according to the Model Climatology Index (MCI) and Model Variability Index (MVI) criteria applied to four precipitation extremes indices for the Coordinated Regional Downscaling Experiment (CORDEX) dataset evaluated among CORDEX models.[Four precipitation extreme indices used in model evaluation consist of annual maxima consecutive precipitation for durations of 1, 3, 5, and 7 days]
Table 11.
Best models according to the Model Climatology Index (MCI) and Model Variability Index (MVI) criteria applied to four precipitation extremes indices for the Localized Constructed Analogs (LOCA) dataset evaluated among LOCA models.[Four precipitation extreme indices used in model evaluation consist of annual maxima consecutive precipitation for durations of 1, 3, 5, and 7 days]
Table 12.
Best models according to the Model Climatology Index (MCI) and Model Variability Index (MVI) criteria applied to four precipitation extremes indices for the Multivariate Adaptive Constructed Analogs (MACA) dataset evaluated among MACA models.[Four precipitation extreme indices used in model evaluation consist of annual maxima consecutive precipitation for durations of 1, 3, 5, and 7 days. BC, bias-correction]
Table 13.
Best models according to the Model Climatology Index (MCI) and Model Variability Index (MVI) criteria applied to four precipitation extremes indices for all datasets evaluated together.[Four precipitation extreme indices used in model evaluation consist of annual maxima consecutive precipitation for durations of 1, 3, 5, and 7 days. BC, bias-correction; CORDEX, Coordinated Regional Downscaling Experiment; LOCA, Localized Constructed Analogs; MACA, Multivariate Adaptive Constructed Analogs; NA, not applicable]
In table 10, it is notable that most of the best CORDEX models for climate region 5 (south Florida) are bias-corrected with Daymet. The best models for both climate region 4 (south-central Florida) and climate region 5 include twice as many high-resolution models (NAM-22i) as low-resolution models (NAM-44i). For LOCA (table 11), about half of the best models in climate region 4 are also in climate region 5. For MACA (table 12), in climate region 4 the best models are 12 from MACA-gridMET and 4 from MACA-Livneh, whereas in climate region 5, the best models are 7 from MACA-Livneh and 5 from MACA-gridMET. Only three models are considered best in both climate regions 4 and 5 for MACA: HADGEM2-CC365 (gridMET), IPSL-CM5A-MR (gridMET), and bcc-csm1-1-m (Livneh). When all datasets are evaluated together (table 13), only 4 LOCA models are considered best in climate region 4 and 0 are considered best in climate region 5. For climate region 4, the best models are 16 from CORDEX and 19 from MACA. For climate region 5, the best models are 12 from CORDEX and 31 from MACA. It is important to note that when MCI and MVI are computed using all of the precipitation extremes indices in table 9 considering all datasets together as a single group, no LOCA models had negative values for both indices, indicating that all LOCA models performed worse than the median model across all datasets and regions.
Change Factors
Change factors in DDF precipitation depths for the period 2050–89 with respect to the period 1966–2005 were computed for all model grid cells associated with NOAA Atlas 14 stations in central and south Florida from all four downscaled climate datasets evaluated as part of this study. The change factors generated as part of this study are available in Irizarry-Ortiz and Stamm (2022). Figures 30A, 31A, 32A, 33A show median change factors for climate regions 4 (south-central Florida) and 5 (south Florida) considering all RCPs and all models or only the best models. Median change factors and their range generally increase with increasing return period and are similar across duration for climate region 4. For climate region 5, median change factors and their range increase with increasing return period and mostly decrease with increasing duration. The increase in change factors with return period is consistent with Lopez-Cantu and others (2020), who found that at the continental scale, high-end daily extremes generally increase more than low-end extremes, as determined by evaluating various downscaled climate datasets for the period 2044–99 with respect to 1951–2005. That is, heavy precipitation events get even heavier under future conditions. The exception is JupiterWRF (which is primarily based on CMIP6 GCMs) for which 1-day change factors do not vary much with return period in both climate regions. The Sixth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC, 2021, p. 15) also states that “There will be an increasing occurrence of some extreme events unprecedented in the observational record with additional global warming, even at 1.5 °C of global warming. Projected percentage changes in frequency are higher for rarer events (high confidence).”
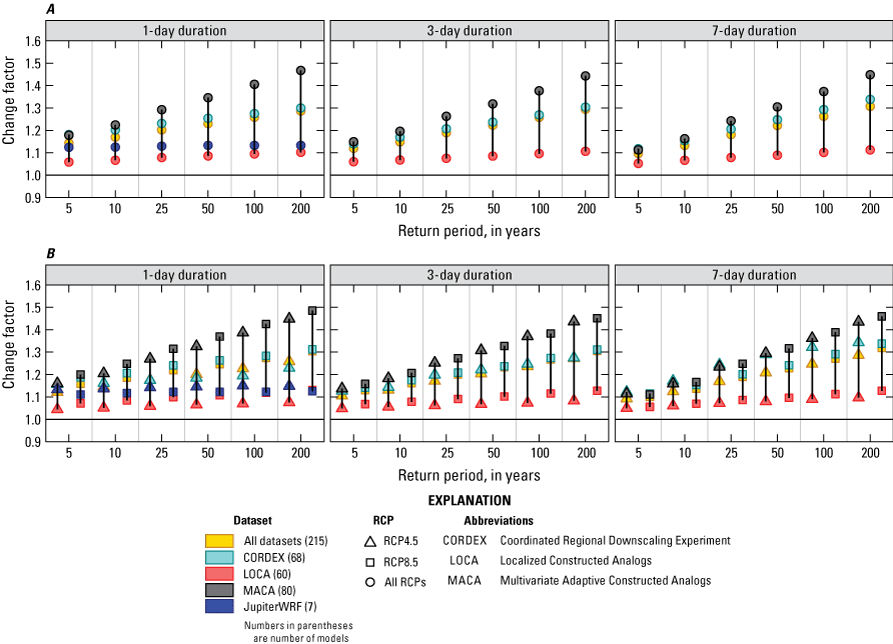
Median change factors across datasets for all stations in climate region 4 (south-central Florida) considering, A, all models and all representative concentration pathways (RCPs) combined, and, B, all models split by RCP. The number of models considered is shown in parentheses next to the dataset name.
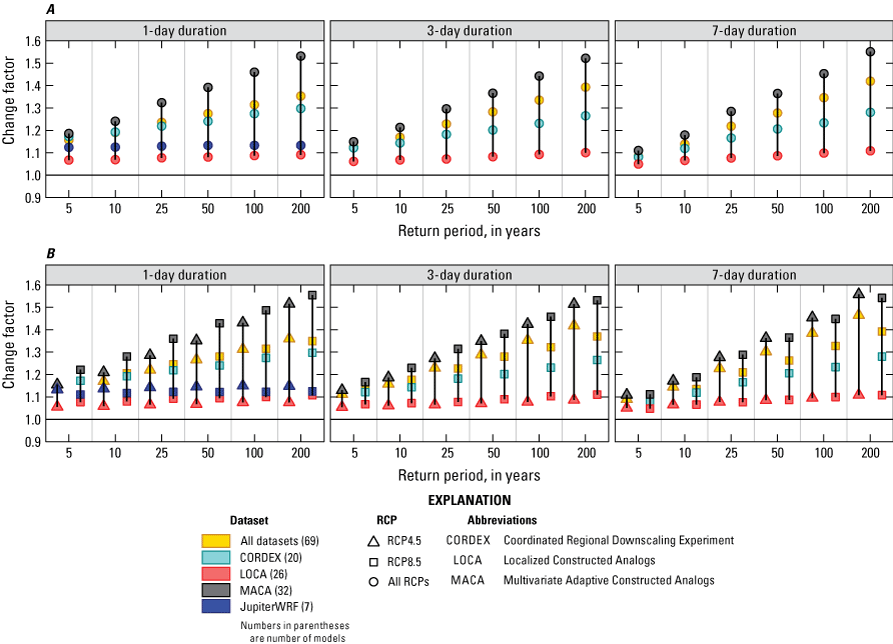
Median change factors across datasets for all stations in climate region 4 (south-central Florida) considering, A, only best models and all representative concentration pathways (RCPs) combined, and, B, only best models split by RCP. The number of models considered is shown in parentheses next to the dataset name.
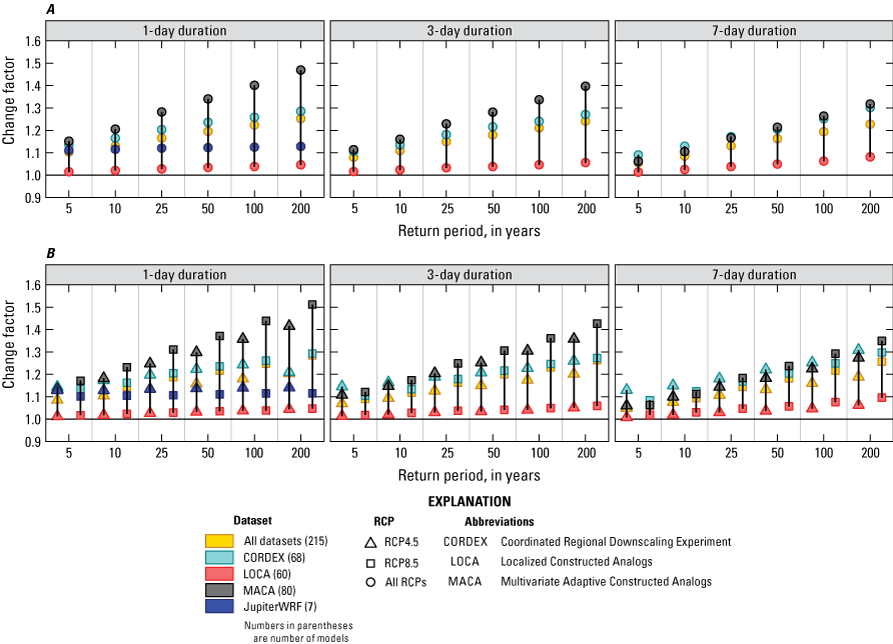
Median change factors across datasets for all stations in climate region 5 (south Florida) considering, A, all models and all representative concentration pathways (RCPs) combined, and, B, all models split by RCP. The number of models considered is shown in parentheses next to the dataset name.
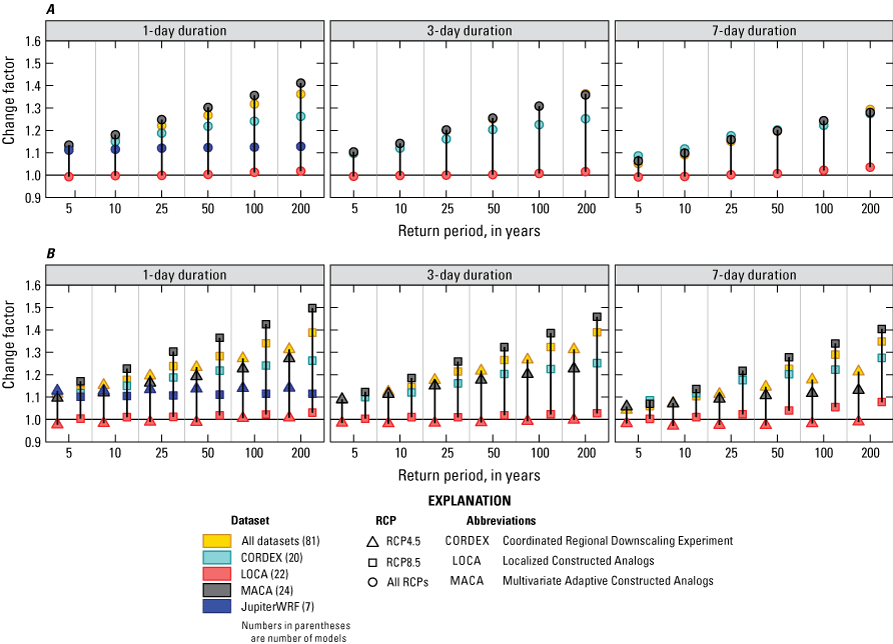
Median change factors across datasets for all stations in climate region 5 (south Florida) considering, A, only best models and all representative concentration pathways (RCPs) combined, and, B, only best models split by RCP. The number of models considered is shown in parentheses next to the dataset name.
Median change factors from LOCA are generally the lowest, followed by those from JupiterWRF (1-day duration only), CORDEX, and MACA, which has the highest change factors. One exception is the median change factors from CORDEX being slightly larger than those from MACA for the 5- and 10-year, 7-day event in climate region 5 (fig. 32A). When only the historically best-performing models are considered in climate region 4 (fig. 31A), the median increases across most durations and return periods for MACA but decreases slightly for CORDEX and LOCA compared to the case for all models (fig. 30A), resulting in a larger inter-model range after culling. If all datasets are considered together, the median increases and gets closer to that of MACA after culling. When only the best models are considered in climate region 5 (fig. 33A), the medians for all datasets are reduced compared to the case for all models (fig. 32A), with the median for LOCA falling slightly below one for the more frequent extreme events. If all datasets are considered together, the median increases to almost that of MACA after culling. This happens because, for climate region 5, when all downscaled datasets are considered together in evaluating precipitation index performance, the best models are 12 from CORDEX and 31 from MACA. Overall, climate region 4 has higher median change factors (1.05–1.55 depending on dataset, duration, and return period) than climate region 5 (1.0–1.4 depending on dataset, duration, and return period) when considering the best models and all RCPs for both areas. The extension of the projected Caribbean drying described in the “Downscaled Climate Datasets” section may be a possible explanation for the lower change factors obtained for south Florida.
Figures 34–38 show maps of median change factors interpolated from the median at-station change factors based on best models from CORDEX, LOCA, MACA, all models from JupiterWRF, and best models selected from the evaluation of precipitation extreme indices when considering all datasets together, respectively. These maps were developed using multiquadric radial basis function interpolation from the geospt R package (Melo and others, 2012). Median change factors at the 10 closest NOAA Atlas 14 stations to each pixel location on an equally spaced 200- × 200-pixel grid were used in the interpolation. The parameter values of the multiquadric radial basis function were chosen so that the interpolation was exact at the locations of the NOAA Atlas 14 stations and so that values were not extrapolated beyond the range of the station values. The choice of interpolation method was subjective because the intent was to be able to show general patterns in median change factors rather than precise values at unsampled locations. These maps show that median change factors based on best models are slightly lower for south Florida than for south-central Florida, as shown in figures 31A and 33A. This is most evident for LOCA as shown in figure 35, which shows some areas with change factors less than one in large portions of south Florida. The exception is JupiterWRF for which a north-south gradient in median change factors is not evident (fig. 37). The fact that MACA contributes the largest proportion of best models when all downscaled datasets are considered together in evaluating precipitation index performance in climate region 5 is evident when comparing the maps of median change factors in south Florida (figs. 36 and 38). The increase in median change factors with return period shown in figures 31A and 33A is most evident in the maps for MACA (fig. 36), followed by the maps for all datasets (fig. 38) and CORDEX (fig. 34).
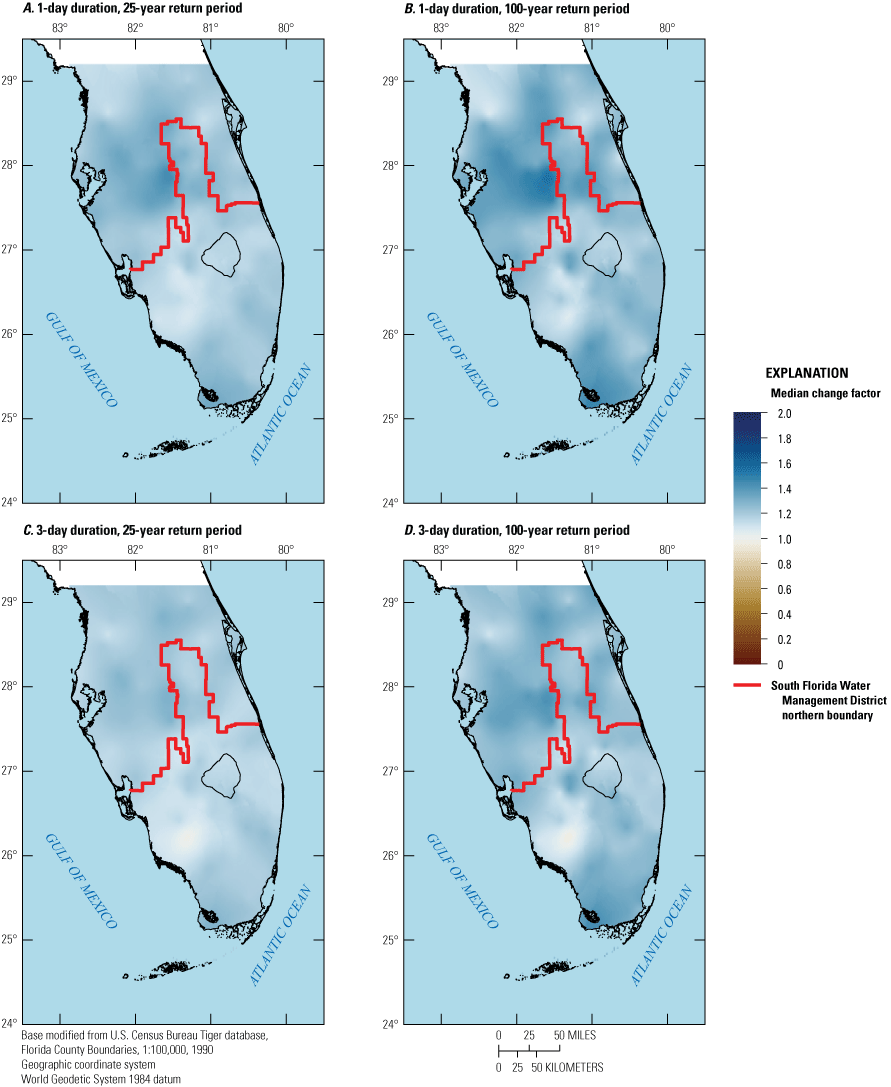
Median change factors based on best Coordinated Regional Downscaling Experiment (CORDEX) models and all representative concentration pathways (RCPs).
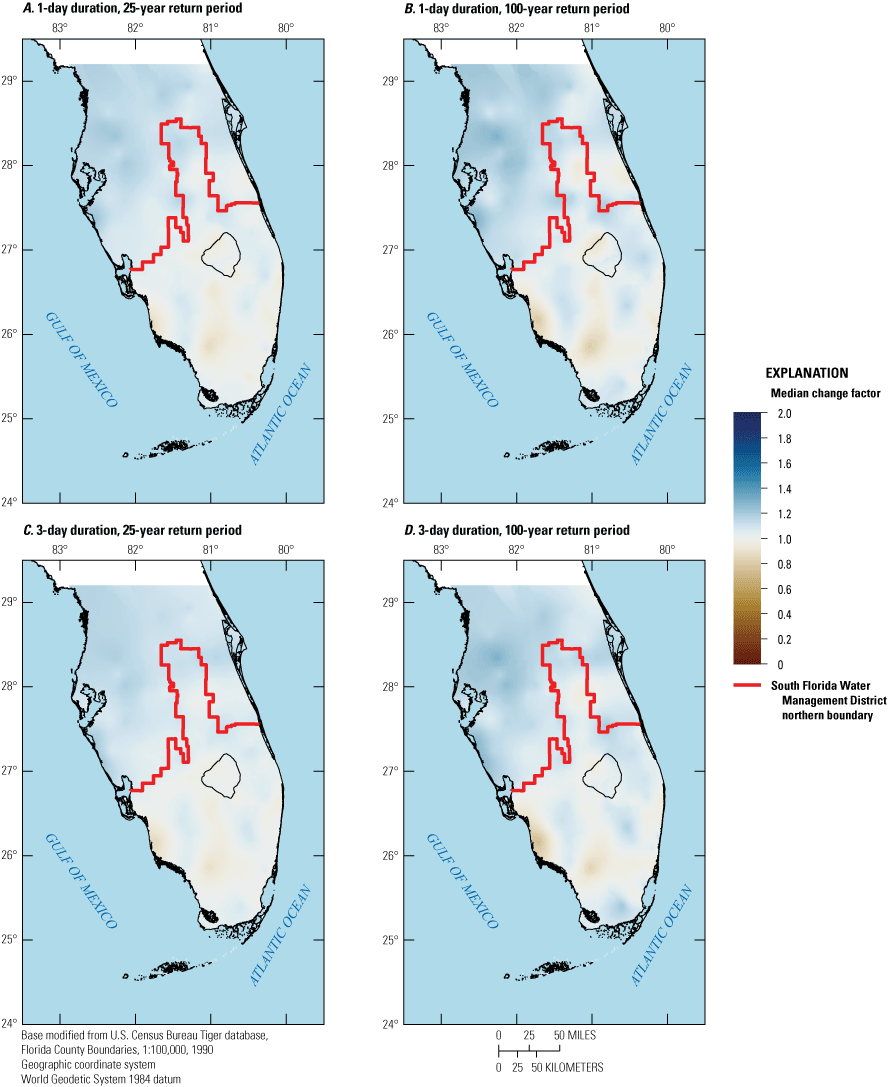
Median change factors based on best Localized Constructed Analogs (LOCA) models and all representative concentration pathways (RCPs).
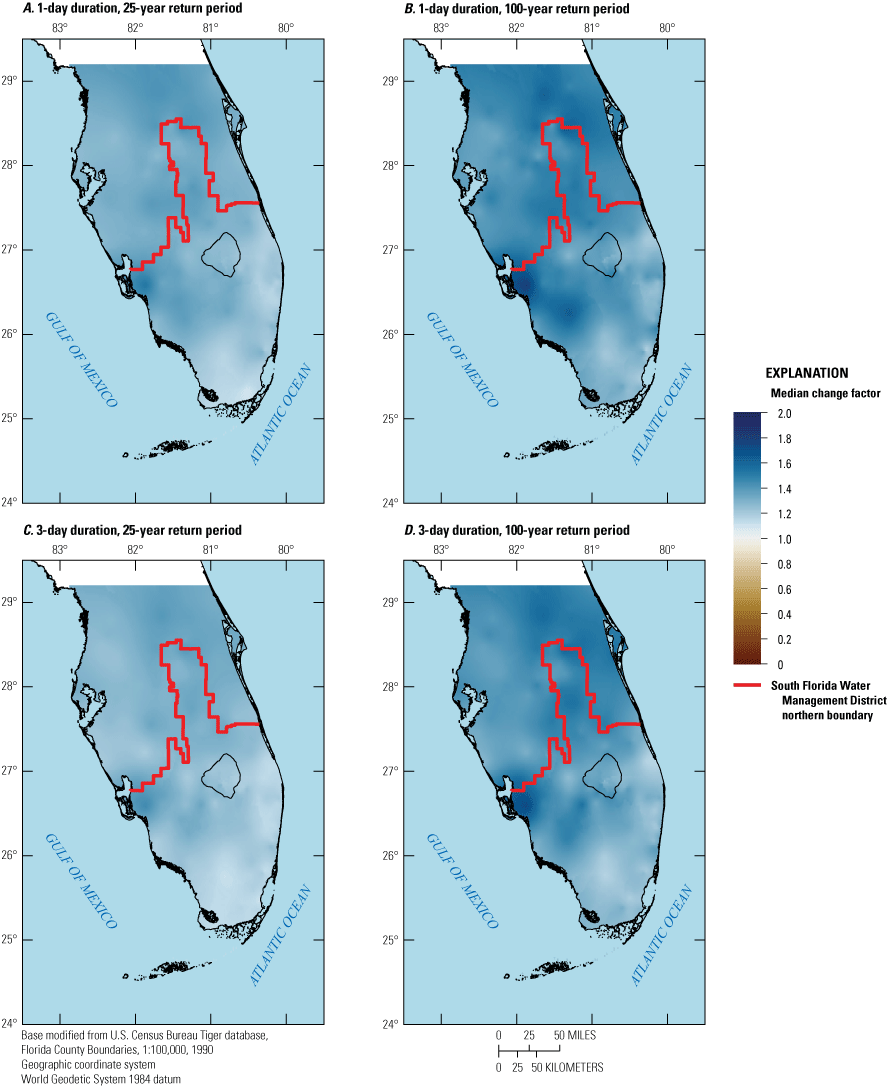
Median change factors based on best Multivariate Adaptive Constructed Analogs (MACA) models and all representative concentration pathways (RCPs).
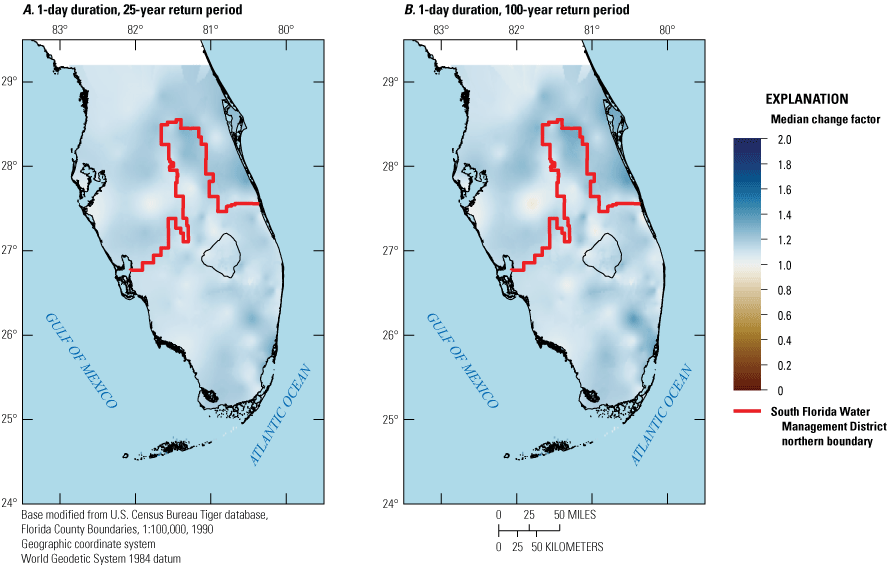
Median change factors based on all models and all representative concentration pathways (RCPs) from the Analog Resampling and Statistical Scaling method by Jupiter Intelligence using the Weather Research and Forecasting model (JupiterWRF).
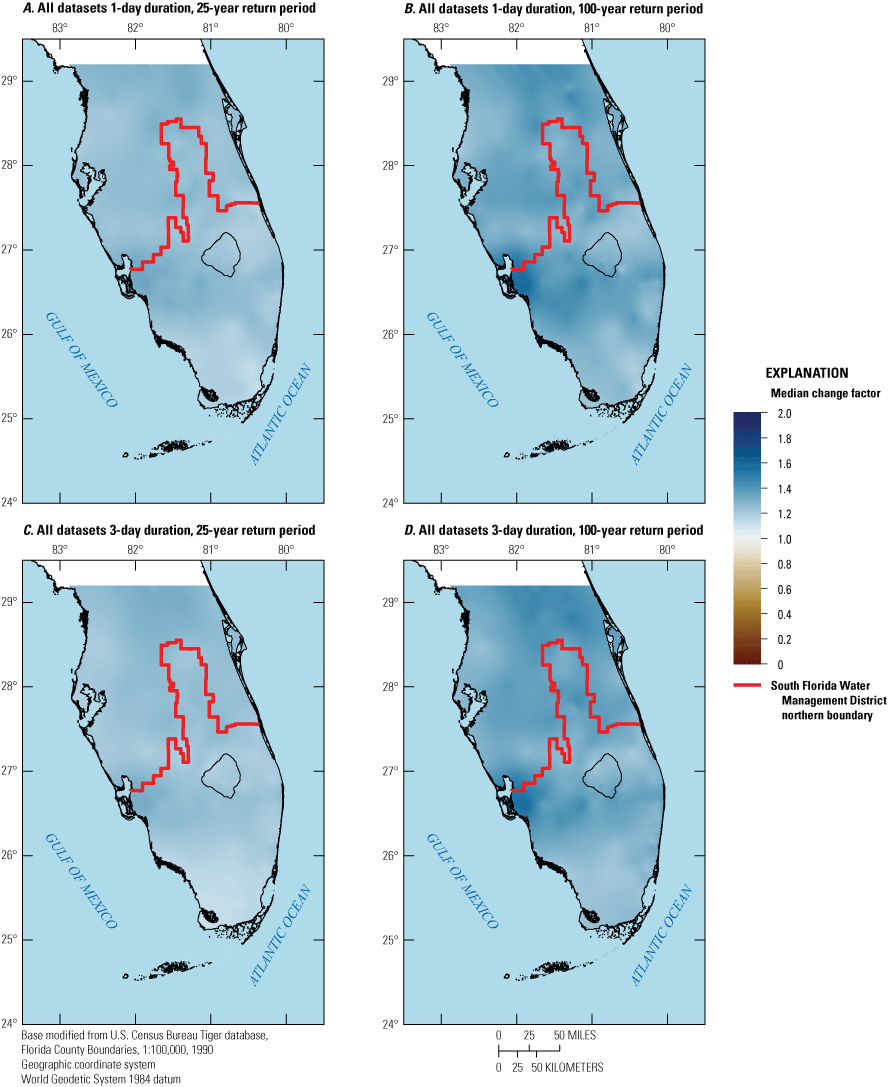
Median change factors based on best models when all datasets are compared against each other (with the exception of the Analog Resampling and Statistical Scaling method by Jupiter Intelligence using the Weather Research and Forecasting model, JupiterWRF, for which all models are considered) and all representative concentration pathways (RCPs).
For the entire continental United States, Lopez-Cantu and others (2020) found that, despite being the least-biased overall compared to observed extremes, the MACA-gridMET multimember mean change factors (for the period 2044–99 with respect to 1951–2005) are also considerably larger than the other datasets evaluated, which include BCCA version 2, LOCA, and CORDEX without bias correction (called “CORDEXnoBC” hereafter). They found that BCCA version 2 results in the lowest change factors for the continental United States, followed by LOCA, low-resolution CORDEXnoBC models, high-resolution CORDEXnoBC models, and MACA-gridMET models. Furthermore, Lopez-Cantu and others (2020) found that the downscaled climate datasets somewhat preserve the pattern of the change signal in the native GCM change factors; however, the magnitude of the signal is reduced in BCCA version 2 and increased in MACA-gridMET. For the southeastern United States, using the CanESM2 GCM as an example, they found for RCP4.5 that LOCA and low-resolution CORDEXnoBC models tend to preserve the GCM change signal the best, whereas MACA-gridMET amplifies the change signal, especially for longer return periods. High-resolution CORDEXnoBC models were found to amplify the change signal more evenly across return periods. Their findings were similar for RCP8.5, but they found that LOCA tends to mute the change signal whereas its amplification in MACA-gridMET and the high-resolution CORDEXnoBC models is slightly lower than in RCP4.5.
As shown in figures 30B–33B, change factors are generally somewhat higher in RCP8.5 than in RCP4.5 for all downscaled climate datasets in both climate regions when all or only the best models are considered, with some exceptions. For climate region 5, figure 32B shows higher change factors for CORDEX models in RCP4.5 than in RCP8.5 for 1- and 3-day events with return periods shorter than 25 years, and for all durations in the 7-day event when all models are considered. However, the number of CORDEX models available for each RCP and summarized in this figure is imbalanced, with only 14 models available for RCP4.5 out of a total of 68 when all models are considered. When the 14 CORDEX models available for both RCPs are compared, RCP8.5 generally shows larger median change factors compared to RCP4.5 for climate regions 4 and 5. For climate region 5, median change factors are as much as 0.11 higher in RCP8.5 than in RCP4.5 for the 1-day duration, between 0.02 lower and 0.09 higher for the 3-day duration, and between 0.03 lower and 0.07 higher for the 7-day duration. For climate region 4, median change factors from these same 14 models are as much as 0.11 higher in RCP8.5 than in RCP4.5 for the 1-day duration, as much as 0.07 higher for the 3-day duration, and between 0.02 lower and 0.04 higher for the 7-day duration. No best CORDEX models are available for RCP4.5; therefore, the RCP4.5 markers for CORDEX are missing from figures 31B and 33B. It is also notable that JupiterWRF results in slightly larger median change factors in RCP4.5 compared to RCP8.5 in both climate regions (figs. 30B and 32B), with differences ranging from 0.02 to 0.03.
NOAA’s Physical Sciences Laboratory provides a Climate Change Web Portal (NOAA, 2022b) that summarizes climate change projections for key variables from the RCP4.5 and RCP8.5 CMIP5 scenarios. The output is provided as time series for predefined regions or as zoomable global maps. Projections of key variables and their anomalies are provided for predefined periods. Using this tool, the median temperature increase from 1956–2005 to 2070–99 expected for south and central Florida, based on the ensemble of CMIP5 models, ranges between 1.4 and 1.6 °C for RCP4.5, and between 2 and 2.25 °C for RCP8.5, with the largest increases in the central Florida region. Temperature increases between 1956–2005 and 2040–69 are very similar. Assuming that the Clausius-Clapeyron (CC) relation holds for precipitation extremes, an approximately 7-percent increase in precipitation would be expected per degree Celsius of warming. This would correspond to change factors of 1.10–1.11 for RCP4.5 and of 1.14–1.16 RCP8.5 based on the median temperature increase projections from the CMIP5 ensemble. The median LOCA change factors shown in figures 30–33 are generally lower than the expected range if the extremes followed the CC relation, indicating a sub-CC relation. Conversely, the median change factors from MACA and CORDEX are generally higher than expected based on the median temperature increase projections from the CMIP5 ensemble, especially for the longest return periods, indicating a super-CC relation. These deviations from CC cannot be attributed to physical factors such as moisture convergence and enhanced convection because they are based on statistically and dynamically downscaled projections, which have been bias-corrected, and therefore any links to physics have been severed. The median change factors from JupiterWRF are more in line with expectations from the CC relation alone; however, this does not imply that they are more accurate than change factors obtained from other downscaled climate datasets. The generally higher median change factors obtained for RCP8.5 than for RCP4.5 are in line with expectations from sole consideration of the CC relation.
Figure 39 shows boxplots of change factors for all models and stations in climate region 5 (south Florida). The variability in change factors increases with increasing return period when all datasets are considered together because of the influence of MACA models. Change factors as high as 8 in south Florida for the 1-day, 200-year event (fig. 39) and as high as 10 in south-central Florida for the 7-day, 200-year event are estimated for individual stations by MACA. CORDEX also shows change factors as high as 6.5 for the 7-day, 200-year event in south Florida (fig. 39) and as high as 6 for the 7-day, 200-year event in south-central Florida. The highest outlier change factors from CORDEX are slightly lower and occur less frequently than in MACA. When these very high change factors are multiplied by NOAA Atlas 14 DDF curves, the resulting future projected DDF values are beyond record high precipitation accumulations being recorded around the globe in the last decade. For example, record precipitation accumulations were observed during Hurricane Harvey in Texas and Louisiana in 2017 with the highest storm-total rainfall reported as 60.6 in. at two locations in Texas exceeding the previously accepted U.S. tropical cyclone storm total rainfall record (NOAA, 2018). The estimated return period for rainfall of this magnitude in southeast Texas is 1,000–10,000 years (Emanuel, 2017). Rainfall during Hurricane Florence in North Carolina in 2018 exceeded 30 in. near landfall with a localized maximum of 35.9 in. that set a State record for tropical cyclone rainfall (NOAA, 2019). The 3- and 4-day rainfall totals for this event surpassed the 1,000-year event at a particular site (Griffin and others, 2019). Hurricane Dorian in 2019 produced storm-total rainfall of 22.8 in. at a location in the Bahamas (NOAA, 2020). For an August 2016 storm in Louisiana, radar rainfall indicated more than 34 in. of rainfall at a location during the storm duration, well over the estimated 1,000-year return interval (Brown and others, 2020). A shift toward more frequent extremes, especially for rarer events, was documented in the Intergovernmental Panel on Climate Change’s (IPCC’s) Fifth Assessment Report (Collins and others, 2013) and further validated in their Sixth Assessment Report (IPCC, 2021). Attribution studies have determined that climate change has increased the intensity of these historical events and made them more likely. (See van der Wiel and others [2017] for the August 2016 Louisiana event; van Oldenborgh and others, [2017] for Hurricane Harvey; Reed and others [2020] for Hurricane Florence; and Reed and others [2021] for Hurricane Dorian.)
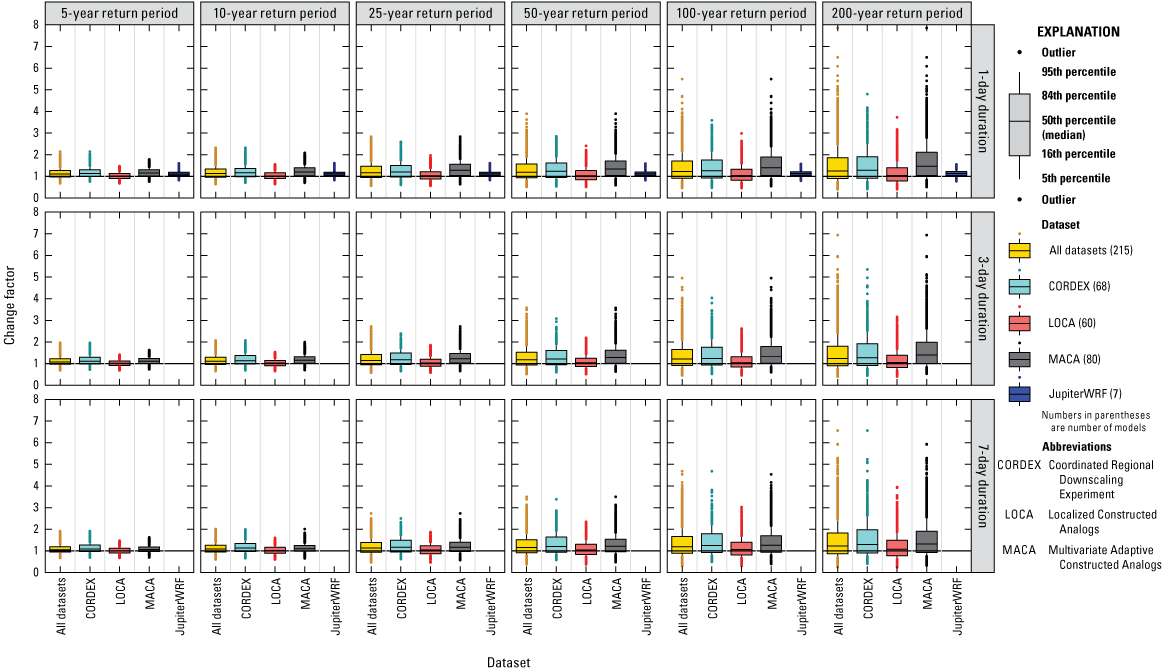
Boxplots showing change factors for all models and stations in climate region 5 (south Florida).
Evidence of record-breaking precipitation extremes and their links to climate change has been accumulating over the last few decades. However, given that the very high change factors computed here were generated by statistical downscaling or bias-corrected dynamical downscaling, the confidence in them is not as high as it would be if they had been generated by a purely physically based model. In addition, the highest change factors are associated with very long return periods, which are much longer than the number of years of data used in DDF fitting and are highly uncertain despite the use of a POT approach in this study. The boxplots of median station change factors across models for climate region 5 (south Florida) (fig. 40) show the central tendency of the station change factors across models in the region. Although the influence of individual station outliers is removed when looking at medians across stations as in this figure, it is evident that MACA still results in higher change factors than CORDEX and LOCA, especially for 1- and 3-day durations. From these two figures, it is evident that change factors below one (that is, drier extremes) are possible as indicated by CORDEX, LOCA, and MACA, with the median for LOCA being very close to a change factor of one. Although a similar boxplot is not shown here for climate region 4 (south-central Florida), it can be inferred from figures 30 and 32, that overall, climate region 4 has higher change factors than climate region 5. In particular, the median for LOCA is above one for all durations and return periods in climate region 4. In fact, it is the 16th percentile for LOCA that is very close to one for climate region 4.
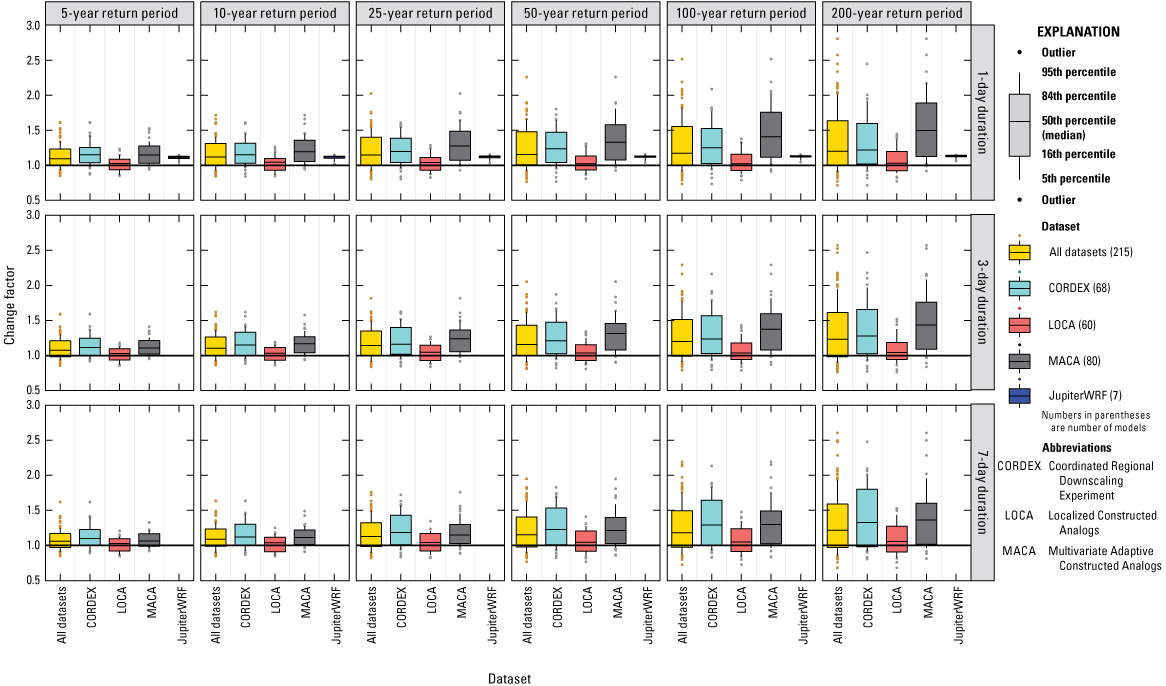
Boxplots showing median station change factors across models for climate region 5 (south Florida).
Spot checks of the data associated with some of the extremely high change factors in MACA show that they are the result of extremely high outlier events in the future projection period 2050–89. The specific case of a change factor of 10 in MACA is due to 35 in. of precipitation during a 3- to 7-day event in the future projection period at a grid cell in southwest Florida. The DDF fit at this station results in an extrapolation to 164 in. of precipitation for the 200-year event, whereas 35 in. of precipitation are fitted for an event with a return period of between 25 and 50 years. This is a limitation arising from fitting DDF curves for a limited future 40-year projection period based on local data, in that it is possible that this very high event only happened once in a much longer period than the 40 years analyzed. However, these very high precipitation events appear to be much more common in MACA than in the other downscaled climate datasets and are likely a result of the downscaling method.
Wootten (2018) shows how subtle decisions performed in the process of statistical downscaling such as tail adjustment, trace adjustment, and interpolation can affect the skill of the prediction and increase the uncertainty in future projections, especially for extremes and event occurrence. Wang and others (2020) found that MACA projects significant increases in the 20-year daily event in New England compared to LOCA for which the projected changes are inconclusive over most of the area. In LOCA, model consensus is lacking over most of the region, but where models do agree, the projected changes have a smaller magnitude than in MACA. Their finding is generally consistent with this study’s findings for Florida. Wang and others (2020) note that projected changes in the mean annual maximum daily event are quite close between MACA-Livneh and MACA-gridMET but differ significantly between LOCA and MACA-Livneh. As a result, they conclude that differences in the projected changes are primarily caused by differences in the downscaling method, rather than the observational data used in training. However, LOCA and MACA used two different versions of the Livneh dataset for bias correction, which complicates the comparison.
The factors identified as potentially contributing to biases in DDF curves for the historical period, in addition to other factors such as scenario uncertainty, contribute to the total uncertainty in derived change factors. Wootten and others (2017) attempt to characterize the sources of uncertainty from global climate models and downscaling techniques. In particular, they evaluate the sources of uncertainty in the decadal mean of the annual number of days with extreme precipitation (more than 1 in.) for central Florida across various downscaled climate datasets, including some analyzed in this study and others that were not. Based on data from an idealized scenario that only compares 16 common GCMs and two common emission scenarios from MACA and BCCA, they find that, for the 2070s, GCM model uncertainty dominates, followed by natural variability and downscaling uncertainty. The emission scenario contributes the least to the total uncertainty, although its contribution increases with time whereas the contribution of natural variability decreases with time. Although a quantitative uncertainty analysis has not been performed as part of this study, Wootten and others (2017) findings seem qualitatively consistent with this study’s findings for change factors on the basis of an examination of figures 39 and 40. Once the station median is computed, the range of variation across models is reduced. The difference in median between datasets is smaller than between models within a dataset, and the difference between RCPs is even smaller. The DDF fitting methodology introduces additional uncertainty in the estimated change factors.
Because of the large uncertainties in the derived change factors and associated future DDF curves, methods for decision making under deep uncertainty could be used to increase the flexibility in the planning process. These methods are documented by Marchau and others (2019) and include decision scaling, robust decision making, and dynamic adaptive policy pathways, among others. Flexibility in the phasing and design of various flood control adaptation measures could reduce long-term costs while considering the evolution in climate science as well as local and global changes in climate and sea-level rise with consideration for potential tipping points. Research gaps and recommendations have also been outlined by Florida International University’s Sea Level Solutions Center (Florida International University, 2021).
Summary and Conclusions
The wide range of change factors computed in this study represent a set of plausible changes in extreme precipitation in central and southern Florida. Given the wide range of change factors computed, users are encouraged to make application-specific judgments when deciding whether to use individual change factors or a range of them for their projects. It is important to consider the many sources of uncertainty and that change factors obtained by statistical downscaling of general circulation model (GCM) output, such as in Localized Constructed Analogs (LOCA) and Multivariate Adaptive Constructed Analogs (MACA), may not respect the physics of the precipitation-generating processes. For example, in statistical downscaling, precipitation amounts are not limited by the amount of precipitable water in the atmosphere or the presence or absence of moisture convergence. Although the raw Coordinated Regional Downscaling Experiment (CORDEX) data prior to bias correction are generated by physically based dynamic downscaling of GCM output using regional climate models, Srivastava and others (2022) show that some CORDEX models are not able to capture the annual cycle of precipitation in Florida, with some models completely out of phase or not able to capture the cycle amplitude. The bias-correction algorithm used by CORDEX generally fixes the seasonality problem, but the links to the physics are broken, also reducing confidence in the bias-corrected CORDEX output.
LOCA performs the worst in terms of being able to reproduce historical precipitation extremes indices and generally predicts the lowest change factors. MACA, which results in the highest change factors, tends to better capture the historical precipitation extremes indices than LOCA in south-central Florida and capture these indices better than CORDEX and LOCA in south Florida. Extremely high change factors obtained from MACA are likely a result of the way the MACA procedure is known to amplify the change signal in the native GCMs. This issue is exacerbated by the extrapolation of high quantiles in the upper tail of the fitted probability distribution. Because these extremely high change factors estimated from MACA happen at isolated stations instead of large regions, confidence in their magnitude is low. Because of large differences between depth-duration-frequency (DDF) values derived from observations and DDF values derived from downscaled model precipitation for the historical period compared to the magnitude of the change from historical to future projection periods, estimates should be used with caution, because differences with respect to observations may be amplified in future projections in a nonmultiplicative manner.
Median change factors across regions and (or) datasets may be more reliable than values at individual stations from individual models or individual datasets. Because of the large uncertainties in the derived change factors and associated future DDF curves, users may wish to rely on the ensemble median of change factors as well as the range of change factors provided by the boxes in the boxplots, which were selected to include two-thirds of the data. A benefit-risk analysis may help clarify a suitable range of change factors. Outliers at individual stations could be identified by comparison with change factors at other nearby locations and across models. It is well-known that return levels and change factors for the longest return periods (100 and 200 years) are the most uncertain and spatially variable. Confidence in a return level decreases rapidly when the return period is more than about twice the length of the original dataset. Even with the peaks-over-threshold approach used as part of this study, which increases the sample size used in fitting, change factors for the 100- and 200-year events are highly uncertain and most spatially variable. The use of median change factors is especially recommended for these rarer events. For return periods above 100 years, one may need to rely on an extension or adjustment of the percent change for lower return periods to higher return periods.
Code written in R language is provided as part of the data release associated with this report (Irizarry-Ortiz and Stamm, 2022), and the code allows users to be able to generate boxplots of change factors by station, or for all stations in a South Florida Water Management District ArcHydro Enhanced Database basin or county. The user has flexibility in defining the percentiles associated with the box and whiskers, including change factors based on all models or only the best models, and including data from one or more representative concentration pathways. National Oceanic and Atmospheric Administration Atlas 14 stations in the Florida Keys are inactive in the downscaled model grids. Data from the closest mainland grid cells to these four stations were used in developing DDF curves at these four locations. Therefore, change factors developed for these four locations are highly uncertain and should be used with caution.
When applying change factors to the historical National Oceanic and Atmospheric Administration Atlas 14 DDF curves to derive future precipitation DDF curves for the entire range of durations and return periods evaluated as part of this study, there is a possibility that the resulting future DDF curves may have fitted precipitation depths that decrease, rather than increase, for longer durations. Depending on the change factors used, this may happen in as much as 6 percent of cases. In such a case, the higher of the future precipitation depths derived for the duration of interest and the previous shorter duration may be a more conservative choice.
Because of the large uncertainties in the derived change factors and associated future DDF curves, methods for decision making under deep uncertainty could be used to increase the flexibility in the planning process. These methods include decision scaling, robust decision making, and dynamic adaptive policy pathways, among others. Flexibility in the phasing and design of various flood control adaptation measures could reduce long-term costs while considering the evolution in climate science as well as local and global changes in climate and sea-level rise with consideration for potential tipping points.
In the longer-term, the development of a high-resolution (1- to 2-kilometer) nonhydrostatic (convection-resolving) regional climate model for the State of Florida, which can better capture local microclimatic conditions including sea- and lake-breeze interactions, land use changes, and so forth, could reduce some of the uncertainties associated with the existing coarse-resolution dynamically downscaled data products and especially with the statistical-downscaling methods. Higher-resolution convection-permitting models have been shown to improve the representation of extreme precipitation, especially on subdaily timescales and for summer high-precipitation intensity events compared to coarser-scale regional models with parameterized convection, such as those used by CORDEX, which tend to produce rainfall that is too light and widespread. In addition, the simulation of tropical cyclones has been shown to be improved when using convection-permitting models.
References Cited
Abatzoglou, J.T., 2013, Development of gridded surface meteorological data for ecological applications and modeling: International Journal of Climatology, v. 33, no. 1, p. 121–131, accessed July 7, 2022, at https://doi.org/10.1002/joc.3413. [Data available at http://thredds.northwestknowledge.net:8080/thredds/reacch_climate_MET_aggregated_catalog.html.]
Abatzoglou, J.T., and Brown, T.J., 2012, A comparison of statistical downscaling methods suited for wildfire applications: International Journal of Climatology, v. 32, no. 5, p. 772–780, accessed July 7, 2022, at https://doi.org/10.1002/joc.2312.
Akaike, H., 1973, Information theory and an extension of the maximum likelihood principle, in International Symposium on Information Theory, 2d, Tsahkadsor, Armenia, USSR, September 2–8, 1971 [Proceedings]: Budapest, Hungary, Akademiai Kiado, p. 267–281. [Reprinted in 1998. Also available at https://doi.org/10.1007/978-1-4612-1694-0_15.]
Ali, H., Fowler, H.J., Pritchard, D., Lenderink, G., Blenkinsop, S., and Lewis, E., 2022, Towards quantifying the uncertainty in estimating observed scaling rates: Geophysical Research Letters, v. 49, article e2022GL099138, 8, p., accessed August 2, 2022, at https://doi.org/10.1029/2022GL099138.
Asadieh, B., and Krakauer, N.Y., 2015, Global trends in extreme precipitation—Climate models versus observations: Hydrology and Earth System Sciences, v. 19, no. 2, p. 877–891, accessed July 7, 2022, at https://doi.org/10.5194/hess-19-877-2015.
Asquith, W.H., 1998, Depth-duration frequency of precipitation for Texas: U.S. Geological Survey Water Resources Investigations Report 98–4404, 107 p., accessed July 7, 2022, at https://doi.org/10.3133/wri984044.
Asquith, W.H., 2020, lmomco—L-moments, censored L-moments, trimmed L-moments, L-comoments, and many distributions—R package, v. 2.3.6: Lubbock, Tex., Texas Tech University, accessed July 7, 2022, at http://cran.r-project.org/package=lmomco.
Asquith, W.H., and Roussel, M.C., 2004, Atlas of depth-duration frequency of precipitation annual maxima for Texas: U.S. Geological Survey Scientific Investigations Report 2004–5041, 114 p., accessed July 7, 2022, at https://pubs.usgs.gov/sir/2004/5041/.
Avery, C.W., Reidmiller, D.R., Kolian, M., Kunkel, K.E., Herring, D., Sherman, R., Sweet, W.V., Tipton, K., and Weaver, C., 2018, Data tools and scenario products, in Reidmiller, D.R., Avery, C.W., Easterling, D.R., Kunkel, K.E., Lewis, K.L.M., Maycock, T.K., and Stewart, B.C., eds., Impacts, risks, and adaptation in the United States—Fourth National Climate Assessment (v. 2): Washington, D.C., U.S. Global Change Research Program, p. 1413–1430, accessed July 7, 2022, at https://doi.org/10.7930/NCA4.2018.AP3.
Ayuso-Muñoz, J.L., García-Marín, A.P., Ayuso-Ruiz, P., Estévez, J., Pizarro-Tapia, R., and Taguas, E.V., 2015, A more efficient rainfall intensity-duration-frequency relationship by using an at-site regional frequency analysis—Application at Mediterranean climate locations: Water Resources Management, v. 29, no. 9, p. 3243–3263, accessed July 7, 2022, at https://doi.org/10.1007/s11269-015-0993-z.
Baigorria, G.A., Jones, J.W., and O’Brien, J.J., 2007, Understanding rainfall spatial variability in southeast USA at different timescales: International Journal of Climatology, v. 27, no. 6, p. 749–760, accessed July 7, 2022, at https://doi.org/10.1002/joc.1435.
Baker, R.C., Lynn, B.H., Boone, A., Tao, W.-K., and Simpson, J., 2001, The influence of soil moisture, coastline curvature, and land-breeze on circulations on sea-breeze-initiated precipitation: Journal of Hydrometeorology, v. 2, no. 2, p. 193–211, accessed July 7, 2022, at https://doi.org/10.1175/1525-7541(2001)002<0193:TIOSMC>2.0.CO;2.
Behnke, R., Vavrus, S., Allstadt, A., Albright, T., Thogmartin, W.E., and Radeloff, V.C., 2016, Evaluation of downscaled, gridded climate data for the conterminous United States: Ecological Applications, v. 26, no. 5, p. 1338–1351, accessed July 7, 2022, at https://doi.org/10.1002/15-1061.
Bell, F.C., 1976, The areal reduction factor in rainfall frequency estimation: Wallingford, U.K., Natural Environment Research Council, Institute of Hydrology Report no. 35, 62 p., accessed July 7, 2022, at https://nora.nerc.ac.uk/id/eprint/5751.
Bhatia, K.T., Vecchi, G.A., Knutson, T.R., Murakami, H., Kossin, J., Dixon, K.W., and Whitlock, C.E., 2019, Recent increases in tropical cyclone intensification rates: Nature Communications, v. 10, no. 635, 9 p., accessed July 7, 2022, at https://doi.org/10.1038/s41467-019-08471-z.
Brown, V.M., Keim, B.D., Kappel, W.D., Hultstrand, D.M., Peyrefitte, A.G., Jr., Black, A.W., Steinhilber, K.M., and Muhlestein, G.A., 2020, How rare was the August 2016 south-central Louisiana heavy rainfall event?: Journal of Hydrometeorology, v. 21, no. 4, p. 773–790, accessed July 7, 2022, at https://doi.org/10.1175/JHM-D-19-0225.1.
Bukovsky, M.S., Gao, J., Mearns, L.O., and O’Neill, B.C., 2021, SSP-based land-use change scenarios—A critical uncertainty in future regional climate change projections: Earth’s Future, v. 9, no. 3, article e2020EF001782, 18 p., accessed August 2, 2022, at https://doi.org/10.1029/2020EF001782.
Bureau of Reclamation, 2013, Downscaled CMIP3 and CMIP5 climate and hydrology projections—Release of downscaled CMIP5 climate projections, comparison with preceding information, and summary of user needs: Denver, Colo., U.S. Department of the Interior, Bureau of Reclamation, Technical Services Center, 47 p., accessed July 7, 2022, at https://gdo-dcp.ucllnl.org/downscaled_cmip_projections/techmemo/downscaled_climate.pdf.
Burnham, K.P., and Anderson, D.R., 2002, Model selection and multimodel inference—A practical information-theoretic approach (2d ed.): New York, Springer Science and Business Media, 488 p., accessed July 7, 2022, at https://doi.org/10.1007/b97636.
Burnham, K.P., Anderson, D.R., and Huyvaert, K.P., 2011, AIC model selection and multimodel inference in behavioral ecology—Some background, observations, and comparisons: Behavioral Ecology and Sociobiology, v. 65, no. 1, p. 23–35, accessed July 7, 2022, at https://doi.org/10.1007/s00265-010-1029-6.
Byrne, M.P., Pendergrass, A.G., Rapp, A.D., and Wodzicki, K.R., 2018, Response of the Intertropical Convergence Zone to climate change—Location, width, and strength: Current Climate Change Reports, v. 4, no. 4, p. 355–370, accessed July 7, 2022, at https://doi.org/10.1007/s40641-018-0110-5.
Cadavid, L.G., Van Zee, R., White, C., Trimble, P., and Obeysekera, J.T.B., 1999, Operational hydrology in south Florida using climate forecast: Annual Geophysical Union Hydrology Days, 19th, Fort Collins, Colo., August 16–20, 1999 [Proceedings]: Fort Collins, Colo., Colorado State University, 17 p., accessed February 1, 2022, at https://www.sfwmd.gov/sites/default/files/documents/opln_hyd_web.pdf.
Campbell, J.D., Taylor, M.A., Bezanilla-Morlot, A., Stephenson, T.S., Centella-Artola, A., Clarke, L.A., and Stephenson, K.A., 2021, Generating projections for the Caribbean at 1.5, 2.0, and 2.5 °C from a high-resolution ensemble: Atmosphere, v. 12, no. 328, 27 p., accessed July 7, 2022, at https://doi.org/10.3390/atmos12030328.
Cannon, A.J., 2018, Multivariate quantile mapping bias correction—An N-dimensional probability density function transform for climate model simulations of multiple variables: Climate Dynamics, v. 50, no. 1–2, p. 31–49, accessed July 7, 2022, at https://doi.org/10.1007/s00382-017-3580-6.
Cannon, A.J., Sobie, S.R., and Murdock, T.Q., 2015, Bias correction of GCM precipitation by quantile mapping—How well do methods preserve changes in quantiles and extremes?: Journal of Climate, v. 28, no. 17, p. 6938–6959, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-14-00754.1.
Carney, M., 2016, Bias correction to GEV shape parameters used to predict precipitation extremes: Journal of Hydrologic Engineering, v. 21, no. 10, article 04016035, accessed July 7, 2022, at https://doi.org/10.1061/(ASCE)HE.1943-5584.0001416.
Carter, L., Terando, A., Dow, K., Hiers, K., Kunkel, K.E., Lascurain, A., Marcy, D., Osland, M., and Schramm, P., 2018, Southeast, in Reidmiller, D.R., Avery, C.W., Easterling, D.R., Kunkel, K.E., Lewis, K.L.M., Maycock, T.K., and Stewart, B.C., eds., Impacts, risks, and adaptation in the United States—Fourth National Climate Assessment (v. 2): Washington, D.C., U.S. Global Change Research Program, p. 743–808, accessed July 7, 2022, at https://doi.org/10.7930/NCA4.2018.CH19.
Cavanaugh, N., Gershunov, A., Panorska, A., and Kozubowski, T.J., 2015, The probability distribution of intense daily precipitation: Geophysical Research Letters, v. 42, 8 p., accessed August 11, 2022, at http://dx.doi.org/10.1002/2015GL063238.
Chen, C.-T., and Knutson, K., 2008, On the verification and comparison of extreme rainfall indices from climate models: Journal of Climate, v. 21, no. 7, p. 1605–1621, accessed July 7, 2022, at https://doi.org/10.1175/2007JCLI1494.1.
Chen, L., and Singh, V.P., 2017, Generalized beta distribution of the second kind for flood frequency analysis: Entropy (Basel, Switzerland), v. 19, no. 6, p. 254, accessed July 7, 2022, at https://doi.org/10.3390/e19060254.
Chen, W., Jiang, Z., and Li, L., 2011, Probabilistic projections of climate change over China under SRES A1B scenario using 28 AOGCMs: Journal of Climate, v. 24, no. 17, p. 4741–4756, accessed July 7, 2022, at https://doi.org/10.1175/2011JCLI4102.1.
Choulakian, V., and Stephens, A., 2001, Goodness-of-fit tests for the Generalized Pareto Distribution: Technometrics, v. 43, no. 4, p. 478–484, accessed July 7, 2022, at https://doi.org/10.1198/00401700152672573.
Chowdhury, J.U., Stedinger, J.R., and Lu, L.-H., 1991, Goodness-of-fit tests for regional generalized extreme value flood distributions: Water Resources Research, v. 27, no. 7, p. 1765–1776, accessed July 7, 2022, at https://doi.org/10.1029/91WR00077.
Claps, P., and Laio, F., 2003, Can continuous streamflow data support flood frequency analysis?—An alternative to the partial duration series approach: Water Resources Research, v. 39, no. 8, article 1216, accessed July 7, 2022, at https://doi.org/10.1029/2002WR001868.
Coles, S., 2001, An introduction to statistical modeling of extreme values: Springer-Verlag, 219 p. [Also available at https://doi.org/10.1007/978-1-4471-3675-0.]
Collins, M., Knutti, R., Arblaster, J., Dufresne, J.-L., Fichefet, T., Friedlingstein, P., Gao, X., Gutowski, W.J., Johns, T., Krinner, G., Shongwe, M., Tebaldi, C., Weaver, A.J., and Wehner, M., 2013, Long-term climate change—Projections, commitments and irreversibility, in Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P.M., eds., Climate Change 2013—The physical science basis—Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change: Cambridge, U.K., and New York, Cambridge University Press, p. 1029–1136, accessed July 7, 2022, at https://doi.org/10.1017/CBO9781107415324.024.
Courty, L.G., Wilby, R.L., Hillier, J.K., and Slater, L.J., 2019, Intensity-duration-frequency curves at the global scale: Environmental Research Letters, v. 14, article 084045, p. 1–10, accessed July 7, 2022, at https://doi.org/10.1088/1748-9326/ab370a.
Cubasch, U., Wuebbles, D., Chen, D., Facchini, M.C., Frame, D., Mahowald, N., and Winther, J.-G., 2013, Introduction, in Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P.M., eds., Climate Change 2013—The physical science basis—Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change: Cambridge, U.K., and New York, Cambridge University Press, p. 119–158, accessed July 7, 2022, at https://doi.org/10.1017/CBO9781107415324.007.
Cunnane, C., 1973, A particular comparison of annual maxima and partial duration series methods of flood frequency prediction: Journal of Hydrology, v. 18, no. 3–4, p. 257–271, accessed July 7, 2022, at https://doi.org/10.1016/0022-1694(73)90051-6.
D’Agostino, R.B., and Stephens, M.A., 1986, Tests based on EDF statistics, in Goodness of fit techniques—Statistics texthooks and monographs (v. 68): New York, Marcel Dekker, p. 110. [Also available at https://doi.org/10.1201/9780203753064.]
Daly, C., Doggett, M.K., Smith, J.I., Olson, K.V., Halbleib, M.D., Dimcovic, Z., Keon, D., Loiselle, R.A., Steinberg, B., Ryan, A.D., Pancake, C.M., and Kaspar, E.M., 2021, Challenges in observation-based mapping of daily precipitation across the conterminous United States: Journal of Atmospheric and Oceanic Technology, v. 38, no. 11, p. 1979–1992, accessed July 7, 2022, at https://doi.org/10.1175/JTECH-D-21-0054.1.
Daly, C., Halbleib, M., Smith, J.I., Gibson, W.P., Doggett, M.K., Taylor, G.H., Curtis, J., and Pasteris, P.P., 2008, Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States: International Journal of Climatology, v. 28, no. 15, p. 2031–2064, accessed July 7, 2022, at https://doi.org/10.1002/joc.1688.
Davison, A.C., and Smith, R.L., 1990, Models for exceedances over high thresholds: Journal of the Royal Statistical Society, Series B, Methodological, v. 52, no. 3, p. 393–425, accessed July 7, 2022, at https://doi.org/10.1111/j.2517-6161.1990.tb01796.x.
Dawdy, D.R., and Gupta, V.K., 1995, Multiscaling and skew separation in regional floods: Water Resources Research, v. 31, no. 11, p. 2761–2767, accessed July 7, 2022, at https://doi.org/10.1029/95WR02078.
DeGaetano, A.T., 2009, Time-dependent changes in extreme-precipitation and return-period amounts in the continental United States: Journal of Applied Meteorology and Climatology, v. 48, no. 10, p. 2086–2099, accessed July 7, 2022, at https://doi.org/10.1175/2009JAMC2179.1.
Dixon, K.W., Lanzante, J.R., Nath, M.J., Hayhoe, K., Stoner, A., Radhakrishnan, A., Balaji, V., and Gaitán, C.F., 2016, Evaluating the stationarity assumption in statistically downscaled climate projections—Is past performance and indicator of future results?: Climatic Change, v. 135, no. 3–4, p. 395–408, accessed July 7, 2022, at https://doi.org/10.1007/s10584-016-1598-0.
Donat, M.G., Alexander, L.V., Yang, H., Durre, I., Vose, R., Dunn, R.J.H., Willett, K.M., Aguilar, E., Brunet, M., Caesar, J., Hewitson, B., Jack, C., Klein Tank, A.M.G., Kruger, A.C., Marengo, J., Peterson, T.C., Renom, M., Oria Rojas, C., Rusticucci, M., Salinger, J., Elrayah, A.S., Sekele, S.S., Srivastava, A.K., Trewin, B., Villarroel, C., Vincent, L.A., Zhai, P., Zhang, X., and Kitching, S., 2013, Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century—The HadEX2 dataset: Journal of Geophysical Research, Atmospheres, v. 118, no. 5, p. 2098–2118, accessed July 7, 2022, at https://doi.org/10.1002/jgrd.50150.
Donat, M.G., Sillmann, J., Wild, S., Alexander, L.V., Lippmann, T., and Zwiers, F.W., 2014, Consistency of temperature and precipitation extremes across various global gridded in situ and reanalysis datasets: Journal of Climate, v. 27, no. 13, p. 5019–5035, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-13-00405.1.
Donders, T.H., de Boer, H.J., Finsinger, W., Grimm, E.C., Dekker, S.C., Reichart, G.J., and Wagner-Cremer, F., 2011, Impact of the Atlantic Warm Pool on precipitation and temperature in Florida during North Atlantic cold spells: Climate Dynamics, v. 36, no. 1–2, p. 109–118, accessed July 7, 2022, at https://doi.org/10.1007/s00382-009-0702-9.
Dougherty, E., and Rasmussen, K.L., 2019, Climatology of flood-producing storms and their associated rainfall characteristics in the United States: Monthly Weather Review, v. 147, no. 11, p. 3861–3877, accessed July 7, 2022, at https://doi.org/10.1175/MWR-D-19-0020.1.
Emanuel, K., 2017, Assessing the present and future probability of Hurricane Harvey’s rainfall: Proceedings of the National Academy of Sciences of the United States of America, v. 114, no. 48, p. 12681–12684, accessed July 7, 2022, at https://doi.org/10.1073/pnas.1716222114.
Emanuel, K.A., 2013, Downscaling CMIP5 climate models shows increased tropical cyclone activity over the 21st century: Proceedings of the National Academy of Sciences of the United States of America, v. 110, no. 30, p. 12219–12224, accessed July 7, 2022, at https://doi.org/10.1073/pnas.1301293110.
Enfield, D.B., and Cid-Serrano, L., 2010, Secular and multidecadal warmings in the North Atlantic and their relationships with major hurricane activity: International Journal of Climatology, v. 30, p. 174–184, accessed July 7, 2022, at https://doi.org/10.1002/joc.1881.
Enfield, D.B., Mestas-Nuñez, A.M., and Trimble, P.J., 2001, The Atlantic Multidecadal Oscillation and its relation to rainfall and river flows in the continental U.S.: Geophysical Research Letters, v. 28, no. 10, p. 2077–2080, accessed July 7, 2022, at https://doi.org/10.1029/2000GL012745.
Eyring, V., Bony, S., Meehl, G.A., Senior, C.A., Stevens, B., Stouffer, R.J., and Taylor, K.E., 2016, Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization: Geoscientific Model Development, v. 9, no. 5, p. 1937–1958, accessed July 7, 2022, at https://doi.org/10.5194/gmd-9-1937-2016.
Falgout, J.T., and Gordon, J., 2020, USGS Advanced Research Computing—USGS Yeti supercomputer: U.S. Geological Survey web page, accessed January 15, 2022, at https://doi.org/10.5066/F7D798MJ.
Faraway, J., Marsaglia, G., Marsaglia, J., and Baddeley, A., 2019, goftest—Classical goodness-of-fit tests for univariate distributions—R package, v. 1.2–2: R Foundation for Statistical Computing software release, accessed July 7, 2022, at https://cran.r-project.org/web/packages/goftest/index.html.
Ferro, C.A.T., 2003, Statistical methods for clusters of extreme values: Lancaster, England, Lancaster University, Ph.D. dissertation, 180 p., accessed October 15, 2020, at http://empslocal.ex.ac.uk/people/staff/ferro/Publications/Thesis/thesis.pdf.
Ferro, C.A.T., and Segers, J., 2003, Inference for clusters of extreme values: Journal of the Royal Statistical Society, Series B, Statistical Methodology, v. 65, no. 2, p. 545–556, accessed July 7, 2022, at https://doi.org/10.1111/1467-9868.00401.
Filliben, J.J., 1975, The probability plot correlation test for normality: Technometrics, v. 17, no. 1, p. 111–117, accessed July 7, 2022, at https://doi.org/10.1080/00401706.1975.10489279.
Fisher, R.A., and Tippett, L.H.C., 1928, Limiting forms of the frequency distribution of the largest or smallest member of a sample: Mathematical Proceedings of the Cambridge Philosophical Society, v. 24, no. 2, p. 180–190, accessed July 7, 2022, at https://doi.org/10.1017/S0305004100015681.
Flato, G., Marotzke, J., Abiodun, B., Braconnot, P., Chou, S.C., Collins, W., Cox, P., Driouech, F., Emori, S., Eyring, V., Forest, C., Gleckler, P., Guilyardi, E., Jakob, C., Kattsov, V., Reason, C., and Rummukainen, M., 2013, Evaluation of climate models, in Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P.M., eds., Climate Change 2013—The physical science basis—Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change: Cambridge, U.K., and New York, Cambridge University Press, p. 741–866, accessed July 7, 2022, at https://doi.org/10.1017/CBO9781107415324.020.
Gibbon, J.D., and Holm, D.D., 2011, Extreme events in solutions of hydrostatic and non-hydrostatic climate models: Philosophical Transactions, Royal Society, Mathematical, Physical, and Engineering Sciences, v. 369, no. 1939, p. 1156–1179, accessed July 7, 2022, at https://doi.org/10.1098/rsta.2010.0244.
Gibson, P., 2021, Python code to compute ETCCDI climate indices [ETCCDI_precip.py, CPC_ETCCDI_Wrapper.py]: NCAR web page, accessed February 12, 2021, at https://github.com/Peter-Gibson/climate/tree/CLIMATE-937/examples.
Gilleland, E., and Katz, R.W., 2016, extRemes 2.0—An extreme value analysis package in R: Journal of Statistical Software, v. 72, no. 8, p. 1–39, accessed July 7, 2022, at https://doi.org/10.18637/jss.v072.i08.
Giorgi, F., 2010, Uncertainties in climate change projections, from the global to the regional scale: EPJ Web of Conferences, v. 9, p. 115–129, accessed August 2, 2022 at https://doi.org/10.1051/epjconf/201009009.
Giorgi, F., Jones, C., and Asrar, G.R., 2009, Addressing climate information needs at the regional level—The CORDEX framework: World Meteorological Society Bulletin, v. 58, no. 3, p. 175–183, accessed July 7, 2022, at https://public.wmo.int/en/bulletin/addressing-climate-information-needs-regional-level-cordex-framework.
Gleckler, P.J., Taylor, K.E., and Doutriaux, C., 2008, Performance metrics for climate models: Journal of Geophysical Research, v. 113, no. D6, article D06104, accessed July 7, 2022, at https://doi.org/10.1029/2007JD008972.
Goldenberg, S.B., Landsea, C.W., Mestas-Nuñez, A.M., and Gray, W.M., 2001, The recent increase in Atlantic hurricane activity—Causes and implications: Science, v. 293, no. 5529, p. 474–479, accessed July 7, 2022, at https://doi.org/10.1126/science.1060040.
Goly, A., 2013, Influences of climate variability and change on precipitation characteristics and extremes: Florida Atlantic University, College of Engineering and Computer Science, Ph.D. dissertation, 345 p., accessed December 30, 2020, at https://fau.digital.flvc.org/islandora/object/fau%3A4189/datastream/OBJ/view/Influences_of_climate_variability_and_change_on_precipitation_characteris tics_and_extremes.pdf.
Goly, A., and Teegavarapu, R.S., 2014, Individual and coupled influences of AMO and ENSO on regional precipitation characteristics and extremes: Water Resources Research, v. 50, no. 6, p. 4686–4709, accessed July 7, 2022, at https://doi.org/10.1002/2013WR014540.
Griffin, M., Malsick, M., Mizzell, H., and Moore, L., 2019, Historic rainfall and record-breaking flooding from Hurricane Florence in the Pee Dee Watershed: Journal of South Carolina Water Resources, v. 6, no. 1, p. 28–35, accessed July 7, 2022, at https://doi.org/10.34068/JSCWR.06.03.
Griffis, V.W., and Stedinger, J.R., 2007, Log-pearson type 3 distribution and its application in flood frequency analysis. I—Distribution characteristics: Journal of Hydrologic Engineering, v. 12, no. 5, p. 482–491, accessed July 7, 2022, at https://doi.org/10.1061/(ASCE)1084-0699(2007)12:5(482).
Gubareva, T.S., and Gartsman, B.I., 2010, Estimating distribution parameters of extreme hydrometeorological characteristics by L-moment method: Water Resources, v. 37, no. 4, p. 437–445, accessed July 7, 2022, at https://doi.org/10.1134/S0097807810040020.
Guttman, N., and Quayle, R.G., 1996, A historical perspective on U.S. climate divisions: Bulletin of the American Meteorological Society, v. 77, no. 2, p. 293–304, accessed July 7, 2022, at https://doi.org/10.1175/1520-0477(1996)077<0293:AHPOUC>2.0.CO;2.
Hall, T.M., and Kossin, J.P., 2019, Hurricane stalling along the North American coast and implications for rainfall: NPJ Climate and Atmospheric Science, v. 2, no. 17, accessed July 7, 2022, at https://doi.org/10.1038/s41612-019-0074-8.
Hart, E.M., and Bell, K., 2015, prism—R package, v. 0.06: Corvallis, Ore., Oregon State University, PRISM Climate Data project, accessed July 7, 2022, at https://github.com/ropensci/prism. [Data available at https://doi.org/10.5281/zenodo.33663.]
Heffernan, J.E., and Stephenson, A.G., 2018, ismev—An introduction to statistical modeling of extreme values—R package, v. 1.42: R Foundation for Statistical Computing software release, accessed July 7, 2022, at https://cran.r-project.org/web/packages/ismev/index.html.
Heo, J.-H., Kho, Y.W., Shin, H., Kim, S., and Kim, T., 2008, Regression equations of probability plot correlation coefficient test statistics from several probability distributions: Journal of Hydrology, v. 355, no. 1–4, p. 1–15, accessed July 7, 2022, at https://doi.org/10.1016/j.jhydrol.2008.01.027.
Hosking, J., and Wallis, J., 1997, Regional frequency analysis—An approach based on L-moments: Cambridge University Press, 238 p., accessed July 7, 2022, at https://doi.org/10.1017/CBO9780511529443.
Hosking, J.R.M., 1990, L-moments—Analysis and estimation of distributions using linear combinations of order statistics: Journal of the Royal Statistical Society, Series B, Methodological, v. 52, no. 1, p. 105–124, accessed July 7, 2022, at https://doi.org/10.1111/j.2517-6161.1990.tb01775.x.
Hosking, J.R.M., 2019, L-moments—R package, v. 2.8: R Foundation for Statistical Computing software release, accessed July 7, 2022, at https://cran.r-project.org/web/packages/lmom/index.html.
Hosking, J.R.M., and Wallis, J.R., 1987, Parameter and quantile estimation for the generalized Pareto distribution: Technometrics, v. 29, no. 3, p. 339–349, accessed July 7, 2022, at https://doi.org/10.1080/00401706.1987.10488243.
Hosking, J.R.M., Wallis, J.R., and Wood, E.F., 1985, Estimation of the generalized extreme-value distribution by the method of probability weighted moments: Technometrics, v. 27, no. 3, p. 251–261, accessed July 7, 2022, at https://doi.org/10.1080/00401706.1985.10488049.
Hourdin, F., Mauritsen, T., Gettelman, A., Golaz, J.-C., Balaji, V., Duan, Q., Folini, D., Ji, D., Klocke, D., Qian, Y., Rauser, F., Rio, C., Tomassini, L., Watanabe, M., and Williamson, D., 2017, The art and science of climate model tuning: Bulletin of the American Meteorological Society, v. 98, no. 3, p. 589–602, accessed July 7, 2022, at https://doi.org/10.1175/BAMS-D-15-00135.1.
Hsing, T., 1991, On tail index estimation using dependent data: Annals of Statistics, v. 19, no. 3, p. 1547–1569, accessed July 7, 2022, at https://doi.org/10.1214/aos/1176348261.
Infanti, J.M., Kirtman B.P., Aumen, N.G., Stamm, J., and Polsky, C., 2020, Aligning climate models with stakeholder needs—Advances in communicating future rainfall uncertainties for south Florida decision makers: Earth and Space Science, v. 7, no. 7, article e2019EA000725, accessed July 7, 2022, at https://doi.org/10.1029/2019EA000725.
Intergovernmental Panel on Climate Change [IPCC], 2000, Emissions scenarios—A special report of Working Group III of the Intergovernmental Panel on Climate Change [Nakicenovic, N. and Swart, R., eds.]: Cambridge University Press, 570 p., https://www.ipcc.ch/site/assets/uploads/2018/03/emissions_scenarios-1.pdf.
Intergovernmental Panel on Climate Change [IPCC], 2013, Summary for policymakers, in Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P.M., eds., Climate Change 2013—The physical science basis—Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change: Cambridge, U.K., and New York, Cambridge University Press, p. 1029–1136, accessed October 1, 2022, at https://doi.org/10.1017/CBO9781107415324.004.
Intergovernmental Panel on Climate Change [IPCC], 2021, Summary for policymakers, in Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L, Gomis, M.I., Huang, M., Leitzell, K., Lonnoy, E., Matthews, J.B.R., Maycock, T.K., Waterfield, T., Yelekçi, O., Yu, R., and Zhou, B., eds., Climate change 2021—The physical science basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change: Cambridge U.K., and New York, N.Y., Cambridge University Press, p. 3–32, accessed July 7, 2022, at https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_SPM.pdf.
Irizarry, M.M., Obeysekera, J., and Dessalegne, T., 2016, Determination of future intensity-duration-frequency curves for level of service planning projects—Task 2 of SFWMD Purchase order 4500095433—Deliverable 2.1. Conduct an extreme precipitation analysis in climate model outputs to determine temporal changes in IDF curves: South Florida Water Management District, 435 p.
Irizarry-Ortiz, M.M., Obeysekera, J., Park, J., Trimble, P., Barnes, J., Park-Said, W., and Gadzinski, E., 2013, Historical trends in Florida temperature and precipitation: Hydrological Processes, v. 27, no. 16, p. 2225–2246, accessed July 7, 2022, at https://doi.org/10.1002/hyp.8259.
Irizarry-Ortiz, M.M., and Stamm, J.F., 2022, Change factors to derive projected future precipitation depth-duration-frequency (DDF) curves at 174 National Oceanic and Atmospheric Administration (NOAA) Atlas 14 stations in central and south Florida: U.S. Geological Survey data release, accessed August 31, 2022, at https://doi.org/10.5066/P935WRTG.
Jeevanjee, N., 2017, Vertical velocity in the gray zone: Journal of Advances in Modeling Earth Systems, v. 9, no. 6, p. 2304–2316, accessed July 7, 2022, at https://doi.org/10.1002/2017MS001059.
Jenkinson, A.F., 1955, The frequency distribution of the annual maximum (or minimum) values of meteorological elements: Quarterly Journal of the Royal Meteorological Society, v. 81, no. 348, p. 158–171, accessed July 7, 2022, at https://doi.org/10.1002/qj.49708134804.
Jiang, Z., Li, W., Xu, J., and Li, L., 2015, Extreme precipitation indices over China in CMIP5 models. Part I-model evaluation: Journal of Climate, v. 28, no. 21, p. 8603–8619, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-15-0099.1.
Kao, S.-C., DeNeale, S.T., Yegorova, E., Kanney, J., and Carr, M.L., 2020, Variability of precipitation areal reduction factors in the conterminous United States: Journal of Hydrology X, v. 9, article 100064, accessed July 7, 2022, at https://doi.org/10.1016/j.hydroa.2020.100064.
Katz, R.W., Parlange, M.B., and Naveau, P., 2002, Statistics of extremes in hydrology: Advances in Water Resources, v. 25, no. 8–12, p. 1287–1304, accessed July 7, 2022, at https://doi.org/10.1016/S0309-1708(02)00056-8.
Kharin, V.V., Flato, G.M., Zhang, X., Gillett, N.P., Zwiers, F., and Anderson, K.J., 2018, Risks from climate extremes change differently from 1.5°C to 2.0°C depending on rarity: Earth’s Future, v. 6, p. 704–715, accessed July 7, 2022, at https://doi.org/10.1002/2018EF000813.
Kharin, V.V., Zwiers, F.W., Zhang, X., and Wehner, M., 2013, Changes in temperature and precipitation extremes in the CMIP5 ensemble: Climatic Change, v. 119, no. 2, p. 345–357, accessed July 7, 2022, at https://doi.org/10.1007/s10584-013-0705-8.
Kirtman, G.P., Misra, V., Burgman, R.J., Infanti, J., and Obeysekera, J., 2017, Florida climate variability and prediction, chap. 17 of Chassignet, E.P., Jones, J.W., Misra, V., and Obeysekera, J., eds., Florida’s climate—Changes, variations & impacts: Gainesville, Fla., Florida Climate Institute, p. 511–532. [Also available at https://doi.org/10.17125/fci2017.ch17.]
Koutsoyiannis, D., 2004a, Statistics of extremes and estimation of extreme rainfall—I. Theoretical investigation: Hydrological Sciences Journal, v. 49, no. 4, p. 575–590, accessed July 7, 2022, at https://doi.org/10.1623/hysj.49.4.575.54430.
Koutsoyiannis, D., 2004b, Statistics of extremes and estimation of extreme rainfall—II. Empirical investigation of long precipitation records: Hydrological Sciences Journal, v. 49, no. 4, p. 591–610, accessed July 7, 2022, at https://doi.org/10.1623/hysj.49.4.591.54424.
Koutsoyiannis, D., 2020, Revisiting the global hydrological cycle—Is it intensifying?: Hydrology and Earth System Sciences, v. 24, no. 8, p. 3899–3932, accessed July 7, 2022, at https://doi.org/10.5194/hess-24-3899-2020.
Kozar, M., and Misra, V., 2013, Evaluation of twentieth-century Atlantic Warm Pool simulations in historical CMIP5 runs: Climate Dynamics, v. 41, no. 9–10, p. 2375–2391, accessed July 7, 2022, at https://doi.org/10.1007/s00382-012-1604-9.
Langbein, W.B., 1949, Annual floods and the partial-duration flood series: Transactions, American Geophysical Union, v. 30, no. 6, p. 879, accessed July 7, 2022, at https://doi.org/10.1029/TR030i006p00879.
Lanzante, J.R., Dixon, K.W., Adams-Smith, D., Nath, M.J., and Whitlock, C.E., 2021, Evaluation of some distributional downscaling methods as applied to daily precipitation with an eye towards extremes: International Journal of Climatology, v. 41, no. 5, p. 3186–3202, accessed July 7, 2022, at https://doi.org/10.1002/joc.7013.
Leadbetter, M.R., 1983, Extremes and local dependence in stationary sequences: Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete, v. 65, no. 2, p. 291–306, accessed July 7, 2022, at https://doi.org/10.1007/BF00532484.
Leadbetter, M.R., Lindgren, G., and Rootzen, H., 1983, Extremes and related properties of random sequences and processes: Springer Series in Statistics, 348 p., accessed July 7, 2022, at https://doi.org/10.1007/978-1-4612-5449-2.
Li, H., Sheffield, J., and Wood, E.F., 2010, Bias correction of monthly precipitation and temperature fields from Intergovernmental Panel on Climate Change AR4 models using equidistant quantile matching: Journal of Geophysical Research, v. 115, no. D10101, accessed July 7, 2022, at https://doi.org/10.1029/2009JD012882.
Liu, C., Ikeda, K., Rasmussen, R., Barlage, M., Newman, A.J., Prein, A.R., Chen, F., Chen, L., Clark, M., Dai, A., Dudhia, J., Eidhammer, T., Gochis, D., Gutmann, E., Kurkute, S., Li, Y., Thompson, G., and Yates, D., 2017, Continental-scale convection-permitting modeling of the current and future climate of North America: Climate Dynamics, v. 49, no. 1–2, p. 71–95, accessed July 7, 2022, at https://doi.org/10.1007/s00382-016-3327-9.
Livneh, B., Bohn, T.J., Pierce, D.W., Munoz-Arriola, F., Nijssen, B., Vose, R., Cayan, D.R., and Brekke, L., 2015, A spatially comprehensive, hydrometeorological data set for Mexico, the U.S., and Southern Canada 1950–2013: Scientific Data, v. 2, no. 1, article 150042, accessed July 7, 2022, at https://doi.org/10.1038/sdata.2015.42. [Data available at https://data.nodc.noaa.gov/cgi-bin/iso?id=gov.noaa.nodc:0129374.]
Livneh, B., Rosenberg, E.A., Lin, C., Nijssen, B., Mishra, V., Andreadis, K.M., Maurer, E.P., and Lettenmaier, D.P., 2013, A long-term hydrologically based dataset of land surface fluxes and states for the conterminous United States—Update and extensions: Journal of Climate, v. 26, no. 23, p. 9384–9392, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-12-00508.1. [Data available at http://thredds.northwestknowledge.net:8080/thredds/catalog/NWCSC_INTEGRATED_SCENARIOS_ALL_CLIMATE/macav2livneh/livneh_CANv1.1_USv1.0/catalog.html.]
Lopez-Cantu, T., Prein, A.F., and Samaras, C., 2020, Uncertainties in future U.S. extreme precipitation from downscaled climate projections: Geophysical Research Letters, v. 47, no. 9, article e2019GL086797, 11 p., accessed July 7, 2022, at https://doi.org/10.1029/2019GL086797.
Lu, L.-H., and Stedinger, J.R., 1992, Variance of two- and three-parameter GEV/PWM quantile estimators—Formulae, confidence intervals, and a comparison: Journal of Hydrology, v. 138, no. 1–2, p. 247–267, accessed July 7, 2022, at https://doi.org/10.1016/0022-1694(92)90167-T.
Lumley, T., Diehr, P., Emerson, S., and Chen, L., 2002, The importance of the normality assumption in large public health datasets: Annual Review of Public Health, v. 23, no. 1, p. 151–169, accessed July 7, 2022, at https://doi.org/10.1146/annurev.publhealth.23.100901.140546.
Madaus, L., McDermott, P., Hacker, J., and Pullen, J., 2020, Hyper-local, efficient extreme heat projection and analysis using machine learning to augment a hybrid dynamical-statistical downscaling technique: Urban Climate, v. 32, article 100606s, accessed July 7, 2022, at https://doi.org/10.1016/j.uclim.2020.100606.
Madsen, H., Rasmussen, P.F., and Rosbjerg, D., 1997, Comparison of annual maxima series and partial duration series methods for modeling extreme hydrologic events—1. At-site modeling: Water Resources Research, v. 33, no. 4, p. 747–757, accessed July 7, 2022, at https://doi.org/10.1029/96WR03848.
Mahjabin, T., and Abdul-Aziz, O.I., 2020, Trends in the magnitude and frequency of extreme rainfall regimes in Florida: Water (Basel), v. 12, no. 9, article 2582, accessed July 7, 2022, at https://doi.org/10.3390/w12092582.
Mann, M.E., Steinman, B.A., Brouillette, D.J., and Miller, S.K., 2021, Multidecadal climate oscillations during the past millennium driven by volcanic forcing: Science, v. 371, no. 6533, p. 1014–1019, accessed July 7, 2022, at https://doi.org/10.1126/science.abc5810.
Mann, M.E., Steinman, B.A., and Miller, S.K., 2020, Absence of internal multidecadal and interdecadal oscillations in climate model simulations: Nature Communications, v. 11, no. 49, 18 p., accessed July 7, 2022, at https://doi.org/10.1038/s41467-019-13823-w.
Maraun, D., 2013, Bias correction, quantile mapping and downscaling—Revisiting the inflation issue: Journal of Climate, v. 26, no. 6, p. 2137–2143, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-12-00821.1.
Marchau, V.A.W.J., Walker, W.E., Bloemen, P.J.T.M., and Popper, S.W., eds., 2019, Decision making under deep uncertainty from theory to practice (1st ed.): Cham, Switzerland, Springer Cham, 405 p., accessed July 7, 2022, at https://doi.org/10.1007/978-3-030-05252-2.
Marshall, C.H., Pielke, R.A., Sr., Steyaert, L.T., and Willard, D., 2004, The impact of anthropogenic land-cover change on the Florida peninsula sea breezes and warm season sensible weather: Monthly Weather Review, v. 132, no. 1, p. 28–52, accessed July 7, 2022, at https://doi.org/10.1175/1520-0493(2004)132<0028:TIOALC>2.0.CO;2.
Martinkova, M., and Kysely, J., 2020, Overview of observed Clausius-Clapeyron scaling of extreme precipitation in midlatitudes: Atmosphere (Basel), v. 11, no. 8, p. 786, accessed July 7, 2022, at https://doi.org/10.3390/atmos11080786.
Martins, E.S., and Stedinger, J.R., 2000, Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data: Water Resources Research, v. 36, no. 3, p. 737–744, accessed July 7, 2022, at https://doi.org/10.1029/1999WR900330.
Mastrandrea, M.D., Field, C.B., Stocker, T.F., Edenhofer, O., Ebi, K.L., Frame, D.J., Held, H., Kriegler, E., Mach, K.J., Matschoss, P.R., Plattner, G.-K., Yohe, G.W., and Zwiers, F.W., 2010, Guidance note for lead authors of the IPCC Fifth Assessment Report on consistent treatment of uncertainties: Intergovernmental Panel on Climate Change [IPCC], 7 p., accessed July 7, 2022, at https://www.ipcc.ch/site/assets/uploads/2018/05/uncertainty-guidance-note.pdf.
Maurer, E.P., Brekke, L., Pruitt, T., and Duffy, P.B., 2007, Fine-resolution climate projections enhance regional climate change impact studies: Eos (Washington, D.C.), v. 88, no. 47, p. 504, accessed July 7, 2022, at https://doi.org/10.1029/2007EO470006.
Mauritsen, T., Stevens, B., Roeckner, E., Crueger, T., Esch, M., Giorgetta, M., Haak, H., Jungclaus, J., Klocke, D., Matei, D., Mikolajewicz, U., Notz, D., Pincus, R., Schmidt, H., and Tomassini, L., 2012, Tuning the climate of a global model: Journal of Advances in Modeling Earth Systems, v. 4, no. 3, article M00A01, accessed July 7, 2022, at https://doi.org/10.1029/2012MS000154.
Max Planck Institute for Meteorology, 2022a, CDO{rb,py}: Max Planck Institute for Meteorology web page, accessed August 1, 2022, at https://code.mpimet.mpg.de/projects/cdo/wiki/Cdo%7Brbpy%7D.
Max Planck Institute for Meteorology, 2022b, Climate Data Operators: Max Planck Institute for Meteorology web page, accessed August 1, 2022, at https://code.mpimet.mpg.de/projects/cdo.
McLeod, A.I., 2011, Kendall—Kendall rank correlation and Mann-Kendall trend test—R package, v. 2.2: R Foundation for Statistical Computing software release, accessed July 7, 2022, at https://cran.r-project.org/web/packages/Kendall/index.html.
Mearns, L.O., and others, 2017, The NA-CORDEX dataset (ver. 1.0): Boulder, Colo., NCAR Climate Data Gateway web page, accessed January 2022 at https://doi.org/10.5065/D6SJ1JCH. [Bias correction error documented at https://na-cordex.org/bias-correction-error.html.]
Melo, C., Santacruz, Z., and Melo, O., 2012, geospt—An R package for spatial statistics—R package, v. 1.0-0: R Foundation for Statistical Computing software release, accessed July 7, 2022, at https://cran.r-project.org/web/packages/geospt/index.html.
Misra, V., Carlson, E., Craig, R.K., Enfield, D., Kirtman, B., Landing, W., Lee, S.-K., Letson, D., Marks, F., Obeysekera, J., Powell, M., and Shin, S.-I., 2011, Climate scenarios—A Florida-centric view: Florida Climate Change Task Force, 71 p., accessed July 7, 2022, at http://www.ces.fau.edu/publications/pdfs/climate_scenario.pdf.
Misra, V., and Mishra, A., 2016, The oceanic influence on the rainy season of peninsular Florida: Journal of Geophysical Research, Atmospheres, v. 121, no. 13, p. 7691–7709, accessed July 7, 2022, at https://doi.org/10.1002/2016JD024824.
Misra, V., Selman, C., Waite, A.J., Bastola, S., and Mishra, A., 2017, Terrestrial and ocean climate of the 20th century, chap. 16 of Chassignet, E.P., Jones, J.W., Misra, V., and Obeysekera, J., eds., Florida’s climate—Changes, variations & impacts: Gainesville, Fla., Florida Climate Institute, p. 485–509, accessed July 7, 2022, at https://doi.org/10.17125/fci2017.ch16.
Müller, P., 2018, Extreme value analysis of non-stationary timeseries—Quantifying climate change using observational data throughout Germany: Dresden, Germany, Technical University of Dresden, Faculty of Mathematics and Natural Sciences, Ph.D. dissertation, 208 p., accessed October 15, 2020, at https://pure.mpg.de/rest/items/item_3152627_1/component/file_3152628/content.
Nadarajah, S., 2005, Extremes of daily rainfall in west central Florida: Climatic Change, v. 69, no. 2–3, p. 325–342, accessed August 11, 2022 at https://doi.org/10.1007/s10584-005-1812-y.
Nadarajah, S., Anderson, C.W., and Tawn, J.A., 1998, Ordered multivariate extremes: Journal of the Royal Statistical Society, Series A (Statistics in Society), v. 60, no. 2, p. 473–496, accessed August 10, 2022 at https://www.jstor.org/stable/2985951.
National Center for Atmospheric Research [NCAR], 2021, Climate Data Gateway at NCAR [NA-CORDEX Search: Variable: prec, pr; Experiment: hist; Frequency: day; Grid: NAM-22i, NAM-44i; Bias Correction: mbcn-gridMET, mbcn-Daymet]: NCAR web page, accessed November 22, 2021, at https://www.earthsystemgrid.org/search/cordexsearch.html.
National Center for Atmospheric Research [NCAR], 2022, Climate Data Gateway at NCAR [NA-CORDEX Search: Variable: prec, pr; Experiment: rcp45, rcp85; Frequency: day; Grid: NAM-22i, NAM-44i; Bias Correction: mbcn-gridMET, mbcn-Daymet]: NCAR web page, accessed January 13, 2022, at https://www.earthsystemgrid.org/search/cordexsearch.html.
National Oceanic and Atmospheric Administration [NOAA], 2011, NOAA/NCEI U.S. climate division data plotting page—Division boundaries and county relationships: NOAA National Centers for Environmental Information web page, accessed April 21, 2021, at https://psl.noaa.gov/data/usclimdivs/boundaries.html.[Data available at ftp://ftp.ncdc.noaa.gov/pub/data/cirs/climdiv/CONUS_CLIMATE_DIVISIONS.shp.zip.]
National Oceanic and Atmospheric Administration [NOAA], 2018, National Hurricane Center tropical cyclone report, Hurricane Harvey (AL092017): NOAA web page, accessed February 9, 2022, at https://www.nhc.noaa.gov/data/tcr/AL092017_Harvey.pdf.
National Oceanic and Atmospheric Administration [NOAA], 2019, National Hurricane Center tropical cyclone report, Hurricane Florence (AL062018): NOAA web page, accessed February 9, 2022, at https://www.nhc.noaa.gov/data/tcr/AL062018_Florence.pdf.
National Oceanic and Atmospheric Administration [NOAA], 2020, National Hurricane Center tropical cyclone report, Hurricane Dorian (AL052019): NOAA web page, accessed February 9, 2022, at https://www.nhc.noaa.gov/data/tcr/AL052019_Dorian.pdf.
National Oceanic and Atmospheric Administration [NOAA], 2022a, Analysis of impact of nonstationary climate on NOAA Atlas 14 estimates—Assessment Report: NOAA, National Weather Service, Office of Water Prediction, 275 p., accessed February 11, 2022, at https://hdsc.nws.noaa.gov/hdsc/files25/NA14_Assessment_report_202201v1.pdf.
National Oceanic and Atmospheric Administration [NOAA], 2022b, Physical Sciences Laboratory—NOAA’s Climate Change Web Portal: NOAA database, accessed February 17, 2022, at https://psl.noaa.gov/ipcc/cmip5/maps.html.
National Weather Service, 2020, Precipitation Frequency Data Server: National Oceanic and Atmospheric Administration web page, accessed December 10, 2020, at https://hdsc.nws.noaa.gov/hdsc/pfds/index.html.
NIST/SEMATECH, 2022a, E-handbook of statistical methods: U.S. Department of Commerce, National Institute of Standards and Technology web page, accessed April 15, 2022, at https://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm.
NIST/SEMATECH, 2022b, E-handbook of statistical methods: U.S. Department of Commerce, National Institute of Standards and Technology web page, accessed April 15, 2022, at https://www.itl.nist.gov/div898/handbook/eda/section3/eda35e.htm.
Northwest Knowledge Network [NKN], 2021, THREDDS data server [Climatic Modeling - MACAv2Livneh - Aggregated Data Catalog]: NKN web page, accessed February 3, 2021, at http://thredds.northwestknowledge.net:8080/thredds/nw.csc.climate-macav2livneh.aggregated.html.
Nover, D.M., Witt, J.W., Butcher, J.B., Johnson, T.E., and Weaver, C.P., 2016, The effects of downscaling method on the variability of simulated watershed response to climate change in five U.S. basins: Earth Interactions, v. 20, no. 11, p. 1–27, accessed July 7, 2022, at https://doi.org/10.1175/EI-D-15-0024.1.
Obeysekera, J., Trimble, P., Cadavid, L., Santee, R., and White, C., 2000, Use of climate outlook for water management in south Florida, USA: South Florida Water Management District, 13 p., accessed August 3, 2020, at https://www.sfwmd.gov/sites/default/files/documents/obeyspaper.pdf.
Olivera, F., Dongkyun, K., Janghwoan, C., and Ming-Han, L., 2006, Calculation of areal reduction factors using NEXRAD precipitation estimates: Texas Transportation Institute, Report No. FHWA/TX–07/0–4642–3, 84 p., accessed November 16, 2020, at https://static.tti.tamu.edu/tti.tamu.edu/documents/0-4642-3.pdf.
Omolayo, A.S., 1993, On the transposition of areal reduction factors for rainfall frequency estimation: Journal of Hydrology, v. 145, no. 1–2, p. 191–205, accessed July 7, 2022, at https://doi.org/10.1016/0022-1694(93)90227-Z.
Overeem, A., Buishand, T.A., and Holleman, I., 2008, Rainfall depth-duration-frequency curves and their uncertainties: Journal of Hydrology, v. 348, no. 1–2, p. 124–134, accessed July 7, 2022, at https://doi.org/10.1016/j.jhydrol.2007.09.044.
Overeem, A., Buishand, T.A., and Holleman, I., 2009, Extreme rainfall analysis and estimation of depth-duration-frequency curves using weather radar: Water Resources Research, v. 45, no. 10, article W10424, 15 p., accessed July 7, 2022, at https://doi.org/10.1029/2009WR007869.
Overeem, A., Buishand, T.A., Holleman, I., and Uijlenhoet, R., 2010, Extreme value modeling of areal rainfall from weather radar: Water Resources Research, v. 46, no. 9, article W09514, 10 p., accessed July 7, 2022, at https://doi.org/10.1029/2009WR008517.
Oyler, J.W., and Nicholas, R.E., 2018, Time of observation adjustments to daily precipitation may introduce undesired statistical issues: International Journal of Climatology, v. 38, no. S1, p. e364–e377, accessed August 11, 2022, at https://doi.org/10.1002/joc.5377.
Papalexiou, S.M., and Koutsoyiannis, D., 2012, Entropy based derivation of probability distributions—A case study to daily rainfall: Advances in Water Resources, v. 45, p. 51–57, accessed July 7, 2022, at https://doi.org/10.1016/j.advwatres.2011.11.007.
Papalexiou, S.M., and Koutsoyiannis, D., 2013, Battle of extreme value distributions—A global survey on extreme daily rainfall: Water Resources Research, v. 49, no. 1, p. 187–201, accessed July 7, 2022, at https://doi.org/10.1029/2012WR012557.
Pathak, C.S., Onderlinde, M., and Fuelberg, H.E., 2009, Use of NEXRAD rainfall data to develop climatologically homogeneous rain areas for central and south Florida, in Starrett, S.E., ed., World Environmental and Water Resources Congress 2009—Great rivers, American Society of Civil Engineers, Kansas City, Mo., May 17–21, 2009 [Proceedings]: American Society of Civil Engineers, 1 p., accessed July 7, 2022, at https://doi.org/10.1061/41036(342)618.
Pavlovic, S., Perica, S., St. Laurent, M., and Mejía, A., 2016, Intercomparison of selected fixed-area areal reduction factor methods: Journal of Hydrology, v. 537, p. 419–430, accessed July 7, 2022, at https://doi.org/10.1016/j.jhydrol.2016.03.027.
Paxton, C.H., Collins, J.M., Williams, A.N., and Noah, D.G., 2009, Southwest Florida warm season tornado development in American Meteorological Society Annual Meeting, 89th, Phoenix, Ariz., January 9–11, 2009 [Proceedings]: American Meteorological Society, 4p., accessed July 7, 2022, at https://ams.confex.com/ams/pdfpapers/148536.pdf.
Pendergrass, A.G., and Hartmann, D.L., 2014a, Changes in the distribution of rain frequency and intensity in response to global warming: Journal of Climate, v. 27, no. 22, p. 8372–8383, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-14-00183.1.
Pendergrass, A.G., and Hartmann, D.L., 2014b, Two modes of change of the distribution of rain: Journal of Climate, v. 27, no. 22, p. 8357–8371, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-14-00182.1.
Pendergrass, A.G., and Knutti, R., 2018, The uneven nature of daily precipitation and its change: Geophysical Research Letters, v. 45, no. 21, p. 11980–11988, accessed July 7, 2022, at https://doi.org/10.1029/2018GL080298.
Pendergrass, A.G., Knutti, R., Lehner, F., Deser, C., and Sanderson, B.M., 2017, Precipitation variability increases in a warmer climate: Scientific Reports, v. 7, no. 1, article 17966, accessed July 7, 2022, at https://doi.org/10.1038/s41598-017-17966-y.
Perica, S., Martin, D., Pavlovic, S., Roy, I., St. Laurent, M., Trypaluk, C., Unruh, D., Yekta, M., and Bonnin, G., eds., 2013, Precipitation-frequency atlas of the United States, southeastern States: National Weather Service, National Oceanic and Atmospheric Administration Atlas 14, v. 9, version 2.0, 163 p., accessed July 7, 2022, at https://www.weather.gov/media/owp/oh/hdsc/docs/Atlas14_Volume9.pdf.
Pickands, J., 1975, Statistical inference using extreme order statistics: Annals of Statistics, v. 3, p. 119–131, accessed July 7, 2022, at https://doi.org/10.1214%2faos%2f1176343003.
Piechota, T.C., and Dracup, J.A., 1996, Drought and regional hydrologic variation in the United States—Associations with the El Niño-Southern Oscillation: Water Resources Research, v. 32, no. 5, p. 1359–1373, accessed July 7, 2022, at https://doi.org/10.1029/96WR00353.
Pielke, R.A., 1974, A three-dimensional numerical model of the sea breezes over south Florida: Monthly Weather Review, v. 102, no. 2, p. 115–139, accessed July 7, 2022, at https://doi.org/10.1175/1520-0493(1974)102<0115:ATDNMO>2.0.CO;2.
Pierce, D.W., Cayan, D.R., Maurer, E.P., Abatzoglou, J.T., and Hegewisch, K.C., 2015, Improved bias correction techniques for hydrological simulations of climate change: Journal of Hydrometeorology, v. 16, no. 6, p. 2421–2442, accessed July 7, 2022, at https://doi.org/10.1175/JHM-D-14-0236.1.
Pierce, D.W., Cayan, D.R., and Thrasher, B.L., 2014, Statistical downscaling using Localized Constructed Analogs (LOCA): Journal of Hydrometeorology, v. 15, no. 6, p. 2558–2585, accessed July 7, 2022, at https://doi.org/10.1175/JHM-D-14-0082.1.
Pierce, D.W., Su, L., Cayan, D.R., Risser, M.D., Livneh, B., and Lettenmaier, D.P., 2021, An extreme-preserving long-term gridded daily precipitation dataset for the conterminous United States: Journal of Hydrometeorology, v. 22, no. 7, p. 1883–1895, accessed July 7, 2022, at https://doi.org/10.1175/JHM-D-20-0212.1.
Poore, R.Z., Quinn, T., Richey, J., and Smith, J.L., 2007, Cycles of hurricane landfalls on the eastern United States linked to changes in Atlantic sea-surface temperatures, chap. 2A in Farris, G.S., Smith, G.J., Crane, M.P., Demas, C.R., Robbins, L.L., and Lavoie, D.L., eds., Science and the storms—The USGS response to the hurricanes of 2005: U.S. Geological Survey Circular 1306, 6 p., accessed July 7, 2022, at https://doi.org/10.3133/cir13062A.
Prein, A.F., Langhans, W., Fosser, G., Ferrone, A., Ban, N., Goergen, K., Keller, M., Tölle, M., Gutjahr, O., Feser, F., Brisson, E., Kollet, S., Schmidli, J., van Lipzig, N.P.M., and Leung, R., 2015, A review on regional convection-permitting climate modeling—Demonstrations, prospects, and challenges: Reviews of Geophysics, v. 53, no. 2, p. 323–361, accessed July 7, 2022, at https://doi.org/10.1002/2014RG000475.
Rahmstorf, S., Foster, G., and Cahill, N., 2017, Global temperature evolution—Recent trends and some pitfalls: Environmental Research Letters, v. 12, no. 5, article 054001, accessed July 7, 2022, at https://doi.org/10.1088/1748-9326/aa6825.
Rasmussen, K.L., Prein, A.F., Rasmussen, R.M., Ikeda, K., and Liu, C., 2020, Changes in the convective population and thermodynamic environments in convection-permitting regional climate simulations over the United States: Climate Dynamics, v. 55, no. 1–2, p. 383–408, accessed July 7, 2022, at https://doi.org/10.1007/s00382-017-4000-7.
R Core Team, 2020, R—A language and environment for statistical computing: Vienna, Austria, R Foundation for Statistical Computing software release, accessed July 7, 2022, at https://www.R-project.org/.
Reed, K.A., Stansfield, A.M., Wehner, M.F., and Zarzycki, C.M., 2020, Forecasted attribution of the human influence on Hurricane Florence: Science Advances, v. 6, no. 1, article eaaw9253, 8 p., accessed July 7, 2022, at https://doi.org/10.1126/sciadv.aaw9253.
Reed, K.A., Wehner, M.F., Stansfield, A.M., and Zarzycki, C.M., 2021, Anthropogenic influence on Hurricane Dorian’s extreme rainfall, in Herring, S.C., Christidis, N., Hoell, A., Hoerling, M.P., and Stott, P.A., eds., Explaining extreme events of 2019 from a climate perspective: Bulletin of the American Meteorological Society, v. 102, no. 1, p. S9–S15, accessed July 7, 2022, at https://doi.org/10.1175/BAMS-D-20-0160.1.
Ren, H., Hou, Z.J., Wigmosta, M., Liu, Y., and Leung, R., 2019, Impacts of spatial heterogeneity and temporal non-stationarity on intensity-duration-frequency estimates—A case study in a mountainous California-Nevada watershed: Water (Basel), v. 11, no. 6, article 1296, accessed July 7, 2022, at https://doi.org/10.3390/w11061296.
Ribatet, M., and Dutang, C., 2019, POT—Generalized Pareto distribution and peaks over threshold—R package, v. 1.1-7: R Foundation for Statistical Computing software release, accessed July 7, 2022, at https://cran.r-project.org/web/packages/POT/index.html.
Ribereau, P., Naveau, P., and Guillou, A., 2011, A note of caution when interpreting parameters of the distribution of excesses: Advances in Water Resources, v. 34, no. 10, p. 1215–1221, accessed July 7, 2022, at https://doi.org/10.1016/j.advwatres.2011.05.003.
Rigby, R.A., and Stasinopoulos, D.M., 2005, gamlss—Generalized additive models for location, scale and shape—R package, v. 5.2.0: R Foundation for Statistical Computing software release, accessed July 7, 2022, at https://cran.r-project.org/web/packages/gamlss/index.html.
Schaefer, M.G., 1990, Regional analyses of precipitation annual maxima in Washington State: Water Resources Research, v. 26, no. 1, p. 119–131, accessed July 7, 2022, at https://doi.org/10.1029/WR026i001p00119.
Schurer, A.P., Mann, M.E., Hawkins, E., Tett, S.F.B., and Hegerl, G.C., 2017, Importance of the pre-industrial baseline in determining the likelihood of exceeding the Paris limits: Nature Climate Change, v. 7, no. 8, p. 563–567, accessed August 1, 2022, at https://doi.org/10.1038%2Fnclimate3345.
Seneviratne, S.I., Nicholls, N., Easterling, D., Goodess, C.M., Kanae, S., Kossin, J., Luo, Y., Marengo, J., McInnes, K., Rahimi, M., Reichstein, M., Sorteberg, A., Vera, C., and Zhang, X., 2012, Changes in climate extremes and their impacts on the natural physical environment, in Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D.J., Ebi, K.L, Mastrandrea, M.D., Mach, K.J., Plattner, G.-K., Allen, S.K., Tignor, M., and Midgley, P.M., eds., Managing the risks of extreme events and disasters to advance climate change adaptation—A special report of working groups I and II of the Intergovernmental Panel on Climate Change (IPCC): Cambridge, U.K., and New York, Cambridge University Press, p. 109–230, accessed July 7, 2022, at https://www.ipcc.ch/site/assets/uploads/2018/03/SREX-Chap3_FINAL-1.pdf.
Serinaldi, F., and Kilsby, C.G., 2014, Rainfall extremes—Toward reconciliation after the battle of distributions: Water Resources Research, v. 50, no. 1, p. 336–352, accessed July 7, 2022, at https://doi.org/10.1002/2013WR014211.
Serinaldi, F., and Kilsby, C.G., 2015, Stationarity is undead—Uncertainty dominates the distribution of extremes: Advances in Water Resources, v. 77, p. 17–36, accessed July 7, 2022, at https://doi.org/10.1016/j.advwatres.2014.12.013.
Shane, R., and Lynn, W., 1964, Mathematical model for flood risk evaluation: Journal of the Hydraulics Division, v. 90, no. 6, p. 4119–4122, accessed July 7, 2022, at https://doi.org/10.1061/JYCEAJ.0001127.
Shepherd, J.M., 2005, A review of current investigations or urban-induced rainfall and recommendations for the future: Earth Interactions, v. 9, no. 12, p. 1–7, accessed July 7, 2022, at https://doi.org/10.1175/EI156.1.
Sillmann, J., Kharin, V.V., Zhang, X., Zwiers, F.W., and Bronaugh, D., 2013a, Climate extremes indices in the CMIP5 multimodel ensemble—Part 1. Model evaluation in the present climate: Journal of Geophysical Research, Atmospheres, v. 118, no. 4, p. 1716–1733, accessed July 7, 2022, at https://doi.org/10.1002/jgrd.50203.
Sillmann, J., Kharin, V.V., Zwiers, F.W., Zhang, X., and Bronaugh, D., 2013b, Climate extremes indices in the CMIP5 multimodel ensemble—Part 2. Future climate projections: Journal of Geophysical Research, Atmospheres, v. 118, no. 6, p. 2473–2493, accessed July 7, 2022, at https://doi.org/10.1002/jgrd.50188.
Simmons, A., Uppala, S., Dee, D., and Kobayashi, S., 2007, ERA-Interim—New ECMWF reanalysis products from 1989 onwards: ECMWF Newsletter, v. 110, p. 25–35, accessed July 7, 2022, at https://doi.org/10.21957/pocnex23c6.
Skamarock, W.C., Klemp, J.B., Dudhia, J., Gill, D.O., Liu, Z., Berner, J., Wang, W., Powers, J.G., Duda, M.G., Barker, D.M., and Huang, X.-Y., 2019, A description of the Advanced Research WRF version 4: NCAR Tech. No. NCAR/TN-556+STR, 145 p., accessed July 7, 2022, at https://doi.org/10.5065/1dfh-6p97.
Smith, R.L., 1986, Extreme value theory based on the r largest annual events: Journal of Hydrology, v. 86, no. 1–2, p. 27–43, accessed July 7, 2022, at https://doi.org/10.1016/0022-1694(86)90004-1.
Southeast Florida Regional Climate Compact, 2020, Unified sea level projection for southeast Florida: Southeast Florida Regional Climate Change Compact’s Sea Level Rise Ad Hoc Work Group, accessed August 2, 2022, at https://southeastfloridaclimatecompact.org/wp-content/uploads/2020/04/Sea-Level-Rise-Projection-Guidance-Report_FINAL_02212020.pdf.
South Florida Engineering and Consulting, LLC [SFEC], 2016, Review of future rainfall extremes—Estimating the impact of projected global warming on magnitude and frequency of extreme rainfall events within the South Florida Water Management District: South Florida Water Management District, Task 3 report, 27 p., prepared by South Florida Engineering and Consulting, LLC, Lake Worth, Fla.
South Florida Water Management District [SFWMD], 2005, Documentation of the South Florida Water Management Model—Version 5.5: South Florida Water Management District, 325 p., accessed July 7, 2022, at https://www.sfwmd.gov/sites/default/files/documents/sfwmm_final_121605.pdf.
South Florida Water Management District [SFWMD], 2016, Environmental resource permit applicant’s handbook—Volume 2: South Florida Water Management District, 58 p. [Also available at https://www.sfwmd.gov/sites/default/files/documents/swerp_applicants_handbook_vol_ii.pdf.]
South Florida Water Management District [SFWMD], 2021, Water and climate resiliency metrics, phase 1—Long-term observed trends: South Florida Water Management District, 115 p. [Also available at https://www.sfwmd.gov/sites/default/files/Water-and-Climate-Resilience-Metrics-Final-Report-2021-12-17.pdf.]
Srivastava, A., Grotjahn, R., and Ullrich, P.A., 2020, Evaluation of historical CMIP6 model simulations of extreme precipitation over contiguous US regions: Weather and Climate Extremes, v. 29, article 100268, accessed July 7, 2022, at https://doi.org/10.1016/j.wace.2020.100268.
Srivastava, A.K., Grotjahn, R., Ullrich, P.A., and Zarzycki, C., 2022, Evaluation of precipitation indices in suites of dynamically and statistically downscaled regional climate models over Florida: Climate Dynamics, v. 58, p. 1587–1611, accessed July 7, 2022, at https://doi.org/10.1007/s00382-021-05980-w.
Stephens, G.L., L’Ecuyer, T., Forbes, R., Gettelmen, A., Golaz, J.-C., Bodas-Salcedo, A., Suzuki, K., Gabriel, P., and Haynes, J., 2010, Dreary state of precipitation in global models: Journal of Geophysical Research, v. 115, no. D24, p. 1–14, accessed July 7, 2022, at https://doi.org/10.1029/2010JD014532.
Stephens, M.A., 1993, Aspects of goodness-of-fit: Stanford University, Department of Statistics, Technical report no. 474, 14 p., accessed October 15, 2020, at https://purl.stanford.edu/dj948gs6343.
Svensson, C., and Jones, D.A., 2010, Review of methods for deriving areal reduction factors: Journal of Flood Risk Management, v. 3, no. 3, p. 232–245, accessed July 7, 2022, at https://doi.org/10.1111/j.1753-318X.2010.01075.x.
Taylor, K.E., 2001, Summarizing multiple aspects of model performance in a single diagram: Journal of Geophysical Research, v. 106, no. D7, p. 7183–7192, accessed July 7, 2022, at https://doi.org/10.1029/2000JD900719.
Taylor, K.E., Stouffer, R.J., and Meehl, G.A., 2012, An overview of CMIP5 and the experiment design: Bulletin of the American Meteorological Society, v. 93, no. 4, p. 485–498, accessed July 7, 2022, at https://doi.org/10.1175/BAMS-D-11-00094.1.
Taylor, M.A., Clarke, L.A., Centella, A., Bezanilla, A., Stephenson, T.S., Jones, J.J., Campbell, J.D., Vichot, A., and Charlery, J., 2018, Future Caribbean climates in a world of rising temperatures—The 1.5 vs. 2.0 dilemma: Journal of Climate, v. 31, no. 7, p. 2907–2926, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-17-0074.1.
Teegavarapu, R.S.V., Goly, A., and Obeysekera, J., 2013, Influences of Atlantic multidecadal oscillation phases on spatial and temporal variability of regional precipitation extremes: Journal of Hydrology, v. 495, p. 74–93, accessed July 7, 2022, at https://doi.org/10.1016/j.jhydrol.2013.05.003.
Terando, A., Reidmiller, D., Hostetler, S.W., Littell, J.S., Beard, T.D., Jr., Weiskopf, S.R., Belnap, J., and Plumlee, G.S., 2020, Using information from global climate models to inform policymaking—The role of the U.S. Geological Survey: U.S. Geological Survey Open-File Report 2020–1058, 25 p., accessed July 7, 2022, at https://doi.org/10.3133/ofr20201058.
Thornton, P.E., Thornton, M.M., Mayer, B.W., Wei, Y., Devarakonda, R., Vose, R.S., and Cook, R.B., 2016, Daymet-Daily surface weather data on a 1-km grid for North America, version 3: Oak Ridge, Tenn., Oak Ridge National Laboratory Distributed Active Archive Center [ORNL DAAC] database, accessed Jan 31, 2022, at https://doi.org/10.3334/ORNLDAAC/1328. [Data available at https://thredds.daac.ornl.gov/thredds/catalog/ornldaac/1328/catalog.html.]
Trimble, P., 1990, Frequency analysis of one and three day rainfall maxima for central and southern Florida: South Florida Water Management District Technical Memorandum, 29 p., accessed July 7, 2022, at http://dpanther.fiu.edu/sobek/FI12090289/00001.
U.S. Geological Survey [USGS], 2020a, USGS Water Resources Mission Area THREDDS data server [Dataset: USGS THREDDS Holdings/LOCA Statistical Downscaling (Localized Constructed Analogs) Statistically downscaled CMIP5 climate projections for North America/Historical LOCA]: USGS Center for Integrated Data Analytics web page, accessed December 4, 2020, at https://cida.usgs.gov/thredds/catalog.html?dataset=cida.usgs.gov/loca_histocial.
U.S. Geological Survey [USGS], 2020b, USGS Water Resources Mission Area THREDDS data server [Dataset: USGS THREDDS Holdings/LOCA Statistical Downscaling (Localized Constructed Analogs) Statistically downscaled CMIP5 climate projections for North America/Future LOCA]: USGS Center for Integrated Data Analytics web page, accessed December 4, 2020, at https://cida.usgs.gov/thredds/catalog.html?dataset=cida.usgs.gov/loca_future.
U.S. Geological Survey [USGS], 2021a, USGS Water Resources Mission Area THREDDS data server [Dataset: USGS THREDDS Holdings/Multivariate Adaptive Constructed Analogs (MACA) CMIP5 Statistically Downscaled Data for Coterminous USA/Daily Historical MACAv2METDATA]: USGS Center for Integrated Data Analytics web page, accessed February 3, 2021, at https://cida.usgs.gov/thredds/catalog.html?dataset=cida.usgs.gov/macav2metdata_daily_historical.
U.S. Geological Survey [USGS], 2021b, USGS Water Resources Mission Area THREDDS data server [Dataset: USGS THREDDS Holdings/Multivariate Adaptive Constructed Analogs (MACA) CMIP5 Statistically Downscaled Data for Coterminous USA/Daily Future MACAv2METDATA]: USGS Center for Integrated Data Analytics web page, accessed February 3, 2021, at https://cida.usgs.gov/thredds/catalog.html?dataset=cida.usgs.gov/macav2metdata_daily_future.
Ushey, K., 2018, RcppRoll—Efficient rolling/windowed operations—R package, v. 0.3.0: R Foundation for Statistical Computing software release, accessed July 7, 2022, at https://CRAN.R-project.org/package=RcppRoll.
U.S. Weather Bureau, 1958, Rainfall intensity-frequency regime—Part 2—Southeastern United States: Washington, D.C., U.S. Department of Commerce Technical Paper No. 29, 64 p., accessed July 7, 2022, at https://www.weather.gov/media/owp/oh/hdsc/docs/TP29P2.pdf.
van der Wiel, K., Kapnick, S.B., van Oldenborgh, G.J., Whan, K., Philip, S., Vecchi, G.A., Singh, R.K., Arrighi, J., and Cullen, H., 2017, Rapid attribution of the August 2016 flood-inducing extreme precipitation in south Louisiana to climate change: Hydrology and Earth System Sciences, v. 21, no. 2, p. 897–921, accessed July 7, 2022, at https://doi.org/10.5194/hess-21-897-2017.
van Oldenborgh, G.J., van der Wiel, K., Sebastian, A., Singh, R., Arrighi, J., Otto, F., Haustein, K., Li, S., Vecchi, G., and Cullen, H., 2017, Attribution of extreme rainfall from Hurricane Harvey, August 2017: Environmental Research Letters, v. 12, no. 124009, p. 1–11, accessed July 7, 2022, at https://doi.org/10.1088/1748-9326/aa9ef2.
Veneziano, D., Langousis, A., and Lepore, C., 2009, New asymptotic and preasymptotic results on rainfall maxima from multifractal theory: Water Resources Research, v. 45, no. 11, article W11421, 12 p., accessed July 7, 2022, at https://doi.org/10.1029/2009WR008257.
Veneziano, D., Lepore, C., Langousis, A., and Furcolo, P., 2007, Marginal methods of intensity-duration-frequency estimation in scaling and nonscaling rainfall: Water Resources Research, v. 43, no. 10, article W10418, 14 p., accessed July 7, 2022, at https://doi.org/10.1029/2007WR006040.
Vogel, R.M., 1986, The probability plot correlation coefficient test for the Normal, Lognormal, and Gumbel distributional hypothesis: Water Resources Research, v. 22, no. 4, p. 587–590, accessed July 7, 2022, at https://doi.org/10.1029/WR022i004p00587.
Vogel, R.M., and Fennessey, N.M., 1993, L moment diagrams should replace product moment diagrams: Water Resources Research, v. 29, no. 6, p. 1745–1752, accessed July 7, 2022, at https://doi.org/10.1029/93WR00341.
Vogel, R.M., and Kroll, C.N., 1989, Low-flow frequency analysis using probability-plot correlation coefficients: Journal of Water Resources Planning and Management, v. 115, no. 3, p. 338–357, accessed July 7, 2022, at https://doi.org/10.1061/(ASCE)0733-9496(1989)115:3(338).
von Storch, H., and Navarra, A., 1995, Misuses of statistical analysis in climate research, chap. 2 in Analysis of climate variability—Applications of statistical techniques: Berlin, Springer-Verlag, p. 11–26, accessed July 7, 2022, at https://doi.org/10.1007/978-3-662-03167-4_2.
Walsh, J., Wuebbles, D., Hayhoe, K., Kossin, J., Kunkel, K., Stephens, G., Thorne, P., Vose, R., Wehner, M., Willis, J., Anderson, D., Doney, S., Feely, R., Hennon, P., Kharin, V., Knutson, T., Landerer, F., Lenton, T., Kennedy, J., and Somerville, R., 2014, Our changing climate, chap. 2 in Melillo, J.M., Richmond, T.C., and Yohe, G.W., eds., Climate change impacts in the United States: Third National Climate Assessment, U.S. Global Change Research Program, p. 735–789, accessed July 7, 2022, at https://doi.org/ 10.7930/J0KS6PHH.
Walton, D.B., Sun, F., Hall, A., and Capps, S., 2015, A hybrid dynamical-statistical downscaling technique. Part I—Development and validation of the technique: Journal of Climate, v. 28, no. 12, p. 4597–4617, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-14-00196.1.
Wang, C., Enfield, D.B., Lee, S., and Landsea, C.W., 2006, Influences of the Atlantic Warm Pool on western hemisphere summer rainfall and Atlantic hurricanes: Journal of Climate, v. 19, no. 12, p. 3011–3028, accessed July 7, 2022, at https://doi.org/10.1175/JCLI3770.1.
Wang, C., Lee, S., and Enfield, D.B., 2008a, Atlantic Warm Pool acting as a link between Atlantic multidecadal oscillation and Atlantic tropical cyclone activity: Geochemistry, Geophysics, Geosystems, v. 9, no. 5, 17 p., accessed July 7, 2022, at https://doi.org/10.1029/2007GC001809.
Wang, D., Hagen, S.C., and Alizad, K., 2013, Climate change impact and uncertainty analysis of extreme rainfall events in the Apalachicola River basin, Florida: Journal of Hydrology, v. 480, p. 125–135, accessed July 7, 2022, at https://doi.org/10.1016/j.jhydrol.2012.12.015.
Wang, G., Kirchhoff, C.J., Seth, A., Abatzoglou, J.T., Livneh, B., Pierce, D.W., Fomenko, L., and Ding, T., 2020, Projected changes of precipitation characteristics depend on downscaling method and training data—MACA versus LOCA using the U.S. Northeast as an example: Journal of Hydrometeorology, v. 21, no. 12, p. 2739–2758, accessed July 7, 2022, at https://doi.org/10.1175/JHM-D-19-0275.1.
Wang, G., Wang, D., Trenberth, K.E., Erfanian, A., Yu, M., Bosilovich, M.G., and Parr, D.T., 2017, The peak structure and future changes of the relationships between extreme precipitation and temperature: Nature Climate Change, v. 7, p. 268–274, accessed August 1, 2022, at https://doi.org/10.1038/nclimate3239.
Wang, J.-W., Wang, K., Pielke, R.A., Sr., Lin, J.C., and Matsui, T., 2008b, Towards a robust test on North America warming trend and precipitable water content increase: Geophysical Research Letters, v. 35, no. 18, article L18804, 5 p, accessed July 7, 2022, at https://doi.org/10.1029/2008GL034564.
Weiss, L.L., 1964, Ratio of true to fixed-interval maximum rainfall—American Society of Civil Engineers: Journal of the Hydraulics Division, v. 90, no. 1, p. 77–82, accessed July 7, 2022, at https://doi.org/10.1061/JYCEAJ.0001008.
Weissman, I., 1978, Estimation of parameters of large quantiles based on the k largest observations: Journal of the American Statistical Association, v. 73, no. 364, p. 812–815, accessed July 7, 2022, at https://doi.org/10.1080/01621459.1978.10480104.
White, A.A., Hoskins, B.J., Roulstone, I., and Staniforth, A., 2005, Consistent approximate models of the global atmosphere—Shallow, deep, hydrostatic, quasi-hydrostatic and non-hydrostatic: Quarterly Journal of the Royal Meteorological Society, v. 131, no. 609, p. 2081–2107, accessed July 7, 2022, at https://doi.org/10.1256/qj.04.49.
Wilby, R.L., and Wigley, T.M.L., 1997, Downscaling general circulation model output—A review of methods and limitations: Progress in Physical Geography, v. 21, no. 4, p. 530–548, accessed July 7, 2022, at https://doi.org/10.1177/030913339702100403.
Wilby, R.L., Wigley, T.M.L., Conway, D., Jones, P.D., Hewitson, B.C., Main, J., and Wilks, D.S., 1998, Statistical downscaling of general circulation model output—A comparison of methods: Water Resources Research, v. 34, no. 11, p. 2995–3008, accessed July 7, 2022, at https://doi.org/10.1029/98WR02577.
Winsberg, M.D., 2020, Anticipating heavy rain in Florida: Tallahassee, Fla., Florida State University, Florida Climate Center web page, accessed December 21, 2020, at https://climatecenter.fsu.edu/topics/specials/anticipating-heavy-rain-in-florida.
Wootten, A.M., 2018, The subtle processes in statistical downscaling and the potential uncertainty: U.S. Climate Variability and Predictability (CLIVAR) Project Office, Variations, v. 16, no. 3, p. 8–13, accessed July 7, 2022, at https://doi.org/10.5065/D62N513R.
Wootten, A.M., Dixon, K.W., Adams-Smith, D.J., and McPherson, R.A., 2021, Statistically downscaled precipitation sensitivity to gridded observation data and downscaling technique: International Journal of Climatology, v. 41, no. 2, p. 980–1001, accessed July 7, 2022, at https://doi.org/10.1002/joc.6716.
Wootten, A.M., Terando, A., Reich, B.J., Boyles, R.P., and Semazzi, F., 2017, Characterizing sources of uncertainty from global climate models and downscaling techniques: Journal of Applied Meteorology and Climatology, v. 56, no. 12, p. 3245–3262, accessed July 7, 2022, at https://doi.org/10.1175/JAMC-D-17-0087.1.
World Meteorological Organization, 2009, Guidelines on analysis of extremes in a changing climate in support of informed decisions for adaptation: World Meteorological Organization, Climate Data and Monitoring WCDMP–No. 72, 55 p., accessed July 7, 2022, at https://www.ecad.eu/documents/WCDMP_72_TD_1500_en_1.pdf.
Wuebbles, D., Meehl, G., Hayhoe, K., Karl, T.R., Kunkel, K., Santer, B., Wehner, M., Colle, B., Fischer, E.M., Fu, R., Goodman, A., Janssen, E., Kharin, V., Lee, H., Li, W., Long, L.N., Olsen, S.C., Pan, Z., Seth, A., Sheffield, J., and Sun, L., 2014, CMIP5 climate model analyses—Climate extremes in the United States: Bulletin of the American Meteorological Society, v. 95, no. 4, p. 571–583, accessed July 7, 2022, at https://doi.org/10.1175/BAMS-D-12-00172.1.
Xu, Y.-P., and Tung, Y.-K., 2009, Constrained scaling approach for design rainfall estimation: Stochastic Environmental Research and Risk Assessment, v. 23, no. 6, p. 697–705, accessed July 7, 2022, at https://doi.org/10.1007/s00477-008-0250-6.
Zhang, M., de Leon, C., and Migliaccio, K., 2018, Evaluation and comparison of interpolated gauge rainfall data and gridded rainfall data in Florida, USA: Hydrological Sciences Journal, v. 63, no. 4, p. 561–582, accessed July 7, 2022, at https://doi.org/10.1080/02626667.2018.1444767.
Zhang, X., Alexander, L., Hegerl, G.C., Jones, P., Klein Tank, A., Peterson, T.C., Trewin, B., and Zwiers, F.W., 2011, Indices for monitoring changes in extremes based on daily temperature and precipitation data: Wiley Interdisciplinary Reviews, Climate Change, v. 2, accessed July 7, 2022, at no. 6, p. 851–870, https://doi.org/10.1002/wcc.147.
Zhang, X., and Zwiers, F.W., 2013, Statistical indices for the diagnosing and detecting changes in extremes, v. 65 in AghaKouchak, A., Esterling, D., Hsu, K., Schubert, S., and Sorooshian, S., eds., Extremes in a changing climate: Dordrecht, Holland, Springer, Water Science and Technology Library, p. 1–14, accessed July 7, 2022, at https://doi.org/10.1007/978-94-007-4479-0_1.
Appendix 1. National Oceanic and Atmospheric Administration Atlas 14 Stations
Appendix 2. Description of Analog Resampling and Statistical Scaling Method by Jupiter Intelligence Using the Weather Research and Forecasting Model
Event Files
Jupiter Intelligence selected 1,044 historical extreme events in south Florida for downscaling using their 4-km WRF model. The events were chosen as days where the daily precipitation at any Global Historical Climatology Network (Menne and others, 2018) station around southern Florida exceeded 30 millimeters. If multiple consecutive days exceeded this threshold, those days were merged to form single event files. The events were simulated using WRF and an additional 1-day spin-up and spin-down of the model. Overall, events of duration as long as 108 hours were simulated for a total simulation length of 156 hours including spin-up and spin-down times. Although events longer than 1 day were simulated by Jupiter Intelligence, because the analogs were developed for daily events and not for multiday events, only extreme events for 1-day duration were analyzed as part of this study.
It is important to note that although the 174 National Oceanic and Atmospheric Administration (NOAA) Atlas 14 stations of interest in this study are all located within the 4-km Jupiter WRF model, four of them were excluded from further analysis. This was necessary because these four stations were located too close to the northern boundary of the model and the statistics of the 1,044 events simulated at these four locations were significantly different from nearby stations (having a much lower mean, maximum, and standard deviation). This discrepancy is likely a result of not using any Global Historical Climatology Network stations close to the northern model boundary to identify extreme precipitation days for downscaling.
Analogs File
Jupiter Intelligence used the ECMWF ERA5 daily reanalysis dataset (Hersbach and others, 2020) to determine historical weather analogs for each future simulated day in a GCM simulation within a 10- × 10-degree region that includes Florida. The historical period used from ERA5 was 1979–2017. The analog matching was based on a comparison of large-scale meteorological variables between ERA5 and climate models including sea-level pressure, precipitation, and zonal and meridional wind components. Detrended daily anomalies for each meteorological variable were normalized by their monthly standard deviation to compute a normalized z-score anomaly for each day in both the ERA5 and the GCM datasets. A z-score is also called a “standard score” and is calculated by subtracting the mean from a value and then dividing the result by its standard deviation. In computing z-scores, the sample mean and standard deviation are used when the true population values are unknown. Here, the values are the detrended daily anomalies—which, by definition, should have a mean of zero if the base period over which the trend in the mean was computed is the same as the period over which the detrending is performed—and the standard deviation is computed from the detrended anomalies. Next, the GCM z-scores are regridded to the ERA5 grid. Only days within 1 month before and after the GCM day are considered as potential analogs. Of these, the 5 historical days with the smallest mean of the spatial root-mean-square difference of the z-scores across the four meteorological variables are chosen as analogs for each future simulated day in the GCM. The data are provided as a csv file that contains analog dates for each day in various future CMIP5 and CMIP6 GCM simulations being considered.
Climate Scaling File
The statistical scaling method developed by Jupiter Intelligence uses output from 13-year simulations performed using a 4-km WRF model of North America. The 13-year simulations include a historical simulation of the period 2000–13 with initial and boundary conditions from the ECMWF ERA-Interim reanalysis (Simmons and others, 2007) and a future climate sensitivity simulation for which the ERA-Interim initial and boundary conditions are modified by adding the CMIP5 ensemble mean RCP8.5 climate change. These 4-km North America simulations are documented in Liu and others (2017) and Rasmussen and others (2020). Hourly precipitation data from the 4-km North America simulations over Florida were extracted by Jupiter Intelligence to generate a gridded dataset of historical and projected hourly precipitation quantiles to be used in quantile mapping for statistical scaling. According to the future simulation design, the future quantiles are expected to capture increases in precipitation resulting from increases in the atmospheric water holding capacity under global warming. This methodology provides more information on localized climate changes than simply using output from a coarse GCM.
Processing Steps
The process to obtain historical and future projected depth-duration-frequency curves for daily duration based on the analog resampling and statistical scaling method is as follows:
-
1. For each of the 1,044 historical extreme events in the 39-year period 1979–2017, obtain the 24-hour maximum precipitation at grid cells closest to the 170 NOAA Atlas 14 stations in the region of interest. This is considered the historical 24-hour maximum event precipitation. For the future projection period, first convert historical hourly precipitation quantiles to future hourly precipitation quantiles by using data obtained from Rasmussen and others (2020), and then compute 24-hour maxima. This is considered the future 24-hour maximum event precipitation resulting from changes in the atmospheric moisture holding capacity alone.
-
2. For each NOAA Atlas 14 station grid cell, pick a threshold for the historical 24-hour maximum event precipitation that would result in 2.5 exceedances per year or 98 exceedances for the 39-year period. Then pick a separate threshold for the future 24-hour maximum event precipitation that would also result in 2.5 exceedances per year or 98 exceedances for the 39-year period.
-
3. Fit the generalized Pareto (GP) distribution for historical 24-hour maximum event precipitation exceeding the historical threshold at each NOAA Atlas 14 station grid cell. Also, fit the GP distribution for the future 24-hour maximum event precipitation exceeding the future threshold at each NOAA Atlas 14 station grid cell.
-
4. For the period 2016–20, for each NOAA Atlas 14 station grid cell, and for all ensemble members in a GCM, count all of the times when the dates of the 98 historical threshold exceedances were analog dates in the csv analog file; this is the base analog rate (Rb). For the period 2068–72, centered in the future year of interest (2070), and for all ensemble members in a GCM, count all of the times when the dates of the 98 historical threshold exceedances were analog dates in the csv analog file; this is the future analog rate (Rf). The ratio of the two analog rates is the rate scaling factor, Sr=Rf/Rb, which can be used to adjust the actual baseline historical threshold exceedance rate, λ, to be more appropriate for the new expected frequency in the future year of interest. The adjusted threshold exceedance rate accounts for projected future changes in large-scale meteorological fields that are conducive to precipitation at a station.
-
5. Obtain historical precipitation quantiles for return periods of interest using the standard formula for the GP distribution: p = 1 − 1/(Tr * λ), where p is the probability of exceedance, Tr is the return period of interest in years, and λ is the threshold exceedance frequency (2.5 exceedances per year). Future precipitation quantiles are instead obtained by using the formula p = 1 − 1/(Tr * λ * Sr), where Sr is the rate scaling factor that was calculated in the previous step.
References Cited
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., De Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R.J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thépaut, J.-N., 2020, The ERA5 global reanalysis: Quarterly Journal of the Royal Meteorological Society, v. 146, no. 730, p. 1999–2049, accessed July 7, 2022, at https://doi.org/10.1002/qj.3803.
Liu, C., Ikeda, K., Rasmussen, R., Barlage, M., Newman, A.J., Prein, A.R., Chen, F., Chen, L., Clark, M., Dai, A., Dudhia, J., Eidhammer, T., Gochis, D., Gutmann, E., Kurkute, S., Li, Y., Thompson, G., and Yates, D., 2017, Continental-scale convection-permitting modeling of the current and future climate of North America: Climate Dynamics, v. 49, no. 1–2, p. 71–95, accessed July 7, 2022, at https://doi.org/10.1007/s00382-016-3327-9.
Menne, M.J., Williams, C.N., Gleason, B.E., Rennie, J.J., and Lawrimore, J.H., 2018, The Global Historical Climatology Network Monthly Temperature Dataset, version 4: Journal of Climate, v. 31, no. 24, p. 9835–9854, accessed July 7, 2022, at https://doi.org/10.1175/JCLI-D-18-0094.1.
Rasmussen, K.L., Prein, A.F., Rasmussen, R.M., Ikeda, K., and Liu, C., 2020, Changes in the convective population and thermodynamic environments in convection-permitting regional climate simulations over the United States: Climate Dynamics, v. 55, no. 1–2, p. 383–408, accessed July 7, 2022, at https://doi.org/10.1007/s00382-017-4000-7.
Simmons, A., Uppala, S., Dee, D., and Kobayashi, S., 2007, ERA-Interim—New ECMWF reanalysis products from 1989 onwards: ECMWF Newsletter, v. 110, p. 25–35, accessed July 7, 2022, at https://doi.org/10.21957/pocnex23c6.
Appendix 3. Parametric Bootstrapping
-
1. Fit the GP for precipitation depth exceedances xi,d (i = 1,…, nd; d = 1, 3, and 7 days) for the three durations of interest simultaneously using the CML approach. Here, it is assumed that the scale and shape parameters vary linearly with duration (eqs. 18 and 19) and that parameter combinations that result in crossing of the cumulative distribution function (CDF) for different durations are invalid. The number of exceedances for each duration (nd) are generally similar for all durations but not exactly the same because they are based on prespecified thresholds, ud, computed from percentiles of precipitation depth data for each duration of interest and runs declustering to assure independence between events within a duration.
-
2. Compute return levels (DDFT,d) for durations d (1, 3, and 7 days) and return periods, T, of interest (5, 10, 25, 50, 100, and 200 years) based on parameters fit in step 1, the threshold ud, and number of threshold exceedances per year.
-
3. Compute the Kolmogorov-Smirnov (KS), Anderson-Darling (AD), Cramér-von Mises (CVM), Pearson product moment correlation coefficient on quantile-quantile plots (PPCCQQ), and Pearson product moment correlation coefficient on probability-probability plots (PPCCPP) statistics for each duration by comparing the sample empirical distribution function (EDF) with the CDF of the GP distribution fit in step 1. Note: Weibull plotting position is used for the sample EDF.
-
For each duration, generate a replicate (i = 1,…,nd; d = 1, 3, and 7 days) based on the fitted GP parameters and threshold ud.
-
Fit a GP to the replicate for the three durations of interest at once using the CML approach. Obtain the intercept and slope parameters () that define the variation of the GP distribution scale and shape parameters with duration (and , respectively). This is a critical step for the case when the parameters of the distribution are not prespecified.
-
4. Compute the goodness of fit (KS*, AD*, CVM*, PPCCQQ* and PPCCPP*) for each duration by comparing the replicate EDF with the CDF of the GP distribution fit in step 5 (as opposed to the CDF of the GP distribution fit for the original sample in step 1). This is a critical step for the case when the parameters of the distribution are not prespecified. Note that the Weibull plotting position is used for the replicate EDF.
-
Save the parameters fit in step 5 and compute return levels for durations and return periods of interest based on those parameters, threshold ud, and the number of exceedances per year.
-
5. Repeat steps 4–7, R times.
-
6. Determine the fraction of KS* exceeding KS for each duration. This is the p-value for KS statistic. Do the same for the AD and CVM test statistics. Determine the fraction of PPCCPP* less than PPCCPP as its p-value, and similarly for PPCCQQ.
-
Sort the and independently for each duration. The and sorted values for each duration are the 100(1 – α) percent confidence intervals.
-
Sort the return levels independently for each duration. The and sorted values for each duration are the 100(1 – α) percent confidence intervals.
Conversion Factors
Temperature in degrees Celsius (°C) may be converted to degrees Fahrenheit (°F) as follows: °F = (1.8 × °C) + 32.
Temperature in degrees Fahrenheit (°F) may be converted to degrees Celsius (°C) as follows: °C = (°F – 32) / 1.8.
Datum
Horizontal coordinate information is referenced to the World Geodetic System 1984 (WGS84) datum and the North American Datum of 1983.
Supplemental Information
Precipitation depth totals are given in inches (in.), and precipitation intensities are given in inches per day (in/d).
Abbreviations
AD
Anderson-Darling
AEP
annual exceedance probability
AHED
ArcHydro Enhanced Database
AIC
Akaike Information Criterion
AMO
Atlantic Multidecadal Oscillation
ARF
areal reduction factor
AWP
Atlantic Warm Pool
BCCA
Bias-Corrected Constructed Analog
CC
Clausius-Clapeyron
CDF
cumulative distribution function
CDO
Climate Data Operators
CMIP3
Coupled Model Intercomparison Project Phase 3
CMIP5
Coupled Model Intercomparison Project Phase 5
CMIP6
Coupled Model Intercomparison Project Phase 6
CML
constrained maximum likelihood
CORDEX
Coordinated Regional Downscaling Experiment
csv
comma-separated value
CVM
Cramér-von Mises
DDF
depth-duration-frequency
ECMWF
European Centre for Medium-Range Weather Forecasts
EDF
empirical distribution function
ENSO
El Niño Southern Oscillation
ETCCDI
Expert Team on Climate Change Detection and Indices
FAWN
Florida Automated Weather Network
FPLOS
Flood Protection Level of Service
GCM
general circulation model
GEV
generalized extreme value
GHG
greenhouse gas
GOF
goodness of fit
GP
generalized Pareto
IPCC
Intergovernmental Panel on Climate Change
JupiterWRF
Jupiter Intelligence Weather Research and Forecasting model
KACF
Kendall auto-correlation coefficient
KS
Kolmogorov-Smirnov
LOCA
Localized Constructed Analogs
MACA
Multivariate Adaptive Constructed Analogs
MCI
Model Climatology Index
MK
Mann-Kendall trend test
ML
maximum likelihood
MQDM
multiplicative quantile delta mapping
MVI
Model Variability Index
netCDF
Network Common Data Form format
NA CORDEX
North American Coordinated Regional Downscaling Experiment
NCEI
National Centers for Environmental Information
NEXRAD
Next-Generation Radar
NOAA
National Oceanic and Atmospheric Administration
PDO
Pacific Decadal Oscillation
PDS
partial-duration series
POT
peaks-over-threshold
PP
point process
PPCCPP
Pearson product moment correlation coefficient on probability-probability plots
PPCCQQ
Pearson product moment correlation coefficient on quantile-quantile plots
PRISM
Parameter-elevation Regressions on Independent Slopes Model
QDM
quantile delta mapping
QM
quantile mapping
RCM
regional climate model
RCP
representative concentration pathway
RMSD
root-mean-square difference
RMSE
root-mean-square error
SFEC
South Florida Engineering and Consulting
SFWMD
South Florida Water Management District
SSP
shared socioeconomic pathway
USGS
U.S. Geological Survey
WRF
Weather Research and Forecasting model
For more information about this publication, contact
Director, Caribbean-Florida Water Science Center
U.S. Geological Survey
4446 Pet Lane, Suite 108
Lutz, FL 33559
For additional information, visit
https://www.usgs.gov/centers/car-fl-water
Publishing support provided by
Lafayette Publishing Service Center
Disclaimers
Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Although this information product, for the most part, is in the public domain, it also may contain copyrighted materials as noted in the text. Permission to reproduce copyrighted items must be secured from the copyright owner.
Suggested Citation
Irizarry-Ortiz, M.M., Stamm, J.F., Maran, C., and Obeysekera, J., 2022, Development of projected depth-duration frequency curves (2050–89) for south Florida: U.S. Geological Survey Scientific Investigations Report 2022–5093, 114 p., https://doi.org/10.3133/sir20225093.
ISSN: 2328-0328 (online)
Study Area
| Publication type | Report |
|---|---|
| Publication Subtype | USGS Numbered Series |
| Title | Development of projected depth-duration frequency curves (2050–89) for south Florida |
| Series title | Scientific Investigations Report |
| Series number | 2022-5093 |
| DOI | 10.3133/sir20225093 |
| Publication Date | October 18, 2022 |
| Year Published | 2022 |
| Language | English |
| Publisher | U.S. Geological Survey |
| Publisher location | Reston, VA |
| Contributing office(s) | Caribbean-Florida Water Science Center |
| Description | Report: xii, 114 p.; 1 Table; Data Release |
| Country | United States |
| State | Florida |
| Online Only (Y/N) | Y |


