Improving Time of Concentration Estimates for Small Rural Watersheds in the Appalachian Plateaus Physiographic Province, West Virginia
Links
- Document: Report (11.5 MB pdf) , HTML , XML
- Data Release: USGS data release - Streamflow and precipitation data and characteristics of selected storms for four stream basins in West Virginia, 2017-2020
- NGMDB Index Page: National Geologic Map Database Index Page (html)
- Download citation as: RIS | Dublin Core
Acknowledgments
Mike Pumphrey and Andrew Thompson, of the West Virginia Department of Transportation, helped us install equipment at a study site near Ripley, West Virginia. Wes Justice, Carson Wright, Katherine Grindle, Chris Grindle, and Fred Brogan, of the U.S. Geological Survey, helped prepare the site at Wallback, W. Va. Nuttall LLC of Fayetteville, W. Va., graciously allowed the research team access to the basin near Hico, W. Va. Technical reviews were completed by Aaron Porter of the U.S. Geological Survey, Niroj Shrestha of Michael Baker International, Eric Brown of the Federal Highway Administration, and Isaac Wait of Marshall University, who served on the Technical Advisory Committee organized by the West Virginia Department of Transportation.
Abstract
The U.S. Geological Survey (USGS), in cooperation with the West Virginia Department of Transportation, Division of Highways, compared time of concentration (Tc) and related runoff characteristics measured at four field sites in West Virginia to estimates of these values made using accepted methods. These four sites were selected to represent a range of basin size, length, and slope, and a range of estimated Tc. Instrumentation included a rain gage and a streamgage at all sites. Two streamgages, USGS station number (no.) 03159718 Grasslick Creek tributary above Interstate 77 near Fairplain, West Virginia, (referred to as Fairplain in this report) and USGS station no. 03159823 Grass Run tributary above Interstate 77 near Ripley, W. Va., (referred to as Ripley in this report) were near each other in northwestern West Virginia at the outlets of small basins with moderate slope. The largest, longest, and flattest basin in the study was upstream from USGS station no. 03190307 Hedricks Creek Tributary above US–19 near Hico, W. Va. (Hico). The final gaged basin in the study, that of USGS station no. 03197062 Cookman Fork at Interstate 79 near Wallback, W. Va., (Wallback) in central West Virginia, had a drainage area nearly as large as Hico, but the basin was more compact.
Precipitation and streamflow data were collected at the streamgages between October 2017 and July 2020. Storms were identified and classified through an iterative process relying on inspecting graphs created from the precipitation and streamflow data. Three hydrograph time metrics that represent Tc were computed for this study: time to rise, time to recede from a high point on the hydrograph to an inflection on the recession, and the time between an inflection on the hyetograph and an inflection on the recession of the hydrograph (precipitation inflection to recession inflection or PI-to-RI).
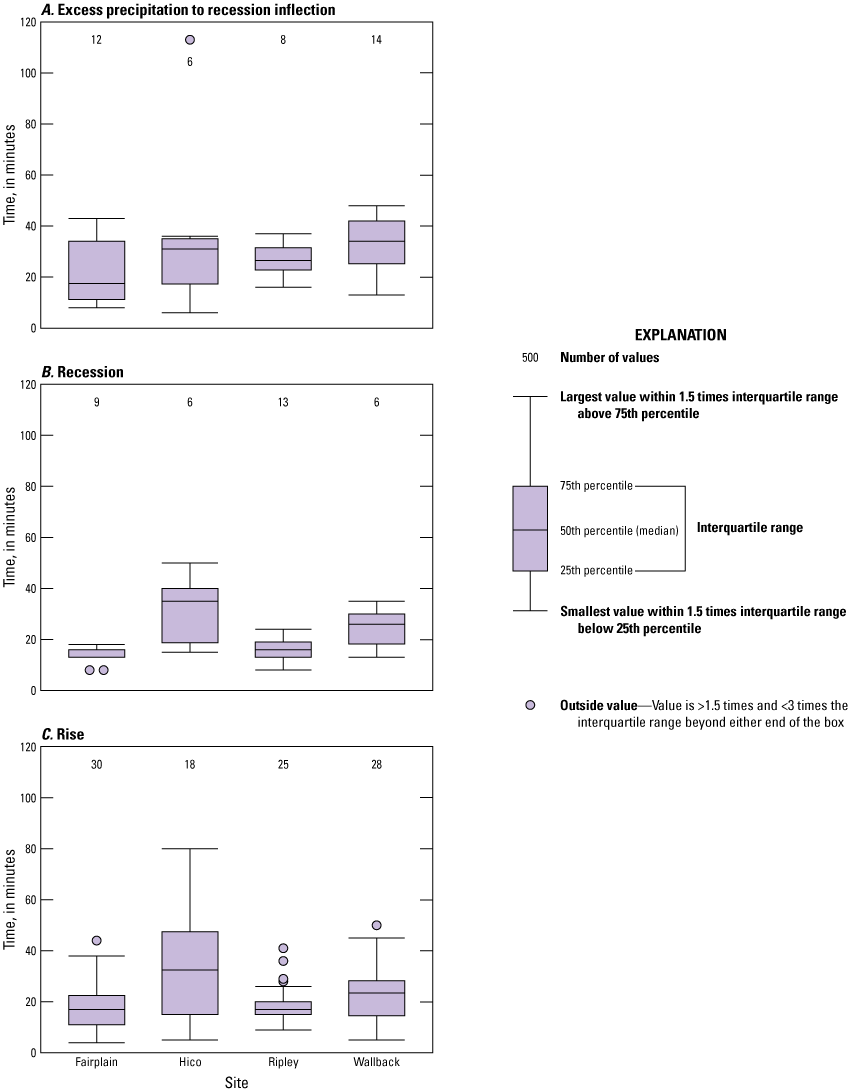
Hico had the slowest time metrics: the streamgage had an average Tc of 34 and 32 minutes for time to rise and time to recede, respectively. The time between the PI-to-RI at Hico, 38 minutes, was the longest for any of the characteristics at any of the streamgages. Wallback had the second slowest time metrics. At Wallback, average Tc for time to rise and time to recede was similar, 23 and 25 minutes, respectively. The average time between the PI-to-RI for Wallback was greater than its time to rise or time to recede, 32 minutes. At Fairplain and Ripley, time to rise was 18 and 19 minutes, time to recede was 14 and 16 minutes, and time between the PI-to-RI was 22 and 27 minutes, respectively. At Ripley, PI-to-RI and time to rise were significantly different from each other. Differences in metrics were not statistically significant (p ≤0.05) among streamgages.
At all streamgages, predictions made with the “Rational Method” were within one average standard deviation of the overall mean Tc. The Rational Method was applied following two different procedures— (1) channel geometry was estimated using professional judgment and (2) channel geometry estimates were adjusted using regional equations. The three different time metrics had an inconsistent relation with the estimates. Some of the predictions differed from individual hydrograph time metrics by more than one standard deviation. Predicted values for the 10-year storm were within the interquartile range (IQR) for 4 of 12 combinations of streamgages and time metrics. Adjusted Tc predictions were within the IQR of PI-to-RI for Fairplain and Wallback, longer than the IQR of observed PI-to-RI at Hico, and shorter than the IQR of observed PI-to-RI at Ripley. The adjusted predictions of Tc were within the IQR of time-to-rise for Hico and Fairplain and were longer than the IQR for Ripley and Wallback. At Ripley, the predictions were not within the IQR for either PI-to-RI or time to rise, but instead, were between them. These lines of evidence do not indicate large, systematic errors in Tc estimates.
Introduction
Discharge estimates are used in the design of culverts and other drainage structures (Holmes and Chintala, 2007). These discharge estimates are made using the “Rational Method” or the Natural Resources Conservation Service Technical Release 55 (TR-55) method: both methods require estimates of the time of concentration (Tc) to estimate discharge (Holmes and Chintala, 2007). These methods are widely used and well accepted (Natural Resources Conservation Service, 1986; McCuen and others, 2002). However, estimating Tc requires estimating variables like flow-segment length and channel geometry that are poorly characterized for small basins, and therefore require individual judgment. Characterizing small, rural, predominantly forested watersheds could help the West Virginia Department of Transportation, Division of Highways (WVDOH) improve Tc estimates by refining individual judgment.
Tc has been variously defined. Black (1991, p. XXII) considered Tc to be 1 of 11 concepts in hydrology that are “relatively easy to define abstractly, difficult to illustrate comprehensively, often are impossible to measure or predict accurately, yet are absolutely essential to the thorough understanding of watershed hydrology.” He went on to provide four different definitions of Tc, including both conceptual and computational definitions. One of the most common conceptual definitions of Tc, and the definition used in TR-55, is the time surface runoff requires to reach the outlet (or other point of interest) from the most hydraulically remote part of the basin (Chow, 1964; Dunne and Leopold, 1978; Natural Resources Conservation Service, 1986; McCuen and others, 2002). Another conceptual definition of Tc, and the definition used in the Rational Method, is the minimum time it takes for an entire basin to contribute flow at the outlet (Hayes and Young, 2005). These are the two principal conceptual definitions of Tc used in this report. Various computational definitions of Tc have been used as well. A computational definition of Tc has a specific metric that can be computed from precipitation and streamflow data that will allow measurement of Tc.
The WVDOH and U.S. Geological Survey (USGS) cooperated to study Tc in the part of West Virginia in the Appalachian Plateaus physiographic province. Streamflow and precipitation data were collected at four field sites intended to represent the study area. Time metrics representing Tc were computed from these streamflow and precipitation data and compared among and within streamgages. Time metrics were compared to storm characteristics and Tc estimates.
Purpose and Scope
The purpose of this report is to compare measurements of Tc and related runoff characteristics to estimates of Tc and related runoff characteristics made using accepted methods. Objectives of this report are to:
-
1. Report Tc measurements at four small basins (less than [<] 200 acres) in the Appalachian Plateaus physiographic province in West Virginia that represent typical basin conditions as represented in Rational Method and TR-55 documentation.
-
2. Compare the measured Tc values from this study to Tc values computed for those watersheds using WVDOH methods.
-
3. Compare relations between observed and estimated Tc as they relate to physical watershed characteristics in a way that allows WVDOH to determine if their current procedures produce accurate Tc estimates, and if not, how to modify them.
Study Design and Site Selection
Sites were selected to represent a range of size, length, slope, and estimated Tc that were typical of basin conditions in West Virginia. All sites had to be in basins that were predominantly forested to represent the principal land cover in the broader study area and that contained negligible amounts of impervious or other non-forested land surfaces. Sites also needed to be within 90 minutes of the USGS Virginia and West Virginia Water Science Center office in Charleston, W. Va., to allow quick response to storms, and culverts at the sites were required to have a generally clean apron and solid wingwalls.
Four sites that met these criteria were chosen for the study (table 1; fig. 1; fig. 2). Two streamgages, USGS station number (no.) 03159718 Grasslick Creek tributary above Interstate 77 near Fairplain, W. Va. (referred to as Fairplain in this report), and USGS station no. 03159823 Grass Run tributary above Interstate 77 near Ripley, W. Va. (referred to as Ripley in this report), were established at the outlets of small basins with moderate slopes and near each other in northwestern West Virginia. These two basins had similar lengths (2,180 and 1,880 feet [ft.]), respectively, along their principal flow paths; principal flow paths were determined using a 1/9 arc-second digital elevation map (U.S. Geological Survey, 2012). Fairplain has a drainage area nearly three times (0.0761 square mile [mi2] or 48.7 acres) that of Ripley (0.0280 mi2 or 17.9 acres), and the two streams flow in nearly opposite directions.
Table 1.
Location and basin/channel characteristics of the four field sites in West Virginia used for this study from October 2017 to July 2020.[USGS, U.S. Geological Survey; DD, decimal degrees; mi2, square mile; EqPct NHD+HW, equivalent percentile of the basin among NHDPlus V.1 (Wieczorek, and LaMotte, 2010) headwater catchments less than 250 acres; ft, feet; W. Va., West Virginia; >, greater than]
Map showing physiographic provinces, selected highways, cities, and other features in West Virginia.
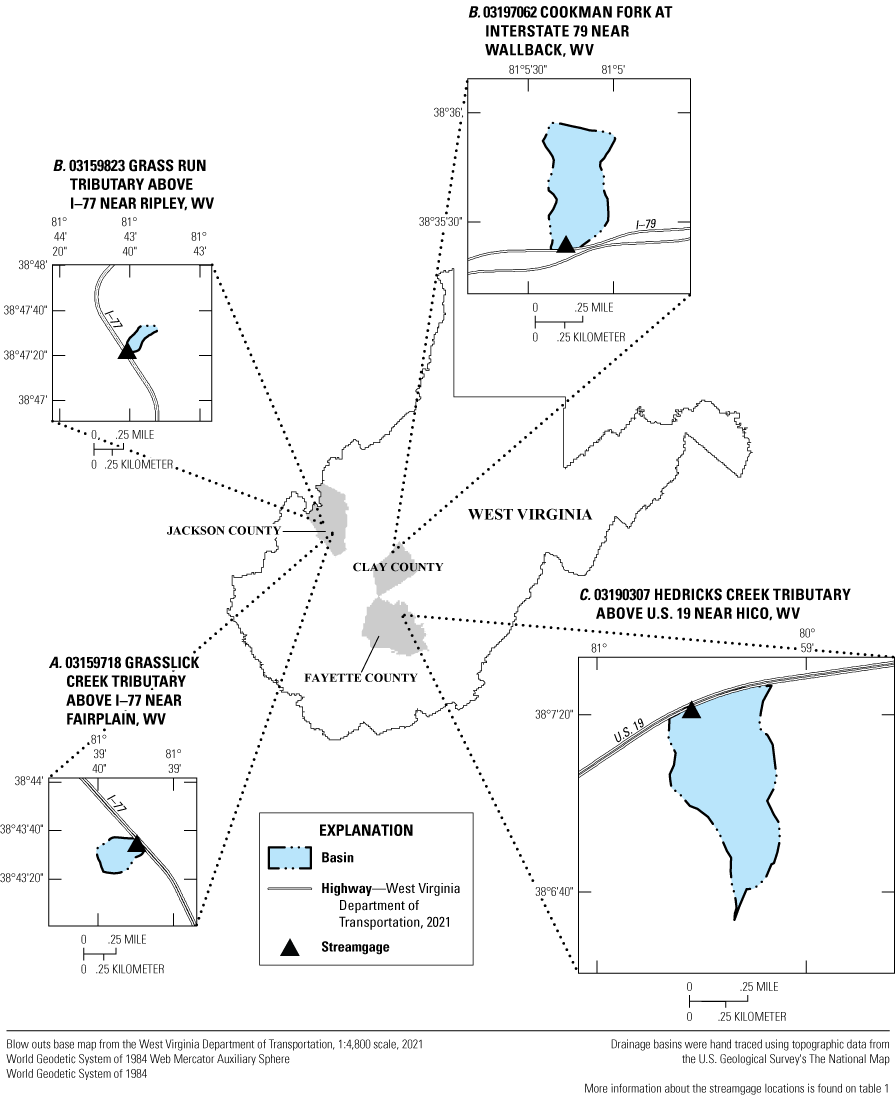
Maps showing the locations of the four field sites (A–D) in West Virginia where time of concentration was measured. WV, West Virginia.
The largest and longest basin in the study drained to the stream cross section where USGS station no. 03190307 Hedricks Creek tributary above U.S. Highway 19 near Hico, W. Va. was established (referred to as Hico in this report). This basin drains 0.213 mi2 or 136 acres and runs 6,010 ft along its principal flow path. Hico is on the uplands of the plateau area near the New River Gorge, where erosion-resistant sandstones have been incised only by the largest rivers in the area so that basins of smaller streams have flatter terrain and less relief than in most of the Appalachian Plateaus physiographic province (Lessing, 1997). Lastly, USGS station no. 03197062 Cookman Fork at Interstate 79 near Wallback, W. Va. (referred to as Wallback in this report), in central West Virginia, was established at the outlet of a basin with a drainage area similar to Hico (0.178 mi2 or 114 acres) but that is more compact and has a principal flow path length of 4,290 ft.
Basin and channel slope were the primary consideration during site selection. Basin slope, as computed with the ArcMap Spatial Analyst Slope geoprocessing tool, represents the average of the slopes computed from an elevation grid. In ArcMap, slope is calculated for each cell inside a polygon in comparison to the eight adjacent grid cells; the slope value for all the cells inside the polygon are then averaged (Esri, 2017). Basin slope was already computed for all National Hydrography Dataset Plus (NHDPlus) catchments, including those for the study area (Wieczorek and LaMotte, 2010). NHD-Plus catchments include headwater catchments, which are drainage basins, but also downstream catchments that begin at the outlet of a headwater catchment. Slope was computed for the candidate basins using data from a 10-meter (m) digital elevation model (U.S. Geological Survey, 2012). These slopes were compared to those of NHDPlus headwater catchments that drained <250 acres. The basin for Hico was steeper than only 11 percent of the NHD-Plus headwater catchments, flat relative to the rest of the area. Ripley (43rd percentile) and Fairplain (86th percentile) represented typical conditions. Wallback was steep, and if it had been an NHDPlus headwater catchment, it would have been the second steepest basin that drained <250 acres within the part of West Virginia in the Appalachian Plateaus physiographic province. Basin slope was assumed to be an imperfect surrogate for the slope of the principal flow paths, but determining the slope of principal flow paths among comparable streams within the entire part of West Virginia in the Appalachian Plateaus physiographic province would have been labor- and time-prohibitive. To underscore the imperfection of basin slope as a surrogate, the four sites in this study ranked differently with respect to principal flow path and basin slope.
Methods of Data Collection and Quality Assurance
Time of concentration field sites were established at the four study basins. The field sites included streamgages that were instrumented to measure instantaneous stage and velocity and rain gages to measure precipitation (fig. 2). Two sets of stage sensors were placed at each site (appendix 1, appendix 2, appendix 3, appendix 4). Vented nonsubmersible pressure transducers (NTRANs) were placed upstream from the culverts and operated according to established USGS methods (Sauer and Turnipseed, 2010). Area-velocity (AV) sensors were placed in each culvert and operated according to the manufacturer’s specifications (Teledyne Isco, 2016). A tipping-bucket rain gage was used to measure rainfall volume. The equipment for the streamgage and rain gage shared a common recorder at each site, and timing was synchronized by Global Positioning Systems (GPS) every 30 minutes. Data were transmitted hourly to the Geostationary Operational Environmental Satellite (GOES) then to the USGS National Water Information System (NWIS) database. Provisional data were made available on the NWIS web page in real time (U.S. Geological Survey, 2017). Streamflow and rainfall data were reviewed daily. Backup data were retrieved from the recorders at least every 2 months and stored in NWIS.
Streamgages were instrumented with submersible TIENet 350 AV sensors that were installed inside each culvert (Teledyne Isco, 2016). The sensors require uniform flow, and to avoid drawdown caused by the culvert, they were installed at cross sections located three times the maximum width of the culvert from the upstream opening, 12 ft at Ripley and Hico and 18 ft at Fairplain and Wallback. The AV sensor’s range of stage measurement is from 0.03 to 10 ft with an accuracy of ±0.10-percent full scale. The AV sensor can measure velocities from −5 to +20 feet per second with an accuracy of 2 percent of the reading. Recorded velocity represents an average of velocity measurements made each second for 30 seconds before the data were saved. These AV sensors measure velocity in an expanding bubble about 20 degrees above the face of the sensor and 10 degrees wide. When flow was shallow, the sensor focused on a small area, and as depth increased, the size of the bubble increased to a maximum of about 1 ft in diameter. Velocity was measured and averaged for the entire bubble. The sensor and recorder system then computed average cross-sectional velocity by applying a velocity coefficient based on the relation of culvert dimensions to measured velocity and depth. The average velocity was applied to cross-sectional areas using a rating that was developed from measured culvert dimensions. The sensor only measured velocity directly at stages greater than (>) 0.08 ft. At lower stages, it interpolated velocities. Velocities at stages between 0.08 and 0.10 ft were erratic. All stage and velocity measurements from the AV sensors at stages less than 0.10 ft were reviewed to ensure the sensors were working properly, then deleted because they were not needed to characterize high flows.
Velocity measurements from the AV sensors were verified with simultaneous independent surface velocity measurements made with a radar gun at the sensor (Stalker, 2018). These surface velocity measurements were made during site visits when depth at the AV sensors exceeded 0.08 ft. Verification measurements could only be made at medium and medium-high flows, because going into the culverts to measure velocities at the highest flows was not safe. During verification, the range of surface velocities was expected to exceed or overlap with the range of simultaneous values from the AV sensors. Surface velocities less than AV velocities were considered an indication that the AV sensors were malfunctioning.
The NTRAN sensors, used at all streamgages, were bubbler gages made by OTT (OTT HydroMet, 2016). OTT bubbler gages can measure stages from 0 to 50 ft with an accuracy of 0.02 ft. These sensors used a vented pressure line to equilibrate with atmospheric pressure. All NTRANs were installed outside and upstream from the culverts. The NTRAN orifice was mounted about 0.10 ft above the apron at Ripley, Fairplain, and Wallback. When the water level was below the orifice at these streamgages, gage height was deleted, and discharge was not determined. At Hico, the orifice was submerged in a pool upstream from a stable streambed feature formed primarily from small boulders. The stage-flow rating was used to determine flow at two streamgages, Hico and Wallback. The ratings were developed from conventional flow measurements made at these two streamgages every routine site visit when there was enough water. At Wallback, the upper end of the rating was developed from the relation between NTRAN stage and AV flow during high-flow periods in September 2018 when the stage-flow relationship was unaffected by sediment deposition and the AV sensor was verified as working properly. At Hico, the upper end of the rating was defined by a slope-area measurement made from floodmarks left by the June 2020 peak, the largest observed there. At both streamgages, ratings were shifted on the basis of flow measurements, changes to the control that were observed during site visits, and ongoing control observations made using the site cameras. At Wallback, a large amount of sand and gravel moved through the apron and culvert, and every time the site cameras showed substantial sediment deposition, a visit was made to clean the control.
The NTRAN was used as the stage sensor at Hico throughout the study period because flow at the AV sensor inside the culvert was too turbulent for the sensor to provide reliable data, and equally important, the NTRAN orifice was installed in a pool with a stable control. The AV sensors were used to generate the primary flow records at three streamgages: Fairplain, Ripley, and Wallback. At Fairplain and Ripley, flow records from the AV meters were largely complete. At Wallback, the AV meter malfunctioned at times, so the record from the NTRAN was substituted at these times to complete the record. Substituting NTRAN data for AV data resulted in a less detailed flow record. The AV sensor could make stage and velocity measurements every minute. The NTRAN needed 5 minutes between stage measurements. At Hico, 5-minute measurement intervals resulted in little or no loss of information. The NTRAN orifice was in a pool with a solid and stable control, the water surface over the orifice was smooth except at the highest flows, and water level changed slowly enough that 1-minute data would have added little information under normal conditions. However, at Wallback, 5-minute data were nonideal. Flows at Wallback were somewhat flashier than those at Hico, but the bigger problem was that Wallback did not have a pool to install an NTRAN orifice in. Instead, the orifice was attached to the apron. Flow over the orifice was turbulent, and a standing wave formed over the orifice at some flows making the stage data noisy.
The rain gages were installed in open spaces near the streamgages, in areas where rainfall patterns would be least affected by vehicles along roadways and by nearby trees. WaterLOG H-3401 8-inch (in.) tipping-bucket rain gages were used at all sites (Yellow Springs Instruments [YSI], 2019). These rain gages measure rainfall rates between 0 and 25 inches per hour (in/h). The bucket tips when it receives 0.01 in. of rain. Calibration of rain gages was checked twice a year by pouring a known quantity of water through the funnel; all calibration checks were successful, and no data needed to be corrected. The funnel and screens were inspected at each site visit. Additional site visits were made when National Weather Service radar indicated rain at a site, but rain either was not recorded by the rain gage or was delayed relative to the radar track; either condition suggested that the funnel was plugged. Typically, the funnel became plugged during extended dry periods, but the exact timing of the plugs during these periods is unknown. Data from periods when the funnel was plugged were deleted and are not in NWIS. The rain gages were unheated, so snow only melted when ambient temperatures were above freezing.
Preprocessing and review steps included applying automated thresholds to screen out spikes, negatives, and other physically impossible values and applying screens to filter out file processing artifacts such as those caused by dropped characters. Preliminary streamflow and precipitation data were reviewed daily, and backup data were reviewed when they were uploaded into NWIS. Streamflow data were deleted when (1) sensors were malfunctioning (this deletion included the entire period after the last inspection when they were working properly), (2) streams were frozen and assumptions of the stage-streamflow relation were violated, or (3) stage at AV sensors was less than 0.10 ft. Precipitation and streamflow records are available for download from the NWIS website (U.S. Geological Survey, 2024a, 2024b, 2024c, 2024d).
Precipitation and Streamflow Results
The following sections describe and summarize precipitation and streamflow data collected during this study (Messinger and Scott, 2024). Precipitation totals from this study are summarized and compared to long-term averages. The largest storms from each site are compared to a standard intensity-depth-frequency atlas to characterize their approximate frequencies (Bonnin and others, 2006). The range and timing of precipitation and streamflow magnitudes are discussed in this section of this report.
Precipitation
The 2018 water year was unusually wet at all sites, ranging from 53 to 59 in., compared to the 1991–2020 normal precipitation of 46 in. at a nearby long-term weather station at Charleston, W. Va., Yeager Airport (table 2; National Centers for Environmental Information, 2021). The 2018 calendar year was the wettest year on record at Charleston, W. Va., with a total of 67 in. of precipitation (National Oceanic and Atmospheric Administration, 2018). Total annual precipitation for the 2019 water year was moderately drier than normal, ranging from 42 to 43 in. at all sites. September 2019, however, was unusually dry, which accounted for most of the precipitation deficit for the year (National Centers for Environmental Information, 2021). Total precipitation for September 2019 ranged from 0.10 in. at Ripley to 0.42 in. at Wallback, in comparison to the 1991–2020 September normal precipitation at Charleston, W. Va., Yeager Airport of 3.46 in. The 2020 water year, like the 2018 water year, was unusually wet at all sites. Rainfall totals for the partial year of 2020 ranged from 39 to 50 in., but some of the differences among sites were caused by differences in the duration of data collection and dates when data collection was discontinued (fig. 3). Data collection ended on June 17, 2020, at Ripley, June 26, 2020, at Fairplain, June 30, 2020, at Hico, and July 2, 2020, at Wallback. Also, some annual and monthly precipitation totals include periods of missing record, which were not adjusted by estimation. The study period’s rainfall totals were normal to wetter than normal overall, except for September 2019.
Table 2.
Total precipitation at the four field sites in West Virginia used for this study from October 2017 to July 2020 (U.S. Geological Survey, 2024a, 2024b, 2024c, 2024d).[in., inch; Fairplain, U.S. Geological Survey (USGS) station number (no.) 03159718 Grasslick Creek tributary above Interstate 77 near Fairplain, West Virginia; Ripley, USGS station no. 03159823 Grass Run tributary above Interstate 77 near Ripley, West Virginia; Hico, USGS station no. 03190307 Hedricks Creek tributary above U.S.–19 near Hico, West Virginia; Wallback, USGS station no. 03197062 Cookman Fork at Interstate 79 near Wallback, West Virginia; --, not measured]
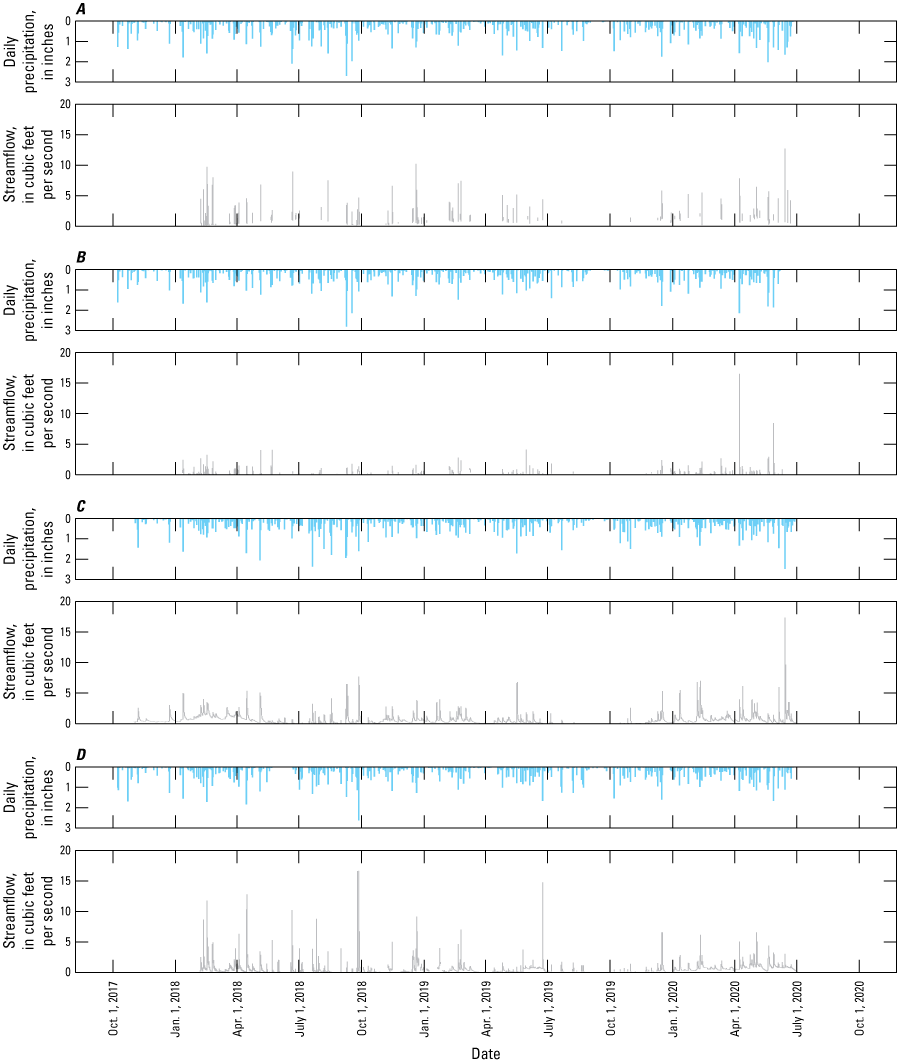
Graphs showing daily precipitation and streamflow at four field sites in West Virginia, October 2017–July 2020: A, U.S. Geological Survey (USGS) station number (no.) 03159718 Grasslick Creek Tributary above Interstate 77 near Fairplain, West Virginia; B, USGS station no. 03159823 Grass Run Tributary above Interstate 77 near Ripley, West Virginia; C, USGS station no. 03190307 Hedricks Creek Tributary above U.S.–19 near Hico, West Virginia; and D, 03197062 Cookman Fork at Interstate 79 near Wallback, West Virginia.
As would be expected in a generally wet period, many days had storms and substantial total precipitation. Daily precipitation exceeded 2 in. between 1 and 4 times at all sites (table 3). Daily precipitation exceeded 1.5 in. between 9 and 11 times at all sites and exceeded 1 in. between 24 and 36 times at all sites. The number of days with substantial total precipitation varied spatially but was also affected by slight differences in study duration. Even though the closest pair of sites, Ripley and Fairplain, were only about 7.5 miles apart, the number of days with 1-inch or greater rainfall varied—Ripley had 26 days and Fairplain had 35. Four of the days when Fairplain received more than an inch of precipitation were days when the rain gage at Ripley was not operational or had been discontinued, compounding the differences that were to be expected because of spatial variance.
Table 3.
Number of days when precipitation exceeded selected thresholds and the maximum daily precipitation at the four field sites in West Virginia used for this study from October 2017 to July 2020.[Dates shown as month/day/year. in., inches; Fairplain, U.S. Geological Survey (USGS) station number (no.) 03159718 Grasslick Creek tributary near Fairplain; USGS station no. 03159823 Grass Run tributary near Ripley; Hico, USGS station no. 03190307 Hedricks Creek Tributary near Hico; Wallback, USGS station no. 03197062 Cookman Fork near Wallback]
Precipitation totals for selected durations for each site were compared to intensity-duration-frequency values commonly used in design (Bonnin and others, 2006). The storm on June 14, 2020, at Fairplain yielded 0.57 in. of rain in 5 minutes and 1.54 in. of rain in 30 minutes. This storm exceeded the 10-year return interval for durations of 5, 10, 15, and 30 minutes; the largest 15-minute total during that storm was between the 50- and 100-year return interval for that duration (table 4). For the longer durations that were compared (60 minutes and 2, 3, 6, 12, and 24 hours), however, the largest totals were only between the 1- and 2-year and 2- and 5-year recurrence intervals. At Fairplain, five storms exceeded the 1-year recurrence interval for durations of 5, 10, and 15 minutes, and three storms exceeded the 2-year recurrence interval for these same durations.
Table 4.
Storm duration, maximum observed storm characteristics, and number of storms exceeding threshold magnitudes for storms with 1- and 2-year recurrence intervals and durations of 1 day or less at the four field sites in West Virginia used for this study from October 2017 to July 2020.[Recurrences from National Oceanic and Atmospheric Administration, 2022. Recurrence values are for the respective rain gage locations. Storms with incomplete precipitation or flow data are excluded. Fairplain, U.S. Geological Survey (USGS) station number (no.) 03159718 Grasslick Creek tributary above Interstate 77 near Fairplain, West Virginia; Ripley, USGS station no. 03159823 Grass Run tributary above Interstate 77 near Ripley, West Virginia; Hico, USGS station no. 03190307 Hedricks Creek tributary above U.S.–19 near Hico, West Virginia; Wallback, USGS station no. 03197062 Cookman Fork at Interstate 79 near Wallback, West Virginia]
At Ripley, the storm of July 7, 2019, yielded 0.85 in. of rain in 10 minutes and 1.33 in. of rain in 30 minutes (table 4). This storm was between the 10- and 25-year recurrence intervals for 10-minute durations and the 5- and 10-year recurrence intervals for 5-, 15-, and 30-minute durations. At Ripley, the largest storms for durations of 1, 2, 3, 6, 12, and 24 hours were between the 1- and 2-year and the 2- and 5-year recurrence intervals. Either 2 or 3 storms exceeded the 1-year return interval for 5- through 60-minute durations at Ripley, and either 1 or 2 storms exceeded the 2-year recurrence interval for these same durations.
Hico received some intense storms during the study. At Hico, the storm of June 5, 2020, yielded 0.48 in. of rain in 5 minutes and was between the 5- and 10-year and 25- and 50-year recurrence intervals for the durations of 12 hours or less that were available for comparison (table 4). Hico was the only site where a storm with a duration >30 minutes exceeded the 5-year recurrence interval. Either 3 or 4 storms exceeded the 1-year recurrence interval for durations of 1 hour or less, and 1 to 2 storms exceeded the 2-year recurrence interval for the same durations.
Storms at Wallback were somewhat less intense, or had a lesser sustained intensity, than at the other sites. The maximum storms for all durations that were compared at Wallback were between the 1- and 2-year and 2- and 5-year recurrence intervals. Either 5 or 6 storms exceeded the 1-year recurrence interval for durations of 15 minutes or less. Of these storms, 4 exceeded the 2-year recurrence interval for 5 minutes, 3 exceeded the 2-year recurrence interval for 10 minutes, but only 1 exceeded the 2-year recurrence interval for 15 minutes.
Streamflow
Streamflow data collection began November 1, 2017, at Hico; January 11, 2018, at Ripley; February 6, 2018, at Wallback; and February 7, 2018, at Fairplain. Data collection ended June 25, 2020, at Fairplain; June 17, 2020, at Ripley; June 30, 2020, at Hico; and July 2, 2020, at Wallback.
Dry channels and zero flows were observed at all four streamgages during field visits. Only one streamgage, Hico, was able to accurately record values of zero flow (table 5). At the other three streamgages, stage could be too low to reach either stage sensor in use at a given time. In this report, the minimum flow that could be measured accurately in each stream is referred to as the “detection level” for that streamgage. The minimum flows recorded at the other three streamgages were 0.02 cubic foot per second (ft3/s) at Wallback and Ripley and 0.15 ft3/s at Fairplain. The number of days when flow was above the detection level for part of the day ranged from 117 days at Fairplain to 851 days at Hico, whereas the number of days when flow remained above the detection level all day ranged from 7 days at Fairplain to 708 days at Hico (table 5). The low number of measured flow values at Fairplain was directly related to the high detection level of flow (0.15 ft3/s) needed to submerse the AV sensor deeply enough for measurements to be accurate.
Table 5.
Number of days when flow was recorded and maximum recorded flow for the four streamgages in West Virginia used for this study from October 2017 to July 2020.[Dates shown as month/day/year. ft3/s, cubic foot per second; Fairplain, U.S. Geological Survey (USGS) station number (no.) 03159718 Grasslick Creek tributary above Interstate 77 near Fairplain, West Virginia; Ripley, USGS station no. 03159823 Grass Run tributary above Interstate 77 near Ripley, West Virginia; Hico, USGS station no. 03190307 Hedricks Creek tributary above U.S.–19 near Hico, West Virginia; Wallback, USGS station no. 03197062 Cookman Fork at Interstate 79 near Wallback, West Virginia]
When flows were high for several days at one streamgage, they generally were high at the other streamgages. However, the maximum flows for the study period were on different days for all four streamgages (fig. 3). The maximum flow for Wallback resulted from a series of storms in September 2018 that produced a peak on September 25 with a flow of 16.6 ft3/s and another peak on September 27 with a flow of 16.7 ft3/s. Thunderstorms in spring of 2020 produced the maximum flow for the other three streamgages. The maximum flow at Ripley (16.5 ft3/s), on April 8, 2020, was nearly twice the magnitude of the second largest peak 8.43 ft3/s recorded on May 29, 2020. The largest peaks at Fairplain were produced by different storms than at Ripley and were closer to each other in magnitude than the largest peaks at the other streamgages: 12.7 ft3/s on June 14, 2020, and 8.93 ft3/s, 9.74 ft3/s, and 10.2 ft3/s on June 22, 2018, February 16, 2018, and December 12, 2018, respectively. At Hico, the maximum flow (17.4 ft3/s), on June 14, 2020, was more than twice the magnitude of the second largest peak, 7.71 ft3/s on September 27, 2018.
The longest period with uninterrupted low flows at all streamgages was in August–September 2019. A period between August 23 and October 5 when no rain gage received more than 0.67 in. of rain resulted in sustained zero flows at Hico and flows below the detection level at the other three streamgages during September and early October 2019 (fig. 3). Flows increased at Hico and Wallback after rain in October 2019. Flows in the smaller streams at Ripley and Fairplain receded below the detection level earlier in August than in the two larger streams and also remained generally dry later until December.
At Hico, a recorder malfunction caused data recorded at 1-minute and 5-minute intervals on the backup recorder between August 31 and October 3, 2018, to be lost, so that only the subset of data transmitted through the GOES system was available for this period. Satellite-transmitted data were only available at 15-minute intervals, instead of 1-minute or 5-minute intervals. This September 2018 period included two large, extended storms and the second highest peak streamflow recorded at Hico. For precipitation, the 15-minute totals were accurate because the rain gage recorded tips throughout the interval and transmitted total precipitation every 15 minutes. The 1-minute precipitation subtotals, however, were lost, and information on precipitation timing was less precise than for any of the other data discussed in this report. For streamflow, not only was information on timing limited to 15-minute intervals, but the recorded value was the instantaneous stage reading from the NTRAN at the 15-minute reading, so that information on rises or falls in stage between those measurements was lost.
Storms and Storm Characteristics
Storms were classified using an iterative, interactive process involving both the precipitation and flow records. Periods when precipitation data were missing, when flow data were estimated, or when no precipitation records were available were not used when classifying storms. Storms were designated as beginning when precipitation began after a period of 6 or more hours without rain. Periods of intermittent rain were classified as part of the same storm if breaks between the rain were less than 6 hours. This amount of time was chosen because inspection of this study’s graphs confirmed that a 6-hour break in precipitation was enough time for stormflows to end at all streamgages. Subsequent periods without rain were included in the previous storm until another storm began or until flows reached the detection level. Cumulative total precipitation was computed for each storm, and storms that did not result in measurable flow at the streamgages were identified and excluded from further analysis. The use of this process led to the identification of 529 storms. Storms were then ranked by the peak flows they caused at the streamgages. Only the 50 biggest storms at each streamgage were retained as being relevant for this analysis.
Finally, storm hydrographs and hyetographs were subdivided into segments. This part of the process was also iterative. Because many storms were long enough that the hydrographs and hyetographs that represented them had compressed scales that made details difficult to distinguish, these graphs were broken into segments that could be plotted on a single page at a convenient scale to analyze. The hydrographs and hyetographs were broken during lulls in the storms when rain had paused and flow was stable. Final storm segment lengths varied so that complex, active hydrographs could be kept on the same plot. This meant that time scales were different on different plots. Running precipitation totals were computed for storm segments.
Hydrographs varied in complexity based on the characteristics of the storm they were depicting. Hydrographs were categorized as simple, extended, or complex (fig. 4). Simple hydrographs showed a single peak that quickly receded; these peaks resulted from a single, often intense pulse of rain. Simple hydrographs were the easiest of the three categories to delineate and, therefore, the most likely to provide useful information, but they were infrequent and represented only some of the largest storms (Messinger and Scott, 2024; tables 1, 2). Extended peaks were produced by storms with generally steady, sustained rainfall. A storm that produced an extended peak typically began with light to moderate rainfall. Stormflow began after basin storage was exceeded, then reached a peak that was sustained by generally steady rainfall. Rises and recessions of stormflow were sometimes easy to identify in graphs showing these storms. The inflection representing the end of excess precipitation was often indistinct on the hyetograph, especially when precipitation intensity decreased during the storm.
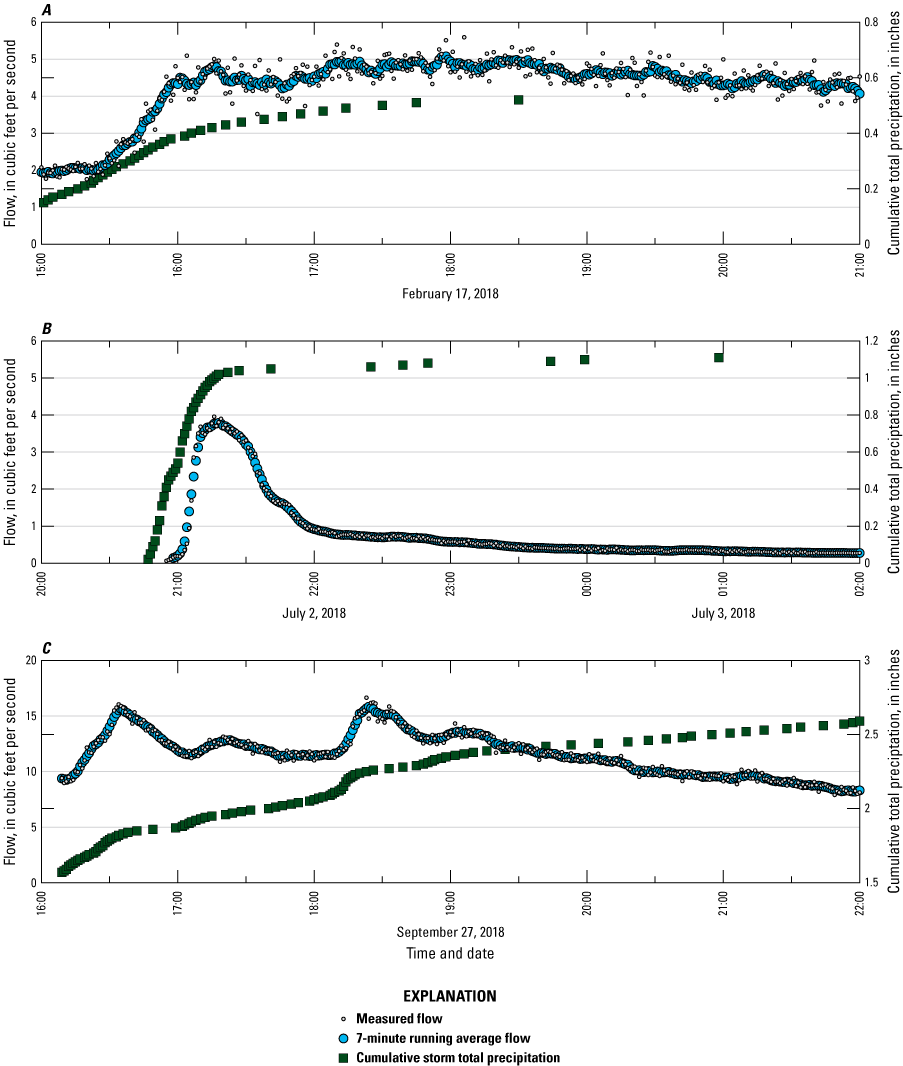
Graphs showing flow and cumulative storm precipitation for selected storms at U.S. Geological Survey station number 03197062 Cookman Fork at Interstate 79 near Wallback, West Virginia, that produced A, extended (February 17, 2018); B, simple (July 2, 2018); and C, complex (September 27, 2018) hydrographs.
Most storms produced complex peaks. Complex peaks were produced by storms with variation in precipitation intensity, including those with breaks in the rain; those with pulses of intense rain coming amidst moderate or light rain; and those with intensifying rain amidst already intense rain. Increases in precipitation intensity might come at any time during a storm, including times when the basin was saturated and flow was rising, when moderate peaks were being sustained, or when peaks were receding. Many of the largest peaks measured during the study were produced by complex storms shown by complex hydrographs. Because these hydrographs were complex, interpreting them was inherently challenging and subjective and required analytic judgment. The information from these hydrographs was necessary to meet study objectives, so data from complex hydrographs were used in analyses.
Hydrograph Time Metrics
Three hydrograph time metrics were used in this study to compute Tc: time to rise, time to recede to an inflection on the recession, and the time between the inflection on the hyetograph at the end of major precipitation (the precipitation inflection) and the inflection on the falling limb of the hydrograph (the recession inflection). The time from the precipitation inflection to the recession inflection is abbreviated in this report as PI-to-RI. These three time metrics represent the two primary conceptual definitions of Tc used in this report.
Time to rise is intended to represent the time needed for a particle of water to travel to the outlet from the most hydraulically remote part of the watershed (Hayes and Young, 2005). Time to rise is most likely to give a good estimate of Tc when the assumptions of the Rational Method are closest to being met in a small basin. Among these assumptions are that the basin area is <200 acres, streamflow peaks when the entire basin contributes stormflow, a storm that has a duration equal to Tc produces the highest peak discharge for a given precipitation intensity, and precipitation intensity is uniform for a storm that has a duration equal to Tc (McCuen, 2002).
The other two time metrics (as previously mentioned) can also be used to compute Tc when Tc is defined as the end of excess precipitation until the end of direct runoff or stormflow (McCuen, 2009). The two primary conceptual definitions of Tc used in this study are related if the rain in the most remote part of a basin when excess precipitation ends is also the last stormflow to leave the basin. In hydrograph analysis, the end of stormflow is taken to be the inflection on the falling limb of the hydrograph from steeply receding flows, representing stormflow, and gradually receding flows, representing mixed base flow and interflow (Natural Resources Conservation Service, 2010). PI-to-RI is a computational definition of Tc that directly corresponds to this conceptual definition (Hayes and Young, 2005; McCuen, 2009).
Time to recede has been used previously as a surrogate for time from the end of excess precipitation to the end of stormflow (Hayes and Young, 2005). The assumption underlying this surrogacy is that in small basins, peaks closely follow the end of excess precipitation. One benefit of using this computational method is that it relies only on the hydrograph and, therefore, one environmental sensor. This was most important in studies done when the best available precipitation and stage recorders used separate clocks that sometimes became unsynchronized, causing errors in time measurement to be an important source of overall error. In this study, the rain gages and stage sensors shared a common recorder that was synchronized with GPS satellites, which allowed a comparison between time to recede and PI-to-RI that was not affected by possible errors in time measurement. Hydrograph time metrics were computed using inflections that were identified on graphs that represent the beginning and end of hydrograph events. In this report, the phrase hydrograph event describes an individual rise, recession, or PI-to-RI that was identified as part of a storm graph. Graphs were plotted in R (R Core Team, 2021) using the package “lattice” (Sarkar, 2021). For most storms, a fixed, site-specific flow range was assigned as a common scale for graphs. The largest storms from all streamgages, those that would not plot properly on the fixed scale for the streamgage in question, were analyzed as a group and plotted using the lattice autoscaling algorithm. The maximum discharge from the 50th ranked storm at a streamgage was plotted on the graphs as a reference line. Inflections were identified onscreen using “lattice,” and codes developed as unique identifiers for the inflections were copied and pasted into a Microsoft Excel spreadsheet to associate them with time and other relevant information. The time at the beginning of each hydrograph event was subtracted from the time at the end of the event in Microsoft Excel.
All three types of hydrograph events were identified at and included in analyses for all four streamgages. However, hydrograph events were not identified for all storms. When a complex storm had multiple rises and recessions in precipitation that met the criteria for a continuous storm, multiple hydrograph events were identified, and hydrograph time metrics were computed multiple times. Hydrograph events from different times during a long, complex storm were judged to represent different antecedent conditions. The amount of water in storage in the basins at the beginning of stormflow is the most important consideration concerning antecedence, not the amount of water in storage hours or days earlier.
In general, 7-minute running averages were used to compute time metrics for Fairplain, Ripley, and Wallback—the streamgages with flow data collected at 1-minute intervals. Running averages were computed as the unit value at the nominal measurement time, the three unit values before the nominal measurement time, and the three unit values following the nominal measurement time. High flows inside culverts were turbulent, and standing waves moved back and forth across the AV sensors. The 1-minute interval data were affected by the turbulence and therefore noisy, which masked patterns. Running averages of several durations, from 3 to 9 minutes, were examined, but 7-minute running averages were determined to be the best compromise among resolution, responsiveness, and smoothing.
At Hico, the flow data collected at 5-minute intervals from the NTRAN were not smoothed and were used as the flow record throughout the study period at this streamgage. At Wallback, when 1-minute interval data from the AV sensor were available, they were used with smoothing. Periods of missing data from the AV sensor, however, used 5-minute interval data from the NTRAN, which was used without smoothing. At both streamgages, the use of 5-minute interval data instead of 1-minute interval data introduced some uncertainty when determining time metrics because the greater the period between measurements meant a greater chance of missing the true peak or inflection. At Wallback, the 5-minute interval measurements collected by the NTRAN had many of the same problems seen in the 1-minute interval measurements from the AV sensor, but without the dense cloud of points to smooth that increased uncertainty in the timing of inflections in hydrographs from this streamgage.
There were 14 exceptions to the 7-minute averaging rule when 1-minute data were available. In 6 storms at Ripley and 8 storms at Fairplain, intense precipitation at the beginning of a storm caused a rapid initial rise in flow less than 7 minutes after precipitation began and, therefore, before enough values were available to compute a running average. For these storms, three 1-minute observed values were added at the beginning of stormflow so that time-to-rise calculations would be accurate (Messinger and Scott, 2024; table 1).
A few times to rise at Fairplain might be slightly, but incorrectly, faster than at other streamgages because the streamgage had a high threshold for minimum flow, and the time needed to bring flow above the detection level is not included in events from this streamgage. Times to rise at Hico might be slightly slower than the other streamgages because flows went all the way to zero, and a few times to rise might include a measurement at the beginning of a hydrograph that would not have been recorded at the other streamgages. Computation of times to rise began at the absolute beginning of stormflow only a few times; notable exceptions were the storms for which the 7-minute averages were supplemented with unit flow values at the beginning of the storm.
The rise and recession metrics were unreasonably long for nearly all storms if they were computed from either the initial increase in flow at the beginning of a storm to the absolute peak or from the absolute peak to pre-stormflow magnitudes. The time from initial rise to absolute peak was not determined for all storms but was more frequently measured in hours or even days than in minutes. Time to rise was highly inconsistent among storms because the absolute peak of a storm could be delayed depending on several factors including how many spates of rain came, time between the spates, and variations in precipitation intensity. Times to rise measured in hours or days were judged to be unrepresentative of how long water took to move through the small basins of interest in this study.
Instead of treating the entire time that flow rose during a complex storm or series of storms as representative of Tc, time to rise and time to recede were determined from inflections on the rising and falling limbs, respectively, of hydrographs (fig. 5; table 3 in Messinger and Scott, 2024). A rise, for purposes of delineating a hydrograph event, was counted as the time where flow clearly inflected upward in response to a spate of intense rain until a point where the slope of that rise caused by that spate of rain levelled or decreased. To be included in analyses, the rise needed to be (1) steady, (2) clearly the result of a specific spate of rain, (3) visually distinct, and (4) representative of a meaningful change in flow magnitude. A distinct rise as a section of a rising limb of a hydrograph should represent Tc because the initial rise represents the arrival of the first stormflow and the slope changes at the end of the rise because water from that spate has traveled from the most remote part of the basin to the outlet. Time to recede was assessed like time to rise, with the additional constraint that when repeated or sustained rain fell during the recession and caused flow to rise or remain stable, the event was excluded. The time between PI-to-RI was defined as the difference between a (1) final inflection on the hyetograph before a visually distinct storm peak and (2) the inflection on the receding limb of the hydrograph from a steep decrease in stormflow to a part of the hydrograph with a flatter slope. The inflection in the recession represents the point where stormflow from the most hydraulically remote point in the basin passes through the outlet. Generally, this recession inflection was selected at the first unit flow value with zero change in flow that followed the peak. Exceptions included extended hydrographs, when flow remained near peak due to continued steady rain; some complex hydrographs, when the basin received rain before the hydrograph appeared to reach an inflection; hydrographs when excessive turbulence or surges in flow at the recorder masked changes in flow, even after smoothing; and peaks that represented generally minor rises that exceeded the flow threshold because of high initial base flow at the beginning of stormflow. All precipitation inflections were chosen visually. The inflection in the plot of cumulative precipitation, referred to as “precipitation inflection” on figure 5, marks a decrease in storm intensity and is taken to represent the end of excess precipitation (fig. 5). Excess precipitation is defined as precipitation that exceeds available detention storage in the basin and, therefore, results in stormflow (Black, 1991). The primary quality-assurance metric for precipitation inflections was the amount of precipitation received during the storm segment after the inflection. Values for post-inflection precipitation ranged from 0 to 0.28 in. (table 4 in Messinger and Scott, 2024). Hydrograph events that included post-inflection precipitation exceeding 0.10 in. were identified and ultimately included in analyses.
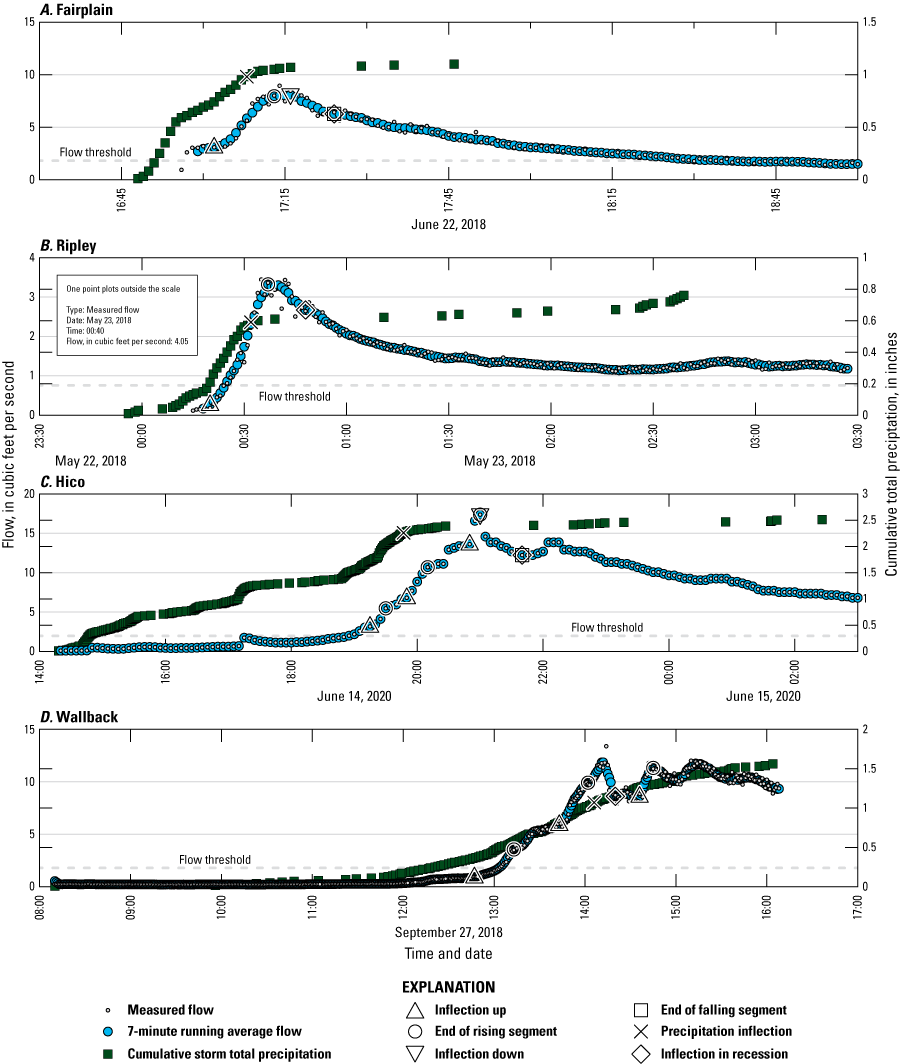
Graphs showing flow, cumulative precipitation, and inflections for hydrograph events during selected storms at the four study sites in West Virginia: A, U.S. Geological Survey (USGS) station number (no.) 03159718 Grasslick Creek tributary above Interstate 77 near Fairplain, West Virginia, June 22, 2018; B, USGS station no. 03159823 Grass Run tributary above Interstate 77 near Ripley, West Virginia, May 22, 2018; C, USGS station no. 03190307 Hedricks Creek tributary above U.S.–19 near Hico, West Virginia, June 14, 2020; and D, USGS station no. 03197062 Cookman Fork at Interstate 79 near Wallback, West Virginia, September 27, 2018.
Hydrograph events were included in analyses if (1) their maximum values were large enough to be among the 50 largest peaks at each streamgage; (2) the event was not affected by snow; (3) the slope of the rise or recession was consistent and steady during a relevant part of an event; (4) the flow record during the hydrograph event was complete without estimated values; (5) the event in question represented a meaningful change in flow; (6) rain that continued while flow receded was minimal and did not appear to interrupt recessions with secondary rises in flow; and (7) the changes between successive unit flow measurements during the hydrograph event were either primarily increases or decreases, indicating that it was primarily stormflow, in contrast to events that were largely stable, which characterized the minor rises and recessions that exceeded flow thresholds only because they began when base flow was already high. Quality-assurance metrics were developed and computed to show how well the hydrograph events met these criteria (Messinger and Scott, 2024). Hydrograph events provisionally identified through inspection of graphs, but that failed to meet quality-assurance criteria, were not included in summary statistics or further analyses.
The quality-assurance metrics that confirmed that hydrograph events had large enough maximum flow values, were affected by snow, or had a complete flow record applied to all three types of hydrograph time metrics. Thresholds for flows were used because the purpose of the study was to characterize high flows. Snow-affected storms were excluded because limited information was available for when the snow melted in the basins or for how much an effect the melted snow had on runoff timing. Days when snow was recorded by the National Oceanic and Atmospheric Administration climate station nearest each streamgage (either Charleston, Beckley, or Gassaway) were identified. Precipitation records for the next storms after snow was recorded were assumed to include snowmelt and excluded from analysis. A complete or mostly complete flow record was needed to identify inflections on hydrographs because estimated values were made by linear interpolation, making them unsuitable for identifying inflections.
Quality-assurance metrics for rises and recessions included the number of increases in unit flow values during a recession, the number of decreases in unit flow values during a rise, and the number of unit flow values with zero change during both types of events. For computing these quality-assurance metrics, a unit flow value was an individual unit of flow either at a 1-minute increment in the 7-minute running average for streamgages and periods where flow data were available at 1-minute increments or a 5-minute increment for the streamgages and periods for which flow data were available at 5-minute increments. Recessions could have no more than three unit rises, rises could have no more than three unit decreases, and no more than 25 percent of unit value changes in flow equal to zero.
A meaningful change in flow was evaluated by comparing the initial and final unit value of flow for each event that was delineated (Messinger and Scott, 2024). This metric was also used to determine if the change in flow was sufficient for inflections to be distinct throughout the hydrograph event. Meaningful changes in flows increased by 25 percent or more during a rise, decreased by 10 percent or more during a recession, and had to equal or exceed 25 percent of the maximum flow during a PI-to-RI event.
In general, hydrograph events were subjectively easier to delineate from simple hydrographs than from extended or complex hydrographs. Events from simple hydrographs were more consistent with delineation criteria than events delineated from extended hydrographs, but about the same in consistency as complex hydrographs (Messinger and Scott, 2024). For simple hydrographs, 13 of 51 provisionally identified events were inconsistent with delineation criteria. For extended hydrographs, 24 of 51 provisionally identified events were inconsistent with delineation criteria, whereas 38 of 148 provisionally identified events from complex hydrographs were inconsistent with delineation criteria.
Judgments made about how to treat quality-assurance metrics for hydrograph events affected Tc computation at all streamgages. Metrics were developed for this project after initial graphical delineation of hydrograph events. The metrics were developed to quantify the criteria used to delineate events and used to eliminate events that analysts were not fully confident met delineation criteria. Several of the events that were provisionally delineated but later excluded were inconsistent with multiple criteria.
Time of Concentration
All the time metrics used to compute Tc varied substantially among storms at all streamgages (table 6). All three metrics were slower at Hico than they were at any of the other streamgages. At Hico, average time to rise and time to recede were 34 and 32 minutes, respectively. The average time from PI-to-RI at Hico, 38 minutes, was the longest for any of the characteristics at any of the streamgages. Hico had the most variation of any streamgage in its time to rise and PI-to-RI values; PI-to-RI had the greatest range of values of any time metrics at any streamgage (fig. 6).
Table 6.
Time of concentration, in minutes, for the four streamgages in West Virginia used for this study during the 2018–20 water years.[PI-to-RI, precipitation inflection to recession inflection; n, number; Fairplain, U.S. Geological Survey (USGS) station number (no.) 03159718 Grasslick Creek tributary above Interstate 77 near Fairplain, West Virginia; Ripley, USGS station no. 03159823 Grass Run tributary above Interstate 77 near Ripley, West Virginia; Hico, USGS station no. 03190307 Hedricks Creek tributary above U.S.–19 near Hico, West Virginia; Wallback, USGS station no. 03197062 Cookman Fork at Interstate 79 near Wallback, West Virginia; und, undefinable because value would have to be divided by zero]
Boxplots showing ranges of time of concentration values for four streamgages in West Virginia, 2018–20. A, precipitation inflection to recession inflection; B, time to recede; and C, time to rise. >, greater than; <, less than.
Wallback had the second slowest time metrics of all the streamgages. Average time to rise and time to recede were similar, 23 and 25 minutes, respectively. As at Hico, the average time from PI-to-RI for Wallback was greater than the time to rise or time to recede, 32 minutes. Time metrics at Wallback varied less than Hico, but more than Fairplain and Ripley.
Time metrics were similar at Fairplain and Ripley. At these two streamgages, average time to rise was 18 and 19 minutes, average time to recede was 14 and 16 minutes, and average time from PI-to-RI was 22 and 27 minutes, respectively. Ripley had the smallest standard deviation in time to rise and time from PI-to-RI among all streamgages, whereas Fairplain had the smallest standard deviation in time to recede.
Hydrograph events that had been provisionally delineated but failed to meet the quality-assurance criteria were examined to see if they were systematically different from those that met the criteria (table 6). Some differences were negligible or slight. At Fairplain, average time to recede was identical, and PI-to-RI was 3 minutes shorter for hydrograph events that failed to meet quality assurance criteria than for those that met criteria. At Ripley, average time to rise was 1 minute longer for hydrograph events that failed to meet quality-assurance criteria than for those that met criteria. At Wallback, average time to recede was 1 minute shorter for hydrograph events that failed to meet quality-assurance criteria than for those that met criteria. Other differences were greater, and for them, the differences between the two groups of hydrograph events were inconsistent in direction. At Fairplain, time to rise was 8 minutes longer for hydrograph events that did not meet quality-assurance criteria than for those that met criteria. At Ripley, PI-to-RI was 6 minutes shorter, but time to recede was 9 minutes longer for hydrograph events that did not meet quality-assurance criteria than for those that met criteria. Time to rise (13-minutes difference) and PI-to-RI (27-minutes difference) at Wallback, however, were both substantially longer for storms that failed to meet criteria, and the storms that caused most of the difference between the categories were unrepresentative of the largest storms at this streamgage. The difference in time to rise at Wallback was primarily because of a 90-minute rise that was affected by snow during a storm that began on January 23, 2019, and the difference in PI-to-RI was because of a 65-minute event that included more than 25-percent unit flows with zero change and little overall change in flow, during a storm that began on December 16, 2019.
At Hico, storms that were excluded from the Tc summaries were generally longer than those that met all criteria for inclusion. These storms did not meet the criterion that fewer than 25 percent of unit flows had zero change (10 of 57 provisionally identified events) and included some major storms. Among excluded storms, average time to recede was only 3 minutes longer than among included storms, but time to rise was 17 minutes longer and PI-to-RI was 127 minutes longer. Storm hydrographs at Hico could be separated into two distinct groups, those that rose quickly and those that rose slowly. Many of the slow rises started with either high base flow or were caused by steady light or moderate rain. Some of them, though, were generated by sustained hard rain, including the second largest peak flow measured at this streamgage, 7.71 ft3/s on September 27, 2018. Slow rises frequently rose and receded by less than the resolution of the water-level recorder during a time step between measurements, which was expressed as successive unit flow values with zero difference. The fast rises resulted from intense rain, and sometimes they were followed by a smaller, broader secondary peak that resembled the slow rises. Two storms from September 2018, for which only 15-minute data were available, were examples of storms with intense early rain (0.36 in. or 1.44 inches per hour (in/hr) for a storm that began on September 8, 2018, just before midnight, and 0.40 in. or 1.60 in/hr for a storm that began on September 10, 2018) that resulted in a small initial rise followed by broad, sustained secondary peaks that exceeded the initial peak (fig. 7). These major storms, and two other major storms from the same period (a second storm segment on September 9 and a storm on September 27), were not included in the Tc computations because the 15-minute precipitation data lacked enough resolution to delineate hydrograph events that were comparable to others in the study. If the events from these storms that met the other criteria were included, however, they would change the average times for PI-to-RI from 38 to 64 minutes and time to rise from 34 to 44 minutes. Time to recede would be unchanged, because no events were delineated for these storms that met other criteria. The largest storm at Hico, on June 5, 2020, was a quick storm with intense rain that caused a large immediate peak; the peak had a time to rise of 10 minutes, a time to recede of 15 minutes, and a PI-to-RI of 6 minutes. Either a quick, intense storm or a protracted storm could cause a large flood in this basin.
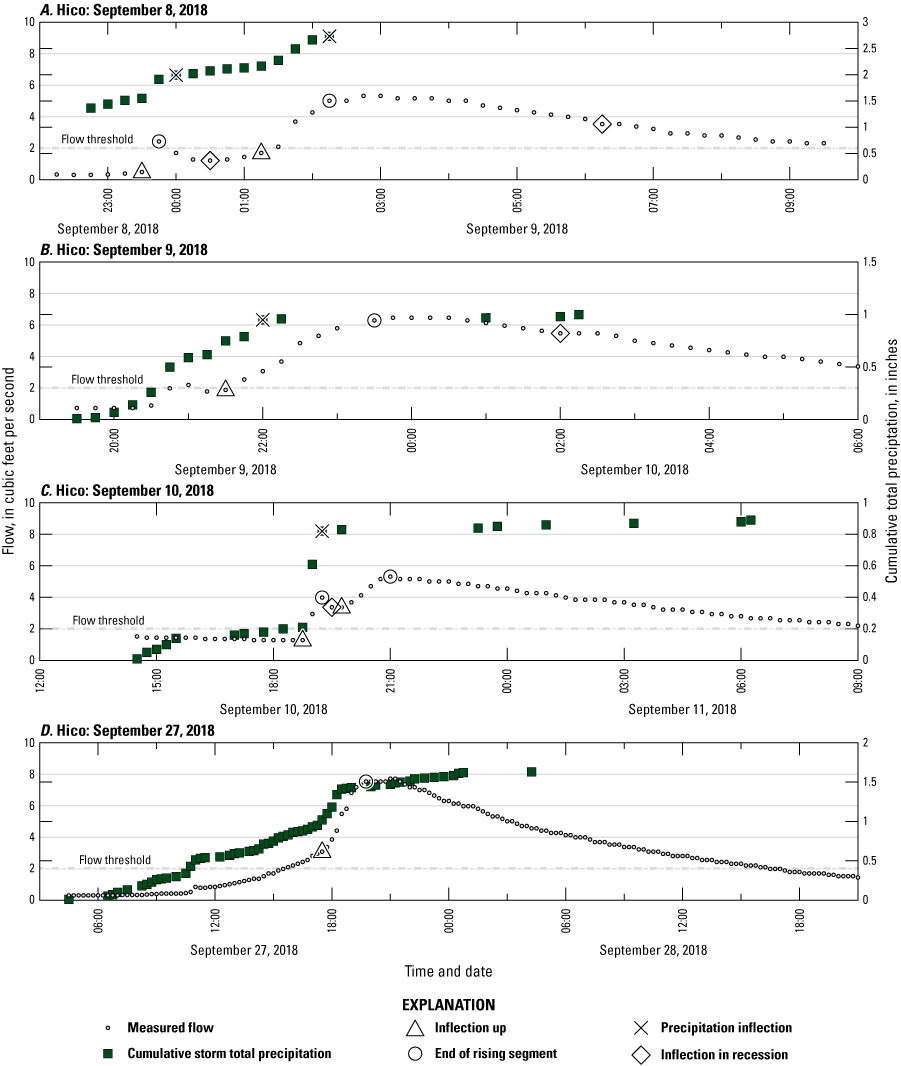
Graphs showing cumulative precipitation, flow, and inflections for hydrograph events for selected storm segments at U.S. Geological Survey station number 03190307 Hedricks Creek tributary above U.S.–19 near Hico, West Virginia: A, September 8, 2018; B, September 9, 2018; C, September 10, 2018; and D, September 27, 2018.
At most streamgages, differences among the time metrics were not statistically significant. The Kruskal-Wallis test was used to explore possible differences among the three time metrics within streamgages. Probability values (p-values) were 0.281, 0.012, 0.102, and 0.899 for Fairplain, Ripley, Wallback, and Hico, respectively; these values indicate that differences among the time metrics were significant for Ripley (values <0.05 being significant and values >0.05 being not significant), but not for the other streamgages.
Further testing for significant differences within streamgages was done with the paired Wilcoxon rank-sum test and Dunn’s all-pairs test, using Benjamini and Hochberg (BH) and Bonferroni false-discovery corrections to adjust p-values for the possibility of finding a falsely significant difference in repeated post-hoc hypothesis testing (Helsel and others, 2020). Most pairings of time metrics from the same streamgage were not significantly different from each other. The paired Wilcoxon rank-sum test with BH false-discovery correction was used to test for differences in all pairwise combinations of time metrics within streamgages. Two p-values were <0.05, both at Ripley, between time to rise and PI-to-RI (p=0.025) and between time to recede and PI-to-RI (p=0.011). P-values ranged from 0.15 to 0.87 for the other within-streamgage pairings of time metrics. Dunn’s all-pairs test with Bonferroni false-discovery correction was used to test if one time metric was different from the other time metrics at each streamgage. The same pairings of time metrics had p-values <0.05 as for the Wilcoxon rank-sum test: between time to rise and PI-to-RI (p=0.040) and between time to recede and PI-to-RI (p=0.012) for Ripley. For the other within-streamgage combinations of time metrics, p-values ranged from 0.11 to 1.00.
The same analytical approaches used to determine differences within streamgages were taken to explore possible differences among streamgages for the three time metrics. The Kruskal-Wallis test found that p-values were 0.017, 0.057, and 0.238 for time to recede, time to rise, and PI-to-RI, respectively. These values indicate that differences among streamgages were likely for time to recede, and possible for time to rise, but that they were unlikely for PI-to-RI.
Further testing confirmed that most pairings of streamgages were not significantly different from each other for any of the three time metrics, indicating that variance within time metrics at each streamgage exceeded differences among streamgages. According to paired Wilcoxon rank-sum tests with BH false-discovery corrections, p-values ranged from 0.14 to 0.85 for pairwise combinations of sites. Dunn’s all-pairs test with the Bonferroni false-discovery correction showed that time to recede was significantly different for one pairing of streamgages, Hico and Fairplain (p=0.036), but for all the other combinations of streamgages, p-values ranged from 0.077 to 1.000.
Hydrograph Time Metrics Compared to Storm Characteristics
The time metrics used to compute Tc were compared to total storm and storm segment precipitation, maximum streamflow during the storm segment, and precipitation intensity terms representing 1-minute, 5-minute, 15-minute, and 60-minute durations. Relations among time metrics and other storm characteristics were inconsistent within and among streamgages (figs. 8, 9, 10, 11; table 7). Precipitation intensity was the storm characteristic most often significantly correlated (p<0.05) with Tc. At least one of the precipitation intensity terms was significantly correlated with at least one time metric at three of the streamgages (table 7). All the significant correlations were negative, indicating that Tc was faster with the increasing values of storm characteristics.
Table 7.
Spearman's rho correlation coefficients and probability values (p-values) for correlations between time of concentration and maximum values of selected characteristics of selected storms for the four streamgages in West Virginia used for this study from October 2017 to July 2020.[PI-to-RI, precipitation inflection to recession inflection; rho, Spearman's rho correlation coefficient; p, for correlations, the probability of observing a correlation as strong or stronger as the one observed; n, number of observations; Fairplain, U.S. Geological Survey (USGS) station number (no.) 03159718 Grasslick Creek tributary near Fairplain; Ripley, USGS station no. 03159823 Grass Run tributary near Ripley; Hico, USGS station no. 03190307 Hedricks Creek tributary near Hico; Wallback, USGS station no. 03197062 Cookman Fork near Wallback]
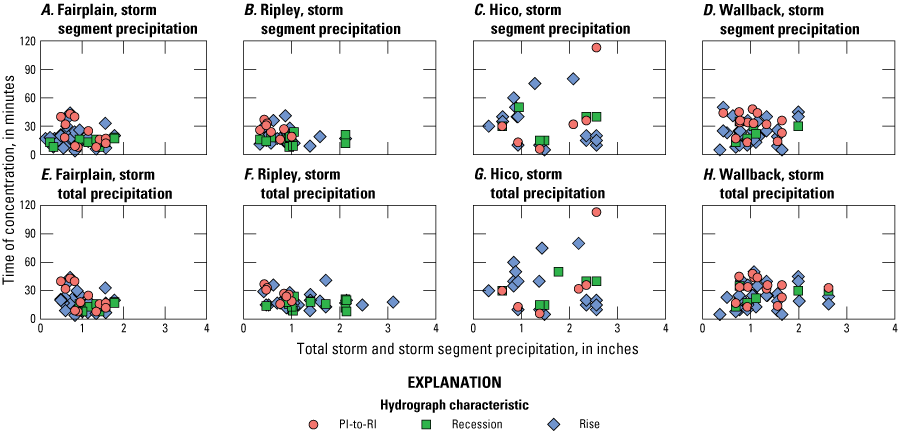
Graphs showing hydrograph characteristics and total storm and storm segment precipitation during selected storms at four streamgages (A–H) in West Virginia from October 2017 to June 2020. PI-to-RI, precipitation inflection to recession inflection.

Graphs showing hydrograph characteristics and maximum running total precipitation during selected storms for 5−, 15−, and 60−minute intervals at four streamgages in West Virginia (A–L) from October 2017 to July 2020.
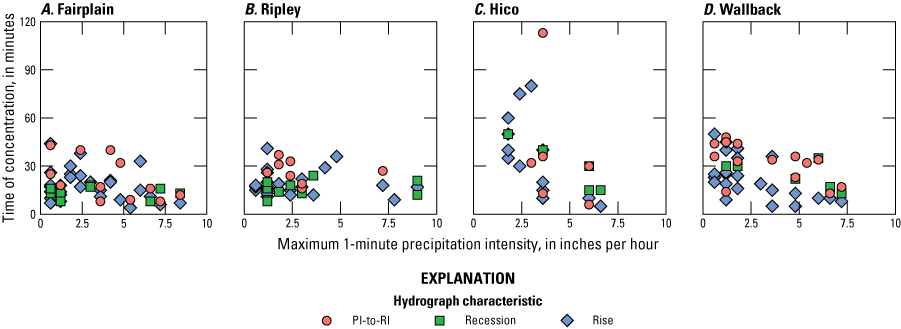
Graphs showing hydrograph characteristics and maximum 1−minute precipitation intensity during selected storms at four streamgages in West Virginia from October 2017 to July 2020.
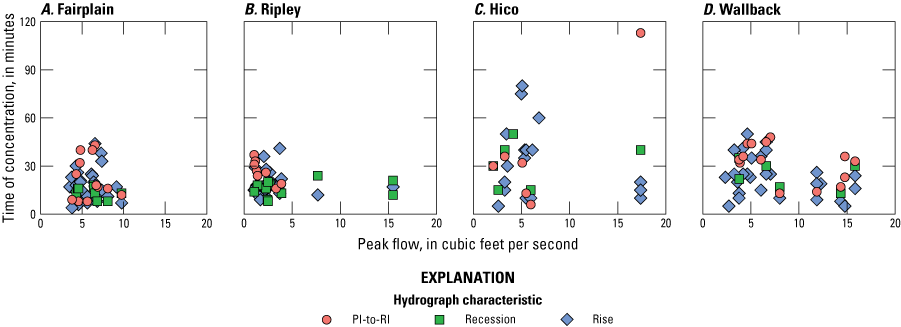
Graphs showing hydrograph characteristics and peak flow during selected storms at four streamgages in West Virginia from October 2017 to July 2020.
At Hico, all three time metrics were significantly correlated (p<0.05) with one or more precipitation intensity terms; the significant correlation coefficients ranged from −0.570 to −0.985. At Wallback, PI-to-RI and time to rise were significantly correlated to all the precipitation intensity terms; the significant correlation coefficients ranged in value from −0.454 to −0.598. None of the other storm characteristics (total storm precipitation, storm segment precipitation, and streamflow) were significantly correlated with Tc at either Hico or Wallback, and the correlation coefficients included both positive and negative values (table 7).
At Fairplain, PI-to-RI was significantly correlated (p<0.05) with total storm precipitation and storm segment precipitation and all the precipitation intensity terms. At Ripley, PI-to-RI was significantly correlated with total storm precipitation and maximum streamflow for the storm segment. Correlations between time to recede and time to rise for Fairplain and Ripley included both positive and negative values and were generally weak; none were significant.
Stronger relations between time metrics and precipitation intensity at Hico than at the other streamgages may result from a greater range in Tc values computed at this streamgage, which is related to the differences in the two populations of hydrographs and how the basin responds differently to high-intensity and low-intensity precipitation. Wallback also had some short Tcs for some intense storms that resulted in large peaks. Ripley and Fairplain generally had a smaller range of Tc values than the two larger basins, though some of the shortest times at these two streamgages were associated with some of the most intense storms. Separate processes may have generated flows at Ripley and Fairplain in response to storms with distinct characteristics, but there was little variability in Tc between flows generated by different processes.
The general patterns between time metrics, precipitation, and peak flows may be unclear because of this study’s short period of record and the small number of large storms available for analysis. Peak flow magnitudes were weakly related to total precipitation and precipitation intensity among the storm segments (storm segments were created to help delineate hydrograph events; fig. 12). This weak relation is likely because total storm precipitation and precipitation intensity were only weakly related to each other, especially during moderate storms. At three streamgages, the largest peak streamflows were measured during the storms with the greatest precipitation intensity. If the storms with the greatest precipitation intensity were excluded from analysis, correlations between peak streamflow and precipitation intensity were weak. Among storms with moderate total precipitation, the most intense storms did not necessarily produce the greatest total precipitation, and either a short, intense storm or a long storm with moderate intensity might produce similar peak magnitudes. More moderate storms than large storms were included in the analysis. Only a few storms had spates of rain that exceeded the 2-year or 5-year recurrence interval for a given duration (table 4). Although these particular storms generally caused the largest peak streamflows at each streamgage, they may or may not have been representative of the full range of large storms.
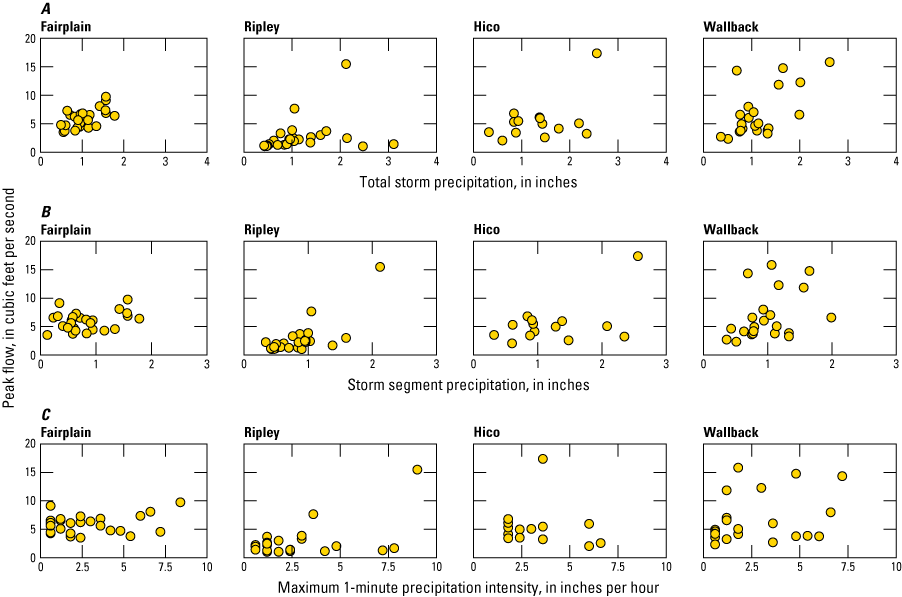
Graphs showing peak flow and A, total storm precipitation; B, storm segment precipitation; and C, maximum 1−minute precipitation intensity during selected storms at the four streamgages used for this study in West Virginia from October 2017 to July 2020.
Measured and Estimated Time of Concentration
Times of concentration that were estimated during site selection were compared to the measurements made during the study. The estimates are compared to time to rise, time to recede, and PI-to-RI. Comparisons are made among time metrics at the same streamgage and among streamgages.
Estimated Time of Concentration
Time of concentration (Tc) and peak discharge were estimated for a design storm with a recurrence interval of 1, 2, 5, 10, 25, 50, and 100 years using the guidance for application of the Rational Method at each of the watersheds from the WVDOH drainage manual (Holmes and Chintala, 2007; table 8). Two sets of estimates were made for each watershed. Both estimate sets examined the sheet-flow, shallow-concentrated-flow, and channel-flow segments from the most hydraulically distant point in the watershed. The individual channel-flow segments were partitioned by meaningful changes in the stream slope and points of confluence with shorter contributing channels within a watershed. The two sets of estimates differed because different methods were used to estimate cross-section geometry for the channel-flow segments. One set utilized an initial estimate of the geometry based on a photo taken at the prospective road crossing, engineering experience, and engineering judgment. The second set utilized bankfull-channel characteristics to estimate the geometry. These characteristics were based on previously published regional-regression equations developed for the Appalachian Plateaus physiographic province in West Virginia (Messinger, 2009). The Tc values (for the two sets of estimates common to all four streamgages) were used to obtain a precipitation intensity for the design-storm recurrence intervals. This intensity value was based on National Oceanic and Atmospheric Administration Atlas 14 (Bonnin and others, 2006). The design-storm recurrence interval affects the sheet-flow segment travel time, causing a minor variance in overall Tc.
Table 8.
Initial and adjusted estimates for time of concentration and peak flow for design storms at selected recurrence intervals for the four streamgages in West Virginia used for this study.[Methods for estimating time of concentration are described in Holmes and Chintala (2007). Tc, time of concentration; Tc sheet, time of concentration for the sheet flow segment; ft3/s, cubic foot per second; Fairplain, U.S. Geological Survey (USGS) station number (no.) 03159718 Grasslick Creek tributary above Interstate 77 near Fairplain, West Virginia; Ripley, USGS station no. 03159823 Grass Run tributary above Interstate 77 near Ripley; Hico, USGS station no. 03190307 Hedricks Creek tributary above U.S.–19 near Hico, West Virginia; Wallback, USGS station no. 03197062 Cookman Fork at Interstate 79 near Wallback, West Virginia]
For the design storm with a 2-year recurrence interval, initial Tc estimates ranged among sites from 17.2 minutes at Fairplain to 51.1 minutes at Hico (table 8). The Tc estimates derived from bankfull-channel characteristics adjusted by regional equations were longer for Fairplain, Ripley, and Wallback, but shorter for Hico. For the 2-year storm, they ranged from 19.5 minutes at Fairplain to 40.9 minutes at Hico. Differences within streamgages but among storm recurrence intervals were less than differences among streamgages. The Tc estimates differed by less than 3 minutes at each streamgage across the range of design storms, and shorter Tc times were estimated for larger, less frequent storms.
In the initial estimate, flows estimated for the 2-year storms ranged from 16 ft3/s at Ripley to 92 ft3/s at Wallback. Flows estimated using bankfull-channel characteristics adjusted by regional equations were slightly smaller at each design flow than the initial estimates for Fairplain (92 to 95 percent of the initial), Ripley (94 to 96 percent of the initial), and Wallback (83 to 84 percent of the initial), but slightly larger for Hico (114 to 118 percent of the initial). Peak flows from the 100-year design storm are between 2.2 and 2.5 times larger than peak flows from the 1-year design storm of values derived from both estimation procedures for all streamgages.
Comparison Between Estimated and Measured Time of Concentration
All Tc estimates for all design flows for both estimation procedures were within the range of observations for their respective streamgage; design flows for only the 10-year flood are shown for clarity (fig. 13). All estimates were also within one standard deviation of the overall average for their streamgage, computed as the average of the averages of the three time metrics. Overall averages and averaged standard deviations of the Tc values for the three time metrics were 18 and 10 minutes for Fairplain, 21 and 7 minutes for Ripley, 35 and 24 minutes for Hico, and 27 and 11 minutes for Wallback, respectively. The general pattern contains a great deal of variation, however.
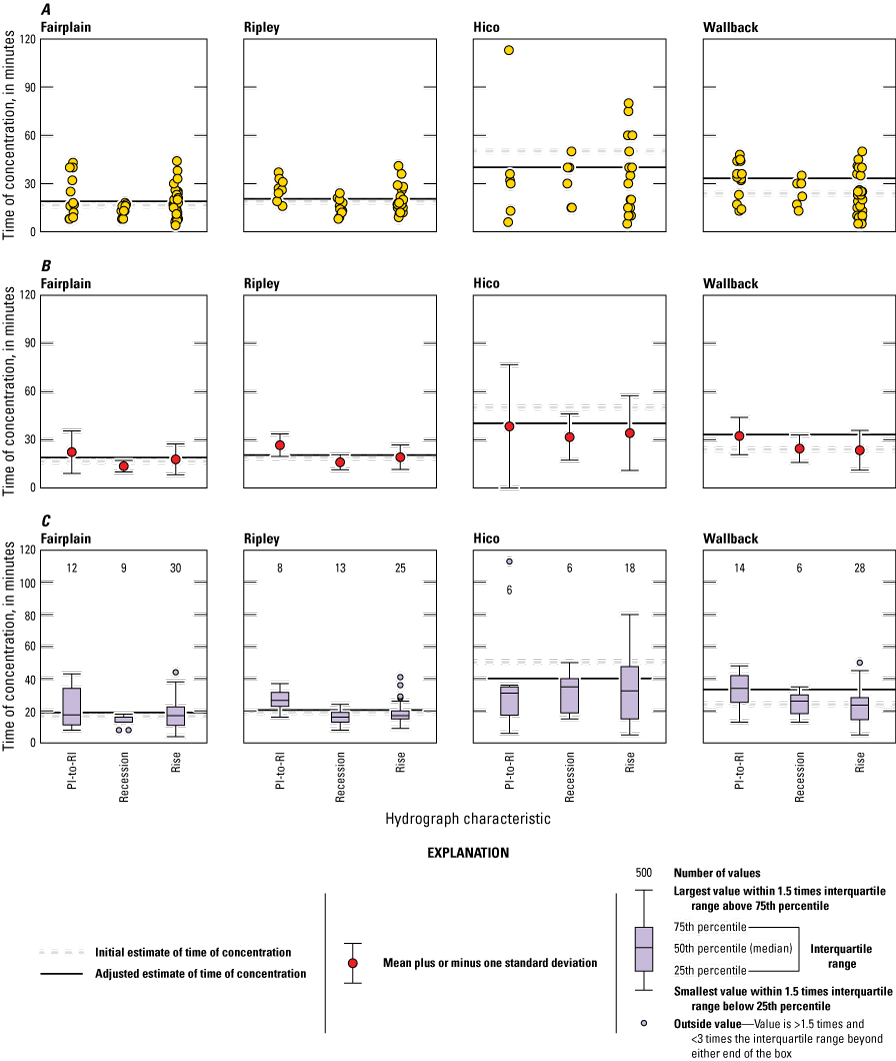
Graphs showing estimated time of concentration for the 10−year storm compared to measured values from selected storms for four streamgages in West Virginia from October 2017 to July 2020: A, jitter plot showing all measured values for all three time metrics for all four streamgages; B, means and standard deviations of each set of time metrics for all four streamgages; and C, boxplots of each set of time metrics for all four streamgages. >, greater than; <, less than; PI-to-RI, precipitation inflection to recession inflection.
Fairplain had an average Tc value that matched Tc estimates from the initial procedure for frequent, moderate storms, whereas the Tc value for Ripley and Wallback had the closest match with estimates from the initial procedure for infrequent, large storms. Adjusting the initial estimate with regional bankfull-channel characteristics provided shorter and less accurate Tc estimates for Fairplain, Ripley, and Wallback. For Hico, however, adjusting the Tc estimates made them longer and closer to the overall measured averages.
None of the three time metrics had a consistent relationship with the estimates. Time to rise and time to recede were generally similar, both among streamgages and to each other, as demonstrated by the testing discussed in the “Time of Concentration” section. Averages for time to rise and time to recede were shorter than PI-to-RI for Fairplain, Ripley, and Wallback (fig. 13). For Fairplain and Ripley, average PI-to-RI was longer than both estimates; for Hico, average PI-to-RI was slightly shorter than both estimates; and for Wallback, average PI-to-RI was longer than the initial estimate but slightly shorter than the adjusted estimate. All Tc estimates were within one standard deviation of the mean for time to rise. Most estimates for time to recede were within one standard deviation of the mean, except for regionally adjusted estimates for Fairplain and initial estimates for Hico. Hico was different from the other basins. Average time from the PI-to-RI, which was longer than time to rise and time to recede, had the best match with estimates. The range of initial estimates for Hico were more than one standard deviation from the mean of both time to rise and time to recede. At Hico, however, the incomplete storms in September 2018 appeared to include hydrograph events with long enough times that, if the record had been complete and the events were included in analyses, could have lengthened the average, median, and interquartile range (IQR) for PI-to-RI and time to rise.
Average Tcs were largely derived from storms that had magnitudes less than those for the 1-year recurrence-interval storm (table 4). Correlations between individual hydrograph time metrics and precipitation intensity were weak everywhere but Hico and, to a lesser extent, at Wallback. At all streamgages, some of the shortest Tcs were for some of the most intense storms, which included some of the largest peak flows in the study (fig. 12). Estimated Tc values decreased slightly with increasing storm magnitude and intensity, but all estimates were developed for storm intensities that exceeded the 1-year recurrence interval.
Averages and standard deviations, both overall and of the separate time metrics, are useful analytical tools to compare broad patterns. However, these measures of variance and central tendency can be affected by outliers (Helsel and others, 2020). Some of the combinations of time metrics and streamgages have apparent outliers among small numbers of observations. The small number of observations make it difficult to assess whether the apparent outliers are truly rare or are rare only among observations from a short study period. The interquartile range (IQR) represents 50 percent of the observations in a group, the range between the 25th and 75th percentiles, and is a commonly used measure of variance that is resistant to outliers.
Predicted values for the 10-year storm, one of the key recurrence intervals in design, were within the IQR for 4 of 12 combinations of streamgages and time metrics (fig. 13). Two of these observations were for observed time metrics for Fairplain, one was for Wallback, and the other was for Hico. At Ripley, which was the streamgage where time metrics were significantly different from each other, the adjusted prediction was not within the IQR for any of the time metrics, but it was shorter than one IQR and longer than the other two. The adjusted prediction was shorter than the IQR for one time metric at one streamgage (PI-to-RI at Ripley), and it was longer than the IQR for seven combinations of streamgages and time metrics.
Comparisons between predictions and individual time metrics showed differences. Adjusted predictions of Tc were within the IQR of PI-to-RI for Fairplain and Wallback, longer than the IQR of observed PI-to-RI at Hico, and shorter than the IQR of observed PI-to-RI at Ripley. The adjusted predictions of Tc were within the IQR of time to rise for Hico and Fairplain but were longer than the IQR of time to rise for Ripley and Wallback. The IQR for time to recede was shorter than the adjusted prediction for each streamgage.
Five of the eight adjusted predictions of Tc that were outside the IQR for their combination of streamgage and time metric were for combinations that had fewer than 10 observations, whereas all four of the adjusted predictions that were within the IQR for a time metric at a streamgage were for combinations with more than 10 observations. The small number of observations for some of the metrics may indicate that the study did not run long enough to provide reliable estimates of median and IQR. The study ran long enough, though, to confirm that the time metrics generally have high variance and wide range.
As a metric, PI-to-RI seems to match one of the most used conceptual definitions of Tc, the time between the end of excess precipitation and the end of stormflow. Concerns about PI-to-RI include whether timing of precipitation can be adequately measured for a basin with a single rain gage at the outlet, whether inflections in the hyetograph truly represent the end of excess precipitation, and whether using two different datasets results in unacceptable increases in measurement error, particularly in time measurement. The sensors used in this study were synchronized with GPS clocks so that errors in time measurement were negligible, addressing a concern in studies that used older technology. However, use of a single rain gage might be a source of error in timing of precipitation throughout the basins relative to changes in streamflow.
Time to rise and time to recede avoid some of the questions about differences in precipitation timing across basins. Although basins in this study were small, precipitation across them was not uniform in space and time. To accept the timing of storms measured with a single rain gage at the basin outlet, it is necessary to assume that differences in timing across the basins were inconsequential. Even these hydrograph-derived metrics incorporated precipitation data, however. Delineation of hydrograph events for time to rise and time to recede included examining hyetographs to exclude recessions complicated by excessive rain and rises that were interrupted or extended by breaks in rain.
Time to recede is intended to quantify the same conceptual definition as PI-to-RI, the time between the end of excess precipitation and the end of stormflow, without requiring detailed precipitation data. It is to be expected that time to recede was faster than PI-to-RI; as an individual hydrograph event in a single storm, it could only be longer than PI-to-RI for that storm if the precipitation inflection follows peak streamflow. Time to recede may represent Tc well if it meets the assumption that in small basins, peak flow is a good surrogate for the end of excess precipitation. For storms measured in this study, it was an imperfect surrogate. For all storms analyzed in this study, precipitation intensity decreased from storm maxima before flows peaked, although in many of the most intense storms, only a minute or two before peaks. Decreases in precipitation intensity may not be ideal measures of the end of excess precipitation in storms when rain continues, but they would seem to be better measures than the timing of peak flow. Additionally, the number of observations for time to recede was generally small. Only 34 such events were identified for the entire study. Time to recede was the least frequently delineated time metric for Fairplain, Hico, and Wallback. This metric is useful to consider, but it probably represents a secondary line of evidence, rather than strong evidence that the true Tc values for these basins are shorter than estimates.
The predictions of peak flow for selected precipitation intensities and durations did not match observed peak flows as accurately as predictions matched observations for Tc. Maximum peak flows during the study period were 12.7, 16.5, 17.4, and 16.7 ft3/s for Fairplain, Ripley, Hico, and Wallback, respectively. Maximum precipitation totals at all streamgages reached the range of 2- to 5-year recurrence intervals for some durations, and maximum storm intensity exceeded the 50-year recurrence interval for a 15-minute duration at Fairplain. The maximum peaks recorded at Fairplain, Ripley, and Hico coincided with the most intense storms at each of those streamgages, and the maximum peak at Wallback coincided with one of the most intense storms. The only streamgage where the maximum observed stormflow for a streamgage reached 50 percent of the smallest prediction was at Ripley, during the April 8, 2020, storm. Although relating peak streamflow to channel and floodplain elevations was not a focus of the study, field inspections included checks for evidence of out-of-bank flow, which was noted only following the two largest storms at Hico and Wallback. Maximum depths at stage sensors during the study were 0.44 ft at Fairplain and 1.17 ft at Ripley, for the AV sensor inside the culverts, and 1.81 ft at Hico and 1.51 ft at Wallback, for the NTRAN upstream from the culverts; these depths are not indicative of major floods, even for such small streams.
More of the predictions seemed too slow than too fast, but that is in comparison to a high-variance set of data. The variance is demonstrated not just by values of standard deviations and IQR, but also by the absence of a metric that was significantly different among streamgages, even though the streamgages were selected to represent different basin slopes and shapes. Differences among streamgages were expected, yet for all time metrics, the differences within streamgages were greater than the differences among streamgages. Time to recede accounted for four of the seven combinations of time metrics and streamgages for which the IQR of observations was shorter than the adjusted estimates for the 10-year storm; however, PI-to-RI better represents assumptions of the same conceptual definition of Tc. If time to recede is considered a secondary line of evidence, then the IQR for three combinations of time metrics and streamgages is shorter than estimates, compared with one that was longer, and the IQR for four combinations included the estimates. All predictions were within one average standard deviation of the overall mean for the streamgage in question, and within the range of observations for all time metrics at all streamgages. These lines of evidence do not indicate large, systematic errors in Tc estimates.
Summary
The U.S. Geological Survey (USGS), in cooperation with the West Virginia Department of Transportation, Division of Highways, compared time of concentration (Tc) and related runoff characteristics measured at four field sites in West Virginia to estimates made using accepted methods. The sites were selected to represent a range of basin size, length, slope, and a range of estimated Tc. Four sites that met these criteria were chosen for the study. Instrumentation included a rain gage and a streamgage at all sites. Two streamgages, USGS station number (no.) 03159718 Grasslick Creek tributary above Interstate 77 near Fairplain, West Virginia (referred to as Fairplain in this report), and USGS station no. 03159823 Grass Run tributary above Interstate 77 near Ripley, W. Va. (referred to as Ripley in this report), were established near each other at the outlets of small basins with moderate slopes in northwestern West Virginia. The largest, longest, and flattest basin in the study drained to a point where USGS station no. 03190307 Hedricks Creek tributary above U.S.–19 near Hico, W.Va. (referred to as “Hico” in this report) was established. The final gaged basin in the study, that of USGS station no. 03197062 Cookman Fork at Interstate 79 near Wallback, W.Va. (referred to as “Wallback” in this report), in central West Virginia, had a drainage area nearly as large as Hico, but the basin was more compact, and the principal flow path was shorter and steeper.
Precipitation and streamflow data were collected during the 2017–20 water years. Precipitation data collection began in 2017 at all sites before streamflow instrumentation was complete. Streamflow data collection began in November 2017 at Hico, and in January 2018 at the other three streamgages. All sites were equipped with a rain gage and two independent streamflow sensors: an area-velocity (AV) sensor and a bubble gage. At two streamgages, all flow data were collected at 1-minute intervals with the AV sensor. At Hico, channel and flow conditions were more favorable for data collection with the bubble gage, so all flow data were collected at 5-minute intervals with the bubble gage. At Wallback, a part of the streamgage’s data record was collected at 1-minute intervals with the AV sensor, but much of the record was collected with the backup bubble gage when it performed better than the AV sensor.
The 2018 water year was unusually wet at all sites; precipitation ranged from 53 to 59 inches throughout the water year, without adjusting for missing periods. The 2019 water year was drier than normal and had nearly identical precipitation measurements among sites, ranging only from 42 to 43 inches, without adjusting for missing periods. Unusually low precipitation in August to September 2019 caused most of the precipitation deficit for the water year. The 2020 water year, like 2018, was unusually wet at all sites. Precipitation totals for the partial year ranged from 39 to 50 inches, although much of the difference among site totals was caused by differences in when data collection was discontinued. At least two, but fewer than five storms exceeded the magnitude of the 1-year storm for selected durations of precipitation at each site, and at least one, but fewer than four storms exceeded the magnitude of the 2-year storm.
When flows were high for several days at one streamgage, they generally were high at the other streamgages. However, the maximum flows for the study period were on different days for all four streamgages. The maximum flow for Wallback resulted from a series of storms in September 2018 that produced a peak on September 25 with a flow of 16.7 ft3/s and another peak on September 27 with a flow of 16.6 ft3/s. Thunderstorms in spring of 2020 produced the maximum flow for the other three streamgages.
Three hydrograph time metrics were used in this study to compute Tc: time to rise, time to recede to an inflection on the recession, and the time between the inflection on the hyetograph at the end of major precipitation (the precipitation inflection) and the inflection on the falling limb of the hydrograph (the recession inflection). The time from the precipitation inflection to the recession inflection is abbreviated in this report as PI-to-RI.
Hico had the slowest Tc according to all three characteristics; its average Tc was 34 and 32 minutes for time to rise and time to recede, respectively. The time between PI-to-RI at Hico, 38 minutes, was the longest metric at any of the streamgages. Storm hydrographs at Hico could be separated into two distinct groups, those that rose quickly and those that rose slowly. These groups were the result of storms with different precipitation intensity.
Wallback had the second slowest Tc according to all three metrics. At Wallback, average Tc for time to rise and time to recede were similar, 23 and 25 minutes, respectively. As at Hico, Wallback’s PI-to-RI, 32 minutes, was more than the time to rise or time to recede.
Fairplain and Ripley’s time metrics were similar: time to rise was 18 and 19 minutes, respectively; time to recede was 14 and 16 minutes, respectively; and time from PI-to-RI was 22 and 27 minutes, respectively. At Ripley, two pairings of time metrics were significantly different from each other: time to rise and PI-to-RI (p=0.025) and between time to recede and PI-to-RI (p=0.011).
Overall averages and average standard deviations of all Tc values were 18 and 10 minutes for Fairplain, 21 and 7 minutes for Ripley, 35 and 24 minutes for Hico, and 27 and 11 minutes for Wallback. Measured Tc values were compared to estimates made with the Rational Method. The Rational Method was applied following two different estimation procedures, one in which channel geometry was estimated using professional judgment and the other in which channel geometry estimates were adjusted using regional equations. All the overall average Tc values from the study were between the range of estimates for different design flows for one of the two estimation procedures. Measured values from different sites did not match the same procedure or design flow, however. All the estimates made using either of the two procedures for applying the Rational Method were within one standard deviation of the overall measured mean Tc for their respective streamgage. The three measured time metrics did not have a consistent relation with the estimates. Time to rise and time to recede were shorter than time from PI-to-RI for all streamgages. None of the time metrics were significantly (p>0.05) different among streamgages, either individually or in aggregate.
The predictions of peak flow for selected precipitation intensities and durations did not match observed peak flows as accurately as predictions matched observations for Tc. The only streamgage where the maximum observed stormflow for a streamgage reached 50 percent of the smallest prediction was at Ripley, during the April 8, 2020, storm.
Predicted values for the 10-year storm, one of the key recurrence intervals in this study’s design, were within the interquartile range (IQR) for 4 of 12 combinations of streamgages and time metrics. Two of these values were for observed time metrics for Fairplain, one was for Wallback, and the other was for Hico. At Ripley, where PI-to-RI and time to rise were significantly different (p=0.025) from each other, their IQRs did not overlap; the predictions were not within the IQR for either metric, but instead, were between them. The adjusted prediction of Tc was shorter than the IQR for one time metric at one streamgage (PI-to-RI at Ripley), and it was longer than the IQR for seven combinations of streamgages and time metrics. Adjusted predictions of Tc were within the IQR of observed PI-to-RI for Fairplain and Wallback, longer than the IQR of observed PI-to-RI at Hico, and shorter than the IQR of observed PI-to-RI at Ripley. The adjusted predictions of Tc were within the IQR of time to rise for Hico and Fairplain but were longer than the IQR for Ripley and Wallback. These lines of evidence do not indicate large, systematic errors in Tc estimates.
References Cited
Bonnin, G.M., Martin, D., Lin, B., Parzybok, T., Yekta, M., and Riley, D., 2006, Delaware, District of Columbia, Illinois, Indiana, Kentucky, Maryland, New Jersey, North Carolina, Ohio, Pennsylvania, South Carolina, Tennessee, Virginia, West Virginia, v. 2 of Precipitation-frequency atlas of the United States (version 3.0, 2006): National Oceanic and Atmospheric Administration, National Weather Service Atlas 14, 295 p. [Also available at https://www.weather.gov/media/owp/oh/hdsc/docs/Atlas14_Volume2.pdf.]
Esri, 2017, ArcGIS 10.6: Esri software release, accessed August 11, 2017, at https://www.esri.com/en-us/arcgis/products/arcgis-desktop/overview.
Esri, 2019, Slope—ArcMap 10.6: Esri software release, accessed August 11, 2017, at https://desktop.arcgis.com/en/arcmap/10.6/tools/spatial-analyst-toolbox/slope.htm.
Hayes, D.C., and Young, R.L., 2005, Comparison of peak discharge and runoff characteristic estimates from the rational method to field observations for small basins in central Virginia: U.S. Geological Survey Scientific Investigations Report 2005–5254, 38 p. [Also available at https://pubs.usgs.gov/sir/2005/5254/sir05_5254.pdf.]
Helsel, D.R., Hirsch, R.M., Ryberg, K.R., Archfield, S.A., and Gilroy, E.J., 2020, Statistical methods in water resources: U.S. Geological Survey Techniques and Methods, book 4, chapter A3, 458 p., https://doi.org/10.3133/tm4a3. [Supersedes U.S. Geological Survey Techniques of Water-Resources Investigations, book 4, chapter A3, version 1.1.]
Holmes, D., and Chintala, R., 2007, West Virginia Division of Highways drainage manual (June 2, 2015, addendum; 3d ed.): West Virginia Division of Highways, 579 p. [Also available at http://www.transportation.wv.gov/highways/engineering/Manuals/Drainage/WVDOH%202007%20Drainage%20Manual%20with%20Addendum%201%20and%202.pdf.]
Lessing, P., 1997, Geology of the New River Gorge: West Virginia Geological & Economic Survey, accessed December 13, 2023, at http://www.wvgs.wvnet.edu/www/geology/geoles01.htm.
McCuen, R.H., 2009, Uncertainty analyses of watershed time parameters: Journal of Hydraulic Engineering, v. 14, no. 5, p. 490–498. [Also available at https://ascelibrary.org/doi/abs/10.1061/(ASCE)HE.1943-5584.0000011.]
McCuen, R.H., Johnson, P.A., and Ragan, R.M., 2002, Highway hydrology—Hydraulic design series no. 2 (2d ed.): Federal Highway Administration Publication No. FHWA–NHI–02–001, 426 p. [Also available at https://www.fhwa.dot.gov/engineering/hydraulics/pubs/hif02001.pdf.]
Messinger, T., and Scott, J.D., 2024, Streamflow and precipitation data and characteristics of selected storms for four stream basins in West Virginia, 2017-2020: U.S. Geological Survey data release, https://doi.org/10.5066/P9SIF6L9.
National Centers for Environmental Information, 2021, U.S. Climate Normals: National Oceanic and Atmospheric Administration website, accessed March 22, 2022, at https://www.ncei.noaa.gov/products/land-based-station/us-climate-normals.
National Oceanic and Atmospheric Administration, 2018, Climatological data—Annual summary—West Virginia 2018: v. 126, no. 13, ISSN 0364-5371 GHCND Ver: 3.27-upd-2019051518, accessed March 22, 2022, at https://www.ncdc.noaa.gov/IPS/cd/cd.html.
National Oceanic and Atmospheric Administration, 2022, NOAA atlas 14 point precipitation frequency estimates—WV: National Oceanic and Atmospheric Administration website, accessed March 22, 2022, at https://hdsc.nws.noaa.gov/pfds/pfds_map_cont.html?bkmrk=wv.
Natural Resources Conservation Service, 2010, Time of concentration—Part 630 Hydrology National Engineering Handbook: Natural Resources Conservation Service, chap. 15, 29 p., accessed November 15, 2021, at https://directives.nrcs.usda.gov/sites/default/files2/1712930617/14081.pdf.
OTT HydroMet, 2016, Operating instructions bubble sensor OTT CBS, ver. 04–0211: Ott HydroMet, accessed September 16, 2020, at https://www.ott.com/download/operating-instructions-bubble-sensor-ott-cbs-version-04-0211/.
R Core Team, 2021, R—A language and environment for statistical computing: Vienna, R Foundation for Statistical Computing, accessed July 1, 2021, at http://www.R-project.org/.
Sarkar, D., 2021, Lattice—Trellis Graphics for R, v. 0.20–45: The Comprehensive R Archive Network, accessed July 1, 2021, at https://cran.r-project.org/web/packages/lattice/index.html.
Stalker, 2018, Hand-held, portable surface flow velocity radar: Richardson, Tex., Applied Concepts, Inc. [Stalker Radar], 2 p., accessed July 1, 2021, at https://www.stalkerradar.com/oem/downloads/006-0427-00-SVR-brochure.pdf. [Also available at https://asin.com.vn/media/lib/006-0427-00-svr-brochure.pdf.]
Teledyne Isco, 2016, TIENet 350 area velocity sensor—Installation and operation guide: Teledyne Isco, accessed March 1, 2021, at https://www.teledyneisco.com/en-us/Water_/Flow%20Meter%20Documents/Manuals/TIENet%20350%20Area%20Velocity%20Sensor.pdf.
U.S. Geological Survey, 2012, USGS NED ned19_n38x25_w081x00_wv_statewide_2003 1/9 arc-second 2012 15 x 15 minute IMG: U.S. Geological Survey National Elevation Dataset, accessed March 16, 2017, at https://ned.usgs.gov/. [Also available at https://www.usgs.gov/the-national-map-data-delivery/gis-data-download.]
U.S. Geological Survey, 2017, USGS water data for the Nation: U.S. Geological Survey National Water Information System database, accessed November 2, 2017, at http://doi.org/10.5066/F7P55KJN.
U.S. Geological Survey, 2024a, USGS 03159718 Grasslick Creek Tributary near Fairplain WV, in USGS water data for the Nation: U.S. Geological Survey National Water Information System database, accessed June 24, 2024, at https://doi.org/10.5066/F7P55KJN. [Site information directly accessible at https://waterdata.usgs.gov/nwis/uv?referred_module=sw&site_no=03159718.]
U.S. Geological Survey, 2024b, USGS 03159823 Grass Run Tributary near Ripley WV, in USGS water data for the Nation: U.S. Geological Survey National Water Information System database, accessed June 24, 2024, at https://doi.org/10.5066/F7P55KJN. [Site information directly accessible at https://waterdata.usgs.gov/nwis/uv?referred_module=sw&site_no=03159823.]
U.S. Geological Survey, 2024c, USGS 03190307 Hedricks Creek Tributary near Hico WV, in USGS water data for the Nation: U.S. Geological Survey National Water Information System database, accessed June 24, 2024, at https://doi.org/10.5066/F7P55KJN. [Site information directly accessible at https://waterdata.usgs.gov/nwis/uv?referred_module=sw&site_no=03190307.]
U.S. Geological Survey, 2024d, USGS 03197062 Cookman Fork near Wallback WV, in USGS water data for the Nation: U.S. Geological Survey National Water Information System database, accessed June 24, 2024, at https://doi.org/10.5066/F7P55KJN. [Site information directly accessible at https://waterdata.usgs.gov/nwis/uv?referred_module=sw&site_no=03197062.]
West Virginia Department of Transportation, 2021, Roads—1:4800 scale, major roads (WV DOT): West Virginia GIS Technical Center web page, accessed August 19, 2021, at https://wvgis.wvu.edu/data/dataset.php?ID=284.
Wieczorek, M.E., and LaMotte, A.E., 2010, Attributes for NHDPlus catchments (ver. 1.1)—Basin characteristics, 2002: U.S. Geological Survey Digital Data Series DS–490–03, accessed March 14, 2017, at https://water.usgs.gov/GIS/metadata/usgswrd/XML/nhd_bchar.xml.
Yellow Springs Instruments (YSI), 2019, H-3401SDI—Smart SDI-12 tipping bucket rain gage: Yellow Springs, Ohio, Yellow Springs Instruments, 31 p., accessed September 16, 2020, at https://www.ysi.com/File%20Library/Documents/Manuals/H-3401-Tipping-Bucket-User-Manual-D61.pdf.
Appendix 1. Instrumentation for U.S. Geological Survey Station Grasslick Creek Tributary Above Interstate 77 near Fairplain, West Virginia, Number 03159718

Photographs showing the instrumentation for U.S. Geological Survey station number 03159718 Grasslick Creek tributary near Fairplain, West Virginia. A, Culvert opening and apron shown as seen from the right bank of the tributary. The orifice of the nonsubmersible transducer (NTRAN) is at the center, and the crest-stage gage is the vertical pipe at the right. B, The culvert opening as seen from upstream. The NTRAN orifice is shown at left, the crest-stage pipe is left of the opening, and the flexible conduit for the area-velocity (AV) sensor is upper left. C, The AV sensor and installation hardware as seen from upstream. D, The AV sensor at a depth of 0.10 feet. E, The rain gage is at the top of the pole. The instrument shelter is the open box mounted on the pole.
Appendix 2. Instrumentation for U.S. Geological Survey Station Grass Run Tributary Above Interstate 77 near Ripley, West Virginia, Number 03159823

Photographs showing the instrumentation for U.S. Geological Survey station number 03159823 Grass Run tributary above Interstate 77 near Ripley, West Virginia. A, The rain gage is at the top of the furthest pole, and the instrument shelter and solar panel are on the nearest pole. B, The area-velocity (AV) sensor and mounting ring are shown as seen from downstream. C, The culvert opening and apron as seen from inside the culvert. The orifice of the nonsubmersible transducer (NTRAN) is at the center of the photograph. D, The culvert opening and apron as seen from upstream. The crest-stage gage is the vertical pipe at the left of the culvert, the flexible conduit for the AV sensor cable is at the upper right corner of the culvert, and the NTRAN orifice is at bottom center of the photograph. E, James Scott, U.S. Geological Survey hydrologic technician, measuring discharge at the culvert opening.
Appendix 3. Instrumentation for U.S. Geological Survey Station Hedricks Creek Tributary Above U.S.–19 near Hico, West Virginia, Number 03190307

Photographs showing the instrumentation for U.S. Geological Survey station number 03190307 Hedricks Creek Tributary above U.S.–19 near Hico, West Virginia. A, The rain gage is at the top of the pole, the solar panel is just below it, and the instrument shelter is mounted on the left side. B, The area-velocity (AV) sensor as seen from upstream during turbulent flow; installation hardware can also be seen (record from the AV sensor was not used at this site). C, The gaging pool as seen from downstream. The orifice of the nonsubmersible transducer (NTRAN) is at the left, the crest-stage gage is the vertical pipe left of center. D, The stream reach upstream from the streamgage.
Appendix 4. Instrumentation for U.S. Geological Survey Station Cookman Fork at Interstate 79 near Wallback, West Virginia, Number 03197062

Photographs showing the instrumentation for U.S. Geological Survey station number 03197062 Cookman Fork near Wallback, West Virginia. A, The culvert opening and apron. The orifice of the nonsubmersible transducer (NTRAN) is at the lower center, the crest-stage gage is the vertical pipe at the right, and the flexible conduit for the area-velocity (AV) sensor cable is at the upper right corner of the culvert. B, The orifice of the NTRAN as seen from inside the culvert facing upstream. C, The AV sensor at a depth of 0.10 feet. D, The AV sensor photographed from upstream. Installation hardware is shown. E, Rain gage at the top of the pole.
Conversion Factors
U.S. customary units to International System of Units
Datum
Vertical coordinate information is referenced to the North American Vertical Datum of 1988 (NAVD 88).
Horizontal coordinate information is referenced to the North American Datum of 1983 (NAD 83).
Altitude, as used in this report, refers to distance above the vertical datum.
Abbreviations
AV
area-velocity
GPS
Global Positioning System
NHDPlus
National Hydrography Dataset Plus
NTRAN
nonsubmersible pressure transducers
NWIS
National Water Information System
PI-to-RI
precipitation inflection to recession inflection
Tc
time of concentration
USGS
U.S. Geological Survey
WVDOH
West Virginia Department of Transportation, Division of Highways
For additional information, contact:
Director, Virginia and West Virginia Water Science Center
U.S. Geological Survey
1730 East Parham Road
Richmond, VA 23228
Or visit our website at:
https://www.usgs.gov/centers/virginia-and-west-virginia-water-science-center
Publishing support provided by the Baltimore Publishing Service Center
Disclaimers
Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Although this information product, for the most part, is in the public domain, it also may contain copyrighted materials as noted in the text. Permission to reproduce copyrighted items must be secured from the copyright owner.
Suggested Citation
Messinger, T., Holmes, D.A., Scott, J.D., and Kirk, D.W., 2024, Improving time of concentration estimates for small rural watersheds in the Appalachian Plateaus physiographic province, West Virginia: U.S. Geological Survey Scientific Investigations Report 2024–5051, 34 p., https://doi.org/10.3133/sir20245051.
ISSN: 2328-0328 (online)
Study Area
| Publication type | Report |
|---|---|
| Publication Subtype | USGS Numbered Series |
| Title | Improving time of concentration estimates for small rural watersheds in the Appalachian Plateaus physiographic province, West Virginia |
| Series title | Scientific Investigations Report |
| Series number | 2024-5051 |
| DOI | 10.3133/sir20245051 |
| Publication Date | December 19, 2024 |
| Year Published | 2024 |
| Language | English |
| Publisher | U.S. Geological Survey |
| Publisher location | Reston, VA |
| Contributing office(s) | Virginia and West Virginia Water Science Center |
| Description | Report: vii, 34 p.; Data Release |
| Country | United States |
| State | West Virginia |
| Other Geospatial | Appalachian Plateaus Physiographic Province |
| Online Only (Y/N) | Y |
| Additional Online Files (Y/N) | N |


