Computation of Bromide Concentrations at the Kansas River at De Soto, Kansas, January 2021 through October 2023
Links
- Document: Report (2.65 MB pdf) , HTML , XML
- Appendix: Appendix 1 —Model Archival Summary for Bromide Concentration at U.S. Geological Survey Streamgage 06892350, Kansas River at De Soto, Kansas, during January 2021 through October 2023
- Dataset: USGS National Water Information System database —USGS water data for the Nation
- Download citation as: RIS | Dublin Core
Acknowledgments
The authors thank the Water District No. 1 of Johnson County, Kansas, for sample analysis and a beneficial and lasting partnership in monitoring water-quality conditions in the Kansas River.
The authors also thank U.S. Geological Survey reviewers Kyle Juracek (Lawrence, Kansas), Teresa Rasmussen (Lawrence, Kans.), Kirk Smith (Northborough, Massachusetts), Mandy Stone (Lawrence, Kans.), and Jonathan Wedel (Lawrence, Kans.) for reviewing previous drafts of this report. Lastly, this report would not have been possible without the hard work of past and present U.S. Geological Survey staff at the Kansas Water Science Center who assisted with data collection, analyses, and project and database management.
Abstract
The Kansas River is an essential water resource that provides drinking water to more than 950,000 people in northeastern Kansas. Water suppliers that rely on the Kansas River as a water-supply source use physical and chemical water-treatment strategies to remove contaminants before distribution. Water District No. 1 of Johnson County, Kansas (WaterOne), is the largest water supplier in the State and uses the Kansas and Missouri Rivers as water-supply sources to provide drinking water to the Kansas City metropolitan area. WaterOne has been using ozone disinfection as a primary water-treatment strategy since the summer of 2020. Water suppliers that rely on ozone disinfection have become increasingly concerned with the presence of elevated dissolved bromide (the negatively charged form of bromine; hereafter referred to as “bromide”) concentrations in their water-supply source. Ozone disinfection of source water containing elevated concentrations of bromide can lead to the formation of bromate, a regulated disinfection byproduct and probable carcinogen. Real-time computations of bromide concentrations upstream from the WaterOne source-water intake in the Kansas River can be used to assist WaterOne with proactive adjustment of water-treatment strategies. These computations can also be used to advance understanding of hydrologic processes affecting ozone disinfection and formation of bromate.
This report documents the development of the surrogate-regression model that computes bromide concentrations in real time at De Soto, Kansas, and characterizes daily and monthly bromide concentrations at this location during the study period. The U.S. Geological Survey (USGS), in cooperation with WaterOne, collected specific conductance and discrete bromide sample data at the USGS streamgage Kansas River at De Soto, Kans. (06892350; hereafter referred to as “De Soto”), during January 2021 through October 2023 to develop a surrogate-regression model using ordinary least-squares regression that computes bromide concentrations at De Soto, which is about 15 miles upstream from the WaterOne source-water intake in the Kansas River. Specific conductance explained about 85 percent of the variance in bromide concentrations at De Soto during the study period. The surrogate-regression model documented in this report estimated that bromide concentrations at De Soto were likely to exceed the WaterOne water-treatment level of concern (150 micrograms per liter [µg/L]) when specific conductance was greater than or equal to about 930 microsiemens per centimeter at 25 degrees Celsius. Surrogate-regression model computations of bromide concentrations documented in this report are available at the USGS National Real-Time Water-Quality website (https://nrtwq.usgs.gov).
Bromide concentrations in discrete samples ranged from 31.9 to 251 µg/L and exceeded the water-treatment level of concern in about 34 percent of the 41 samples collected at De Soto during January 2021 through October 2023. Computed daily bromide concentrations ranged from 38.2 to 277 µg/L and exceeded the water-treatment level of concern about 46 percent of the time during January 2021 through October 2023. Generally, an inverse relation was observed between bromide and streamflow during the study period. Higher bromide concentrations were observed during September through February, and lower bromide concentrations were observed during March through August. Seasonal median bromide concentrations were significantly different in all pairwise seasonal combinations, except for summer versus spring. Computed median bromide concentrations were highest during winter, followed by fall, then spring and summer.
Introduction
The Kansas River is an essential water resource for eastern Kansas that provides recreational and industrial uses, food procurement, groundwater recharge, irrigation, wildlife habitat, livestock water use, and drinking water for more than 950,000 people in northeastern Kansas (Kansas Department of Health and Environment, 2017; Josh Olson, Kansas Water Office, written commun., July 21, 2022). Water suppliers that rely on the Kansas River as a water-supply source use various water-treatment strategies, depending on source-water-quality characteristics, to remove contaminants before distribution. An early-notification system of changes in source-water quality upstream from water-supply intakes has been previously developed and maintained in the Kansas River (Rasmussen and others, 2005; Foster and Graham, 2016; Williams, 2021, 2023) to assist water suppliers with proactive adjustment of water-treatment strategies. Surrogate-regression models that use in situ continuous real-time water-quality data to compute concentrations of total dissolved solids, major ions, hardness as calcium carbonate, nutrients, chlorophyll a, total suspended solids, suspended sediment, and fecal indicator bacteria densities have recently been developed at three U.S. Geological Survey (USGS) streamgages: the Kansas River at Wamego, Kansas (06887500; Williams, 2021); the Kansas River above Topeka Weir at Topeka, Kans. (06888990; Williams, 2023); and the Kansas River at De Soto, Kans. (06892350; hereafter referred to as “De Soto”; Williams, 2021). This previously published early-notification system provides hourly computations of water-quality constituent concentrations or densities that are not easily measured in real time. Model computations can be compared to associated Federal and State water-quality criteria and are useful to the public for cultural and recreational purposes. Real-time computations of these concentrations or densities are available at the USGS National Real-Time Water-Quality website (U.S. Geological Survey, 2024a). The water-quality data used to develop this early-notification system have also been used to characterize water-quality conditions in the Kansas River over time (Graham and others, 2018; Williams and others, 2024a, b).
Water District No. 1 of Johnson County, Kansas (WaterOne), is the largest water supplier in Kansas and uses the Kansas and Missouri Rivers as water-supply sources to provide drinking water to the Kansas City metropolitan area (Water District No. 1 of Johnson County, 2024b). WaterOne began using ozone as a primary disinfection-treatment strategy in the summer of 2020 (Water District No. 1 of Johnson County, 2024a). Water suppliers that rely on ozone disinfection have become increasingly concerned with the presence of elevated dissolved bromide (the negatively charged form of bromine; hereafter referred to as “bromide”) concentrations in their water-supply source. The sources of bromide in the Kansas River basin are likely from natural saline water intrusion from underlying bedrock, oil-field brine contamination during the 1910s to 1940s, and the dissolution of deicing and water-softener salts (Whittemore, 2007; Donald Whittemore, Kansas Geological Survey, written commun., March 4, 2024). Bromide itself does not pose a risk to human health (World Health Organization, 2009). However, ozone disinfection of source water containing elevated concentrations of bromide can lead to the formation of bromate (Agus and others, 2009), a regulated disinfection byproduct and probable carcinogen (U.S. Environmental Protection Agency, 2009). The formation of bromate during ozone disinfection can be affected by the bromide concentration and pH of the water-supply source (New York State Department of Health, 2006). The U.S. Environmental Protection Agency has established a National Primary Drinking Water Regulation for bromate, setting the maximum contaminant level (MCL) and public health goal for finished drinking water at 10 micrograms per liter (µg/L) and 0 µg/L, respectively (U.S. Environmental Protection Agency, 2009). WaterOne uses a threshold of 150 µg/L for bromide in the Kansas River as a water-treatment level of concern (Greg Totzke, WaterOne, written commun., April 1, 2023).
No surrogate models for bromide concentration in the Kansas River have been previously published. However, Baldys and others (2010) developed and published surrogate models that compute bromide concentration for three USGS streamgages along the Red River in Texas, and Stone and Klager (2023) developed similar models for three USGS streamgages along the Little Arkansas River in Kansas. Real-time computations of bromide concentrations upstream from the WaterOne source-water intake in the Kansas River can be used to enhance the existing early-notification system of changes in source-water quality (Williams, 2021, 2023) by assisting WaterOne with proactive adjustment of water-treatment strategies. These computations can also be used to advance understanding of hydrologic processes affecting ozone disinfection and formation of bromate.
The USGS, in cooperation with WaterOne, collected continuous (15-minute interval) and discrete water-quality data at De Soto during January 2021 through October 2023 to develop a surrogate-regression model that computes bromide concentrations at De Soto. Bromide concentrations computed from the surrogate-regression model documented in this report are available at the USGS National Real-Time Water-Quality website (U.S. Geological Survey, 2024a).
Purpose and Scope
The purpose of this report is to document a surrogate-regression model that computes bromide concentrations in real time at De Soto and to characterize daily and monthly bromide concentrations at this location during the study period. The surrogate-regression model was developed using in situ specific conductance and bromide sample data collected by the USGS at De Soto during January 2021 through October 2023. The surrogate-regression model documented in this report provides computations of bromide concentrations that are not easily measured in real time. Historical bromide concentrations were computed during January 2021 through October 2023 and summarized in relation to the WaterOne water-treatment level of concern, streamflow, and seasonality. The model-development data and model computations documented in this report can be used to characterize water-quality conditions that affect drinking-water treatment at WaterOne, provide early notification of changing conditions that can be used to proactively adjust water treatment, and evaluate potential changes in bromide concentrations in the Kansas River over time.
Description of Study Area
The Kansas River Basin covers about 60,100 square miles (mi2) of northern Kansas, southern Nebraska, and northeastern Colorado (fig. 1). The Kansas River is about 174 miles long and flows east from the confluence of the Republican and Smoky Hill Rivers near Junction City, Kans., to its confluence with the Missouri River (not shown) in Kansas City, Kans. (fig. 1). The study area, or lower Kansas River Basin, covers about a 5,450-mi2 area east of Junction City, Kans., which includes four reservoirs (Milford Lake, Tuttle Creek Lake, Perry Lake, and Clinton Lake; fig. 1). These reservoirs regulate streamflow in the Kansas River and were constructed during the 1960s through 1970s for flood control, public water supply, and recreation (U.S. Army Corps of Engineers, 2017). The study area is primarily used for agricultural purposes (cropland [primarily corn, soybeans, and wheat; Kansas Department of Agriculture, 2023] and grassland). The rest of the study area consists of four major urban areas that are along the Kansas River: Manhattan, Topeka, Lawrence, and the Kansas City metropolitan area (fig. 1). These cities, along with several smaller municipalities, use the Kansas River or its associated alluvial aquifer as a water-supply source.
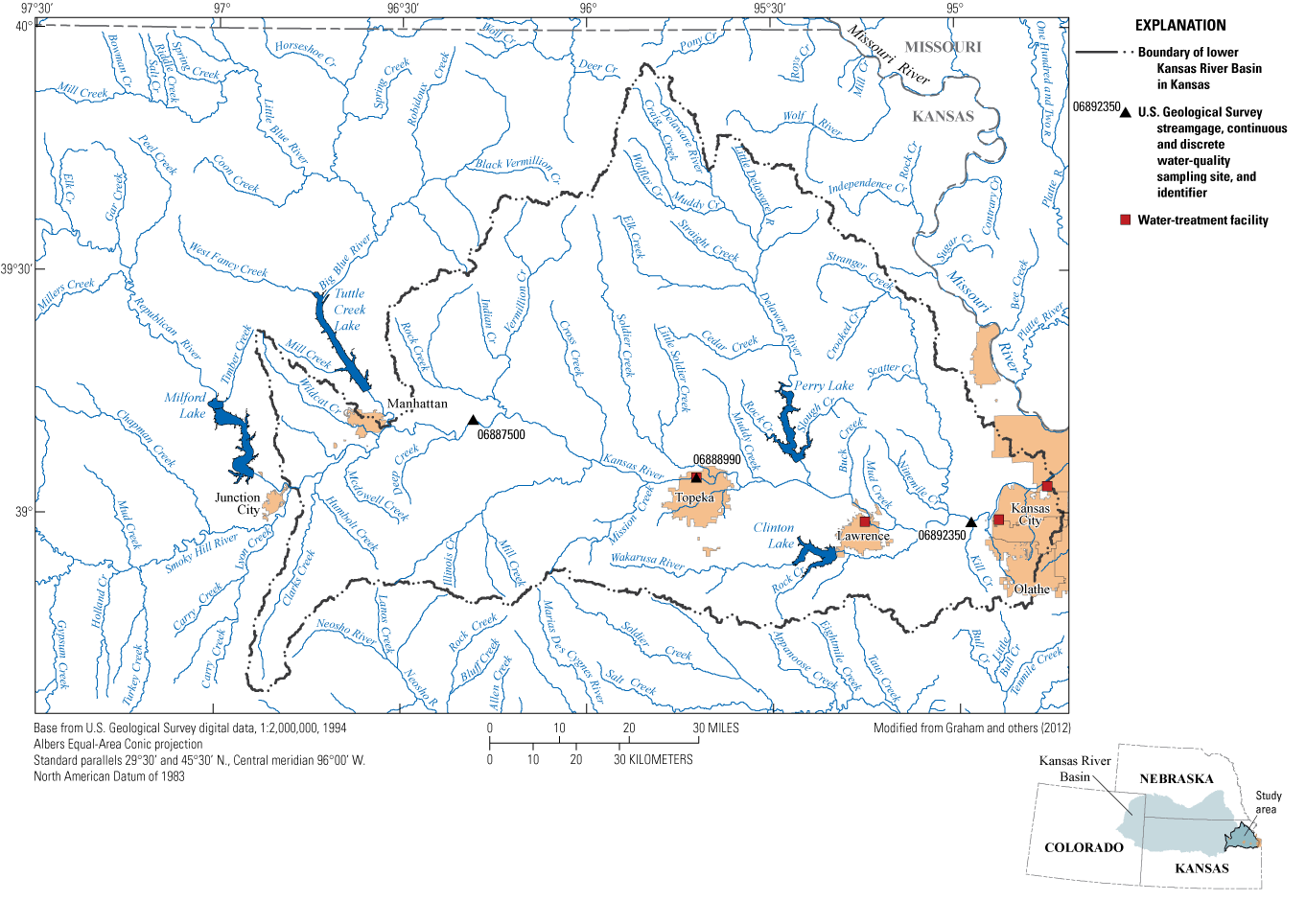
Location of the U.S. Geological Survey streamgage Kansas River at De Soto, Kansas (06892350), and discrete water-quality sampling station in the lower Kansas River Basin. To the west, two additional U.S. Geological Survey streamgages (Kansas River at Wamego, Kans. [06887500], and Kansas River above Topeka Weir at Topeka, Kans. [06888990]) are shown.
A surrogate-regression model that computes bromide concentrations was developed at De Soto, which has a drainage area of about 59,800 mi2 (Graham and others, 2018). De Soto is about 15 miles upstream from the WaterOne source-water intake in the Kansas River. The instream travel time from De Soto to the WaterOne source-water intake in the Kansas River during low-flow conditions (near 1,500 cubic feet per second) was estimated to range from about 12 hours (Chantelle Davis, U.S. Geological Survey, written commun., July 8, 2024) to about 20 hours (Jobson, 1996; U.S. Geological Survey, 2022). The study area is described in additional detail by Rasmussen and Christensen (2005), Rasmussen and others (2005), and Graham and others (2012).
Methods
The USGS collected continuous and discrete water-quality data at De Soto over a range of streamflow and specific-conductance conditions observed during January 2021 through October 2023 (figs. 2 and 3). These data were used to develop a surrogate-regression model that computes bromide concentrations at De Soto.
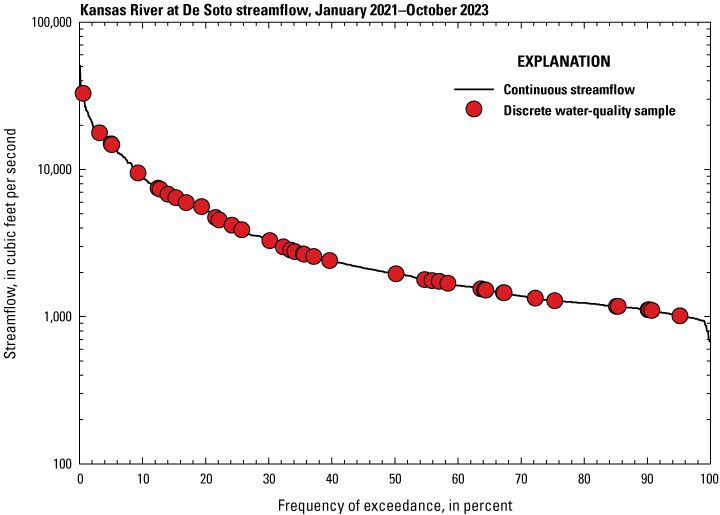
Streamflow duration curve and discrete water-quality samples at the U.S. Geological Survey streamgage Kansas River at De Soto, Kansas (06892350), during January 2021 through October 2023. Data from U.S. Geological Survey (2024b).
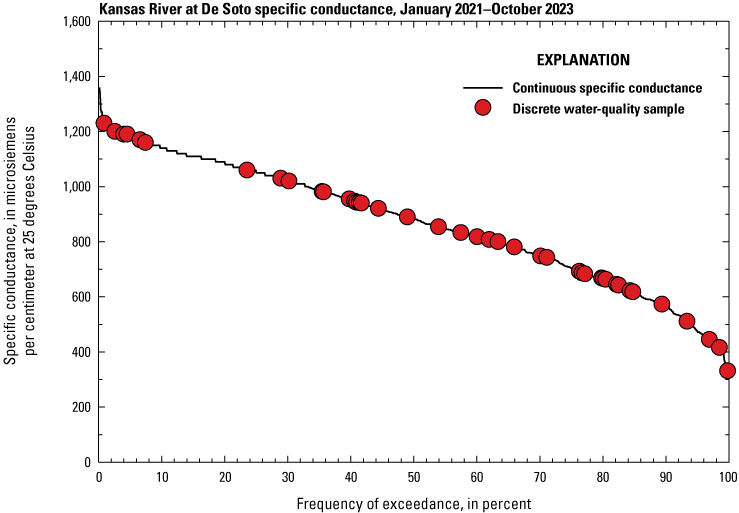
Specific-conductance duration curve and discrete water-quality samples at the U.S. Geological Survey streamgage Kansas River at De Soto, Kansas (06892350), during January 2021 through October 2023. Data from U.S. Geological Survey (2024b).
Continuous Streamflow and Water-Quality Monitoring
Continuous (15-minute interval) streamflow data have been collected at De Soto since October 1990 (U.S. Geological Survey, 2024b). Continuous streamflow data during January 2021 through October 2023 were collected using standard USGS methods (Sauer and Turnipseed, 2010; Turnipseed and Sauer, 2010). These data are available in near real time (hourly) from the USGS National Water Information System database at https://doi.org/10.5066/F7P55KJN (U.S. Geological Survey, 2024b) using station identifier 06892350.
The USGS began collecting continuous (15-minute interval) water-quality data at De Soto during July 1999 through September 2004 and resumed in July 2012 (U.S. Geological Survey, 2024b). A YSI EXO2 water-quality monitor (YSI, Inc., 2017), equipped with sensors for water temperature, specific conductance, dissolved oxygen, pH, turbidity, and chlorophyll and phycocyanin fluorescence, was deployed by suspension from a bridge about 1 to 3 feet below the water surface near the area of deepest and fastest streamflow at De Soto during January 2021 through October 2023 (fig. 4). Continuous water-quality data were collected and quality assured using standard USGS methods (Wagner and others, 2006; Bennett and others, 2014). A nitrate sensor (Hach Nitratax plus sc), equipped with a 5-millimeter path length (Hach, 2022), was installed alongside the water-quality monitor during January 2021 through October 2023. Continuous nitrate data were collected and quality assured using the methods described by Pellerin and others (2013). All continuous water-quality data at De Soto are available in near-real time (hourly) from the USGS National Water Information System database at https://doi.org/10.5066/F7P55KJN (U.S. Geological Survey, 2024b) using station identifier 06892350.

Continuous water-quality monitor deployment at the U.S. Geological Survey streamgage Kansas River at De Soto, Kansas (06892350), during January 2021 through October 2023. Photograph by Ryan Waters, U.S. Geological Survey.
Discrete Water-Quality Sampling
Water-quality samples were collected by the USGS at De Soto on a biweekly to bimonthly basis during January 2021 through October 2023 and analyzed for bromide concentrations. A fixed-schedule sampling approach, affected by the seasonal streamflow characteristics, allowed for 41 water-quality samples to be collected over a range of streamflow and specific-conductance conditions observed at De Soto during the study period (figs. 2 and 3). All water-quality samples were collected using the equal-width increment method, which is a depth-integrated, isokinetic sampling technique (U.S. Geological Survey, variously dated) that is representative of the average chemical composition of the sampled stream cross section. All water-quality samples collected by the USGS at De Soto during January 2021 through October 2023 were analyzed for bromide concentrations by the WaterOne Laboratory in Kansas City, Kans., using U.S. Environmental Protection Agency Method 300.1 (U.S. Environmental Protection Agency, 1997). Results of bromide concentrations from water-quality samples collected by the USGS at De Soto are available from the USGS National Water Information System database at https://doi.org/10.5066/F7P55KJN (U.S. Geological Survey, 2024b) using station identifier 06892350.
Quality Assurance and Quality Control of Continuous and Discrete Water-Quality Data
All continuous specific conductance and discrete bromide data collected during January 2021 through October 2023 were reviewed and approved quarterly, following USGS guidance (U.S. Geological Survey, 2012, 2017; Rasmussen and others, 2014). Continuous specific-conductance data occasionally were corrected, missing, or deleted because of excessive fouling, sensor calibration drift (Wagner and others, 2006; Bennett and others, 2014), equipment malfunction, or temporary removal of equipment to prevent loss or damage during icy conditions. About 6 percent of the continuous specific-conductance data at De Soto were missing or deleted during January 2021 through October 2023 (U.S. Geological Survey, 2024b).
Concurrent replicate samples were collected for about 10 percent of all discrete water-quality samples for quality-control purposes. Concurrent replicate samples were used to characterize variability in bromide concentrations that could have been potentially introduced by sample collection, processing, or analytical methods (Rasmussen and others, 2014; Mueller and others, 2015). Relative percentage difference was used to quantify the variability in concurrent replicate pairs of sampled bromide concentrations and was calculated by dividing the absolute difference of the paired samples by their mean value and multiplying by 100 (Zar, 1999). Three concurrent replicate pairs of sampled bromide concentrations were collected at De Soto during January 2021 through October 2023, with median and mean relative percentage differences equaling about 4 and 11 percent, respectively.
Field- and equipment-blank samples also were collected for about 10 percent of all discrete water-quality samples for quality-control purposes to characterize bias in bromide concentrations that could have been potentially introduced by sampling and analytical methods (Mueller and others, 2015). During January 2021 through October 2023, three field-blank samples were collected at De Soto, and two equipment-blank samples were collected at the USGS Kansas Water Science Center water-quality sample-processing laboratory and analyzed for bromide concentrations by the WaterOne Laboratory; all results were less than the laboratory minimum reporting limit of 25 µg/L.
Development of Bromide Regression Model
A surrogate-regression model that relates continuous in situ specific-conductance sensor measurements to discrete sample bromide concentrations was developed for De Soto using data collected by the USGS during January 2021 through October 2023. The model was developed using ordinary least-squares regression (Helsel and others, 2020) and R programming language (R Core Team, 2024). No bromide data collected during the study period were reported as estimated or less than the laboratory minimum reporting limit.
Continuous (15-minute interval) streamflow data, water-quality data (water temperature, specific conductance, pH, dissolved oxygen, turbidity, chlorophyll and phycocyanin fluorescence, and nitrate), and seasonal components were considered as potential explanatory variables for bromide concentrations at De Soto. Potential explanatory variables were interpolated by discrete water-quality sample time within the 15-minute continuous time series record. For example, if the water-quality sample time was 12:20, then the explanatory variable value was interpolated between values recorded at 12:15 and 12:30 in the continuous time series record. No discrete water-quality sample times coincided with a gap in the continuous record exceeding 1 hour (because of excessive fouling, equipment malfunction, or equipment removal). Potential explanatory variables were evaluated individually and in combination.
Potential surrogate-regression models for bromide concentrations were evaluated based on the range and distribution of model-calibration data, patterns in residual plots, adjusted coefficient of determination (R2), and root mean square error (RMSE; Rasmussen and others, 2009; Helsel and others, 2020). Potential outliers in the model-calibration dataset were initially identified in bivariate plots of the explanatory and response variables (Rasmussen and others, 2009). Model-computed studentized residual values greater than three or less than negative three (Pardoe, 2020) also were used to identify potential outliers in the dataset. Computations of leverage, Cook’s distance, and difference in fits statistics were used to estimate outlier effect on a potential surrogate-regression model (Cook, 1977; Helsel and others, 2020). After identification, outliers were investigated for possible removal from the model-calibration dataset by confirming correct database entry, evaluating relevant laboratory quality-control and quality-assurance data, and reviewing sample-field notes for abnormalities that could have affected the result (Rasmussen and others, 2009). Using this approach, no outliers were determined to have errors associated with sample collection, processing, or analysis and were retained in the model-calibration dataset.
The best surrogate-regression model was selected when the amount of variance in bromide concentrations explained by the explanatory variable (as indicated by adjusted R2) was maximized, the probability (p) value of the explanatory variable was less than 0.05, uncertainty in the model computations was minimized (as indicated by RMSE), and heteroscedasticity (irregular scatter) in residual plots was minimized (Rasmussen and others, 2009; Helsel and others, 2020). A logarithmic transformation (logarithm with base 10 [log] transformation) was considered if it reduced heteroscedasticity in residual plots. However, log transformations can introduce negative bias in model computations (Helsel and others, 2020). Therefore, if a log transformation was used, a bias correction factor was needed for the retransformation of log-transformed model computations back into their original unit (Duan, 1983). A multiple linear regression model (containing more than one explanatory variable) was not selected because there was no combination of explanatory variables in which the extra variable increased the adjusted R2 by more than 5 percent and minimized the RMSE and residual heteroscedasticity. Model-development methodology is described in additional detail in appendix 1.
Computation of Historical Bromide Concentrations
Daily bromide concentrations at De Soto were computed during January 2021 through October 2023 using the surrogate-regression model documented in this report and daily mean specific-conductance data. Occasionally, daily mean specific-conductance data were missing or deleted because of excessive fouling, equipment malfunction, or temporary removal of the continuous water-quality monitor to avoid damage or loss during subfreezing surface-water temperatures. About 10 percent of daily mean specific-conductance data were missing or deleted during the study period. During these periods, daily bromide concentrations were computed using the Weighted Regressions on Time, Discharge, and Season method with Kalman filtering (WRTDS–K; Kalman, 1960; Hirsch and others, 2010; Hirsch and De Cicco, 2015; Zhang and Hirsch, 2019). Daily bromide concentrations computed using the WRTDS–K method can be recomputed using the Exploration and Graphics for RivER Trends (or EGRET) R package (Hirsch and De Cicco, 2015), daily mean streamflow, and the results of bromide concentrations from water-quality samples collected at De Soto during January 2021 through October 2023 (U.S. Geological Survey, 2024b). The WRTDS–K method has been determined to be more accurate compared to other regression-based methods using streamflow as the explanatory variable (Lee and others, 2019). However, the WRTDS–K method is a retrospective approach intended to be used for the computation of daily concentration and cannot be used to compute hourly bromide concentrations in real time. The Wilcoxon signed rank (Wilcoxon, 1945) and Mann-Whitney rank sum (Mann and Whitney, 1947) tests were used to determine if there were statistical differences between daily bromide concentrations computed using the specific-conductance based surrogate regression and WRTDS–K methods during days when computations from both methods were available.
Historical daily bromide computations were used to characterize bromide concentrations during the study period relative to the WaterOne water-treatment level of concern of 150 µg/L (Greg Totzke, WaterOne, written commun., April 1, 2023). This threshold is specific to WaterOne’s Kansas River treatment facility and is based on their ozone disinfection strategies. It was estimated that when bromide concentrations in the Kansas River exceed the WaterOne water-treatment level of concern (150 µg/L), the formation of bromate concentrations greater than the MCL of 10 µg/L (U.S. Environmental Protection Agency, 2009) during ozonation is likely. When bromide concentrations in the Kansas River approached or exceeded the water-treatment level of concern, WaterOne adjusted their water-treatment strategies to ensure the bromate MCL was not exceeded.
Monthly and seasonal patterns in computed bromide concentrations were also investigated during the study period. Monthly median bromide concentrations were calculated using the daily bromide concentrations computed from the specific-conductance based surrogate-regression and WRTDS–K methods during January 2021 through October 2023. Monthly median bromide concentrations were then compared to monthly median streamflow (computed using daily mean streamflow data). To investigate seasonal patterns in computed bromide concentrations, seasonal median values were computed and compared using a Kruskal-Wallis one-way analysis-of-variance on ranks test (Helsel and others, 2020). For the purposes of this test, seasons were defined as follows: winter consisted of December through February, spring consisted of March through May, summer consisted of June through August, and fall consisted of September through November. If differences in seasonal median values were determined to be significantly different (p-value less than [<] 0.05), then a Dunn’s test was used to test all pairwise differences among each season and identify which season(s) differed (Dunn, 1964; Helsel and others, 2020).
Bromide Regression Model Results
A surrogate-regression model that computes bromide concentrations was developed for De Soto using data collected during January 2021 through October 2023. Specific conductance was selected as the single explanatory variable, which explained about 85 percent of the variance (as indicated by R2) in bromide concentrations at De Soto (table 1; app. 1). Specific conductance is a measure of the electrical conductivity of water and is positively correlated with bromide and other charged ionic species (Hem, 1985). Using the surrogate-regression model documented in this report (table 1; app. 1), bromide concentrations at De Soto were likely to exceed the WaterOne water-treatment level of concern (150 µg/L) when specific conductance was greater than or equal to about 930 microsiemens per centimeter at 25 degrees Celsius. Specific conductance was also the single explanatory variable for bromide concentration in surrogate-regression models developed by Baldys and others (2010) for three USGS streamgages along the Red River in Texas (explained about 92–97 percent of the variance in bromide concentrations), and by Stone and Klager (2023) for three USGS streamgages along the Little Arkansas River in Kansas (explained about 72–89 percent of the variance in bromide concentrations). The final selected surrogate-regression model for bromide concentrations at De Soto, associated model-diagnostic statistics, and summary statistics of the model-calibration dataset are listed in table 1. A model archival summary that documents model-development information, statistical output (R Core Team, 2024), and the model-calibration dataset is provided in appendix 1. Surrogate-regression model computations of bromide concentrations are available at the USGS National Real-Time Water-Quality website (U.S. Geological Survey, 2024a).
Table 1.
Surrogate-regression model and summary statistics for computing bromide concentrations at the U.S. Geological Survey streamgage Kansas River at De Soto, Kansas (06892350), using data collected during January 2021 through October 2023.[R2, coefficient of determination; MSE, mean square error; RMSE, root mean square error; MSPE, model standard percentage error; n, number of discrete samples used in model-development dataset; μg/L, microgram per liter; log, logarithm with base 10; Br, bromide, in micrograms per liter; SC, sensor-measured specific conductance, in microsiemens per centimeter at 25 degrees Celsius; NA, not applicable]
| Regression model | Model archival summary | Adjusted R2 | MSE | RMSE | Upper MSPE | Lower MSPE | Bias correction factor (Duan, 1983) | Discrete data used in model-development dataset | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | Percentage of censored data | Range of values in variable measurements | First quartile | Mean | Median | Third quartile | Percentage of data greater than 150 µg/L1 | ||||||||
| log(Br)=1.224log(SC)−1.460 | Appendix 1 | 0.854 | 0.00457 | 0.0676 | 16.9 | 14.4 | 1.012 | 41 | 0 | Br: 31.9–251 | 94.3 | 131 | 136 | 166 | 34.2 |
| SC: 359–1,240 | 656 | 823 | 830 | 975 | NA | ||||||||||
Historical Bromide Concentrations
Bromide concentrations in discrete samples ranged from 31.9 to 251 µg/L (mean=131 µg/L; median=136 µg/L) and exceeded the water-treatment level of concern (150 µg/L) in about 34 percent of the 41 samples collected at De Soto during January 2021 through October 2023 (table 1). Daily bromide concentrations were computed at De Soto using daily mean specific-conductance data and the surrogate-regression model documented in this report during January 2021 through October 2023. When daily mean specific-conductance data were missing at De Soto during this time, daily bromide concentrations were computed using the WRTDS–K method (Kalman, 1960; Hirsch and others, 2010; Hirsch and De Cicco, 2015; Zhang and Hirsch, 2019). The Wilcoxon signed rank (Wilcoxon, 1945) and Mann-Whitney rank sum (Mann and Whitney, 1947) tests did not indicate significant differences (p-value<0.05) between pairs of daily bromide concentrations (Wilcoxon signed rank test p-value=0.218; table 2) or daily bromide concentration datasets (Mann-Whitney rank sum test p-value=0.177; table 2) computed using either method. Therefore, the use of WRTDS–K computed daily bromide concentrations during days when daily mean specific-conductance data were missing or deleted was a suitable approach for computing a complete daily record of bromide concentrations during January 2021 through October 2023. Computed daily bromide concentrations ranged from 38.2 to 277 µg/L (mean=142 µg/L; median=145 µg/L; table 2) and exceeded the water-treatment level of concern about 46 percent of the time during January 2021 through October 2023 (fig. 5). Summary statistics and results of statistical difference tests for bromide concentrations computed using the specific-conductance based surrogate-regression and WRTDS–K methods during January 2021 through October 2023 are listed in table 2.
Table 2.
Summary statistics for bromide concentrations computed using the specific-conductance based surrogate-regression and the Weighted Regressions on Time, Discharge, and Season with Kalman filtering methods at the U.S. Geological Survey streamgage Kansas River at De Soto, Kansas (06892350), during January 2021 through October 2023.[WRTDS–K, Weighted Regressions on Time, Discharge, and Season with Kalman filtering; p, probability; NA, not applicable]
Summary statistics were computed using daily data when bromide concentrations from both computation methods were available.
Computations of bromide concentrations using the WRTDS–K method (Kalman, 1960; Hirsch and others, 2010; Hirsch and De Cicco, 2015; Zhang and Hirsch, 2019) were included only when daily mean specific-conductance data were unavailable.
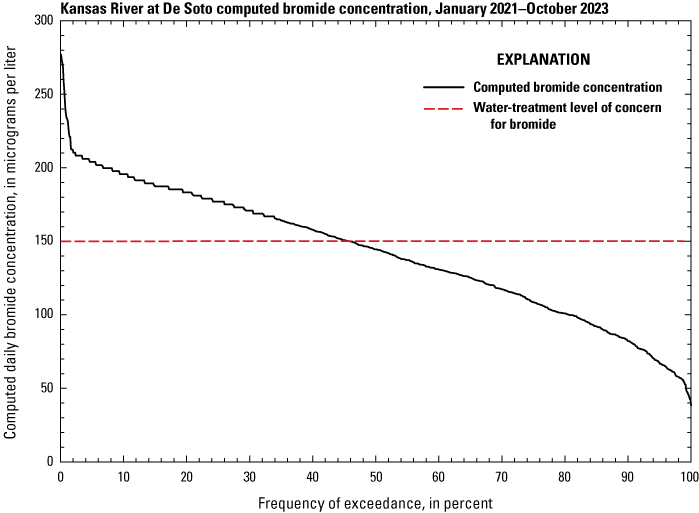
Computed bromide duration curve for the U.S. Geological Survey streamgage Kansas River at De Soto, Kansas (06892350), during January 2021 through October 2023.
Computations of monthly median bromide concentrations were compared to monthly median streamflow at De Soto during January 2021 through October 2023. Generally, an inverse relation was observed between bromide and streamflow during the study period. Higher bromide concentrations were observed during September through February, and lower bromide concentrations were observed during March through August (fig. 6). The opposite was observed for streamflow; higher streamflow was observed during May through July (fig. 6). Computations of seasonal median bromide concentrations were compared using the Kruskal-Wallis one-way analysis-of-variance on ranks (Helsel and others, 2020) and Dunn’s tests (Dunn, 1964; Helsel and others, 2020) to investigate seasonal patterns further. Seasonal median bromide concentrations were significantly different (p-value<0.05) in all pairwise seasonal combinations (p-values<0.001), except for summer versus spring (p-value=0.518). Computed median bromide concentrations were highest during winter, followed by fall, followed by spring and summer.
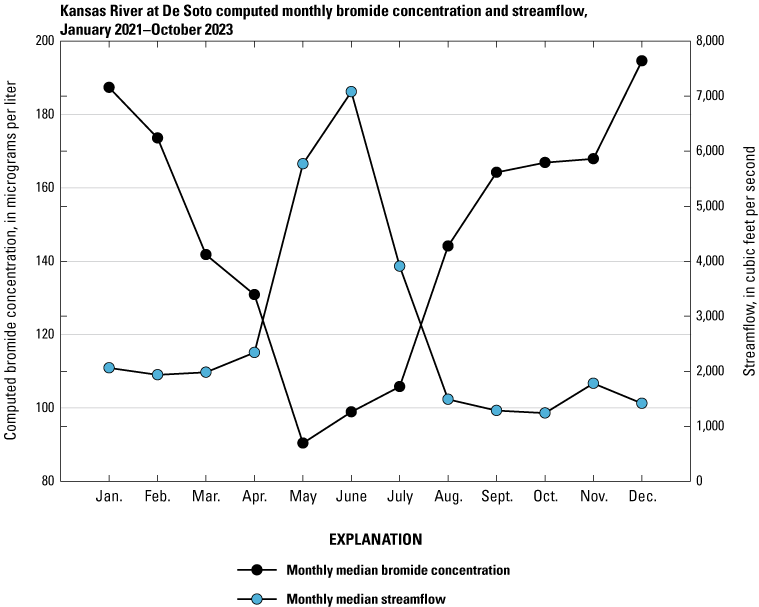
Monthly median computed bromide and streamflow at the U.S. Geological Survey streamgage Kansas River at De Soto, Kansas (06892350), during January 2021 through October 2023.
Patterns in historical computed bromide concentrations in the Kansas River relative to streamflow and seasonality can be helpful to water suppliers using ozone disinfection. Increases in specific conductance and decreases in streamflow are likely to correspond to increases in bromide concentrations at De Soto. The real-time computations of bromide concentrations using the model documented in this report and the observed historical patterns in bromide at De Soto can aid water suppliers in proactively adjusting water-treatment strategies to reduce the risk of bromate formation during ozone disinfection and evaluating potential changes in bromide concentrations in the Kansas River over time. These computations can also be used to advance understanding of hydrologic processes affecting ozone disinfection and formation of bromate.
Summary
The Kansas River is an essential water resource for eastern Kansas that provides recreational and industrial uses, food procurement, groundwater recharge, irrigation, wildlife habitat, livestock water use, and drinking water for more than 950,000 people in northeastern Kansas. Water suppliers that rely on the Kansas River as a water-supply source use various water-treatment strategies, depending on source-water-quality characteristics, to remove contaminants before distribution. Water District No. 1 of Johnson County, Kansas (WaterOne), is the largest water supplier in Kansas and uses the Kansas and Missouri Rivers as water-supply sources to provide drinking water to the Kansas City metropolitan area. WaterOne has been using ozone as a primary disinfection-treatment strategy since the summer of 2020. However, water suppliers that rely on ozone disinfection have become increasingly concerned with the presence of elevated dissolved bromide (the negatively charged form of bromine; hereafter referred to as “bromide”) concentrations in their water-supply source. Ozone disinfection of source water containing elevated concentrations of bromide can lead to the formation of bromate, a regulated disinfection byproduct and probable carcinogen. Real-time computations of bromide concentrations upstream from the WaterOne source-water intake in the Kansas River can be used to assist WaterOne with proactive adjustment of water-treatment strategies. These computations can also be used to advance understanding of hydrologic processes affecting ozone disinfection and formation of bromate.
This report documents the development of the surrogate-regression model that computes bromide concentrations in real time at De Soto, Kansas, and characterizes daily and monthly bromide concentrations at this location during the study period. The U.S. Geological Survey (USGS), in cooperation with WaterOne, collected continuous and discrete water-quality data at the USGS streamgage Kansas River at De Soto, Kans. (06892350; hereafter referred to as “De Soto”), during January 2021 through October 2023 to develop a surrogate-regression model that computes bromide concentrations at De Soto, which is about 15 miles upstream from the WaterOne source-water intake in the Kansas River. Model-development data and model computations documented in this report can be used to characterize water-quality conditions that affect drinking-water treatment at WaterOne, provide early notification of changing conditions that can be used to proactively adjust water-treatment strategies, and evaluate potential changes in bromide concentrations in the Kansas River over time.
Continuous (15-minute interval) streamflow and water-quality (water temperature, specific conductance, pH, dissolved oxygen, turbidity, chlorophyll and phycocyanin fluorescence, and nitrate) data were collected at De Soto during January 2021 through October 2023. Water-quality samples were collected on a biweekly to bimonthly basis at De Soto during this time and analyzed for bromide concentrations. These data were used to develop a surrogate-regression model that computes bromide concentrations at De Soto. This model was developed using ordinary least-squares regression. Daily bromide concentrations at De Soto were computed during January 2021 through October 2023 using the surrogate-regression model documented in this report and daily mean specific-conductance data. During periods when daily mean specific-conductance data were missing (because of excessive fouling, equipment malfunction, or temporary removal of the continuous water-quality monitor), daily bromide concentrations were computed using the Weighted Regressions on Time, Discharge, and Season method with Kalman filtering. Historical daily bromide computations were used to characterize bromide concentrations during the study period relative to the WaterOne water-treatment level of concern of 150 micrograms per liter (µg/L).
A surrogate-regression model that computes bromide concentrations was developed for De Soto using data collected during January 2021 through October 2023. Specific conductance was selected as the single explanatory variable and explained about 85 percent of the variance in bromide concentrations at De Soto. The surrogate-regression model documented in this report estimated that bromide concentrations at De Soto were likely to exceed the WaterOne water-treatment level of concern when specific conductance was greater than or equal to about 930 microsiemens per centimeter at 25 degrees Celsius. Surrogate-regression model computations of bromide concentrations are available at the USGS National Real-Time Water-Quality website (https://nrtwq.usgs.gov).
Bromide concentrations in discrete samples ranged from 31.9 to 251 µg/L (mean=131 µg/L; median=136 µg/L) and exceeded the water-treatment level of concern (150 µg/L) in about 34 percent of the 41 samples collected at De Soto during January 2021 through October 2023. Computed daily bromide concentrations ranged from 38.2 to 277 µg/L (mean=142 µg/L; median=145 µg/L) and exceeded the water-treatment level of concern (150 µg/L) about 46 percent of the time during January 2021 through October 2023. Generally, an inverse relation was observed between bromide and streamflow during the study period. Higher bromide concentrations were observed during September through February, and lower bromide concentrations were observed during March through August. The opposite was observed for streamflow; higher streamflow was observed during May through July. Seasonal median bromide concentrations were significantly different in all pairwise seasonal combinations (probability values less than 0.001), except for summer versus spring (probability value=0.518). Computed median bromide concentrations were highest during winter, followed by fall, followed by spring and summer.
Patterns in historical computed bromide concentrations in the Kansas River relative to streamflow and seasonality can be helpful to water suppliers using ozone disinfection. Increases in specific conductance and decreases in streamflow are likely to correspond to increases in bromide concentrations at De Soto. Real-time computations of bromide concentrations and observed historical patterns in bromide at De Soto can aid water suppliers in proactively adjusting water-treatment strategies to reduce the risk of bromate formation during ozone disinfection and for evaluating potential changes in bromide concentrations in the Kansas River over time.
References Cited
Agus, E., Voutchkov, N., and Sedlak, D.L., 2009, Disinfection by-products and their potential impact on the quality of water produced by desalination systems—A literature review: Desalination, v. 237, nos. 1–3, p. 214–237, accessed May 2024 at https://doi.org/10.1016/j.desal.2007.11.059.
Baldys, S., III, Churchill, C.J., Mobley, C.A., and Coffman, D.K., 2010, Bromide, chloride, and sulfate concentrations and loads at U.S. Geological Survey streamflow-gaging stations 07331600 Red River at Denison Dam, 07335500 Red River at Arthur City, and 07336820 Red River near DeKalb, Texas, 2007–09: U.S. Geological Survey Scientific Investigations Report 2010–5120, 30 p., accessed March 2024 at https://doi.org/10.3133/sir20105120.
Bennett, T.J., Graham, J.L., Foster, G.M., Stone, M.L., Juracek, K.E., Rasmussen, T.J., and Putnam, J.E., 2014, U.S. Geological Survey quality-assurance plan for continuous water-quality monitoring in Kansas, 2014: U.S. Geological Survey Open-File Report 2014–1151, 34 p. plus appendixes, accessed May 2024 at https://doi.org/10.3133/ofr20141151.
Cook, R.D., 1977, Detection of influential observation in linear regression: Technometrics, v. 19, no. 1, p. 15–18, accessed May 2024 at https://doi.org/10.1080/00401706.1977.10489493.
Duan, N., 1983, Smearing estimate—A nonparametric retransformation method: Journal of the American Statistical Association, v. 78, no. 383, p. 605–610, accessed May 2024 at https://doi.org/10.1080/01621459.1983.10478017.
Dunn, O.J., 1964, Multiple comparisons using rank sums: Technometrics, v. 6, no. 3, p. 241–252, accessed May 2024 at https://doi.org/10.1080/00401706.1964.10490181.
Foster, G.M., and Graham, J.L., 2016, Logistic and linear regression model documentation for statistical relations between continuous real-time and discrete water-quality constituents in the Kansas River, Kansas, July 2012 through June 2015: U.S. Geological Survey Open-File Report 2016–1040, 27 p., accessed May 2024 at https://doi.org/10.3133/ofr20161040.
Graham, J.L., Foster, G.M., Williams, T.J., Mahoney, M.D., May, M.R., and Loftin, K.A., 2018, Water-quality conditions with an emphasis on cyanobacteria and associated toxins and taste-and-odor compounds in the Kansas River, Kansas, July 2012 through September 2016: U.S. Geological Survey Scientific Investigations Report 2018–5089, 55 p., accessed May 2024 at https://doi.org/10.3133/sir20185089.
Graham, J.L., Ziegler, A.C., Loving, B.L., and Loftin, K.A., 2012, Fate and transport of cyanobacteria and associated toxins and taste-and-odor compounds from upstream reservoir releases in the Kansas River, Kansas, September and October 2011: U.S. Geological Survey Scientific Investigations Report 2012–5129, 65 p., accessed May 2024 at https://doi.org/10.3133/sir20125129.
Hach, 2022, Nitratax sc—User manual (edition 7): Loveland, Colo., Hach Company, 38 p., accessed June 2024 at https://cdn.bfldr.com/7FYZVWYB/at/gkcc3tf3wc8bnnwp939jrjp/DOC0235403211_ed7.pdf.
Helsel, D.R., Hirsch, R.M., Ryberg, K.R., Archfield, S.A., and Gilroy, E.J., 2020, Statistical methods in water resources: U.S. Geological Survey Techniques and Methods, book 4, chap. A3, 458 p., accessed May 2024 at https://doi.org/10.3133/tm4A3. [Supersedes USGS Techniques of Water-Resources Investigations, book 4, chap. A3, version 1.1.]
Hem, J.D., 1985, Study and interpretation of the chemical characteristics of natural water (3d ed.): U.S. Geological Survey Water-Supply Paper 2254, 263 p., 4 pls., accessed March 2024 at https://doi.org/10.3133/wsp2254.
Hirsch, R.M., and De Cicco, L.A., 2015, User guide to exploration and graphics for rivEr trends (EGRET) and dataRetrieval—R packages for hydrologic data (ver. 2.0, February 2015): U.S. Geological Survey Techniques and Methods, book 4, chap. A10, 93 p., accessed April 2024 at https://doi.org/10.3133/tm4A10.
Hirsch, R.M., Moyer, D.L., and Archfield, S.A., 2010, Weighted regressions on time, discharge, and season (WRTDS), with an application to Chesapeake Bay River inputs: Journal of the American Water Resources Association, v. 46, no. 5, p. 857–880, accessed April 2024 at https://doi.org/10.1111/j.1752-1688.2010.00482.x.
Jobson, H.E., 1996, Prediction of traveltime and longitudinal dispersion in rivers and streams: U.S. Geological Survey Water-Resources Investigations Report 96–4013, 69 p., accessed July 2024 at https://doi.org/10.3133/wri964013.
Kalman, R.E., 1960, A new approach to linear filtering and prediction problems: Journal of Basic Engineering, v. 82, no. 1, p. 35–45, accessed April 2024 at https://doi.org/10.1115/1.3662552.
Kansas Department of Agriculture, 2023, Kansas farm facts 2023: Kansas Department of Agriculture, 144 p., accessed July 2024 at https://www.agriculture.ks.gov/home/showpublisheddocument/166/638441481201900000.
Kansas Department of Health and Environment, 2017, Kansas-Lower Republican River Basin [total maximum daily load]: Kansas Department of Health and Environment web page, accessed May 2024 at https://www.kdhe.ks.gov/1455/Kansas-Lower-Republican-River-Basin.
Lee, C.J., Hirsch, R.M., and Crawford, C.G., 2019, An evaluation of methods for computing annual water-quality loads: U.S. Geological Survey Scientific Investigations Report 2019–5084, 59 p., accessed April 2024 at https://doi.org/10.3133/sir20195084.
Mann, H.B., and Whitney, D.R., 1947, On a test of whether one of two random variables is stochastically larger than the other: The Annals of Mathematical Statistics, v. 18, no. 1, p. 50–60, accessed April 2024 at https://doi.org/10.1214/aoms/1177730491.
Mueller, D.K., Schertz, T.L., Martin, J.D., and Sandstrom, M.W., 2015, Design, analysis, and interpretation of field quality-control data for water-sampling projects: U.S. Geological Survey Techniques and Methods, book 4, chap. C4, 54 p., accessed May 2024 at https://doi.org/10.3133/tm4C4.
New York State Department of Health, 2006, Bromate in drinking water—Information fact sheet: Troy, N.Y., New York State Department of Health, 2 p., accessed May 2024 at https://www.health.ny.gov/environmental/water/drinking/bromate.htm.
Pardoe, I., 2020, Applied regression modeling (3d ed.): New York, Wiley, 336 p. [Also available at https://doi.org/10.1002/9781119615941.]
Pellerin, B.A., Bergamaschi, B.A., Downing, B.D., Saraceno, J.F., Garrett, J.D., and Olsen, L.D., 2013, Optical techniques for the determination of nitrate in environmental waters—Guidelines for instrument selection, operation, deployment, maintenance, quality assurance, and data reporting: U.S. Geological Survey Techniques and Methods, book 1, chap. D5, 37 p., accessed May 2024 at https://doi.org/10.3133/tm1D5.
R Core Team, 2024, R—A language and environment for statistical computing: Vienna, Austria, R Foundation for Statistical Computing. [Also available at https://www.r-project.org/.]
Rasmussen, P.P., and Christensen, V.G., 2005, Hydrologic and water-quality conditions in the Kansas River, northeast Kansas, November 2001–August 2002, and simulation of ammonia assimilative capacity and bacteria transport during low flow: U.S. Geological Survey Scientific Investigations Report 2005–5188, 111 p., accessed May 2024 at https://doi.org/10.3133/sir20055188.
Rasmussen, P.P., Gray, J.R., Glysson, G.D., and Ziegler, A.C., 2009, Guidelines and procedures for computing time-series suspended-sediment concentrations and loads from in-stream turbidity sensor and streamflow data: U.S. Geological Survey Techniques and Methods, book 3, chap. C4, 53 p., accessed May 2024 at https://doi.org/10.3133/tm3C4.
Rasmussen, T.J., Bennett, T.J., Stone, M.L., Foster, G.M., Graham, J.L., and Putnam, J.E., 2014, Quality-assurance and data-management plan for water-quality activities in the Kansas Water Science Center, 2014: U.S. Geological Survey Open-File Report 2014–1233, 41 p., accessed May 2024 at https://doi.org/10.3133/ofr20141233.
Rasmussen, T.J., Ziegler, A.C., and Rasmussen, P.P., 2005, Estimation of constituent concentrations, densities, loads, and yields in lower Kansas River, northeast Kansas, using regression models and continuous water-quality monitoring, January 2000 through December 2003: U.S. Geological Survey Scientific Investigations Report 2005–5165, 117 p., accessed May 2024 at https://doi.org/10.3133/sir20055165.
Sauer, V.B., and Turnipseed, D.P., 2010, Stage measurement at gaging stations: U.S. Geological Survey Techniques and Methods, book 3, chap. A7, 45 p., accessed May 2024 at https://doi.org/10.3133/tm3A7.
Stone, M.L., and Klager, B.J., 2023, Long-term water-quality constituent trends in the Little Arkansas River, south-central Kansas, 1995–2021: U.S. Geological Survey Scientific Investigations Report 2023–5102, 103 p., accessed May 2024 at https://doi.org/10.3133/sir20235102.
Turnipseed, D.P., and Sauer, V.B., 2010, Discharge measurements at gaging stations: U.S. Geological Survey Techniques and Methods, book 3, chap. A8, 87 p., accessed May 2024 at https://doi.org/10.3133/tm3A8.
U.S. Army Corps of Engineers, 2017, Kansas City district lakes: U.S. Army Corps of Engineers web page, accessed May 2024 at https://www.nwk.usace.army.mil/Locations/District-Lakes/.
U.S. Environmental Protection Agency, 1997, Method 300.1—Determination of inorganic anions in drinking water by ion chromatography: Cincinnati, Ohio, National Exposure Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency, 40 p., accessed March 2024 at https://www.epa.gov/sites/production/files/2015-06/documents/epa-300.1.pdf.
U.S. Environmental Protection Agency, 2009, National primary drinking water regulations: U.S. Environmental Protection Agency 816–F–09–004, 7 p., accessed May 2024 at https://19january2021snapshot.epa.gov/sites/static/files/2016-06/documents/npwdr_complete_table.pdf.
U.S. Geological Survey, 2012, Update of policy on review and publication of discrete water data: U.S. Geological Survey Office of Water Quality Technical Memorandum no. 2012.03, 4 p., accessed May 2024 at https://water.usgs.gov/admin/memo/QW/qw12.03.pdf.
U.S. Geological Survey, 2017, Procedures for processing, approving, publishing, and auditing time-series records for water data: U.S. Geological Survey Office of Water Quality Technical Memorandum no. 2017.07, 5 p., accessed March 2024 at https://water.usgs.gov/admin/memo/QW/qw2017.07.pdf.
U.S. Geological Survey, 2022, Time of travel beta application: U.S. Geological Survey web page, accessed July 2024 at https://www.usgs.gov/tools/time-travel-beta-application.
U.S. Geological Survey, 2024a, Kansas real-time water quality: U.S. Geological Survey National Real-Time Water Quality web page, accessed July 2024 at https://nrtwq.usgs.gov/ks/.
U.S. Geological Survey, 2024b, USGS water data for the Nation: U.S. Geological Survey National Water Information System database, accessed May 2024 at https://doi.org/10.5066/F7P55KJN.
U.S. Geological Survey, [variously dated], National field manual for the collection of water-quality data: U.S. Geological Survey Techniques of Water-Resources Investigations, book 9, chaps. A1–A9 [variously paged], accessed May 2024 at https://water.usgs.gov/owq/FieldManual/.
Wagner, R.J., Boulger, R.W., Jr., Oblinger, C.J., and Smith, B.A., 2006, Guidelines and standard procedures for continuous water-quality monitors—Station operation, record computation, and data reporting: U.S. Geological Survey Techniques and Methods, book 1, chap. D3, 51 p. plus 8 attachments, accessed May 2024 at https://doi.org/10.3133/tm1D3. [Supersedes USGS Water-Resources Investigations Report 2000–4252.]
Water District No. 1 of Johnson County, 2024a, Ozone treatment facilities: Water District No. 1 of Johnson County web page, accessed May 2024 at https://www.waterone.org/291/Ozone-Treatment-Facilities.
Water District No. 1 of Johnson County, 2024b, Water quality report 2024: Water District No. 1 of Johnson County web page, accessed May 2024 at https://www.waterone.org/ArchiveCenter/ViewFile/Item/155.
Whittemore, D.O., 2007, Fate and identification of oil-brine contamination in different hydrogeologic settings: Applied Geochemistry, v. 22, no. 10, p. 2099–2114, accessed May 2024 at https://doi.org/10.1016/j.apgeochem.2007.04.002.
Wilcoxon, F., 1945, Individual comparisons by ranking methods: Biometrics Bulletin, v. 1, no. 6, p. 80–83, accessed April 2024 at https://doi.org/10.2307/3001968.
Williams, T.J., 2021, Linear regression model documentation and updates for computing water-quality constituent concentrations or densities using continuous real-time water-quality data for the Kansas River, Kansas, July 2012 through September 2019: U.S. Geological Survey Open-File Report 2021–1018, 18 p., accessed May 2024 at https://doi.org/10.3133/ofr20211018.
Williams, T.J., 2023, Linear regression model documentation for computing water-quality constituent concentrations or densities using continuous real-time water-quality data for the Kansas River above Topeka Weir at Topeka, Kansas, November 2018 through June 2021: U.S. Geological Survey Scientific Investigations Report 2022–5130, 14 p., accessed May 2024 at https://doi.org/10.3133/sir20225130.
Williams, T.J., Klager, B.J., and Stiles, T.C., 2024a, Water-quality data and computed flow-normalized and low-flow concentrations and loads in the Kansas River, Kansas, 1972–2020: U.S. Geological Survey data release, accessed July 2024 at https://doi.org/10.5066/P9WVZ8X1.
Williams, T.J., Klager, B.J., and Stiles, T.C., 2024b, Water-quality trends in the Kansas River, Kansas, since enactment of the Clean Water Act, 1972–2020: U.S. Geological Survey Scientific Investigations Report 2024–5050, 29 p., accessed July 2024 at https://doi.org/10.3133/sir20245050.
World Health Organization, 2009, Bromide in drinking-water—Background document for development of WHO guidelines for drinking-water quality: World Health Organization, 7 p., accessed May 2024 at https://iris.who.int/handle/10665/70169.
YSI, Inc., 2017, EXO user manual—Advanced water quality monitoring platform (rev. G): Yellow Springs, Ohio, YSI, Inc., 154 p., accessed May 2024 at https://www.ysi.com/file%20library/documents/manuals/exo-user-manual-web.pdf.
Zar, J.H., 1999, Biostatistical analysis (4th ed.): Upper Saddle River, N.J., Prentice Hall, 663 p. [Also available at https://archive.org/details/biostatisticalan0000zarj.]
Zhang, Q., and Hirsch, R.M., 2019, River water-quality concentration and flux estimation can be improved by accounting for serial correlation through an autoregressive model: Water Resources Research, v. 55, no. 11, p. 9705–9723, accessed April 2024 at https://doi.org/10.1029/2019WR025338.
Appendix 1. Model Archival Summary for Bromide Concentration at U.S. Geological Survey Streamgage 06892350, Kansas River at De Soto, Kansas, during January 2021 through October 2023
Conversion Factors
Supplemental Information
Specific conductance is given in microsiemens per centimeter at 25 degrees Celsius (µS/cm at 25 °C).
Concentrations of bromide in water are given in micrograms per liter (µg/L).
For more information about this publication, contact:
Director, USGS Kansas Water Science Center
1217 Biltmore Drive
Lawrence, KS 66049
785–842–9909
For additional information, visit: https://www.usgs.gov/centers/kswsc
Publishing support provided by the
Rolla and Baltimore Publishing Service Centers
Disclaimers
Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Although this information product, for the most part, is in the public domain, it also may contain copyrighted materials as noted in the text. Permission to reproduce copyrighted items must be secured from the copyright owner.
Suggested Citation
Williams, T.J., and Totzke, G.S., 2024, Computation of bromide concentrations at the Kansas River at De Soto, Kansas, January 2021 through October 2023: U.S. Geological Survey Scientific Investigations Report 2024–5078, 18 p., https://doi.org/10.3133/sir20245078.
ISSN: 2328-0328 (online)
Study Area
| Publication type | Report |
|---|---|
| Publication Subtype | USGS Numbered Series |
| Title | Computation of bromide concentrations at the Kansas River at De Soto, Kansas, January 2021 through October 2023 |
| Series title | Scientific Investigations Report |
| Series number | 2024-5078 |
| DOI | 10.3133/sir20245078 |
| Publication Date | August 26, 2024 |
| Year Published | 2024 |
| Language | English |
| Publisher | U.S. Geological Survey |
| Publisher location | Reston, VA |
| Contributing office(s) | Kansas Water Science Center |
| Description | Report: vii, 18 p.; Appendix; Dataset |
| Country | United States |
| State | Kansas |
| City | De Soto |
| Other Geospatial | Kansas River |
| Online Only (Y/N) | Y |
| Additional Online Files (Y/N) | Y |


