 |
Shear Stress Calculated from Hydrodynamic Model Output
In order to estimate mobility, the combined wave-current shear stress must be calculated for the modeled hydrodynamic conditions. A formulation was developed by Soulsby (1997) to parameterize four methods, which provide good overall performance for estimating wave-current stress, based on original formulations by Grant and Madsen (1979), Fredsøe (1984), Davies and others (1988), and Huynh-Thanh and Temperville (1991). The combined wave-current stress (twc) for the individual components of wave and current stress was calculated for hydrodynamic model output (depth-averaged velocity magnitude and direction, wave bottom orbital velocity, wave period, wave direction, and water depth) following the method prescribed in Soulsby (1997) for each of the four formulations. The density of water used in the calculations was as assumed to be 1,027 kilograms per cubic meter (kg/m3), and the grain-size roughness contribution (z0) was calculated to be (Soulsby, 1997) the diameter of the particle (either surface residual ball (SRB) or surficial sediment) divided by 12. The mean value of the four formulations was used to estimate the combined wave-current shear stress for each hydrodynamic scenario and for all time-steps of the time varying simulations. Evaluation of the standard deviation of the four methods indicated the uncertainty introduced by calculation method is low compared with the magnitude of the calculated stress (less than 1 percent).
Critical Stress for Incipient Motion
Most research into critical thresholds for incipient motion of noncohesive sediment (including large grains such as gravel and cobbles, in a similar size range to SRBs) has at least partial basis in the work of Shields (1936) who created a dimensionless parameter (θcr) based on the shear stress (τcr). The shear stress balances the gravitational weight of the particle (described in Soulsby, 1997):
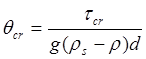 , , |
(3-1) |
where
| g |
is the acceleration due to gravity (9.81 meters per second squared (m/s2)), |
| ρs |
is the density of the sediment, |
| ρ |
is the density of water, and |
| d |
is the diameter of the grain of the sediment. |
Soulsby empirically determined the relation between this critical value and the grain diameter and density; the equation was subsequently updated by Soulsby and Whitehouse (1997) to cover a wider range of conditions.
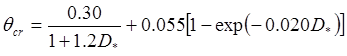 , , |
(3-2) |
where D* is the dimensionless grain size, calculated as follows:
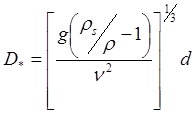 , , |
(3-3) |
where &nu: is the kinematic viscosity of water, 1.36×10-6 m2/s.
The high critical stress estimate for each SRB class (and the only critical stress value used for sand) was attained by replacing θcr in equation 3–1 with the value of θcr from equation 3–2 and solving for τcr; the estimate is appropriate for the conditions for which the formulation was calibrated, for example, particles not protruding above the bed into the flow.
Experiments have demonstrated that the extent to which any individual particle protrudes from the bed (such as could be expected for a single SRB on a seabed of sand) can lower that particle's critical shear stress (τcr) value (Fenton and Abbott, 1977; Andrews, 1983; Wiberg and Smith, 1987; Wilcock, 1998; Bottacin-Busolin and others, 2008). Empirical studies of cobbles have indicated that the dimensionless critical shear stress (θcr) approaches a minimum value of 0.01 to 0.02 (Fenton and Abbott, 1977; Andrews, 1983; Wiberg and Smith, 1987; Wilcock, 1998; Bottacin-Busolin and others, 2008). Note that, although the dimensionless Shields parameter θcr is constant for the exposed particle stress case, the conversion to the physically meaningful force (in pascals) includes a dependence on grain size; thus, the critical stress compared with modeled stress forcing increases for large particles. For the analysis of SRB mobility, when particle extrusion is important, the critical stress value is calculated from a θcr of 0.02 (medium threshold) and 0.01 (low threshold) to provide a limit on the uncertainty in mobility for the range of conditions from an SRB in a relatively uniform bed of SRBs such as a mat (for example, little particle extrusion) to an isolated SRB sitting relatively high in the flow.
SRB Density
For sediment mixed with oil, Operational Science Advisory Team (OSAT3) data were used to constrain the density of observed SRBs (L. Bruce, British Petroleum Corporation, GCRO, Science NRDA Team, unpub. data, 2012). Composition data provide the percentage of moisture (fH2O) and the percentage of oil by dry weight (foil,dry) of the sampled SRBs; the total percentage of oil of the original (wet weight) sample is taken as foil = (1 – fH2O) × foil,dry. To estimate the density of the samples, an assumed density of 1,027 kg/m3 was assigned to the moisture fraction, an assumed density of 900 kg/m3 was assigned to the oil fraction, and the remaining fraction of 1 – fH2O – (1 – fH2O) × foil,dry was assumed to consist of quartz sand with a density of 2,650 kg/m3. The approximate density (ρSRB) of each sample in the dataset was therefore estimated to be:
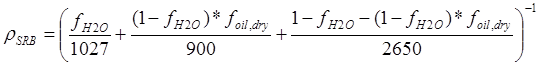 , , |
(3-4) |
The densities calculated in this manner for all the observed SRB data were used in assessing the variability of SRBcritical stress.
|